Tunable reverse electrodialysis microplatform with geometrically controlled self-assembled nanoparticle network†
Eunpyo
Choi
,
Kilsung
Kwon
,
Daejoong
Kim
* and
Jungyul
Park
*
Department of Mechanical Engineering, Sogang University, 35 Baekbeom-ro, Mapo-gu, Seoul, 121-742, Korea. E-mail: sortpark@sogang.ac.kr; daejoong@sogang.ac.kr
First published on 1st October 2014
Abstract
Clean and sustainable energy generation from ambient environments is important not only for large scale systems, but also for tiny electrical devices, because of the limitations of batteries or external power sources. Chemical concentration gradients are promising energy resources to power micro/nanodevices sustainably without discharging any pollutants. In this paper, an efficient microplatform based on reverse electrodialysis, which enables high ionic flux through three dimensional nanochannel networks for high power energy generation, is demonstrated. Highly effective cation-selective nanochannel networks are realized between two microfluidic channels with geometrically controlled in situ self-assembled nanoparticles in a cost-effective and simple way. The nano-interstices between the assembled nanoparticles have a role as collective three-dimensional nanochannel networks and they allow higher ionic flux under concentration gradients without decreasing diffusion potential, compared to standard one-dimensional nanochannels. An in-depth experimental study with theoretical analysis shows that the electrical power of the presented system can be flexibly tuned or further optimized by changing the size, material, and shape of the assembled nanoparticles or by the geometric control of the microchannel. This microfluidic power generation system can be readily integrated with existing lab on a chip systems in the near future and can also be utilized to investigate nanoscale electrokinetics.
Introduction
Environment-friendly, non-combustion energy harvesting is promising because of limited fossil fuel sources and global warming.1,2 Current sustainable energy harvesting techniques that have been intensively studied, include solar,3,4 wind,5,6 biomass,7,8 thermal,9,10 and mechanical vibration.11,12 In addition, other renewable energy sources arise in fluidic systems, such as salinity gradients,13,14 and wave and tidal power.15,16 Reverse electrodialysis (RED) based on salinity gradients has received significant attention because it is, in principle, clean and sustainable and does not discharge any pollutants or CO2.17 The potential capacity for generating energy from salinity gradients by mixing fresh water and salt water (seawater) is vast. Each cubic meter of fresh water can generate 1.4 MJ of energy when mixed with the same amount of seawater, and 2.25 MJ when mixed with an excess of seawater.1 Since it also does not rely on any mechanical moving parts, such as turbines or motors, damage from wear and tear and replacement for these parts can be avoided. The conventional RED technology based on organic membranes was proposed in the 1950s,18 and since then, many researchers have developed large-scale systems focused on ion-exchange membranes.19–21 However, this large-scale organic membrane based technology has several problems, such as the high membrane cost, shrinkage effect,22–24 and low power density.17,25,26 For these reasons, even if these organic membranes were scaled down to a small-scale system such as a lab on a chip or micro/nanodevice,11 there may be not enough power due to their lower power density (0.0072 mW cm−2 from Sales et al.26 obtained with an 8-cell stacked structure, and 0.00002 mW cm−2 from Sadeghian et al.25 obtained with a half-cell structure, which only has one kind of ion-selectivity membrane) and changes to the nanopore size by membrane shrinkage. Recently, solid-state nanochannels or ion track-etched nanopores with half-cell structures (with only a cation-exchange membrane) have been proposed as an alternative technique to membrane based RED, which enhances the power generation performance in a small-scale due to a higher power density.27–29 These techniques enable greatly improved performance and also show the potential of powering micro/nanodevices without the limitations of batteries or external power supplies, such as microelectromechanical systems (MEMS), biomedical implant microdevices, portable personal electronics, and micro/nanorobots.17,30In this study, we demonstrate a microfluidic based platform that advances the power generation performance significantly by producing high ionic flux through three dimensional nanochannel networks. Highly effective cation-selective nanochannel networks are created between two microfluidic channels using geometrically controlled in situ self-assembled nanoparticles in a cost-effective and simple fabrication method, compared to previous nanochannel or nanoporous systems requiring extensive fabrication processes or expensive and special equipment. Ouyang and co-workers31 suggested a half-cell RED system using the assembled nanoparticles in the micropore from KOH-etched silicon wafers. However, there are several disadvantages, as follows: it is difficult to (1) obtain the arbitrary desired shape because of the limitation of the KOH etching process, (2) quantitatively control the thickness of the nanoparticle assembly because the nanoparticles are self-assembled by the gravitational sedimentation process,32 and (3) locate the micropore in a demanded position between the source and the sink channel precisely, and even more difficult to integrate with other components in MicroTAS for further applications. (4) It is impossible to visualize ion transport using a fluorescent dye through the micropore.
The proposed system can intrinsically achieve high power generation, because the nano-interstices between the assembled nanoparticles have a role as collective three-dimensional nanochannel networks compared to the conventional single nanochannel27,33 or nanopore17,28 corresponding to thin one-dimensional pathways. The nanochannel networks may have a slightly lower transference number and open circuit voltage, but they significantly augment the ion current at the same time so that the harvesting power can increase. Another advantage of our system is that electrical performance such as the maximum power (Pmax) and the energy conversion efficiency (ηmax) can be tuned quantitatively or optimized by changing the geometry of the microchannel and selecting the size and material of the assembled nanoparticles. Especially, the materials of a nanochannel and an ion track-etched nanoporous membrane were confined to silica and organic polymers, respectively, but various materials, from organic to inorganic, can be adopted in our system. The measured maximum generated power is 327.11 pW when carboxylate polystyrene nanoparticles (C-PSNP) are used. The microfluidic based power generation system has the potential to be readily integrated with existing lab on a chip or in vitro diagnostic microdevices, so we expect that self-powered micro/nanodevices with a reduced volume and weight can be realized in the near future. Moreover, like previous visualization studies for the ion transport phenomenon using fluorescent dyes,34–36 the ion transport according to the variations of surface properties and geometrical changes can not only be measured with current recording but can also be visualized with fluorescent dyes using the proposed system, so that it can contribute to revealing the still-unclear fundamental mechanism of power-generation.
Materials and methods
Fabrication process of the PDMS microfluidic channels
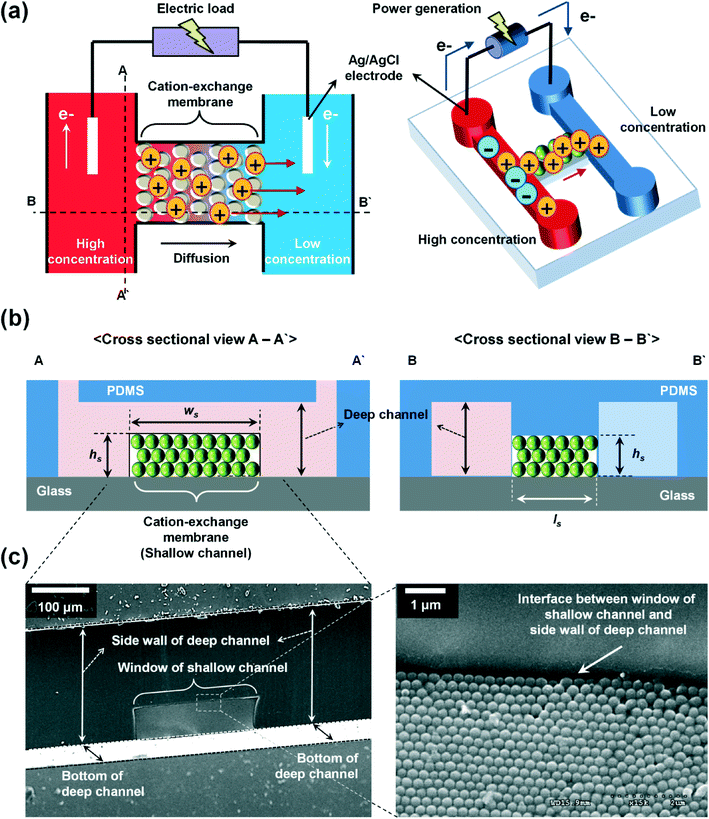
The PDMS microfluidic chip was fabricated using a standard soft lithography. The details of the fabrication process are provided in Fig. S1 in the ESI.† Briefly, Fig. S1(a)–(d)† show the fabrication process for a multilayered design: (a) a 4-inch silicon wafer was patterned with a SU-8 resist. The height of the first layer for the shallow channel that can form the desired patterns for the nanochannel networks was approximately 25 μm or 50 μm. Subsequently, SU-8 2050 was patterned on the first SU-8 layer (target: 200 μm, this layer is for the deep channel). (b) The PDMS mixture was poured onto the master and cured at 95 °C for 1 h. (c) The PDMS was then peeled off. (d) Finally, it was bonded with a slide glass, followed by O2 plasma treatments.In situ formation of nanochannel networks using nanoparticles
We formed the nanochannel networks using nanoparticles within the shallow channel, as reported previously.37 For a more detailed fabrication process, see section S.2 in the ESI.† Briefly, Fig. S2† shows the fabrication process for the in situ formation of the nanochannel networks using the self-assembly of particles within the PDMS channel: (a) the PDMS device with shallow and deep channels was molded from a SU-8 master with two different heights. (b) Diluted nanoparticles were introduced into one side of deep channel-A by capillary pressure. (c) The diluted nanospheres at the intersection between the shallow and deep channels experience a sudden pressure drop, which tries to drag the solution in the deep channel into the shallow channel.38 However, this flow of diluted nanoparticles in the shallow channel cannot move forward toward the deep channel because of the effects of the capillary stop valve from 90° of the expansion angle (β) and the difference in the channel heights. (d) After the solution stops at the neck, evaporation of the solvent (70% ethanol) is induced through deep channel-B. Then the solvent with the convective transport of nanoparticles is introduced from deep channel-A toward the neck to compensate for the solvent lost by evaporation. This influx of the nanoparticles promotes the unidirectional growth of the ordered lattice (FCC structure) from the neck to deep channel-A. (e) When the growth of the nanoparticle assembly reaches the interface between the shallow channel and deep channel-A, the residual solution in deep channel-A is gently removed. (f) Finally, the self-assembled nanoparticles are dried out at room temperature for one day.Experimental setup
The picometer/voltage source (6487, Keithley Instrument) was used as the electronic load and controlled by using a general purpose interface bus (GPIB) and Labview 9.0 (National Instruments). The voltage signal and current signal were recorded by a computer connected to the picometer/voltage source through the GPIB card (PCI-GPIB, National Instruments). For the electrolyte solutions, potassium chloride (KCl) was prepared by dissolving a target solute in deionized (DI) water. A precise scale (AB 264-S/31. Mettler Toredo) with a resolution of 0.01 mg was utilized to accurately meter the concentration of the electrolyte solutions. We measured the pH for the electrolyte solutions using a pH meter (SevenMulti™ S47, Mettler Toredo). The pH of the electrolyte solutions was 5.6–6.0, similar to the pH of the DI water. We let the electrolyte solutions cool down enough after mixing and kept them sealed at room temperature before the experiments.Experimental procedure
Before the initial use of nanochannel networks, we fixed the concentration of the KCl solution at 0.1 mM and gently filled all the channels with this solution. Subsequently, KCl solutions with different ionic strengths (0.1, 5, 10, 50, and 100 mM) were sequentially introduced into the high concentration side of the deep channel. We obtained each I–V curve in a galvanostatic mode. The voltage steps were applied according to the concentrated solution and each step was maintained for 30 s. The electrical signal was measured without fluid flow, so that the decrease of the concentration gradient across the nanochannel network and the hindrance of ion transport by the concentration polarization might have occurred over time. However, since we focused on the variation of the generated power according to the change of geometry in the microchannel and the material/size of the nanoparticles in this study, we ignored this effect and analyzed the experimental results based on the maximum values from the measured electric signals.Results and discussion
Fig. 1 shows the configuration of the proposed microplatform and the working principle. The parallel straight microchannels are interconnected with the nanochannel network formed with the self-assembled nanoparticles, as indicated in Fig. 1(b). The nano-interstices between the close-packed nanoparticles with homogeneous sizes and negative surface charges serve as the pores of cation-selective membranes. Since the electric double layers are overlapped in these nano-interstices, cations are preferentially transported. Cations diffuse from high to low concentrations and this asymmetric ion-transport induces the electrochemical redox reactions on the electrode surfaces to satisfy electro-neutrality. Finally, electrons are transferred along the external circuit and electrical power is generated. Fig. 1(c) shows the SEM images of the fabricated device from a cross sectional view in the A–A′ direction, and the enlarged image of the interface between the window of the shallow channel and the side wall of the deep channel. The nanoparticles were self-assembled in face centered cubic (FCC) structures only within the shallow channel and the shallow channel was fully close-packed by the control of microdroplets and evaporation. Interestingly, the crystallized nanoparticles do not cross over the interface between the shallow and deep channels as we originally intended. The nano-interstices between these close-packed nanoparticles consist of equivalent nanopores (~15% of the sphere size39) and negative surface charges create the ion selective ability since the diffuse layer in electrical double layer (EDL) was overlapped. By using this ion-selective membrane as RED cells, we systematically studied the dependence of the transference number, open circuit voltage, electric conductance, maximum power, and energy conversion efficiency on the concentration gradient, the diameter of the nanoparticles, the height of the nanochannel network (height of the shallow channel, hs), and the different materials of the nanoparticles.When the high concentration solution diffuses into the low concentration solution through the nanopores, cations diffuse more rapidly than anions due to the ion selective transport property of the nanochannel networks.27 Finally, according to the principle of Gibbs free energy from this net ion diffusion, electric potential in the nanochannel networks (Enetworks) is generated and it can be described as follows:27
| Enetworks = Esource − Eredox = Ediff − InetworksRnetworks | (1) |
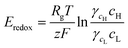 | (2) |
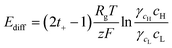 | (3) |
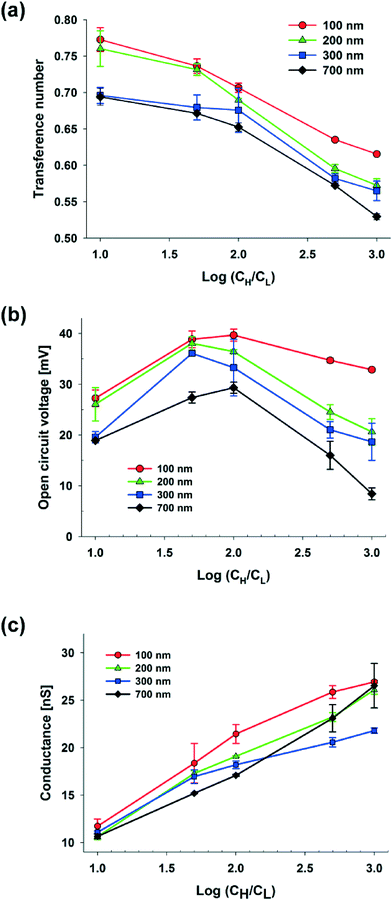
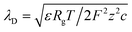 . Here, ε is the permittivity of the electrolyte solutions. In this equation, the EDL thickness is reduced with the increase in cH (cL is fixed with 0.1 mM and λD is 30.7 nm): the calculated λD values are 4.34 nm at 5 mM, 3.1 nm at 10 mM, 1.4 nm at 50 mM, and 1.0 nm at 100 mM. The ion selectivity with transference number therefore decreases as the concentration increases. Moreover, as the nanopore size increases with the same concentration, the effect of the overlapped EDLs (major cause of the charge selectivity) is gradually reduced and the ion selectivity becomes weakened with the lower transference number. Here, we used diameters of 100, 200, 300, and 700 nm with expected nanopore sizes between the nanoparticles of 15, 30, 45, and 105 nm, respectively.
. Here, ε is the permittivity of the electrolyte solutions. In this equation, the EDL thickness is reduced with the increase in cH (cL is fixed with 0.1 mM and λD is 30.7 nm): the calculated λD values are 4.34 nm at 5 mM, 3.1 nm at 10 mM, 1.4 nm at 50 mM, and 1.0 nm at 100 mM. The ion selectivity with transference number therefore decreases as the concentration increases. Moreover, as the nanopore size increases with the same concentration, the effect of the overlapped EDLs (major cause of the charge selectivity) is gradually reduced and the ion selectivity becomes weakened with the lower transference number. Here, we used diameters of 100, 200, 300, and 700 nm with expected nanopore sizes between the nanoparticles of 15, 30, 45, and 105 nm, respectively.
Fig. 2(b) shows the open circuit voltage against the concentration gradient with various diameters of S-NPs. According to the theory of Gibbs free energy, the maximum voltage should steadily increase as the concentration gradient becomes higher in the case of the ideal solution, whose transference number is fixed, and the ideal ion-selective membrane (t+ = 1). However, in a real experiment, as the transference number dropped dramatically at higher concentrations and with larger nanoparticle diameters, the maximum voltage shows a non-linear dependency. When the diameters of the S-NPs were varied at 100, 200, 300, and 700 nm at a fixed hs (25 μm), Ediff was maximized at different concentration gradients with the values of 39.68 ± 1.20, 38.05 ± 1.30, 36.10 ± 0.18, and, 29.31 ± 1.09 mV, respectively, and it was thus reduced as the concentration continuously increased.
The electric conductance is strongly influenced by the net diffusion through the nanochannel network.28 It depends on the two following mechanisms. One is the ion separation within EDLs (diffuse layer) at the surface. The other is asymmetric ion diffusion on the EDLs (bulk layer) which occurs due to the mobility difference between the positive and negative ions. When EDLs are overlapped in nanopores, the electric conductance depends on the charge separation within the EDLs. As shown in Fig. 2(c), at a fixed hs (25 μm), the maximum conductance steadily increases as the concentration difference increases due to the enhancement of ion diffusion. A higher maximum conductance at the smaller diameter of nanoparticles can also be indebted to the following: as the diameter decreases, the counter-ion concentration in the nanopore increases and it results in the higher conductivity. Also, irrespective of the diameter of the nanoparticles, the close-packed nanoparticles with an FCC structure have the same packing efficiency (volume of space occupied by the spheres/total volume) and its value is 74.05%. Therefore, when the nanoparticles are ideally self-assembled within the same volume of the shallow channel, nanoparticles with smaller diameters have a larger surface area, which induces the increase of ionic conductance. However, when the concentration at the cH side is higher than 10 mM, the increase in conductance is greater in the case of S-NPs with a diameter of 700 nm than those with a diameter of 300 nm. It seems that the dramatic collapse of the overlapped EDLs in the nanopores between 700 nm S-NPs at electrolyte concentrations greater than 10 mM results in higher diffusive flux from the cH to the cL side through the nanochannel network. Consequently, this results in the increase of the concentration at the cL side with a higher conductance within the nanochannel network.
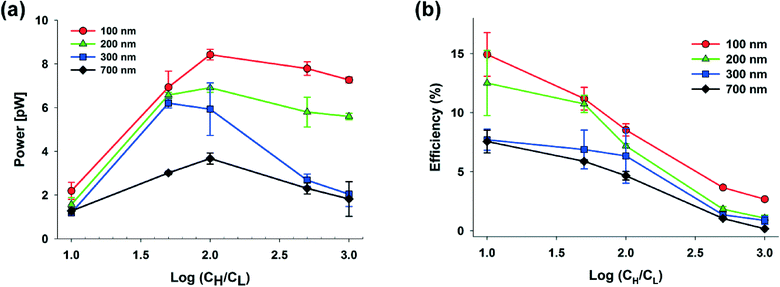
The power generation from the nanochannel networks is given by P = Enetworks·Inetworks and we denoted its maximum value as Pmax. Fig. 3(a) shows the plots of maximum powers and they become higher as the concentration gradient increases or the diameter of nanoparticles decreases. Therefore, when hs was 25 μm, we obtained the highest maximum power, 8.62 pW, with S-NPs with a diameter of 100 nm. Furthermore, when the nanoparticles are ideally close-packed in the FCC structure, the effective cross sectional area is always the same regardless of the nanoparticle size (21.50% of the cross sectional area of the shallow channel, Ashallow). Hence, since we used the shallow channel with a cross sectional area Ashallow of 200 × 25 μm2, the highest power density measured was ~0.00080 mW cm−2. The energy conversion efficiency is defined as the ratio of the output electrical energy to the input energy (Gibbs free energy of mixing) and this efficiency for the maximum power, ηmax, can be simply expressed by the following formula:27
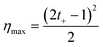 | (4) |
 | ||
| Fig. 3 Dependence of (a) the maximum power, and (b) the energy conversion efficiency on the concentration gradient and diameter of silica nanoparticles (S-NP: 100, 200, 300, and 700 nm). | ||
According to eqn (4), the value of the energy conversion efficiency for the complete cation selectivity system is 50%. As shown in Fig. 3(b), at a fixed hs (25 μm), the efficiency increases when the concentration is decrease due to the increase of the transference number. The maximum efficiency measured in the present work reaches up to 16.76% with an S-NP diameter of 100 nm.
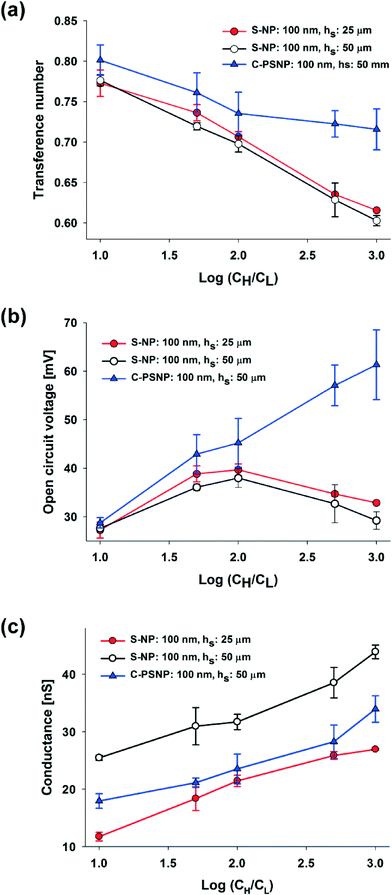
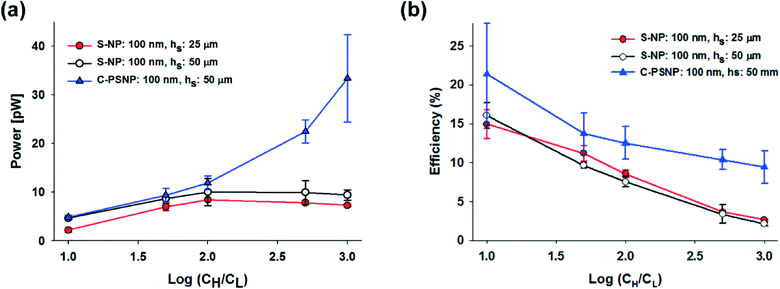
In our systems, we can easily obtain a higher maximum power and energy conversion efficiency by changing the geometry and by selecting the optimal materials for the nanoparticles. First, we changed the hs and performed the experiments using only 100 nm S-NPs, because we obtained the highest power generation at the shallow channel height of 25 μm with this S-NP diameter. Fig. 4(a) and (b) show the plots of the transference number and the open circuit voltage, respectively, comparing between the shallow channel heights of 25 μm (line, ●) and 50 μm (dash, ○). In the case of the ideal solution, where the transference number is fixed, and the ideal ion-selective membrane (t+ = 1), both the values should be similar regardless of the shallow channel height. However, at a higher hs, the transference number and the open circuit voltage were slightly lower, as shown in the present results. It seems that the higher hs results in the increase in the number of the diffused ions: the bulk concentration ratio (cH/cL) should decrease with the higher diffusion and therefore by eqn (2) and (3), t+ and Ediff should be reduced. Also, since the diffusivity of chloride ions (2.03 × 10−5 cm2 s−1) is higher than that of potassium ions (1.96 × 10−5 cm2 s−1), the increase in ion diffusion may result in a greater number of chloride ions in the nanochannel networks, and it can probably hinder the diffusion of potassium ions. Fig. 4(c) shows that the maximum conductance for varying hs depends on the concentration. As can be expected, the maximum conductance becomes higher as the hs increases for the same diameter of nanoparticle and at the same concentration gradient. The conductance at a height of 50 μm was almost twice that at a height of 25 μm. Fig. 5(a) and (b) show the maximum power and energy conversion efficiency, respectively, for varying hs. The harvested energy increases as hs increases, due to the increase in the maximum conductance and the best value is as high as 12.82 pW at a shallow channel height of 50 μm.
Second, we increased the maximum power with varying materials of nanoparticles. Negatively charged carboxylate polystyrene nanoparticles (C-PSNP) with a diameter of 100 nm were used at a fixed shallow channel height of 50 μm to compare with the S-NPs. Fig. 4(a) and (b) show the plots of the transference number and the open circuit voltage, respectively, comparing between the carboxylate polystyrene nanoparticles and silica nanoparticles. Basically, the C-PSNPs show higher t+ and Ediff than the S-NPs as the concentration gradient increases. However, although electrical conductance with all the nanoparticles is barely within the error range, the average conductance of the C-PSNPs is slightly lower than that of the S-NPs, as shown in Fig. 4(c). These results can be explained by the different surface properties, i.e., the hydrophilic (S-NP) and hydrophobic (C-PSNP) surfaces. Over the past years, researchers have demonstrated that a thin water depletion layer is exhibited close to a hydrophobic surface and it results in hydrodynamic slippage at solid surfaces, which is often quantified by the so-called slip length, b (a few tens of nanometers).43,44 On the hydrophilic surface, the zeta potential ζ is indistinguishable from the electrostatic surface potential ψ0, and thereby ζ represents the electric properties of the surface. On the hydrophobic surface, ζ is amplified by ζ = ψ0(1 + b/λD) with the slip length, b.44 However, since we measured the zeta potential with a zetameter for pure water, where λD is much higher than the slip-length, the zeta potential becomes similar to the surface potential (ζ ≈ ψ0). In our experimental conditions, the measured zeta potentials of the C-PSNPs and S-NPs for pure water were −53.7 and −40.4 mV, respectively. This means that the surface potential, ψ0, for the C-PSNPs was originally higher than that of the S-NPs, and consequently promotes the ion-selectivity with higher transference numbers and open circuit voltages, as shown in Fig. 4(a) and (b). On the other hand, due to this slip length with the water depletion layer near the hydrophobic surface of the C-PSNPs, the nanopore size (below 15% of diameter) and effective cross sectional area (below 21.50% of Ashallow) of the close-packed C-PSNPs are lower than those of the S-NPs. This decreased surface area induces lower conductance. Therefore, despite the higher surface potential, the average conductance of the C-PSNPs is slightly lower than that for the S-NPs. Nevertheless, the maximum power and energy conversion efficiency were improved by using the C-PSNPs because of its dramatically increased transference number compared to the S-NPs. As shown in Fig. 5(a), Pmax, which is measured in the present work using C-PSNPs, reached a best value of 42.38 pW when the concentration gradient was 0.1 mM/100 mM and the highest power density measured was ~0.0020 mW cm−2. Fig. 5(b) shows the maximum energy conversion efficiency and the best value is 27.03%.
Based on all these experimental results and an approximated formula for shallow channel conductance, we can perform model calculations to investigate a way to improve the maximum power. The electrical conductance of the nanochannel networks (Knetworks) can be expressed by the bulk conductance contribution and the surface conductance contribution from both the counter ions, K+ and H+, inside the nano-interstice as follows:45,46
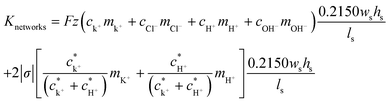 | (5) |
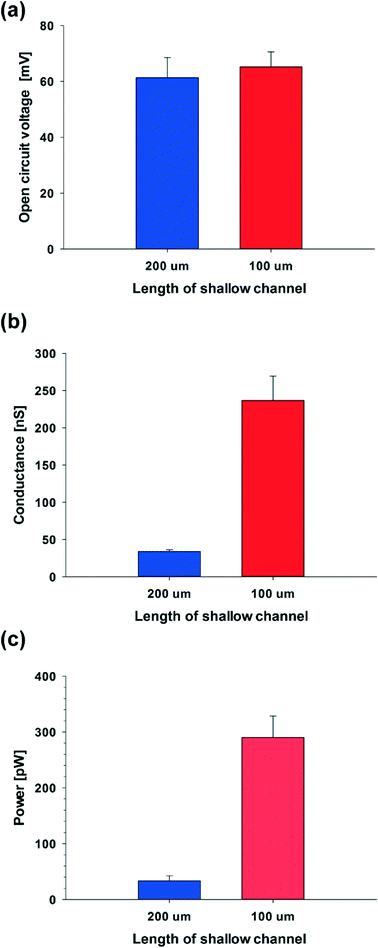
To verify this theoretical result, we shortened the length of the shallow channel (ls) up to 100 μm and performed the experiments with 100 nm diameter C-PSNPs, a hs of 50 μm, a ws of 200 μm, and a KCl concentration gradient of 0.1 mM/100 mM. As shown in Fig. 6(a)–(c), open circuit voltages (Ediff) at two different ls were barely within the error range. The conductance, however, increased dramatically after decreasing the length of the shallow channel and the Pmax was also enhanced up to 327.11 pW (290.25 ± 36.86 pW), which is greater than we predicted using eqn (5) (the theoretical value is ~85 pW). This nonlinear behavior against the Ohm's law seems to occur because the diffusion through the nanoparticle assembly is decreased severely by the physical confinement of the ions inside the nanopore cluster.48–50 The pure steric exclusion and hydrodynamic drag lead to the hindered diffusivity and Renkin's equation provides a fraction (α0), which demonstrates the relationship between the nanopore diffusivity (Dpore) and the bulk diffusivity (Dbulk) when an ion is transported through a single nanopore, as shown below:51
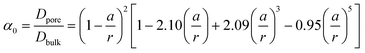 | (6) |
| αtotal = α0τ·n·κ | (7) |
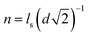 , wherein d is the diameter of the nanoparticle), and κ is the empirical constant which are relevant to the enhancement of the diffusivity in nanopores due to the electrostatic attraction by the counter-charge on the surface of the nanoparticles. Unlike the conventional organic membrane, we can easily infer the number of nanopores because the proposed membrane has a highly ordered and close-packed FCC structure. As shown in Fig. S5(a), in the ESI,† we roughly assumed that when the ion transport across the membrane occurs in the shortest path toward the low concentration channel, it may experience four nanopores (τ = 4). κ is evaluated by performing the experiment for the ion transport through the proposed membrane using a fluorescent dye. For a more detailed experiment, see section S.4 in the ESI.† In brief, we introduced the positively charged fluorescent dye, rhodamine 6G (R6G), which represents the potassium ion at one side of the deep channel (cH) and subsequently, we measured the time taken for the R6G to reach the opposite side of the deep channel (cL) through the membrane by using a fluorescent microscope. Fig. S5(b)† shows the time sequence fluorescent images. Finally, we obtained the diffusivity of the R6G (DR6G.membrane) in the membrane and evaluated κ from eqn (7), i.e., DR6G.membrane/DR6G.bulk = α0τ·n·κ where the DR6G.bulk is the bulk diffusivity of the R6G.
, wherein d is the diameter of the nanoparticle), and κ is the empirical constant which are relevant to the enhancement of the diffusivity in nanopores due to the electrostatic attraction by the counter-charge on the surface of the nanoparticles. Unlike the conventional organic membrane, we can easily infer the number of nanopores because the proposed membrane has a highly ordered and close-packed FCC structure. As shown in Fig. S5(a), in the ESI,† we roughly assumed that when the ion transport across the membrane occurs in the shortest path toward the low concentration channel, it may experience four nanopores (τ = 4). κ is evaluated by performing the experiment for the ion transport through the proposed membrane using a fluorescent dye. For a more detailed experiment, see section S.4 in the ESI.† In brief, we introduced the positively charged fluorescent dye, rhodamine 6G (R6G), which represents the potassium ion at one side of the deep channel (cH) and subsequently, we measured the time taken for the R6G to reach the opposite side of the deep channel (cL) through the membrane by using a fluorescent microscope. Fig. S5(b)† shows the time sequence fluorescent images. Finally, we obtained the diffusivity of the R6G (DR6G.membrane) in the membrane and evaluated κ from eqn (7), i.e., DR6G.membrane/DR6G.bulk = α0τ·n·κ where the DR6G.bulk is the bulk diffusivity of the R6G.
Using experimental conditions where the diameter of the potassium ion is 0.300 nm,52 and the nanopore is around 15 nm (~15% of the diameter of the nanoparticle), one can see that as the length of the shallow channel is shortened from 200 μm to 100 μm, the diffusivity at 100 μm increases ~9-fold than at 200 μm. We can therefore calculate the theoretical value of the power when the ls is 100 μm, 306.73 ± 82.67 pW, from the experimental value when the ls is 200 μm (33.39 ± 8.99 pW), because the diffusivity is proportional to the electrical conductance and the resulting power. This theoretical calculation shows good agreement with the experimental results, where the power is 290.25 ± 36.86 pW when the ls is 100 μm. Moreover, as the ls is shortened, the maximum power density is enhanced from ~0.0020 to ~0.015 mW cm−2 (Pmax is 327.11 pW). From these tendencies, if the C-PSNP has a diameter smaller than 100 nm to improve the ion-selectivity or the geometry of the shallow channel, especially when the ls is adjusted and the shallow channel is parallel integrated to scale up the conductance, tens of nanowatts could be readily obtained.
According to the comparison of these results with previously reported values obtained with a half-cell structure in different scales, we think that our system has the potential to fill the gap of the scale between bulk and single nano-scale RED platforms. We obtained a much higher power than a nano-scale system with a half-cell structure such as the straight nanofluidic channel reported by Kim et al. (~1 pW)27 and the ion-selective nanopore reported by Cao et al. (~45 pW).17 This is because the nano-interstices between the assembled nanoparticles have a role as the networks between the integrated single nanochannels or nanopores in parallel and this achieves the high ionic flux. However, the power density is lower than that for nano-scale RED systems (0.77 mW cm−2 from Kim et al.,27 0.83–1.43 mW cm−2 from Cao et al.17). Cao and co-workers estimated that the ion-selective nanopore by track-etching process will have a power density of 3–260 mW cm2 if its pore density is 108–1010 cm−2.17,28 However, unlike their expectations, Kwon et al. recently showed that although the power is increased, the energy density decreases to 0.0058 mW cm−2 when the track-etched nanoporous membrane (the diameter of 10 mm in the opening area, 78.5 mm2) with a pore density of ~6 × 108 cm−2 is used.29 This is because of the reduction of the diffusion potential and the current density (Kwon et al. obtained a diffusion potential that was 2 times lower and a current density (μA cm−2) that was 100-fold lower than that of the single-pore in Cao's work). As aforementioned, the higher working area may result in the increase in the number of diffused ions but it also results in a greater number of co-ions in the nanopore networks, and it can probably hinder the diffusion of counter-ions. Our result from the comparison study between different hs also shows that as the hs increases (higher working area), the power is enhanced but the voltage and the power density decrease slightly (Fig. 4(b)). From this point of view, with the half-cell structure, the power density of the micro-scale RED system will be between the nano (0.77–1.43 mW cm−2)17,27 and sub-micron scale (0.00002–0.0058 mW cm−2),25,29 and our results (micro-scale, ~0.015 mW cm−2) show good agreement with this trend.
Conclusions
In this paper, we proposed a nanofluidic reverse electrodialysis platform that includes crystallized nanoparticles that are geometrically controlled. This can efficiently convert the salinity-gradient energy into electricity with high power by allowing high ionic flux without decreasing the transference number and open circuit voltage. Although solid state nanochannels and nanopores have enhanced the power density of RED techniques, there were obvious limitations in their intrinsic surface materials due to their specific fabrication processes. Since the presented microplatform can adopt freely selected materials and a modified surface a priori, we believe that there is a greater possibility for improvement. It was experimentally proved and theoretically supported that the further improved performance can be achieved when using a small size and high surface charged nanoparticles that are close-packed in a microchannel with a large cross-sectional area and especially the length of the channel. Interestingly, it was also observed that the hydrophobic surface from the polymer has a high surface charge that induces high ion selectivity and open circuit voltage but reduces ionic conductance slightly due to the reduction of an effective cross sectional area by slip length. A more in-depth study about the dependency of size and material of the nanoparticles, and the design of the microchannel on ionic behavior is possible. The configuration of the microplatform is easily adaptable to existing microfluidic based systems. Therefore, it is expected to have potential applications in supplying electricity to next generation microdevices for health care or environment monitoring in the near future.Acknowledgements
This work was supported by Basic Science Research Program (2013R1A1A2073271), Research Program for Solving Social Problem (2013M3C8A3078815), and by National Nuclear R&D Program (2012M2A8A4055325) through the National Research Foundation of Korea funded by Ministry of Science ICT & Future Planning.References
- J. W. Post, H. V. M. Hamelers and C. J. N. Buisman, Environ. Sci. Technol., 2008, 42, 5785–5790 CrossRef CAS.
- F. La Mantia, M. Pasta, H. D. Deshazer, B. E. Logan and Y. Cui, Nano Lett., 2011, 11, 1810–1813 CrossRef CAS PubMed.
- P. V. Kamat, J. Phys. Chem. C, 2007, 111, 2834–2860 CAS.
- B. Z. Tian, X. L. Zheng, T. J. Kempa, Y. Fang, N. F. Yu, G. H. Yu, J. L. Huang and C. M. Lieber, Nature, 2007, 449, 885–U888 CrossRef CAS PubMed.
- Z. Chen, J. M. Guerrero and F. Blaabjerg, IEEE Trans. Power Electron., 2009, 24, 1859–1875 CrossRef.
- G. M. J. Herbert, S. Iniyan, E. Sreevalsan and S. Rajapandian, Renewable Sustainable Energy Rev., 2007, 11, 1117–1145 CrossRef PubMed.
- R. C. Saxena, D. K. Adhikari and H. B. Goyal, Renewable Sustainable Energy Rev., 2009, 13, 167–178 CrossRef PubMed.
- R. P. John, G. S. Anisha, K. M. Nampoothiri and A. Pandey, Bioresour. Technol., 2011, 102, 186–193 CrossRef CAS PubMed.
- A. Majumdar, Science, 2004, 303, 777–778 CrossRef CAS PubMed.
- A. J. Minnich, M. S. Dresselhaus, Z. F. Ren and G. Chen, Energy Environ. Sci., 2009, 2, 466–479 CAS.
- S. Xu, Y. Qin, C. Xu, Y. G. Wei, R. S. Yang and Z. L. Wang, Nat. Nanotechnol., 2010, 5, 366–373 CrossRef CAS PubMed.
- Y. Qi and M. C. McAlpine, Energy Environ. Sci., 2010, 3, 1275–1285 CAS.
- J. N. Weinstein and F. B. Leitz, Science, 1976, 191, 557–559 CAS.
- W. Sparreboom, A. van den Berg and J. C. T. Eijkel, Nat. Nanotechnol., 2009, 4, 713–720 CrossRef CAS PubMed.
- R. Pelc and R. M. Fujita, Mar. Policy, 2002, 26, 471–479 CrossRef.
- A. F. D. Falcao, Renewable Sustainable Energy Rev., 2010, 14, 899–918 CrossRef PubMed.
- L. X. Cao, W. Guo, W. Ma, L. Wang, F. Xia, S. T. Wang, Y. G. Wang, L. Jiang and D. B. Zhu, Energy Environ. Sci., 2011, 4, 2259–2266 CAS.
- R. E. Pattle, Nature, 1954, 174, 660 CrossRef CAS.
- G. D. Mehta, J. Membr. Sci., 1982, 11, 107–120 CrossRef CAS.
- J. J.-G. R. Kramer, Ind. Eng. Chem. Process Des. Dev., 1986, 25, 443–449 Search PubMed.
- M. T. B. Bandura, Desalination, 2007, 205, 67–74 CrossRef PubMed.
- T. Okada, H. Satou, M. Okuno and M. Yuasa, J. Phys. Chem. B, 2002, 106, 1267–1273 CrossRef CAS.
- H. G. Haubold, T. Vad, H. Jungbluth and P. Hiller, Electrochim. Acta, 2001, 46, 1559–1563 CrossRef CAS.
- P. W. Majsztrik, M. B. Satterfield, A. B. Bocarsly and J. B. Benziger, J. Membr. Sci., 2007, 301, 93–106 CrossRef CAS PubMed.
- R. B. Sadeghian, O. Pantchenko, D. Tate and A. Shakouri, Appl. Phys. Lett., 2011, 99 Search PubMed.
- B. B. Sales, M. Saakes, J. W. Post, C. J. N. Buisman, P. M. Biesheuvel and H. V. M. Hamelers, Environ. Sci. Technol., 2010, 44, 5661–5665 CrossRef CAS PubMed.
- D.-K. Kim, C. Duan, Y.-F. Chen and A. Majumdar, Microfluid. Nanofluid., 2010, 9, 1215–1224 CrossRef CAS.
- W. Guo, L. Cao, J. Xia, F.-Q. Nie, W. Ma, J. Xue, Y. Song, D. Zhu, Y. Wang and L. Jiang, Adv. Funct. Mater., 2010, 20, 1339–1344 CrossRef CAS.
- K. Kwon, S. J. Lee, L. Li, C. Han and D. Kim, Int. J. Energy Res., 2014, 38, 530–537 CrossRef CAS.
- Z. L. Wang, Sci. Am., 2008, 298, 82–87 CrossRef PubMed.
- W. Ouyang, W. Wang, H. Zhang, W. Wu and Z. Li, Nanotechnology, 2013, 24, 345401 CrossRef PubMed.
- Y. Lei, F. Xie, W. Wang, W. Wu and Z. Li, Lab Chip, 2010, 10, 2338–2340 RSC.
- C. H. Duan and A. Majumdar, Nat. Nanotechnol., 2010, 5, 848–852 CrossRef CAS PubMed.
- R. Kwak, G. Guan, W. K. Peng and J. Han, Desalination, 2013, 308, 138–146 CrossRef CAS PubMed.
- O. Demirer and C. Hidrovo, Microfluid. Nanofluid., 2014, 16, 109–122 CrossRef CAS.
- R. Kwak, V. S. Pham, K. M. Lim and J. Han, Phys. Rev. Lett., 2013, 110, 114501 CrossRef.
- E. Choi, H. K. Chang, C. Y. Lim, T. Kim and J. Park, Lab Chip, 2012, 12, 3968–3975 RSC.
- S. Chung, H. Yun and R. D. Kamm, Small, 2009, 5, 609–613 CrossRef CAS PubMed.
- Y. Zeng and D. J. Harrison, Anal. Chem., 2007, 79, 2289–2295 CrossRef CAS PubMed.
- P. Läuger, Angew. Chem., Int. Ed. Engl., 1969, 8, 42–54 CrossRef PubMed.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley, 2000 Search PubMed.
- D. Dash, S. Kumar, C. Mallika and U. K. Mudali, ISRN Chem. Eng., 2012, 5, DOI:10.5402/2012/730154.
- D. M. Huang, C. Sendner, D. Horinek, R. R. Netz and L. Bocquet, Phys. Rev. Lett., 2008, 101 Search PubMed.
- C. I. Bouzigues, P. Tabeling and L. Bocquet, Phys. Rev. Lett., 2008, 101 Search PubMed.
- C. C. Chang, C. P. Yeh and R. J. Yang, Electrophoresis, 2012, 33, 758–764 CrossRef CAS PubMed.
- R. B. Schoch and P. Renaud, Appl. Phys. Lett., 2005, 86 Search PubMed.
- R. F. Probstein, Physicochemical hydrodynamics: an introduction, ed. R. F. Probstein, Butterworths, Boston, 1989 Search PubMed.
- J. Han, J. Fu and R. B. Schoch, Lab Chip, 2008, 8, 23–33 RSC.
- Y. Y. Kievsky, B. Carey, S. Naik, N. Mangan, D. Ben-Avraham and I. Sokolov, J. Chem. Phys., 2008, 128, 151102 CrossRef CAS PubMed.
- V. V. Swaminathan, L. R. Gibson, M. Pinti, S. Prakash, P. W. Bohn and M. A. Shannon, J. Nanopart. Res., 2012, 14 Search PubMed.
- E. M. Renkin, J. Gen. Physiol., 1954, 38, 225–243 CAS.
- A. Achilli, T. Y. Cath and A. E. Childress, J. Membr. Sci., 2010, 364, 233–241 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Fabrication process for PDMS microfluidic channels with multilayered design, in situ formation of nanochannel network membrane using nanoparticles, electrode calibration, evaluation of empirical constant, κ. See DOI: 10.1039/c4lc01031k |
| This journal is © The Royal Society of Chemistry 2015 |