A kinetic model of gene transfer via natural transformation of Azotobacter vinelandii
Nanxi
Lu†
a,
Arash
Massoudieh
 *b,
Xiaomeng
Liang
b,
Tamir
Kamai
c,
Julie L.
Zilles
a,
Thanh H.
Nguyen
a and
Timothy R.
Ginn
d
*b,
Xiaomeng
Liang
b,
Tamir
Kamai
c,
Julie L.
Zilles
a,
Thanh H.
Nguyen
a and
Timothy R.
Ginn
d
aDepartment of Civil and Environmental Engineering, University of Illinois, Urbana–Champaign, USA
bDepartment of Civil Engineering, The Catholic University of America, Washington DC, USA. E-mail: arashmassoudieh@gmail.com
cInstitute of Soil, Water and Environmental Sciences, Agricultural Research Organization, Bet Dagan, Israel
dDepartment of Civil and Environmental Engineering, University of California, Davis, USA
First published on 12th March 2015
Abstract
Horizontal gene transfer allows antibiotic resistance and other genetic traits to spread among bacteria in the aquatic environment. Despite this important role, quantitative models are lacking for one mechanism of horizontal gene transfer, which is natural transformation. The rates of horizontal gene transfer of a tetracycline resistance gene through natural transformation were experimentally determined for motile and non-motile strains of Azotobacter vinelandii. We developed a mathematical model adapted from the mass action law that successfully described the experimentally determined rates of natural transformation of a tetracycline resistance gene for motile and non-motile strains of Azotobacter vinelandii. Transformation rates showed a rapid initial increase, followed by a decrease in the first 30 minutes of the experiment, and then a constant rate was maintained at a given cell and DNA concentration. The proposed model also described the relationship between transformation frequency and varied DNA or cell concentrations. The modeling results revealed that under the given experimental conditions, the gene transformation rate was limited both by the abundance of the tetracycline resistance gene and by cellular activities associated with cell–DNA interactions. This work establishes a quantitative model of natural transformation, suggests a need to further investigate the cell properties affecting transformation rates, and provides a basis for development of comprehensive models of horizontal gene transfer and quantitative risk assessment of antibiotic resistance gene dissemination in the aquatic environment.
Water impactAntibiotic resistance is an important water quality issue that is compounded by horizontal gene transfer among microorganisms. Among the known mechanisms of horizontal gene transfer, only natural transformation, the uptake and expression of extracellular DNA, lacks a quantitative model. This manuscript presents the first quantitative model of natural transformation, based on experimental data obtained with a tetracycline resistance gene and the model bacterium Azotobacter vinelandii. We found that only a small fraction of DNA participates in the transformation, and the rate is controlled by the abundance of the resistance gene. Our results contribute to the development of comprehensive models for horizontal gene transfer, providing a basis for understanding and ultimately risk assessment of antibiotic resistance dissemination in the aquatic environment. |
Introduction
In the aquatic environment, horizontal gene transfer (HGT) can be facilitated, contributing to the development of an important environmental reservoir of antibiotic resistance (reviewed in ref. 1). More generally, HGT is an important mechanism of bacterial adaptation (e.g., ref. 2–4) and facilitates the spread of metabolic traits throughout a microbial community. Therefore, HGT is fundamental to our understanding of microbial processes and fates influencing water quality and public health, including biodegradation of pollutants and dissemination of antibiotic resistance genes. While substantial effort has been devoted to modeling conjugation and transduction, to our knowledge, mathematical models of the third mechanism of HGT, natural transformation, are not available, leaving a critical gap in our ability to understand the occurrence of HGT in the environment.Natural transformation requires extracellular DNA and competent cells, both of which are present in sediments and soils.5–8 There is limited knowledge of natural transformation in aquatic systems, but aquatic biofilms and sediment microbial communities where conjugation is important also provide appropriate conditions for natural transformation.1 Despite being adsorbed on environmental surfaces,6,7,9 extracellular DNA is still accessible to microorganisms, as has been documented for Pseudomonas stutzeri,10Bacillus subtilis,11 and Azotobacter vinelandii.12,13 The development of competence is typically regulated by bacteria, and hence the availability of competent cells depends on the growth conditions.5 In the current work, A. vinelandii was used as the model organism because it is environmentally relevant (native to soil), naturally competent/transformable, non-sequence-specific in its uptake of DNA,14 and motile due to its peritrichous flagella.15 For A. vinelandii, one condition that induces competence is iron limitation.16 Natural transformation rates also typically depend on the concentration of DNA, with the transformation frequency of A. vinelandii leveling off at around 0.1 μg of DNA per 107 cells.17
Because transformation requires contact between extracellular DNA and the cell, bacterial motility might also be expected to influence transformation rates. A connection between natural transformation and twitching motility, which is mediated by type IV pili and occurs on a surface, has been documented in multiple microorganisms. However, this connection appears to be due to an involvement of some of the components of the pilus in DNA uptake, rather than an effect of movement.18 Although flagellar motility affects bacterial transport and deposition,19–22 to our knowledge, the effect of flagellar motility on natural transformation frequencies or rates has not been examined previously.
Several models have been developed to describe rate-limited conjugation.23–26 Most of these models are based on the mass action relationship proposed by Levin et al.,23 where it is assumed that the gene transfer rate is proportional to the product of local donor and recipient cell number densities. Subsequent modifications have added plasmid transfer from newly formed transconjugants,27 growth and decay of donors, recipients and transconjugants,26 and consideration of mating pair formation, donor recovery, and transconjugant maturation times.28,29 In more recent modeling studies, the impacts of attachment to surfaces, biofilm formation, and heterogeneity on conjugation have been incorporated into models based on Levin's mass action transfer.25,30–33
However, conjugation does not always follow Levin's mass action model (e.g.ref. 34); instead, a brief period of rapid conjugation may be observed after which no further increase in the number of transconjugants follows. Turner35 showed that the conjugation rate of plasmid pB15 in E. coli in poorly mixed environments was not linearly proportional to the recipient cell density. Ponciano et al.32 considered the conjugation rate to be not linearly dependent on the recipient density but via a Monod-type relationship, while Zhong et al.36 considered mating pair formation as an intermediate step and a rate limiting process in conjugative transfer. Kinetic models for transduction have also been developed.37,38
The kinetics of horizontal gene transfer through natural transformation has not, to our knowledge, been modeled quantitatively. Also, although the impact of bacterial motility on the rate of conjugation has been recognized,34 to our knowledge, no studies have compared the natural transformation rates of motile vs. non-motile bacteria. These knowledge gaps limit our ability to understand and predict the fate and transport of genes in the environment, whether these genes encode beneficial or harmful traits. In this study, we developed a new kinetic model of transformation, built from models of conjugation but included dynamically changing available DNA, and applied the new model to transformation data collected under controlled laboratory conditions. This new model was used to test the hypothesis that DNA limitation is the controlling factor in the rate. Our experiments also used different strains of A. vinelandii to specifically investigate the effects of flagellar motility.
Materials and methods
Strains and growth conditions
Three strains of A. vinelandii were used in this work. These bacterial strains were chosen to test the influence of swimming motility on natural transformation. DJ is a wild-type, motile strain. DJ77 contains a 128 bp deletion in nifH, resulting in a defect in nitrogen fixation in the presence of molybdenum.39 DJ77 exhibits reduced motility as compared to DJ. Looking at their mean squared displacement, which is a metric for quantifying movement,40 DJ77 has an approximately one order of magnitude smaller mean squared displacement than DJ.15 Both of these strains were obtained from Dr. Dennis Dean and were used as recipients in the transformation experiments. The third strain was JZ52, which contains the tetA(C) tetracycline resistance gene inserted in the flhC gene.15 Chromosomal DNA was extracted from JZ52 for use in the transformation experiments via standard phenol–chloroform extraction methods.41 For a given experiment, the concentration of donor DNA was measured with a Nanodrop® ND-1000 (Thermo Scientific) or a Qubit® 2.0 fluorometer (Life Technologies, Thermo Fisher Scientific Inc.). The A. vinelandii strains were routinely cultivated in Burke's medium.42 Competent cells were prepared by growing in Burke's medium plates (without molybdenum) with addition of 13 mM ammonium acetate at 30 °C for 2 days and then inoculating in Burke's liquid medium without molybdenum or iron, and shaking at 170 rpm for 18 to 20 h. These conditions are known to induce competence.39,43 To quantify the starting cell concentration, a hemocytometer was used for direct counting of suspended cells in a controlled volume under a light microscope. The starting cell concentration was then adjusted as desired through dilution.Transformation assays
Transformation assays were conducted by mixing 200 μL of competent cells (with varying target concentrations), 200 μL of MOPS buffer with 1 mM Mg2+, and 10 μL of donor chromosomal DNA (with varying concentrations) sequentially. After incubating at room temperature for 30 min (standard conditions) or varying amounts of time (kinetic experiments), the transformation reaction was terminated by adding 2 enzyme units of DNase I and incubating for 10 min. The resulting mixture was diluted 10 times in Burke's medium with 13 mM ammonium acetate and incubated at 30 °C for 24 h before being plated. Transformants were quantified by duplicate plating in a selective medium (Burke's medium with 12.5 μg mL−1 tetracycline and 13 mM ammonium acetate). Viable cells were quantified by duplicate plating in a non-selective medium (Burke's medium with 13 mM ammonium acetate). The cells were grown at 30 °C for 3–5 days. Transformation frequencies were determined by dividing the number of transformants by that of viable cells. Parallel transformations were conducted within a batch of competent cells for each condition (duplicate transformations), and each experiment was repeated twice with independent preparations of competent cells (biological replicates). Spontaneous mutations and selectivity of the plates were tested with no-DNA controls in each set of experiments. Control experiments comparing the transformation frequency for DJ77 and JZ52 using wild type chromosomal DNA and selection for nitrogen fixation demonstrated that the flhC mutation does not impair transformation.Three sets of natural transformation experiments with dissolved DNA were conducted to investigate the influence of cell concentration, DNA concentration, and transformation time. In the first set, the cell concentration was varied from 3.7 × 107 to 9.8 × 108 cells per mL and from 6.0 × 107 to 8.7 × 108 cells per mL for DJ and DJ77, respectively. The cell concentration range between 3.0 × 107 to 1.0 × 109 cells per mL allows transformant detection. The DNA concentration was held constant at 0.25 μg mL−1 and the transformation time was 30 min. The second set was carried out with varying DNA concentrations from 0.00025 to 2.5 μg mL−1 for both recipient strains. For these experiments, the cell concentration averaged 1.0 × 107 ± 8.2 × 106 cells per mL for DJ (± standard deviation, n = 20) and 7.8 × 106 ± 3.3 × 106 cells per mL for DJ77 (± standard deviation, n = 20). These biological replicates differed in their transformation time, 15 min and 30 min. The final set was conducted with transformation times ranging from 0 to 90 min and with 0.25 μgDNA mL−1. In the first biological replicates (panels a and c), the cell concentrations were 3.4 × 107 ± 2.8 × 107 cells per mL for DJ (± standard deviation, n = 20) and 4.6 × 107 ± 8.6 × 106 cells per mL for DJ77 (± standard deviation, n = 20). In the second replicates (panels b and d), the cell concentrations were 1.7 × 108 ± 2.5 × 107 cells per mL for DJ (± standard deviation, n = 12) and 1.7 × 108 ± 3.7 × 107 cells per mL for DJ77 (± standard deviation, n = 12).
Mathematical model
From the kinetic data (described in Results and discussion (Transformation experiments)), a few observations can be made: 1) the increase in transformation frequency is time-dependent, with a higher slope at the beginning that decreases with time and eventually approaches zero as the incubation time approaches 30 minutes. 2) There is a strong concave non-linear relationship between the cell concentration and transformation frequency. This means that transformation per unit cell concentration decreases as the cell concentration increases. 3) The maximum observed transformation constitutes only a small fraction of the total number of viable cells. 4) Different batches of cells have different transformation frequencies with dissolved DNA under similar conditions as reported previously.12Considering that only a fraction of genomic DNA fragments hold the tetracycline resistance gene required for detection of a transformation event in our assay, Levin's mass action model can be applied to express the temporal change in the concentration of transformants as:
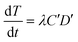 | (1) |
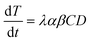 | (2) |
The value of α is the fraction of the tetracycline resistance gene that was eventually expressed in the cells over the total DNA, and the value of β is the ratio of bacterial cells involved in transformation to the number of viable cells. The balance equations for D and C can be written as:
| αD = αD0 − T | (3a) |
| βC = βC0 − T | (3b) |
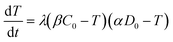 | (4) |
The analytical solution to eqn (4) with the initial condition of T(t = 0) = 0 can be found as:
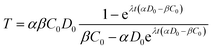 | (5) |
If dimensionless quantities including dimensionless initial concentration of DNA, effective transformation frequency, and dimensionless time are defined respectively as D*0 = αD0/βC0, T* = T/βC0, and t* = λtβC0, the dimensionless form of eqn (5) expressing the effective transformation frequency (transformation per unit competent and viable cell concentration) can be written as:
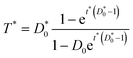 | (6) |
Based on eqn (5) and (6), when βC0 ≫ αD0, the ultimate concentration of transformed cells will be equal to αD0 and when βC0 ≪ αD0, the ultimate number concentration will be equal to βC0. Fig. 1 provides a graphical depiction of the variation of effective transformation frequency as a function of D*0 and t*. When D < 1, the limiting transformed cell concentration at t* ≫ 1 approaches D*0 which indicates DNA limitation and it approaches 1 (i.e. T = βC0) when D* > 1, representing cell limiting conditions.
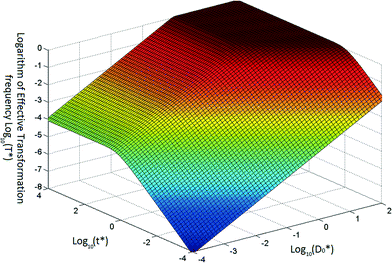 | ||
| Fig. 1 Typical variation of transformation frequency as a function of dimensionless transferable DNA number concentration and dimensionless time. | ||
Parameter estimation
To estimate the model parameters (i.e. α, β and λ), maximum likelihood estimation via an optimization algorithm was used, minimizing the sum of squared differences between the measured and modeled log-transformed transformant number densities. The combined data from all transformation experiments were used as the measured values. Log-transformation was performed because the distributions of the observed transformants were closer to a log-normal distribution than to a normal distribution, and with proportional errors, log-transformation is expected to render errors more approximately normal. Initially, a single set of parameters was considered for the two strains, but the agreement between the modeled and measured transformant concentrations (not shown here) was not acceptable. Since the parameters quantified the changes in transformation frequency in response to DNA and cell concentrations, this indicates that DJ and DJ77 responded differently to DNA and cell concentrations, despite showing no significant difference in their overall transformation frequency. Different parameters were therefore considered for the two strains.Due to the uncertainties associated with the measured viable cell and transformed cell concentrations, there are also uncertainties associated with the maximum likelihood estimates of the model parameters. To assess these uncertainties, a Bayesian inference using the Markov Chain Monte Carlo (MCMC) approach was employed to find the joint probability distributions of the model parameters. Assuming conditional independence of observed transformant concentrations, non-informative priors for the parameters, and log-normal and multiplicative error structures, the posterior distribution of the model parameters can be written as:44
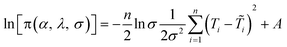 | (7) |
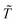 are respectively the modeled and observed transformant concentration in sample i, and A is a constant that only depends on the observed data and is irrelevant when using MCMC to draw samples from the posterior distribution.
are respectively the modeled and observed transformant concentration in sample i, and A is a constant that only depends on the observed data and is irrelevant when using MCMC to draw samples from the posterior distribution.
The Metropolis–Hastings MCMC algorithm45 was used to sample from the posterior distribution. The algorithm draws a large number of samples from the posterior distribution (eqn (5)).
Results and discussion
Transformation experiments
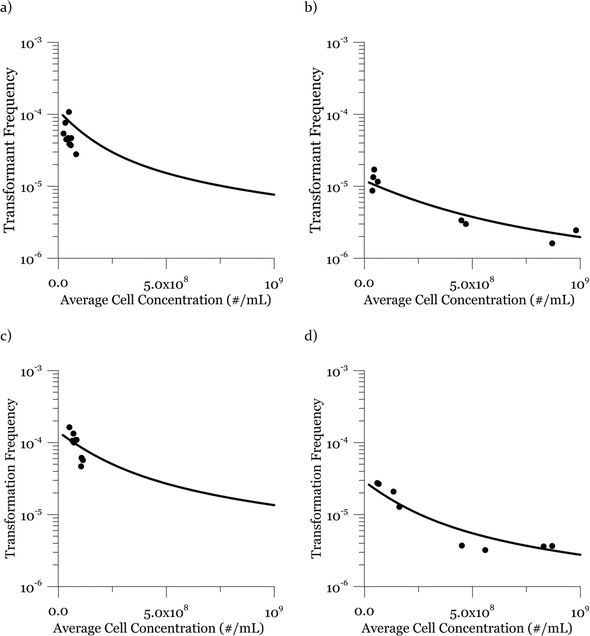
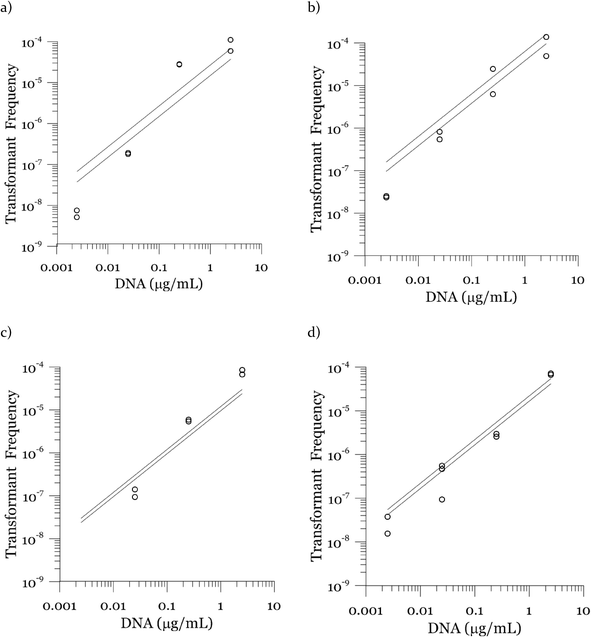
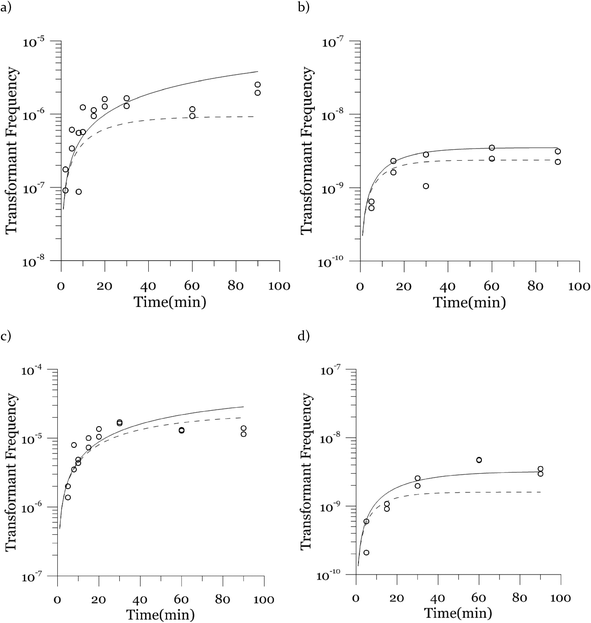
Due to a known variation between batches of competent cells,13 biological replicates are presented separately rather than being averaged. The results from both biological replicates were used for modeling. For both replicates, the transformation frequencies dropped as the concentrations of cells increased (Fig. 2). Because the transformation frequency was defined as transformants normalized by viable cells, this decrease reflects the fact that increasing the number of viable cells in the experiment did not generate a corresponding increase in transformants; there was a non-linear relationship between the rate of increase in the number of transformations and the increasing cell concentration. The decreased transformation frequencies with more viable cells can be explained by postulating that the access of each competent cell to a transforming gene on the DNA molecule decreases as the competent cell number increases. Alternatively, with higher cell concentrations, one individual cell could experience less contact with DNA because of the competition or impedance from the surrounding cells. In contrast, for DNA concentrations ranging from 0.00025 to 2.5 μg mL−1, the transformation frequencies for both strains showed an almost linear relationship (Fig. 3). The relationship between the transformation frequency and DNA concentration was consistent with Levin's original mass action relationship and indicated that transformation kinetics were limited by DNA under our experimental conditions.The plot of transformation frequency versus time shows that the transformation frequencies increased rapidly at the beginning, and then the increase slowed down, stabilizing after about 30 minutes for both biological replicates of both strains (Fig. 4). The plateau in transformation frequency versus time occurred at a lower transformation frequency than expected; several hypotheses were investigated to explain this observation. One hypothesis was that this lower plateau was due to the loss of competence. This hypothesis was tested by incubating competent cells under the reaction conditions but without DNA for varying times before being used in a transformation experiment. Under these conditions, the cells maintained both viability and competence for 48 h, well beyond the duration of the experiments described here, disproving this hypothesis. In another hypothesis, we tested the possibility that mixing limitations affected the transformation kinetics. In our standard transformation assay, the transformation reactions were only mixed once, at the beginning of the transformation period. An additional transformation experiment was therefore conducted where a second round of mixing and 30 minute incubation was performed after the initial mixing and incubation. The transformation rate for this case was compared with that for a case where the second set had 30 minutes of incubation without mixing. No statistically significant difference was observed. This rejects the mixing limitation hypothesis. We then considered the hypothesis that the secretion of nucleases from Azotobacter vinelandii competent cells damaged the transforming DNA. Secretion of nucleases was not directly tested here, but a previous report suggests that A. vinelandii does not produce extracellular nucleases during natural transformation.46 Considering this information, we hypothesize that the temporal decrease in the transformation rate was a result of depletion of the transforming gene pool. The concave relationship between transformation frequency and time suggested that the transforming genes were consumed given enough time; this result was consistent with the results of the experiments varying either DNA or cell concentrations.
The transformation frequencies were lower for both strains in the second replicate because the viable cell concentrations in the second replicate were higher than those in the first replicate (4.9 and 3.8 times higher for DJ and DJ77, respectively). As observed in the previous cell concentration experiments, the transformation frequency was lower at higher cell concentrations.
Modeling results
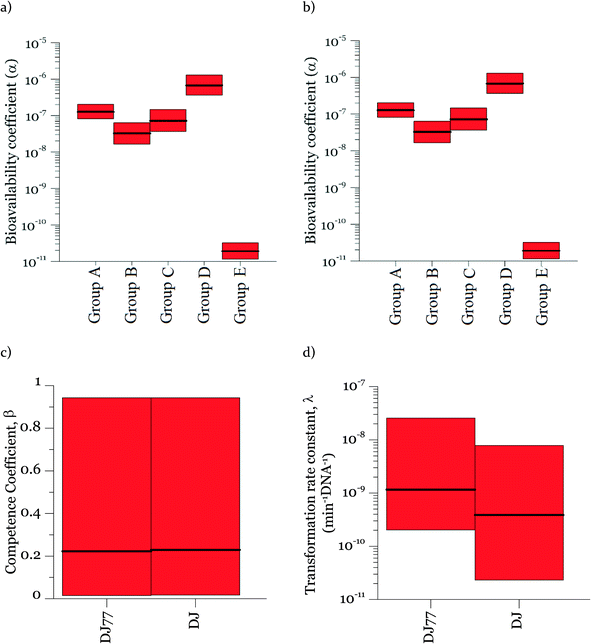
Parameters α, β, and λ were estimated from the combined data in Fig. 2–4 using maximum likelihood estimation with an optimization algorithm as detailed in Materials and methods. Coefficient α varied substantially for different experimental groups (Fig. 5). The experimental groups A–E belong to different batches of competent cells (group A and B: varying cell concentrations; C: varying DNA concentrations; D and E: transformation kinetics) with an exception that the transformations with varying DNA concentrations at 15 min and 30 min of transformation time (group C) were grouped together for simplicity since they gave very close transformation frequency magnitudes and dynamics. In particular, α was much lower for the second set of biological replicates for the kinetic experiments (group E in Fig. 5a and b), which were conducted several weeks after all other experiments. This was surprising, since coefficient α influences the number of transforming DNA molecules and not the cell concentration or abundance of competent cells. Two potential causes for this are: variation in the fraction of DNA containing the tetracycline resistance gene from experiment to experiment, and/or variation in cellular activity from batch to batch of competent cells. The fraction of tetracycline resistance genes was well-controlled, since DNA from multiple extractions was pooled and then aliquoted for the transformation experiments. There could have been changes in the pooled DNA over time. However, the concentration of DNA did not change over that time period. We therefore conclude that the variation of α likely reflects not only variation in the properties of DNA, but also batch-to-batch variability in cellular activity associated with DNA–cell interactions, such as DNA contact with cells, transport into cells, incorporation into the genome, and/or gene expression.Fig. 5 shows the 95% credible intervals (C.I.) and medians of the parameters obtained from the posterior distributions of the model parameters α and λ. The range of values of α was consistent for the experiments with the motile and non-motile strains. This observation agrees with our definition of α as reflecting the fraction of DNA producing detectable transformation events in our assay, which should not be dependent on motility. The highest value of α was around 10−6. Since A. vinelandii possesses a chromosome size of 5365 kb (ref. 47) and that of the tetracycline resistance gene is 1.2 kb, 2 × 10−4 genomic DNA would be expected to contain the tetracycline resistance gene. The fact that α was even lower than 2 × 10−4 suggests that either not all copies of the genome contain the tetracycline resistance gene or other characteristics of the cells limit the ultimate expression of the tetracycline resistance gene. These characteristics could affect DNA uptake or its subsequent incorporation into the recipient cell genome and the expression for assay detection. The 95% intervals of λ and β are wide, indicating equifinality (i.e., the non-unique combination of the two parameters can result in equally good agreement between modeled and measured values). For the experimental results shown here, a model without β could explain the data, but considering the broader range of cell concentrations in the environment, a cell concentration parameter was included for versatility. As shown in Fig. 5c, the 95% interval value of β varied between almost zero to 0.93 for DJ77 and zero to 0.92 for DJ, with expected average values of ~0.2 and ~0.1, respectively.
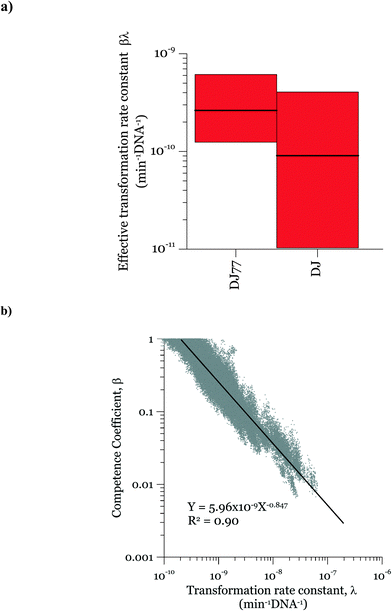
In the posterior distributions, β and λ were correlated, which means that a decrease in β and a proportional increase in λ resulted in the same numbers of transformation events. This correlation is due to the fact that the concentration of competent cells did not control the ultimate transformed cell concentrations in these experiments. Fig. 6a shows the 95% confidence interval of the quantity βλ (referred to as the effective transformation rate constant).
Fig. 6b shows the possibility space of β and λ obtained using the outcome of the MCMC analysis and a strong correlation between the posterior distributions of the logarithms of the two parameters is evident. The 95% brackets for the product of the two parameters are much narrower than that for λ, indicating its better identifiability. Theoretically, a narrower confidence interval could be obtained regarding β by conducting the experiments either with a much larger DNA concentration or with a much smaller cell concentration, so that viable and competent cells become the limiting factor of the ultimate transformation frequency. However, this solution was not feasible due to the amount of DNA required and the detection limits in the transformation assay. The βλ value for the two strains overlapped, with the expected average value of βλ for DJ77 roughly two times larger. The p-value for the hypothesis that the βλ for DJ77 is larger than that for DJ (i.e. the probability that the βλ for DJ is larger) was 0.00751. We attribute this difference to the difference in motility between the two strains, rather than to DJ77's Nif− phenotype, because fixed nitrogen was provided throughout the experiment. A motility defect could affect transformation by allowing a longer contact time between the cells and extracellular DNA. However, this difference was not substantial enough to lead to a distinctive model structure.
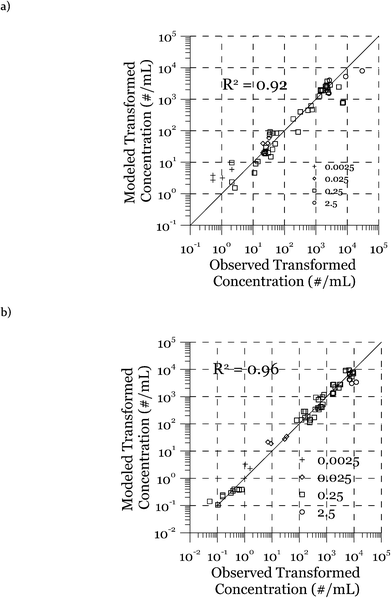
The modeled transformation frequencies were compared to the experimental results using all measured data (Fig. 7) as well as data from the transformation experiments featuring only cell concentrations (Fig. 2), DNA concentrations (Fig. 3), or transformation kinetics (Fig. 4). The R2 values reported in Fig. 7 were calculated based on the log-transformed transformed cell concentrations. Using all of the measured data (Fig. 7), the predicted values are the likeliest parameter sets obtained through minimization of the squared error between measured and modeled data. R2 values of 0.92 (DJ) and 0.96 (DJ77) were obtained using the log-transformed modeled and measured transformed cell concentrations. In addition to the proposed model, we tested alternative models including Levin's mass action model without considering the reduction of DNA as well as a few other models where the relationship between the transformation rate and D and C was considered non-linear through power law relationships. The proposed model was able to reproduce the observed data significantly better, as evaluated using R2 and the Bayesian information criterion.
Next, we explore the transformation kinetics. Fig. 4 shows modeled and observed transformation kinetics. Since the cell concentrations showed some variation around the target concentrations, each of the points in Fig. 4 is from a different cell concentration. Therefore, we present two modeled transformation frequency curves, one based on the minimum experimental viable cell concentration (the solid curve) and the other one based on the maximum experimental viable cell concentration (the dashed curve). The values of α, β and λ used to generate these plots are the likeliest values obtained through deterministic maximization of the likelihood function.
Considering the effect of cell concentration, in one set of experiments for each strain (DJ and DJ77), the cell concentration was varied by less than one order of magnitude (Fig. 2, panels a and c), while in the second set of experiments (Fig. 2, panels b and d), the cell concentration was varied by about two orders of magnitude from 3.7 × 107 to 9.8 × 108 cells per mL. For both strains, the model describes the decreasing trend in transformation frequency as a result of an increase in the cell concentration well.
Fig. 3 shows modeled vs. measured transformation frequencies in the experiment where the DNA concentrations were varied by four orders of magnitude. Similar to Fig. 7, the model predictions based on the largest and the smallest cell concentrations in each experiment are presented. The sensitivity towards cell concentration is small compared to that towards DNA concentration, indicating DNA limitation. The almost linear (slightly convex) relationship between transformation frequency and DNA concentration is captured by the model.
Environmental implications
Considering the experimental data and the modified Levin's mass action model developed in this work, the most reasonable conclusion which can be made is that transformation frequencies are limited primarily by the abundance of the transforming gene. In the environment, however, a broader range of cell concentrations could lead to cell concentration also being a limiting parameter. The lower than predicted values for α suggest an additional limit on transformation that is related to the DNA concentration; identification of the molecular mechanism(s) underlying this limit requires further study. Swimming motility appeared to reduce transformation, based on the smaller estimated βλ values of the motile strain DJ compared to those of the motility-impaired strain DJ77. In addition to this effect on transformation, swimming motility could affect environmental transformation rates through its effects on cell transport.In aquatic environments, HGT can contribute to the dissemination of antibiotic resistance genes, virulence genes, and new biodegradation capabilities. In particular, the dissemination of antibiotic resistance genes in aquatic environments presents a current and pressing public health concern for which risk assessment and identification of appropriate control measures require an understanding of horizontal gene transfer and the parameters that control it. The quantitative model of natural transformation presented in this work provides a basis for identifying the parameters controlling natural transformation rates in the environment. In combination with existing models of conjugation and transduction, this model will allow the development of a comprehensive predictive model of horizontal gene transfer.
Acknowledgements
This project research was supported by the NSF (project award number 1114274, “Collaborative Research: Horizontal Gene Transfer in Porous Media: Experiments and Modeling” and project award number 1215756, “Collaborative Research: Near-Surface Repulsion and Mixing-Limitations: Upscaling of Colloid Transport in Non-Uniform Media under Unfavorable Conditions”).References
- E. Marti, E. Variatza and J. L. Balcazar, The role of aquatic ecosystems as reservoirs of antibiotic resistance, Trends Microbiol., 2014, 22(1), 36–41 CrossRef CAS PubMed.
- P. Marri, W. Hao and G. B. Golding, The role of laterally transferred genes in adaptive evolution, BMC Evol. Biol., 2007, 7(Suppl 1), S8 CrossRef PubMed.
- E. Skippington and M. A. Ragan, Lateral genetic transfer and the construction of genetic exchange communities, FEMS Microbiol. Rev., 2011, 35(5), 707–735 CrossRef CAS PubMed.
- R. I. Aminov, The extent and regulation of lateral gene transfer in natural microbial ecosystems, In Horizontal Gene Transfer in Microorganisms, ed. M. P. Francino, Caister Academic Press, 2012 Search PubMed.
- M. G. Lorenz and W. Wackernagel, Bacterial gene transfer by natural genetic transformation in the environment, Microbiol. Rev., 1994, 58(3), 563–602 CAS.
- E. Paget and P. Simonet, On the track of natural transformation in soil, FEMS Microbiol. Ecol., 1994, 15(1–2), 109–117 CrossRef CAS PubMed.
- D. J. Levy-Booth, R. G. Campbell, R. H. Gulden, M. M. Hart, J. R. Powell, J. N. Klironomos, K. P. Pauls, C. J. Swanton, J. T. Trevors and K. E. Dunfield, Cycling of extracellular DNA in the soil environment, Soil Biol. Biochem., 2007, 39(12), 2977–2991 CrossRef CAS PubMed.
- G. Pietramellara, J. Ascher, F. Borgogni, M. T. Ceccherini, G. Guerri and P. Nannipieri, Extracellular DNA in soil and sediment: fate and ecological relevance, Biol. Fertil. Soils, 2009, 45(3), 219–235 CrossRef CAS.
- W. H. Yu, N. Li, D. S. Tong, C. H. Zhou, C. X. Lin and C. Y. Xu, Adsorption of proteins and nucleic acids on clay minerals and their interactions: A review, Appl. Clay Sci., 2013, 80–81, 443–452 CrossRef CAS PubMed.
- M. G. Lorenz and W. Wackernagel, Natual genetic transformation of Pseudomonas stutzeri by sand bound DNA, Arch. Microbiol., 1990, 154(4), 380–385 CrossRef CAS.
- M. Khanna and G. Stotzky, Transformation of Bacillus subtilis by DNA bound on Montmorillonite and effect of DNase on the transforming ability of bound DNA, Appl. Environ. Microbiol., 1992, 58(6), 1930–1939 CAS.
- N. Lu, S. E. Mylon, R. Kong, R. Bhargava, J. L. Zilles and T. H. Nguyen, Interactions between dissolved natural organic matter and adsorbed DNA and their effect on natural transformation of Azotobacter vinelandii, Sci. Total Environ., 2012, 426, 430–435 CrossRef CAS PubMed.
- N. Lu, J. L. Zilles and T. H. Nguyen, Adsorption of extracellular chromosomal DNA and its effects on natural transformation of Azotobacter vinelandii, Appl. Environ. Microbiol., 2010, 00193-10 Search PubMed.
- C. S. Renaud, J. Pasternak and B. R. Glick, Integration of exogenous DNA into the genome of Azotobacter vinelandii, Arch. Microbiol., 1989, 152(5), 437–440 CrossRef CAS.
- N. Lu, T. Bevard, A. Massoudieh, C. Zhang, A. C. Dohnalkova, J. L. Zilles and T. H. Nguyen, Flagella-Mediated Differences in Deposition Dynamics for Azotobacter vinelandii in Porous Media, Environ. Sci. Technol., 2013, 47(10), 5162–5170 CrossRef CAS PubMed.
- W. J. Page and M. Vontigerstrom, Induction of transformation competence in Azotobacter vinelandii iron-limited cultures, Can. J. Microbiol., 1978, 24(12), 1590–1594 CrossRef CAS.
- J. L. Doran, W. H. Bingle, K. L. Roy, K. Hiratsuka and W. J. Page, Plasmid transfermation of Azotobacter vinelandii, J. Gen. Microbiol., 1987, 133, 2059–2072 CAS.
- I. Chen and D. Dubnau, DNA uptake during bacterial transformation, Nat. Rev. Microbiol., 2004, 2(3), 241–249 CrossRef CAS PubMed.
- T. A. Camesano and B. E. Logan, Influence of fluid velocity and cell concentration on the transport of motile and nonmotile bacteria in porous media, Environ. Sci. Technol., 1998, 32(11), 1699–1708 CrossRef CAS.
- B. Z. Haznedaroglu, O. Zorlu, J. E. Hill and S. L. Walker, Identifying the Role of Flagella in the Transport of Motile and Nonmotile Salmonella enterica Serovars, Environ. Sci. Technol., 2010, 44(11), 4184–4190 CrossRef CAS PubMed.
- A. Massoudieh, N. Lu, X. Liang, T. H. Nguyen and T. R. Ginn, Bayesian Process-Identification in Bacteria Transport in Porous Media, J. Contam. Hydrol., 2013 Search PubMed , (In press).
- J. W. McClaine and R. M. Ford, Characterizing the adhesion of motile and nonmotile Escherichia coli to a glass surface using a parallel-plate flow chamber, Biotechnol. Bioeng., 2002, 78(2), 179–189 CrossRef CAS PubMed.
- B. R. Levin, F. M. Stewart and V. A. Rice, Kinetics of conjungative plasmid transmission - fit of a simple mass action model, Plasmid, 1979, 2(2), 247–260 CrossRef CAS.
- A. Massoudieh, C. Crain, E. Lambertini, K. E. Nelson, T. Barkouki, P. L'Amoreaux, F. J. Loge and T. R. Ginn, Kinetics of conjugative gene transfer on surfaces in granular porous media, J. Contam. Hydrol., 2010, 112(1–4), 91–102 CrossRef CAS PubMed.
- A. Massoudieh, A. Mathew, E. Lambertini, K. E. Nelson and T. R. Ginn, Horizontal gene transfer on surfaces in natural porous media: Conjugation and kinetics, Vadose Zone J., 2007, 6(2), 306–315 CrossRef.
- G. R. Knudsen, M. V. Walter, L. A. Porteous, V. J. Prince, J. L. Armstrong and R. J. Seidler, Predictive model of conjungative plasmid transfer in the rhizosphere and phyllosphere, Appl. Environ. Microbiol., 1988, 54(2), 343–347 CAS.
- R. Freter, R. R. Freter and H. Brickner, Experimental and mathematical models of Escherichia coli plasmid transfer in vitro and in vivo, Infect. Immun., 1983, 39(1), 60–84 CAS.
- L. Andrup, L. Smidt, K. Andersen and L. Boe, Kinetics of conjugative transfer: A study of the plasmid pXO16 from Bacillus thuringiensis subsp. israelensis, Plasmid, 1998, 40(1), 30–43 CrossRef CAS PubMed.
- L. Andrup and K. Andersen, A comparison of the kinetics of plasmid transfer in the conjugation systems encoded by the F plasmid from Escherichia coli and plasmid pCF10 from Enterococcus faecalis, Microbiology, 1999, 145, 2001–2009 CrossRef CAS PubMed.
- C. Lagido, I. J. Wilson, L. A. Glover and J. I. Prosser, A model for bacterial conjugal gene transfer on solid surfaces, FEMS Microbiol. Ecol., 2003, 44(1), 67–78 CrossRef CAS.
- M. Imran, D. Jones and H. Smith, Biofilms and the plasmid maintenance question, Math. Biosci., 2005, 193(2), 183–204 CrossRef CAS PubMed.
- J. M. Ponciano, L. Gelder, E. M. Top and P. Joyce, The population biology of bacterial plasmids: A hidden Markov model approach, Genetics, 2007, 176(2), 957–968 CrossRef PubMed.
- K. R. Philipsen, L. E. Christiansen, H. Hasman and H. Madsen, Modelling conjugation with stochastic differential equations, J. Theor. Biol., 2010, 263(1), 134–142 CrossRef CAS PubMed.
- T. R. Licht, B. B. Christensen, K. A. Krogfelt and S. Molin, Plasmid transfer in the animal intestine and other dynamic bacterial populations: the role of community structure and environment, Microbiology, 1999, 145, 2615–2622 CAS.
- P. E. Turner, Phenotypic plasticity in bacterial plasmids, Genetics, 2004, 167(1), 9–20 CrossRef.
- X. Zhong, J. E. Krol, E. M. Top and S. M. Krone, Accounting for mating pair formation in plasmid population dynamics, J. Theor. Biol., 2010, 262(4), 711–719 CrossRef CAS PubMed.
- B. Bajaj, P. Lei and S. T. Andreadis, High efficiencies of gene transfer with immobilized recombinant retrovirus: Kinetics and optimization, Biotechnol. Prog., 2001, 17(4), 587–596 CrossRef CAS PubMed.
- V. S. Tayi, B. D. Bowen and J. M. Piret, Mathematical Model of the Rate-Limiting Steps for Retrovirus-Mediated Gene Transfer Into Mammalian Cells, Biotechnol. Bioeng., 2010, 105(1), 195–209 CrossRef CAS PubMed.
- M. R. Jacobson, K. E. Brigle, L. T. Bennett, R. A. Setterquist, M. S. Wilson, V. L. Cash, J. Beynon, W. E. Newton and D. R. Dean, Physical and genetic map of the major nif gene cluster from Azotobacter vinelandii, J. Bacteriol., 1989, 171(2), 1017–1027 CAS.
- H. Qian, M. P. Sheetz and E. L. Elson, Single particle tracking. Analysis of diffusion and flow in two-dimensional systems, Biophys. J., 1991, 60(4), 910–921 CrossRef CAS.
- A. Contreras and J. Casadesus, Tn10 Mutagenesis in Azotobacter vinelandii, Mol. Gen. Genet., 1987, 209(2), 276–282 CrossRef CAS.
- G. W. Strandberg and P. W. Wilson, Formation of the nitrogen-fixing enzyme system in Azotobacter vinelandii, Can. J. Microbiol., 1968, 14(1), 25–31 CrossRef CAS.
- W. J. Page, Optimal conditions for induction of competence in nitrogen-fixing Azotobacter vinelandii, Can. J. Microbiol., 1982, 28(4), 389–397 CrossRef CAS.
- J. Kaipio and E. Somersalo, Statistical and Computational Inverse Problems (Applied Mathematical Sciences), Springer, 2005, p. 344 Search PubMed.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, Equations of State Calculations by Fast Computing Machines, J. Chem. Phys., 1953, 21(6), 1087–1092 CrossRef CAS PubMed.
- J. L. Doran and W. J. Page, Heat sensitivity of Azotobacter vinelandii genetic transformation, J. Bacteriol., 1983, 155(1), 159–168 CAS.
- J. C. Setubal, P. dos Santos, B. S. Goldman, H. Ertesvåg, G. Espin, L. M. Rubio, S. Valla, N. F. Almeida, D. Balasubramanian, L. Cromes, L. Curatti, Z. Du, E. Godsy, B. Goodner, K. Hellner-Burris, J. A. Hernandez, K. Houmiel, J. Imperial, C. Kennedy, T. J. Larson, P. Latreille, L. S. Ligon, J. Lu, M. Mærk, N. M. M. Miller, S. Norton, I. P. O'Carroll, I. Paulsen, E. C. Raulfs, R. Roemer, J. Rosser, D. Segura, S. Slater, S. L. Stricklin, D. J. Studholme, J. Sun, C. J. Viana, E. Wallin, B. Wang, C. Wheeler, H. Zhu, D. R. Dean, R. Dixon and D. Wood, Genome Sequence of Azotobacter vinelandii, an Obligate Aerobe Specialized To Support Diverse Anaerobic Metabolic Processes, J. Bacteriol., 2009, 191(14), 4534–4545 CrossRef CAS PubMed.
Footnote |
| † The first and the second authors equally contributed to this work. |
| This journal is © The Royal Society of Chemistry 2015 |