Open Access Article
Open Access ArticleOperational constraints and strategies for systems to effect the sustainable, solar-driven reduction of atmospheric CO2
Yikai
Chen
,
Nathan S.
Lewis
* and
Chengxiang
Xiang
*
Joint Center for Artificial Photosynthesis, Beckman Institute, Kavli Nanoscience Institute and Division of Chemistry and Chemical Engineering, California Institute of Technology, Pasadena, CA 91125, USA. E-mail: nslewis@caltech.edu; cxx@caltech.edu
First published on 8th October 2015
Abstract
The operational constraints for a 6-electron/6-proton CO2 reduction system that operates at the concentration of CO2 in the current atmosphere (pCO2 = 400 ppm) have been evaluated on a variety of scale lengths that span from laboratory scale to global scale. Due to the low concentration of CO2 in the atmosphere, limitations due to mass transport of CO2 from the tropopause have been evaluated through five different regions, each with different characteristic length scales: the troposphere; the atmospheric boundary layer (ABL); the canopy layer; a membrane layer; and an aqueous electrolyte layer. The resulting CO2 conductances, and associated physical transport limitations, will set the ultimate limit on the efficiency and areal requirements of a sustainable solar-driven CO2 reduction system regardless of the activity or selectivity of catalysts for reduction of CO2 at the molecular level. At the electrolyte/electrode interface, the steady-state limiting current density and the concomitant voltage loss associated with the CO2 concentration overpotential in a one-dimensional solar-driven CO2 reduction cell have been assessed quantitatively using a mathematical model that accounts for diffusion, migration and convective transport, as well as for bulk electrochemical reactions in the electrolyte. At pCO2 = 400 ppm, the low diffusion coefficient combined with the low solubility of CO2 in aqueous solutions constrains the steady-state limiting current density to <0.1 mA cm−2 in a typical electrochemical cell with natural convection and employing electrolytes with a range of pH values. Hence, in such a system, the CO2 capture area must be 100- to 1000-fold larger than the solar photon collection area to enable a >10% efficient solar-driven CO2 reduction system (based on the solar collection area). This flux limitation is consistent with estimates of oceanic CO2 uptake fluxes that have been developed in conjunction with carbon-cycle analyses for use in coupled atmosphere/ocean general circulation models. Two strategies to improve the feasibility of obtaining efficient and sustainable CO2 transport to a cathode surface at pCO2 = 400 ppm are described and modeled quantitatively. The first strategy employs yet unknown catalysts, analogous to carbonic anhydrases, that dramatically accelerate the chemically enhanced CO2 transport in the aqueous electrolyte layer by enhancing the acid–base reactions in a bicarbonate buffer system. The rapid interconversion from bicarbonate to CO2 in the presence of such catalysts near the cathode surface would in principle yield significant increases in the steady-state limiting current density and allow for >10% solar-fuel operation at the cell level. The second strategy employs a thin-layer cell architecture to improve the diffusive transport of CO2 by use of an ultrathin polymeric membrane electrolyte. Rapid equilibration of CO2 at the gas/electrolyte interface, and significantly enhanced diffusive fluxes of CO2 in electrolytes, are required to increase the steady-state limiting current density of such a system. This latter approach however only is feasible for gaseous products, because liquid products would coat the electrode and therefore thicken the hydrodynamic boundary layer and accordingly reduce the diffusive CO2 flux to the electrode surface. Regardless of whether the limitations due to mass transport to the electrode surface are overcome on the laboratory scale, at global scales the ultimate CO2 flux limitations will be dictated by mass transport considerations related to transport of atmospheric CO2 to the boundary plane of the solar-driven reactor system. The transport of CO2 across the troposphere/ABL interface, the ABL/canopy layer interface, and the canopy layer/electrolyte interface have therefore been assessed in this work, to provide upper bounds on the ultimate limits for the solar-to-fuel (STF) conversion efficiency for systems that are intended to effect the reduction of atmospheric CO2 in a sustainable fashion at global scale.
Broader contextDevelopment of a sustainable, solar-driven CO2 reduction system is still in the proof-of-concept stage, and faces significant challenges both in fundamental materials discovery and engineering designs of cell and system architectures. Despite the lack of active, selective and stable electrocatalysts for the CO2 reduction reaction (CO2RR), it is important to understand the operational constraints and attainable system efficiencies based on the CO2 mass transport properties from the atmosphere towards the electrode surface for atmospheric cell operation. In this work, we describe two strategies that could significantly enhance the CO2 transport and increase the steady-state limiting current density at pCO2 = 400 ppm. We have additionally evaluated analytically the transport limitations of CO2 from the tropopause down to the cathode surface, through five different regions with five different length scales (from tens of nanometers to tens of kilometers), to understand the transport limitations of the CO2RR for a system that might eventually be deployed at global scale. |
I. Introduction
A solar-fuels generation system designed to effect the sustainable reduction of CO2 includes components for light absorption and charge separation, electrocatalysis of both the CO2-reduction reaction (CO2RR) and the oxygen-evolution reaction (OER), and a mechanism to transport ions between the two reaction chambers while maintaining robust product separation for both efficiency and safety reasons. Efficient electrochemical or photoelectrochemical conversion of CO2 into usable fuels under mild pressure and temperature conditions entails greater physical and chemical constraints than efficient solar-driven water-splitting systems that can generate renewable H2(g).At the laboratory scale, no currently known catalyst can perform the multi-electron, multi-proton, electrochemical or photoelectrochemical CO2RR efficiently and selectively. Polycrystalline metal electrodes are among the most studied class of materials for electrocatalysis of the CO2RR, and most metals have been classified as being selective for CO, HCOO−, or H2.1 Copper and copper-containing metal alloys have shown promise for forming hydrocarbons and C–C coupled products with a wide array of major and minor products, albeit at high overpotentials and with limited stability under operating conditions.2 Recent work on single-crystal,3 nanostructured Au substrates4 or oxide-derived Cu substrates5 has shown the preferred formation of certain products with limited selectivity and activity. The low activity for the hydrogen-evolution reaction (HER) of semiconductor surfaces may provide opportunities to improve the electrocatalytic performance of GaAs,6–8 GaP,9,10 InP,6,11 and of other semiconductors for the CO2RR.
Assuming the discovery of a suitable catalyst, robust and efficient couplings between the CO2RR, the oxygen-evolution reaction (OER), and the necessary ionic transport processes between two potentially different electrolytes or solvent environments will be required for operation of a full, efficient, sustainable CO2RR system. Traditional three-electrode, two-compartment electrochemical cells are typically employed to study the catalytic and energy-conversion performance of electrocatalysts and semiconductor/catalyst assemblies.12 However, the transport of ions between the working electrode compartment (cathode chamber) and the counter electrode compartment (anode chamber) is often far from ideal, and the resistive losses and concentration overpotentials are typically compensated for by the additional external bias applied by the potentiostat.13 The efficient and sustainable coupling of the CO2RR and OER, with low potential losses and minimal product crossover between the two chambers, has been investigated only to a very limited degree. Moreover, in the absence of perfectly selective catalysts for both the CO2RR and OER, a robust and efficient separator needs to be developed to prevent product crossover and thus provide efficient and safe operation of a CO2RR system. While traditional membrane separators such as Nafion™14–19 are highly conductive and effective for preventing gas crossover in water-splitting systems, Nafion membranes yield high crossover losses in direct methanol fuel cells and would not be suitable for solar-driven CO2RR devices that produce alcohols as products. Development of membranes with the desired permeability and ionic conductivity in the presence of a variety of solution species thus constitutes a significant research opportunity for CO2RR systems.
Regardless of the performance of the full electrochemical cell at the laboratory scale, the sustainable reduction of CO2 at global scale will additionally require effective mass transport and uptake of atmospheric CO2 on large areas of the Earth's surface. The large-scale, sustainable reduction of CO2 requires a robust and cost-effective method for the delivery of CO2 to the cathode surface of the device. Whereas liquid water or water vapor is readily able to produce sufficient reactant flux to allow for construction of an efficient solar-driven water-splitting system,20 the low concentration of CO2 in the atmosphere (∼400 ppm), and the low solubility of CO2 in aqueous solutions (∼34 mM at standard temperature and pressure), present significant physical limitations to obtaining sufficient reactant transport to achieve technologically relevant efficiencies for the operation of a solar-driven CO2RR system with atmospheric CO2. Passage of 10 mA cm−2 of current density for 5 h of solar-driven water splitting would consume a column height of 0.018 cm of liquid water, whereas in the absence of transport, the same total amount of charge passed for a 6-electron CO2RR would consume all of the atmospheric 400 ppm CO2 in a column extending 160 m above the earth's surface. To produce a reasonable partial pressure of CO2 by direct air capture, the surface area for the CO2 collection and concentration is likely to be many orders of magnitude larger than the surface area for the solar photon collection and conversion part of the system. Use of separate CO2 concentration and reduction systems would present additional challenges for integration and coupling of the two technologies. While active research and development has been pursued to achieve efficient capture of CO2 from air,21–25 significant advances are still needed to make such technologies cost effective and functional in the presence of humidity and temperature variations in the atmosphere.
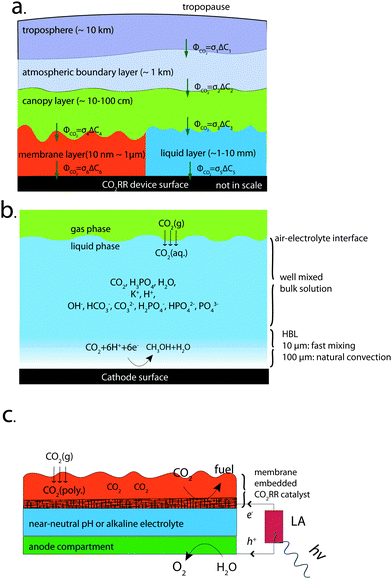
In this work, we have evaluated analytically the transport limitations of CO2 from the tropopause down to a cathode surface, through five different regions with five different length scales (from tens of nanometers to tens of kilometers) (Fig. 1a) that are coupled in series from a mass transport perspective. In each case, an effective mass transfer coefficient, σi, has been obtained. The mass transfer coefficients will add reciprocally to produce the reciprocal of the overall CO2 mass transfer coefficient of the system, σsystem:
 | (1) |
II. Modeling
2.1 CO2 transport
Fig. 1a shows a schematic illustration of the CO2 transport from tropopause towards the surface of a CO2RR device. Five different layers with different characteristic length scales are coupled in series with the same CO2 flux. Three distinctive types of phase boundaries: gas/gas (troposphere/atmospheric boundary layer (ABL), ABL/canopy layer), gas/electrolyte (canopy layer/membrane layer, or canopy layer/liquid layer) and electrolyte/electrode interface (liquid layer/cathode surface, or membrane layer/cathode surface) were included in the transport schematics. The CO2 concentrations within the troposphere, the ABL, and the canopy layer were assumed to separately be constant due to rapid turbulent mixing within each layer, while the net CO2 flux across the troposphere/ABL interface and across the ABL/canopy interface results in CO2 concentration differentials between the different gas-phase layers. The equilibrium CO2 concentrations at the various gas/electrolyte interfaces were assumed to follow Henry's law. At the electrolyte/electrode interfaces, a 4-electron/4-proton OER was assumed and a 6-electron/6-proton CO2RR was assumed, to represent a favorable situation for the ratio of CO2 molecules to electrons in the electrochemical cell.At the phase boundaries, the CO2 flux across the interface, ΦCO2[mol cm−2 s−1] was expressed as ΦCO2 = σΔC, where σ is an effective mass transfer coefficient [cm s−1] and ΔC is the concentration differential of CO2 [moles cm−3] between the two neighboring layers. Two transport pathways, one containing the membrane layer (σ1, σ2, σ4 and σ6) and the other containing the liquid layer (σ1, σ2, σ3 and σ5), were modeled and evaluated in this study. The CO2 flux across all of the interfaces, ΦCO2, can be expressed as ΦCO2 = σsystem(Ctroposphere − Ccathode), where σsystem is the overall effective mass transfer coefficient of the system, which can be expressed as  for the system that contains the liquid layer and as
for the system that contains the liquid layer and as  for the system that contains the membrane layer. As a result of the reciprocal summation relation, the overall effective mass transfer coefficient of the system, σsystem, is smaller than any individual mass transfer coefficient, and is dominated by the process with the smallest mass transfer coefficient in the system.
for the system that contains the membrane layer. As a result of the reciprocal summation relation, the overall effective mass transfer coefficient of the system, σsystem, is smaller than any individual mass transfer coefficient, and is dominated by the process with the smallest mass transfer coefficient in the system.
2.2 One-dimensional traditional cell design
Fig. 1b illustrates the one-dimensional (1-D) model used in this work to evaluate the CO2 transport near a cathode performing a 6-electron/6-proton CO2RR. The electrode was assumed to have a sufficiently high catalytic activity that under operating conditions the CO2 concentration was driven to zero at the electrode surface. A well-mixed bulk solution was assumed, and two hydrodynamic boundary layers (HBL), that accounted for forced convective mixing (lHBL = 10 μm) or natural convection (lHBL = 100 μm), respectively, were introduced near the cathode surface. Rapid equilibration of CO2 was assumed at the air–electrolyte interface, and the acid–base equilibria for the carbonate buffer and for the phosphate buffer, as well as the equilibria for the corresponding chemical reactions, were included in the model for the liquid regions. The same configuration, representing a well-mixed bulk solution layer and two HBLs, was assumed for the OER at the anode.Table 1 summarizes the forward and reverse rate constants for the bicarbonate buffer solution, that were used in the simulation.26,27 Note that the total CO2 concentration in Table 1 has been defined as the sum of the dissolved CO2 in aqueous solution, CO2(aq), and the carbonic acid concentration, H2CO3. The forward and reverse reaction rate constants, k1+ and k1−, respectively, fully describe the acid–base equilibrium between CO2(aq), H2CO3 and HCO3− in the buffer system.26,27 The transport loss in the system was assumed to be independent of the detailed electrocatalytic parameters for the cathode and anode, and was assumed to be a function only of the operating current density at the electrode surfaces. In some situations, an interconversion enhancement factor was introduced to increase both the forward and reverse rates for reactions (1–4) in Table 1, to represent the behavior of a hypothetical catalyst for these reactions with the catalyst having a reactivity analogous to that exhibited by the enzyme carbonic anhydrase.
2.3 Catalyst-embedded, thin-layer membrane assembly for rapid transport of CO2
Fig. 1c illustrates a conceptually distinct system that consists of a CO2-reduction reactor based on a catalyst-embedded, thin-layer membrane device architecture. The cell consists of a solar-driven CO2RR reactor that incorporates a light absorber (LA), a catalyst-embedded thin-layer membrane assembly, an anode compartment, and an electrolyte that is either buffered at near-neutral pH or is maintained under alkaline conditions. The LA (red) captures the solar photons and converts them into energetic electrons and holes for the fuel-forming reactions. The device has been designed to achieve large mass transport fluxes of CO2 to the electrode surface, based purely on diffusional transport of CO2 in the ultrathin electrolyte, because the catalyst-embedded, thin-layer membrane assembly (orange) reduces the length of the pathways for CO2 transport within the polymer electrolyte.In this device, the equilibrium CO2 concentration at the gas/polymer electrolyte interface was assumed to follow Henry's law. Three different permeabilities for CO2 transport in the polymer electrolyte were assumed. The buffered near-neutral pH or alkaline electrolytes (blue) were chosen so that the small proton concentration at the cathode surface would suppress the rate of the hydrogen-evolution reaction (HER) relative to the rate of the CO2RR. The anode compartment (green) performed the OER and provided the necessary proton source for the cathode. The anode compartment also contained an anion-exchange membrane for alkaline operation or a bi-polar membrane for CO2RR and OER at two different pHs, to facilitate the ionic transport and reduce the product crossover in the system.
2.4 Governing equations
Ionic species and neutral species in the electrolyte solution were modeled using the Nernst–Planck equation,12 in which the diffusion, migration and bulk reactions of water and buffer dissociation were explicitly included. Forced convection was approximated by the use of the hydrodynamic boundary layers.The total voltage requirement (Δϕcell) for the electrochemical cell was calculated as the sum of the equilibrium potential (E0), kinetic overpotentials (η), solution potential drop losses (Δϕsolution), and the Nernstian potential losses associated with pH gradients, (ΔϕpH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gradient), as well as the potential drops associated with CO2 concentration gradients, (ΔϕCO2
gradient), as well as the potential drops associated with CO2 concentration gradients, (ΔϕCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gradient) at the surface of the electrodes:
gradient) at the surface of the electrodes:
Δϕcell = E0 + ηOER − ηHER + Δϕsolution + ΔϕpH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gradient + ΔϕCO2 gradient + ΔϕCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gradient gradient | (2) |
The solution losses, (Δϕsolution), were calculated as the sum of the ohmic resistive loss (first term) and the electrodialysis loss (second term). These losses can be expressed as:
 | (3) |
The Nernstian potential losses associated with the pH gradients (ΔϕpH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gradient) and CO2 concentration gradients (ΔϕCO2
gradient) and CO2 concentration gradients (ΔϕCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gradient) at the surface of the electrodes can be expressed as:
gradient) at the surface of the electrodes can be expressed as:
 | (4) |
III. Results
3.1 Limiting performance of cells operated using a 400 ppm CO2 feedstock
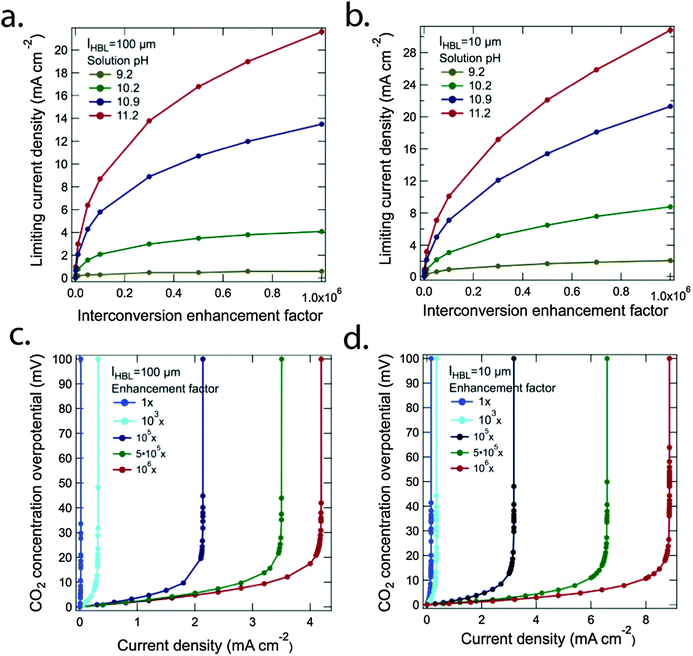
At 400 ppm of CO2 in the reactant atmosphere, CO2 transport at the electrolyte/electrode interface, specifically, ΦCO2 = σ5ΔC5 in Fig. 1a, produced significant concentration polarization and limited the device efficiency. Fig. 2a shows the steady-state limiting current density as a function of the electrolyte pH for a 6-electron/6-proton CO2 reduction process. Two HBL thicknesses, 100 μm (red) and 10 μm (blue) were used to account for natural convection and forced convection, respectively. In addition to the bicarbonate buffer system, in which the dissolved CO2 concentration was set to the solubility limit, the electrolyte solution was buffered at different pHs with a 1.0 M phosphate buffer. The steady-state limiting current density was <0.2 mA cm−2 for all cases, which is ∼2 orders of magnitude smaller than the current density required to produce a CO2RR reactor with a 10% solar-to-fuels efficiency. In the higher pH solutions (pH > 10.2), a slight increase in the obtainable steady-state limiting current densities was observed. The higher concentration of bicarbonate in higher pH electrolytes at pCO2 = 400 ppm resulted in an enhanced conversion from bicarbonate species to CO2.Fig. 2b shows the change of the CO2 concentration at the cathode surface relative to the bulk equilibrium value, Δ[CO2], as a function of the operating current density for a 6-electron/6-proton CO2 reduction process at two different partial pressures of CO2. A linear relationship between Δ[CO2] and the operating current density was observed for two different partial pressures of CO2. At a given HBL thickness, a constant slope was observed at different partial pressures of CO2. When Δ[CO2] approached the solubility limit for CO2, a steady-state limiting current density was reached. For a cell fed by a 25-fold higher CO2 partial pressure than found in air, i.e., pCO2 = 0.01 atm, the limiting current densities were 0.3 mA cm−2 and 3 mA cm−2 for lHBL = 100 μm and lHBL = 10 μm, respectively. Although numerous solution species and chemical reactions in the liquid layer are associated with the inter-conversion of CO2 species, a linear relation, ΦCO2 = σ5ΔC5, was sufficient to describe the CO2 transport process at the gas/electrolyte interface. Effective mass transfer coefficients, σ5 = 0.002 cm s−1 and 0.018 cm s−1, were obtained for lHBL = 100 μm and lHBL = 10 μm, respectively. Note that the value of the effective mass transfer coefficient reflected both the diffusive transport of the neutral CO2 species and the chemically enhanced transport due to the interconversion of CO2 and the bicarbonate ion.
3.2 Effect of enhancing the rates of interconversion for the bicarbonate buffer system
The low mass transfer coefficient, σ5, at the electrolyte/electrode interface significantly limited the attainable operating current density in the system. One approach to in principle accelerate the rate of chemically enhanced transport in the system involves the development of catalysts that can rapidly interconvert dissolved CO2, carbonic acid, and bicarbonate.Fig. 3a and b show the steady-state limiting current density as a function of a hypothetical interconversion-enhancement factor for the bicarbonate buffer system for lHBL = 100 μm and lHBL = 10 μm, respectively. The bulk CO2 concentration was equilibrated with pCO2 = 400 ppm and was set to 14 μM. The situation for four different pH values, 9.2, 10.2, 10.9 and 11.2, which correspond to bicarbonate concentrations of 0.01 M, 0.1 M, 0.5 M and 1.0 M, respectively, were evaluated. A significant increase in the steady-state limiting current density required an increase of 6 orders of magnitude in the rates for the interconversion of carbon dioxide and bicarbonate (or vice versa) relative to the natural interconversion rate. In particular, in higher pH solutions, where the bicarbonate concentration was higher, the reverse reactions, H+ + HCO3− → CO2 + H2O and HCO3− → CO2 + OH−, were significantly increased at higher interconversion-enhancement factors. For instance, for lHBL = 10 μm, the steady-state limiting current density exceeded 20 mA cm−2 for pH = 10.9 and 11.2 in the presence of this hypothetical million-fold increase in equilibration rate relative to the natural situation.
Fig. 3c and d show the Nernstian potential losses associated with the development of CO2 gradients near the surface of a cathode in contact with an electrolyte with pH = 10.2, as a function of the operational current density, for five different interconversion-enhancement factors with lHBL = 100 μm and lHBL = 10 μm, respectively. The CO2 concentration overpotential increased exponentially when the operating current density approached the steady-state limiting current density according to the Nernst equation. Minimization of the potential losses (<100 mV) due to concentration overpotentials requires that the operating current densities remain below the values at which the concentration-overpotential curves rise nearly vertically in Fig. 3c and d. The solution loss and the Nernstian potential losses associated with pH gradients at the electrode surfaces were small (<50 mV) in the assumed cell design, and were additionally minimized by the use of a phosphate buffer and a convected electrolyte. Similar results were also reported recently in an analytical assessment of solar driven water-splitting systems at near-neutral pH.28
Fig. 4 shows the spatially resolved concentration profile of the ionic and neutral species between the cathode surface and the hydrodynamic boundary layer (HBL) at an operational current density of 1 mA cm−2. At the bulk-solution edge of the HBL, the concentration of the dissolved CO2 was set to 14 μM. In a cell fed by air with pCO2 = 400 ppm, and containing a pH = 10.2 solution and 1.0 M phosphate buffer, minimal pH gradients were observed (Fig. 4a). Fig. 4b shows the steady-state CO2 generation/consumption rate within the HBL. As the enhancement factor increased, a rapid increase of the CO2 generation rate near the cathode surface, and a rapid increase of uptake of CO2 at the edge of the HBL, were observed. In the middle region, an acid–base equilibrium with near-zero CO2 generation/consumption was observed. The increased CO2 generation rate near the cathode surface increased the steady-state limiting current density of the system at higher enhancement factors. Fig. 4c and d also depict the corresponding CO2 concentration and the bicarbonate concentration profile, respectively.
3.3 Performance of the catalyst-embedded, thin-layer membrane assembly for rapid transport of CO2
Instead of dramatically accelerating the chemically enhanced transport in aqueous solutions, an alternative strategy to significantly improve the CO2 transport would involve the use of a thin-layer electrochemical cell design (Fig. 1c). The CO2 transport at the polymer-electrolyte/electrode interface, specifically, ΦCO2 = σ6ΔC6 in Fig. 1c, and the resulting limiting current density, can in principle be significantly enhanced by use of a thin-layer membrane electrolyte, and consequently relying on purely diffusive fluxes to achieve the desired current density at sufficiently small membrane thicknesses.Fig. 5 shows the limiting current density as a function of the membrane thickness for three different permeabilities of CO2 in the polymer electrolytes of the catalyst-embedded thin-layer membrane-assembly design (Fig. 1c). The solubility and the diffusion coefficient of CO2 in the polymer electrolytes, i.e., Nafion, are highly dependent on the polymer morphology, the polymer segmental dynamics, the hydration conditions, and the operating temperature.29–32 The permeability of CO2 and other gases for Nafion membranes is the product of the diffusion coefficient and the solubility. The permeability is the key figure of merit for CO2 transport in membrane-based systems, and has been measured experimentally by others under various conditions. The black curve used a typical value, 3 × 10−11 [cm3(STP) cm cm−2 s−1 Pa−1], for the permeability of CO2 in Nafion near room temperature.31,32 The red and green curves represent results for permeability values of 3 × 10−10 and 3 × 10−12 [cm3(STP) cm cm−2 s−1 Pa−1], respectively, and represent the upper and lower bounds for the calculation. The attainable current density in the membrane-based system was independent of the pH conditions and was determined by the solubility and the diffusion coefficient of CO2 in the membrane, as well as by the thickness of the membrane. The effective mass transfer coefficient at the polymer-electrolyte/electrode interface, σ6, at a membrane thickness of 100 nm was 0.038 cm s−1 and 3.8 cm s−1 for the upper and lower limit of the membrane permeability values, respectively. The thin layer of the catalyst-embedded membrane minimized the CO2 transport losses in the aqueous solution or polymeric media, and enabled the direct electrochemical reduction of CO2 from air at current densities in excess of 10 mA cm−2 without mass transport limitations in the liquid layer.
 | ||
| Fig. 5 The calculated limiting current density as a function of the membrane thickness for three different permeabilities of CO2 in the membrane. | ||
IV. Discussion
4.1 Assumptions and limitations of the treatment of CO2RR systems
The limiting electrochemical current densities and concentration polarization losses obtained in this study pertain solely to the cathode and the electrolyte region near the cathode, in a fashion analogous to evaluating the flux-limited current densities at the working electrode in a traditional 3-electrode electrochemical experiment. In an actual two-electrode photoelectrosynthetic system comprised of catalysts that effect the CO2RR and OER, the current density at the cathode is likely to be nonuniform,33 resulting in even higher local CO2 flux demands by a factor of 10 or more than those assumed herein for an isopotential electrode surface. The cathodic reduction products and CO2RR intermediates were assumed to have negligible reactivity with O2(g) in the atmosphere, and despite the much higher concentration of O2 relative to CO2 in ambient air, O2(g) was assumed to be electroinactive at the cathode at potentials required to effect the CO2RR, despite the >1 V driving force for O2(g) reduction to H2O and the ease of reducing O2(g) to H2O2 at these potentials. No CO2 catalysts or electrode systems known to date meet any of these criteria. The CO2RR products and intermediates at the cathode were assumed to be separated from the anode, which was assumed to have 100% faradaic efficiency for O2(g) evolution. The ohmic resistive loss, pH gradients, and electrodialysis due to the incorporation of an cation exchange membrane or an anion exchange membrane in the near-neutral pH system,28 such as the bicarbonate buffer system, which can individually or collectively produce significant and in some cases overwhelming voltage losses in the operating cell, have not been considered in the present assessment.Standard temperature conditions 273.15 K were assumed for the operational temperature of the CO2RR systems in the simulations performed herein. Solar-driven CO2RR systems may operate at elevated temperatures. The solubility of CO2 in water is strongly temperature dependent, and the Henry's law constant for CO2 decreases from 34 mM atm−1 to 13 mM atm−1 when the operational temperature is increased from 273 K to 333 K.34 Hence, at elevated temperatures, the decreased solubility of CO2 in water would lead to a further reduction the mass-transport-limited current density in the cell. One approach to increase the solubility of CO2 in the electrolyte is to use ionic liquids. For instance, the solubility of CO2 in imidazolium-based ionic liquids can be ∼40 fold larger than the CO2 solubility in aqueous bicarbonate solutions at standard temperature.35 However, the ∼10–20 fold lower diffusion coefficient of CO236,37 in ionic liquids as compared to in aqueous solutions, combined with the lack of chemically enhanced CO2 transport in the ionic liquids, will produce mass-transport limited current densities in such media that are on the same order of magnitude as those in aqueous solutions (Fig. 2).
4.2 Conductance at the atmosphere/aqueous electrolyte interface
Regardless of the ideal activity, selectivity and coupling between the OER and CO2RR in the full electrochemical cells, the CO2 flux at the atmosphere/aqueous electrolyte interface imposes constraints on the mass transfer and thus on the efficiency for the system. For aqueous electrolytes that have thicknesses larger than the width of the hydrodynamic boundary layer, the low solubility of CO2 in water, combined with the relatively small diffusion coefficient of CO2 in liquid water compared to in the gas phase, produces very low CO2 fluxes and conductances. Hence, over large areas, either with natural convection or with forced convection sufficient to thin the hydrodynamic boundary layer in the aqueous phase to 10 μm, a value comparable to that obtained according to the Levich equation with a rotating disk electrode at a rotation velocity of 106 rpm,12 the steady-state limiting CO2 flux even with a 6-electron reduction of each CO2 molecule is 100–1000 fold lower than the 10 mA cm−2 current density produced by the solar photon flux in an efficient single or tandem photoelectrode system.38,39 Hence regardless of the activity of an electrocatalyst for CO2 reduction, the solar-to-fuels conversion efficiency of such a system will be limited to <0.1% based on the active area of the solar collection component. Additionally, the concentration overpotential will require higher voltages for a complete CO2 reduction system than are expected based on the potential differences between the CO2RR half-reaction and the OER half-reaction alone, including their associated kinetic overpotentials at each electrode surface.This conclusion is in accord with the CO2 uptake fluxes that have been established previously for the air/ocean boundary for use in assessing the global carbon cycle in coupled air/ocean general circulation models. Specifically, extensive studies of CO2 exchange at the air–sea interface have shown that the effective mass transfer coefficient of CO2 across the air–liquid interface, specifically, σ3, in Fig. 1c, is on the order of 10−3–10−2 cm s−1, corresponding to a current density of ∼10–100 μA cm−2 for a 6-electron/6-proton CO2RR, over a large range of temperatures, wind velocities, salinities and pH conditions.40–42 In situations where the effective mass transfer coefficient, σ3 or σ4, presents a transport limitation, the air/electrolyte interface equilibrium according to Henry's law may not be achieved. In this case, the device efficiency would be yet lower and would ultimately be limited by the rate of CO2 transport across the air/electrolyte interface. Hence, without strategies to circumvent the inherently low CO2 conductance at the air/water interface, very low solar-to-fuel conversion efficiencies will be obtained and/or the CO2 capture and collection area will have to greatly exceed, by a factor of 100–1000, the active solar photon collection area of a sustainable solar-driven, aqueous-based, CO2RR system.
4.3 Enhancement of interconversion rates for the bicarbonate buffer system
One strategy to circumvent the conductance limit imposed by liquid-phase transport, specifically by, ΦCO2 = σ5ΔC5, involves chemically enhancing the rate of CO2 uptake by equilibrating the dissolved CO2 with the bicarbonate and carbonic acid reservoirs in aqueous solutions buffered to pH values >7. Carbonic anhydrases are among the most well-known metalloenzymes that catalyze the rapid interconversion of carbon dioxide and water to bicarbonate and protons.43 In the absence of a catalyst, the reversible reaction occurs relatively slowly, as reflected in the rate constants tabulated in Table 1. At a CO2 concentration of 14 μM, the catalyzed rate for the buffer interconversion reaction, as described using Michaelis–Menten kinetics for carbonic anhydrases, is ∼200 s−1 (assuming a maximum rate of conversion of 4 × 105 s−1 and a Michaelis constant of 26 mM).44,45 As a result, a carbonic anhydrase concentration of ∼2.5 mM would be required to achieve an interconversion enhancement factor of 106 relative to the uncatalyzed case. The concentration of carbonic anhydrase in sea water is estimated to be <∼100 nM,46 so a 106 enhancement of the interconversion rate using such enzymes would require an enzyme concentration ∼25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-fold higher than the peak value in sea water systems.46
000-fold higher than the peak value in sea water systems.46
A hypothetical catalyst that had analogous catalytic activity to carbonic anhydrase, and that extremely rapidly replenished dissolved CO2 near the cathode surface due to enhanced rates for the reverse reactions, reaction H+ + HCO3− → CO2 + H2O and reaction HCO3− → CO2 + OH−, could in principle produce significant increases in the limiting current density for a CO2RR reactor, even when lHBL = 100 μm, i.e., for the natural convection case. As shown in Fig. 3, an interconversion-enhancement factor of at least 105 would however be needed before a CO2RR cell with 10% solar-to-fuels conversion efficiency could be constructed, other transport limitations notwithstanding (vide infra). The heretofore unknown interconversion catalyst must of course itself be robust, electrochemically inert at both of the electrodes in the system, and operate under conditions with which the other components of the CO2RR device are compatible.
4.4 Implemenation of thin-layer membrane assembly
The required CO2 flux to the cathode could in principle alternatively be obtained by use of a thin-layer membrane-based system (Fig. 5). The efficient transport in a thin-layer (tens of nanometers thick) membrane (Fig. 5) exploits the very small distance between the gas phase CO2 and the catalyst at the cathode surface. Due to the required short length of the pathways, the implementation of this strategy in the CO2RR cell constrains the reduction products to be highly volatile/gaseous species such as methane or ethylene. Liquid fuel products, such as methanol or ethanol, which will form a liquid layer of the product at the electrocatalyst surface, will impede the CO2 reactant transport towards the catalyst, and hence will result in unacceptably low CO2 fluxes to the electrode surface, as in the case when the electrode is coated with a layer of liquid water (vide supra).4.5 Transport between the canopy layer and the electrolyte
The gas-phase transport of CO2 near the electrode surface, specifically, at the canopy layer/membrane layer interface, ΦCO2 = σ4ΔC4, or the canopy layer/liquid layer interface, ΦCO2 = σ3ΔC3, does not impose significant limitations on the ability to deliver CO2 to the CO2RR reactor. According to the kinetic theory of gases, the rate of surface bombardment of CO2 molecules at pCO2 = 400 ppm is ∼1020 molecules cm2 s−1, which could produce a mass-transport-limited current density many orders of magnitude higher than the photon flux in unconcentrated solar illumination. Another more practical estimation of the CO2 flux at the air/membrane or air/liquid interfaces can be obtained by using Fick's first law: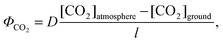 | (5) |
The rapid transport between the canopy layer and the electrolyte is a result of the relatively high gas-phase diffusion coefficient of CO2. In the natural photosynthetic system, the terrestrial plant-based CO2 fixation rate is significantly higher than the CO2 flux across the air/ocean interface. Terrestrial plant-based photosynthesis thus takes advantage of the rapid CO2 transport in the gas-phase as well as the 3-dimensional structure of the plants and trees on an ∼1 m height scale, which leads to a significant increase in the contact area per unit of geometric area on the earth's surface and results in a more optimal “contactor” design than can be achieved at a planar air/water boundary over large horizontal length scales.
4.6 Gas-phase transport of CO2 between the troposphere and the ABL and between the ABL and the canopy layer for regional-scale deployment of CO2-reduction reactors
The fluxes of CO2 between the troposphere and the atmospheric boundary layer (ABL), and between the ABL and the canopy layer, specifically, ΦCO2 = σ1ΔC1 and ΦCO2 = σ2ΔC2, in Fig. 1c, also impose a constraint on the CO2 conductance of CO2RR systems deployed at regional-scale, for which the length-scale of the CO2RR system is larger than the scale height of the atmosphere, broadly defined in the range between 104 and 106 km2 (i.e. when vertical transport in the atmospheric column is more important than advection in determining the CO2 concentration in the column), regardless of strategies used to enhance the conductance at the air/water or air/polymer interfaces. An estimate of the CO2 mass transport limitation on scale lengths comparable to or larger than the scale height of the atmosphere can also be obtained by eqn (5), where now D is the turbulent diffusion coefficient of the atmosphere and l is the vertical gradient scale height. The minimal value for l is set by the scale height of the atmosphere, which is ∼100 km. In conjunction with an approximate value for the atmospheric turbulent diffusivity, D, of 106 cm2 s−1, the maximum CO2 flux is thus ∼1015 molecules cm−2 s−1, which for a 6-electron/6-proton CO2RR corresponds to a CO2-transport-limited current density of ∼1 mA cm−2.Another estimation of the mass-transport-limited CO2 flux can be obtained by reference to the net ecosystem-exchange (NEE) rate for CO2, which has been directly measured and monitored by various techniques, including eddy covariance methods, over long periods (months or years) in different regions worldwide.49–52 Satellite retrieval methods that allow extraction of the vertical profile of CO2 in an atmospheric column in turn allow formulation of a flux relationship between the CO2 concentration differential “i.e. draw-down” in the ABL relative to the CO2 concentration in the troposphere, as a function of the local NEE rate. A quasi-linear relationship at regional spatial scales between the net CO2 flux and the CO2 draw-down between the troposphere and the ABL has been observed, as expected.49,53 On average, an ∼2 μmol m−2 s−1 net CO2 flux between the troposphere and the ABL results in ∼10 ppm reduction in the CO2 concentration in the ABL,49 which corresponds to an effective mass transfer coefficient of 0.44 cm s−1. If a sustained 10% solar-to-fuel (STF) conversion efficiency were achieved for a 6-electron/6-proton CO2 reduction process at the cell level, and such a system were deployed on a regional scale, extrapolation of this linear relationship indicates that a daily average CO2 draw-down of ∼130 ppm would be produced between the troposphere and the entire (well-mixed) ABL, 2–2.5 km in height (assuming a 20% capacity factor for the CO2RR reactor), by the sustained mass flux, and consumption, of CO2 at the electrode surface. During the peak operation of a solar-driven CO2RR system deployed on a regional scale, a significantly larger drawdown of CO2 and a large temporal variation of the CO2 concentration near the surface of CO2RR reactor would be expected. The decreased CO2 levels at the electrode surface would in turn require even more active catalysts. Moreover, the height of the ABL and the concentration of CO2 in the ABL are also highly dependent on storms, and weather conditions in the atmosphere, etc. The flux into the ABL can even under some conditions invert in sign. Hence, the significant alteration of the CO2 concentration in the ABL, and concomitant spatial and temporal variations in the attainable CO2 uptake flux at the surface of the Earth, present significant practical and engineering impediments to the deployment of regional-scale systems that would involve rapid CO2 consumption rates at the electrode surface, assuming that such a system can be achieved through unprecedented catalyst development, along with aggressive strategies to increase the CO2 uptake flux into the reactor (i.e., new CO2 reservoir interconversion catalysts and/or for gaseous products implementing an ultra-thin polymeric cathode electrolyte) to significantly enhance the diffusive CO2 flux relative to the value observed for natural air/ocean boundaries. It is reasonable to surmise that the peak net primary productivity of plant-based photosynthesis is constrained, in part due to down-regulation of photosynthesis at high light intensities, to minimize the sensitivity of the system to atmospheric CO2 concentration and transport fluctuations, because otherwise these fluctuations that occur as a function of changes in the physical state of the atmosphere due to weather, storms, and other processes would significantly affect the CO2 concentration in the ABL and thus the performance of the CO2RR system at the Earth's surface.
The CO2 flux between the ABL and the canopy layer has an effective mass transfer coefficient, σ2 = 0.44 cm s−1 that is comparable to the mass transfer coefficient, σ1, at the troposphere/ABL interface. Hence, at the CO2 flux required to sustain a 10% efficient CO2RR cell at the electrode surface, a daily average CO2 concentration differential of 260 ppm would be produced between the canopy layer and the troposphere. The lower CO2 concentration in the canopy layer, to which the dissolved CO2 concentration in electrolytes is equilibrated, would further increase the CO2 concentration overpotential by ∼100–200 mV in the system, but at peak operation, the transient and temporal depletion of CO2 at the surface of the CO2RR reactor system would produce a much larger overpotential.
V. Conclusions
The limited CO2 transport in the presence of bulk electrolyte layers (>10 μm) at a cathode surface serves as a physical limitation to the construction of a sustainable, scalable solar-driven CO2RR cell with a technologically relevant efficiency that operates at pCO2 = 400 ppm. Rapid replenishment of CO2(aq) near a cathode surface using catalysts with activities and reactivities analogous to the carbonic anhydrase enzymes, that enhance the interconversion between the bicarbonate and CO2, could hypothetically significantly increase the achievable steady-state limiting current density and concomitantly reduce the CO2 concentration overpotential for such a system. For instance, an interconversion enhancement factor of 106 could in principle increase the steady-state limiting current density to >20 mA cm−2 in a pH = 11.2 aqueous solution. Alternatively, a catalyst-embedded, thin-layer architecture that minimizes the CO2 transport pathways in electrolyte layers could in principle also produce large and sustainable CO2 reduction current densities at pCO2 = 400 ppm, for gas-phase products and reactants. The CO2 flux at the troposphere/ABL interface and at the ABL/canopy layer interface imposes significant physical constraints on the realization of an efficient, sustainable, and globally scalable CO2RR solar-fuels system. Large-scale implementation of CO2RR cells with a 10% solar-to-fuel (STF) conversion efficiency for a 6-electron/6-proton CO2 reduction process would entail a 130 ppm steady-state troposphere/ABL drawdown of the CO2 concentration over the entire 2.5 km high ABL, with much higher depletion of the CO2 concentration during periods of high solar insolation onto the reactors. This level of CO2 depletion would have profound environmental impacts in the region, and would produce a system performance that was subject to large variability in response to the weather conditions as well as to the presence and intensity of storms, etc. and other conditions that affect the CO2 transport at the troposphere/ABL boundary as well as in the ABL.Acknowledgements
This material is based upon work performed by the Joint Center for Artificial Photosynthesis, a DOE Energy Innovation Hub, supported through the Office of Science of the U.S. Department of Energy under Award Number DE-SC0004993 as well as by the Gordon and Betty Moore Foundation, grant 1225. We also thank Dr Ken Caldeira and Dr Joe Berry of the Carnegie Institution for Science, Department of Global Ecology, for numerous stimulating and valuable discussions regarding the ocean/air CO2 flux and the ABL/troposphere CO2 transport properties.References
- Y. Hori, Electrochemical CO2 Reduction on Metal Electrodes. In Modern Aspects of Electrochemistry, Springers, 2008 Search PubMed.
- K. P. Kuhl, E. R. Cave, D. N. Abram and T. F. Jaramillo, Energy Environ. Sci., 2012, 5, 7050–7059 CAS.
- K. J. P. Schouten, Z. S. Qin, E. P. Gallent and M. T. M. Koper, J. Am. Chem. Soc., 2012, 134, 9864–9867 CrossRef CAS PubMed.
- Y. H. Chen, C. W. Li and M. W. Kanan, J. Am. Chem. Soc., 2012, 134, 19969–19972 CrossRef CAS PubMed.
- C. W. Li and M. W. Kanan, J. Am. Chem. Soc., 2012, 134, 7231–7234 CrossRef CAS PubMed.
- K. Hirota, D. A. Tryk, T. Yamamoto, K. Hashimoto, M. Okawa and A. Fujishima, J. Phys. Chem. B, 1998, 102, 9834–9843 CrossRef CAS.
- K. W. Frese and D. Canfield, J. Electrochem. Soc., 1984, 131, 2518–2522 CrossRef CAS PubMed.
- B. Aurianblajeni, M. Halmann and J. Manassen, Sol. Energy Mater., 1983, 8, 425–440 CrossRef CAS.
- S. Ikeda, A. Yamamoto, H. Noda, M. Maeda and K. Ito, Bull. Chem. Soc. Jpn., 1993, 66, 2473–2477 CrossRef CAS.
- H. Noda, A. Yamamoto, S. Ikeda, M. Maeda and K. Ito, Chem. Lett., 1990, 1757–1760, DOI:10.1246/Cl.1990.1757.
- H. Yoneyama, K. Sugimura and S. Kuwabata, J. Electroanal. Chem., 1988, 249, 143–153 CrossRef.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods, Fundamentals and Applications, Wiley, 2nd edn, 2000 Search PubMed.
- B. A. Rosen, A. Salehi-Khojin, M. R. Thorson, W. Zhu, D. T. Whipple, P. J. A. Kenis and R. I. Masel, Science, 2011, 334, 643–644 CrossRef CAS PubMed.
- M. S. Dresselhaus, G. W. Crabtree and M. V. Buchanan, MRS Bull., 2005, 30, 518–524 CrossRef CAS.
- S. J. Hamrock and M. A. Yandrasits, Polym. Rev., 2006, 46, 219–244 CAS.
- M. A. Hickner and B. S. Pivovar, Fuel Cells, 2005, 5, 213–229 CrossRef CAS PubMed.
- J. M. Spurgeon, M. G. Walter, J. F. Zhou, P. A. Kohl and N. S. Lewis, Energy Environ. Sci., 2011, 4, 1772–1780 CAS.
- A. Z. Weber, M. M. Mench, J. P. Meyers, P. N. Ross, J. T. Gostick and Q. H. Liu, J. Appl. Electrochem., 2011, 41, 1137–1164 CrossRef CAS.
- http://www.sc.doe.gov/bes/hydrogen.pdf .
- C. Xiang, Y. Chen and N. S. Lewis, Energy Environ. Sci., 2013, 6, 3713–3721 CAS.
- S. Choi, J. H. Drese, P. M. Eisenberger and C. W. Jones, Environ. Sci. Technol., 2011, 45, 2420–2427 CrossRef CAS PubMed.
- D. W. Keith, Science, 2009, 325, 1654–1655 CrossRef CAS PubMed.
- S. Stucki, A. Schuler and M. Constantinescu, Int. J. Hydrogen Energy, 1995, 20, 653–663 CrossRef CAS.
- R. Baciocchi, G. Storti and M. Mazzotti, Chem. Eng. Process., 2006, 45, 1047–1058 CrossRef CAS PubMed.
- F. Zeman, Environ. Sci. Technol., 2007, 41, 7558–7563 CrossRef CAS.
- K. S. Johnson, Limnol. Oceanogr., 1982, 27, 849–855 CrossRef CAS.
- K. G. Schulz, U. Riebesell, B. Rost, S. Thoms and R. E. Zeebe, Mar. Chem., 2006, 100, 53–65 CrossRef CAS PubMed.
- M. R. Singh, K. Papadantonakis, C. X. Xiang and N. S. Lewis, Energy Environ. Sci., 2015, 8, 2760–2767 CAS.
- K. Broka and P. Ekdunge, J. Appl. Electrochem., 1997, 27, 117–123 CrossRef CAS.
- J. S. Chiou and D. R. Paul, Ind. Eng. Chem. Res., 1988, 27, 2161–2164 CrossRef CAS.
- V. A. Sethuraman, S. Khan, J. S. Jur, A. T. Haug and J. W. Weidner, Electrochim. Acta, 2009, 54, 6850–6860 CrossRef CAS PubMed.
- S. Ma and E. Skou, Solid State Ionics, 2007, 178, 615–619 CrossRef CAS PubMed.
- S. Haussener, C. X. Xiang, J. M. Spurgeon, S. Ardo, N. S. Lewis and A. Z. Weber, Energy Environ. Sci., 2012, 5, 9922–9935 CAS.
- CRC Handbook of Chemistry and Physics, 96th edn, 2015 Search PubMed.
- C. Cadena, J. L. Anthony, J. K. Shah, T. I. Morrow, J. F. Brennecke and E. J. Maginn, J. Am. Chem. Soc., 2004, 126, 5300–5308 CrossRef CAS PubMed.
- Y. Hou and R. E. Baltus, Ind. Eng. Chem. Res., 2007, 46, 8166–8175 CrossRef CAS.
- S. S. Moganty and R. E. Baltus, Ind. Eng. Chem. Res., 2010, 49, 9370–9376 CrossRef CAS.
- L. C. Seitz, Z. B. Chen, A. J. Forman, B. A. Pinaud, J. D. Benck and T. F. Jaramillo, ChemSusChem, 2014, 7, 1372–1385 CrossRef CAS PubMed.
- S. Hu, C. X. Xiang, S. Haussener, A. D. Berger and N. S. Lewis, Energy Environ. Sci., 2013, 6, 2984–2993 CAS.
- B. J. H. Matthews, PhD thesis, University of East Anglia, Norwich, 1999 Search PubMed.
- M. Frankignoulle, Limnol. Oceanogr., 1988, 33, 313–322 CrossRef CAS.
- R. H. Wanninkhof and L. F. Bliven, J. Geophys. Res.: Oceans, 1991, 96, 2785–2796 CrossRef.
- M. R. Badger and G. D. Price, Annu. Rev. Plant Physiol., 1994, 45, 369–392 CrossRef CAS.
- J. M. Berg, J. L. Tymoczko and L. Stryer, Biochemistry, W. H. Freeman, 5th edn, 2002 Search PubMed.
- C. K. Mathews, K. E. Van Holde and K. G. Ahern, Biochemistry, Prentice Hall, 4th edn, 1999 Search PubMed.
- J. T. Hardy, The Sea Surface and Global Change, Cambridge UP, 1997 Search PubMed.
- J. Newman and K. Thomas-Alyea, Electrochemical Systems, Wiley & Sons, 2004 Search PubMed.
- S. V. Patankar, Numerical Heat Transfer and Fluid Flow, McGraw-Hill, New York, 1980 Search PubMed.
- B. R. Helliker, J. A. Berry, A. K. Betts, P. S. Bakwin, K. J. Davis, A. S. Denning, J. R. Ehleringer, J. B. Miller, M. P. Butler and D. M. Ricciuto, J. Geophys. Res.: Atmos., 2004, 109, 607–618 CrossRef.
- S. C. Wofsy, M. L. Goulden, J. W. Munger, S. M. Fan, P. S. Bakwin, B. C. Daube, S. L. Bassow and F. A. Bazzaz, Science, 1993, 260, 1314–1317 CAS.
- J. Grace, J. Lloyd, J. Mcintyre, A. C. Miranda, P. Meir, H. S. Miranda, C. Nobre, J. Moncrieff, J. Massheder, Y. Malhi, I. Wright and J. Gash, Science, 1995, 270, 778–780 CAS.
- M. L. Goulden, J. W. Munger, S. M. Fan, B. C. Daube and S. C. Wofsy, Science, 1996, 271, 1576–1578 CAS.
- C. T. Lai, A. J. Schauer, C. Owensby, J. M. Ham, B. Helliker, P. P. Tans and J. R. Ehleringer, Tellus, Ser. B, 2006, 58, 523–536 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2015 |