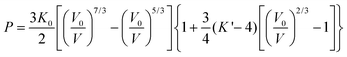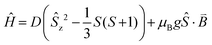A high-pressure crystallographic and magnetic study of Na₅[Mn(L-tart)₂]·12H₂O (L-tart = L-tartrate)

Abstract

The crystal structure and magnetic properties of the compound Na₅[Mn(L-tart)₂]·12H₂O (1, L-tart = L-tartrate) have been investigated over the pressure range 0.34–3.49 GPa. The bulk modulus of 1 has been determined as 23.9(6) GPa, with a compression of the coordination spheres around the Na⁺ ions observed. 1 is therefore relatively incompressible, helping it to retain its magnetic anisotropy under pressure.

---

Recent years have seen an increased interest in high pressure crystallographic studies of coordination compounds.¹ This is due to the wide array of structural features that can be modified by the application of hydrostatic pressure, and has been aided by technological developments.² In addition, diamond anvil cells (DACs)³ allow access to a huge range of pressures, spanning atmospheric pressure to tens of gigapascals, offering a much wider window over which to study the physical properties of materials, particularly when compared to variation of temperature. Hydrostatic pressure has been used to modulate non-covalent interactions,^4–6 switch the spin state of Fe(II) complexes,⁷ reveal piezochromism,^8–10 and bring about the polymerisation of discrete complexes.^11,12

For several years, we have been interested in the way in which pressure can affect high spin transition metal complexes, particularly those with pronounced Jahn–Teller axes.^13–17 Recently, we demonstrated that the compound Na₅[Mn(L-tart)₂]·12H₂O (1, L-tart = L-tartrate)¹⁸ shows slow relaxation of magnetisation under an applied direct current (dc) field.¹⁹ As such, it forms part of a wider family of transition metal complexes that show single-molecule magnet (SMM) behaviour²⁰ arising from a single transition metal ion in an appropriate ligand field.²¹ The presence in the crystal lattice of Na⁺ ions, Mn(III) ions, a flexible organic ligand in L-tartrate, and an extended network involving water molecules, make 1 an attractive candidate for high pressure crystallographic studies. Hydrated sodium salts have been shown to undergo substantial changes to their coordination environments on applying pressure,²² while pressure-induced flipping of the orientation of one of the Mn(III) Jahn–Teller axes in a Mn₁₂ SMM has been observed.²³ Herein, we describe the effect on the crystal structure of 1 of hydrostatic pressure ranging from 0.34 to 3.49 GPa. The static and dynamic magnetic properties of 1 are also investigated as a function of pressure. The bulk modulus of 1 is derived, and it is found to be relatively incompressible when compared to other compounds of its type, with the effect of pressure largely being observed around the Na⁺ ions in the lattice. As a result, 1 retains the axial anisotropy associated with the Mn(III) ion, and continues to display slow relaxation of the magnetisation under a direct current (dc) field, despite the pressure applied.

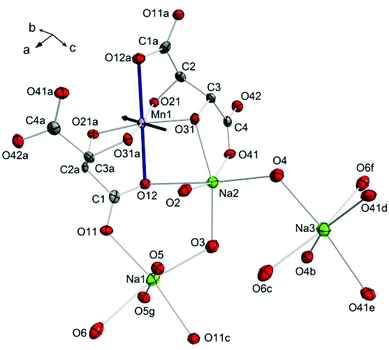
Compound 1 crystallises in the monoclinic space group C2. The central Mn(III) ion lies on a two-fold rotation axis in a distorted octahedral geometry, in which three O-donor atoms are provided each by two fully deprotonated L-tartrate ligands (Fig. 1). The room temperature, ambient pressure crystal structure of 1 has been described elsewhere,¹⁸ so here we detail the structure at the first pressure point collected, 0.34 GPa. The equatorial positions of the transition metal ion are occupied by the alkoxo atoms O21, O31, and their symmetry equivalent counterparts from the second L-tartrate ligand, with an average bond length of 1.909(7) Å. The axial positions are filled by O12 of the carboxylate, with a bond length of 2.319(2) Å. The clear tetragonal elongation is a consequence of the Jahn–Teller effect in the d⁴ ion.

Fig. 1 The structure of 1 at 0.34 GPa. Ellipsoids are shown at the 70% probability level, and hydrogen atoms are omitted for clarity. The Jahn–Teller axis is shown with thicker bonds. The black arrow represents the largest component of the strain tensor (see text). Lower case letters represent the symmetry operations for duplicate atoms: a = (1 − x, y, −z), b = (1 − x, y, 1 − z), c = (1.5 − x, 0.5 + y, 1 − z), d = (x, −1 + y, z), e = (1 − x, −1 + y, 1 − z), f = (−0.5 + x, −0.5 + y, z), g = (1.5 − x, 0.5 + y, 1 − z).

These [Mn(L-tart)₂]⁵⁻ complexes are linked through an extended network of Na⁺ ions and H₂O molecules. The Na1 ion is octahedrally coordinated, with the oxygen atoms O11 and O11c in a trans-arrangement, contributed from two different L-tart ligands, and four water molecules occupying the remaining four positions: O5 and O5g atoms in a trans-arrangement, and O3 and O6 also in a trans-configuration. The O11 atom, together with the water molecule containing O5, bridges two symmetry equivalent Na1 ions. The water molecules containing O3 and O6 bridge to Na2 and Na3, respectively. The Na1–O bond lengths range from 2.317(10)–2.730(3) Å. Na2 is coordinated by three donor atoms the L-tart ligands: in a cis-manner by the alkoxo-group O31 and carboxylato-O41 from one ligand, and by O12 from the other. The remaining three sites are occupied water molecules O2, O3, and O4. The water molecule containing O2 is terminal, and O4 bridges to Na3. The Na–O bond lengths around Na2 range from 2.332(3) to 2.677(10) Å. Na3 is surrounded by three pairs of O-atom donors: two water molecules containing O4, in a cis-arrangement; two carboxylato-O41 atoms in a cis-arrangement, and finally two water molecules containing O6 in a trans-configuration. The Na3–O bond lengths range from 2.397(8)–2.569(9) Å.

The effect of hydrostatic pressure on the structure of 1 was investigated at 10 further pressure points, reaching a maximum of 3.49 GPa. Selected crystallographic data are provided in Table 1. The structure remains in the monoclinic space group C2 over the full pressure range examined. All three unit cell lengths decrease with increasing pressure, with the b-axis being the most sensitive, displaying a decrease of 5.2% between 0.34 and 3.49 GPa (Fig. 2). There is a resultant reduction in the unit cell volume of 106.4(4) ų. The pressure dependence of the volume of the unit cell was fitted²⁴ to a third order Birch–Murnaghan equation of state:

yielding a bulk modulus K₀ of 23.9(6) GPa, with its pressure derivative (K′) equal to 4.2(5). The bulk modulus gives a measure of how incompressible a material is: diamond has K₀ = 440 GPa.²⁵ Typically, K₀ is found to be lower than 30 GPa for molecular solids and in this class of material, 1 is relatively incompressible. As a comparison, the molecular complexes [bis(3-fluorosalicylaldoximato)nickel(II)] and Co₃(dpa)₄Br₂·CH₂Cl₂ were found to have K₀ = 9.1(17) GPa⁹ and 6.4(7) GPa,²⁶ respectively. The bulk modulus found for the metal–organic framework [Zn₂(C₃H₃N₂)₄]_n was 14 GPa,²⁷ and the strongly hydrogen-bonded system L-alanine has K₀ = 13.4(7) GPa.²⁸ It is interesting that 1 is perhaps less compressible than could have been anticipated, given the conformational flexibility of the L-tartrate ligand.

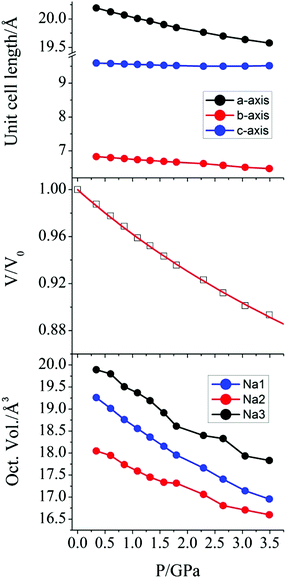Fig. 2 (top) Variation of the crystallographic unit cell lengths in 1 as a function of applied pressure. (middle) Pressure dependence of the relative unit cell volume of 1. The value at P = 0 is taken from the original crystal structure determination,¹⁸ and the solid line is a fit to a Birch-Murnaghan equation of state. (bottom) The pressure dependence of the octahedral volume around the Na⁺ ions in 1.

Table 1 Selected crystallographic data for compound 1. A full table for all of the data-sets collected is given in the ESI

	0.34 GPa	3.49 GPa
Crystal system	Monoclinic
Space group	C2
λ/Å	0.4859
a/Å	20.1905(14)	19.5753(19)
b/Å	6.830(2)	6.476(3)
c/Å	9.5946(7)	9.5153(10)
β/°	112.981(4)	114.033(6)
V/Å^3	1218.0(4)	1101.7(5)
Z	2
D calc/g cm^−3	1.849	2.044
Reflections	4189	3086
Unique reflections	1044	921
R int	0.046	0.059
R	0.041	0.049
R w	0.064	0.078
S	0.99	1.00
Flack parameter	0.06(6)	0.06(10)
ρ max, ρmin/e Å^−3	0.55, −0.58	1.43, −1.32

---

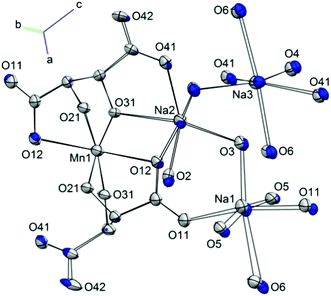
1 displays a pronounced Jahn–Teller (JT) effect along the axis of the Mn1–O12, O12a bonds. Previous studies of molecular nanomagnets have shown that the application of pressure can lead to switching of the orientation of JT axes.²³ However, the geometry around the central Mn(III) ion in 1 was found to be largely unaffected by pressure. The variation in the Mn–O bond lengths as pressure is increased is shown in Fig. S1.† The axial Mn1–O12 bond lengths (Å) decrease from 2.319(2) at 0.34 GPa to 2.283(4) at 3.49 GPa, and the average equatorial bond length changes from 1.909(7) to 1.884(14), at 0.34 GPa and 3.49 GPa, respectively. Therefore, the difference between the axial and average equatorial bond lengths is 0.410 and 0.399 Å for the lowest and highest pressures measured. The retention of the coordination environment around the Mn(III) ion is shown by the overlay of the structures at 0.34 and 3.49 GPa in Fig. 3. While there is almost full overlap of the Mn(III) ions, the six oxygen donor atoms, and the carbon atom backbone of the L-tartrate ligand at the starting and final pressures, more pronounced displacements are observed in the positions of the Na⁺ ions, particularly Na1. Calculation of the strain tensor,²⁹ which describes the magnitude of compression and its anisotropy, showed that its largest component lies along the b-axis, approximately in the equatorial plane of the Mn(III) ion, bisecting the O31–Mn1–O31a angle (Fig. 1). The application of pressure from 0.34 to 3.49 GPa leads to a very slight increase in the O31–Mn1–O31a (93.8(4) to 95.5(7)°, at 0.34 and 3.49 GPa, respectively) and O21–Mn1–O21a angles (96.6(4) to 97.2(8)°), accompanied by a decrease in the O21–Mn1–O31 angles (85.4(2) to 84.1(3)°).

Fig. 3 Overlay of the structure of 1 at 0.34 GPa (blue) and 3.49 GPa (light grey). Ellipsoids are shown at the 30% probability level, hydrogen atoms are omitted for clarity, and only heteroatoms are labelled.

A more pronounced contraction in bond lengths is observed around each of the sodium ions in the lattice. At 3.59 GPa, the average Na–O bond lengths around Na1, Na2, and Na3 are 2.358(13), 2.357(10), and 2.426(10) Å, representing a decrease of 0.100, 0.066, and 0.083 Å, when compared to the values at 0.34 GPa. The effect of this change is observed as a compression of the coordination octahedra around the three Na⁺ cations (Fig. 2) for which the largest decrease in volume was observed in Na1 (19.260 to 16.955 ų, as calculated using PLATON³⁰).

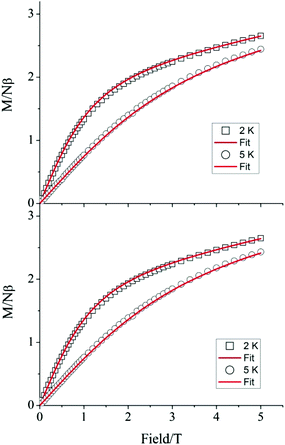
To verify whether the structural modifications induced by the application of pressure lead to changes in the magnetic properties of 1, both the direct current (dc) and alternating current (ac) susceptibilities were studied at four different applied pressures, ranging from 0 to 1.6 GPa. Consistent with our preceding work,¹⁹ variable field magnetisation measurements performed at 2 and 5 K were not found to reach saturation at ambient pressure. Indeed, increasing the applied pressure to 0.5, 1.0, and 1.6 GPa appeared to have no effect on the M vs. H curves (Fig. 4). Employing the program Phi,³¹ the data were fitted according to the Hamiltonian:

yielding a value for the axial zero-field splitting (zfs) parameter D of −3.23 cm⁻¹ at each pressure point investigated, in line with the ambient pressure value previously determined through high-field EPR spectroscopy.¹⁹ Thus, as was found for the distorted octahedral environment of the Mn(III) ion in the crystal structures, the axial anisotropy of the Mn(III) ion in 1 appears insensitive to pressure to 1.6 GPa. The magnitude of the axial anisotropy is one of the determining factors in the size of the barrier to slow relaxation of the magnetisation, U_eff. Correspondingly the barrier in 1, determined under an applied dc field of 2500 Oe, was also found to be invariant on applying pressure in the available ac frequency range (Fig. 5, S3 and Table S3†).

Fig. 4 Magnetisation of 1 as a function of applied field at (top) ambient pressure inside the pressure cell and (bottom) 1.6 GPa. Solid lines correspond to fits of the data, performed with the program Phi.

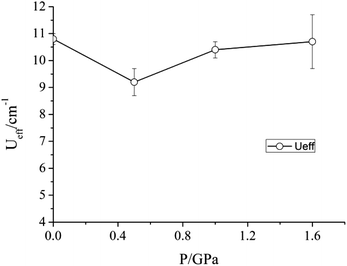Fig. 5 Variation of the barrier to relaxation U_eff of 1 under an applied dc field of 2500 Oe as a function of pressure.

Given the modifications induced in the crystal structure of 1 by the application of pressure, we propose that the Na⁺ ions shield the central transition metal ion from the effects of compression. As a result, the principal effect of the hydrostatic pressure is to squeeze the coordination octahedra around the three Na⁺ ions, rather than lead to any significant distortion around the Mn(III) ion. Accordingly, while pressure has been shown to alter the magnetic properties of other coordination complexes containing Mn(III), no such effect is found here. Soft ionic sites, such as the Na⁺ ions in the lattice of 1, could therefore be envisaged to play a role in helping preserve important physical properties of other lattice entities – in this case the slow relaxation of the magnetisation of Mn(III) ions. Work is underway to investigate whether substitution of the Na⁺ ions for other mono-cationic species would lead to more pronounced distortions in the coordination environment of the Mn(III) ion on the application of pressure.

Experimental details

Compound 1 was synthesised as reported previously.¹⁸ A crystal of 1 (0.20 × 0.15 × 0.10 mm³) was loaded into a Merrill-Bassett diamond anvil cell equipped with 600 mm culet-cut diamonds and conically-ground WC backing plates.^3,32 The hydrostatic medium was Daphne oil, and the pressure was measured by ruby fluorescence.³³ High pressure single-crystal X-ray diffraction data were collected at room temperature on beamline I19 at Diamond Light Source (λ = 0.4859 Å). The data were integrated using the program SAINT³⁴ while employing dynamic masks to account for regions shaded by the pressure cell³⁵ and absorption corrections were carried out with SADABS.³⁶ The structures were refined against F² using CRYSTALS.³⁷ All non-H atoms were refined anisotropically. Bond angles and distances in the L-tart ligand were restrained for the structure solution at 0.34 GPa, but refined freely at all of the other pressure points. All metal–ligand distances, angles, and torsion angles were refined freely. Thermal and vibrational similarity restraints were applied to the L-tart ligand and the O atoms of the water molecules. H atoms were fixed in geometrically calculated positions.

Magnetic measurements under pressure were carried out using a Quantum Design MPMS-XL5 SQUID Magnetometer. The sample, in the form of a crystalline powder, was loaded into the CuBe piston-cylinder-type high-pressure capsule cell. Daphne 7373 oil was used as a pressure-transmitting medium. A background measurement was performed using a complete, assembled cell with no sample contained in the cell. Alternating current (ac) susceptibility measurements were performed under an applied direct current (dc) field of 2500 Oe, with a drive field of 3 Oe.

Acknowledgements

The UK Engineering and Physical Sciences Research Council are thanked for financial support (grant ref. EP/K033662/1; EP/K033646/1; EP/K033549/1). We thank Diamond Light Source for access to beamline I19 (proposal number MT10392) that contributed to the results presented here. The data which underpin this work are available at http://dx.doi.org/10.5525/gla.researchdata.209.

Notes and references

1. J. P. Tidey, H. L. S. Wong, M. Schröder and A. J. Blake, Coord. Chem. Rev., 2014, 277–278, 187–207.
2. A. Katrusiak, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 135–148.
3. S. A. Moggach, D. R. Allan, S. Parsons and J. E. Warren, J. Appl. Crystallogr., 2008, 41, 249–251.
4. C. H. Woodall, S. Fuertes, C. M. Beavers, L. E. Hatcher, A. Parlett, H. J. Shepherd, J. Christensen, S. J. Teat, M. Intissar, A. Rodrigue-Witchel, Y. Suffren, C. Reber, C. H. Hendon, D. Tiana, A. Walsh and P. R. Raithby, Chem. – Eur. J., 2014, 20, 16933–16942.
5. H. L. S. Wong, D. R. Allan, N. R. Champness, J. McMaster, M. Schröder and A. J. Blake, Angew. Chem., Int. Ed., 2013, 52, 5093–5095.
6. G. Mínguez Espallargas, L. Brammer, D. R. Allan, C. R. Pulham, N. Robertson and J. E. Warren, J. Am. Chem. Soc., 2008, 130, 9058–9071.
7. P. Guionneau and E. Collet, in Spin-Crossover Materials: Properties and Applications, ed. M. A. Halcrow, John Wiley & Sons Ltd., Oxford, UK, 2013, p. 508.
8. A. Jaffe, Y. Lin, W. L. Mao and H. I. Karunadasa, J. Am. Chem. Soc., 2015, 137, 1673–1678.
9. P. J. Byrne, P. J. Richardson, J. Chang, A. F. Kusmartseva, D. R. Allan, A. C. Jones, K. V. Kamenev, P. A. Tasker and S. Parsons, Chem. – Eur. J., 2012, 18, 7738–7748.
10. K. W. Galloway, S. A. Moggach, P. Parois, A. R. Lennie, J. E. Warren, E. K. Brechin, R. D. Peacock, R. Valiente, J. Gonzalez, F. Rodriguez, S. Parsons and M. Murrie, CrystEngComm, 2010, 12, 2516–2519.
11. S. A. Moggach, K. W. Galloway, A. R. Lennie, P. Parois, N. Rowantree, E. K. Brechin, J. E. Warren, M. Murrie and S. Parsons, CrystEngComm, 2009, 11, 2601–2604.
12. D. R. Allan, A. J. Blake, D. Huang, T. J. Prior and M. Schroder, Chem. Commun., 2006, 4081–4083.
13. J. A. Gould, M. J. Rosseinsky and S. A. Moggach, Dalton Trans., 2012, 41, 5464–5467.
14. A. Prescimone, J. Sanchez-Benitez, K. V. Kamenev, S. A. Moggach, J. E. Warren, A. R. Lennie, M. Murrie, S. Parsons and E. K. Brechin, Dalton Trans., 2010, 39, 113–123.
15. A. Prescimone, J. Sanchez-Benitez, K. V. Kamenev, S. A. Moggach, A. R. Lennie, J. E. Warren, M. Murrie, S. Parsons and E. K. Brechin, Dalton Trans., 2009, 7390–7395.
16. A. Prescimone, C. J. Milios, J. Sanchez-Benitez, K. V. Kamenev, C. Loose, J. Kortus, S. Moggach, M. Murrie, J. E. Warren, A. R. Lennie, S. Parsons and E. K. Brechin, Dalton Trans., 2009, 4858–4867.
17. A. Prescimone, C. J. Milios, S. Moggach, J. E. Warren, A. R. Lennie, J. Sanchez-Benitez, K. Kamenev, R. Bircher, M. Murrie, S. Parsons and E. K. Brechin, Angew. Chem., Int. Ed., 2008, 47, 2828–2831.
18. S. Kaizaki, M. Urade, A. Fuyuhiro and Y. Abe, Inorg. Chim. Acta, 2006, 359, 374–378.
19. G. A. Craig, J. J. Marbey, S. Hill, O. Roubeau, S. Parsons and M. Murrie, Inorg. Chem., 2015, 54, 13–15.
20. Molecular Nanomagnets and Related Phenomena, ed. S. Gao, Springer-Verlag, 2014.
21. G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147.
22. M. Walker, C. A. Morrison, D. R. Allan, C. R. Pulham and W. G. Marshall, Dalton Trans., 2007, 2014–2019.
23. P. Parois, S. A. Moggach, J. Sanchez-Benitez, K. V. Kamenev, A. R. Lennie, J. E. Warren, E. K. Brechin, S. Parsons and M. Murrie, Chem. Commun., 2010, 46, 1881–1883.
24. R. J. Angel, M. Alvaro and J. Gonzalez-Platas, Z. Kristallogr., 2014, 229, 405–419.
25. C. Slebodnick, J. Zhao, R. Angel, B. E. Hanson, Y. Song, Z. Liu and R. J. Hemley, Inorg. Chem., 2004, 43, 5245–5252.
26. S. R. Madsen, J. Overgaard, D. Stalke and B. B. Iversen, Dalton Trans., 2015, 44, 9038–9043.
27. E. C. Spencer, R. J. Angel, N. L. Ross, B. E. Hanson and J. A. K. Howard, J. Am. Chem. Soc., 2009, 131, 4022–4026.
28. N. P. Funnell, A. Dawson, D. Francis, A. R. Lennie, W. G. Marshall, S. A. Moggach, J. E. Warren and S. Parsons, CrystEngComm, 2010, 12, 2573–2583.
29. S. Parsons, STRAIN, program for calculation of linear strain tensors, 2003.
30. A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155.
31. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175.
32. L. Merrill and W. A. Bassett, Rev. Sci. Instrum., 1974, 45, 290–294.
33. G. J. Piermarini, S. Block, J. D. Barnett and R. A. Forman, J. Appl. Phys., 1975, 46, 2774–2780.
34. Bruker, Bruker AXS, Madison, Wisconsin, USA, 2007.
35. A. Dawson, D. R. Allan, S. Parsons and M. Ruf, J. Appl. Crystallogr., 2004, 37, 410–416.
36. G. M. Sheldrick, SADABS Version 2008-1, University of Gottingen, Gottingen, Germany, 2008.
37. P. W. Betteridge, J. R. Carruthers, R. I. Cooper, K. Prout and D. J. Watkin, J. Appl. Crystallogr., 2003, 36, 1487.

---

Footnote

† Electronic supplementary information (ESI) available: Additional magnetic and crystallographic data. CCDC 1419429–1419439. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5dt03320a

---