Open Access Article
Open Access ArticleThe impact of doping rates on the morphologies of silver and gold nanowires grown in helium nanodroplets
Alexander
Volk
a,
Philipp
Thaler
a,
Daniel
Knez
b,
Andreas W.
Hauser
*a,
Johannes
Steurer
a,
Werner
Grogger
b,
Ferdinand
Hofer
b and
Wolfgang E.
Ernst
*a
aInstitute of Experimental Physics, Graz University of Technology, Petersgasse 16, A-8010 Graz, Austria. E-mail: andreas.w.hauser@gmail.com; wolfgang.ernst@tugraz.at; Fax: +43 (316) 873 108140; Tel: +43 (316) 873 8157 Tel: +43 (316) 873 8140
bInstitute for Electron Microscopy and Nanoanalysis & Graz Centre for Electron Microscopy, Graz University of Technology, Steyrergasse 17, A-8010 Graz, Austria
First published on 12th November 2015
Abstract
Silver and gold nanowires are grown within superfluid helium nanodroplets and investigated by high resolution electron microscopy after surface deposition. The wire morphologies depend on the rate of metal atom doping in the pickup sequence. While high doping rates result in a polycrystalline face-centered cubic nanowire structure, at lower doping rates the initial fivefold-symmetry seems to be preserved. An explanation for this observation is given by computer simulations, which allow the derivation of timescales for the nanowire growth process inside helium nanodroplets.
1 Introduction
Quantized vortices, accessory phenomena of superfluidity, were predicted by Onsager and Feynman around 1950.1,2 Despite earlier experimental evidence for their existence,3,4 it took until 2006 to finally image them in bulk superfluid helium (He II) using hydrogen particles as tracers.5 The fact that impurities get pinned to the vortices as a consequence of a pressure gradient around the vortex cores6 can be exploited to investigate processes such as vortex reconnection and quantum turbulence in He II.7–9 In a more applied approach, the use of the directed growth of nanoparticles in the presence of vortices in He II was proposed for the production of nanowires.10 Single and bundled metal nanowires were obtained from laser ablation of metal targets immersed in He II and subsequently characterized in terms of structure, electrical properties and thermal stability.11–20Helium nanodroplets (HeN), on the other hand, were extensively used as weakly perturbing cryogenic matrices for the spectroscopy of atoms, molecules and small clusters in molecular beam experiments (see ref. 21–24 for detailed reviews). The possibility of sequential doping and local confinement of different species at 0.37 K makes HeN also a unique environment for cluster growth.21–23,25,26 The first surface deposition of HeN-grown metal clusters27,28 triggered a series of experimental studies on cluster growth and follow-up surface deposition.29–33 Gomez et al. found that Ag nanoparticles (Agn), synthesized in single helium droplets and subsequently deposited on a substrate, tend to agglomerate equidistantly along distinct lines.34 In the absence of external guiding forces, this can be taken as the first experimental evidence for the existence of vortices inside of HeN. This confirms several preceding computational studies on this issue (see ref. 35–38 and references therein). Further proof for the presence of vortices or even vortex lattices in the droplets was given by recent X-ray diffraction experiments on a Xe-doped HeN-beam and complementary density functional theory (DFT) calculations.39,40 Utilizing these vortices as inert templates, continuous monometallic nanowires with lengths of several hundred nanometers were synthesized inside HeN,41 as well as bimetallic core–shell nanowires.42 As an intrinsic property of the growth process, the diameter of these wires is ≈3–10 nm. In a recent study on the stability of HeN-grown Ag nanowires we could show that these thin structures segment due to thermally induced Ag atom diffusion after their deposition on a surface.43
Despite these experimental achievements, little is known about the actual growth process of nanowires inside the droplets.41,44 Our group was able to deduce a possible growth mechanism for pure Agn inside of vortex-free HeN by analyzing high resolution transmission electron microscopy (HRTEM) images of the deposited clusters.30 A computational survey of the landing process revealed that small Agn (diameter dAg < 3 nm) presumably undergo reconstruction upon deposition, while for larger clusters the pronounced soft landing conditions28,45,46 favour the conservation of the initial morphology.47 Only recently we modelled the collision process between two coinage metal dopants in small HeN with a molecular dynamics (MD) simulation.48 The obtained timescales for dimer collisions were subsequently used in a model suitable for larger droplet sizes. It shows that for large HeN, multicenter aggregation leads to well separated clusters in one droplet for long timescales.49
In the present study we extend our previous work by investigating the influence of the doping conditions on the cluster growth and aggregation inside of large HeN. We further give timescales for the pinning of clusters due to attractive forces exerted by vortices present in the droplets, which causes the nanowire-growth. The obtained results are compared to HRTEM images of bare Ag and Au clusters and nanowires. Experiment and calculations indicate that an alteration in the amount of metal dopants induces different growth scenarios, which finally influences the morphology of the produced nanowires. To our belief a good understanding of the underlying growth process of nanowires in HeN is one of the key questions to be addressed in order to be able to synthesize more elaborate structures with this technique.
2 Experimental
The experimental setup is described in detail elsewhere.50 In brief, HeN are produced by the supersonic jet expansion of gaseous He (99.9999% purity) through a precooled nozzle with a 5 μm orifice into high vacuum. The helium stagnation pressure (p0) was kept at 20 bar for all experiments discussed in this work. By variation of the nozzle temperature (T0) it is possible to alter the mean droplet size (![[N with combining overline]](https://www.rsc.org/images/entities/i_char_004e_0305.gif) ).21 In our experiments, vortices have exclusively been observed for T0 ≤ 6.5 K at p0 = 20 bar. Therefore, it can be assumed that they are efficiently created and preserved only when large HeN (
).21 In our experiments, vortices have exclusively been observed for T0 ≤ 6.5 K at p0 = 20 bar. Therefore, it can be assumed that they are efficiently created and preserved only when large HeN (![[N with combining overline]](https://www.rsc.org/images/entities/i_char_004e_0305.gif) > 108 atoms) are formed via breakup of liquid He during the expansion process.34,51,52 For experiments on vortex-free HeN we therefore keep T0 at 8 K. In all other cases, T0 is set to 5.4 K. This corresponds to
> 108 atoms) are formed via breakup of liquid He during the expansion process.34,51,52 For experiments on vortex-free HeN we therefore keep T0 at 8 K. In all other cases, T0 is set to 5.4 K. This corresponds to ![[N with combining overline]](https://www.rsc.org/images/entities/i_char_004e_0305.gif) ≈ 7 × 106 atoms (droplet diameter
≈ 7 × 106 atoms (droplet diameter ![[d with combining overline]](https://www.rsc.org/images/entities/i_char_0064_0305.gif) D ≈ 85 nm) and
D ≈ 85 nm) and ![[N with combining overline]](https://www.rsc.org/images/entities/i_char_004e_0305.gif) ≈ 1.7 × 1010 atoms (
≈ 1.7 × 1010 atoms (![[d with combining overline]](https://www.rsc.org/images/entities/i_char_0064_0305.gif) D ≈ 1100 nm) respectively.21,51,53 We note that recent calculations also suggest vortex nucleation in small HeN (N = 1000) by ionization of attached dopants54,55 or during the doping process with neutral atoms.56 However, in the latter case theory suggests limited vortex-lifetimes in the picosecond range.
D ≈ 1100 nm) respectively.21,51,53 We note that recent calculations also suggest vortex nucleation in small HeN (N = 1000) by ionization of attached dopants54,55 or during the doping process with neutral atoms.56 However, in the latter case theory suggests limited vortex-lifetimes in the picosecond range.
The HeN-beam passes a 400 μm skimmer into a separate vacuum chamber where the droplets are doped with the desired metal. Ag or Au atoms are evaporated from separate resistively heated alumina ovens of 2.3 cm length. They are captured by the passing droplets, in which they subsequently agglomerate to clusters. After the pickup, the droplet beam enters a UHV chamber (base pressure <6 ≈ 10−10 mbar) and is terminated on commercial TEM grids (Ted Pella, Inc., Prod. No. 01824). This leads to the disintegration of the droplet and a soft deposition of the contained aggregates on the amorphous carbon (a-c) surface.28,45–47
The disintegration of the HeN causes a rise in the He background pressure pHe, which can be monitored with an ionization pressure gauge (Leybold Heraeus IM 220) and a quadrupole residual gas analyzer (Balzers QMA 200/QME 200), both mounted off the beam axis. Due to evaporative cooling,53 the HeN size and accordingly the total He flux ΦHe into the last chamber are reduced with increasing Ag/Au doping rate. Following ref. 28, we calculate the mean number of metal dopant atoms ![[n with combining overline]](https://www.rsc.org/images/entities/i_char_006e_0305.gif) X per HeN as
X per HeN as
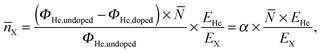 | (1) |
![[n with combining overline]](https://www.rsc.org/images/entities/i_char_006e_0305.gif) X as obtained for the attenuations used in this work. We note that EX is dependent on the cluster size and considerably smaller at the beginning of cluster growth.58 This is taken into account for the small HeN (
X as obtained for the attenuations used in this work. We note that EX is dependent on the cluster size and considerably smaller at the beginning of cluster growth.58 This is taken into account for the small HeN (![[N with combining overline]](https://www.rsc.org/images/entities/i_char_004e_0305.gif) ≈ 7 × 106) in Table 1.
≈ 7 × 106) in Table 1.
![[n with combining overline]](https://www.rsc.org/images/entities/i_char_006e_0305.gif) X per HeN for different droplet sizes
X per HeN for different droplet sizes ![[N with combining overline]](https://www.rsc.org/images/entities/i_char_004e_0305.gif) and attenuations α as calculated with eqn (1)
and attenuations α as calculated with eqn (1)
| α |
![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif)
|
n Ag | n Au |
|---|---|---|---|
| 0.75 | 1.7 × 1010 | 2.6 × 106 | 2.0 × 106 |
| 0.5 | 7 × 106 | — | 650 |
| 0.2 | 1.7 × 1010 | 6.8 × 105 | 5.4 × 105 |
| 0.04 | 1.7 × 1010 | — | 1.1 × 105 |
For the given average droplet speed vD ≈ 173 m s−1 at T0 = 5.4 K51 the pickup rates reach up to 2 × 1010 atoms per s. The energy transferred to the droplet this way leads to an estimated increase of the droplet temperature from 0.37 K59 to ≈1.05 K.53,60 Since this temperature is still below the He superfluid transition temperature of 2.17 K, quantized vortices are preserved during the pickup.
As for a previous study,30 we use a Tecnai TF20 from FEI Company for TEM and HRTEM measurements on the deposited clusters and nanowires. The microscope is equipped with an FEG source and a high resolution Gatan imaging filter with an UltraScan CCD camera (2048 px × 2048 px). All images are recorded with 200 kV acceleration voltage and a current density as low as 1 pA nm−2 to prevent morphology changes of the particles during the imaging process.
Since the breakup of Ag nanowires becomes noticeable already at ≈260 K,43 some substrates are cooled via the substrate holder to liquid nitrogen (LN2) temperature for the investigation of continuous wires. After nanowire deposition, cooled substrates are immersed into LN2 within 5 s after the substrate holder has been detached from its mount in the chamber. These substrates are subsequently transferred to a suited cryo-TEM holder (Gatan, Model 792) without being removed from the LN2 bath. Other substrates are exposed to ambient conditions for times shorter than 5 min when transferred to the TEM. In all cases, the chamber is vented with gaseous N2 (grade 5).
3 Computational details
3.1 Cluster growth and aggregation
Recently, we investigated the time dependence of two-particle-collisions in HeNvia a combination of helium density functional theory and molecular dynamics simulations.48 While it is computationally feasible to simulate the collision of just two dopants within a droplet on quantum-chemistry level, a similar description of the actual particle growth process is not possible due to the large time-scale (milliseconds) and the system size (up to 106 metal atoms). Instead, we use the collision times calculated in ref. 48 as input for a simplified, global model of multiple cluster growth in large helium droplets. We study the number and mass of all metal particles as a function of time without keeping track of actual particle positions. Qualitatively, the model is the same for simulations of Au and Ag dopants. Therefore, only the Ag case shall be described here in greater detail.According to the real experiment, cluster growth in HeN starts by the pickup of single atoms in a locally defined region. In the computer simulation we therefore add ![[n with combining overline]](https://www.rsc.org/images/entities/i_char_006e_0305.gif) Ag (see Table 1) atoms with a fixed doping frequency. The latter is determined by the length of the pickup region and the velocity of the droplets in the HeN beam. Benchmark calculations show that the shrinking of the droplet due to evaporative cooling has a negligible impact on the doping cross-section for a fixed dopant vapor pressure. Therefore a constant doping frequency can be assumed. The dopants are spawned within the HeN volume at Landau velocity vλ ≈ 56 m s−1.61 The time it takes for two atoms to aggregate Δta(2) is taken from ref. 48 and adjusted as follows: as more dopant-atoms are added to the droplet, the nucleation rate will increase until equilibrium conditions are reached. In our model, the nucleation frequency
Ag (see Table 1) atoms with a fixed doping frequency. The latter is determined by the length of the pickup region and the velocity of the droplets in the HeN beam. Benchmark calculations show that the shrinking of the droplet due to evaporative cooling has a negligible impact on the doping cross-section for a fixed dopant vapor pressure. Therefore a constant doping frequency can be assumed. The dopants are spawned within the HeN volume at Landau velocity vλ ≈ 56 m s−1.61 The time it takes for two atoms to aggregate Δta(2) is taken from ref. 48 and adjusted as follows: as more dopant-atoms are added to the droplet, the nucleation rate will increase until equilibrium conditions are reached. In our model, the nucleation frequency 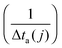 increases with the number of pairs that can be formed by j particles, hence
increases with the number of pairs that can be formed by j particles, hence
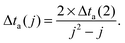 | (2) |
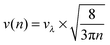 | (3) |
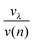 .
.
An individual “aggregation timer” is defined for every particle enclosed in the droplet, which reflects the actual droplet size and its current loading with dopants, i.e. the size-dependent velocities of all clusters which are currently present in the droplet. For the first two atoms picked up by the droplet this timer is set to Δta(2), but it is reevaluated after every additional pickup following eqn (2) and (3). Whenever an aggregation timer expires, the corresponding particle merges with another particle randomly chosen from the current set, but with a probability proportional to the velocity of the second particle (i.e. mergers with smaller particles are preferred). The merging leads to the growth of the first particle and to a reevaluation of its aggregation timer according to eqn (3), while the second particle is removed from the set.
In order to study structural changes in our set of metal particles over time, we further keep track of the shape of each resulting particle, which is determined by the amount of binding energy released during coalescence. While the addition of single atoms to a preexisting cluster is treated in a way that yields a new spherical particle, two clusters only coalesce into a spherical particle if the released energy is large enough to completely melt at least one of the involved clusters. This treatment is based on the findings in ref. 14 and 16. The authors of the respective studies showed that the surface energy released upon coagulation of two small metal clusters in He II can lead to melting and a subsequent merging of the individual particles into a single sphere. For larger clusters the released energy may not be sufficient for a complete melting, so that the clusters stick together and form nanowires.
We use a slightly different approach to calculate the energy released upon coagulation, as this allows us a better implementation of coagulation events between different sized clusters. To start, we calculate the binding energy per atom Eb(n) in a cluster consisting of n atoms using the empirical relation62
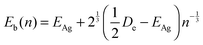 | (4) |
| ΔEb = (n1 + n2) × Eb(n1 + n2) − (n1 × Eb(n1) + n2 × Eb(n2)). | (5) |
It is evident that without additional effects, given sufficient time, such an algorithm inevitably leads to one single final particle. In the real experiment the growth rates are damped due to the presence of vortices in large HeN. Particles caught by vortices are pinned to the vortex core and their motion is subsequently restricted to the direction along the vortex line.5,65 The coalescence of captured particles along the vortex core is the reason for the formation of continuous nanowires, but is not directly captured in the presented model. However, we can choose the maximum simulation time to be equal to the mean time it takes for a particle to get trapped by a vortex contained in the HeN, which will be derived in the next section. This enables us to follow the growth of the building blocks of the final nanowires.
3.2 Cluster capture by vortices
Due to a pressure gradient around the vortex core,6 a vortex exhibits an attractive force on particles in the droplet, whose magnitude is given by66–68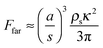 | (6) |
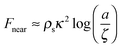 | (7) |
![[s with combining overline]](https://www.rsc.org/images/entities/i_char_0073_0305.gif) can be given analytically as
can be given analytically as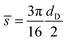 | (8) |
4 Results and discussion
4.1 HRTEM images
In order to ensure that the fundamental growth process for different coinage metal clusters in vortex-free HeN (![[N with combining overline]](https://www.rsc.org/images/entities/i_char_004e_0305.gif) ≈ 7 × 106 atoms) is the same, we repeat our previous experiment,30 but dope the droplets with Au instead of Ag. The TEM substrate is exposed to the Au-doped (α = 0.5) HeN-beam for 480 s. Following the routine of ref. 30, the mean diameter of deposited Aun is measured using the image processing package FIJI.69 The obtained diameter
≈ 7 × 106 atoms) is the same, we repeat our previous experiment,30 but dope the droplets with Au instead of Ag. The TEM substrate is exposed to the Au-doped (α = 0.5) HeN-beam for 480 s. Following the routine of ref. 30, the mean diameter of deposited Aun is measured using the image processing package FIJI.69 The obtained diameter ![[d with combining overline]](https://www.rsc.org/images/entities/i_char_0064_0305.gif) Au ≈ 2.9(1) nm corresponds to
Au ≈ 2.9(1) nm corresponds to ![[n with combining overline]](https://www.rsc.org/images/entities/i_char_006e_0305.gif) Au ≈ 750 assuming a spherical cluster shape and bulk density of the metal.30 The discrepancy between this value and the one given in Table 1 lies within the measurement uncertainties. We note that even small deviations in either of the variables in eqn (1) lead to a reasonable change in the estimated absolute number of dopants. Fortunately, this becomes less crucial for the larger droplets investigated.
Au ≈ 750 assuming a spherical cluster shape and bulk density of the metal.30 The discrepancy between this value and the one given in Table 1 lies within the measurement uncertainties. We note that even small deviations in either of the variables in eqn (1) lead to a reasonable change in the estimated absolute number of dopants. Fortunately, this becomes less crucial for the larger droplets investigated.
HRTEM images are recorded and compared to the corresponding simulations30,70 in order to determine the morphologies of the clusters. While a complete analysis of the Aun morphology distribution lies beyond the scope of this article, we report that the findings are in good agreement with the measurements on Agn.30 Above all, we can clearly identify icosahedral (Ih) and decahedral (Dh) clusters for large cluster diameters (dAu > 3 nm) in numerous cases, two of which are exemplary depicted in Fig. 1. As will be shown later, these structures can be identified as building blocks in conglomerated nanowires.
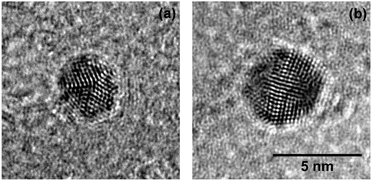 | ||
Fig. 1 Decahedral (a) and icosahedral (b) Aun synthesized in HeN free from vortices (![[N with combining overline]](https://www.rsc.org/images/entities/i_char_004e_0305.gif) ≈ 7 × 106 atoms), observed after deposition on a TEM substrate. The morphologies found agree well with those of Agn produced under comparable conditions.30 Scale is the same for both images. ≈ 7 × 106 atoms), observed after deposition on a TEM substrate. The morphologies found agree well with those of Agn produced under comparable conditions.30 Scale is the same for both images. | ||
In order to investigate the aggregation process in the presence of vortices, large HeN (![[N with combining overline]](https://www.rsc.org/images/entities/i_char_004e_0305.gif) ≈ 1.7 × 1010 atoms) are doped with Ag or Au atoms, respectively. In both cases, the doping rate was adjusted so as to obtain either heavy (α = 0.75) or weak (α = 0.2) loading of the droplets. Subsequently, the TEM substrates are exposed to the droplet beam for 5 s. This time is chosen in order to obtain a decent surface coverage on one hand and to ensure an insignificant overlap between nanowires carried by different droplets.
≈ 1.7 × 1010 atoms) are doped with Ag or Au atoms, respectively. In both cases, the doping rate was adjusted so as to obtain either heavy (α = 0.75) or weak (α = 0.2) loading of the droplets. Subsequently, the TEM substrates are exposed to the droplet beam for 5 s. This time is chosen in order to obtain a decent surface coverage on one hand and to ensure an insignificant overlap between nanowires carried by different droplets.
Fig. 2(a) shows continuous Ag nanowires with a total length of several hundred nanometers and a mean diameter ![[d with combining overline]](https://www.rsc.org/images/entities/i_char_0064_0305.gif) nw ≈ 5 nm (as obtained with α = 0.75). Cryo-HRTEM measurements on these wires reveal multiple domains of face centered cubic (fcc) morphology (Fig. 2(b)). Blurred parts along the wire are due to thickness oscillations, i.e. the structure is visible in the HRTEM measurements only for areas with similar thickness for a chosen defocus. Due to these perturbations in diameter, the wires break up via a surface diffusion process already below room temperature, as shown recently.43 The outcome of this so-called Rayleigh breakup is the occurrence of chains of Ag segments as depicted in Fig. 3(a) and (d), and previously found in other HeN34,41,44 and He II bulk experiments.18 HRTEM images reveal that in the case of heavy doping (α = 0.75, left column of Fig. 3) these segments can either adopt polycrystalline fcc morphologies (Fig. 3(b)) or exhibit large monocrystalline fcc domains (Fig. 3(c)). No clusters with Ih or Dh morphology were found under these doping conditions.
nw ≈ 5 nm (as obtained with α = 0.75). Cryo-HRTEM measurements on these wires reveal multiple domains of face centered cubic (fcc) morphology (Fig. 2(b)). Blurred parts along the wire are due to thickness oscillations, i.e. the structure is visible in the HRTEM measurements only for areas with similar thickness for a chosen defocus. Due to these perturbations in diameter, the wires break up via a surface diffusion process already below room temperature, as shown recently.43 The outcome of this so-called Rayleigh breakup is the occurrence of chains of Ag segments as depicted in Fig. 3(a) and (d), and previously found in other HeN34,41,44 and He II bulk experiments.18 HRTEM images reveal that in the case of heavy doping (α = 0.75, left column of Fig. 3) these segments can either adopt polycrystalline fcc morphologies (Fig. 3(b)) or exhibit large monocrystalline fcc domains (Fig. 3(c)). No clusters with Ih or Dh morphology were found under these doping conditions.
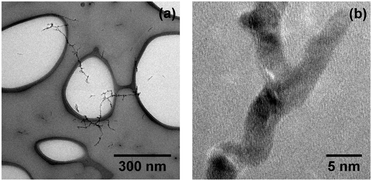 | ||
Fig. 2 Ag nanowires synthesized in HeN (![[N with combining overline]](https://www.rsc.org/images/entities/i_char_004e_0305.gif) ≈ 1.7 × 1010), deposited and imaged on a LN2 cooled (a-c) TEM grid. Continuous branched wires (a) show polycrystalline domains in HRTEM mode (b). ≈ 1.7 × 1010), deposited and imaged on a LN2 cooled (a-c) TEM grid. Continuous branched wires (a) show polycrystalline domains in HRTEM mode (b). | ||
 | ||
| Fig. 3 Chains of Ag segments resulting from the breakup of nanowires as depicted in Fig. 2. Left column: (a) heavy doping of the droplet (α = 0.75). HRTEM measurements reveal either polycrystalline morphology (b) or large monocrystalline domains (c). Right column: (d) weak doping (α = 0.2). Silver segments resulting from the breakup of small nanowires often exhibit fivefold symmetry, i.e. icosahedral ((e), top of (f)) or decahedral (bottom of (f)) morphologies. | ||
This is completely different from the findings obtained with Ag and α = 0.2 as depicted in the right column of Fig. 3. The existence of large Ihs (Fig. 3(e) and top of Fig. 3(f)) and Dhs (bottom of Fig. 3(f)) is dominating, being followed by particles with large monocrystalline domains. In contrast to the observations made for α = 0.75 we find only a very small amount of polycrystalline particles for weak loading of the droplets.
For large Au nanowires (α = 0.75) at LN2 temperature, we find the same branched structures as depicted in Fig. 2(a) for Ag. During the heat-up to room temperature Au nanowires undergo a surface smoothing but do not break into multiple segments (see Fig. 4(a)). The inner morphology (Fig. 4(b)) resembles that of continuous Ag wires, i.e. multiple fcc domains can be found. The wires resemble those found in bulk He II experiments in diameter, shape and morphology.12,13,17,19 Under low doping conditions (α = 0.2) we find short but continuous Au wires of slightly smaller diameter (Fig. 4(c)). In numerous cases, these wires contain spherical enclosures of ambiguous morphology, while the rest of the wire consists of multiple fcc domains (Fig. 4(d)).
Further reduction of the amount of doped Au atoms (α = 0.04) leads to the observation of segmented Au nanowires (Fig. 5). Assuming conserved volumes, we calculate the mean diameter of the initial wires as ![[d with combining overline]](https://www.rsc.org/images/entities/i_char_0064_0305.gif) nw ≈ 3.0(1) nm. The distance between the centers of neighboring segments λ ≈ (13 ± 4) nm is in very good agreement with the theoretically derived relationship 2λ/d = 8.89 for the Rayleigh breakup of an ideal cylinder.71 The HRTEM image in Fig. 5 shows a small decahedral cluster (marked by an arrow) between two clusters of indistinct morphology.
nw ≈ 3.0(1) nm. The distance between the centers of neighboring segments λ ≈ (13 ± 4) nm is in very good agreement with the theoretically derived relationship 2λ/d = 8.89 for the Rayleigh breakup of an ideal cylinder.71 The HRTEM image in Fig. 5 shows a small decahedral cluster (marked by an arrow) between two clusters of indistinct morphology.
 | ||
| Fig. 5 Segmented Au nanowire resulting from very weak doping (α = 0.04). The arrow marks a small decahedral cluster in the HRTEM image. | ||
As shown in our previous work,43 the breakup of Ag nanowires can be explained by the diffusion of wire surface atoms from thinner to thicker parts of the wire due to a gradient of the chemical potential. It is therefore convenient to assume that the observed morphologies are present already inside the initially continuous wires, and that they become clearly visible in the course of the breakup. It has been shown in several theoretical studies that the icosahedral shape is energetically preferred for small metal clusters, while intermediate and large clusters seem to be more stable in Dh and fcc morphologies, respectively (see ref. 72–74 and references therein). Further, it has been determined by MD simulations that the fcc morphology is preferred over the icosahedral morphology for Ag clusters with sizes larger than 1590 atoms (dAg ≈ 3.7 nm).75 The Ihs depicted in Fig. 3(e) and (f) both exhibit diameters larger than 5 nm (n > 3900 atoms). Therefore, it can be excluded that they were formed from fcc particles via a restructuring process. Such a growth sequence would further strongly contradict MD simulations recently performed by our own group.47 In simulations of silver clusters we could observe the conversion of Ihs and Dhs into fcc particles during surface deposition due to a recrystallization process, but not a single event of an inverse transformation from fcc into a particle of fivefold symmetry.
4.2 Simulation of the growth process
In order to explain the different morphologies observed we simulate the cluster growth process for different doping rates, i.e. different attenuation coefficients α. The maximum simulation time is chosen to equal the mean time it takes for a particle to get trapped by a vortex (ttrap). The pickup of atoms and their coagulation into clusters lead to shrinking of the droplets, which influences![[s with combining overline]](https://www.rsc.org/images/entities/i_char_0073_0305.gif) given in eqn (8). It turns out that ttrap is long compared to the timescale of cluster growth, which equals the timescale of the doping process (≈130 μs) determined by the flight time of the HeN through the pickup region. It is therefore convenient to calculate
given in eqn (8). It turns out that ttrap is long compared to the timescale of cluster growth, which equals the timescale of the doping process (≈130 μs) determined by the flight time of the HeN through the pickup region. It is therefore convenient to calculate ![[s with combining overline]](https://www.rsc.org/images/entities/i_char_0073_0305.gif) and subsequently ttrap using the droplet diameters of the attenuated droplet beam dD,α. The results for ttrap are summarized in Table 2.
and subsequently ttrap using the droplet diameters of the attenuated droplet beam dD,α. The results for ttrap are summarized in Table 2.
![[N with combining overline]](https://www.rsc.org/images/entities/i_char_004e_0305.gif) = 1.7 × 1010 atoms.
= 1.7 × 1010 atoms. ![[s with combining overline]](https://www.rsc.org/images/entities/i_char_0073_0305.gif) is calculated using eqn (8) and dD,α
is calculated using eqn (8) and dD,α
| Element | α | d D/nm | t trap/ms |
|---|---|---|---|
| Ag | 0.75 | 720 | 1.4 |
| 0.2 | 1060 | 3.0 | |
| Au | 0.75 | 720 | 1.8 |
| 0.2 | 1060 | 4.0 | |
| 0.04 | 1130 | 4.6 | |
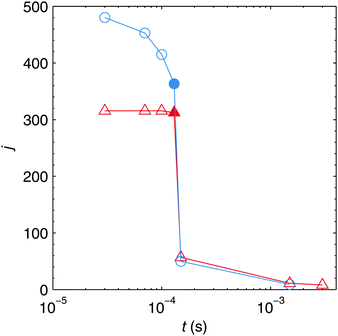
The time evolution of the total number of particles j present in one helium droplet is depicted in Fig. 6 for the attenuations realized in the experiment. It can be seen that in both cases the number of individual particles quickly drops after the pickup of new atoms has ended and that the following agglomeration takes place on a much longer timescale. The reason for this behaviour lies in the slow velocities of large clusters (see eqn (3)) compared to the Landau velocity assumed for freshly spawned metal atoms in the simulation. This finding has also been verified experimentally by the observation of bimetallic core–shell clusters with single or double cores.49 In order to realize the latter case two clusters have to grow in the droplet in the first of two consecutive pickup regions and have to stay separated until the droplets reach the second pickup cell. The corresponding HeN flight time can be estimated as ≈1 ms in our apparatus.50
Fig. 6 also reveals a decrease of j during the pickup process for larger attenuations, while j seems to stay nearly constant for α = 0.2. This behaviour can be explained by the shrinking of HeN which is much more prominent for α = 0.75 as can be seen from Table 2. The HeN flight time between the pickup cell and the TEM substrate is ≈6 ms. Comparing this to the timescale of cluster growth and to ttrap, it is evident that most clusters have to grow outside the vortex in a multicenter aggregation process, and that nearly all clusters will be captured by the vortex before substrate deposition.
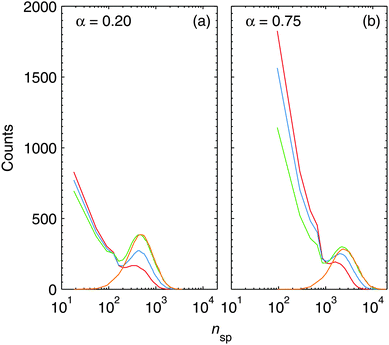
The monitoring of the number of particles contained in spherical clusters nsp can give us a further important insight into the agglomeration process. Fig. 7 depicts the absolute occurrence of a certain value of nsp for all spherical particles contained in a single HeN. The lines shown correspond to the smoothed envelopes of histograms. Every histogram is calculated from several simulation runs for every depicted time of the aggregation process. Snapshots are taken during the pickup process at 30, 70, 130 (end of the pickup) and at 150 μs. As explained in the computational details, spherical clusters which do not melt during agglomeration are treated as elongated particles, built from the initially spherical collision partners. nsp includes all spherical clusters, regardless of whether they are present as building blocks of elongated structures or as individual spheres. From this, it follows that Fig. 7 directly reflects the sizes of the last complete melting of the clusters. A merging event which does not lead to molten clusters does affect j, but not the depicted histograms of nsp.
The large amount of small clusters present in the droplets during the pickup process is efficiently reduced after the addition of new atoms has ended, which is in good agreement with the behaviour depicted in Fig. 6. In fact, the final distribution of spherical building blocks is reached after 150 μs. This means that melting processes are practically limited to the pickup time, and that 20 μs after the end of pickup melting is negligible. After 150 μs, the spherical clusters still coagulate to form the final nanoparticles. This process takes the time which we calculated as ttrap earlier.
The most striking feature in Fig. 7 is that the positions of the histogram maxima are determined by the attenuation, i.e. the doping rate. A high doping rate in the case of α = 0.75 leads to a stronger heating of the clusters as more atoms impinge within a given time while the cooling rate rc is the same as for weaker doping. The effect is further enhanced by the pronounced shrinking of the droplet under heavy doping conditions, and leads to a slight shift of the histogram maxima towards higher values of nsp in Fig. 7. We can extract from the histograms ![[n with combining overline]](https://www.rsc.org/images/entities/i_char_006e_0305.gif) sp ≈ 600 (
sp ≈ 600 (![[d with combining overline]](https://www.rsc.org/images/entities/i_char_0064_0305.gif) Ag ≈ 2.7 nm) for α = 0.2 and
Ag ≈ 2.7 nm) for α = 0.2 and ![[n with combining overline]](https://www.rsc.org/images/entities/i_char_006e_0305.gif) sp ≈ 3000 (
sp ≈ 3000 (![[d with combining overline]](https://www.rsc.org/images/entities/i_char_0064_0305.gif) Ag ≈ 4.6 nm) for α = 0.75, which are also in good agreement with the diameters observed for deposited nanowires in the cryo-TEM images. As explained above, the fcc structure is energetically preferred over the Ih morphology for cluster sizes larger than 1590 atoms (dAg ≈ 3.7 nm).75 Since the clusters solidify from a molten state, it is justified to assume that the formation of Ihs is much more probable at α = 0.2 than it is for α = 0.75. This explains the exclusive findings of particles of fivefold symmetry under weak doping conditions in the experiment.
Ag ≈ 4.6 nm) for α = 0.75, which are also in good agreement with the diameters observed for deposited nanowires in the cryo-TEM images. As explained above, the fcc structure is energetically preferred over the Ih morphology for cluster sizes larger than 1590 atoms (dAg ≈ 3.7 nm).75 Since the clusters solidify from a molten state, it is justified to assume that the formation of Ihs is much more probable at α = 0.2 than it is for α = 0.75. This explains the exclusive findings of particles of fivefold symmetry under weak doping conditions in the experiment.
5 Conclusions
Experimentally observed morphologies of HeN-grown Au and Ag nanowires depend on the rate of doping with metal atoms during the pickup process. In the first step of the growth process, multiple clusters are formed within a droplet in a multicenter aggregation process. At low doping rates, a large portion of these clusters exhibits fivefold symmetry, while at high rates the presence of the fcc structure is dominating. In the second step of the growth process these clusters are captured by vortices and coagulate into nanowires. According to our simulations, their coagulation does not result in a complete melting of the single clusters. This is related to the large cluster sizes and the relatively low collision rates at this stage of the nanowire growth. Therefore, the morphologies of the initial building blocks, i.e. the coagulating clusters, are preserved within the nanowires.We believe that our experimental findings and the computational model presented will be of use in future attempts of gaining better control over the synthesis and the design of nanostructures within HeN. It would also be desirable to determine the morphologies of clusters enclosed in the HeN before substrate deposition, e.g. by X-ray scattering, a technique which has been exploited recently to investigate the morphologies of large free Ag nanoparticles.76
Acknowledgements
The authors thank Dr Markus Koch and Dr Florian Lackner for fruitful discussions and Manuel Paller for creating 3D graphics. This research has been supported by the Austrian Science Fund (FWF) under Grant FWF-E-P22962, by the European Commission and the Styrian Government within the ERDF program as well as by the European Union within the 7th Framework Programme (FP7/2007-2013) under Grant Agreement No. 312483 (ESTEEM2). The authors gratefully acknowledge support from NAWI Graz.References
- L. Onsager, Proc. Int. Conf. Theor. Phys., Science Council of Japan, Tokyo, 1953, pp. 877–880 Search PubMed.
- R. P. Feynman, in Progress in Low Temperature Physics, ed. C. J. Gorter, North-Holland, Amsterdam, 1955, pp. 17–53 Search PubMed.
- G. A. Williams and R. E. Packard, Phys. Rev. Lett., 1974, 33, 280–283 CrossRef CAS.
- E. J. Yarmchuk, M. J. V. Gordon and R. E. Packard, Phys. Rev. Lett., 1979, 43, 214–217 CrossRef CAS.
- G. P. Bewley, D. P. Lathrop and K. R. Sreenivasan, Nature, 2006, 441, 588 CrossRef CAS PubMed.
- R. J. Donelly, Quantized Vortices in Helium II, Cambridge University Press, Cambridge, 1991 Search PubMed.
- G. P. Bewley, M. S. Paoletti, K. R. Sreenivasan and D. P. Lathrop, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 13707–13710 CrossRef CAS PubMed.
- M. S. Paoletti, M. E. Fisher, K. R. Sreenivasan and D. P. Lathrop, Phys. Rev. Lett., 2008, 101, 154501 CrossRef CAS PubMed.
- M. S. Paoletti, M. E. Fisher and D. P. Lathrop, Phys. D, 2010, 239, 1367–1377 CrossRef CAS.
- E. B. Gordon and Y. Okuda, J. Low Temp. Phys., 2009, 35, 209–213 CrossRef CAS.
- E. B. Gordon, A. V. Karabulin, V. I. Matyushenko, V. D. Sizov and I. I. Khodos, J. Low Temp. Phys., 2010, 36, 590–595 CrossRef CAS.
- P. Moroshkin, V. Lebedev, B. Grobety, C. Neururer, E. B. Gordon and A. Weis, EPL, 2010, 90, 34002 CrossRef.
- V. Lebedev, P. Moroshkin, B. Grobety, E. Gordon and A. Weis, J. Low Temp. Phys., 2011, 165, 166–176 CrossRef CAS.
- E. B. Gordon, A. V. Karabulin, V. I. Matyushenko, V. D. Sizov and I. I. Khodos, J. Exp. Theor. Phys., 2011, 112, 1061–1070 CrossRef CAS.
- E. B. Gordon, A. V. Karabulin, V. I. Matyushenko, V. D. Sizov and I. I. Khodos, Appl. Phys. Lett., 2012, 101, 052605 CrossRef.
- E. Gordon, A. Karabulin, V. Matyushenko, V. Sizov and I. Khodos, Chem. Phys. Lett., 2012, 519–520, 64–68 CrossRef CAS.
- E. B. Gordon, A. V. Karabulin, A. A. Morozov, V. I. Matyushenko, V. D. Sizov and I. I. Khodos, J. Phys. Chem. Lett., 2014, 5, 1072–1076 CrossRef CAS PubMed.
- E. Gordon, A. Karabulin, V. Matyushenko, V. Sizov and I. Khodos, Phys. Chem. Chem. Phys., 2014, 16, 25229–25233 RSC.
- E. B. Gordon, A. V. Karabulin, V. I. Matyushenko and I. I. Khodos, J. Phys. Chem. A, 2015, 119, 2490–2501 CrossRef CAS PubMed.
- E. B. Gordon, A. V. Karabulin, V. I. Matyushenko, V. D. Sizov and I. I. Khodos, Laser Phys. Lett., 2015, 12, 096002 CrossRef.
- J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef CAS.
- J. Tiggesbäumker and F. Stienkemeier, Phys. Chem. Chem. Phys., 2007, 9, 4748–4770 RSC.
- C. Callegari and W. E. Ernst, in Handbook of High Resolution Spectroscopy, ed. F. Merkt and M. Quack, John Wiley & Sons, Chichester, 2011, vol. 3, pp. 1551–1594 Search PubMed.
- M. Mudrich and F. Stienkemeier, Int. Rev. Phys. Chem., 2014, 33, 301–339 CrossRef CAS.
- M. Theisen, F. Lackner and W. E. Ernst, J. Phys. Chem. A, 2011, 115, 7005–7009 CrossRef CAS PubMed.
- M. Ratschek, M. Koch and W. E. Ernst, J. Chem. Phys., 2012, 136, 104201 CrossRef PubMed.
- V. Mozhayskiy, M. N. Slipchenko, V. K. Adamchuk and A. F. Vilesov, J. Chem. Phys., 2007, 127, 094701 CrossRef PubMed.
- E. Loginov, L. F. Gomez and A. F. Vilesov, J. Phys. Chem. A, 2011, 115, 7199–7204 CrossRef CAS PubMed.
- A. Boatwright, C. Feng, D. Spence, E. Latimer, C. Binns, A. M. Ellis and S. Yang, Faraday Discuss., 2013, 162, 113–124 RSC.
- A. Volk, P. Thaler, M. Koch, E. Fisslthaler, W. Grogger and W. E. Ernst, J. Chem. Phys., 2013, 138, 214312 CrossRef PubMed.
- S. Yang, A. M. Ellis, D. Spence, C. Feng, A. Boatwright, E. Latimer and C. Binns, Nanoscale, 2013, 5, 11545–11553 RSC.
- S. B. Emery, K. B. Rider, B. K. Little, A. M. Schrand and C. M. Lindsay, J. Chem. Phys., 2013, 139, 054307 CrossRef PubMed.
- S. B. Emery, K. B. Rider and C. M. Lindsay, Propellants, Explos., Pyrotech., 2014, 39, 161–165 CrossRef CAS.
- L. F. Gomez, E. Loginov and A. F. Vilesov, Phys. Rev. Lett., 2012, 108, 155302 CrossRef PubMed.
- F. Dalfovo, R. Mayol, M. Pi and M. Barranco, Phys. Rev. Lett., 2000, 85, 1028–1031 CrossRef CAS PubMed.
- K. K. Lehmann and R. Schmied, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 224520 CrossRef.
- F. Ancilotto, M. Barranco and M. Pi, Phys. Rev. Lett., 2003, 91, 105302 CrossRef PubMed.
- E. Sola, J. Casulleras and J. Boronat, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 052507 CrossRef.
- L. F. Gomez, K. R. Ferguson, J. P. Cryan, C. Bacellar, R. M. P. Tanyag, C. Jones, S. Schorb, D. Anielski, A. Belkacem, C. Bernando, R. Boll, J. Bozek, S. Carron, G. Chen, T. Delmas, L. Englert, S. W. Epp, B. Erk, L. Foucar, R. Hartmann, A. Hexemer, M. Huth, J. Kwok, S. R. Leone, J. H. S. Ma, F. R. N. C. Maia, E. Malmerberg, S. Marchesini, D. M. Neumark, B. Poon, J. Prell, D. Rolles, B. Rudek, A. Rudenko, M. Seifrid, K. R. Siefermann, F. P. Sturm, M. Swiggers, J. Ullrich, F. Weise, P. Zwart, C. Bostedt, O. Gessner and A. F. Vilesov, Science, 2014, 345, 906–909 CrossRef CAS PubMed.
- F. Ancilotto, M. Pi and M. Barranco, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 100503 CrossRef.
- E. Latimer, D. Spence, C. Feng, A. Boatwright, A. M. Ellis and S. Yang, Nano Lett., 2014, 14, 2902–2906 CrossRef CAS PubMed.
- P. Thaler, A. Volk, F. Lackner, J. Steurer, D. Knez, W. Grogger, F. Hofer and W. E. Ernst, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155442 CrossRef.
- A. Volk, D. Knez, P. Thaler, A. W. Hauser, W. Grogger, F. Hofer and W. E. Ernst, Phys. Chem. Chem. Phys., 2015, 17, 24570–24575 RSC.
- D. Spence, E. Latimer, C. Feng, A. Boatwright, A. M. Ellis and S. Yang, Phys. Chem. Chem. Phys., 2014, 16, 6903–6906 RSC.
- M. P. de Lara-Castells, N. F. Aguirre, H. Stoll, A. O. Mitrushchenkov, D. Mateo and M. Pi, J. Chem. Phys., 2015, 142, 131101 Search PubMed.
- V. N. Popok, I. Barke, E. E. B. Campbell and K.-H. Meiwes-Broer, Surf. Sci. Rep., 2011, 66, 347–377 CrossRef CAS.
- P. Thaler, A. Volk, M. Ratschek, M. Koch and W. E. Ernst, J. Chem. Phys., 2014, 140, 044326 CrossRef PubMed.
- A. W. Hauser, A. Volk, P. Thaler and W. E. Ernst, Phys. Chem. Chem. Phys., 2015, 17, 10805–10812 RSC.
- G. Haberfehlner, P. Thaler, D. Knez, A. Volk, F. Hofer, W. E. Ernst and G. Kothleitner, Nat. Commun., 2015, 6, 8779 CrossRef CAS PubMed.
- P. Thaler, A. Volk, D. Knez, F. Lackner, G. Haberfehlner, J. Steurer, M. Schnedlitz and W. E. Ernst, J. Chem. Phys., 2015, 143, 134201 CrossRef PubMed.
- L. F. Gomez, E. Loginov, R. Sliter and A. F. Vilesov, J. Chem. Phys., 2011, 135, 154201 CrossRef PubMed.
- H. Buchenau, E. L. Knuth, J. Northby, J. P. Toennies and C. Winkler, J. Chem. Phys., 1990, 92, 6875–6889 CrossRef CAS.
- D. M. Brink and S. Stringari, Z. Phys. D, 1990, 15, 257–263 CrossRef CAS.
- A. Leal, D. Mateo, A. Hernando, M. Pi, M. Barranco, A. Ponti, F. Cargnoni and M. Drabbels, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224518 CrossRef.
- D. Mateo, A. Leal, A. Hernando, M. Barranco, M. Pi, F. Cargnoni, M. Mella, X. Zhang and M. Drabbels, J. Chem. Phys., 2014, 140, 131101 Search PubMed.
- A. Leal, D. Mateo, A. Hernando, M. Pi and M. Barranco, Phys. Chem. Chem. Phys., 2014, 16, 23206–23213 RSC.
- C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, Hoboken, 2005 Search PubMed.
- M. D. Morse, Chem. Rev., 1986, 86, 1049–1109 CrossRef CAS.
- M. Hartmann, R. E. Miller, J. P. Toennies and A. Vilesov, Phys. Rev. Lett., 1995, 75, 1566–1569 CrossRef CAS PubMed.
- M. Hartmann, N. Pörtner, B. Sartakov, J. P. Toennies and A. F. Vilesov, J. Chem. Phys., 1999, 110, 5109–5123 CrossRef CAS.
- N. B. Brauer, S. Smolarek, E. Loginov, D. Mateo, A. Hernando, M. Pi, M. Barranco, W. J. Buma and M. Drabbels, Phys. Rev. Lett., 2013, 111, 153002 CrossRef PubMed.
- H. Müller, H.-G. Fritsche and L. Skala, in Clusters of Atoms and Molecules I, ed. H. Haberland, Springer-Verlag, Berlin Heidelberg, 1995 Search PubMed.
- C. M. Lindsay and R. E. Miller, J. Chem. Phys., 2005, 122, 104306 CrossRef CAS PubMed.
- I. Scheele, A. Conjusteau, C. Callegari, R. Schmied, K. K. Lehmann and G. Scoles, J. Chem. Phys., 2005, 122, 104307 CrossRef PubMed.
- E. Popov, M. Mammetkuliyev and J. Eloranta, J. Chem. Phys., 2013, 138, 204307 CrossRef PubMed.
- D. P. Meichle and D. P. Lathrop, Rev. Sci. Instrum., 2014, 85, 073705 CrossRef PubMed.
- T. V. Chagovets and S. W. Van Sciver, Phys. Fluids, 2011, 23, 107102 CrossRef.
- Y. A. Sergeev and C. F. Barenghi, J. Low Temp. Phys., 2009, 157, 429–475 CrossRef CAS.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J.-Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682 CrossRef CAS PubMed.
- K. Koga and K. Sugawara, Surf. Sci., 2003, 529, 23–35 CrossRef CAS.
- F. A. Nichols and W. W. Mullins, Trans. Metall. Soc. AIME, 1965, 233, 1840–1848 CAS.
- F. Baletto and R. Ferrando, Rev. Mod. Phys., 2005, 77, 371–423 CrossRef CAS.
- F. Baletto, R. Ferrando, A. Fortunelli, F. Montalenti and C. Mottet, J. Chem. Phys., 2002, 116, 3856–3863 CrossRef CAS.
- F. Baletto, C. Mottet and R. Ferrando, Chem. Phys. Lett., 2002, 354, 82–87 CrossRef CAS.
- C. Amano, H. Niina and Y. Mikami, THEOCHEM, 2009, 904, 64–68 CrossRef CAS.
- I. Barke, H. Hartmann, D. Rupp, L. Flückiger, M. Sauppe, M. Adolph, S. Schorb, C. Bostedt, R. Treusch, C. Peltz, S. Bartling, T. Fennel, K.-H. Meiwes-Broer and T. Müller, Nat. Commun., 2015, 6, 6187 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2016 |