Quantum chemical insights into the dependence of porphyrin basicity on the meso-aryl substituents: thermodynamics, buckling, reaction sites and molecular flexibility

Abstract

The chemical and sensing properties of porphyrins are frequently tuned via the introduction of peripheral substituents. In the context of the exceptionally fast second protonation step in the case of 5,10,15,20-tetraphenylporphyrin (TPP), as compared to porphin and 5,10,15,20-tetramesitylporphyrin (TMesP), we investigated the macrocycle-substituent interactions of these three porphyrin derivatives in detail. Using quantum chemical thermodynamics calculations, the analysis of geometric structures, torsional profiles, electrostatic potential distributions, and particularly the analysis of molecular flexibilities via ab initio molecular dynamics simulations, we obtained a comprehensive picture of the reactivities of the studied porphyrins and how these are influenced by the meso-substituents. As compared to porphin and TMesP the second protonation of TPP is energetically more favorable and is particularly energetically comparable to its first protonation, instead of being significantly less favorable like in the case of porphyrin and TMesP. Additionally, the second TPP protonation is facilitated by an interplay between out-of-plane (oop) distortion of the protonation site and a pronounced electrostatic binding spot at the protonation site. Furthermore, the second protonation is particularly facilitated in the case of TPP by the large oop-flexibility of the diprotonated species as unraveled by ab initio molecular dynamics simulations.

---

Introduction

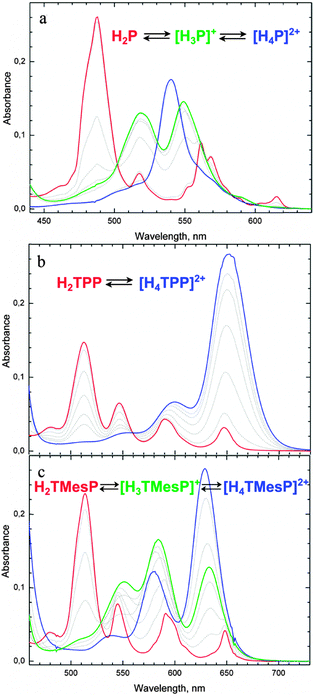
The photophysical and chemical properties of porphyrins and related tetrapyrrolic macrocycles can be tuned over a wide range via peripheral functionalization, control of the acid–base equilibria of the porphyrin core, and the core size.^1–20 Thus, a large variety of reports on tetrapyrrolic compounds can be found in the literature, like the occurrence of Fe-protoporphyrin IX as the prosthetic group of the hemeproteins in nature,²¹ the application as photosensitizers in photodynamic therapy,²² including the fast developing field of two-photon excitation,^23–25 as active materials for organic solar cells^26,27 or light emitting diodes,²⁸ and in chemical sensors. Sensing applications can utilize the chelating core of the macrocycles or their acid–base equilibria, thus enabling e.g. optical pH-sensing with porphyrins.^29–34

To optimize porphyrin structures for the above-mentioned applications, particularly for sensing, control over the chemical properties of the porphyrin core, such as the acid–base equilibria shown in Scheme 1, is necessary. Therefore, possibilities to tune binding and reactivity properties of the macrocycle core via electronic and steric influences of the peripheral substituents have been extensively studied.^35–42 Interestingly, the relative rates of the two possible subsequent protonations of the porphyrin core can be controlled by the meso-aryl substituents.^43,44 In addition to the effect of protonation, the meso-substituents might cause nonplanar distortions of the macrocycle and change the molecular flexibility, as studied in-depth for diprotonated porphyrins.^{21,32,36,37,41,45} The type and extent of nonplanar distortions of the macrocycle have been extensively discussed in terms of molecular flexibility,^32,37,41 the peripheral substitution pattern,^{21,32,36,37,41} and the strength of intermolecular interactions with acid residues or other anionic species in solution.^10,36,43,46 The relationship between the molecular structure and the macrocycle acid–base equilibrium has also been investigated.^36,46–52 The monoprotonated forms of porphyrins are, however, much less studied with respect to molecular conformation, stability, and optical properties.^{47,51,53–55} For the porphine (H₂P) and alkyl-substituted porphyrins, both mono- and diprotonated forms were reported (see Fig. 1).^53,55

Scheme 1 Acid–base equilibria of different porphyrin derivatives. Carbon atoms 5, 10, 15, and 20 are the meso-carbons.

Fig. 1 Ground-state absorption spectra of the free base, mono- and diprotonated species (red, green and blue colors, respectively). Panels from top to bottom: porphine (H₂P, [H₃P]⁺, [H₄P]²⁺), tetra-meso-phenylporphyrin (H₂TPP, [H₄TPP]²⁺), and tetra-meso-mesitylporphyrin (H₂TMesP, [H₃TMesP]⁺, [H₄TMesP]²⁺).

Particularly, comparing the evolution of the UV-vis absorption spectra in the course of acid–base titration of tetra-meso-mesitylporphyrin and tetra-meso-phenylporphyrin, TMesP and TPP, respectively (Fig. 1), demonstrates the dramatic influence of the type of meso-aryl substituents on the basicity of the porphyrin core. While the titration of TMesP yields three well distinguishable UV-vis absorption spectra in different pH ranges, that are attributed, respectively, to the free base (H₂TMesP), monoprotonated (H₃TMesP⁺) and diprotonated (H₄TMesP²⁺) species⁵² (as known from porphine and alkyl-substituted porphyrins), no spectral signature of the monoprotonated form (H₃TPP⁺) was found for TPP and also not for the structurally very similar tetra-meso-(4-N-methylpyridyl)porphyrin (H₂TMpyP⁴⁺) in the course of titration.^43,44 To obtain stable monoprotonated derivatives of TPP, structural modifications are necessary, such as introducing hydrocarbon-capped moieties that face the macrocyclic plane⁵⁶ or complexation of the diprotonated form with bulky and poorly coordinating anions followed by dilution to decrease the acidity.⁵⁴

It was reported by Pasternack et al. as well as by Stone and Fleischer that the experimental titration data of TPP and (TMpyP)⁴⁺ are consistent with the following set of equilibria:^43,44

H₂P ⇌ *H₂P

*H₂P + H⁺ ⇌ H₃P⁺

H₃P⁺ + H⁺ ⇌ H₄P²⁺ very fast

where *H₂P represents an activated form of the free base. The authors assumed that this activated form was buckled and that it dominates protonation, while similar mechanisms were not discussed for the mono-protonated form, as the second protonation is “very fast”. However, since we observed a significant difference in the second protonation between P, TMesP and TPP,⁵² the second protonation needs to be analyzed in more detail to understand how it is influenced by the meso-aryl substituents.

Therefore, we have first treated the thermodynamics of the acid–base equilibria of P, TMesP and TPP quantum chemically within the present paper. Since the base strength pK_B depends linearly on the Gibbs free energy ΔG at a given temperature T according to ΔG = −RT ln K = −RT ln 10 lg K = −RT ln 10lg(K_A/[H₂O = 55.5]) = RT ln 10(pK_A + lg 55.5), thus pK_A = ΔG/(RT ln 10) − 1.74 (R is the gas constant and K the equilibrium constant), ΔG needs to be calculated carefully under consideration of the solvent environment.⁵⁷ We compared the energies of isolated molecules and those enclosed by a dielectric continuum solvent environment (COSMO) in the conductor limit and additionally involved the interaction of surface elements to better account for intermolecular interactions, i.e. we applied a statistical thermodynamics treatment for more realistic solvation (RS) simulations.^58–60

If buckling or any kind of out-of-plane distortion determines the kinetics of the first protonation,^43,44 it might also be important for the second protonation. Therefore, we analyzed the pyrrole out-of-plane distortions along with the meso-aryl tilts. The buckling might accelerate protonation, either because it increases structural similarity between the mono- and diprotonated forms, or because it increases accessibility of the protonable nitrogen. The latter was analyzed by means of reactivity volumes. In any case, the meso-aryl substituents must play an essential role, possibly in terms of the porphyrin flexibility, as studied by means of ab initio molecular dynamics and analysis of the torsional profiles of the meso-substituents.

Methods

Quantum chemical structure optimizations, polarizable continuum solvation, and calculations of electrostatic potential distributions were performed using density functional theory (DFT) implemented in Turbomole^61,62 and applying the GGA (generalized gradient approximation) B-P86 exchange–correlation functional, the def2-TZVP triple-ζ basis set^63,64 and the MARI-J approximation.⁶⁵ This combination has been shown to give reliable geometries, electron density distributions and spectroscopic properties in many cases at a very reasonable computational cost.^66–72 For simulation of solvent environments, the conductor like screening model (COSMO, performed in the conductor limit, i.e. ε = ∞) and additionally COSMO for realistic solvation (COSMO-RS) implemented in COSMOtherm were used to model the dissolution of porphyrins in water and tetrahydrofuran (THF) that was used in the experiments.^57–59Ab initio molecular dynamics (MD) were run at 298 K to determine the range of variation of internal molecular coordinates as estimates for molecular flexibility. Therefore the highly efficient program TeraChem was used.^73,74 For analyzing electrostatic potential distributions and MD trajectories, Mathematica⁷⁵ Version 8 was used.

Results and discussion

The experimentally observed differences in spectroscopic responses upon acid addition between porphine and both differently meso-substituted porphyrins might originate from thermodynamics and/or kinetics. First, we compared DFT-calculated energies of the porphyrin derivatives involved in the acid–base equilibria with the experimental basicity relations. In the next step, we analyzed the steady state geometries of the porphyrin derivatives involved in the acid–base equilibria and estimated molecular flexibility from the distribution of internal coordinate values as sampled by MD runs. Thus, we will ascertain if the exceptionally fast second protonation in the case of tetra-meso-phenylporphyrin is due to a high structural similarity between the mono- and diprotonated species. Additionally, a high molecular out-of-plane (oop) flexibility would promote the formation of stable saddle-type geometries of diprotonated species and would facilitate exceptional oop-exposure of the reaction site in [H₃TPP]⁺.

Protonation energies and pK_B values

The Gibbs free energy difference of dissociation, ΔG_diss, that drives the protonation in the acid–base equilibria [H_2+nP]ⁿ⁺ + [H₃O]⁺ ⇌ [H_3+nP]⁽ⁿ⁺¹⁾⁺ + H₂O, exemplarily shown for porphyrin (P) with n = 0 or 1 for the first or second protonation, is defined according to eqn (1), with B being the base.

ΔG_diss = G(B) − G([HB]⁺) + [G([H₃O]⁺) − G(H₂O)] (1)

The differences in ΔG_diss between the porphyrin derivatives P, TMesP, and TPP dissolved in the same solvent equal the differences in corresponding ΔG values defined as ΔG = G(B) − G([HB]⁺). To better understand the origin of these ΔG differences between the protonation of P, TMesP and TPP, we discuss the independent contributions from the isolated molecules , the dielectric energies, E_diel, of protonated and non-protonated species according to COSMO at ε = ∞, i.e. the energy contribution that is caused by the dielectric screening of charges at a solvent-excluded surface (SAS) in the conductor limit, and the chemical potentials obtained by COSMO-RS, μ.⁵⁸

The pseudo gas-phase energy difference, , is defined as .⁵⁸ As shown in Table 1, for the first protonation step is similar for all the three derivatives H₂P, H₂TMesP, and H₂TPP (; differences in this series: 36 and 3 kJ mol⁻¹), with a particular small difference between the tetra-meso-aryl-substituted porphyrins. The differences for the second protonation step between [H₃P]⁺, [H₃TMesP]⁺, and [H₃TPP]⁺ are larger (; differences in this series: 83 and 8 kJ mol⁻¹) but their relations are similar. Consequently, in the gas phase, meso-aryl-substitution leads to a significantly increased stabilization of the protonated species (first/second protonation: ), but the second protonation step for TPP is energetically only slightly favored as compared to TMesP and the second proton affinities are generally smaller than the first ones.

Table 1 Gas-phase, conductor, COSMO and COSMO-RS energies, chemical potentials and Gibbs free energies for the free base and protonated states of porphine and the tetra-meso-aryl-substituted derivatives

	Pseudo-gas	COSMO		COSMO-RS H2O
		ΔEdiel	ΔECOSMO	Δμ	ΔΔG	pKB
	[kJ mol^−1]	[kJ mol^−1]		[kJ mol^−1]
H2P → [H3P]^+	−1034	−127.9	−1162	9	−1153	11
[H3P]^+ →[H4P]^2+	−680	−453.9	−1134	4	−1130	14
H2TMesP → [H3TMesP]^+	−1070	−96.9	−1167	12	−1155	11
[H3TMesP]^+ → [H4TMesP]^2+	−763	−381.9	−1145	5	−1140	13
H2TPP → [H3TPP]^+	−1073	−104.2	−1177	13	−1164	10
[H3TPP]^+ → [H4TPP]^2+	−771	−395.3	−1166	5	−1162	10

---

The energy gains due to dielectric screening E_diel increase approximately linearly with the molecular size of the free bases. However, in the case of the protonated species, E_diel of the pristine porphyrin significantly exceeds the E_diel stabilization of the tetra-meso-aryl-substituted derivatives, while the E_diel stabilization in the case of TPP is slightly larger than in the case of TMesP. Thus, ΔE_COSMO for the first protonation is similar for P and TMesP (−1162 and −1167 kJ mol⁻¹), while it is largest for TPP (−1177 kJ mol⁻¹) and in the case of the second protonation ΔE_COSMO increases from P to TMesP to TPP (−1134, −1145 and −1166 kJ mol⁻¹), as shown in Table 1. Consequently, the highest basicity for TPP as compared to P and TMesP observed experimentally is reproduced by the COSMO-energies for protonation, but the ΔE_COSMO values are again smaller for the second protonation as compared to the first one. However, this ΔΔE_COSMO difference is the smallest, i.e. the energy gains due to the first and second protonation are almost similar, for TPP (ΔΔE_COSMO between the second and first protonation for P, TMesP, TPP: −28, −22, −10 kJ mol⁻¹).

Additional accounting of interactions of molecular surface elements in real solutions using COSMO-RS slightly alters the protonation energies, which now even better match the experimental findings. The ΔE_COSMO relations are approximately preserved, but particularly ΔG values for the first protonation are reduced due to the consideration of the chemical potentials of the solutes in water determined via COSMO-RS. Thus, the COSMO-RS derived ΔG values for the first and second protonation of TPP are almost identical (−1164 and −1162 kJ mol⁻¹). The ΔΔG value between the first and second protonation of TPP equates to −2 kJ mol⁻¹, while ΔΔG-values for P and TMesP are both significantly higher, −23 and −15 kJ mol⁻¹, respectively. The same relation is mirrored by the corresponding pK_B values reported in Table 1.

As detailed in Table 2, the mean interaction energies decrease with subsequent protonation, which is mainly driven by hydrogen-bond-interactions that are most energetically beneficial for the diprotonated species. Opposingly, the surface charges are best compensated in the case of the free-bases (misfit energy E_mf), while van der Waals interactions E_VdW are energetically most favorable for the mono-protonated species. However, both contributions to the mean interaction energy, as well as their changes, are small as compared to hydrogen bonds. The energetic benefit upon improved hydrogen bonding of the diprotonated species is similar for TMesP and TPP, thus their change in the mean interaction energy at the second protonation is virtually identical. Just small differences in the mean interaction energy between TMesP and TPP at the first protonation contribute to the larger similarity between the Gibbs free energies of the first and the second protonation of TPP as compared to TMesP.

Table 2 Solute–water interactions as calculated via COSMO-RS. E_i is the mean interaction energy, E_mf, E_H, and E_VdW refer to the misfit, hydrogen bonding, and van der Waals energy contributions, respectively. All energies and potentials are given in kJ mol⁻¹

	ΔEi	ΔEmf	ΔEH	ΔEVdW	Δμ	ΔG	pKB
H2P → [H3P]^+	−6.4	1.1	−7.0	−0.5	8.7	−1153.4	11.0
[H3P]^+ → [H4P]^2+	−29.5	0.1	−30.7	1.2	3.6	−1130.1	14.3
H2TMesP → [H3TMesP]^+	−3.6	1.8	−4.9	−0.6	12.2	−1154.9	10.8
[H3TMesP]^+ → [H4TMesP]^2+	−22.2	0.3	−24.6	2.1	4.8	−1139.8	12.9
H2TPP → [H3TPP]^+	−5.1	1.9	−7.2	0.2	13.0	−1163.9	9.5
[H3TPP]^+ → [H4TPP]^2+	−22.2	−0.2	−24.0	2.0	4.8	−1161.7	9.8

---

The energetic contributions due to hydrogen bonds with tetrahydrofuran (THF) are smaller for the free bases but larger for the diprotonated species as compared to water as shown in Table 3. Their changes upon protonation are slightly larger in the case of THF as solvent as compared to water. van der Waals interactions of the solutes with THF are generally larger than in the case of water, hence causing similar energetic changes upon protonation. The compensation of surface-charges depends more strongly on the protonation state and its energetic change upon protonation is generally more unfavorable than in the case of water. However, the relations between the changes in the mean interaction energies upon protonation are very similar to the ones discussed above for water. Finally, THF yields porphyrins with higher basicity when dissolved in water, but the pK_B-difference between the first and second protonation is again smaller for TPP (ΔpK_B = 1.3) as compared to TMesP (ΔpK_B = 3.2).

Table 3 Solute–tetrahydrofuran (THF) interactions as calculated via COSMO-RS. E_i is the mean interaction energy, E_mf, E_H, and E_VdW refer to the misfit, hydrogen bonding, and van der Waals energy contributions, respectively. All energies and potentials are given in kJ mol⁻¹

	ΔEi	ΔEmf	ΔEH	ΔEVdW	Δμ	ΔG	pKB
H2P → [H3P]^+	−9.3	5.4	−14.6	−0.1	−2.7	−1164.8	11.0
[H3P]^+ → [H4P]^2+	−26.9	6.3	−35.1	1.9	−3.8	−1137.5	12.5
H2TMesP → [H3TMesP]^+	−5.8	6.7	−12.1	−0.4	0.1	−1166.9	8.1
[H3TMesP]^+ → [H4TMesP]^2+	−17.2	7.8	−27.4	2.4	−0.4	−1145.0	11.4
H2TPP → [H3TPP]^+	−6.7	6.7	−13.6	0.2	1.1	−1175.8	6.8
[H3TPP]^+ → [H4TPP]^2+	−17.2	7.1	−27.0	2.7	−0.8	−1167.3	8.1

---

In conclusion, the experimentally observed thermodynamic relations between the successive protonation of P, TMesP and TPP could be reproduced by using COSMO-RS and are predominantly determined by the interplay between gas-phase and dielectric screening energies. These gas-phase energies themselves depend on the interplay between steric interactions and molecular π-conjugation, while the dielectric screening energies are determined by the charge distribution at the molecular surface, hence depending also on the molecular geometry and electron delocalization. To identify the molecular origin of the outstanding protonation thermodynamics and kinetics of TPP, we subsequently focused on the geometric and electronic properties of the tetra-meso-aryl-substituted porphyrins.

Structural features and geometric similarity between different protonation states

One contribution to the fast second protonation of TPP might be a larger structural similarity between its mono- and diprotonated form as compared to P and TMesP, what is discussed after presentation of the basic structural features of each investigated derivative.

The oop-exposures of all pyrroles are quantified by the dihedral angles defined by α-, meso-, α- and either β-carbons or nitrogen as the fourth point (θ^βC or θ^N). As shown by these angles, given in Table 4, H₂P and H₂TMesP are planar, while H₂TPP is slightly distorted (θ < 1°). In [H₃P]⁺ and [H₃TMesP]⁺ the protonated pyrroles B are tilted out of plane to a virtually identical extent (θ^N ≈ −9°). Pyrroles A and C (for assignment see Scheme 1) are both tilted oop less and in the opposite direction than pyrrole B ([H₃P]⁺: θ^N = 3°, [H₃TMesP]⁺: θ^N = 5°). The protonated pyrrole B is bent slightly more (Δθ = |θ^βC| − |θ^N| = 3 to 4°) in all mono-protonated porphyrins than all other pyrroles A, C and D (Δθ < 2°). In both mono-protonated derivatives [H₃P]⁺ and [H₃TMesP]⁺, the non-protonated pyrrole D is almost in plane, but with a very small oop-distortion towards a saddle-type geometry ([H₃P]⁺: θ^N = 0°, [H₃TMesP]⁺: θ^N = −2°). In contrast to [H₃P]⁺ and [H₃TMesP]⁺, the non-protonated pyrrole D in [H₃TPP]⁺ is tilted oop considerably (θ^N = −8°), thus possessing a oop-distorted structure similar to the saddle-type geometry of the diprotonated pristine porphyrin [H₄P]²⁺. For all diprotonated derivatives the saddle-type geometry is energetically most favourable, see Table 4 (|θ| for [H₄P]²⁺, [H₄TMesP]²⁺, [H₄TPP]²⁺: 10, 15, 20°).

Table 4 Dihedral angles θ (in degrees) within the porphyrin macrocycle (pyrrole tilt) and between the tetra-meso-aryl substituents and the porphyrin macrocycle (aryl twist). The values of the tilting angle for nonprotonated pyrrole D and twisting angles of adjacent aryls in monoprotonated species are given in bold

		H2P	H3P^+	H4P^2+	H2TMesP	H3TMesP^+	H4TMesP^2+	H2TPP	H3TPP^+	H4TPP^2+
a Numbering is according to Scheme 1. The pyrrole tilts are measured by dihedral angles separately for nitrogen (N21–24) and Cβ carbon atoms (C2,3,7,8,12,13,17,18) on the basis of the bonds between the respective Cα (C1,4,6,9,11,14,16,19) and Cm carbons (C5,10,15,20) averaged for the left and right side of each pyrrole. Pyrroles A and C are protonated in the free bases (H2P, H2TPP, and H2TMesP). Pyrrole B is additionally protonated in the monoprotonated forms (H3P^+, H3TPP^+, and H3TMesP^+) and all four pyrroles are protonated in the diprotonated forms (H4P^2+, H4TPP^2+, and H4TMesP^2+). b Root mean square deviation from planar, i.e. θ = 0°, geometries: . c RMSD difference between two differently protonated species. d The aryl substituent is labelled by the meso-position (C5,10,15,20) to which it is attached. The basis for these dihedral angles is again the bond between the respective carbon atoms in alpha- (C1,4,6,9,11,14,16,19) and meso-positions (C5,10,15,20) and the C1′- and C2′-carbon atoms in the aryl ring. Thereby, for counterclockwise order the sign of the angle has been taken as negative.
Pyrrole A^a	C2,3	0.0	−1.9	−9.6	0.0	−3.6	−14.2	0.0	−9.5	−19.5
	N21	0.0	2.7	9.6	0.0	4.6	14.8	0.4	10.3	20.5
Pyrrole B^a	C7,8	0.0	12.2	9.5	0.0	12.7	14.5	0.7	17.9	19.0
	N22	0.0	−8.5	−9.2	0.0	−9.7	−15.0	−0.2	−15.2	−20.1
Pyrrole C^a	C12,13	0.0	−2.1	−9.3	0.0	−4.1	−14.4	0.5	−9.6	−19.4
	N23	0.0	2.9	9.5	0.0	5.1	15.0	0.3	10.5	20.1
Pyrrole D^a	C17,18	0.0	0.8	9.3	0.0	1.3	14.5	0.6	5.5	19.1
	N24	0.0	−0.3	−9.0	0.0	−1.6	−15.1	−0.7	−8.3	−20.1
RMSD^b		0.0	5.5	9.4	0.0	6.5	14.7	0.5	11.5	19.7
ΔRMSD^c			5.5	3.8		6.5	8.2		11.0	8.3
5-Aryl^d					−90.0	−82.4	−71.4	−71.2	−55.6	−45.6
10-Aryl^d					90.0	81.8	70.4	70.5	55.1	45.6
15-Aryl^d					−90.0	−88.5	−71.8	−70.8	−60.1	−45.6
20-Aryl^d					90.0	88.1	71.2	69.7	60.3	45.2

---

The change in the macrocycle oop-geometry upon protonation is concisely reflected in the root-mean-square-deviations (RMSD) of the above mentioned dihedral angles from the planar geometry. These RMSDs clearly show that the total macrocycle oop-deformations increase from P to TMesP to TPP for each protonation step, respectively. The changes in these RMSDs upon the first protonation are small for P and TMesP (5.5° and 6.5°), but significantly larger for TPP (11.5°). The second protonation causes further oop-deformation, but the oop-geometry-change ΔRMSD is actually smaller for P and TPP (3.8° and 8.3°), but slightly larger for TMesP (8.2°) than in the case of the first protonation. Thus, TPP undergoes an exceptional structural rearrangement during the first protonation, which is significantly smaller for the second protonation. This relation might contribute to the fact that the second protonation is significantly faster than the first one in the case of TPP, hence leading to a domination of H₂TPP and [H₄TPP]²⁺ related absorption features in the course of the titration experiment. However, since the ΔRMSD-values for the second protonation are almost identical for TPP and TMesP, the macrocycle geometry of mono-protonated TPP is not closer to its diprotonated form than in the case of TMesP.

Macrocycle flexibility

After discussing the similarities between the energetically most favorable geometries of the mono- and diprotonated species and the accessibilities of the non-protonated nitrogen atoms, the conclusions drawn were reappraised in view of molecular flexibilities as derived from ab initio molecular dynamics (AIMD) simulations. To analyze the geometries sampled during the AIMD runs, histograms of θ^N angles for each geometry are plotted in Fig. 2.

Fig. 2 Histograms of dihedral angles θ^N, which quantify the oop-distortion and are determined by the flexibility of the macrocycle. For each pyrrole two dihedral angles involving the same nitrogen, but α-, meso-, and next α-carbons in opposing directions can be defined, as indicated in the protonated structures at the top of the figure. Thus, two identically colored lines represent the smoothed histograms of these two dihedral angles.

In the case of all investigated free base porphyrins, the histograms are almost fully superposed and show maxima at 0° and a full-width-at-half maximum of roughly 16°, i.e. predominantly planar macrocycles with similar flexibilities are present for all investigated derivatives. Upon subsequent protonation, saddle-type structures are formed, while in the case of the mono-protonated porphin [H₃P]⁺, the non-protonated pyrrole D stays planar. In contrast, in [H₃TMesP]⁺ and [H₃TPP]⁺ the meso-aryl groups transmit the tilts of pyrroles A and C to D so that the non-protonated pyrrole D is tilted oop by about 10°. Significant differences between the oop-tilt of the non-protonated pyrrole D between [H₃TMesP]⁺ and [H₃TPP]⁺ are not present. In contrast, the histograms of [H₄TMesP]²⁺ and [H₄TPP]²⁺ are vastly different. While the histograms of [H₄TMesP]²⁺ are smooth Gaussian profiles with virtually full superposition for B, D and A, C and maxima at ca. ±15°, respectively, the histograms of [H₄TPP]²⁺ are significantly broader with larger contributions at small θ^N tilt angles. Thus, we conclude that [H₄TPP]²⁺ has a significantly larger oop-flexibility than [H₄TMesP]²⁺ and can more easily adopt to the geometry of its mono-protonated form than the mesityl-substituted derivative. In other words, the weaker restriction in aryl-torsions in the case of TPP as compared to TMesP causes an exceptionally high oop-flexibility of diprotonated TPP,³⁶ what is likely to be an important reason for the exceptionally fast second protonation step in TPP.

The energies that are necessary to distort the mono-protonated forms to the geometry of the diprotonated form, without the second proton, and, opposing, those energies that are necessary to distort the diprotonated form to match the geometry of the mono-protonated form are shown in Fig. 3. The given energies on the left side of each panel, respectively, refer to summed educt energies while those on the right side of each panel refer to the products, respectively, according to the chemical reactions shown below.

Fig. 3 Energies of geometry-optimized mono- and diprotonated species as well as states with geometries matching those of the neighboring protonation state. ^‡labels: mono-protonated species that are distorted to match the geometries of their diprotonated forms (via removing one proton from the diprotonated forms). ^‡′labels: diprotonated species that are distorted to match the geometries of their mono-protonated forms (via constraint geometry optimization after adding a proton to the mono-protonated forms).

Oop-distortions of the mono-protonated forms so that they match the geometries of the diprotonated species [H₃P]^+‡ according to the reaction shown below, necessitate energies of about 50 kJ mol⁻¹ in the gas phase and about 100 to 170 kJ mol⁻¹ if dielectric screening is considered.† This hypothetic reaction path is indicated by dashed lines in Fig. 3.

[H₃P]⁺ + H₃O⁺ → [H₃P]^+‡ + H₃O⁺ → [H₄P]²⁺ + H₂O

In contrast, if the geometry of the mono-protonated form is preserved and a proton is attached according to the reaction below‡ (see dotted lines in Fig. 3),

[H₃P]⁺ + H₃O⁺ → [H₄P]^2+‡′ + H₂O → [H₄P]²⁺ + H₂O

an energetic downhill reaction results for the tetra-meso-aryl-substituted porphyrins in case of a gas-phase calculation. In contrast, dielectric screening in the conductor limit strongly increases the energies, relative to the monoprotonated species, of the hypothetical transient diprotonated species at the geometries of their mono-protonated forms. Essentially, these COSMO-energies show that the energies of the [H₄P]^2+‡′ states and those of the tetra-meso-aryl derivatives are more sensitive towards their solvent environment than the energies of the [H₃P]^+‡ state and those of the tetra-meso-aryl derivatives. It appears reasonable to assume that in a realistic picture, the transient species are not perfectly screened as in the COSMO-calculation. Thus, we obtain a picture in between the gas-phase and the COSMO results, shown in Fig. 3, where the protonation kinetics are substantially influenced by the energy of [H₄P]^2+‡′ related states, i.e. by the flexibility of the diprotonated species. This is in excellent agreement with both the AIMD result, that particularly [H₄TPP]²⁺ has an outstandingly large flexibility, and the experimental findings of an exceptional fast second protonation in the case of TPP as compared to P and TMesP.

Steric interactions between the meso-aryl substituents and the macrocycle

To unravel the influence of the meso-aryl substituents on the above discussed geometric and energetic features, as well as their interplay and the impact of electronic changes on the porphyrin induced by the substituents, the impact of their torsions against the porphyrins on molecular properties are analyzed in the following.

In the case of H₂TMesP, the mesityl groups are perpendicular to the porphyrin and get successively twisted reaching the saddle-type geometry in [H₄TMesP]²⁺, as shown in Table 4. The two mesityls (meso-C5 and meso-C10) next to pyrrole B, which is protonated first, tilt constantly with protonation (H₂TMesP, [H₃TMesP]⁺, [H₄TMesP]²⁺: |δ| ≈ 90, 82, 71°), while the mesityls next to the non-protonated pyrrole D in [H₃TMesP]⁺ (meso-C15 and meso-C20) change their tilt only little compared to the free base structure (H₂TMesP, [H₃TMesP]⁺: |δ| ≈ 90, 88°). This change in the mesityl tilt upon the first protonation is small because the neighboring pyrroles A and C do not get tilted significantly oop upon protonation of H₂TMesP and the non-protonated pyrrole D stays approximately in plane in [H₃TMesP]⁺, thus transmitting little torsion to the mesityls neighboring the non-protonated pyrrole D. In contrast, the meso-phenyl groups in H₂TPP are tilted significantly already in the free base form (|δ| ≈ 70°) and the meso-C5 and meso-C10 phenyls next to the first protonated pyrrole B constantly tilt in slightly larger steps upon protonation (H₂TPP, [H₃TPP]⁺, [H₄TPP]²⁺: |δ| ≈ 70, 55, 46°) as compared to the mesityl-substituted derivatives discussed above. The two phenyls next to the non-protonated pyrrole D in [H₃TPP]⁺ (at meso-C15 and meso-C20) significantly tilt already in the mono-protonated species [H₃TPP]⁺, thus both sterically interacting with the non-protonated pyrrole D, which tilts oop exceptionally strong in [H₃TPP]⁺ (θ^N = −8°) as compared to [H₃P]⁺ and [H₃TMesP]⁺ (θ^N = 0, −2°).

In the case of TMesP, protonated pyrrole tilts are transmitted via the meso-mesityls to the neighboring pyrroles, thus significantly disturbing the porphyrin geometry and π-electron delocalization already at small tilt angles at which the mesityl groups do not yet extend the porphyrin π-system. Because of the lacking ortho-methyl groups in the meso-phenyl substituents, their tilts and the porphyrin distortion are significantly smaller than in the case of the mesityl groups.

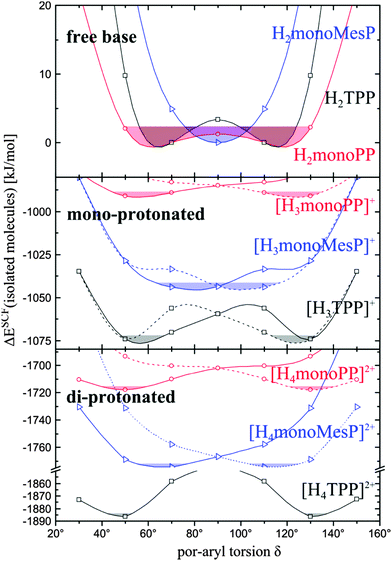
From calculations of torsional profiles of the model substances 5-mono-phenyl- and 5-mono-mesityl-porphyrin (H₂monoPP, H₂monoMesP), which are shown in the upper panel of Fig. 4, it can be concluded that at room temperature the mesityl tilts are approximately 90 ± 10°. In contrast, phenyl tilts are possible between approximately 40° and 140°, with two energetic minima at ∼60° and ∼120° in H₂monoPP. At these tilt angles, considerable π-conjugation between the porphyrin and the meso-phenyls is present⁷⁶ and improves further with co-planarization between both moieties. The energy gain because of this increased π-electron delocalization compensates the energy demand caused by the accompanied oop-tilt of the non-protonated porphyrin according to quantum chemical geometry optimization.

Fig. 4 Torsional profiles of mono-meso-substituted porphyrins. The influence of the different meso-substituents (phenyl, P, and mesityl, Mes) on the SCF energy upon torsion against the porphyrin in the model compounds H₂monoPP and H₂monoMesP and their mono- and diprotonated forms is compared. The torsional profiles of the mono-protonated species refer to protonation of the pyrrole that is closest to the meso-substituent. The dashed graphs are mirrored representatives of the continuous line graphs. Both are asymmetric for the protonated species since the pyrrole oop-twist is different for the two pyrroles neighboring the meso-substituent. The ΔE^SCF values refer to the absolute SCF energies with respect to the energetic minima for H₂monoPP and H₂monoMesP. The gray background (darker: H₂monoPP, lighter: H₂monoMesP) represents torsional angles at which the ΔE^SCF < RT, i.e. which should be the dominant contribution at room temperature.

Upon the first protonation, both monoPP and monoMesP torsional profiles get steeper, which is attributed to the higher steric strain in the protonated macrocycle core. Thus, just one energetic minimum at approximately 50° is obtained for [H₃monoPP]⁺, as shown in the middle panel of Fig. 4. At room temperature (ΔE = kT = 2.4 kJ mol⁻¹), the torsional angle in [H₃monoPP]⁺ varies approximately between 45° and 72° (Δδ ≈ 27°). This variation is similar for [H₃monoPP]⁺ and [H₃monoMesP]⁺ (63° < δ < 95°, Δδ ≈ 32°).

Electronic interactions between the meso-aryl substituents and the macrocycle

While the proton affinities (PAs), which neglect solvent interactions with the porphyrins, for TPP and TMesP are almost identical (cf. differences between pseudo-gas phase energies in Table 1, ), mono-meso-MesP and mono-meso-PP have smaller and significantly different PAs (∼990 and ∼1050 kJ mol⁻¹). Thus, the more meso-aryl substituents are attached to the porphyrin, the better a proton gets stabilized. In the case of the mono-meso-aryl derivatives, the electron-pushing methyl substituents of the meso-mesityl group lead to a significantly larger stabilization (by ∼60 kJ mol⁻¹) of the protonated species than in the case of unsubstituted meso-phenyl functionalization. As shown in Fig. 4, this energy relation holds true for a very broad range of por-aryl torsions, for perpendicular geometries as well as for those around δ = 60°, where considerable π-conjugation between the porphyrin and the meso-aryl groups is present. Thus, improved π-conjugation due to co-planarization between the porphyrin and meso-aryl groups plays a minor role for proton stabilization as compared to the electron pushing influence of the meso-aryl groups.

However, addition of more meso-phenyl groups yields a larger additional cumulative stabilization of the protonated species than addition of meso-mesityl groups, since [H₃TPP]⁺ and [H₃TMesP]⁺ show virtually identical proton affinities . The reason for the similar stabilization by the four meso-phenyls and the four meso-mesityls is the interplay between electronic and geometric stabilization. While the mesityls push more electron density to the core, the porphyrin, with its core crowded with three hydrogens, can sterically relax better towards a saddle-like structure in the case of phenyl- than in the case of mesityl-substitution, as shown by the geometry analysis and the difference in the shape of the torsional potentials discussed above. The difference in sterical relaxation just gets pronounced at multiple meso-aryls attached to the porphyrin core and is negligible for the mono-mesityl-substituted derivatives, where the electronic influence of the meso-substituents dominates the difference in proton affinities.

For the diprotonated species, the torsional profiles get steeper and, in accordance to the geometric features of the energetically most favorable structures discussed above, the positions of the minima slightly shift to larger porphyrin-aryl torsions. Thus, the torsional profiles of monoPP and monoMesP confirm that smaller porphyrin-aryl torsion angles are energetically favorable in monoPP as compared to monoMesP and that these torsional angles generally shift to smaller values on protonation. In the case of TPP, the steric demands of the four meso-phenyls accumulate and cause significantly steeper torsional profiles than those of monoPP, while the energetic minima are approximately at the same torsional angles. Since the minima-positions in the torsional profile of TPP are retained from the one of monoPP, it is assumed that the quantitative comparison between the torsional profile of monoPP and monoMesP can be transferred qualitatively to the comparison of porphyrin-aryl torsions between TPP and TMesP.

Attraction of and accessibility for protons

As briefly mentioned above, the θ^N-oop exposure of the non-protonated pyrrole D in [H₃TPP]⁺ is exceptionally large (−8°, cf.Table 4) as compared to the angles of [H₃P]⁺ and [H₃TMesP]⁺. Thus, it appears probable that the nitrogen atom is sterically and electrically shielded significantly less against protons by the mono-protonated and positively charged macrocycle in the case of TPP as compared to the other derivatives, hence probably contributing to its instantaneous (on the time scale of the titration experiments) protonation. However, in a deeper analysis of accessibility, the molecular surface that can be reached by solvent molecules (the “solvent excluded surface” SES⁷⁷) needs to be considered. This SES is one boundary of the reactivity volume V_react,⁷⁶ while a sphere around the reaction center with a radius of 2 Å that accounts for intermolecular distances is the outer boundary of this reactivity volume. Thus, the V_react accounts for the geometric accessibility of a reaction center for reactants. These reactivity volumes V_react are represented by small 3D-voxels in the molecular representations in Fig. 5 and are divided into one cap above and one beneath the macrocycles.

Fig. 5 van der Waals surface representations of the mono-protonated species [H₃P]⁺, [H₃TMesP]⁺, [H₃TPP]⁺ together with voxels that represent the reactivity volumes V_react. The color coding of the voxels corresponds to the electrostatic potential in the center of each voxel. Color coding of atoms: white, gray, and blue – H, C, and N. Reactivity volumes V_react with their associated mean electrostatic potentials [small phi variant, Greek, macron] are found above and beneath each of the macrocycles and are labelled by solid and dashed lines, respectively, in the bottom panel.

In the free base form, the non-protonated pyrrole D is not tilted oop in H₂P and H₂TMesP, as listed in Table 1. Accordingly, the reactivity caps above and beneath the macrocycle show identical volumes (V_react(H₂P) = 1.88 ų, V_react(H₂TMesP) = 1.87 ų, see gray lines in the bottom panel of Fig. 5). Since the porphyrin in TPP is already distorted in the free base form, the reactivity cap above the macrocycle is larger than the one beneath (V_react(above/beneath): 2.14/1.67 ų). This asymmetry in the V_react of the different caps is present for the mono-protonated species of all considered porphyrin derivatives because of their pyrrole oop-torsion (V_react(above/beneath): [H₃P]⁺: 1.80/1.87 ų, [H₃TMesP]⁺: 1.69/1.77, [H₃TPP]⁺: 2.06/1.44). In accordance with the geometric analysis discussed above (see Table 4), [H₃TPP]⁺ shows an exceptionally large reactivity volume of V_react = 2.06 ų. In contrast to the discussion on dihedral angles, i.e. despite the large dihedral angle of pyrrole D in the mono-protonated form of TPP as compared to the free base, the accessibility volume in [H₃TPP]⁺ is actually slightly smaller than in H₂TPP due to steric shielding in the buckled macrocycle.

For proton transfer not just the geometric accessibility, but also the electron distribution around the reaction center is important. The corresponding mean electrostatic potentials [small phi variant, Greek, macron] within the reactivity volumes of the free bases are slightly positive, [small phi variant, Greek, macron] ≈ 0.05 V, and increase to 1.5–1.9 V for the mono-protonated species. [H₃P]⁺ shows higher [small phi variant, Greek, macron]-values, i.e. stronger proton repulsion, than [H₃TMesP]⁺ and [H₃TPP]⁺. Even if this mean electrostatic potential within the reactivity volumes of these tetra-meso-aryl-substituted derivatives are similar, their φ(r)-distributions differ, as shown in Fig. 5. The purple colored spot of low positive, and for protons weakly repulsive, potentials at the nitrogen lone-pair is larger and has a lower minimum-φ of 0.066 V in [H₃TPP]⁺ as compared to [H₃TMesP]⁺ with φ_min = 0.078 V.

Consequently, the considered nitrogen atom is exceptionally exposed in the free base as well as in the mono-protonated form of TPP as compared to P and TMesP. Additionally, for protons repulsive electrostatic potential shows a large spot with low φ-values, i.e. weak repulsion, at the position of the nitrogen lone pair in [H₃TPP]⁺ in comparison to [H₃TMesP]⁺ and [H₃TPP]⁺. It is expected that both effects contribute to the fact that the second protonation of TPP is faster than for the other derivatives and similarly fast or even faster than the first protonation of TPP, thus explaining why the experimental absorption spectra detected during titration are dominated by H₂TPP and [H₄TPP]²⁺ related absorption features.

Conclusions

In conclusion, the ease of oop-buckling, i.e. molecular flexibility, appears to be the key for understanding the exceptionally fast second protonation of TPP as compared to P and TMesP. Our ab initio molecular dynamics simulations show that particularly [H₄TPP]²⁺ is significantly more flexible than [H₄TMesP]²⁺, while just small differences are found between the mono-protonated species. Thus, the accessible geometric conformational space of [H₄TPP]²⁺ is significantly larger than for [H₄TMesP]²⁺. Accordingly, transitions between geometries of mono- and diprotonated forms are strongly facilitated for TPP as compared to TMesP or P, which corresponds to a lower activation barrier and a faster kinetics of the second protonation. Together with the energetic relations and the pronounced binding spot in [H₃TPP]⁺ mentioned above, the exceptional molecular flexibility of [H₄TPP]²⁺ explains why spectroscopic signatures of just the free base and diprotonated species of TPP are found in the titration experiments, but not [H₃TPP]⁺. Thus, the very similar experimental findings on the exceptional basicities of the monoprotonated form of sterically less demanding meso-aryl porphyrins of Pasternack et al. and of Stone and Fleischer,^43,44 which were discussed focusing on buckling of the free-base forms, need to be reappraised in view of our quantum chemical results focusing on the diprotonated species.

The general conclusions that can be drawn from this work for the development of improved molecular designs are the following. Despite the low π-conjugation between the meso-mesityl substituents and the porphyrin center due to their approximately perpendicular arrangement, the mesityls still significantly push electron density to the porphyrin's core, as shown by quantification of proton stabilization in the section on torsional profiles, i.e. approximately perpendicular geometries between the porphyrin and its substituents do not dramatically disturb their electronic interactions. Nevertheless, those perpendicular geometries are usually caused by steric strain that significantly affects reaction kinetics, as shown by the relative speed of the second protonation between the meso-mesityl and meso-phenyl-porphyrins in this work.

Acknowledgements

This work was supported by an FP-7 grant from the EC for Research, Technological Development and Demonstration Activities, “Dendrimers for Photonic Devices”, under the “International Research Staff Exchange Scheme” IRSES-PEOPLE-2009-247260-DphotoD. W. Maes and W. Dehaen thank the FWO (Fund for Scientific Research – Flanders), the KU Leuven, Hasselt University and the Ministerie voor Wetenschapsbeleid for continuing financial support. M. Presselt acknowledges financial support from the Carl-Zeiss-Foundation. The financial support to Prof. Mikalai Kruk from the State Program of Scientific Researches of the Republic of Belarus “Convergence”, project 3.2.02 “Synthesis of new tetrapyrroles containing supramolecular systems and their applications for the luminescent sensors design”, is also acknowledged. We are also grateful to H. Schwanbeck from the Ilmenau University Computer Center for technical assistance and to Torsten Sachse for providing an efficient code for extraction of dihedral angles from MD-trajectories as well as to Lee-Ping Wang for computational support.

References

1. W. A. Eaton, E. R. Henry, J. Hofrichter and A. Mozzarelli, Nat. Struct. Biol., 1999, 6, 351–358.
2. H. K. Lichtenthaler, Methods Enzymol., 1987, 148, 350–382.
3. M. R. Wasielewski, Chem. Rev., 1992, 92, 435–461.
4. A. Yella, H. W. Lee, H. N. Tsao, C. Y. Yi, A. K. Chandiran, M. K. Nazeeruddin, E. W. G. Diau, C. Y. Yeh, S. M. Zakeeruddin and M. Grätzel, Science, 2011, 334, 629–634.
5. A. Karotki, M. Kruk, M. Drobizhev, A. Rebane, E. Nickel and C. W. Spangler, IEEE J. Sel. Top. Quantum Electron., 2001, 7, 971–975.
6. M. Drobizhev, A. Karotki, M. Kruk and A. Rebane, Chem. Phys. Lett., 2002, 355, 175–182.
7. A. Karotki, M. Khurana, J. R. Lepock and B. C. Wilson, Photochem. Photobiol., 2006, 82, 443–452.
8. M. A. Oar, J. A. Serin, W. R. Dichtel and J. M. J. Frechet, Chem. Mater., 2005, 17, 2267–2275.
9. F. Bedioui and N. Villeneuve, Electroanalysis, 2003, 15, 5–18.
10. M. M. Kruk, A. S. Starukhin, N. Z. Mamardashvili, G. M. Mamardashvili, Y. B. Ivanova and O. V. Maltseva, J. Porphyrins Phthalocyanines, 2009, 13, 1148–1158.
11. B. Saraswathyamma, M. Pajak, J. Radecki, W. Maes, W. Dehaen, K. G. Kumar and H. Radecka, Electroanalysis, 2008, 20, 2009–2015.
12. D. Vlascici, E. Fagadar-Cosma, I. Popa, V. Chiriac and M. Gil-Agusti, Sensors, 2012, 12, 8193–8203.
13. A. Rana and P. K. Panda, RSC Adv., 2012, 2, 12164–12168.
14. A. Ghosh, Angew. Chem., Int. Ed., 2004, 43, 1918–1931.
15. Z. Gross, N. Galili and I. Saltsman, Angew. Chem., Int. Ed., 1999, 38, 1427–1429.
16. D. Aviezer, S. Cotton, M. David, A. Segev, N. Khaselev, N. Galili, Z. Gross and A. Yayon, Cancer Res., 2000, 60, 2973–2980.
17. I. Saltsman, A. Mahammed, I. Goldberg, E. Tkachenko, M. Botoshansky and Z. Gross, J. Am. Chem. Soc., 2002, 124, 7411–7420.
18. A. Mahammed, H. B. Gray, J. J. Weaver, K. Sorasaenee and Z. Gross, Bioconjugate Chem., 2004, 15, 738–746.
19. D. T. Gryko, Eur. J. Org. Chem., 2002, 1735–1743.
20. D. T. Gryko, J. Porphyrins Phthalocyanines, 2008, 12, 906–917.
21. J. A. Shelnutt, X. Z. Song, J. G. Ma, S. L. Jia, W. Jentzen and C. J. Medforth, Chem. Soc. Rev., 1998, 27, 31–41.
22. R. Bonnett, Chemical aspects of photodynamic therapy, Gordon and Breach Science Publishers, Amsterdam, the Netherlands, 2000.
23. M. Drobizhev, A. Karotki, M. Kruk, N. Z. Mamardashvili and A. Rebane, Chem. Phys. Lett., 2002, 361, 504–512.
24. Y. Nakamura, S. Y. Jang, T. Tanaka, N. Aratani, J. M. Lim, K. S. Kim, D. Kim and A. Osuka, Chem. – Eur. J., 2008, 14, 8279–8289.
25. M. Pawlicki, H. A. Collins, R. G. Denning and H. L. Anderson, Angew. Chem., Int. Ed., 2009, 48, 3244–3266.
26. J. R. Stromberg, A. Marton, H. L. Kee, C. Kirmaier, J. R. Diers, C. Muthiah, M. Taniguchi, J. S. Lindsey, D. F. Bocian, G. J. Meyer and D. Holten, J. Phys. Chem. C, 2007, 111, 15464–15478.
27. D. Walker, S. Chappel, A. Mahammed, B. S. Brunschwig, J. R. Winkler, H. B. Gray, A. Zaban and Z. Gross, J. Porphyrins Phthalocyanines, 2006, 10, 1259–1262.
28. G. Li, J. Shinar and G. E. Jabbour, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71.
29. O. Finikova, A. Galkin, V. Rozhkov, M. Cordero, C. Hagerhall and S. Vinogradov, J. Am. Chem. Soc., 2003, 125, 4882–4893.
30. S. Thyagarajan, T. Leiding, S. P. Årsköld, A. V. Cheprakov and S. A. Vinogradov, Inorg. Chem., 2010, 49, 9909–9920.
31. C. J. Medforth, M. O. Senge, K. M. Smith, L. D. Sparks and J. A. Shelnutt, J. Am. Chem. Soc., 1992, 114, 9859–9869.
32. M. O. Senge, J. Photochem. Photobiol., B, 1992, 16, 3–36.
33. M. O. Senge, T. P. Forsyth, L. T. Nguyen and K. M. Smith, Angew. Chem., Int. Ed. Engl., 1995, 33, 2485–2487.
34. C. Y. Li, X. B. Zhang, Z. X. Han, B. Akermark, L. C. Sun, G. L. Shen and R. Q. Yu, Analyst, 2006, 131, 388–393.
35. A. K. Wertsching, A. S. Koch and S. G. DiMagno, J. Am. Chem. Soc., 2001, 123, 3932–3939.
36. A. Rosa, G. Ricciardi, E. J. Baerends, A. Romeo and L. M. Scolaro, J. Phys. Chem. A, 2003, 107, 11468–11482.
37. A. Rosa, G. Ricciardi and E. J. Baerends, J. Phys. Chem. A, 2006, 110, 5180–5190.
38. C. J. Medforth, R. E. Haddad, C. M. Muzzi, N. R. Dooley, L. Jaquinod, D. C. Shyr, D. J. Nurco, M. M. Olmstead, K. M. Smith, J. G. Ma and J. A. Shelnutt, Inorg. Chem., 2003, 42, 2227–2241.
39. M. O. Senge and M. Davis, J. Porphyrins Phthalocyanines, 2010, 14, 557–567.
40. M. O. Senge, C. J. Medforth, T. P. Forsyth, D. A. Lee, M. M. Olmstead, W. Jentzen, R. K. Pandey, J. A. Shelnutt and K. M. Smith, Inorg. Chem., 1997, 36, 1149–1163.
41. B. S. Cheng, O. Q. Munro, H. M. Marques and W. R. Scheidt, J. Am. Chem. Soc., 1997, 119, 10732–10742.
42. O. Q. Munro, H. M. Marques, P. G. Debrunner, K. Mohanrao and W. R. Scheidt, J. Am. Chem. Soc., 1995, 117, 935–954.
43. A. Stone and E. B. Fleisher, J. Am. Chem. Soc., 1968, 90, 2735.
44. R. F. Pasternack, N. Sutin and D. H. Turner, J. Am. Chem. Soc., 1976, 98, 1908.
45. S. Y. Ma, Chem. Phys. Lett., 2000, 332, 603–610.
46. V. N. Knyukshto, K. N. Solovyov and G. D. Egorova, Biospectroscopy, 1998, 4, 121–133.
47. M. M. Kruk and S. E. Braslavsky, J. Phys. Chem. A, 2006, 110, 3414–3425.
48. V. N. Knyukshto, K. N. Solovyov, A. F. Mironov, G. D. Egorova and A. V. Efimov, Opt. Spectrosc., 1998, 85, 540–547.
49. E. B. Fleischer and L. E. Webb, J. Phys. Chem., 1963, 67, 1131.
50. P. Hambrigh and E. B. Fleischer, Inorg. Chem., 1970, 9, 1757.
51. T. Gensch, C. Viappiani and S. E. Braslavsky, J. Am. Chem. Soc., 1999, 121, 10573–10582.
52. M. M. Kruk, A. S. Starukhin and W. Maes, Macroheterocycles, 2011, 4, 69–79.
53. H. Ogoshi, E. Watanabe and Z. Yoshida, Tetrahedron, 1973, 29, 3241–3245.
54. G. De Luca, A. Romeo, L. M. Scolaro, G. Ricciardi and A. Rosa, Inorg. Chem., 2007, 46, 5979–5988.
55. Y. B. Ivanova, A. S. Semeikin and N. Z. Mamardashvili, Russ. J. Gen. Chem., 2009, 79, 1029–1034.
56. O. Almarsson, A. Blasko and T. C. Bruice, Tetrahedron, 1993, 49, 10239.
57. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
58. A. Klamt, F. Eckert, M. Diedenhofen and M. E. Beck, J. Phys. Chem. A, 2003, 107, 9380–9386.
59. F. Eckert and A. Klamt, J. Comput. Chem., 2006, 27, 11–19.
60. F. Eckert, M. Diedenhofen and A. Klamt, Mol. Phys., 2010, 108, 229–241.
61. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
62. M. Von Arnim and R. Ahlrichs, J. Comput. Chem., 1998, 19, 1746–1757.
63. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
64. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
65. M. Sierka, A. Hogekamp and R. Ahlrichs, J. Chem. Phys., 2003, 118, 9136–9148.
66. M. Presselt, C. Schnedermann, M. Schmitt and J. Popp, J. Phys. Chem. A, 2009, 113, 3210–3222.
67. W. Eger, M. Presselt, B. Jahn, M. Schmitt, J. Popp and E. Anders, Inorg. Chem., 2011, 50, 3223–3233.
68. W. J. D. Beenken, F. Herrmann, M. Presselt, H. Hoppe, S. Shokhovets, G. Gobsch and E. Runge, Phys. Chem. Chem. Phys., 2013, 15, 16494–16502.
69. M. Presselt, B. Dietzek, M. Schmitt, A. Winter, M. Chiper, C. Friebe, U. S. Schubert and J. Popp, J. Phys. Chem. C, 2008, 112, 18651–18660.
70. M. Presselt, B. Dietzek, M. Schmitt, S. Rau, A. Winter, M. Jäger, U. S. Schubert and J. Popp, J. Phys. Chem. A, 2010, 114, 13163–13174.
71. W. Beenken, M. Presselt, T. H. Ngo, W. Dehaen, W. Maes and M. Kruk, J. Phys. Chem. A, 2014, 118, 862–871.
72. J. Preiß, M. Jäger, S. Rau, B. Dietzek, J. Popp, T. Martínez and M. Presselt, ChemPhysChem, 2015 DOI:10.1002/cphc.201500223.
73. I. S. Ufimtsev and T. J. Martínez, J. Chem. Theory Comput., 2009, 5, 1004–1015.
74. I. S. Ufimtsev and T. J. Martínez, PetaChem, LLC, Los Altos Hills, CA, v1.5-dev edn, 2012.
75. I. Wolfram-Research, Mathematica Edition: Version 8.0, Wolfram Research, Inc., Champaign, Illinois, 8.0 edn, 2010.
76. M. Presselt, M. Wojdyr, W. J. D. Beenken, M. Kruk and T. J. Martínez, Chem. Phys. Lett., 2014, 603, 21–27.
77. F. M. Richards, Annu. Rev. Biophys. Bioeng., 1977, 6, 151–176.

---

Footnotes

† Theoretical details: Energy calculated by a single-point calculation on a geometry-optimized diprotonated structure with one proton removed.

‡ Theoretical details: Energy derived in a constrained optimization that just allows modification of the second proton coordinates.

---