Spectro-microscopic photoemission evidence of charge uncompensated areas in Pb(Zr,Ti)O₃(001) layers

Abstract

Photoelectron spectroscopy studies of (001) oriented PbTi_0.8Zr_0.2O₃ (PZT) single crystal layers with submicron resolution revealed areas with different Pb 5d binding energies, attributed to the different charge and polarization states of the film surface. Two novel effects are evidenced by using intense synchrotron radiation beam experiments: (i) the progressive increase of a low binding energy component for the Pb core levels (evidenced for both 5d and 4f, on two different measurement setups), which can be attributed to a partial decomposition of the PZT film at its surface and promoting the growth of metallic Pb during the photoemission process, with the eventuality of the progressive formation of areas with downwards ferroelectric polarization; (ii) for films annealed in oxygen under clean conditions (in an ultrahigh vacuum installation) a huge shift of the Pb 5d core levels (by 8–9 eV) towards higher binding energies is attributed to the formation of areas with depleted mobile charge carriers, whose surface density is insufficient to screen the depolarization field. This shift is attenuated progressively with time, as the sample is irradiated with high flux soft X-rays. The formation of these areas with strong internal electric field promotes these films as good candidates for photocatalysis and solar cells, since in the operation of these devices the ability to perform charge separation and to avoid electron–hole recombination is crucial.

---

Introduction

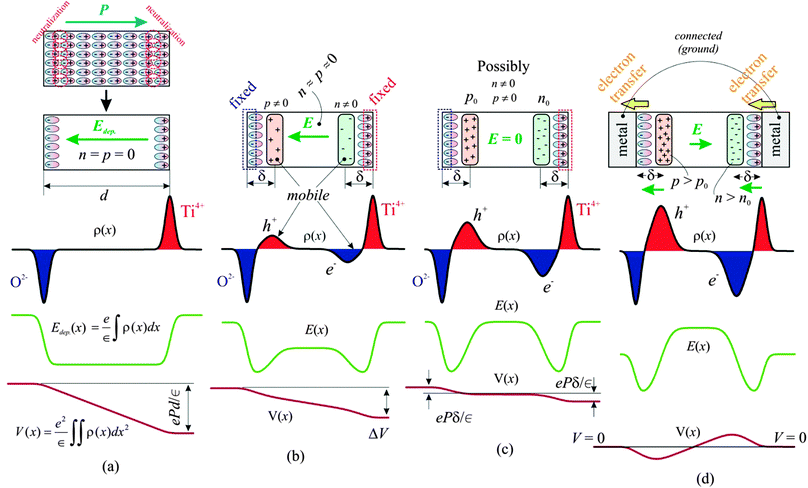
Recently, there has been an increasing interest in using ferroelectric materials in catalysis, photocatalysis¹ and solar energy applications.^2,3 The potential for catalysis is stimulated by the fact that the surface band bending of ferroelectrics exhibiting out-of-plane polarization (see Fig. 4 of ref. 4) stimulates charge transfer, making it possible for oxidation reactions for surfaces exhibiting inwards polarization, and reduction reactions for surfaces exhibiting outwards polarization^4,5 to occur. There is also increasing evidence for adsorption of polar molecules on ferroelectrics,^6,7 and recently the large affinity of areas with outwards polarization for adsorbing sticky contaminant molecules was demonstrated.⁴ An emergent area nowadays is believed to be tunable catalysis, where external electric fields may be used to control the surface reactivity.^8,9 The interplay between mobile charge distribution and surface reconstructions (electronic and atomic) together with stoichiometry variations are still debateds,¹⁰ and one needs deeper surface science and microscopic investigations into these phenomena.

A basic requirement in heterogenous catalysis is a good adsorption of reactant molecules over the catalytic substrate, and this adsorption has been shown to vary strongly with the polarization of ferroelectric supports.^10–12 A next step is the ability of the catalytic material to exhibit reversible charge transfer towards the adsorbed molecules,⁵ and to achieve this aim a good charge separation and, eventually, the existence of an internal field to separate charges inside the solid catalyst is a prerequisite.^1,12 Thus, applications in photocatalysis, solar cells and fuel cells of these materials are due mainly to the ability to separate or to drive charges offered by the intrinsic electric field in the material. Solid oxide fuel cell operation may also be greatly helped by the existence of such an internal field.¹³ In an ideal ferroelectric, this field is called depolarization field and has a sign opposed to the out-of-plane component of the polarization vector, as represented in Fig. 1(a).

Fig. 1 Spatial dependencies of charge density ρ(x), electric field E(x) and potential energies V(x) for the following cases: (a) an uncompensated ferroelectric layer, where only the fixed surface charges produce the depolarization field inside the layer, oriented in the opposite direction with respect to the polarization P. (b) The case of a partial compensation of the fixed charges by the mobile charges (electrons accumulated near the surface with outwards polarization, holes accumulated near the surface with inwards polarization). The overall potential energy dependence decreases in this case. (c) The case of complete compensation of fixed charges by electrons and holes. The electric field vanishes inside the layer, and just a small band bending is manifested near the surfaces of the layer. (d) The case where the potential energy of the two faces is equal, e.g. by using two metal films in electrical contact. Metals pump charges near the surface layers so as to overcompensate the electric field produced by fixed charges. In this case, the electric field inside the ferroelectric layer is weak and oriented in the same direction as the polarization.

In thick ferroelectrics with no metal contacts, the field induced by the static charges (the depolarization field) is compensated for by the formation of thin layers of mobile charges of opposite sign, such that the internal field vanishes, as seen from Fig. 1(c). For thin ferroelectric layers with the ideal structure, i.e. without defects, dislocations or oxygen vacancies, it may so happen that there are not enough charge carriers in the material to generate a mobile charge layer of sufficiently high charge density to compensate for the depolarization field, i.e., in SI units end < P, where e is the elementary charge, n is the charge carrier density, and d the thickness of the layer. In this case, the internal (depolarization) field does not vanish, as represented in Fig. 1(b). This partially compensated situation is suspected to offer considerable potential for photocatalysis, solar and fuel cells.

It is clear that the above simplified picture is valid only for single domain films. The uncompensated depolarization field for thin films is strong enough to suppress the macroscopic polarization.¹⁴ Therefore, uncompensated ferroelectric thin films will exhibit 180° micro- and nanoscopic domains at a macroscopic scale,^14,15 assuming they are strained by the substrate and obliged to feature tetragonal distortion. The question of partial compensation and of the thickness effect is still under debate, and in this respect it is highly desirable to contribute with pictures of the depolarization charge densities at the microscopic level, in addition to the domain structure that might be visualized by standard scanning probe techniques. Pictures of band bending at the microscopic scale are expected to provide more information about these phenomena.

Investigation of band bendings and potential variation by electrical measurements induces an additional perturbation, related to metal–semiconductor Schottky barriers formed at interfaces (which combine with the band bending due to the ferroelectric out-of-plane polarization^16,17), charge injection from the metal into the semiconductor, etc. The situation where two ideal metal contacts are formed on a ferroelectric, with both contacts held at the same potential is represented in Fig. 1(d). In this case, a weaker internal field of magnitude approximately 2Pδ/[∈(d − 2δ)] ≈ 2Pδ/(∈d) will be formed inside the layer, as derived by ‘tilting counter-clockwise’ the potential curve of Fig. 1(c), so as to equalize the potential energy on both sides; this field is oriented in this case in the same direction as the polarization of the ferroelectric. In the above formula and in Fig. 1, δ is the distance between one surface of the layer and the centre of the charge density of mobile carriers accumulated to compensate for the depolarization field (2–20 nm (ref. 18, 19)), and ∈ is the permittivity of the ferroelectric. An internal field will also be present in this case, and the outer electrodes may be transparent, therefore this metal/ferroelectric/metal (MFM) heterostructure offers also some possibilities for photocatalysis and photovoltaics. Also, synergistic effects in catalysis are reported when ferroelectrics are combined with the usual metallic nanoparticles (Pt, Pd)^18,20 and this may be due to the stabilization of charged nanoparticles, again, due to the band bending formed between these nanoparticles and the ferroelectric layer.^21,22

It was recognized more than half a century ago that the surface electronic structure plays a leading role in adsorption–desorption mechanisms,²³ especially under irradiation.²⁴ Therefore, impurities, such as heteroatoms or oxygen vacancies may result in noticeable changes of the surface Fermi energies, inducing different functionalities e.g. in light stimulated adsorption–desorption,²⁴ intimately connected to photocatalysis. Moreover, creation of oxygen vacancies may be accompanied by a reduction of the B-site metal in a perovskite ABO₃,²⁵ an effect which was also connected to the Wolkenstein electronic model of semiconductor catalysts,^23,24 being related to the ability for active electron trapping near the surface. Another related example is the use of co-catalysts such as noble metal nanoparticles (e.g., Pt) selectively adsorbed on faces with well defined P⁽⁺⁾ polarization, which induced the stabilization of reductive areas (by electron accumulation) with highly beneficial effects on photocatalytic reactions such as water splitting.²⁶ As a consequence, it is expected that a wide variety of novel, efficient, catalytic systems will be developed in the near future based on ferroelectric materials.

Before thinking of the exploitation of more complex heterostructures or systems involving the presence of nanoparticles, ferroelectric layers with well defined structure and exhibiting out-of-plane polarization need to be characterized in more detail, possibly by using a non-interacting method. X-ray photoelectron spectroscopy (XPS) was demonstrated recently as a valid method to quantify band bending at metal–semiconductors,²⁷ free ferroelectrics^4,28,29 and metal–ferroelectric heterostructures.^17,21,30,31 The main hypothesis promoting XPS for band bending investigations is the surface sensitivity owing to the low value of photoelectron inelastic mean free path³² (IMFP) and the verified hypothesis that core levels present a rigid shift with the valence band bending to a good approximation (see e.g. Fig. 1(c) from ref. 29 for a principle of this measurement, or Fig. 1(c) from ref. 30 for a demonstration of it). All the previous investigations were performed by using conventional photoelectron spectroscopy, i.e. without spatial resolution. By taking into account that the size of domains formed on usual ferroelectrics is in the sub-μm range,^16,21,31,33 it appears to be desirable to use photoemission spectro-microscopic tools. This work represents the first study aiming to investigate the surface band bendings on single crystal ferroelectric layers with sub-μm resolution by photoemission. The system investigated was lead zirco-titanate PbZr_0.2Ti_0.8O₃ prepared by pulsed laser deposition, and was well characterized from the structural point of view by diffraction methods (X-ray diffraction, reflection high energy electron diffraction RHEED, low energy electron diffraction LEED, and X-ray photoelectron diffraction). Areas with uncompensated polarization by mobile charge were detected on samples, which were cleaned in an ultrahigh vacuum by a well established procedure. Also, the interaction of the high flux synchrotron beam with the sample surface resulted in time-dependent changes of the polarization state of the analyzed areas. These changes offer another possibility for application, namely the ability of triggering the polarization state (and hence, that of the chemical reactivity) by photon impact. This could be important e.g. for lab-on-chip applications.³⁴

Experimental

Samples of lead zirco-titanate (PZT) with the desired composition Pb(Zr_0.2Ti_0.8)O₃ were prepared by pulsed laser deposition (PLD) on SrTiO₃ (STO) (001) single crystal with a 20–30 nm SrRuO₃ (SRO) buffer layer, introduced in order to ground the bottom part of the ferroelectric film by a single crystal conductive layer isomorphic to the STO substrate and to the PZT film, and in order to perform electrical (current–voltage and capacitance–voltage) measurements. The PLD setup (Surface GmbH, Germany) operates with KrF radiation and the preparation conditions are described in greater detail in ref. 21. Special care was paid to the crystallinity of the layers, which is checked in situ during growth by high pressure reflection high energy electron diffraction (HP-RHEED) and also after growth by X-ray diffraction (XRD). Selected samples were investigated with atomic resolution by high resolution transmission electron microscopy (HRTEM). More details are provided in the Supporting Information (SI) of ref. 31 for XRD, and in the ref. 17 (including the SI) for HRTEM. Also, previous investigations by X-ray photoelectron spectroscopy^4,21,29,31 allowed one to infer a fair surface stoichiometry, close to the desired one.

Samples were subjected to ambient pressure between their preparation by PLD and the introduction into ultrahigh vacuum (UHV) photoemission chambers. A detailed study of the contamination of these samples from a few minutes of exposure to environmental conditions up to one week storage time at ambient pressure was presented in ref. 4. In the actual case, the contamination is expected to be even more important, since about 2–5 months are elapsed between the sample preparation and their analysis by photoelectron spectroscopy. After investigation of the samples as introduced, a cleaning procedure consisting of heating at 300–400 °C for three hours in an oxygen partial pressure of 5 × 10⁻⁵ mbar was applied.³⁵ For thin samples (5, 10 and 20 nm), this resulted in reasonable LEED patterns. For thicker samples (such as the 250 nm thick sample, which will be discussed extensively in the spectromicroscopy experiments), LEED was not visible owing to the too insulating character of the film. Nevertheless, X-ray photoelectron diffraction (XPD) was used to probe the existence of crystalline order in as prepared samples. LEED investigations on thinner samples (10 nm) and XPD graphs for thicker samples (250 nm) are presented in the ESI.†

Photoemission experiments were performed in two setups: (i) The SpectroMicroscopy setup the Elettra synchrotron radiation facility in Trieste, Italy. The soft X-ray beam of fixed photon energy (74 eV) is collimated using Schwarzschild optics with a sub-micrometer (0.5 μm FWHM) spot on the sample surface; electrons are detected by using a movable hemispherical mirror analyzer with angular resolution below 0.3 degrees and energy resolution on the order of 50 meV.³⁶ The acquisition software also provides (apart for individual spectra) data cubes, with two spatial coordinates of the sample surface, and the electron kinetic energy as a third axis. It is possible to extract individual spectra from well defined positions of the centre of the beam spot, within a precision of 0.5 μm. (ii) A surface science cluster (Specs) comprising a photoemission chamber (including a Phoibos 150 electron energy analyzer), a scanning tunnelling microscopy (STM) chamber, and a preparation chamber (molecular beam epitaxy, MBE) connected to the SuperESCA beamline also at Elettra.^37–39 In the latter setup, electrons are collected at 45° takeoff angle and the analyzer operates in medium area mode with a pass energy of 20 eV. The estimated experimental resolution under these conditions is about 0.55 eV Gaussian width (FWHM). A flood gun with acceleration voltage of 1 eV and electron current of 0.1 mA was employed to ensure sample neutralization. It has been demonstrated that these flood gun parameters are effective in neutralizing charging effects on highly insulating thin films.^29–31 All ultrahigh vacuum (UHV) chambers operate in low 10⁻¹⁰ mbar vacuum range. The photon flux is estimated to be ∼10¹¹ photons per s at spectromicroscopy (hν = 74 eV) on a circular beam spot of about 0.5 μm diameter, and ∼10¹² photons per s at SuperESCA (hν = 400 eV), with a beam spot defined by an exit slit of 100 × 10 μm².

The XPS data were analyzed with normalized Voigt profiles, which are convolutions of Lorentzian and Gaussian lineshapes.⁴⁰ The inelastic background was simulated with integrals of Voigt lineshapes, also derived from ref. 40. For a doublet, when the spin–orbit splitting exceeds the range of ionization energy or work function of the material, the Lorentzian core level widths are allowed to vary (e.g. from Ti 2p_3/2 to Ti 2p_1/2, separated by about 5.8 eV) to account for the opening of Coster–Kronig decay channels yielding a lower core hole lifetime of the state with higher binding energy.⁴¹ The Lorentzian width is kept the same for a doublet with low spin–orbit splitting separation (Pb 4f, Zr 3d). The same Gaussian width was considered for all components. We mention also that no flood gun was available in the spectromicroscopy experiment.

The morphology and the polarization of the layers are investigated using atomic force microscopy (AFM) and piezoresponse force microscopy (PFM) by using an Asylum Research instrumentation on twin samples prepared in the same PLD run, in air, with no further thermal treatment. A multitude of separate experiments (see e.g.ref. 31) allowed one to infer that the polarization imprint of the film is predominantly oriented outwards.

Results and discussion

As-introduced samples

Fig. 2 presents AFM and PFM images obtained on the 250 nm thick film. From the AFM image analysis, the root mean square (rms) rugosity of the film is derived to be ∼1.0 nm.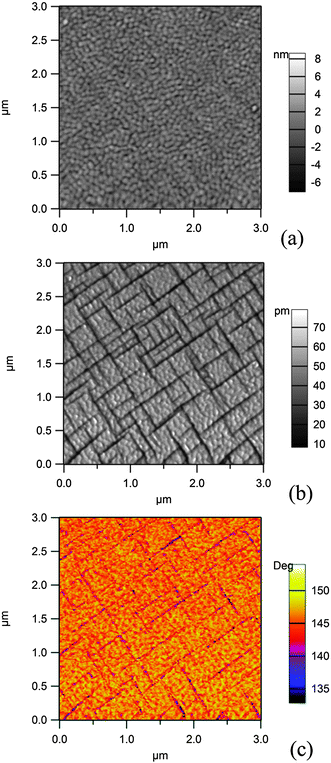

Fig. 2 Scanning probe microscopy (AFM and PFM) investigation of a 250 nm thick PZT(001) layer grown on SRO/STO(001): (a) topography (AFM); (b) amplitude and (c) phase of the PFM signal.

The simultaneous analysis of the amplitude and phase of the PFM signal allows one to infer that the light grey domains in the amplitude signal (Fig. 1(b)), which correspond to the yellow-orange regions of the phase signal (Fig. 1(c)) and representing about 90% of the surface, are a sign of an outward polarization, which will be denoted by P⁽⁺⁾. The dark regions represent areas with in-plane polarization P⁽⁰⁾. Therefore, 90° domain walls are formed. No regions with inward polarization (P⁽⁻⁾) are detected using this method. The maximum size of an area with uniform polarization is about 400 × 400 nm². Therefore, such areas will be of similar size (slightly lower) than the spot at the Spectromicroscopy beamline; thus, there are few chances that the P⁽⁰⁾ areas will be visualized by photoemission microscopy techniques, whereas there are chances to obtain spectra in areas with uniform P⁽⁺⁾ orientation. In the ESI† we also present PFM investigations of a thinner (20 nm) sample. In that case, it is found that the largest amount of the sample surface is in the P⁽⁺⁾ state; this result is at variance with the reported strong decrease of the polarization value for low size nanocrystals of PbTiO₃.^1,42

Before discussing the synchrotron radiation experiments performed on thick (250 nm) layers of PZT further, we will review some results by spatially averaged photoemission obtained for lower thickness samples (20 nm). The choice of this lower thickness was to ensure that the sample is still in a well defined polarization state, while eliminating the eventual problems which might be due to the sample charging during the experiment. Fig. 3 presents X-ray photoelectron spectra recorded at the SuperESCA beamline on a 20 nm thick PZT film as a function of beam exposure time. The spectra are corrected by the Fermi energy. The Zr 3d and Ti 2p signals are decomposed into two different components, one main component and a component with about 0.7–0.8 eV larger binding energy.

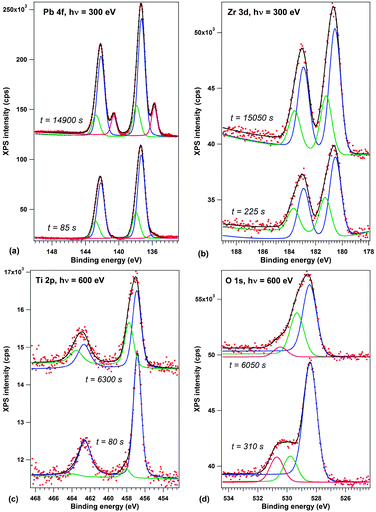Fig. 3 First and last spectra from the recorded time evolution of X-ray photoelectron spectra on a 20 nm PZT film grown on (001)SrTiO₃ covered by a 20 nm SrRuO₃: (a) Pb 4f, recorded with 300 eV photon energy; (b) Zr 3d, 300 eV photon energy; (c) Ti 2p, 600 eV photon energy; (d) O 1s, 600 eV photon energy. The spectra are deconvoluted with Voigt doublets of fixed branching ratios (see the Experimental section for details). Vertical offsets are introduced for clarity. The complete time evolution of XPS spectra is presented in the ESI.†

According to several previous studies,^4,17,31 the main component is attributed to the P⁽⁺⁾ state of the surface. The lower amplitude and higher binding energy component is then attributed to a component with either higher polarization (P⁽⁺⁺⁾) or lower compensation, according to Fig. 1(b and c). The opposite may also be valid, i.e. the P⁽⁺⁺⁾ component represents the completely polarized and screened state of the film, represented in Fig. 1(c), and the P⁽⁺⁾ component represents the state where, owing to some additional charge present at the interfaces, the internal field is reversed, Fig. 1(d). This additional charge may be due to the presence of contaminant molecules⁴ or even some electrons produced by the photoemission process trapped near the sample surface. The shift between the two states is lower than that reported in ref. 17, 21 and 26, and this is consistent with a fraction of the polarization induced band bending ePδ/∈. The O 1s spectra have additionally a component due to contamination, at about 530.5 eV, corresponding to C–O bonds.⁴³ More details about the data analysis and on derivation of stoichiometries for both P⁽⁺⁾ and P⁽⁺⁺⁾ areas are presented in the ESI.† In the following, we shall concentrate more on the origin of the small binding energy component which develops in the Pb 4f spectrum.

One spectrum acquisition lasts about three minutes. The Pb 4f signal, presented in Fig. 3(a), exhibits a clear development of a low binding energy component (about 135.8 eV) with time. During one hour of measurement, the weight of this small binding energy component over the whole Pb 4f signal goes from 2.5% to more than 12%; it evolves up to 18% during the second hour of measurement. We consider that, owing to the IMFP which is evaluated to about 6 Å ≈ 3 atomic layers in the ESI,† the effective number of lead atoms investigated for each elementary cell is about 2 atoms (assuming that the sample is PbO terminated, which is reasonable, if one takes into account the large Pb/(Zr + Ti) signal and IMFP effects). Therefore, the low binding energy signal corresponds to one Pb atom in a different state over 3–4 surface elementary cells (one Pb for 4 elementary cells after one hour, one Pb for 3 elementary cells after two hours).

The main question is the attribution of this low binding energy component.

Hypothesis (i). The first possible attribution would be some photodissociation process occurring at the sample surface, with the formation of metallic Pb, whose tabulated values in the literature for the 4f_7/2 binding energies range between 136.4 eV⁴⁴ and 137.0 eV,⁴⁵ with the most recommended value of 136.82 eV.⁴⁶ Note also that the literature values for Pb 4f in PbTiO₃ range between 137.80 eV⁴⁷ and 138.10 eV,⁴⁸ whereas our previous results for PZT, obtained in a laboratory XPS and by using a flood gun, fall well within these values.^{4,17,21,29–31} Here, the main Pb component has a 4f_7/2 binding energy of 137.3 eV, which is understandable, if one takes into account the intense synchrotron radiation beam. Therefore, the low binding energy component should be ‘re-calibrated’ at about 136.5 eV, and it falls well within the range of reported values for metallic Pb.

A more detailed analysis may be performed by taking into account the reported binding energies for free negatively charged Pb clusters,⁴⁹ where, if one considers also the Pb work function (4.25 eV⁵⁰), the above binding energy with respect to the vacuum level yields 140.75 eV, and this would correspond, according to ref. 49, to (Pb_N)⁻ nanoparticles of about 2 nm size. Let us retain for a later comment that these nanoparticles may be negatively charged. Negatively charged Au nanoparticles were identified to be formed during Au deposition of similar layers of PZT.²¹

At the same time, the main P⁽⁺⁾ component of PZT progressively gets richer in Pb and poorer in oxygen, its stoichiometry evolving such as Pb_1.02Ti_0.90Zr_0.10O_2.80 → Pb_1.81Ti_0.80Zr_0.20O_2.24 (more details are given in the ESI†). This is also quite visible from the evolution of integral amplitudes represented in Fig. 4. Thus, it is reasonable to suppose that Pb–O bonds are somehow broken by interaction with the synchrotron light, oxygen is removed in the form of molecules leaving the UHV chamber, some Pb remains in the perovskite, but also some Pb is ejected in the form of metallic nanoparticles. Formation of Pb metallic nanoparticles was reported also during metal deposition on PZT,⁵¹ and therefore a wide variety of phenomena may yield to the Pb ejection at the sample surface.

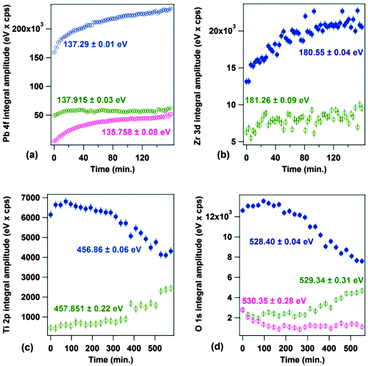Fig. 4 Time evolution of individual integral amplitudes of components extracted from the analysis of the XPS spectra presented in Fig. 2: (a) Pb 4f; (b) Zr 3d; (c) Ti 2p; (d) Zr 3d. The evolution of binding energies is given in the ESI.†

The main argument against this attribution is related to the lack of a similar phenomena when one investigates PZT(111) samples of similar thicknesses, processed under exactly the same conditions. The corresponding Pb 4f spectrum is presented in the ESI.† Therefore, if reduced metallic Pb is formed, somehow this photon induced bond (Pb–O) breaking is highly sensitive to the orientation of the layers. Thus, a second hypothesis connecting this low binding energy peak to a distinct polarization state may be formulated.

Hypothesis (ii). The low binding energy Pb 4f component corresponds to the P⁽⁻⁾ state of the ferroelectric PZT. It has been recently demonstrated by investigating core levels from the substrate in similar structures that photogenerated carriers are efficiently transported across the ferroelectric layer;⁵² however, no photoinduced polarization switch was reported in this experiment (the soft X-ray flux may also different with respect to the actual case). The mechanism for inducing such a polarization switch may be formulated, in a highly exploratory way, as follows: (a) initially, the large majority of the layer is over-compensated,³¹ as represented in Fig. 1(d), with an internal field oriented parallel to the polarization (towards vacuum). Electron–hole generation inside the layer due to the photoabsorption process drives holes near the surface and electrons near the bottom electrode. On some well designed areas, these photogenerated carriers recombine with the existing space charge of opposite sign. Note that the experimental arrangement is such that electrons are escaping from the material, leaving holes near the surface within a few values of the IMFP. These holes must be compensated for by electrons produced by the bottom electrode, but supposing that, owing to electron–hole recombinations, this process is ineffective. Thus, positive charge is still accumulated right under the surface and at a given point its effect would be to produce a switching field, able to reverse the polarization of the layer, at least in some regions. By taking into account the photon flux density of ∼10²¹ photons per (s m²) and the photoionization cross-section of Pb 4f of 3.7 Mbarn (ref. 53) = 3.7 × 10⁻²² m², a Pb atom from the sample undergoes about 0.37 photoionization processes per second. By considering that the photon energy is converted mainly in the kinetic energy of secondary electrons which need about 7 eV to escape from the sample (work function, ∼5.3 eV, plus half of the bandgap, 3.4 eV), each photoionization process produces about 40 pairs of electron and holes, therefore about 15 electron–hole pairs are generated in a second on the area corresponding to an elementary cell (about 15 Ų). This corresponds to the formation of a layer with 1 C m⁻² charge density in 0.07 s if one takes into account only the photoionization processes of a single atomic layer. For about 7 layers containing Pb (the IMFP), the spatial charge needed to reverse the polarization is produced within about 10 ms. Electrons coming from the bottom electrode recombine with the photoinduced holes, but in the actual hypothesis the electron transport across the PZT layer finally yields to an unbalanced charge which is roughly the product of the current defined by the escaping electrons (0.17 μA) and the resistance of the layer (R ∼ up to 10 MΩ¹⁷ for voltages of a few volts). A voltage across the layer of some volts suffices to switch its polarization, whereas the time constant RC is on the order of 10 to 16 seconds.

The main arguments against this attribution are the following two: (a) there is no observation of low binding energy components in the other core level spectra, especially in the Ti 2p and O 1s, which were already shown to be highly sensitive to the P⁽⁻⁾ states;³¹ (b) repeated checks if the low binding energy component of Pb 4f subsists in time, while switching off the synchrotron radiation, yielded the result of an apparent irreversible character of the occurrence of this component. However, this hypothesis could explain the fact that this low binding energy component is not observed in the PZT(111) layer, since the domain structure is more complicated in this case. In the following, with the help of spatially resolved photoemission, we will try to elucidate the origin of this component.

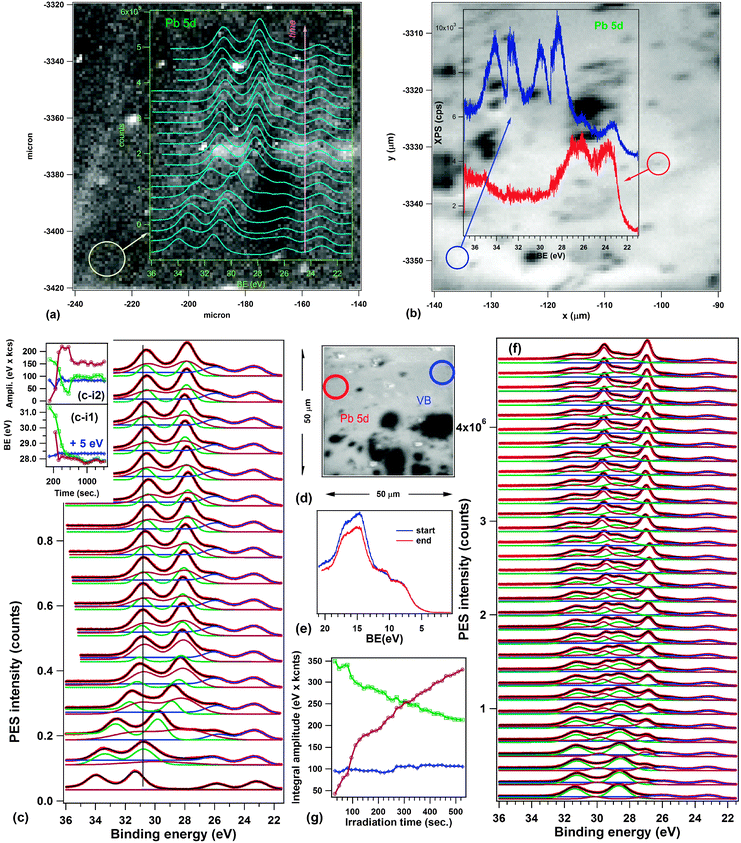
Fig. 5 presents spectromicroscopic data obtained on the 250 nm PZT(001) layer as introduced (i.e., no thermal treatment). The images represent integrals of the photoemitted intensity over the investigated energy area, corresponding to the Pb 5d_5/2 line plus the region before this line, where the low binding energy peak appears. Dark regions represent areas of considerably lower photoemission (see the selected spectra from Fig. 5(a)) and the immediate interpretation of these areas is that they represent regions where the sample is contaminated, yielding to a decrease of the intensity owing electron to IMFP effects. In Fig. 5(b), on two selected areas, one ‘bright’ and one ‘dark’, repeated photoemission spectra have been recorded in order to investigate their time evolution. A spectrum lasts about 40 seconds. One observes the development of the low binding energy component within a much shorter time on the ‘bright’ regions than observed in Fig. 3(a). The binding energy of this peak, uncorrected by the work function, is of 22.2 eV, which compares well with previously reported values for Pb 5d_5/2 in metallic Pb⁰ (22.05 eV for surface and 21.89 eV for bulk).⁵⁴ There are no noticeable differences in the surface sensitivity of the two experiments (the Pb 4f kinetic energy is about 160 eV in the SuperESCA experiment, and the Pb 5d kinetic energy is about 50 eV in the spectromicroscopy experiment, yielding a minimum IMFP of some 4–5 ų²). The only noticeable difference between both experiments is the flux density of photons in the soft X-ray spot, which is of about 5 × 10²⁴ photons per (s m²), i.e. more than three orders of magnitude more intense than at SuperESCA. As a consequence, the same effect as obtained at SuperESCA after about two hours of measurements (44 spectra) is expected to be obtained in the spectromicroscopy setup in a few seconds.

Fig. 5 Spectromicroscopic data obtained on as introduced 250 nm PZT(001): (a) Spectromicroscopy image of PZT(001), representing the total number of counts in the kinetic energy range of Pb 5d_5/2 (49.83–53.66) eV, together with selected spectra in regions outlined by blue circles. (b) Same image as in (a), but with the time evolution of Pb 5d spectra in the regions outlined by blue circles (vertical offsets introduced for clarity). Curve fitting analyses of the time resolved spectra are presented in the ESI.† (c) Another spectromicroscopic image of PZT(001), taken after the analysis of Pb 5d evolution, this time evidencing valence band changes in time in two outlined regions by blue circles. (d) A third spectromicroscopic image of PZT(001), taken after the Pb 5d and the valence band evolution. The regions where longer acquisitions occurred are outlined by blue circles (for Pb 5d) and by green circles (valence band measurements). Full red circles: region used for optimization. Dashed red circle: region which was brighter in (a), but lost intensity after one day of experiments.

Actually, there is a factor close to 1000 in the time constant of the evolution of the low binding energy peak between both experiments. One has also to take into account that the photon energy is lower (by a factor of 4) and the photoionization cross-section of the Pb 5d is higher, some 11.7 Mbarn, yielding on average a lower quantity of emitted secondary electrons for an absorbed photon for the spectromicroscopy experiment. This big difference in the time constant of the increase of the low binding energy peak is not consistent with the assumption formulated in Hypothesis (ii) that the process is governed by the RC time constant of the equivalent circuit of the ferroelectric layer, consisting of a capacitor and a resistance in parallel, connected to a current source (the photoemission process). The RC constant should be the same, no matter what the layer thickness and the investigated area are, and this should be equal to the product between the resistivity and the dielectric permittivity.

Another interesting observation is that on the ‘dark’ (contaminated) areas, the evolution is much slower. If we maintain Hypothesis (i), it means that the contamination layer prevents the formation of metallic Pb. This cannot be attributed to a lower beam intensity effect, since the contamination layer is a few Ångströms thick and the 74 eV beam penetrates inside the sample, the absorption coefficient being on the order of the product of Pb atom density and the absorption cross-section, yielding about 0.02 nm⁻¹. Therefore, one may think about the role of the contamination in preventing the escape of oxygen atoms resulting from photodissociation, and thus less metallic Pb is formed on the surface. At the same time, this process is not completely quenched, since it still happens (according to the left inset of Fig. 5(b)), but with a time constant of at least one order of magnitude higher. In the ESI† a more detailed analysis by curve fitting of the spectra from Fig. 5(b) is provided.

Selected valence band spectra, by performing again a time dependent series, are shown in Fig. 5(c). It may be seen that in the ‘contaminated’ areas there is no visible change in the valence band over almost one hour, whereas in the ‘clean’ areas the valence band evolves, but not dramatically. The Pb 5d core level evolution is much more important. One notices, however, a small shift of the onset of the valence band maximum by some 0.2 eV towards lower binding energies after irradiation, and that the binding energy corresponding to the valence band offset is quite close to the Pb work function (about 4.3 eV). Note also, in Fig. 5(c and d) the clear signs (white spots) of the areas where extended investigations (exceeding one half an hour) were performed. These areas subsist for several hours. The diffuse bright area in the upper right corner of the analyzed area in Fig. 5(a and b) was produced during the optimization procedure of the sample in the focus of the analyzer. Interestingly, this area disappears after a while (in Fig. 5(c and d)). About 20 hours were spent from starting working on this sample and the recording of the image from Fig. 5(d). This means that, if the ‘bright’ areas are due to the formation of surface Pb, in some cases this Pb may recombine after a while, especially when neighboring areas are investigated extensively. In this case, the Pb–O dissociation seems to be a reversible process, at the scale of 10–20 hours.

Interestingly, the same is the scale in which the P⁽⁻⁾ state subsists in several laboratory PFM experiments under air. This pushes us not discard yet completely the hypothesis (ii) from above, namely, the formation of P⁽⁻⁾ areas on the irradiated samples.

Annealed samples

Fig. 6 shows the spectromicroscopy results of the 250 nm PZT(001) after the annealing procedure. The most important result is presented in Fig. 6(a), where the time dependent evolution of the Pb 5d region was superimposed on the spectromicroscopic image. Fig. 6(c) presents the detailed curve fitting analysis of these data. One identifies in the beginning two distinct doublets, one placed at the ‘normal’ binding energy (about 23.2 eV for Pb 5d_5/2) and the other one, more intense, with a huge shift of about 8.2 eV towards higher binding energies. This shift cannot be attributed to a different chemical state, but rather to the realization of an uncompensated situation, as depicted in Fig. 1(a and b). The following hypothesis may be used to explain this behaviour: during the annealing in an oxygen atmosphere, the sample surface becomes clean, the stoichiometry of the layer is rebuilt, and the layer becomes a good insulator. The XPD patterns presented in the ESI† support this hypothesis of a good sample quality. Therefore, it cannot provide enough charge carriers to compensate the depolarization field at microscopic level, as commented in the Introduction. By irradiating with soft X-rays, electrons and holes are produced inside the layer and they migrate near the film surfaces, to establish the depolarization charge sheets. More precisely, electrons generated in the bulk are expected to migrate near the surface and holes near the bottom interface, since the depolarization field is oriented inwards. Thus, the overall band bending of the film decreases in time. Note also that the presence of ferroelectric order is crucial to explain this behaviour: for a ‘normal’ insulating sample, the standard behaviour is that, with progressive photoemission, more and more electrons escape from the sample and the surface becomes positively charged, enhancing the observed binding energies.

Fig. 6 Spectromicroscopic data obtained on the 250 nm PZT(001) layer after annealing in oxygen: (a) Spectromicroscopic image obtained on annealed PZT(001). Superposed: a time evolution of the Pb 5d signal. (b) Spectromicroscopic image obtained over the whole energy range designed in the superposed graph, with two typical spectra obtained on areas outlined with blue and red circles. (c) The analysis of the time evolution of the Pb 5d signal from (a). Inserted in the upper right corner: (c-i1) binding energies and (c-i2) integral amplitudes resulted from deconvolution. (d) An area plot of the total intensity, with the regions where the Pb 5d time evolution was recorded outlined by the red circle, and the time evolution of the valence band, represented in (e) (just the starting and the ending situation) recorded in the area outlined by the blue circle. (f) Time evolution of the Pb 5d signal, together with deconvolutions by using three components, whose integral amplitudes are represented in (g). The binding energies of individual components do not vary considerably in this case and their evolution is not represented.

Thus, Fig. 6(a and c) are direct evidence of the formation of partially compensated areas on the ferroelectric. The nonzero internal field in the sample may be estimated (according to the considerations from the Introduction, and neglecting the δ parameter) as 8.2 V/250 nm ≈ 3.3 × 10⁷ V m⁻¹, and if one multiplies by the permittivity of vacuum and by an estimated dielectric constant of 180,^19,21 the ‘uncompensated’ charge density yields a value of about 5 μC cm⁻². Irradiating with soft X-rays for about 5 minutes decreases this charge density (and the corresponding band bending) to half of the above values. Thus, such layers, processed in UHV, could have potential applications in photocatalysis and in light driven catalytic processes. The estimated carrier density of these layers may be easily evaluated by considering the saturation polarization determined by ferroelectric hysteresis loops¹⁹ (87 μC cm⁻²), from which one subtracts 5 μC cm⁻², divided by the elementary electronic charge and by the thickness of the layer: the result is in the range of 2 × 10¹⁹ cm⁻³, including the photogenerated carriers.

Fig. 6(b) shows how, in some areas, one can still obtain the ‘compensated’ situation (the red photoemission curve), whereas there are areas which present concomitantly two ‘uncompensated’ situations, with overall band bendings of 8.9 eV and 4.5 eV. We still do not have an explanation as to why the second chemical shift (BE2) is nearly half of the first one (BE1).

It is also interesting to note that the time evolution represented in Fig. 6(a) and by scanning along all individual spectra contained in the data from Fig. 6(b) we did not find any trace of the low binding energy peak. It seems that improving the structure and the stoichiometry by treating the sample in oxygen prevents the ejection of Pb⁰ (Hypothesis (i)) or the formation of P⁽⁻⁾ areas (Hypothesis (ii)). However, when we tried to check further this finding on a different area of the sample, we found the situation represented in Fig. 6(d–g). Here one starts with a superposition of the ‘normal’ spectrum and the spectrum with the chemical shift BE2; then, progressively, a lower binding energy sharp structure with respect to the component BE2 develops, whereas the ‘basic’ component remains unaffected. It is hard to believe that a P⁽⁻⁾ component could develop based on a P⁽⁺⁾ component which is only partially compensated. The whole mechanism sketched in the previous paragraph to explain the possible occurrence of the P⁽⁻⁾ component fails in this case, simply because the uncompensated depolarization field would drive photogenerated holes towards the bottom electrode. Therefore, this last figure suggests that the explanation of the sharp component shifted towards lower binding energies is indeed reduced Pb, which in this case occurs on the top of the partially compensated BE2 areas. The fact that the ‘normal’ component does not exhibit this component may be related to a possible migration of Pb atoms, once ejected, towards the BE2 area.

Possibly, the Pb atoms or clusters become slightly negatively charged, as we mentioned when analyzing the first XPS data. It is now worth mentioning that the Pb work function (4.25 eV⁵¹) is considerably lower than that of PZT (5.1–5.3 eV^17,21,31), thus normally electrons should be transferred to PZT from these metallic moieties. In order to explain a reversed charge transfer, one has to consider the fact that the area that ejected Pb is already oxygen depleted (according to the XPS results), therefore the Fermi level is pinned close to the conduction band, owing to a strong local n doping. The valence band spectra from Fig. 6(e) are in line with this assumption. At the same time, we assumed that small Pb nanoparticles of about 2 nm are formed: their ionization energies are higher than the metallic Pb work function, being in the range of 5.3–6.6 eV, and their electron affinities are in the range of 3.8 eV.⁵⁵ Thus, it costs a lower amount of Koopman energy to promote an electron from PZT to a Pb_N nanoparticle than to do the reverse. Other correlation effects, especially the presence of positive fixed charge could contribute to favouring this process of stabilization of the negatively charged nanoparticle. Thus, it is reasonable to suppose that these nanoparticles are attracted more by BE2 areas, which are positively charged.

With this migration mechanism in mind, one may also try to explain the disappearance of the extended bright region from Fig. 5(a) to (d): this region was due, at the beginning, to metallic Pb structures photogenerated during the optimization process; but, progressively, by taking into account that neighbouring areas of the sample are constantly positively charged by photoemission, these Pb atoms migrate there, where other Pb atoms are also ejected, up to the release of the region they occupy initially. This Pb mobility, together with the fact that these clusters are slightly negatively charged (this could explain also the lower binding energy recorded for these entities) could eventually also be exploited in surface chemical reactions. Migration of carbon-containing contaminants was proposed also to explain the evolution of XPS spectra from ‘fresh’ to ‘contaminated’ samples in ref. 4, and lead is isoelectronic with carbon. Also, migration processes may be invoked for the lack of the formation of metallic Pb in PZT(111), according to the results presented in the ESI.† It may happen that, on a (111) surface which also presents Ti(Zr) ions, these strongly positive ions may act as traps for slightly negatively charged Pb atoms or clusters. Thus, migration will be considerably reduced in this case and the formation of Pb nanoparticles is less favourable. Without being able to migrate, Pb progressively recombines with oxygen from the bulk or eventually stabilizes in an inert surface reconstruction. These are open questions to be answered by future experiments.

A last remark is that the valence band recorded in this last experiment (Fig. 6(e)) can also be regarded as a superposition of two components: (i) the ‘basic’ PZT component (lowest binding energy); (ii) the BE2 component (highest binding energy) with a clear signature of the Fermi level due to metallic Pb present on this surface.

Conclusions

Two new phenomena were put in evidence by the actual experiments. First of all, the development of a sharp and low binding energy component in the Pb 4f and Pb 5d spectra is commented by considering two hypotheses, the formation of metallic (reduced) Pb nanoparticles and the promotion of P⁽⁻⁾ areas of the samples. Although initially there were arguments and counter-arguments for each hypothesis, a comparative analysis of the XPS, composition and spectromicroscopy data allowed us to attribute this component to the formation of Pb⁰, also introducing the hypothesis that Pb is found on the surface in the form of clusters of about 2 nm size. New concepts emerged from this analysis, connected to the ability of Pb to migrate on the surface and to the fact that Pb nanoparticles might be negatively charged.

The second phenomenon identified is of more prominent practical interest: it was found that, after an annealing procedure in oxygen by using a UHV setup, one may produce samples with good quality, highly insulating: on some areas of these samples, there is not enough surface charge carrier density at room temperature to build up the two depolarization charge sheets and to screen the depolarization fields. Therefore, a robust internal field value of about 33 V μm⁻¹ subsists inside the ferroelectric layer and might be used to separate photogenerated electron and holes, or to promote considerably different electrode potentials of the two faces of the film. It is easy to estimate that the value of electron/hole acceleration into this field is of about 6 × 10¹⁸ m s⁻² and they may separate ballistically by several μm in a picosecond, which is believed to be a lower bound for the recombination time.² For example, in BiFeO₃ much larger recombination times (tens of microseconds) were recently reported.⁵⁶ Also, the strong dependence of the overall band bending and of the internal field on the soft X-ray beam used for analysis opens new perspectives to investigate the tunable band bending effect by using UV and/or visible sources. The goal of light triggered catalysis, together with other possible applications in photocatalysis or photovoltaics, promote ferroelectric single crystal layers as viable candidates for future applications in these areas. Last but not least, heteroatom mediated band engineering able to trigger photoadsorption and photodesorption processes, based on the venerable work of Wolkenstein,^23,24 may be reconsidered and eventually improved by considering ferroelectricity. This is in order to set up a basic theory suitable for the expected growth in the area of ferroelectrics catalysis and photocatalysis, taking into account the actual performances in the synthesis of single crystal ferroelectric layers with well-defined polarization.

Acknowledgements

Access to the Elettra synchrotron radiation facility was granted through Proposal Nos. 20130333 and 20135077. This work was funded by the Romanian Ministry of Education and Research through the Complex Research Grant PN-II-ID-PCCE-2011-2-0006 (Contract No. 3/2012).

Notes and references

1. L. Li, P. A. Salvador and G. S. Rohrer, Nanoscale, 2014, 6, 24–42.
2. Y. G. Yuan, Z. G. Xiao, B. Yang and J. S. Huang, J. Mater. Chem. A, 2014, 2, 6027–6041.
3. D. W. Cao, C. Y. Wang, F. G. Zheng, L. Fang, W. Dong and M. R. Shen, J. Mater. Chem., 2012, 22, 12592–12598.
4. L. E. Ştoflea, N. G. Apostol, L. Trupinǎ and C. M. Teodorescu, J. Mater. Chem. A, 2014, 2, 14386–14392.
5. Y. F. Cui, J. Briscoe and S. Dunn, Chem. Mater., 2013, 25, 4215–4223.
6. D. G. Li, M. H. Zhao, J. Garra, A. M. Kolpak, A. M. Rappe, D. A. Bonnell and J. M. Vohs, Nat. Mater., 2008, 7, 473–477.
7. K. Garrity, A. M. Kolpak, S. Ismail-Beigi and E. I. Altman, Adv. Mater., 2010, 22, 2969–2973.
8. A. M. Kolpak, I. Grinberg and A. M. Rappe, Phys. Rev. Lett., 2007, 98, 166101.
9. K. Garrity, A. Kakekhani, A. Kolpak and S. Ismail-Beigi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 045401.
10. Y. Yun and E. I. Altman, J. Am. Chem. Soc., 2007, 129, 15684–15689.
11. Y. Yun, L. Kampschulte, M. Li, D. Liao and E. I. Altman, J. Phys. Chem., 2007, 111, 13951–13956.
12. N. V. Burbure, P. A. Salvador and G. S. Rohrer, Chem. Mater., 2010, 22, 5823–5830.
13. S. B. Adler, Chem. Rev., 2004, 104, 4791–4843.
14. B. C. Huang, Y. T. Chen, Y. P. Chiu, Y. C. Huang, J. C. Yang, Y. C. Chen and Y. H. Chu, Appl. Phys. Lett., 2012, 100, 122903.
15. J. Junquera and P. Ghosez, Nature, 2003, 422, 506–509.
16. R. Ahluwalia and D. J. Srolowitz, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 174121.
17. I. Pintilie, C. M. Teodorescu, C. Ghica, C. Chirilǎ, A. G. Boni, L. Hrib, I. Pasuk, R. Negrea, N. G. Apostol and L. Pintilie, ACS Appl. Mater. Interfaces, 2014, 6, 2929–2939.
18. L. Pintilie and M. Alexe, J. Appl. Phys., 2005, 98, 124103.
19. L. Pintilie, I. Boerasu, M. J. M. Gomes, T. Zhao, R. Ramesh and M. Alexe, J. Appl. Phys., 2005, 98, 124104.
20. C. Y. Chao, Z. H. Ren, Y. H. Zhu, Z. Xiao, Z. Y. Liu, G. Xu, J. Q. Mai, X. Li, G. Shen and G. R. Han, Angew. Chem., Int. Ed., 2012, 51, 9283–9287.
21. N. G. Apostol, L. E. Ştoflea, G. A. Lungu, C. Chirilǎ, L. Trupinǎ, R. F. Negrea, C. Ghica, L. Pintilie and C. M. Teodorescu, Appl. Surf. Sci., 2013, 273, 415–425.
22. J. Y. Lan, X. M. Zhou, J. G. Yu, J. C. Zhang, L. J. Zhi and G. J. Nie, Nanoscale, 2011, 3, 5161–5167.
23. T. Wolkenstein, Adv. Catal., 1960, 12, 189–264.
24. T. Wolkenstein, Discuss. Faraday Soc., 1961, 31, 209–218.
25. M. Florea, M. Alifanti, V. Kuncser, D. Macovei, N. Apostol, P. Granger and V. I. Parvulescu, J. Catal., 2014, 316, 130–140.
26. C. Zhen, J. C. Yu, G. Liu and H.-M. Cheng, Chem. Commun., 2014, 50, 10416–10419.
27. H. Sezen and S. Suzer, Thin Solid Films, 2013, 534, 1–11.
28. F. Chen and A. Klein, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 094105.
29. N. G. Apostol, L. E. Ştoflea, G. A. Lungu, C. A. Tache, L. Pintilie and C. M. Teodorescu, Mater. Sci. Eng., B, 2013, 178, 1317–1322.
30. N. G. Apostol, L. E. Ştoflea, G. A. Lungu, L. C. Tǎnase, C. Chirilǎ, L. Frunzǎ, L. Pintilie and C. M. Teodorescu, Thin Solid Films, 2013, 545, 13–21.
31. L. E. Ştoflea, N. G. Apostol, C. Chirilǎ, L. Trupinǎ, R. Negrea, L. Pintilie and C. M. Teodorescu, J. Mater. Sci., 2014, 49, 3337–3351.
32. S. Hüfner, Photoelectron Spectroscopy: Principles and Applications, Springer, Berlin, 3rd edn, 2003, p. 9.
33. I. Vrejoiu, M. Alexe, D. Hesse and U. Gösele, Adv. Funct. Mater., 2008, 18, 3892–3906.
34. R. Ferris, B. Yellen and S. Zauscher, Small, 2012, 8, 28–35.
35. I. Krug, N. Barrett, A. Petraru, A. Locatelli, T. O. Mentes, M. A. Niño, K. Rahmanizadeh, G. Bihlmayer and C. M. Schneider, Appl. Phys. Lett., 2010, 97, 222903.
36. P. Dudin, P. Lacovig, C. Fava, E. Nicolini, A. Bianco, G. Cautero and A. Barinov, J. Synchrotron Radiat., 2010, 17, 445–450.
37. A. Abrami, M. Barnaba, L. Battistello, A. Bianco, B. Brena, G. Cautero, Q. H. Chen, D. Cocco, G. Comelli, S. Contrino, F. DeBona, S. Di Fonzo, C. Fava, P. Finetti, P. Furlan, A. Galimberti, A. Gambitta, D. Giuressi, R. Godnig, W. Jark, S. Lizzit, F. Mazzolini, P. Melpignano, L. Olivi, G. Paolucci, R. Pugliese, S. N. Qian, R. Rosei, G. Sandrin, A. Savoia, R. Sergo, G. Sostero, R. Tommasini, M. Tudor, D. Vivoda, F.-Q. Wei and F. Zanini, Rev. Sci. Instrum., 1995, 66, 1618–1620.
38. S. Lizzit, G. Zampieri, L. Petaccia, R. Larciprete, P. Lacovig, E. D. L. Rienks, G. Bihlmayer, A. Baraldi and P. Hofmann, Nat. Phys., 2010, 6, 345–349.
39. N. G. Gheorghe, G. A. Lungu, R. M. Costescu and C. M. Teodorescu, Phys. Status Solidi B, 2011, 248, 1919–1924.
40. C. M. Teodorescu, J. M. Esteva, R. C. Karnatak and A. El Afif, Nucl. Instrum. Methods Phys. Res., Sect. A, 1994, 345, 141–146.
41. D. Luca, C. M. Teodorescu, R. Apetrei, D. Macovei and D. Mardare, Thin Solid Films, 2007, 515, 8605–8610.
42. E. K. Akdogan, C. J. Rawn, W. D. Porter, E. A. Payzant and A. Safari, J. Appl. Phys., 2005, 97, 084305.
43. M. Iliuţ, C. Leordean, V. Cânpean, C. M. Teodorescu and S. Aştilean, J. Mater. Chem. C, 2013, 1, 4094–4104.
44. L. Ley, S. P. Kowalczyk, F. R. McFeely, R. A. Pollak and D. A. Shirley, Phys. Rev. B: Solid State, 1973, 8, 2392–2402.
45. C. D. Wagner and J. A. Taylor, J. Electron Spectrosc. Relat. Phenom., 1980, 20, 83–93.
46. C. J. Powell, J. Electron Spectrosc. Relat. Phenom., 2012, 185, 1–3.
47. A. P. Dementjev, O. P. Ivanova, L. A. Vasilyev, A. V. Naumkin, D. M. Nemirovsky and D. Y. Shalaev, J. Vac. Sci. Technol., A, 1994, 12, 423–427.
48. C. J. Lu, A. X. Kuang and G. Y. Huang, J. Appl. Phys., 1996, 80, 202–206.
49. J. Bahn, P. Oelßner, M. Köther, C. Braun, V. Senz, S. Palutke, M. martins, E. Rühl, G. Ganteför, T. Möller, B. von Issendorf, D. Bauer, J. Tiggesbäumker and K.-H. Meiwes-Broer, New J. Phys., 2012, 14, 075008.
50. in CRC Handbook of Chemistry and Physics, (Ed.-in-Chief) D. L. Lide, CRC Press, Boca Raton, 75th edn, 1995, p. 12–114.
51. F. Chen, R. Schafranek, W. Wu and A. Klein, J. Phys. D: Appl. Phys., 2011, 44, 255301.
52. C.-L. Wu, P.-W. Lee, Y.-C. Chen, L.-Y. Chang, C.-H. Chen, C.-W. Liang, P. Yu, Q. He, R. Ramesh and Y.-H. Chu, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 020103(R).
53. J. J. Yeh and I. Lindau, At. Data Nucl. Data Tables, 1985, 32, 1–155.
54. D. Jablonskyi, M. Patanen, S. Aksela and H. Aksela, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 041101(R).
55. C. Rajesh and C. Majumder, J. Chem. Phys., 2007, 126, 244704.
56. M. Alexe, Nano Lett., 2012, 12, 2193–2198.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp04546g

---