Tuning spin polarization and spin transport of zigzag graphene nanoribbons by line defects
G. P.
Tang
*,
Z. H.
Zhang
*,
X. Q.
Deng
,
Z. Q.
Fan
and
H. L.
Zhu
Institute of nanomaterial & nanostructure, Changsha University of Science and Technology, Changsha 410114, China. E-mail: guipingtang@163.com; cscuzzh@163.com
First published on 28th October 2014
Abstract
From first-principles methods, the spin-dependent electronic properties of zigzag-edged graphene nanoribbons (ZGNRs) with a line defect (558-defect) are investigated systematically and compared to those of the pristine ZGNR. Results show that the line defect possesses an obvious tuning effect on the spin-polarization of the edge carbon atoms of the defective ZGNRs, and the spin-polarization and spin-transport are sensitive to the position of line defects. The defective ZGNRs can realize a transition from antiferromagnetism (AFM) to ferrimagnetism and ferromagnetism (FM) via changing the position of line defects from the center to the zigzag edge of ZGNRs. More importantly, when the line defect is located at the one edge, the defective ZGNRs exhibit the long-range magnetic ordering at edges with a high Curie temperature up to 276 K, and the defective ZGNR system can generate a high-performance spin-filter effect in the large bias range, 0.0–0.5 V. Such a sensitive modulation for the spin-polarization and spin-transport holds great promise for applications of the graphene-based systems in nano-scale spintronic devices.
1. Introduction
Nanostructured magnetic materials have a wide range of applications in the field of spintronics. There have been continuing efforts to search for new magnetic nanomaterials, and much recent interest has been devoted to the magnetism of carbon-based, especially graphene-based structures.1–6 Graphene has a fairly simple honeycomb atomic structure, a rather unique electronic structure, a long spin relaxation length and lifetime, and can be used as an excellent ballistic spin transport channel.7–10 The magnetic graphene nanostructures are particularly promising for spintronics applications, a very probable future step in the evolution of the electronics industry, which promises information storage, processing and communication at a faster speed and with a lower energy consumption.11–13 Although the pristine two-dimensional (2D) infinite graphene sheet is nonmagnetic (NM), zigzag-edged graphene nanoribbons (ZGNRs) have magnetic edges as a result of electron spin polarization, which have been theoretically predicted and experimentally confirmed.14–17 Magnetic zigzag edges of graphene are considered as a basis for novel spintronics devices. However, for the ground-state electronic configurations of ZGNRs, the spin polarization at the two edges has an opposite orientation,18 and the antiferromagnetic coupling results in no net magnetic moment in the system. This hinders further applications of ZGNRs in spintronics. In addition, the spin-resolved edge magnetism of ZGNRs has been found to be highly unstable owing to lack of the long-range magnetic ordering with a good transition temperature, thus also making it difficult for spintronics applications under ambient conditions, which is also the primary factor that the feasibility of the proposed nanoscale spintronics devices currently based on graphene edge magnetism is questioned.19,20 Therefore it is highly desirable to tune the spin polarization at edges of ZGNRs for realizing transition from antiferromagnetism (AFM) to ferromagnetism (FM), and establishing the long-range magnetic ordering at edges with a high Curie temperature.Currently, a few possible methods have been proposed,21–27 but how to achieve experimentally remains challenging. For example, Sawada et al. found that injecting carriers (electrons or holes) to ZGNR can yield a ferromagnetic coupling between the two edges.21 Transition to FM can also be induced by the substrate magnetic field when ZGNRs are deposited on the graphene/Ni(111) surface.22 However, the exchange energies are very small. Xu et al. demonstrated that the transition to FM is possible when one carbon atom at one edge is saturated by two H atoms and that at the other edge by one H,26 but such a precise control is not easy experimentally.
One of the alternative approaches is to introduce extended defects into the graphene lattice.28–33 The topological line defects composed of octagons and fused pentagons have been observed experimentally in graphene sheets (see Fig. 1(b)).28 The presence of the line defect makes the graphene sheet show the metallic character, which is consistent with the theory proposed by Yazyev et al. based on the momentum conservation rule.34 When the line defect is introduced into ZGNRs, the presence of localized states in the line defect may have different effects on the electronic states of the two spins and change the magnetic behavior of the system. In the present work, using the first-principles approach, we investigate systematically the impact of a line defect on spin-dependent electronic properties of ZGNRs. We try to tune the spin-polarization and spin-transport of ZGNRs via an introduced line defect, and explore the Curie temperature and the spin-filter effect for the ZGNRs with the line defect.
 | ||
| Fig. 1 (a) The structural model of the relaxed ZGNR with an extended topological line defect; the line defect consists of one octagon (filled by blue) and a pair of pentagons (filled by red) periodically repeated along the edge direction. All edge carbon atoms are saturated with hydrogen atoms, the blue (white) spheres represent C (H) atoms, and the area surrounded by the red rectangle is the chosen unit supercell. (b) Scanning tunneling microscope image of the line defect in graphene and the superimposed defect model (image adapted from ref. 28). (c) M1, M2 and M3 are the unit supercell used in the present calculations, respectively. The left number N is the number of zigzag carbon chains of ZGNRs. M1 corresponds to a line defect just located at the center, M2 and M3 correspond to models with the next-closest and closest line defects to the zigzag edge, respectively. | ||
2. Models and methods
The ZGNR model we study is shown in Fig. 1, which contains the 558-defect line, where there are N zigzag carbon chains across the width, denoted as 558-defect-N-ZGNR. After relaxation, the system retains its planar structure, the C–C bond lengths of pentagonal and octagonal rings are within 1.41–1.45 Å, indicating delocalized π bonding. To simplify the investigation, we only consider three different-width ZGNRs with N = 7, 9, and 11, respectively, and mainly focus on the case of N = 9. Choosing four different unit supercells for each case, namely, ZGNR corresponds to the perfect graphene nanoribbon, and M1, M2, and M3 correspond to a line defect at the center, next-closest to the edge, closest to the edge, respectively.We consider well-fledged first-principles calculations using the density functional theory (DFT), and expect it to provide the most detailed and accurate description of the electronic properties. The geometry optimization and electronic properties are calculated by using the non-equilibrium Green's function (NEGF) method combined with the density functional theory (DFT) as implemented in Atomistix ToolKit (ATK). The generalized gradient approximation (GGA) and the double-zeta polarized basis set (DZP) are used. The convergence criteria of energy and force are set to 1 × 10−5 eV and 0.01 eV Å−1, respectively. The k-point sampling is 1 × 10 × 100, the cutoff energy is set to 150 Ry, and the electron temperature is fixed at 300 K. The spin-resolved current Iσ under bias voltage Vb is calculated with the Landauer–Büttiker formula:
 | (1) |
3. Results and discussion
We first investigate the binding energy and compare it with that of the pristine ZGNR in order to clarify the structural stability of the ZGNR with a 558-defect. Here, the binding energy is defined as Eb = (ET − nCEC − nHEH)/(nC + nH), where ET, EC and EH are the total energy of the investigated system, a C atom and a H atom, respectively. nC and nH are the number of C atoms and H atoms, respectively. In the case of N = 9, the calculated binding energies of M1, M2 and M3 are −8.921 eV, −8.914 eV and −8.912 eV, respectively, which are comparable with the case of the pristine 9-ZGNR (−9.018 eV). This indicates that the structure of the ZGNR with a 558-defect line is very stable as ZGNR. Then we calculate the total energies (E) of paramagnetic (PM), ferromagnetic (FM) and antiferromagnetic (AFM) configurations for 9-ZGNR, M1, M2, and M3, respectively. The calculated E displays the following regularities: for 9-ZGNR, M1 and M2, EAFM < EFM < EPM; for M3, EAFM = EFM < EPM. It indicates the ground states of 9-ZGNR, M1 and M2 are all AFM configurations, but that of M3 is FM configuration.We now investigate the electronic band structures of the ZGNR and M1–M3 at the ground state, as shown in Fig. 2(a)–(d). Two important features can be viewed: (i) for 9-ZGNR and M1, the energy bands of majority spin and minority spin degenerate completely. Conversely, for M2 and M3, the energy bands are all split obviously, and some bands get across the Fermi level in M3; this phenomenon implies the intense spin-polarization occurring and 558-defect-9-ZGNRs are all ferrimagnetic or ferromagnetic except the line defect just located at the center. (ii) For 9-ZGNR and M1, there is a about 0.5 eV and 0.25 eV energy gap between the valence band (VB) and the conduction band (CB), respectively. So they are semiconductors. But for M2, there is almost a zero band gap for the majority spin, but a small band gap for the minority spin. This means it is in a half-metallic state. For M3, there is no band gap for either majority spin or minority spin. Thus it is in metallic state obviously. It suggests that the ground state of 558-defect-9-ZGNR can be changed from an initial semiconductor to a half-metallic state or a metallic state just by shifting the position of line defect from the center to edge.
To know the spin-polarization of ZGNRs with a line defect, we calculate the spin polarization density (SPD) ρ↑ − ρ↓ for 558-defect-9-ZGNRs at the ground state, and give the density averaged in the direction perpendicular to the ribbon plane for M1, M2 and M3 in Fig. 3(a)–(c), respectively. Here, the majority spin and minority spin are labeled ↑ and ↓, respectively, and the electron density is denoted as ρ. From Fig. 3, we can observe that the SPD of the bottom edges for 558-defect-9-ZGNRs is of majority spin, with a significant larger value. The SPD of the top edge for the minority spin becomes weaker gradually to zero as the line defect position moves from the center to edge, and the SPD are very weak nearly to zero in other regions except both edges. It shows that the 558-defect-9-ZGNRs exhibit an obvious spin-polarization and can be transformed from AFM to ferrimagnetism, and to the FM state because this intrinsic feature is sensitive to the position of the line defect.
To further analyze the spin-polarization for ZGNRs with a line defect, we define the spin-polarized degree P as:
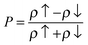 | (2) |
The above results show that a long-range ferromagnetic ordering can be created by employing a line defect located at one edge of ZGNR (see Fig. 3(c) and 4(c)). Next, we investigate the strength and stability of magnetism about ZGNRs with a line defect. Two related physical parameters are magnetic moment (M) and Curie temperature (TC). TC can be estimated by using the mean-field theory and Heisenberg model,35–37
 | (3) |
We now turn to investigate the impact of the line defect on the spin transport for ZGNRs. The spin-resolved current–voltage characteristics for 9-ZGNR, M1, M2 and M3 are presented in Fig. 6(a)–(d), respectively. It can be seen that, for pristine ZGNR, the majority spin-transport is equivalent to the minority spin-transport, both the majority and minority spin electronic conductions comply with Ohm's law of resistance, and the corresponding current–voltage characteristics in Fig. 6(a) are all straight lines and completely overlapping. But for 558-defect-9-ZGNRs, the impacts of the line defect on majority and minority spin-transport are distinct, when the line defect position shifts from the center to the edge of nanoribbons, the minority-spin current becomes smaller significantly, in contrast, the majority-spin current increases. This can be understood from the minority spin-transport pathway becoming narrower while the majority spin-transport pathway getting wider apparently as the line defect position shifts from the center to the edge of nanoribbons. It suggests that the spin-transport can be tuned by varying the line defect position, the line defect near the edge acts as conductors to majority spin-transport but as insulators to the opposite minority spin-transport, which generate a spin-filter effect.
To clearly reveal that the 558-defect-9-ZGNR systems can generate a spin-filter effect, a way to compare the differences of the spin-filter effect between the ribbons is to calculate the spin-filter efficiency (SFE) η, which is defined at zero bias as
 | (4) |
Since the spin-filter effect at finite bias is more valuable for applications than that at zero bias, we define the spin-filter efficiency (SFE) η at finite bias as
 | (5) |
The calculated SFE (η) of 558-defect-9-ZGNR systems are shown in Fig. 7. We can find the η is extremely sensitive to the line defect position and bias voltage (Vb), the η is improved remarkably with the line defect shifting to edge, the η of M3 is the most excellent one (represented by pink in Fig. 7), and changes within 50%–60% as 0.1 ≤ Vb ≤ 0.5 V. We also find that the SFE (η) of ZGNRs with N = 7, 11 display similar behaviors roughly as that of N = 9. It suggests that a stable and high-performance spin-filter device might be designed based on ZGNR with a line defect closest to the zigzag edge.
 | ||
| Fig. 7 Spin-filter efficiency (η) of defective ZGNR systems as functions of bias voltage and line defect position. The insets in the left panel show the corresponding models of unit supercells. | ||
4. Conclusions
Based on first-principles methods, the spin-dependent electronic properties for zigzag-edge graphene nanoribbons (ZGNRs) with a line defect are investigated and are compared to the results for ZGNR without a line defect. Results show that the edge carbon atoms of the defective ZGNRs exhibit intense spin-polarization, and the spin-polarization and spin-transport are sensitive to the position of the line defect. The defective ZGNRs can realize a transition from antiferromagnetism to ferrimagnetism and ferromagnetism via varying the position of line defect from the center to the zigzag edge of nanoribbons. And the ground state can be tuned from an initial semiconductor to a half-metallic state and a metallic state. In addition, the spin-transport can be tuned by varying the line defect position, the line defect near the edge acts as a conductor to majority spin-transport but as an insulator to the opposite minority spin-transport, which generates a spin-filter effect. More importantly, when the line defect is located on one edge, the defective ZGNRs exhibit the long-range magnetic ordering at edges with a high Curie temperature up to 276 K, and the defective ZGNR system can generate high-performance spin-filter effect in the large bias range, 0.0−0.5 V. Such a sensitive modulation for the spin-polarization and spin-transport holds great promise for applications of the graphene-based systems in nano-scale spintronic devices.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 61371065, 61101009, and 61201080), the Hunan Provincial Natural Science Foundation of China (Grant No. 2015JJ2009), the Scientific Research Fund of Hunan Provincial Education Department (Grant No. 14A013), the PhD Research Foundation of Changsha University of Science and Technology, the construct program of the key discipline in Hunan Province, and aid program for Science and Technology Innovative Research Team in Higher Educational Institutions of Hunan Province.References
- Y. W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347–349 CrossRef CAS PubMed.
- K. Nomura and A. H. MacDonald, Phys. Rev. Lett., 2006, 96, 256602 CrossRef.
- L. Brey, H. A. Fertig and S. Das Sarma, Phys. Rev. Lett., 2007, 99, 116802 CrossRef CAS.
- K. S. Novoselov, Z. Jiang, Y. Zhang, S. V. Morozov, H. L. Stormer, U. Zeitler, J. C. Maan, G. S. Boebinger, P. Kim and A. K. Geim, Science, 2007, 315, 1379 CrossRef CAS PubMed.
- O. V. Yazyev and L. Helm, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 125408 CrossRef.
- W. L. Wang, S. Meng and E. Kaxiras, Nano Lett., 2008, 8, 241–245 CrossRef CAS PubMed.
- T. Nikolaos, J. Csaba, P. Mihaita, T. J. Harry and B. J. V. Wees, Nature, 2007, 448, 571–574 CrossRef PubMed.
- W. Han and R. K. Kawakami, Phys. Rev. Lett., 2011, 107, 047207 CrossRef.
- D. H. Hernando, F. Guinea and A. Brataas, Phys. Rev. Lett., 2009, 103, 146801 CrossRef.
- K. M. McCreary, A. G. Swartz, W. Han, J. Fabian and R. K. Kawakami, Phys. Rev. Lett., 2012, 109, 186604 CrossRef.
- S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. V. Molnar, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Science, 2001, 294, 1488–1495 CrossRef CAS PubMed.
- I. Zutic, J. Fabian and S. D. Sarma, Rev. Mod. Phys., 2004, 76, 323–410 CrossRef CAS.
- C. Chappert, A. Fert and F. V. D. Nguyen, Nat. Mater., 2007, 6, 813–823 CrossRef CAS PubMed.
- L. Tapasztó, G. Dobrik, P. Lambin and L. P. Biró, Nat. Nanotechnol., 2008, 3, 397–401 CrossRef PubMed.
- S. S. Datta, D. R. Strachan, S. M. Khamis and A. T. C. Johnson, Nano Lett., 2008, 8, 1912–1915 CrossRef CAS PubMed.
- C. Berger, Z. Song, X. Li, X. Wu, N. Brown, C. Naud, D. Mayou, T. Li, J. Hass, A. N. Marchenkov, E. H. Conrad, P. N. First and W. A. de Heer, Science, 2006, 312, 1191–1196 CrossRef CAS PubMed.
- Y. W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803 CrossRef.
- H. Lee, Y. W. Son, N. Park, S. Han and J. Yu, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 174431 CrossRef.
- N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133 CrossRef CAS.
- J. Kunstmann, C. Özdoǧan, A. Quandt and H. Fehske, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 045414 CrossRef.
- K. Sawada, F. Ishii, M. Saito, S. Okada and T. Kawai, Nano Lett., 2009, 9, 269–272 CrossRef CAS PubMed.
- K. Sawada, F. Ishii and M. Saito, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 245426 CrossRef.
- J. A. Yan and M. Y. Chou, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 125403 CrossRef.
- G. P. Tang, J. C. Zhou, Z. H. Zhang, X. Q. Deng and Z. Q. Fan, Carbon, 2013, 60, 94–101 CrossRef CAS PubMed.
- Z. Li, W. Zhang, Y. Luo, J. Yang and J. G. Hou, J. Am. Chem. Soc., 2009, 131, 6320–6321 CrossRef CAS PubMed.
- B. Xu, J. Yin, Y. D. Xia, X. G. Wan, K. Jiang and Z. G. Liu, Appl. Phys. Lett., 2010, 96, 163102 CrossRef PubMed.
- G. P. Tang, Z. H. Zhang, X. Q. Deng, Z. Q. Fan, Y. C. Zeng and J. C. Zhou, Carbon, 2014, 76, 348–356 CrossRef CAS PubMed.
- J. Lahiri, Y. Lin, P. Bozkurt, I. I. Oleynik and M. Batzill, Nat. Nanotechnol., 2010, 5, 326–329 CrossRef CAS PubMed.
- Q. Q. Dai, Y. F. Zhu and Q. Jiang, J. Phys. Chem. C, 2013, 117, 4791–4799 CAS.
- Q. Q. Dai, Y. F. Zhu and Q. Jiang, Phys. Chem. Chem. Phys., 2014, 16, 10607–10613 RSC.
- S. S. Alexandre, A. D. Lúcio, A. H. C. Neto and R. W. Nunes, Nano Lett., 2012, 12, 5097–5102 CrossRef CAS PubMed.
- C. Su, H. Jiang and J. Feng, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 075453 CrossRef.
- X. L. Sheng, H. J. Cui, F. Ye, Q. B. Yan, Q. R. Zheng and G. Su, J. Appl. Phys., 2012, 112, 074315 CrossRef PubMed.
- O. V. Yazyev and S. G. Louie, Nat. Mater., 2010, 9, 806–809 CrossRef CAS PubMed.
- P. Kurz, G. Bihlmayer and S. Blüge, J. Phys.: Condens. Matter, 2002, 14, 6353–6371 CrossRef CAS.
- T. Hynninen, H. Raebiger and J. Boehm, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 125208 CrossRef.
- J. Kunstmann, C. Özdoǧan, A. Quandt and H. Fehske, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 045414 CrossRef.
- M. Sepioni, R. R. Nair, S. Rablen, J. Narayanan, F. Tuna, R. Winpenny, A. K. Geim and I. V. Grigorieva, Phys. Rev. Lett., 2010, 105, 207205 CrossRef CAS.
- O. V. Yazyev and M. I. Katsnelson, Phys. Rev. Lett., 2008, 100, 047209 CrossRef.
| This journal is © the Owner Societies 2015 |





