Hidden aspects of the Structural theory of chemistry: MC-QTAIM analysis reveals “alchemical” transformation from a triatomic to a diatomic structure

Abstract

The Structural theory of chemistry introduces chemical/molecular structure as a combination of relative arrangement and bonding patterns of atoms in a molecule. Nowadays, the structure of atoms in molecules is derived from the topological analysis of the quantum theory of atoms in molecules (QTAIM). In this context, a molecular structure is varied by large geometrical variations and concomitant reorganization of electronic structure that usually take place in chemical reactions or under extreme hydrostatic pressure. In this report, a new mode of structural variation is introduced within the context of the newly proposed multi-component QTAIM (MC-QTAIM) that originates from the mass variation of nuclei. Accordingly, XCN and CNX series of species are introduced where X stands for a quantum particle with a unit of positive charge and a variable mass that is varied in discrete steps between the mass of a proton and a positron. Ab initio non-Born–Oppenheimer (non-BO) calculations are done on both series of species and the resulting non-BO wavefunctions are used for the MC-QTAIM analysis, revealing a triatomic structure for the proton mass and a diatomic structure for the positron mass. In both series of species, a critical mass between that of proton and positron mass is discovered where the transition from triatomic to diatomic structure takes place. This abrupt structural transformation has a topological nature resembling the usual phase transitions in thermodynamics. The discovered mass-induced structural transformation is a hidden aspect of the Structural theory which is revealed only beyond the BO paradigm, when nuclei are treated as quantum waves instead of clamped point charges.

---

1. Introduction

The original notion of the molecular/chemical structure, as the relative arrangement and bonding pattern of atoms of a molecule, has been probably the most fundamental concept in chemistry since the advent of the Structural theory by Kekulé, Couper and Butlerov over one and a half centuries ago.^1–3 Since the introduction and subsequent development of the Lewis electronic theory of atoms and molecules almost a century ago,⁴ a new dimension, namely electron distribution, has also been incorporated into the very notion of the molecular structure. The notion of molecular structure did not cease to evolve after all the subsequent experimental and theoretical advances, e.g. the emergence of X-ray crystallography and quantum chemistry. Nowadays, it is generally believed that once the equilibrium nuclear configuration and the electronic structure of a molecule are known, the essentials to derive molecular structure are at hand.⁵ Currently, apart from sophisticated experimental methods,^6,7 computational quantum chemistry is also a reliable source for deriving equilibrium nuclear configurations.^8–10 Besides, the resulting ab initio electronic wavefunctions are used as “input” to those quantum chemical methodologies, e.g. natural bond orbital method and its ramifications,^11–14 that aim to obtain a “chemical”/real space picture of electronic structure. Alternatively, the quantum theory of atoms in molecules (QTAIM) that directly deciphers the “atoms in molecules” (AIM) structure from the electronic wavefunctions is a useful methodology which in its approach is similar to the notion of the original Structural theory.^15–17 Through the combination of elements of these two levels of chemical organization, i.e. electronic and the AIM structures, one hopes that a detailed and consistent picture of the molecular structure emerges.

However, all these quantum chemical methodologies and the emerging image of molecular structure have their roots in the familiar Born–Oppenheimer (BO) paradigm.¹⁸ In this paradigm, electrons are considered as quantum waves, whereas nuclei are treated as clamped particles acting as the source of the Coulombic electric field that binds electrons. The “dual” role of electrons and nuclei is attributed to their large mass difference that justifies an adiabatic viewpoint. Recent advances in non-BO ab initio computational methods bypass this paradigm, demonstrating that nuclei may also be treated as quantum waves from the outset of calculations, without any need for an adiabatic picture even at an intermediate stage.^19–28 Then, the question naturally arises that how the familiar notion of molecular structure is derivable from a non-BO wavefunction. To answer this question, novel quantum chemical methodologies must be developed that are capable of using non-BO wavefunctions, instead of adiabatic electronic wavefunctions, as input to extract the essentials of molecular structure. In contrast to some primary progress in this direction,^29–41 currently, such novel non-BO methodologies are in their infancy and it is not clear whether they will survive in the long term as reliable sources to derive the essentials of molecular structure.^18,42–46 A more modest strategy is extending the known BO-based methodologies to the non-BO realm; the use of various “extended population analysis” methodologies using non-BO wavefunctions as input is a prime example.^47–63

The recently proposed multi-component quantum theory of atoms in molecules (MC-QTAIM) also serves as an example of methodologies that aim to bypass the BO paradigm, unraveling the AIM structure from non-BO wavefunctions.^64–70 While the orthodox QTAIM is confined within the BO paradigm,^15–17 the MC-QTAIM is capable of revealing the AIM structure from both the BO and non-BO wavefunctions, unifying the AIM analysis of both realms. In fact, it has been demonstrated that the orthodox QTAIM is just the “asymptote” of the MC-QTAIM when the mass of nuclei tends toward infinity.⁶⁶ On the other hand, the MC-QTAIM is also capable of revealing the AIM structure of exotic species containing new fundamental particles beyond the electrons and the familiar nuclei, of which the positronic and muonic molecular systems are primary examples.^71–74 Thus, the unification domain of the MC-QTAIM methodology extends further, promising the extension of the Structural theory beyond its classic domain.⁶⁹ Particularly, this is a promising and new field of research since high quality ab initio wavefunctions are now accessible for many exotic species.^75–81 On the other hand, one of the main traits of the MC-QTAIM analysis is its mass dependence, namely that the masses of the constituent bodies of the molecular system are directly involved in the underlying formalism. Accordingly, both the gamma density that is used for the topological analysis and unraveling the boundaries of atomic basins, and the property densities yielding properties of atomic basins, are explicitly mass dependent (vide infra).⁶⁶ One of the manifestations of this mass-dependency is the observation of distinct atomic basins for each of the hydrogen isotopes.^64,74

Another opportunity, which is scrutinized in this study, is direct observation of the variation of molecular structure upon the mass variation of constituent bodies. In order to unravel this variation, two series of systems including XCN and CNX series are considered, where in both series X stands for a quantum particle with a unit of positive charge and a variable mass that is varied in discrete steps (vide infra) between the mass of a proton and a positron, m_proton ≈ 1836m_e and m_positron = m_e, respectively. Both extremes correspond to well-known molecular structures. In the case of the proton, both HCN and CNH are linear structures containing three atomic basins, each encompassing one of the nuclei.¹⁵ On the other hand, in the case of the positron, one is faced with positronic cyanide, CN⁻,e⁺, which is a diatomic positronic species with two atomic basins corresponding to the two nuclei, whereas the positron, unable to shape its own atomic basin, is distributed unevenly within these two basins.⁷² Intuitively, one expects that with the mass variation of the positively charged particle (PCP) from one extreme to the other, a structural transition must somehow take place from a triatomic to a diatomic structure. As is demonstrated in the rest of this contribution, this “mass dependent” structural transition has a topologically abrupt nature within the context of the MC-QTAIM and there is a critical mass of the PCP witnessing this sudden/catastrophic transformation.

2. A brief survey on the computational procedures and the mass dependence of the gamma density

The non-BO ab initio computational procedure used in this study is the multi-component Hartree–Fock (HF) method developed within the context of the Nuclear-Electronic-Orbital theory termed NEO-HF,²³ as implemented in the NEO computer code that is now part of the GAMESS suite of programs.⁸² In the NEO-HF method, which is based on the multi-component Hartree–Fock equations, the non-BO wavefunction is approximated as a product of Slater determinants (assuming constituent particles as fermions).²³ In the present study, in both series of species the wavefunction is the product of a Slater determinant, constructed from electronic orbitals, and an orbital describing the PCP all determined from the SCF procedure employing the mean potential field of the multi-component Hartree–Fock equations. As recently detailed elsewhere,⁷⁰ new capabilities have been added to the original NEO code, including the mass variation of the PCP, as well as using a “hybrid” basis set consisting of the usual nuclear centered and “mobile” functions. The concept of mobile function is particularly vital in considering cases where Gaussian basis sets with pre-fixed exponents and positions are not applicable. This is mainly the case in this study considering PCPs with non-standard masses, so they are scrutinized in this section in detail.

In the mobile part of the basis set, all variables of Gaussian functions, which include the exponents, positions, and linear coefficients, were optimized variationally during the SCF procedure of the NEO-HF method. Throughout the ab initio calculations, carbon and nitrogen nuclei were treated as clamped particles whereas electrons and the PCP were treated as quantum waves containing kinetic energy operators in the multi-component HF equations. In the present study, all the centers of the basis functions were placed on an axis going through both the clamped nuclei, and their position variations were restricted only on this axis during the optimization procedure. To describe the electrons around the clamped nuclei, the standard nuclear centered cc-pVDZ electronic basis set was placed on the clamped nuclei.^83,84 On the other hand, the PCP's orbital in the XCN series has been composed of three mobile s-type Gaussian functions each with a different center, one placed between the two clamped nuclei and the two others each behind any of the clamped nuclei. This arrangement of Gaussian functions was used as an “initial guess” in the initial step of the NEO-HF calculations and then varied during the optimization process. For the CNX series, just a single s-type Gaussian function was placed behind the clamped nitrogen nucleus and used in the initial step of the NEO-HF calculations. This strategy was employed since the computational experiences demonstrated that in most cases the variationally optimized SCF coefficients of the three s-type Gaussian functions describing the PCP's orbital prefer the XCN configuration; only the SCF coefficient of the Gaussian function behind the carbon clamped nuclei is non-zero, except the positronic cyanide, CN⁻,e⁺. In order to describe the electronic orbitals surrounding the above mentioned PCP associated mobile functions in both series, nine s-type Gaussians functions were grouped into three subsets as electronic mobile functions, each subset containing three Gaussians, and were placed at three different centers. In the XCN series, these three centers were fixed at the center of the three mobile functions describing the PCP's orbital. For the CNX series, one subset was fixed at the center of the single s-type Gaussian function describing the PCP's orbital while the two others were initially placed one between the clamped nuclei and one behind the clamped carbon nucleus and treated as “ghost” centers (sometimes also called banquet/Bq nuclei). Although these two ghost centers do not in practice describe electronic distribution around the PCP, they are employed to provide the description of electronic structure in the CNX series as flexible as that of the XCN series. At the next stage, during the NEO-HF calculations of each species in both series, in addition to the usual linear optimization of the SCF coefficients of the hybrid basis set,²³ the inter-nuclear distance of the clamped nuclei and the centers and exponents of the mobile functions were all optimized with a non-linear non-gradient optimizer added externally to the NEO code. At the final stage of ab initio calculations, the gradient of energy was computed explicitly to ensure the precision of the external optimizer; the root mean square of forces operative on the nuclei and the PCP was always less than 10⁻⁵ Hartree per Bohr in all considered species while the maximum force was always less than 10⁻⁴ Hartree per Bohr. The designed procedure is a combination of the orthodox NEO-HF, which is usually used with fixed-center basis sets with pre-defined exponents,²³ and the fully variational multi-component Hartree–Fock method that optimizes all variables of a basis set.^{26,27,64–68,70} In the series of the XCN species the mass of the PCP was varied in discrete steps including: m_X = m_e, 25m_e, 50m_e, 60m_e, 65m_e, 70m_e, 75m_e, 80m_e, 85m_e, 90m_e, 95m_e, 100m_e, 200m_e, 600m_e, 1000m_e, 1400m_e, 1836m_e, while in the CNX series these include: m_X = 25m_e, 50m_e, 100m_e, 200m_e, 300m_e, 350m_e, 385m_e, 400m_e, 405m_e, 410m_e, 415m_e, 425m_e, 500m_e, 600m_e, 1000m_e, 1400m_e, and 1836m_e. Apart from the PCPs with m_X = m_e, 200m_e, 1836m_e that correspond to the mass of positron, and almost to muon and proton, respectively, the other members of the “mass spectrum” are fictitious particles just employed to reveal a semi-continuous view of patterns emerging in the MC-QTAIM analysis from the mass variation.

The details of the MC-QTAIM formalism and associated computational analysis have been fully disclosed elsewhere and are not reiterated here.^64–70 However, because the mass dependent topological transitions are a main focus of this study, the mass dependence of the gamma density is reviewed briefly. Since there are two types of quantum particles in the considered systems, i.e. electrons and the PCP, the proper gamma field is: Γ⁽²⁾(q⃑) = ρ_e(q⃑) + (m_e/m_X)ρ_X(q⃑), where ρ_e(q⃑) = 14∫dτ_e′Ψ*Ψ is the one-particle density of electrons while ρ_X(q⃑) = ∫dτ_X′Ψ*Ψ is the one-particle density of the PCP.^67,70 In these equations dτ_t′, t = e, X implies summing over spin variables of all quantum particles and integrating over spatial coordinates of all quantum particles except one arbitrary particle belonging to the subset of electrons, denoted by subscript e, or the PCP, denoted by subscript X. Since Ψ is a non-BO wavefunction, it is important to distinguish the one-particle density of electrons used to construct the gamma density and the usual one-electron density introduced within the context of BO paradigm and employed in the topological analysis of the orthodox QTAIM.^15–17 The mass dependence of the gamma density is of two types; the “explicit” mass dependence originating from the equation of the gamma and an “implicit” mass dependence which stems from the fact that both one-particle densities are also mass dependent themselves. By decreasing the mass of the PCP, in the case of explicit mass dependence, the contribution of the PCP's one-particle density increases in the combined gamma density. However, the implicit mass-dependence dictates that a PCP with a smaller mass, which yields a less localized PCP one-particle density, is less capable of accumulating electrons. This is best exemplified in the above-mentioned extremes in both XCN and CNX series. While the proton is capable of accumulating electrons sufficiently to yield a (3, −3) CP in the gradient vector field of the gamma density and forming a topological atom,⁸⁵ the one-particle density of proton has very little direct contribution to the gamma density. On the other hand, since a positron and an electron have the same mass, the positron's one-particle density is formally contributing equally to the gamma density like the electron's one-particle density but its extreme diffuseness⁷² makes it quite ineffective at accumulating electrons and shaping a topological atom. Among these two extremes there is a competition between the two opposite factors in shaping the topography of the gamma density. Thus, a prior prediction of the critical mass of the PCP where the atomic basin associated to the PCP appears/disappears, without a detailed computational study, is not straightforward. The atomic properties of each atomic basin, M̃(Ω), are determined by basin integrations of the combined property density. Property densities are composed of two contributions originating from electrons, M_(q⃑), and the PCP, M_X(q⃑), thus: 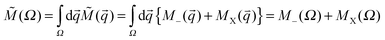. The numerical basin integrations were done using an algorithm disclosed elsewhere and are not reconsidered.^64,72 The computed virial ratios (Table 1), 〈V〉/〈T〉, deviate from the exact value, −2, thus, an ad hoc virial scaling was done in computing atomic energies.^70,72 This stems from the “partial” optimization of the basis function; although all variables of mobile functions were fully optimized, in the case of the nuclear centered function only the SCF coefficients, but not centers and exponents, were optimized. In order to guarantee the accuracy of the basin integration procedure, the numerical parameters of the basin integration were varied until the net flux integral of each basin, , was smaller than 10⁻⁴ in atomic units. Species from both series whose basin integrations, because of numerical instabilities, do not conform to this criterion, i.e. L̃(Ω) > 10⁻⁴, were excluded from the final MC-QTAIM analysis. The accuracy of the basin integrations was double checked comparing the sum of basin properties with associated molecular properties which were computed independently from the ab initio calculations, .

Table 1 Some results of the ab initio calculations on the XCN and CNX series of species, including C–N (N–C) inter-nuclear distances, C–X and N–X mean inter-nuclear distances, and total energies, as well as virial ratios. All results are given in atomic units

XCN					CNX
X-mass	N–C	C–X^a	Energy	Virial ratio	X-mass	C–N	N–X^a	Energy	Virial ratio
a The mean inter-nuclear distance is the distance between the clamped nucleus and the center of the s-type nuclear Gaussian function describing the quantum nucleus. For mX ≤ 80me in the XCN series and mX ≤ 405me in the CNX series, the atomic basin corresponding to X particle disappears; thus the mean inter-nuclear distances are not reported.
1	2.169	—	−92.4612	2.0003	25	2.175	—	−92.6455	2.0013
25	2.136	—	−92.6609	2.0007	50	2.173	—	−92.6940	2.0013
50	2.134	—	−92.7105	2.0007	100	2.173	—	−92.7350	2.0010
60	2.134	—	−92.7222	2.0007	200	2.172	—	−92.7681	2.0011
65	2.133	—	−92.7272	2.0007	300	2.171	—	−92.7843	2.0011
70	2.133	—	−92.7317	2.0007	350	2.171	—	−92.7898	2.0011
75	2.133	—	−92.7358	2.0007	385	2.171	—	−92.7926	2.0012
80	2.133	—	−92.7396	2.0007	400	2.171	—	−92.7939	2.0012
85	2.133	2.222	−92.7431	2.0007	405	2.171	—	−92.7943	2.0012
90	2.133	2.216	−92.7463	2.0007	410	2.171	1.953	−92.7947	2.0012
95	2.133	2.210	−92.7493	2.0007	415	2.171	1.953	−92.7951	2.0012
100	2.133	2.205	−92.7521	2.0007	425	2.171	1.952	−92.7959	2.0012
200	2.132	2.145	−92.7860	2.0007	500	2.171	1.944	−92.8011	2.0012
600	2.131	2.086	−92.8254	2.0007	600	2.171	1.937	−92.8065	2.0012
1000	2.130	2.067	−92.8387	2.0007	1000	2.171	1.919	−92.8196	2.0012
1400	2.130	2.058	−92.8462	2.0007	1400	2.170	1.909	−92.8270	2.0012
1836	2.130	2.051	−92.8514	2.0007	1836	2.170	1.903	−92.8322	2.0012

---

3. Results and discussion

Table 1 offers selected results of the NEO-HF calculations and, considering the mass variation of the PCP, regular patterns are observable in the geometrical parameters and total energies of the considered species in both series. In discussing the patterns throughout the paper, it is always assumed that all trends are described from HCN/CNH to CN⁻,e⁺; thus the phrase “because of the decrease of the mass” is eliminated from corresponding statements. In both series, the C–N inter-nuclear distances, and particularly the mean C–X and N–X distances, are ascending, indicating “spatial expansion” of species containing lighter PCPs in both series. The absolute value of the total energy is descending in both series, which is in line with the observed spatial expansion. This well-known trend is rationalized considering the fact that a heavier PCP accumulates electrons in a smaller region, i.e. tighter orbits, increasing the electronic kinetic energy that dominates the total kinetic energy, 〈T〉, and also the total energy, E_t, through the virial theorem, E_t = −〈T〉.^65,68,70 On the other hand, comparing congener species from both series with the same PCP mass demonstrates that the XCN species are always more stable than CNX species. This observation agrees with the observed “variational collapse” of the three center mobile basis set to the XCN configuration in most of the mass spectrum (vide supra).

The MC-QTAIM analysis begins with the topological analysis of the gamma density, relief maps of which are depicted for selected species from both series in Fig. 1 and 2. The topological analysis of the species of both series clearly demonstrates that one is faced with two distinct types of Molecular Graphs (MGs) when scanning the mass spectrum. In the case of the XCN series, the derived MGs in the mass region 85m_e ≤ m_X ≤ 1836m_e are topologically equivalent to the usual MG that is derived for HCN within the context of the orthodox QTAIM.¹⁵ Three (3, −3) critical points (CPs) reveal three basins of attraction within the vector gradient field of the gamma density which are atomic basins separated with the zero-flux surfaces going through the two (3, −1) CPs. Accordingly, the PCP, though not clamped, is capable of forming an atomic basin in this mass region. On the other hand, in the mass region m_e ≤ m_X ≤ 80m_e, the (3, −3) CP associated to the PCP disappears and the corresponding species are now composed of two atomic basins. Evidently, a topological transformation takes place within the mass region 80m_e ≤ m_X ≤ 85m_e witnessing an abrupt structural transition from a triatomic to a diatomic structure. A similar pattern is also observed in the CNX series, though in this case the structural transition occurs in the mass region 405m_e ≤ m_X ≤ 410m_e. Accordingly, the critical mass of the PCP for the structural transition is quite different in the two series, revealing the interesting fact that the positive muon, m_μ ≈ 206.8m_e, is capable of forming its own basin in the XCN series but not in the CNX series. Table 2, as well as Tables S1 and S2 in the ESI,† gather some quantitative results of the topological analysis including the topological indices at the (3, −3) and (3, −1) CPs. It is evident from Tables S1 and S2 (ESI†) that in both series of species the topological indices of (3, −3) CPs at the clamped nuclei and the (3, −1) CP in between are almost constant and relatively insensitive to the mass variation of the PCP. As has also been stressed recently,⁷⁰ this is a manifestation of the principle of the nearsightedness of the electronic matter,^86,87 which roughly states that a perturbation induced by a variation on a specific site of a molecule damps beyond the region of perturbation when considering the electronic density as well as the property densities. Manifestly, the mass variation of the PCP, which acts similar to a perturbation, is best revealed on the topological indices computed at the PCP associated (3, −3) CP as well as the (3, −1) CP at the boundary of the X basin and its neighboring basin. Inspection of Table 2 reveals that in both series the amount of the gamma density as well as the absolute amount of its Laplacian are both descending at the (3, −3) CP, demonstrating that the lighter PCPs are less capable of concentrating/accumulating electrons around themselves; in order to gain a more detailed picture, Tables S3 and S4 in ESI† offer the separate contributions of electrons and the PCP to the topological indices. The length of the gradient path connecting the (3, −3) CP in the X basin and the (3, −1) CP at the boundary of the X basin and its neighboring basin is also descending in both series and reaches to zero near the critical masses. On the other hand, the topological floppiness index, TF = Γ⁽²⁾(q⃑_(3,−1))/Γ⁽²⁾(q⃑_(3,−3)),⁶⁸ is ascending and approaching its limiting value, TF = 1, near the critical masses in both series. All these conform to the fact that the PCP associated atomic basin “shrinks” and suddenly disappears at the critical mass.

Fig. 1 The relief map of the gamma density of selected species of the XCN series of species when the masses of the PCPs are: 25m_e (a), 200m_e (b), 600m_e (c), and 1836m_e (d). The carbon nucleus is located in the center of the coordinate system while the nitrogen nucleus is located on the negative side of the z-axis.

Fig. 2 The relief map of the gamma density of selected species of the CNX series of species when the masses of the PCPs are: 25m_e (a), 200m_e (b), 600m_e (c), and 1836m_e (d). The carbon nucleus is located on the negative side of the z-axis while the nitrogen nucleus is located in the center of the coordinate system.

Table 2 Some results of the topological analysis of the XCN and CNX series of species, including the gamma density, the combined Lagrangian kinetic energy density (denoted as G), the Laplacian of the gamma density, computed (3, −3) CP located in the X basin and at the (3, −1) linking the (3, −3) CP on the carbon nucleus and the (3, −3) CP within the X basin for the XCN series and at the (3, −1) CP linking the (3, −3) CP on the nitrogen nucleus and the (3, −3) CP within the X basin for the CNX series. The length of the path connecting the mentioned CPs (denoted as L(X-(3, −1))), and the index of the topological floppiness (denoted as TF) are also presented. All results are given in atomic units

X-mass	Gamma		G		Laplacian of gamma		L(X-(3, −1))	TF
	(3, −1)	X-(3, −3)	(3, −1)	X-(3, −3)	(3, −1)	X-(3, −3)
XCN
85	0.197	0.197	0.047	0.045	−1.363	−1.483	0.028	1.0000
100	0.204	0.205	0.053	0.042	−1.145	−2.018	0.176	0.9944
200	0.228	0.239	0.045	0.045	−1.074	−3.746	0.339	0.9538
600	0.255	0.286	0.013	0.061	−1.112	−7.220	0.476	0.8914
1000	0.263	0.304	0.013	0.071	−1.067	−9.172	0.516	0.8656
1400	0.267	0.314	0.013	0.079	−1.047	−10.564	0.533	0.8505
1836	0.270	0.322	0.014	0.087	−1.039	−11.761	0.544	0.8397
CNX
410	0.269	0.269	0.128	0.127	−3.280	−3.416	0.008	1.0000
425	0.271	0.271	0.132	0.124	−3.024	−3.787	0.042	0.9998
500	0.276	0.277	0.138	0.122	−2.740	−4.617	0.096	0.9976
600	0.282	0.284	0.138	0.124	−2.631	−5.382	0.128	0.9942
1000	0.297	0.302	0.117	0.138	−2.642	−7.371	0.178	0.9842
1400	0.306	0.312	0.084	0.150	−2.729	−8.726	0.207	0.9781
1836	0.312	0.320	0.052	0.162	−2.745	−9.850	0.237	0.9733

---

Several atomic properties derived from the basin integrations are gathered in Tables 3–5. Inspection of Table 3 demonstrates that in both series of species the absolute value of basin energies, electronic populations, the population of the PCP and the atomic volumes all reveal a rapidly descending pattern for the X basin. These observations conform to the results of the topological analysis and the annihilation of the X basin below the critical mass. Interestingly, comparison of congener species from both series, those containing PCPs having the same mass, reveals that in the CNX series the X basin is always smaller, containing fewer electrons. This is rationalized taking into account the fact that the nitrogen basin, which is the neighbor of the X basin in the CNX series, has a larger capacity of electron withdrawing/electronegativity than the carbon basin which is the neighbor of the X basin in the XCN series. Accordingly, based on Tables 4 and 5, in both series the atomic charges of the nitrogen basins, resulting from subtracting nitrogen's atomic number and its electronic population,⁶⁸ are always negative, in line with its place on the electronegativity scale, whereas those of the carbon basins are always positive. A more detailed inspection of these tables also reveals that in the set of nitrogen and carbon basins in both series a larger electron population is always accompanied by more negative basin energy. Such a trend, which has also been recently observed in the case of hydrogen basins,^70,74 demonstrates that basin energies are sensitive probes of electron transfer processes, though a detailed theoretical understanding is yet missing. Also, in the CNX series and some lighter species in the XCN series, the PCP is not completely contained within the X basin and “leaks” into the neighboring basin. Evidently, in competition with neighboring basins the capacity of the X basins, containing lighter PCPs, to maintain the electrons and even the PCP itself weakens. The PCP's leakage is also observable in Tables S3 and S4 (ESI†) considering even the mass-scaled PCP's contribution to the gamma density at the (3, −1) CP at the boundary of the X basin and its neighbor. Inspection of Tables 4 and 5 demonstrates that in both series, in line with the principle of nearsightedness, the basin that is next to the X basin is more influenced by the mass variations of the PCP. Whereas, the pattern of property variations of the non-neighboring basins is gradual and virtually “continuous”, at the proximity of the critical mass, the neighboring basin experiences “discontinuous” property variations. These discontinuous property variations originate from the fact that below the critical mass the basin neighboring the X basin completely “absorbs” the X basin, i.e. both its electrons and the PCP, into itself yielding a single basin; the whole process resembles the well-known discontinuous phase transitions in thermodynamics. In this analogy the two topological structures above and below the critical mass act like two distinct phases while the mass of the PCP acts like the control parameter, e.g. temperature. It is timely to emphasize that this analogy was recognized and considered in the original literature of the orthodox QTAIM.¹⁵ However, since the formalism of the orthodox QTAIM is confined to the BO paradigm, the control parameters are only nuclear coordinates and the topological changes are solely induced by molecular geometry variations.

Table 3 The results of the basin integration of the X basin in the XCN and CNX series of species including basin energy, electronic population (donated as e-pop.), the PCP population (denoted as PCP-pop.) and the volume of the atomic basin. All results are given in atomic units

X-mass	Energy	e-pop.	PCP-pop.	Volume
XCN
85	−0.2212	0.325	0.856	24.0
100	−0.2514	0.375	0.915	26.4
200	−0.3083	0.462	0.984	29.3
600	−0.3824	0.582	1.000	32.8
1000	−0.4074	0.621	1.000	33.9
1400	−0.4199	0.640	1.000	34.4
1836	−0.4284	0.652	1.000	34.8
CNX
410	−0.1968	0.220	0.863	14.0
425	−0.2053	0.231	0.880	14.3
500	−0.2200	0.249	0.919	15.1
600	−0.2305	0.261	0.944	15.6
1000	−0.2518	0.286	0.981	16.4
1400	−0.2669	0.305	0.993	17.1
1836	−0.2823	0.326	0.998	17.8

---

Table 4 The results of the basin integration of the nitrogen and carbon basins in the XCN series of species including basin energies, electronic populations (donated as e-pop.), the PCP populations (denoted as PCP-pop.) and the volumes of the atomic basins. The space between m_X = 80m_e and m_X = 85m_e is the border between the triatomic and diatomic structures. All results are given in atomic units

X-mass	N-basin				C-basin
	Energy	e-pop.	PCP-pop.	Volume	Energy	e-pop.	PCP-pop.	Volume
1	−55.5023	8.874	0.618	276.1	−36.9590	5.126	0.382	203.7
25	−55.3891	8.522	0.000	168.9	−37.2719	5.478	1.000	140.9
50	−55.3838	8.510	0.000	168.5	−37.3268	5.490	1.000	134.9
60	−55.3828	8.508	0.000	168.4	−37.3393	5.493	1.000	133.7
65	−55.3817	8.506	0.000	168.3	−37.3455	5.494	1.000	133.3
70	−55.3809	8.506	0.000	168.4	−37.3507	5.495	1.000	132.4
75	−55.3804	8.505	0.000	167.6	−37.3554	5.495	1.000	131.9
80	−55.3799	8.505	0.000	167.5	−37.3597	5.495	1.000	131.5
85	−55.3795	8.504	0.000	167.5	−37.1424	5.171	0.145	107.0
100	−55.3784	8.503	0.000	167.5	−37.1223	5.122	0.085	104.1
200	−55.3754	8.499	0.000	167.2	−37.1022	5.039	0.016	98.6
600	−55.3725	8.495	0.000	167.1	−37.0704	4.923	0.000	92.3
1000	−55.3716	8.494	0.000	167.0	−37.0598	4.884	0.000	89.9
1400	−55.3712	8.494	0.000	167.0	−37.0551	4.866	0.000	88.6
1836	−55.3708	8.494	0.000	167.0	−37.0522	4.854	0.000	87.9

---

Table 5 The results of the basin integration of the nitrogen and carbon basins in the CNX series of species including basin energies, electronic populations (donated as e-pop.), the PCP populations (denoted as PCP-pop.) and the volumes of the atomic basins. The space between m_X = 405m_e and m_X = 410m_e is the border between the triatomic and diatomic structures. All results are given in atomic units

X-mass	C-basin				N-basin
	Energy	e-pop.	PCP-pop.	Volume	Energy	e-pop.	PCP-pop.	Volume
25	−36.8621	4.822	0.000	121.1	−55.7833	9.178	1.000	185.8
50	−36.8588	4.812	0.000	120.2	−55.8351	9.188	1.000	182.1
100	−36.8575	4.807	0.000	119.7	−55.8775	9.193	1.000	179.5
200	−36.8466	4.805	0.000	119.7	−55.9215	9.195	1.000	177.9
300	−36.8455	4.803	0.000	119.5	−55.9387	9.197	1.000	177.4
350	−36.8449	4.802	0.000	119.5	−55.9449	9.198	1.000	177.3
385	−36.8535	4.799	0.000	118.3	−55.9391	9.201	1.000	177.2
400	−36.8535	4.799	0.000	118.2	−55.9404	9.201	1.000	177.2
405	−36.8535	4.799	0.000	118.2	−55.9408	9.201	1.000	177.2
410	−36.8535	4.799	0.000	118.2	−55.7444	8.981	0.137	163.2
425	−36.8534	4.799	0.000	118.1	−55.7371	8.970	0.121	162.7
500	−36.8534	4.798	0.000	117.9	−55.7277	8.953	0.081	161.8
600	−36.8532	4.798	0.000	117.8	−55.7227	8.941	0.056	161.2
1000	−36.8500	4.797	0.000	118.4	−55.7178	8.917	0.019	158.9
1400	−36.8499	4.797	0.000	118.4	−55.7101	8.898	0.007	157.7
1836	−36.8498	4.796	0.000	118.4	−55.7000	8.878	0.002	156.6

---

It is also interesting to comment on the special position of the positronic molecule among the other members of these two series, since it is the only species with which the nitrogen basin shares the population of the PCP (Fig. 3) and its atomic properties are distinctly different from those of species with m_X = 25m_e (Table 4). Although one does not expect a new topological structural transformation to take place between m_X = m_e and m_X = 25m_e, evidently, the PCP's migration into the nitrogen basin begins in this mass region that seems to be the final stage of property variations in the mass spectrum. Attempts to survey this mass region were plagued by the fact that multiple “local” minima with similar energies emerged in the “space” of variables of the mobile functions for each species. Thus, it is hard to unambiguously locate the “global” minimum for each species, i.e. the wavefunction yielding the lowest possible energy. Since the MC-QTAIM analysis of the derived local minima yields distinct atomic properties, it is hard to establish the true patterns of atomic property variations and they are not discussed in this contribution. New computational strategies are now under development in our lab to safely analyze this mass region.

Fig. 3 The mass-scaled one-particle densities of the PCPs for two XCN species including m_X = 25m_e (the blue curve) and m_X = m_e (the red curve). The positions of carbon and nitrogen nuclei are almost identical in both cases and are shown with green and orange circles, respectively.

The recently proposed extended theory of localization/delocalization of electrons and other quantum particles,⁶⁸ applicable within the non-BO domain, was applied for the electrons of both series of species and the results are gathered in Tables 6 and 7. Since there is just a single PCP in the considered species, the localization/delocalization analysis is not applicable to the PCP.⁶⁸ Inspection of both tables demonstrates that, in line with previously observed trends, the localization of electrons in the X basin, as well as the delocalization of the electrons of the X basin into other basins, all diminish. Comparison of the percent localization of the X basin with those for nitrogen and carbon basins clearly reveals much smaller localization capacity of the X basin. However, the best probe of the discontinuous topological transformation is an abrupt increase in the localization index of the neighboring basin of the X basin when crossing the critical mass in both series of species. On the other hand, and in agreement with the nearsightedness principle, the electronic localization of basins that are not neighbors of the X basin, as well as the delocalization of electrons between carbon and nitrogen basins, are much less affected by the mass variation of the PCP and are almost constant in the whole mass spectrum.

Table 6 The electronic localization and delocalization indices as well as the percent localization of the XCN series of species. The space between m_X = 80m_e and m_X = 85m_e is the border between the triatomic and diatomic structures

X-mass	Loc.			% Loc.			Deloc.
	N	C	X	N	C	X	(N,C)	(X,C)	(N,X)
1	7.81	4.06	—	88.0	79.2	—	2.13	—	—
25	7.37	4.32	—	86.4	78.9	—	2.31	—	—
50	7.35	4.33	—	86.4	78.9	—	2.31	—	—
60	7.35	4.34	—	86.4	78.9	—	2.31	—	—
65	7.35	4.34	—	86.4	78.9	—	2.31	—	—
70	7.35	4.32	—	86.4	78.6	—	2.31	—	—
75	7.35	4.32	—	86.4	75.7	—	2.31	—	—
80	7.35	4.32	—	86.4	75.7	—	2.30	—	—
85	7.35	3.76	0.05	86.4	72.9	16.1	2.28	0.52	0.03
100	7.35	3.70	0.07	86.4	72.1	18.2	2.28	0.58	0.04
200	7.34	3.57	0.10	86.4	70.8	22.3	2.27	0.67	0.04
600	7.34	3.40	0.16	86.4	69.1	27.9	2.26	0.78	0.06
1000	7.34	3.35	0.18	86.4	68.6	29.7	2.25	0.81	0.06
1400	7.34	3.33	0.20	86.4	68.4	30.5	2.25	0.83	0.06
1836	7.34	3.31	0.20	86.4	68.2	31.0	2.25	0.84	0.06

---

Table 7 The electronic localization and delocalization indices as well as the percent localization of the CNX series of species. The space between m_X = 405m_e and m_X = 410m_e is the border between the triatomic and diatomic structures

X-mass	Loc.			% Loc.			Deloc.
	C	N	X	C	N	X	(C,N)	(C,X)	(N,X)
25	3.93	8.29	—	81.5	90.3	—	1.78	—	—
50	3.93	8.31	—	81.7	90.4	—	1.77	—	—
100	3.93	8.32	—	81.8	90.5	—	1.75	—	—
200	3.93	8.32	—	81.8	90.5	—	1.75	—	—
300	3.93	8.32	—	81.8	90.5	—	1.75	—	—
350	3.93	8.32	—	81.8	90.5	—	1.75	—	—
385	3.93	8.32	—	81.8	90.5	—	1.74	—	—
405	3.93	8.34	—	81.8	90.6	—	1.74	—	—
410	3.93	7.92	0.02	81.8	88.2	11.1	1.73	0.01	0.39
425	3.93	7.90	0.03	81.8	88.1	11.2	1.73	0.01	0.40
500	3.93	7.87	0.03	81.8	88.0	11.9	1.73	0.01	0.43
600	3.93	7.85	0.03	81.8	87.8	12.5	1.73	0.01	0.44
1000	3.93	7.81	0.04	81.9	87.6	13.7	1.73	0.01	0.48
1400	3.93	7.78	0.04	81.9	87.5	14.6	1.72	0.01	0.51
1836	3.93	7.75	0.05	81.9	87.3	15.5	1.72	0.02	0.54

---

4. Conclusions

In the present study, through introducing the hybrid basis set and mobile functions in addition to the usual nuclear centered basis functions, a large mass spectrum was scanned using the ab initio NEO-HF method. One may conceive the idea of mobile functions as on the “fly” basis set design and this is a particularly useful strategy when applying ab initio non-BO calculations to species with non-standard masses. However, even for real but less familiar quantum particles like the positive muon and associated muonic molecules, employing such a strategy facilitates a “from scratch” basis set design. Since this strategy may be used for both nuclear/PCP and electronic basis sets, the resulting basis functions are not biased, carrying the “fingerprint” of their “environment”, which is a major advantage in contrast to the usual “pre-designed” basis sets with fixed variables. Thus, the large number of basis functions usually used to design flexible basis sets for quantum nuclei could be bypassed and this is particularly desirable and a real saving of computational cost when performing post-NEO-HF calculations. These issues will be addressed in detail in a future study.

The presented MC-QTAIM analysis reveals the detailed nature of the topological structural transformation upon the mass variation of the PCP, which despite some similarities, is distinct from the usual geometry-dependent topological structural transformations. Within the context of the orthodox QTAIM, the one-electron density parametrically depends on the position of the clamped nuclei and the variations of MGs are accomplished by variations of molecular geometry.^15–17 These variations are confined to the rearrangement of a fixed number of AIM and atomic basins do not appear/disappear during geometrical variations except in some very special cases,^88–90 or by applying extremely large hydrostatic pressure to molecules.⁹¹ However, this “AIM conservation” rule is restricted to the BO paradigm and the present study demonstrates that within the context of the MC-QTAIM, beyond the BO paradigm, and upon mass variation of quantum particles, atomic basins may appear/disappear. Thus, the topological transformations considered in the present study are a novel unprecedented type of structural transformations. It is timely to emphasize that the idea of topological transformations has also been utilized recently to disclose the abrupt transition from H⁻, atomic species, to H₂⁺, molecular species, upon the mass variation of the constituent particle.^36,40 However, these topological transitions just disclose “topographical” changes of the used density and no underlying AIM structure was revealed in these studies.

In a very recent study, the AIM structures of some very simple muonic species were considered within the context of the MC-QTAIM and it was proposed that the positive muon is capable of forming its own atomic basin.⁷⁴ In that study, the positive muon competed with hydrogen isotopes, e.g. proton and deuteron, in shaping its own atomic basin. However, in this study it was demonstrated that in competition with the nitrogen atom in the CN moiety it is unable to form an independent atomic basin and is absorbed into the nitrogen basin. Accordingly, it seems legitimate to tentatively assign the following formulas, μCN and CN⁻,μ⁺, to the muonic species considered in the present study in order to emphasize their structural resemblance to HCN and CN⁻,e⁺, respectively; based on the ab initio calculations, μCN is the stable configuration. Before making a final decision on whether from the viewpoint of the AIM structure a positive muon behaves like a lighter isotope of hydrogen or not, more MC-QTAIM studies on species containing the positive muon are needed. Accordingly, in a future contribution, the MC-QTAIM analysis of a diverse set of muonic species will be considered comprehensively, in order to shed some light on this interesting question.

It seems that there is a consensus among theoretical chemists that the concept of chemical structure is applicable straightforwardly within the BO paradigm, while it is not trivial to be applied in the non-BO domain.^18,42,92,93 Recent studies on analyzing non-BO wavefunctions shed light on how one may derive some ingredients of molecular structures in the non-BO domain,^30–41 though serious technical obstacles remain to be tackled.^18,42 The present study, as well as the recent MC-QTAIM analysis of some polyatomic species,⁷⁰ however, shows that the clamped nucleus model is not required in order to derive the AIM structure which is one of the basic ingredients required to propose a chemical/molecular structure. More precisely, insofar as there are some clamped nuclei in a molecule where the total translational and rotational motions are excluded from molecular non-BO wavefunction, assuming certain nuclei as quantum waves does not seem to be an obstacle to introduce molecular structures. Since chemists are usually interested in the non-BO description of certain parts of a molecule,^47–63e.g. isotope substitution in a specific site of a molecule, clamping some nuclei during ab initio non-BO calculations is not a real restriction and the NEO methodology may be applied successfully. The resulting non-BO wavefunctions are classified in a single category, and termed WF1 in a previous contribution,⁶⁵ while the MC-QTAIM analysis is capable of dealing with this class of wavefunctions yielding the underlying AIM structure. However, the subsequent question is: “What will happen if all nuclei are treated as quantum waves?”. Nakai's proposed ab initio nuclear orbital plus molecular orbital method (NOMO) seems to be a powerful methodology in such cases, which eliminates total translational and rotational motions systematically.²⁴ The resulting wavefunctions have been classified as WF2 and WF3 based on details of technicalities,⁶⁵ and after proper modifications of the present formalism of the MC-QTAIM, which will be discussed in a future contribution, the underlying AIM structure is also derivable from the NOMO wavefunctions. All these cast doubt that the BO paradigm and the clamped nucleus model are “the” border for applicability of the concept of molecular structure and, more generally, the Structural theory. However, at the same time, it must be stressed that for the most intricate non-BO wavefunctions that contain total rotational dynamics,¹⁸ termed as WF4,⁶⁵ deriving the AIM structure is still elusive,^40–42 and current MC-QTAIM methodology needs further theoretical developments to deal with such wavefunctions.

Acknowledgements

The authors are grateful to Masumeh Gharabaghi, Cina Foroutan-Nejad, Rohoullah Firouzi and Shahin Sowlati for their detailed reading of a previous draft of this paper and helpful suggestions.

References

1. O. T. Benfey, Classics in the Theory of Chemical Combination, Dover Publication, New York, 1963.
2. C. A. Russell, The History of Valency, Leicester University Press, New York, 1971.
3. P. J. Ramberg, Chemical Structure, Spatial Arrangement: The Early History of Stereochemistry (1874–1914), Ashgate Publishing Company, Burlington, 2003.
4. G. N. Lewis, Valence and the Structure of Atoms and Molecules, Chemical Catalog Company, New York, 1923.
5. V. I. Minkin, Russ. Chem. Bull., 2012, 61, 1265.
6. E. F. Garman, Science, 2014, 343, 1102.
7. R. J. Dwayne Miller, Science, 2014, 343, 1108.
8. T. Helgaker, P. Jørgenson and J. Olsen, Molecular Electronic-Structure Theory, John Wiley & Sons, New York, 2000.
9. P. Pyykkö, Phys. Chem. Chem. Phys., 2012, 14, 14734.
10. A. S. Ivanov and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2012, 14, 15943.
11. F. Weinhold and C. R. Landis, Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective, Cambridge University Press, Cambridge, 2005.
12. F. Weinhold and C. R. Landis, Discovering Chemistry with Natural Bond Orbitals, John Wiley & Sons, New Jersey, 2012.
13. D. Yu. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207.
14. D. Yu. Zubarev and A. I. Boldyrev, J. Org. Chem., 2008, 73, 9251.
15. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990.
16. P. L. A. Popelier, Atoms in Molecules an Introduction, Pearson, London, 2000.
17. C. Matta and R. J. Boyd, Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, Wiley-VCH, Weinheim, 2007.
18. B. T. Sutcliffe and R. G. Woolley, Phys. Chem. Chem. Phys., 2005, 7, 3664.
19. M. Cafiero, S. Bubin and L. Adamowicz, Phys. Chem. Chem. Phys., 2003, 5, 1491.
20. S. Bubin, M. Cafiero and L. Adamowicz, Adv. Chem. Phys., 2005, 131, 377.
21. S. Bubin, M. Pavanello, W.-C. Tung, K. L. Sharkey and L. Adamowicz, Chem. Rev., 2013, 113, 36.
22. J. Mitroy, S. Bubin, W. Horiuchi, Y. Suzuki, L. Adamowicz, W. Cencek, K. Szalewicz, J. Komasa, D. Blume and K. Varga, Rev. Mod. Phys., 2013, 85, 693.
23. S. P. Webb, T. Iordanov and S. Hammes-Schiffer, J. Chem. Phys., 2002, 117, 4106.
24. H. Nakai, Int. J. Quantum Chem., 2007, 107, 2849.
25. T. Krebich, R. van Leeuwen and E. K. U. Gross, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 022501.
26. T. Ishimoto, M. Tachikawa and U. Nagashima, Int. J. Quantum Chem., 2009, 109, 2677.
27. T. Udagawa and M. Tachikawa, Multi-Component Molecular Orbital Theory, Nova Science Publishers, New York, 2009.
28. R. Flores-Moreno, E. Posada, F. Moncada, J. Romero, J. Charry, M. Díaz-Tinoco, S. A. González, N. F. Aguirre and A. Reyes, Int. J. Quantum Chem., 2014, 114, 50.
29. D. M. Bishop and L. M. Cheung, Int. J. Quantum Chem., 1979, 15, 517.
30. F. Arias de Saavedra, E. Buendía, F. J. Gálvez and A. Sarsa, Eur. Phys. J. D, 1998, 2, 181.
31. J. Usukura, K. Varga and Y. Suzuki, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 58, 1918.
32. M. Cafiero and L. Adamowicz, Chem. Phys. Lett., 2004, 387, 136.
33. M. Cafiero and L. Adamowicz, J. Chem. Phys., 2005, 122, 184305.
34. M. Bubin, E. Bednarz and L. Adamowicz, J. Chem. Phys., 2005, 122, 041102.
35. M. Bubin and L. Adamowicz, Chem. Phys. Lett., 2005, 403, 185.
36. U. Müller-Herold, J. Chem. Phys., 2006, 124, 014105.
37. M. Cafiero and L. Adamowicz, Int. J. Quantum Chem., 2007, 107, 2679.
38. U. Müller-Herold, Eur. Phys. J. D, 2008, 49, 311.
39. U. Müller-Herold, Eur. Phys. J. D, 2010, 56, 311.
40. E. Mátyus, J. Hutter, U. Müller-Herold and M. Reiher, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 052512.
41. E. Mátyus, J. Hutter, U. Müller-Herold and M. Reiher, J. Chem. Phys., 2011, 135, 204302.
42. B. T. Sutcliffe and R. G. Woolley, Chem. Phys. Lett., 2005, 408, 445.
43. E. V. Ludeña, L. Echevarría, X. Lopez and J. M. Uglade, J. Chem. Phys., 2012, 136, 084103.
44. M. Becerra, V. Posligua and E. V. Ludeña, Int. J. Quantum Chem., 2013, 113, 1584.
45. C. G. Rodríguez, A. S. Urbina, F. J. Torres, D. Cazar and E. V. Ludeña, Comput. Theor. Chem., 2013, 1018, 26.
46. J. Karwowski, Croat. Chem. Acta., 2013, 86, 531.
47. M. Ishida, M. Tachikawa, H. Tokiwa, K. Mori and A. Ishii, Surf. Sci., 1999, 438, 47.
48. H. Nakai, K. Sodeyama and M. Hoshino, Chem. Phys. Lett., 2001, 345, 118.
49. T. Ishimoto, M. Tachikawa, M. Yamauchi, H. Kitagawa, H. Tokiwa and U. Nagashima, Chem. Phys. Lett., 2003, 372, 503.
50. T. Udagawa, T. Ishimoto, H. Tokiwa, M. Tachikawa and U. Nagashima, Chem. Phys. Lett., 2004, 389, 236.
51. T. Ishimoto, M. Tachikawa, M. Yamauchi, H. Kitagawa, H. Tokiwa and U. Nagashima, J. Phys. Soc. Jpn., 2004, 73, 1775.
52. H. Nakai, M. Hoshino, K. Miyamoto and S. Hyodo, J. Chem. Phys., 2005, 122, 164101.
53. A. Reyes, M. V. Pak and S. Hammes-Schiffer, J. Chem. Phys., 2005, 123, 064104.
54. T. Ishimoto, M. Tachikawa, H. Tokiwa and U. Nagashima, Chem. Phys., 2005, 314, 231.
55. T. Ishimoto, M. Tachikawa, H. Tokiwa and U. Nagashima, J. Phys. Soc. Jpn., 2005, 74, 3112.
56. T. Udagawa, T. Ishimoto, H. Tokiwa, M. Tachikawa and U. Nagashima, J. Phys. Chem. A, 2006, 110, 7279.
57. Y. Kikuta, T. Ishimoto and U. Nagashima, Chem. Phys., 2008, 354, 218.
58. S. A. González, N. F. Aguirre and A. Reyes, Int. J. Quantum Chem., 2008, 108, 1742.
59. T. Udagawa and M. Tachikawa, THEOCHEM, 2009, 912, 63.
60. D. V. Moreno, S. A. González and A. Reyes, J. Phys. Chem. A, 2010, 114, 9231.
61. Y. Kikuta, T. Ishimoto and U. Nagashima, Comput. Theor. Chem., 2011, 975, 138.
62. T. Simazaki and M. Kubo, Chem. Phys. Lett., 2012, 525–526, 134.
63. Y. Kita, H. Kamikubo, M. Kataoka and M. Tachikawa, Chem. Phys., 2013, 419, 50.
64. M. Goli and Sh. Shahbazian, Theor. Chem. Acc., 2011, 129, 235.
65. M. Goli and Sh. Shahbazian, Theor. Chem. Acc., 2012, 131, 1208.
66. M. Goli and Sh. Shahbazian, Theor. Chem. Acc., 2013, 132, 1362.
67. M. Goli and Sh. Shahbazian, Theor. Chem. Acc., 2013, 132, 1365.
68. M. Goli and Sh. Shahbazian, Theor. Chem. Acc., 2013, 132, 1410.
69. Sh. Shahbazian, Found. Chem., 2013, 15, 287.
70. M. Goli and Sh. Shahbazian, Comput. Theor. Chem., 2014 DOI:10.1016/j.comptc.2014.07.019.
71. P. Nasertayoob, M. Goli and Sh. Shahbazian, Int. J. Quantum Chem., 2011, 111, 1970.
72. M. Goli and Sh. Shahbazian, Int. J. Quantum Chem., 2011, 111, 1982.
73. F. Heidar Zadeh and Sh. Shahbazian, Int. J. Quantum Chem., 2011, 111, 1999.
74. M. Goli and Sh. Shahbazian, Phys. Chem. Chem. Phys., 2014, 16, 6602.
75. M. Tachikawa, Y. Kita and R. J. Buenker, Phys. Chem. Chem. Phys., 2011, 13, 2701.
76. K. Koyanagi, Y. Kita and M. Tachikawa, Eur. Phys. J. D, 2012, 66, 121.
77. F. Moncado, D. Cruz and A. Reyes, Chem. Phys. Lett., 2012, 539–540, 209.
78. K. Koyanagi, Y. Takeda, T. Oyamada, Y. Kita and M. Tachikawa, Phys. Chem. Chem. Phys., 2013, 15, 16208.
79. K. Koyanagi, Y. Kita, Y. Shigeta and M. Tachikawa, ChemPhysChem, 2013, 14, 3458.
80. F. Moncado, D. Cruz and A. Reyes, Chem. Phys. Lett., 2013, 570, 16.
81. Y. Oba and M. Tachikawa, Int. J. Quantum Chem., 2014, 114, 1146.
82. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347.
83. T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007.
84. T. Helgaker, P. Jørgenson and J. Olsen, Molecular Electronic-Structure Theory, John Wiley & Sons, New York, 2000.
85. H. Joypazadeh and Sh. Shahbazian, Found. Chem., 2014, 16, 63.
86. R. F. W. Bader, Int. J. Quantum Chem., 1995, 56, 409.
87. R. F. W. Bader, J. Phys. Chem. A, 2008, 112, 13717.
88. R. F. W. Bader, S. G. Anderson and A. J. Duke, J. Am. Chem. Soc., 1979, 101, 1389.
89. R. F. W. Bader, Y. Tal, S. G. Anderson and T. T. Nguyen-Dang, Isr. J. Chem., 1980, 19, 8.
90. C. Foroutan-Nejad and Sh. Shahbazian, THEOCHEM, 2009, 894, 20.
91. P. M. Sánchez, A. Martín Pendás and V. Luaña, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 125103.
92. H. Primas, Acta Polytech. Scand., 1998, 91, 83.
93. H. J. Monkhorst, Int. J. Quantum Chem., 1999, 72, 281.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp03722g

---