Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Polymeric watersplitting photocatalysts; a computational perspective on the water oxidation conundrum†
Pierre
Guiglion
,
Cristina
Butchosa
and
Martijn A.
Zwijnenburg
*
Christopher Ingold Laboratories, Department of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK. E-mail: m.zwijnenburg@ucl.ac.uk
First published on 11th June 2014
Abstract
A computational scheme to predict the thermodynamic ability of photocatalysts to drive both of the watersplitting half reactions, proton reduction and water oxidation, is discussed, and applied to a number of polymeric systems to explain their apparent inability to oxidise water. We predict that the poly(p-phenylene) (PPP) is thermodynamically unable to oxidise water and that PPP is hence unlikely to split water in the absence of an external electrical bias. For other polymers, however, for example carbon nitride, the lack of oxygen evolution activity appears kinetic in origin and hence a suitable co-catalyst could potentially transform them into true watersplitting photocatalysts.
Introduction
Photocatalytic watersplitting offers a renewable route to molecular hydrogen. Sunlight, sometimes in a combination with an electrical bias, is used to split water into molecular hydrogen and oxygen gas, where the former can be separated off and used as fuel. As only sunlight and water are used to generate this hydrogen, and as its combustion results in the formation of only water, hydrogen produced through photocatalytic watersplitting can play a crucial role in an overall greening of the economy. However, to reach this stage, photocatalysts have to be developed that are both efficient in terms of the percentage of light photons successfully converted into hydrogen, and cheap. In this paper we discuss a computational method of analysing the thermodynamic ability of materials to act as photocatalysts for watersplitting, and apply it to a class of photocatalysts that have recently attracted great attention; organic conjugated polymers.Chemically, the overall photocatalytic watersplitting reaction is the combination of two half-reactions:1,2
| 2H+ + 2e− ⇄ H2 | (A) |
| O2 + 4H+ + 4e− ⇄ 2H2O | (B) |
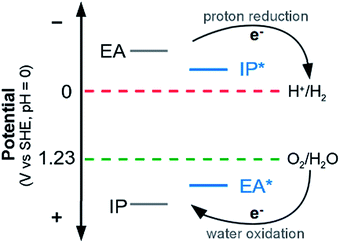
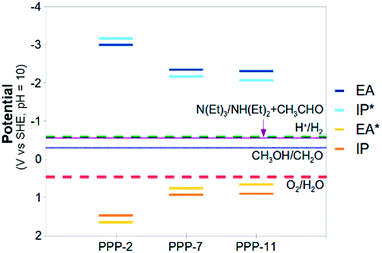
Half-reaction (A) runs in the forward direction, the reduction of protons to hydrogen gas, and (B) backwards, oxidation of water to oxygen gas and protons. In order for both of these half-reactions to take place, a photocatalyst will have to provide electrons for half-reaction (A), and accept electrons, or in other words donate holes, for half-reaction (B). Experimentally, half-reaction (A) has a standard reduction potential of 0 V relative to the Standard Hydrogen Electrode (SHE) and half reaction (B) a standard reduction potential of 1.23 V. A photocatalyst needs therefore to provide at least this amount of potential to split water. In practice, generally, a larger potential (e.g. 2 V) is required to overcome kinetic barriers and energetic losses, the difference between the effective and thermodynamic potentials being the overpotential. Another requirement for a successful watersplitting photocatalyst is that the (standard) reduction potential of its charge-carriers (electrons, holes) straddle those of half-reactions (A) and (B). In other words, the (standard) reduction potential of its electrons should be more negative than that of the proton reduction half-reaction (A) and the potential of its holes more positive than that of water oxidation half-reaction (B) (see Fig. 1).
Following the discovery by Fujishima, Honda and co-workers in 1969 that a TiO2 photoanode, i.e. using a combination of light and electrical bias, could catalyse the splitting of water,3 the search for watersplitting catalysts focussed primarily upon inorganic systems1,2,4 (e.g. besides TiO2; Zn1.44GeN2.08O0.38 (ref. 5) and TaON6). However, in 1985 Yanagida and co-workers7 widened the scope of possible photocatalysts by demonstrating that also an organic conjugated polymer, poly(p-phenylene), could successfully catalyse half-reaction (A) under ultraviolet light.
Organic conjugated polymers offer the long-term vista of solution processable photocatalysts that can be optimized through exploiting the unrivalled synthetic versatility offered by organic chemistry. Also, in contrast to many of their inorganic counterparts, they are based on earth abundant elements. However, until recently, the progress of research into polymeric watersplitting catalysts was very slow compared with that of their inorganic analogues, possibly due to perceived stability issues. This all changed in 2008 with the discovery by Antonietti and co-workers8 that carbon nitride polymers could act as a photocatalyst for both the (A) and (B) half-reactions, although, for the moment, not concurrently. Since this report, there has been a steady stream of publications on polymer systems for photocatalytic watersplitting, including (doped) carbon nitrides,9–16 poly(azomethine),17 polyimides,18 and polymeric disulfides.19
Currently, most of these polymeric photocatalysts only catalyse the proton reduction half-reaction (A) in the presence of a sacrificial electron donor (e.g. methanol or triethylamine) and thus, for the moment, cannot split water as such. Moreover, the one polymeric system in the literature that is reported to split pure water,13 a carbon nitride polymer with polypyrrole nanoparticles on its surface, produces hydrogen and hydrogen peroxide instead of hydrogen and oxygen.
The lack of experimental activity for the water oxidation half-reaction (B) could in principle be thermodynamic in nature, e.g. because the (standard) reduction potential of the polymers holes is not sufficiently positive, or alternatively a kinetic issue. In the latter case, a co-catalyst that either lowers the kinetic barriers for water oxidation (i.e. reduces the required overpotential) or prevents electron–hole recombination, might turn a polymer that only catalyses half-reaction (A) into one that splits pure water. In contrast, if the lack of activity for reaction (B) is due to thermodynamics, a possible route towards true watersplitting would be to use the polymer as a photocathode in combination with an electrical bias and a suitable counter electrode, or as part of a Z-scheme.20,21
In order to resolve if the issue with water oxidation for a given polymer is kinetic or thermodynamic in nature, we develop an approach that not only considers the free electron and holes but also the bound exciton (excited electron–hole pair). We also explicitly consider the effect of the environment and the nuclear relaxation associated with localising an excited electron, hole, or exciton (adiabatic potentials versus vertical potentials). We use our approach here primarily to rationalise the lack of water oxidation activity in the original poly(p-phenylene) (PPP) photocatalyst7,22 of Yanagida and co-workers, but will also briefly touch upon other polymer systems, including carbon nitrides. We will demonstrate that the holes in PPP thermodynamically cannot drive the oxidation of water, but also suggest that for other systems the problem must be kinetic in nature and should be resolvable with the choice of a suitable co-catalyst.
Theoretical approach
In the following section we will outline an approach to predict computationally the thermodynamic ability of a photocatalyst to drive the reduction of protons and the oxidation of water. We will use this approach later on to analyse a number of polymeric watersplitting photocatalysts.Modelling the polymer
When considering the ability of a photocatalyst to drive the reduction of protons and the oxidation of water or alternative sacrificial electron donors, there are four redox half-reactions to consider. These half-reactions, written in line with convention as reduction reactions, are:| P+ + e− ⇄ P* | (C) |
| P* + e− ⇄ P− | (D) |
| P + e− ⇄ P− | (E) |
| P+ + e− ⇄ P | (F) |
In half-reactions (C) and (E) the exciton and free electron act as a reductant; they donate an electron and the half-reaction will run in the opposite direction to that shown above. In the other two half-reactions the exciton and free hole will act as an oxidant; accepting electrons. Finally, the free electrons and holes responsible for half-reactions (E) and (F) could either be formed as a by-product of half-reactions (C) and (D) or directly by thermal or field ionisation of the exciton:
| P* + P → P+ + P− | (G) |
The free energies of half-reactions (C)–(F) and reaction (G) then are:
| ΔG(C) = G(P*) − G(P+) = −IP* | (1) |
| ΔG(D) = G(P−) − G(P*) = −EA* | (2) |
| ΔG(E) = G(P−) − G(P) = −EA | (3) |
| ΔG(F) = G(P) − G(P+) = −IP | (4) |
| ΔG(G) = (G(P+) + G(P−)) − (G(P*) + G(P)) | (5) |
Finally we can calculate the (standard) reduction potentials of the half-reactions via:
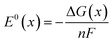 | (6) |
The Gibbs free energies of each relevant species can be considered as a sum of three contributions:
| G(x) = U(x) + Gvib(x) + Gsol(x) | (7) |
Another approximation is to calculate eqn (1)–(5) using the ground state geometry of the neutral photocatalyst for all species; ignoring nuclear relaxation. This would be the so-called vertical approximation, yielding vertical potentials, which can be compared with their full adiabatic counterparts. The vertical approximation is not only a numerical simplification but also physically meaningful. Contrasting vertical and adiabatic values allows one to distinguish what would happen if electron transfer was respectively fast or slow compared with nuclear relaxation.
Now, as alluded to in the introduction, for a photocatalyst to be able to thermodynamically drive both the reduction of protons and the oxidation of water, the potentials of half-reactions (D) and (F) (the potentials EA* and IP) should be more positive than the O2/H2O reduction potential and the potentials of half-reactions (C) and (E) (the potentials IP* and EA) more negative than the H+/H2 reduction potential (see Fig. 1). For either half-reaction to occur at an appreciable rate, like with any electrochemical reaction, an excess overpotential is usually required; i.e. the potentials should be even more positive and negative respectively.
Modelling the potentials of water and sacrificial electron donors
Standard reduction potentials for the reduction of protons, the 4-electron oxidation of water, and the 2-electron oxidation of the sacrificial electron donors methanol and triethylamine,23 can be calculated from their respective half-reactions (A), (B), and:| CH2O + 2H+ + 2e− → CH3OH | (H) |
| NH(CH2CH3)2 + CH3CHO + 2H+ + 2e− → N(CH2CH3)3 + H2O | (I) |
All these half-reactions involve one or more protons. Calculating the free energy of a proton, however, is rather complicated.24,25 Following work of others, we thus use the experimentally determined absolute value of the standard hydrogen electrode for the potential of reaction (A) (4.44 V).26 We determine the proton free-energy (G(H+)) for calculating the potentials of the other half-reactions ((B), (H), (I)) via:
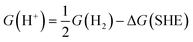 | (8) |
Computational details
To calculate the photocatalyst potentials outlined above, we use a combination of DFT,27,28 for the ground (free) energies including those of the cation and anion, and TD-DFT,29 for the excited state (free) energies. We use a molecular rather than a periodic approach30–32 as this conveniently gives us access to the vacuum reference state and allow us to study cation and anions (P+, P−) without having to introduce additional approximations, such as a neutralising background charge. The molecular approach is also the natural description of the amorphous polymeric photocatalysts studied below, with excited states delocalised over a finite number of polymer units.Our calculations consist effectively of four major steps. First, we perform a conformational search using an interatomic potential to find the lowest energy conformers. Second, we optimise the geometries of these conformers using DFT for its neutral (P), cationic (P+) and anionic state (P−). Third, we optimise the geometry of the conformer in its lowest singlet excited state (S1) using TD-DFT (P*). Fourth, we calculate the vibrational spectra for all four minimum energy geometries (P, P+, P− and P*) to determine the vibrational contribution to the free energy; Gvib(x) in eqn (7). A similar set-up is used to calculate the standard reduction potentials of water and the sacrificial electron donors, except for the lack of a conformer search and no need of TD-DFT calculations.
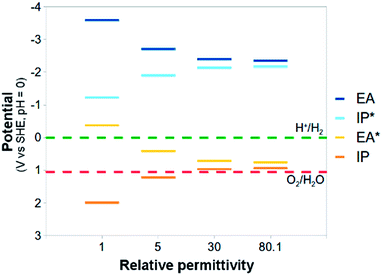
The effect of the solvent, and the environment in general, is included in all calculations, except where explicitly stated, by using the COSMO dielectric continuum solvation model,33,34 allowing us to estimate the Gsol(x) term in eqn (7). We have considered both single point COSMO calculations on the gas phase minimum energy structures and full COSMO geometry optimisations, except in the case of TD-DFT calculations, where no COSMO gradients are available in the code we use, and for which hence only the former option is available. Within the COSMO model, the properties of the environment are characterised by its relative dielectric permittivity (ε). Calculations for the polymers were performed for a range of ε values (ε = 1, 5, 30 and 80.1), while the standard reduction potentials of water and the sacrificial electron donors were only calculated for the case of ε = 80.1; solvation in water.
For the initial conformational search, the OPLS-2005 forcefield35 and the low-mode sampling algorithm36 as implemented in MacroModel 9.9 (ref. 37) were employed. We typically used a combination of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 search steps and minimum and maximum low-mode move distances of 3 and 6 Å respectively. All the structures located within an energy window of 100 kJ mol−1 relative to the lowest energy conformer were saved.
000 search steps and minimum and maximum low-mode move distances of 3 and 6 Å respectively. All the structures located within an energy window of 100 kJ mol−1 relative to the lowest energy conformer were saved.
All the DFT and TD-DFT calculations employed the B3LYP38–41 hybrid Exchange–Correlation (XC) functional and the Turbomole 6.5 code.42–44 The standard basis-set used was the double-ζ DZP45 basis set, but for selected calculations also the larger def2-TZVP46 basis-set was employed. In all TD-DFT calculations, the Tamm–Dancoff47 approximation was used.
Finally, we calculated for selected systems Peach's Λ diagnostic.48 The Λ diagnostic characterises the overlap between the occupied and unoccupied orbitals involved with an excitation, and the likeliness that this excitation is wrongly described in TD-DFT due to it having a charge-transfer (CT-) nature. The Λ scale ranges from 0 (no overlap, CT-excitation) to 1 (full overlap, fully local excitation), and for excitations with Λ > 0.3, TD-B3LYP has been found to normally not suffer from any CT-problems.48 The Λ values obtained, typically 0.4–0.8, suggest that CT-problems are unlikely to be an issue in the TD-B3LYP excited state description of any of the systems studied here.
Results and discussion
We will now discuss the results of the application of the computational approach introduced above to organic polymeric watersplitting photocatalysts.PPP
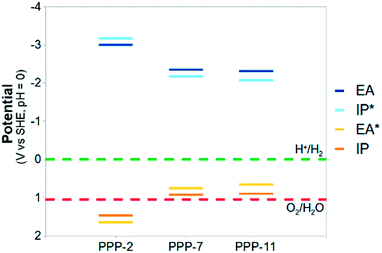
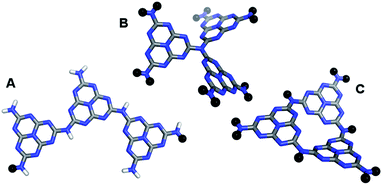
In the follow-up to the original paper of Yanagida and co-workers,7 Shibata et al.22 estimate that the photocatalytically active PPP material consists approximately of p-phenylene chains of 7 and 11 phenylene units (see below). Hence in our calculations, we primarily focus on these molecules, hereafter referred to as PPP-7 and PPP-11. Fig. 2 shows a picture of the DFT optimised structure of the lowest energy conformer of PPP-7. To probe the effect of chain length we will also contrast the properties of these longer chains with those of the p-phenylene dimer, PPP-2.Before discussing our prediction for the (standard) reduction potentials of the exciton and the free charge carriers, we first compare the predicted absorption on-set and luminescence signal of PPP-7 and PPP-11 with experimental data for PPP powder samples from the literature. Different authors22,49 report slightly different powder absorption spectra for PPP. These differences arise probably from slight variations in the PPP chain-length distributions obtained during synthesis, and from the experimental difficulty in characterising this chain-length distribution due to the poor solubility of PPP oligomers and polymers in common solvents. In the case of the PPP samples of Shibata and co-workers,22 the fact that both the PPP-7 and PPP-11 samples have a similar absorption on-set (see Fig. 2B in their paper) and the fact that the fluorescence spectrum they obtain for PPP-11 is bimodal (see their Fig. 3) suggest that both samples most likely contain a distribution of PPP chain lengths. The experimental labels PPP-7 and PPP-11, while probably representative, are hence likely to be a slight simplification of the true complexity of the experimental samples.
When comparing experimental spectra with TD-DFT predicted excitation energies we make, following our previous work,50–52 the implicit assumption that the top of the first peak or shoulder in the absorption spectrum equals the experimental vertical absorption on-set, and that all absorption before this peak arises from vibrational broadening. As can be seen from Table 1, upon making this assumption, TD-B3LYP yields a good match to the experimental data. In line with the literature, adding a dielectric embedding to model the polymer matrix around the chains (assumed to have ε = 5) changes the results only marginally.
The standard reduction potentials involving the exciton (EA* and IP*) show similar behaviour. Upon increasing the relative dielectric permittivity of the environment, the standard reduction potential of the reaction where the exciton donates an electron (IP*), becomes more negative and the standard reduction potential of the reaction where the exciton accepts an electron (EA*) becomes more positive. The difference in potential between EA and IP* and between IP and EA* becomes progressively smaller, approaching zero for water (0.2 eV). For PPP-7 embedded in water, less than 10 kBT of additional energy needs to be provided to ionise the exciton into free charge carriers (compared with more than 100 kBT for the gas phase). Splitting the exciton, required for chemistry involving the free charge carriers, is thus predicted to be much easier in a high dielectric permittivity environment.
The large shifts in predicted potentials with changes in the relative dielectric permittivity of the environment in which the PPP polymer is embedded make physical sense. All potentials involve charged species, the free charge carriers, and those charged species are to a much larger degree stabilised energetically by the dielectric embedding than their neutral counterparts. The predicted adiabatic potentials in Fig. 3 neglect the contribution of Gvib in eqn (7). Data including Gvib can be found in the ESI (section ESI-1†), showing that neglecting Gvib generally results in changes of the order of 0.1 V in the predicted potentials. Ignoring nuclear relaxation, using vertical rather than adiabatic potentials, would introduce a larger error (0.2–0.3 V, see ESI-1†). In the remainder of this paper, all polymer potentials discussed will be adiabatic potentials calculated for an aqueous environment (ε = 80.1), where Gvib is neglected.
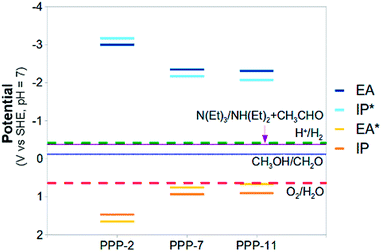
Fig. 5 and 6 also include the predicted potentials for the 2-electron oxidation of methanol and triethylamine (reactions (H) and (I)). Clearly there is a thermodynamic driving force for the oxidation of both by PPP-7 and PPP-11. The driving force is largest for triethylamine, in line with the results of Shibata and co-workers, where its use gave the highest hydrogen yield. One of the expected products of the 2-electron oxidation of triethylamine (ethanol) is indeed observed by Shibata and co-workers to be produced in conjunction with hydrogen,22 while the other (diethylamine) was not measured, as it is unstable under alkaline conditions. The success of triethylamine as a sacrificial electron donor is probably due to its more negative potential than that of water, combined with the fact it involves a 2- rather than a 4-electron reaction.
All results discussed here were obtained using the DZP basis-set. We recalculated some of the potentials for the polymer and all of the solution reaction potentials (reactions (A), (B), (H) and (I)) with the larger def2-TZVP basis and found the effect of increasing the basis-set generally small (see Table 2 and section ESI-4 of the ESI†). The most noticeable change was an even better agreement of the calculated standard reduction potential of water oxidation (1.05 V for DZP and 1.21 V for def2-TZVP) with its experimental value. Finally, while we neglect Gvib for the polymer, we always include it when calculating the solution reaction potentials. Due to the structural differences between reactants and products, the effect of neglecting Gvib would be substantially bigger here.
| DZP | def2-TZVP | def2-QZVP | |
|---|---|---|---|
| O2/H2O | 1.05 | 1.21 | 1.26 |
| H2O/H2O2 | 1.64 | 1.85 | 1.91 |
| TEA | 0.03 | 0.09 | |
| MeOH | 0.29 | 0.25 |
Beyond PPP
Whereas for PPP, in line with our predictions, water oxidation has never been observed, other photocatalysts do oxidise water when using a sacrificial electron acceptor other than protons. Here we discuss some initial results on one such material; carbon nitride. The exact atomic structure of the amorphous/semi-crystalline carbon nitride CNxHy samples used in watersplitting is unknown. The active material might be built from linked triazine or heptazine building blocks, might have a layered graphitic-like structure or consist of linear chains, and could be polymeric or oligomeric. We hence performed calculations on cluster models representative of different possible material structures, focussing on those structures build from heptazine (see Fig. 7).Fig. 8 shows the potentials calculated for the different carbon nitride cluster models using the same set-up as PPP (see section ESI-5 of the ESI† for the potentials at pH = 0). All carbon nitride models are limited to three heptazine units, but calculations on a tetramer, discussed in the ESI (see section ESI-5 of the ESI†), demonstrate that at least for the linear structure, enlarging the cluster model results only in minor changes in the predicted potentials.
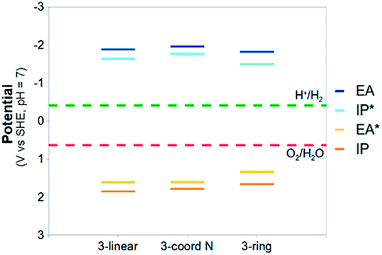 | ||
| Fig. 8 The (TD-)B3LYP predicted IP, EA, IP* and EA* adiabatic potential values of the different carbon nitride trimers in water (ε = 80.1) at pH 7 (all values relative to SHE). | ||
The predicted potentials for the carbon nitride cluster models are significantly different from those for PPP. Now there is not only a clear driving force for proton reduction, but also for water oxidation. While more work needs to be done, e.g. on the effect of stacking,52 our results strongly suggest that with a suitable co-catalyst such materials should be able to photocatalyse both reactions and split pure water into hydrogen and oxygen.
The reason that no carbon nitride photocatalyst has as yet been observed experimentally to split pure water into hydrogen and oxygen must be related to the fact that water oxidation to oxygen is a 4-electron reaction, and that therefore it is likely to be outcompeted by electron–hole recombination in the absence of some mechanism of keeping electron and holes apart. This idea is supported by the fact that in the only experiment in the literature where pure water is split using a polypyrrole co-catalyst,13 hydrogen peroxide rather than oxygen is formed. The oxidation of water to hydrogen peroxide, while thermodynamically much less favourable than the oxidation of water to oxygen, as it involves the larger potential of 1.64 V (overpotential of 0.4–0.6 V), only requires 2 instead of 4 electrons. Clearly, future work on carbon nitride photocatalysts should thus focus on finding suitable co-catalysts and related mechanisms of keeping electrons and holes apart.
Beyond carbon nitrides, focussing on other nitrogen-containing conjugated polymers might be worthwhile. Calculations on a heptamer of poly(pyridine-2,5-diyl)54,55 (PPy-7, see Fig. 9), the pyridine equivalent of PPP-7, suggest that the presence of nitrogen in the backbone of the polymer also in this case leads to a positive shift of the IP and EA* potentials, and thus to a larger thermodynamic driving force for water oxidation (see Fig. 10, and section ESI-6 of the ESI†). PPy has only been observed to catalyse the proton reduction reaction experimentally54,55 in the presence of triethylamine as sacrificial electron donor.
 | ||
| Fig. 10 A comparison between the (TD-)B3LYP predicted IP, EA, IP* and EA* adiabatic potential values of PPP-7 and its PPy-7 equivalent in water (ε = 80.1) at pH 7 (all values relative to SHE). | ||
Our calculations, however, predict a significant overpotential (0.6 V at pH 7), implying that the lack of water oxidation activity could also for PPy be resolved through the addition of a suitable co-catalyst. In summary, we thus believe that nitrogen substitution is a universal method of shifting the water oxidation potential in the desired direction.
Conclusions
Using a newly developed computational approach, we probed the thermodynamic ability of several polymeric watersplitting photocatalysts to drive both the reduction of protons and the oxidation of water. In the case of poly(p-phenylene), our calculations strongly suggests that this material is thermodynamically unable to oxidise water and hence split pure water. For other polymers studied, including carbon nitrides, any issue with water oxidation appears kinetic in nature. We believe that for these materials, the development of suitable co-catalysts that minimises electron–hole recombination and maximises water oxidation kinetics, will result in them being transformed into true watersplitting photocatalysts. Finally, we discuss that incorporation of nitrogen in the polymer backbone appears to offer a general route towards polymers with the ability to oxidise water, and we hence suggest that the study of other nitrogen containing polymers beyond carbon nitrides as photocatalysts might prove very fruitful.Acknowledgements
Dr Dave Adams, Enrico Berardo, Dr Michael Bojdys, Prof. Andy Cooper, Dr Furio Cora, Dr Alex Cowan and Dr Katherine Holt are kindly acknowledged for useful discussion. M.A.Z. thanks the UK Engineering and Physical Sciences Research Council (EPSRC) for a Career Acceleration Fellowship (Grant EP/I004424/1). Computational time on HECToR/ARCHER the UK's national high-performance computing service (via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC grants EP/F067496/1 and EP/L000202/1) and the EPSRC UK National Service for Computational Chemistry Software (NSCCS) at Imperial College London is gratefully acknowledged.References
- K. Maeda and K. Domen, J. Phys. Chem. Lett., 2010, 1, 2655–2661 CrossRef CAS.
- T. Hisatomi, J. Kubota and K. Domen, Chem. Soc. Rev., 2014 10.1039/C3CS60378D.
- A. Fujishima, K. Honda and S. Kikuchi, Kogyo Kagaku Zasshi, 1969, 72, 108–113 CrossRef CAS.
- A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278 RSC.
- Y. Lee, H. Terashima, Y. Shimodaira, K. Teramura, M. Hara, H. Kobayashi, K. Domen and M. Yashima, J. Phys. Chem. C, 2006, 111, 1042–1048 CrossRef.
- Z. Wang, J. Hou, C. Yang, S. Jiao, K. Huang and H. Zhu, Energy Environ. Sci., 2013, 6, 2134–2144 CAS.
- S. Yanagida, A. Kabumoto, K. Mizumoto, C. Pac and K. Yoshino, J. Chem. Soc., Chem. Commun., 1985, 474–475 RSC.
- X. C. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 76–80 CrossRef CAS PubMed.
- J. Zhang, G. Zhang, X. Chen, S. Lin, L. Möhlmann, G. Dołęga, G. Lipner, M. Antonietti, S. Blechert and X. Wang, Angew. Chem., Int. Ed., 2012, 51, 3183–3187 CrossRef CAS PubMed.
- A. B. Jorge, D. J. Martin, M. T. S. Dhanoa, A. S. Rahman, N. Makwana, J. W. Tang, A. Sella, F. Cora, S. Firth, J. A. Darr and P. F. McMillan, J. Phys. Chem. C, 2013, 117, 7178–7185 CAS.
- K. Schwinghammer, B. Tuffy, M. B. Mesch, E. Wirnhier, C. Martineau, F. Taulelle, W. Schnick, J. Senker and B. V. Lotsch, Angew. Chem., Int. Ed. Engl., 2013, 52, 2435–2439 CrossRef CAS PubMed.
- L. Ge, C. Han, X. Xiao, L. Guo and Y. Li, Mater. Res. Bull., 2013, 48, 3919–3925 CrossRef CAS PubMed.
- Y. Sui, J. Liu, Y. Zhang, X. Tian and W. Chen, Nanoscale, 2013, 5, 9150–9155 RSC.
- Z. Hong, B. Shen, Y. Chen, B. Lin and B. Gao, J. Mater. Chem. A, 2013, 1, 11754–11761 CAS.
- S. Chu, Y. Wang, Y. Guo, J. Feng, C. Wang, W. Luo, X. Fan and Z. Zou, ACS Catal., 2013, 3, 912–919 CrossRef CAS.
- K. Kailasam, J. Schmidt, H. Bildirir, G. Zhang, S. Blechert, X. Wang and A. Thomas, Macromol. Rapid Commun., 2013, 34, 1008–1013 CrossRef CAS PubMed.
- M. G. Schwab, M. Hamburger, X. Feng, J. Shu, H. W. Spiess, X. Wang, M. Antonietti and K. Mullen, Chem. Commun., 2010, 46, 8932–8934 RSC.
- S. Chu, Y. Wang, Y. Guo, P. Zhou, H. Yu, L. Luo, F. Kong and Z. Zou, J. Mater. Chem., 2012, 22, 15519–15521 RSC.
- Z. Zhang, J. Long, L. Yang, W. Chen, W. Dai, X. Fu and X. Wang, Chem. Sci., 2011, 2, 1826–1830 RSC.
- A. J. Bard, J. Photochem., 1979, 10, 59–75 CrossRef CAS.
- K. Maeda, ACS Catal., 2013, 3, 1486–1503 CrossRef CAS.
- T. Shibata, A. Kabumoto, T. Shiragami, O. Ishitani, C. Pac and S. Yanagida, J. Phys. Chem., 1990, 94, 2068–2076 CrossRef CAS.
- L. C. Portis, V. V. Bhat and C. K. Mann, J. Org. Chem., 1970, 35, 2175–2178 CrossRef CAS.
- C.-G. Zhan and D. A. Dixon, J. Phys. Chem. A, 2001, 105, 11534–11540 CrossRef CAS.
- V. S. Bryantsev, M. S. Diallo and W. A. Goddard III, J. Phys. Chem. B, 2008, 112, 9709–9719 CrossRef CAS PubMed.
- S. Trasatti, J. Electroanal. Chem. Interfacial Electrochem., 1986, 209, 417–428 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, 864–871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, 1133–1138 CrossRef.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- I. E. Castelli, T. Olsen, S. Datta, D. D. Landis, S. Dahl, K. S. Thygesen and K. W. Jacobsen, Energy Environ. Sci., 2012, 5, 5814–5819 CAS.
- Y. Wu, P. Lazic, G. Hautier, K. Persson and G. Ceder, Energy Environ. Sci., 2013, 6, 157–168 CAS.
- V. Stevanovic, S. Lany, D. S. Ginley, W. Tumas and A. Zunger, Phys. Chem. Chem. Phys., 2014, 16, 3706–3714 RSC.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- V. Barone, M. Cossi and J. Tomasi, J. Comput. Chem., 1998, 19, 404–417 CrossRef CAS.
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657–1666 CrossRef CAS.
- I. Kolossváry and W. C. Guida, J. Am. Chem. Soc., 1996, 118, 5011–5019 CrossRef.
- F. Mohamadi, N. G. J. Richards, W. C. Guida, R. Liskamp, M. Lipton, C. Caufield, G. Chang, T. Hendrickson and W. C. Still, J. Comput. Chem., 1990, 11, 440–467 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem. C, 1994, 98, 11623–11627 CrossRef CAS.
- R. Ahlrichs, M. Baer, M. Haeser, H. Horn and C. Koelmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2004, 121, 12772–12773 CrossRef CAS PubMed.
- C. van Wüllen, J. Comput. Chem., 2011, 32, 1195–1201 CrossRef PubMed.
- A. Schafer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- M. J. Peach, P. Benfield, T. Helgaker and D. J. Tozer, J. Chem. Phys., 2008, 128, 044118 CrossRef PubMed.
- G. Froyer, J. Y. Goblot, J. L. Guilbert, F. Maurice and Y. Pelous, J. Phys. Colloques, 1983, 44, 745–748 Search PubMed.
- M. A. Zwijnenburg, J. Phys. Chem. C, 2012, 116, 20191–20198 CAS.
- M. A. Zwijnenburg, G. Cheng, T. O. McDonald, K. E. Jelfs, J. X. Jiang, S. J. Ren, T. Hasell, F. Blanc, A. I. Cooper and D. J. Adams, Macromolecules, 2013, 46, 7696–7704 CrossRef CAS PubMed.
- C. Butchosa, T. O. McDonald, A. I. Cooper, D. J. Adams and M. A. Zwijnenburg, J. Phys. Chem. C, 2014, 118, 4314–4324 CAS.
- H. Meier, U. Stalmach and K. Kolshorn, Acta Polym., 1997, 48, 379 CrossRef CAS.
- S. Matsuoka, T. Kohzuki, Y. Kuwana, A. Nakamura and S. Yanagida, J. Chem. Soc., Perkin Trans. 2, 1992, 679–685 RSC.
- T. Maruyama and T. Yamamoto, J. Phys. Chem. B, 1997, 101, 3806–3810 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Potentials at different pH values; comparison of vertical, adiabatic, and free-energy corrected potentials for PPP-7; effect of basis-set for PPP-7 and information about PPP conjugation length. See DOI: 10.1039/c4ta02044h |
| This journal is © The Royal Society of Chemistry 2014 |