A study of Yb_0.2Co₄Sb₁₂–AgSbTe₂ nanocomposites: simultaneous enhancement of all three thermoelectric properties

Abstract

The single-filled skutterudite Yb_0.2Co₄Sb₁₂ has been long known as a promising bulk thermoelectric material. In this work, we adopted a melting–milling–hot pressing procedure to prepare nanocomposites that consist of a micrometer-grained Yb_0.2Co₄Sb₁₂ matrix and well-dispersed AgSbTe₂ nanoinclusions on the matrix grain boundaries. Different weight percentages of AgSbTe₂ inclusions were added to optimize the thermoelectric performance. We found that the addition of AgSbTe₂ nanoinclusions systematically and simultaneously optimized the otherwise adversely inter-dependent electrical conductivity, Seebeck coefficient and thermal conductivity. In particular, the significantly enhanced carrier mobility led to a ∼3-fold reduction of the electrical resistivity. Meanwhile the absolute value of Seebeck coefficient was enhanced via the energy filtering effect at the matrix–nanoinclusion interfaces. Moreover there is a topological crossover of the AgSbTe₂ inclusions from isolated nanoparticles to a nano-plating or nano-coating between 6 wt% and 8 wt% of nanoinclusions. Above the crossover, further addition of nanoinclusions degraded the Seebeck coefficient and the electrical conductivity. Meanwhile, the addition of nanoinclusions generally reduced the lattice thermal conductivity. As a result, the power factor of the 6 wt% sample was ∼7 times larger than that of the nanoinclusion-free sample, yielding a room temperature figure of merit ZT ∼ 0.51.

---

1. Introduction

Due to their ability to directly convert heat into electricity and vice versa without moving parts or greenhouse emissions, thermoelectric (TE) materials have drawn much attention in the wake of the energy crisis and the environmental concerns of fossil fuel use. The conversion efficiency of a TE material is determined by its dimensionless figure of merit ZT = α²T/ρκ, where α, ρ, κ, T are the Seebeck coefficient, electrical resistivity, thermal conductivity and absolute temperature, respectively. In the past decade much effort has been exerted toward developing nanostructured thermoelectric materials, and in this vein significant progress has been achieved in supperlattices^1–3 and nanocomposites.^4–6 To date, most of the enhancement of ZT in nanostructured thermoelectric materials has come from lowering the lattice thermal conductivity via strong phonon scattering at interfaces. In some cases the lattice thermal conductivity has been reduced to near the so-called amorphous limit as the phonon mean free path is comparable to the inter-atomic spacing.⁷ For this reason there is limited room for researchers to further enhance ZT by reducing the lattice thermal conductivity, therefore new strategies for increasing the power factor (α²/ρ) while retaining a low lattice thermal conductivity are highly desired.

The goal of this work was to improve the thermoelectric performance of Yb-filled CoSb₃ skutterudite bulk materials via incorporating nanoparticles. Upon appropriate filling, CoSb₃-based skutterudites are well known as a promising class of bulk thermoelectric materials for medium-temperature applications. The skutterudite family of compounds crystallizes in the Im3 space group with the form MX₃, where the metal atom M can be Co, Rh, or Ir and the pnicogen X can be P, As or Sb. A unit cell consists of 32 atoms, in which the M atoms form eight sub-cubes with pnicogen rings occupying six of them leaving the final two sub-cubes or cages empty. Filling the naturally formed voids (i.e., the empty sub-cubes or cages) with rare-earth, alkaline-earth, In, or Tl etc. atoms (i.e., filled skutterudite) leads to a remarkable decrease of the lattice thermal conductivity,^8–12 thereby increasing ZT. However, the lattice thermal conductivity of filled skutterudites, especially that of n-type filled skutterudites, remains relatively high as compared to other state-of-the-art thermoelectric materials.

To further reduce the lattice thermal conductivity, some investigations have been carried out by incorporating nanoparticles into the bulk matrix via both in situ and ex situ preparation methods,^13–16 though the beneficial reduction of the lattice thermal conductivity is often offset by a degradation of the power factor. Importantly, not all nanostructuring processes are thermoelectrically favorable, hence appropriate selection of composition, micro-morphology, and topology of the nano-component is crucial. In this vein, we choose AgSbTe₂ as the nano-component in order to enhance the thermoelectric performance of the single-filled skutterudite Yb_0.2Co₄Sb₁₂. In addition to being an important component of the high-performance thermoelectric materials, LAST and TAGS, AgSbTe₂ is by itself a promising thermoelectric material with low lattice thermal conductivity (∼0.6 W m⁻¹ K⁻¹ at room temperature)¹⁷ and a complicated nano-microstructure similar to LAST.¹⁸

In order to systematically study the impact of AgSbTe₂ nanoinclusions, we adopted an ex situ approach to incorporate different weight percentages of AgSbTe₂ nanoinclusions into bulk micrograined Yb_0.2Co₄Sb₁₂. High temperature thermoelectric property measurements revealed that the electrical conductivity, Seebeck coefficient and thermal conductivity were optimized simultaneously. To obtain a better understanding of the underlying mechanism, low temperature transport property measurements have been performed, in conjunction with microstructure characterization, and we found that the incorporation of AgSbTe₂ nanoinclusions has decoupled the otherwise adversely inter-dependent electrical conductivity, Seebeck coefficient and thermal conductivity; the property optimization has been obtained via improving carrier mobility, energy filtering, and phonon scattering at the interfaces. Meanwhile we observed that the AgSbTe₂ inclusions underwent a topological crossover from isolated nanoparticles to a nano-plating or nano-coating between 6 wt% and 8 wt% of nanoinclusions, which substantially influenced the thermoelectric properties.

2. Experimental procedure

Yb_0.2Co₄Sb₁₂ and AgSbTe₂ were separately synthesized as follows. Stoichiometric amounts of Co powder (99.5%), Sb shot (99.99%), and Yb ingot (99.9%) were mixed and sealed in evacuated quartz tubes, slowly heated to 1323 K and held for 24 h, then cooled to 923 K and held for another 4 days, before furnace-cooling to room temperature. Stoichiometric amounts of Ag powder (99.9%), Sb shot (99.99%), and Te powder (99.99%) were mixed and sealed in evacuated quartz tubes, heated to 1123 K and held for 10 h, then quenched in liquid-nitrogen. To obtain Yb_0.2Co₄Sb₁₂/x wt% AgSbTe₂ composites (x denotes the weight percentage of AgSbTe₂, x = 0, 2, 4, 6, 8), the Yb_0.2Co₄Sb₁₂ ingot, which would serve as the matrix of composites, was pulverized manually in an agate mortar, and the AgSbTe₂ ingot was milled in a planetary mill at 400 rpm for 5 h to yield nano to micro-scale particles. The matrix and AgSbTe₂ particles were then mixed in a planetary mill at 300 rpm for 40 minutes, and hot pressed at 873 K and 100 MPa for 2 h in a vacuum. The density of the obtained samples is about 95% of the theoretical value for all samples.

Phase characterization was performed by X-ray powder diffraction (PANalytical X'pert PRO diffractometer with Cu Kα radiation), and the lattice parameter of the matrix was analyzed from high angle scans using a regression diagnostics method.¹⁹ The fractured surface of the composite was checked by field-emission scanning electron microscopy (FEI: Nano SEM 450). The transmission electron microscopy sample was prepared by polishing, dimpling, and ion milling to obtain a thin specimen for analysis, and the TEM investigations were carried out in Tecnai G2 20 and JEM 2100F microscopes equipped with an energy-dispersive X-ray spectrometer (EDS).

For direct measurements of their thermoelectric properties, the samples were cut, using a diamond saw, into 7 × 2 × 2 mm³ bars for low temperature electrical resistivity and Seebeck coefficient measurements, and 8 × 8 × 1 mm³ squares for room temperature thermal conductivity measurements. The low temperature electrical resistivity and Seebeck coefficient were measured simultaneously from 15 K to 325 K in a custom designed apparatus.²⁰ The room temperature thermal conductivity κ was calculated from the measured thermal diffusivity D, specific heat C_p, and density d using the expression κ = DC_pd, where D and C_p were measured by a laser flash method (Shinkuriko: TC-7000H) in a vacuum, and the density d was measured by the Archimedes method. The Hall coefficient measurements were performed on a Quantum Design PPMS using a 5-probe configuration, with the magnetic field sweeping between ±1.0 tesla.

3. Results and discussion

3.1 Structural characterization

Fig. 1 presents the powder XRD patterns of the liquid-nitrogen quenched AgSbTe₂ ingot and matrix–8 wt% AgSbTe₂ composite. Powder XRD analysis shows that (i) the Yb_0.2Co₄Sb₁₂ ingot is of the single-phase skutterudite structure; (ii) the AgSbTe₂ ingot consists primarily of the rocksalt structure (JCPDS: 00-015-0540) and a minor Ag₂Te phase (JCPDS: 01-081-1820), which is consistent with the report that stoichiometric AgSbTe₂ separates into a two-phase mixture of Ag₂Te in a Sb-rich, rocksalt structure matrix.^21,22 The powder XRD pattern of the matrix–8 wt% AgSbTe₂ composite can be indexed to a minor AgSbTe₂ phase (JCPDS: 00-015-0540) and a primary skutterudite phase (JCPDS: 03-065-3144). For the composites with 0 < x < 8, the peaks from the AgSbTe₂ phase are difficult to detect because of its low concentration as well as peak broadening due to its nanoscale grain size. The lattice parameters of the composites' matrices were calculated and the results are: 9.0424(2), 9.0420(3), 9.0426(2), 9.0418(3), 9.0424(3) Å for x = 0, 2, 4, 6 and 8, respectively.

Fig. 1 Powder XRD patterns of the AgSbTe₂ ingot and the matrix–8 wt% AgSbTe₂ composite.

The fractured surfaces of the hot-pressed samples were analyzed by SEM, and some typical images are shown in Fig. 2. A striking feature in the composite samples is that nanoparticles with size less than 100 nm are well dispersed on the grain boundaries. The nanoparticles are not observed on the Yb_0.2Co₄Sb₁₂ sample (i.e., the reference sample), implying that they originated from AgSbTe₂. Furthermore, the nanoparticle content initially increases with increasing x, and when x reaches 8, however, the nanoparticles are conspicuously absent. This has been attributed to inter-growth/inter-connection of the nanoparticles in the 8 wt% sample, as shown in Fig. 2(d).

Fig. 2 SEM images of the fractured surfaces of (a) Yb_0.2Co₄Sb₁₂, (b) 4 wt% AgSbTe₂ composite, (c) 6 wt% AgSbTe₂ composite, and (d) 8 wt% AgSbTe₂ composite.

To further investigate the composition and microstructure of the nanoparticles, selected area electron diffraction (SAED) and chemical analysis were carried out on the matrix–4 wt% AgSbTe₂ sample. Fig. 3 shows bright-field images and selected area electron diffraction (SAED) patterns of the nanoparticle on the grain boundary. Consistent with the SEM observations, nanoparticles of less than 100 nm size are well dispersed on the grain boundaries. EDS analysis reveals that the grain boundaries are Ag and Te rich. Generally a single phase AgSbTe₂ is considered to be a disordered NaCl-type Fm3̄m structure with Ag and Sb randomly occupying the Na sites. However, recent studies have revealed that primitive cubic Pm3̄m, tetragonal P4/mmm or rhombohedral R3̄mH structures can be formed with a certain degree of Ag and Sb atomic ordering, and long-range atomic ordering has been found.^18,23 Indeed, the SAED patterns in Fig. 3(c) are composed of two distinct patterns, as illustrated in Fig. 3(d). For one pattern the fundamental spots are indexed to a primitive cubic Pm3̄m lattice along a [6 2 1] zone axis with a ≈ 6.26 Å (ICSD #170661 (ref. 23)). Additionally there are extra super-reflection spots arrayed along the [0 −1 2] direction (indicated by a white arrow), characteristic of a double unit cell due to Ag/Sb ordering. The other pattern is indexed to a rhombohedral R3mH AgTe₃ lattice with a ≈ 8.43 Å, c ≈ 5.23 Å (JCPDS: 01-076-2328). It is worth noting that the characteristic XRD peaks of AgTe₃ are close to those of cubic AgSbTe₂, and hence they are masked by those of AgSbTe₂. Fig. 4 shows another bright-field image and a corresponding SAED pattern; electron diffraction reveals that the nanoparticle crystallizes in a monoclinic Ag₂Te lattice along a [5 2 6] zone axis (JCPDS: 01-081-1820). Based on powder XRD, electron microscopy, SAED, and chemical analysis, it is concluded that the composites are composed of a micrometer-grained Yb_0.2Co₄Sb₁₂ matrix along with nanometer-sized grain boundary phases, which, in turn, consist of a primary AgSbTe₂ cubic phase and minor AgTe₃ and Ag₂Te phases. No discernible change in phase has been detected before and after the nanocompositing process.

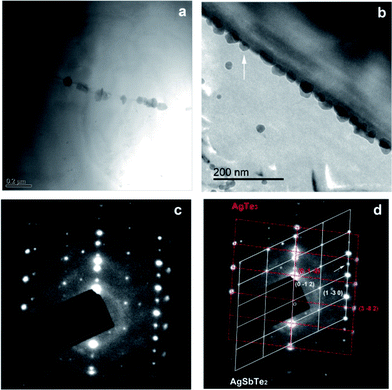Fig. 3 (a and b) Bright-field images of matrix–4 wt% AgSbTe₂ composite and (c) SAED taken on (b) as shown. The two sets of diffraction patterns in (c) are illustrated in (d).

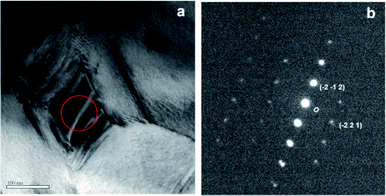Fig. 4 (a) A bright-field image of matrix–4 wt% AgSbTe₂ composite and (b) the corresponding SAED pattern.

3.2 Thermoelectric properties

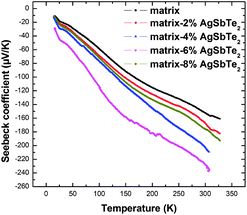
Fig. 5 and 6 present the low temperature electrical resistivity and Seebeck coefficient of all samples from 15 to 325 K. Interestingly, the electrical resistivity is decreased remarkably and the absolute Seebeck coefficient is increased simultaneously in the composites, which is hard to attain in single-phase materials. The electrical resistivity of the composites is decreased by a factor of about three compared to that of the pristine matrix: it decreases with increasing AgSbTe₂ content for x = 2 to 6, and then increases for x = 8. The carrier concentration n was estimated from the measured Hall coefficient R_H using a single parabolic band model via the relation n = 1/eR_H, where e is the electron charge. Furthermore, the Hall mobility μ was calculated from the measured electrical resistivity ρ and carrier concentration n via the relation ρ = 1/neμ. As shown in Fig. 7, the carrier concentration increases with increasing AgSbTe₂ content when x is less than 8 below 250 K, suggesting that the incorporation of AgSbTe₂ introduces a n-type dopant. This doping might be due to the effect of AgSbTe₂ as an inclusion, however, AgSbTe₂ is generally a p-type semiconductor. Therefore it is presumably due to Te from the AgSbTe₂ entering into and doping the matrix through diffusion in the synthesis of the composites, since Te is a common n-type dopant of CoSb₃ that substitutes Sb. The amount of Te substitution has been estimated from the change of carrier concentration. As the largest carrier concentration increment, Δn, in the composites compared with the matrix is less than 2 × 10¹⁹ cm⁻³, the estimated amount of Te substitution is less than y = 0.02 in the form of Yb_0.2Co₄Sb_12−yTe_y, taking into account that each Te atom gives about 0.3–0.4 electron to the structure when it replaces Sb.^24,25 This value is too small to observe any significant increase of the lattice parameters, consistent with the XRD analysis. A similar observation has been reported in CoSb₃–PbTe composites.²⁶

Fig. 5 The low temperature electrical resistivities of the studied samples.

Fig. 6 The low temperature Seebeck coefficients of the studied samples.

Fig. 7 The low temperature carrier concentrations of the studied samples.

Fig. 8 shows the temperature dependence of the Hall mobility. The mobility of the matrix first increases with temperature below about 25 K, and then decreases at elevated temperatures due to acoustic phonon scattering. Similar behaviour has been reported for Yb_0.21Co₄Sb₁₂.²⁷ Here the most surprising observation is that the Hall mobility is significantly enhanced in the composites. The magnitude is increased by about a factor of 3, indicating that the reduction of the electrical resistivity in the composites originates mainly from the enhanced mobility. Actually there are two factors that are disadvantageous to carrier transportation in the composites. Firstly, Te substitution generally leads to decreased mobility owing to increased ionized impurity scattering, as reported in Te-doped CoSb₃,^25,28 Te-doped and Sr-filled Sr_yCo₄Sb_12−xTe_x.²⁹ Besides, the matrix–nanoparticle heterogeneous interfaces serve as a scattering center for charge carriers, which also decrease carrier mobility. Though the exact mechanism underlying the enhancement of the mobility is unclear and requires further investigation, a possible explanation is that the incorporation of AgSbTe₂ nanoparticles has improved grain boundary electrical connectivity. An enhanced mobility has been observed in Ba_0.3Co₄Sb₁₂–Ag nanocomposites,³⁰ owing to Ag nanoparticles promoting the grain boundary connectivity since Ag is a good conductor. In this case AgSbTe₂ is a semiconductor in stead of metallic Ag, however, the matrix is Yb-filled skutterudite, and, as is known, ytterbium is so reactive that insulating ytterbium oxide is readily formed which mostly distributes on the grain boundaries and suppresses the grain boundary connectivity. It has been reported²⁷ that 38% of the total Yb was ended up with the form of oxides on the grain boundaries in the Yb-filled skutterudites. In the composite materials, as mentioned above AgSbTe₂ nanoparticles are evenly distributed on the grain boundaries, therefore the grain boundary conductivity is improved compared with the matrix, giving rise to the mobility enhancement.

Fig. 8 The low temperature carrier mobilities of the studied samples.

In addition to the significant reduction of the electrical resistivity, the absolute Seebeck coefficient of the composites is increased. For example, the absolute Seebeck coefficient of the matrix–6 wt% AgSbTe₂ sample is increased to 228 μV K⁻¹ as compared to 152 μV K⁻¹ for the pristine matrix at 300 K. In general, for a series of samples that share the same exponent of scattering and approximately the same effective mass, the Seebeck coefficient is negatively correlated with the carrier concentration. However, here the carrier concentration of the composites (x = 2, 4, 6) is increased compared with that of the matrix below 250 K, yet the absolute Seebeck coefficient is still enhanced. Fig. 9 presents the Pisarenko relationship of the Seebeck coefficients for some filled skutterudites and the composite materials studied here. The data of the filled skutterudites are from our previously investigated In_xYb_yCo₄Sb₁₂ materials measured with the same method.³¹ The filled skutterudites generally follow the Pisarenko relationship, whereas the absolute Seebeck coefficient values for the matrix–4%, matrix–6% samples lie well above the fitted line. This abnormally enhanced Seebeck coefficient in the composite materials can be explained based on the Mott expression:^32,33

Fig. 9 Pisarenko relationship of the filled skutterudites and the composites. The absolute Seebeck coefficients are used. The fitted line serves to guide the eye.

The Mott relationship gives the Seebeck coefficient of degenerately doped solids as a function of the energy dependence of the electrical conductivity, σ(E) = n(E)eμ(E), taken at the Fermi energy E_F. From eqn (1) it is inferred that there are two mechanisms that can increase α: (i) an increased energy dependence of μ(E), for instance by a scattering mechanism that strongly depends on the energy of the charge carriers or (ii) an increased energy dependence of n(E), for instance by a local increase in the density of states around the Fermi energy. The second mechanism can occur when the valence or conduction band of the host semiconductor resonates with one energy level of a localized atom in the host. As is known, Te is a common dopant in skutterudites and no abnormal doping effect on the electronic transport has been observed.^25,28,29 On the other hand, band bending at the matrix–nanoparticle heterogeneous interfaces produces a potential barrier, which preferentially scatters the charge carriers with lower energy, as, for example, demonstrated in PbTe with Pb precipitates.³⁴

As indicated from the electrical property measurements, the matrix–8% AgSbTe₂ shows different behaviour from the other composites. This can be understood in relation with the corresponding change of the microstructure. As shown from the microstructure analysis, the nanoparticles are well dispersed on the grain boundaries in x = 2 to 6 samples, but are conspicuously absent in the sample x = 8, attributed to inter-growth/inter-connection of the nanoparticles. In other words, there is a topological crossover of the AgSbTe₂ inclusions from isolated nanoparticles to a nano-plating or nano-coating between 6 wt% and 8 wt% of nanoinclusions. As a consequence the composite with high AgSbTe₂ content (matrix–8 wt% AgSbTe₂) turns to behave like a traditional two-phase composite that can be described by an effective-media model.³⁵ Since the measured electrical resistivity of the as-prepared AgSbTe₂ (59 μΩ m at 300 K) is higher than that of the matrix, the electrical resistivity begins to increase as the AgSbTe₂ content reaches x = 8. Additionally, because AgSbTe₂ is a p-type semiconductor, there exists mixed n-type and p-type conduction in the matrix–8 wt% AgSbTe₂ sample, which reduces the nominal absolute Seebeck coefficient and carrier concentration. Therefore further addition of nanoinclusions degrades the Seebeck coefficient and the electrical conductivity.

Fig. 10 presents the power factors of all samples, the power factors of the composites are enhanced considerably due to the significant decrease of the electrical resistivity and the simultaneous increase of the absolute Seebeck coefficient. The maximum power factor is obtained in the matrix–6 wt% AgSbTe₂ composite, which is about 7 times larger than that of the matrix.

Fig. 10 The low temperature power factors of the studied samples.

Table 1 presents the room temperature thermoelectric properties of the studied samples. As mentioned above, one motivation for selecting AgSbTe₂ as the nano-component is its extremely low thermal conductivity, which is expected to help to decrease the lattice thermal conductivity of the composite. The lattice thermal conductivity κ_lattice was obtained by subtracting the carrier thermal conductivity κ_e from the total thermal conductivity κ. The κ_e value is estimated by the Wiedemann–Franz relationship κ_e = L₀T/ρ, where ρ is the electrical resistivity and L₀ is the Lorentz constant, given by L₀ = 2 × 10⁻⁸ V² K⁻², which is suitable for heavily doped semiconductors. It can be seen that the lattice thermal conductivity of the composites decreases with the addition of AgSbTe₂, and it decreases monotonically with increasing AgSbTe₂ content except for matrix–6 wt% AgSbTe₂. Finally due to the significantly enhanced power factor and decreased lattice thermal conductivity the dimensionless figure of merit ZT is increased remarkably, with a maximum ZT of 0.51 at 300 K obtained in the matrix–6 wt% AgSbTe₂ sample.

Table 1 The transport properties of the studied samples at 300 K

Composition	α (μV K^−1)	ρ (μΩ m)	κ (W m^−1 K^−1)	κ lattice (W m^−1 K^−1)	ZT
Matrix	−152	29.2	2.94	2.74	0.08
Matrix–2 wt% AgSbTe2	−167	11.3	3.25	2.72	0.23
Matrix–4 wt% AgSbTe2	−202	9.51	2.62	1.99	0.49
Matrix–6 wt% AgSbTe2	−228	9.18	3.31	2.65	0.51
Matrix–8 wt% AgSbTe2	−176	12.5	2.41	1.93	0.31

---

4. Conclusions

Yb_0.2Co₄Sb₁₂–AgSbTe₂ composites have been prepared through an ex situ melting–milling–hot pressing procedure. A noteworthy feature of the composites is that the AgSbTe₂ nanoparticles are well dispersed on the matrix grain boundaries, and there is a topological crossover of the AgSbTe₂ inclusions from isolated nanoparticles to a nano-plating or nano-coating between 6 wt% and 8 wt% of nanoinclusions. The addition of the AgSbTe₂ nanoparticles has decoupled the inter-dependent electrical conductivity and Seebeck coefficient. The electrical resistivity of the composites is decreased by a factor of about three, largely from a significant increase of the carrier mobility due to improved grain boundary conductivity. Furthermore, the absolute Seebeck coefficient of the composites is enhanced simultaneously through an energy filtering mechanism, which combined with the reduction of the electrical resistivity, leads to a remarkable enhancement of the power factor. The maximum power factor is obtained in the matrix–6 wt% AgSbTe₂ composite, about 7 times larger than that of the pristine matrix. Meanwhile, the lattice thermal conductivity of the composites is decreased with the addition of AgSbTe₂, ascribed to the rather low thermal conductivity of the AgSbTe₂ component. In summary, the ZT value of Yb_0.2Co₄Sb₁₂ is significantly enhanced by the addition of AgSbTe₂ nanoparticles, and a maximum ZT value of 0.51 at 300 K is obtained in the matrix–6 wt% AgSbTe₂ material.

Acknowledgements

This work is co-supported by National Natural Science Foundation of China (51271084, 51072062 and 51272080) and the Natural Science Foundation of Hubei province (2012FFB02215). The work at Clemson University is supported by National Science Foundation of the United States (DMR-1307740). The technical assistance from the Analytical and Testing Center of Huazhong University of Science & Technology is also gratefully acknowledged.

Notes and references

1. R. Venkatasubramanian, E. Siivola, T. Colpitts and B. O'Quinn, Nature, 2001, 413, 597.
2. T. C. Harman, P. J. Taylor, M. P. Walsh and B. E. LaForge, Science, 2002, 297, 2229.
3. G. H. Zeng, J. H. Bahk, J. E. Bowers, H. Lu, A. C. Gossard, S. L. Singer, A. Majumdar, Z. X. Bian, M. Zebarjadi and A. Shakouri, Appl. Phys. Lett., 2009, 95, 083503.
4. K. F. Hsu, S. Loo, F. Guo, W. Chen, J. S. Dyck, C. Uher, T. Hogan, E. K. Polychroniadis and M. G. Kanatzidis, Science, 2004, 303, 818.
5. B. Poudel, Q. Hao, Y. Ma, Y. C. Lan, A. Minnich, B. Yu, X. Yan, D. Z. Wang, A. Muto, D. Vashaee, X. Chen, J. M. Liu, M. S. Dresselhaus, G. Chen and Z. F. Ren, Science, 2008, 320, 634.
6. W. Kim, S. L. Singer, A. Majumdar, J. M. O. Zide, D. Klenov, A. C. Gossard and S. Stemmer, Nano Lett., 2008, 8, 2095.
7. B. C. Sales, D. Mandrus, B. C. Chakoumakos, V. Keppens and J. R. Thompson, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 15081.
8. B. C. Sales, D. Mandrus and R. K. Williams, Science, 1996, 272, 1325.
9. J. Yang, W. Zhang, S. Q. Bai, Z. Mei and L. D. Chen, Appl. Phys. Lett., 2007, 90, 192111.
10. T. He, J. Z. Chen, H. D. Rosenfeld and M. A. Subramanian, Chem. Mater., 2006, 18, 759.
11. J. Y. Peng, W. Xu, Y. G. Yan, J. Y. Yang, L. W. Fu, H. Kang and J. He, J. Appl. Phys., 2012, 112, 024909.
12. X. Shi, J. Yang, J. R. Salvador, M. F. Chi, J. Y. Cho, H. Wang, S. Q. Bai, J. H. Yang, W. Q. Zhang and L. D. Chen, J. Am. Chem. Soc., 2011, 133, 7837.
13. Z. M. He, C. Stiewe, D. Platzek, G. Karpinski, E. Müller, S. H. Li, M. Toprak and M. Muhammed, J. Appl. Phys., 2007, 101, 043707.
14. H. Li, X. F. Tang, X. L. Su and Q. J. Zhang, Appl. Phys. Lett., 2008, 92, 202114.
15. Z. Xiong, X. H. Chen, X. Y. Huang, S. Q. Bai and L. D. Chen, Acta Mater., 2010, 58, 3995.
16. B. Duan, P. C. Zhai, P. F. Wen, S. Zhang, L. S. Liu and Q. J. Zhang, Scr. Mater., 2012, 67, 372.
17. F. D. Rosi, E. F. Hockings and N. E. Lindenblad, RCA Rev., 1961, 22, 82.
18. S. N. Zhang, T. J. Zhu, S. H. Yang, C. Yu and X. B. Zhao, Acta Mater., 2010, 58, 4160.
19. T. J. B. Holland and S. A. T. Redfern, Mineral. Mag., 1997, 61, 65.
20. A. L. Pope, R. T. Littleton IV and T. M. Tritt, Rev. Sci. Instrum., 2001, 72, 3129.
21. R.-M. Marin, G. Brun and J.-C. Tedenac, J. Mater. Sci., 1985, 20, 730.
22. J. D. Sugar and D. L. Medlin, J. Alloys Compd., 2009, 478, 75.
23. E. Quarez, K.-F. Hsu, R. Pcionek, N. Frangis, E. K. Polychroniadis and M. G. Kanatzidis, J. Am. Chem. Soc., 2005, 127, 9177.
24. K. T. Wojciechowski, J. Tobola and J. Leszczynski, J. Alloys Compd., 2003, 361, 19.
25. X. Y. Li, L. D. Chen, J. F. Fan, W. B. Zhang, T. Kawahara and T. Hirai, J. Appl. Phys., 2005, 98, 083702.
26. C. Chubilleau, B. Lenoir, A. Dauscher and C. Godart, Intermetallics, 2012, 22, 47.
27. J. R. Salvador, J. Yang, X. Shi, H. Wang, A. A. Wereszczak, H. Kong and C. Uher, Philos. Mag., 2009, 89(19), 1517.
28. B. Duan, P. C. Zhai, L. S. Liu, Q. J. Zhang and X. F. Ruan, J. Mater. Sci.: Mater. Electron., 2012, 23, 1817.
29. X. Y. Zhao, S. Q. Bai, X. Y. Li, Y. F. Zhou and L. D. Chen, J. Inorg. Mater., 2009, 24, 803.
30. X. Y. Zhou, G. Y. Wang, L. Zhang, H. Chi, X. L. Su, J. Sakamoto and C. Uher, J. Mater. Chem., 2012, 22, 2958.
31. J. Y. Peng, P. N. Alboni, J. He, B. Zhang, Z. Su, T. Holgate, N. Gothard and T. M. Tritt, J. Appl. Phys., 2008, 104, 053710.
32. N. F. Mott and E. A. Davis, Electronic Processes in Non-crystalline Materials, Clarendon, Oxford, 1979.
33. J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Science, 2008, 321, 554.
34. J. P. Heremans, C. M. Thrush and D. T. Morelli, J. Appl. Phys., 2005, 98, 063703.
35. D. J. Bergman and O. Levy, J. Appl. Phys., 1991, 70, 6821.

---