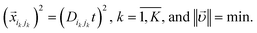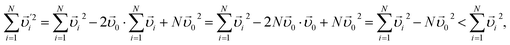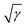Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Random-close packing limits for monodisperse and polydisperse hard spheres
Vasili
Baranau
and
Ulrich
Tallarek
*
Department of Chemistry, Philipps-Universität Marburg, Hans-Meerwein-Strasse, 35032 Marburg, Germany. E-mail: tallarek@staff.uni-marburg.de; Fax: +49-6421-28-27065; Tel: +49-6421-28-25727
First published on 3rd March 2014
Abstract
We investigate how the densities of inherent structures, which we refer to as the closest jammed configurations, are distributed for packings of 104 frictionless hard spheres. A computational algorithm is introduced to generate closest jammed configurations and determine corresponding densities. Closest jamming densities for monodisperse packings generated with high compression rates using Lubachevsky–Stillinger and force-biased algorithms are distributed in a narrow density range from φ = 0.634–0.636 to φ ≈ 0.64; closest jamming densities for monodisperse packings generated with low compression rates converge to φ ≈ 0.65 and grow rapidly when crystallization starts with very low compression rates. We interpret φ ≈ 0.64 as the random-close packing (RCP) limit and φ ≈ 0.65 as a lower bound of the glass close packing (GCP) limit, whereas φ = 0.634–0.636 is attributed to another characteristic (lowest typical, LT) density φLT. The three characteristic densities φLT, φRCP, and φGCP are determined for polydisperse packings with log-normal sphere radii distributions.
I. Introduction
The definition and determination of the random-close packing (RCP) limit for frictionless hard-sphere particles is a long-standing problem. For monodisperse particles, there exist at least three estimates for the RCP limit, with distinct densities φ: (i) φ = 0.634–0.636;1–4 (ii) φ ≈ 0.64;5–8 and (iii) φ ≈ 0.65.9–16 The values of 0.634 and 0.65 are supported theoretically.1,15 In our previous work17 we showed that φ ≈ 0.64 and φ ≈ 0.65 refer to different phenomena and represent the RCP limit and a lower bound of the glass close packing (GCP) limit.18The RCP limit is sometimes interpreted as a special density at which almost every Poisson packing will jam in the process of infinitely fast compressions and is also referred to as the J-point.5 For finite packings, this point is expanded into a J-segment.5,19 The behaviour of the J-segment in the thermodynamic limit is yet unresolved; it may converge to a single J-point5 or preserve a finite width.19 Here we do not investigate this issue, but study finite packings of 104 particles and observe indeed a finite width of the J-segment for our packings. We find that φ = 0.634–0.636 is the lower bound of this segment, whereas φRCP ≈ 0.64 is the upper bound. We also reproduce the density φGCP ≈ 0.65 in our simulations. In addition, we determine the RCP limits and lower bounds of the GCP limits for polydisperse packings.
By jamming we understand in this paper collective jamming in packings of frictionless particles,20–23 equivalent to mechanical stability1 and infinite pressure in systems of particles supplied with velocity.24 The equivalence of isostaticity and jamming is supported experimentally,5,20,25–32 while Salsburg and Wood proved24 that isostaticity is a necessary condition for infinite pressure and jamming. A packing is referred to as jammed if there is at least a subset of particles that is jammed (other particles are rattlers). We do not exclude rattler particles from the packings when computing packing densities.
For polydisperse packings the GCP limit φGCP is defined18 as the infinite-pressure limit for the densest glassy state (the ideal glass state), whereas for monodisperse packings it is the density above the RCP limit with minimal number of jammed packing configurations (as revealed by an entropy minimum).9,17 We will follow these definitions.
In our previous work17 we noticed that the pressure reported during packing generation using the Lubachevsky–Stillinger (LS) algorithm is non-stationary, because any packing generation is a non-equilibrium process. Therefore, infinite non-equilibrium pressure cannot be used as an indicator for jamming. Instead, the packings should be allowed to equilibrate. Indeed, monodisperse LS packings expose an average coordination number below the isostatic value of six for densities lower than 0.644 and can be densified further using low compression rates.17
Research has been conducted recently to describe the pressure relaxation process for monodisperse and polydisperse packings.33 It also shows that LS packings are not always jammed despite very high non-equilibrium pressure. We have suggested17 that stationary pressure after relaxation may be substituted into the equation of state (EOS) of Salsburg and Wood24 to estimate the jamming densities. Some results33 show that the process of pressure relaxation has time scales comparable with the process of macroscopic packing rearrangement. In a certain interval of densities the particles start to form crystalline regions and the estimated jamming density for these packings may be as high as the crystalline packing density (φFCC or φHCP) for monodisperse packings, or as high as the GCP limit φGCP for polydisperse packings.34 Thus, these density estimates do not represent the jamming densities closest to the initial packing configurations and will not assist us in defining the RCP limit φRCP. Here, we modified the LS packing generation algorithm to search for the jammed packing configurations closest to the initial ones (instead of simply estimating their densities by equilibration) and will base our definition of the RCP limit on the results produced with this modification.
The paper is structured as follows. Before we present any experimental results, we use Section II to start with definitions that become relevant for our subsequent discussion. These are inherent structure,35 basin of attraction of an inherent structure, bounding region, bounding surface, and closed bounding region. We will show that an inherent structure for an arbitrary configuration of hard spheres is a jammed configuration that is the closest one to the initial configuration. To emphasize that we are investigating hard particles, not particles with soft potential, we will use throughout this paper the term “closest jammed configuration” instead of “inherent structure” and also refer to the “closest jamming density” instead of the “density of the inherent structure”. In Section III we describe the modification of the LS packing generation algorithm to produce the closest jammed configurations. The subsequent application of this modification to monodisperse and polydisperse packings produced with the LS algorithm36,37 and force-biased (FB) algorithm38,39 is presented in Section IV. It reveals that the closest jamming densities for our finite packings produced with fast compressions are located in narrow density bands depending on the particle size distribution, from φ = 0.634–0.636 to φ ≈ 0.64 for monodisperse packings. We attribute φ ≈ 0.64 to the RCP limit φRCP and interpret φ = 0.634–0.636 as well as similar densities for polydisperse packings as another characteristic density φLT, the lowest typical (LT) jamming density. The definitions of φRCP and φLT are also provided. In addition, we estimate lower bounds of the GCP limits from the results in Section IV by extrapolating packing densities to infinite generation time. We furthermore demonstrate how these three characteristic densities φLT, φRCP, and φGCP depend on the polydispersity for finite hard-sphere packings. Section V presents a summary and conclusions.
The particles in our polydisperse packings have log-normal radii distributions with standard deviations σ from 0.05 to 0.3 in steps of 0.05 (particle mean diameter is normalized to unity). All sphere packings were prepared in a fully periodic cubic box (cf.Fig. 1) and consist of 104 particles. Polydisperse packings are generated in a wide range of compression rates using the LS and FB protocols. Each packing is created from an individual Poisson configuration of points (independent random uniform selection of sphere centre coordinates). The applied source code is available under the MIT free software license.40
We rely on the phase space packing description24 and use the terms “limiting polytope”, “hypersurface”, and “hypercylinder” from that paper.
II. Definitions
In this section we present definitions that will be needed for our discussion of hard-sphere packing problems.Each sphere packing configuration of N monodisperse or polydisperse particles (with predefined nominal radii) can be represented as a point in a 3N-dimensional packing phase space (3 coordinates per particle center). For the packing box sides Lx, Ly, Lz, respectively, the total phase space volume equals Vtot = (LxLyLz)N. The actual particle radii are proportional to the nominal ones and thus are determined only by the proportionality ratio or by the actual packing density.
In our discussion we will rely on the concept of inherent structures. Stillinger introduced it for systems of particles with soft potential.35 The earliest description of this concept can be found in Stillinger et al.41 (eqn (23), Section IV in that paper), though this term is actually not used. A qualitative description is also given in Torquato and Jiao42 (Section IV B in that paper). Inherent structures for systems of particles with soft potential are local potential energy minima in the phase space. The minimum that is reached by the steepest descent energy minimization for an arbitrary system configuration is an inherent structure for this configuration. Potential energy in hard-sphere packings is replaced by the maximum packing density that can be associated with this configuration (i.e., when there are still no intersecting particles), taken with the minus sign.
Inherent structures for hard-sphere packings correspond to jammed configurations. Indeed, if a packing resides in an inherent structure, there are no infinitesimal changes in the configuration that will allow preserving the density; instead, any change will always require decreasing the particle radii (decreasing the density, increasing the energy). Thus, the packing configuration resides in an infinitesimal limiting polytope and is jammed. Because such an inherent structure is reached from an initial configuration through a steepest descent, it is the closest one to the initial configuration.
To emphasize that we are investigating hard particles, not particles with soft potential, we will use throughout this paper the term “closest jammed configuration” instead of the “inherent structure”. We are unaware of precise mathematical definitions of the closest jammed configuration, especially of those accounting for rattler particles, so we provide a mathematical definition in the Appendix (Subsection C). We will not use precise definitions to implement searching for the closest jammed configurations. Instead, we modify the LS algorithm in Section III. The closest jammed configuration is defined uniquely for any unjammed packing configuration, except for saddle points in the potential energy landscape. The precise definition in the Appendix defines the closest jammed configuration uniquely even for saddle points.
An initial packing configuration belongs to a basin of attraction of a given jammed configuration if this jammed configuration is the closest one for the initial packing. Any phase space point belongs to one and only one basin of attraction, because the closest jammed configuration is defined uniquely for any configuration.
Similarly, let us define the bounding region of a given jammed configuration at a given density as the intersection of this configuration's basin of attraction with available phase space (contact hypercylinders for that density excluded). All available phase space is uniquely split into bounding regions. When the particle radii are large enough, bounding regions become closed and are then transformed into limiting polytopes.
We can also define bounding surfaces, i.e., the surfaces of these bounding regions (comprised of hypercylinder surfaces and “wormholes” between bounding regions). The bounding region is closed if the bounding surface is fully formed by hypercylinder surfaces. Any configuration in a closed bounding region is called a glassy state.18 The glass transition occurs when the bounding region becomes closed.
The definitions from this section together with the pressure criterion for jamming24 allow us to transform the conventional definition of the GCP limit for polydisperse particles18 (“the infinite-pressure limit for the densest glassy state”) into a “jammed configuration with the highest density”. Precise definitions for these concepts can also be found in Subsection D of the Appendix.
III. Algorithm used to search for the closest jammed configurations
In this section, we present a modification to the LS packing generation algorithm. This modified LS (MLS) algorithm was used to search for the closest jamming densities.A. General idea
The LS algorithm in its conventional form cannot be used to search for the closest jammed configurations. This algorithm terminates too early for fast compressions because of the non-equilibrium pressure excess. Limiting polytopes have not yet collapsed into single points. If we apply slow compressions to unjammed packings, they will terminate in almost jammed configurations, but the latter will not correspond to the initial bounding regions and will have higher densities than the closest jammed configurations.17Therefore, one way of searching for the closest jammed configuration is to use fast compressions at the beginning of the packing generation (to preserve the configuration point in an initial bounding region) and to use slow compressions at the end of the generation (to arrive at a truly jammed configuration). In order to merge these two regimes, we should gradually reduce the compression rate during the packing generation. We run the LS packing generation with a high compression rate, until the non-equilibrium reduced pressure is high (reaches a conventional value of 1012), then decrease the compression rate and run the LS generation again, until the pressure is high enough again, and repeat this procedure until the compression rate is low enough. High compression rates at the initial stages will lead to a very fast movement of the bounding surfaces and to the closing of most of the wormholes between the bounding regions. Low compression rates at the end of the generation will ensure that the pressure is almost stationary, and the high pressure is a sign of the proximity to jamming. Slow compressions will also allow the configuration point to explore the bounding region and to exit the dead ends formed by concave boundaries and follow the movement of the bounding surfaces.
B. Details of the modified Lubachevsky–Stillinger (MLS) algorithm
We use the following packing generation parameters: the root mean square particle velocity is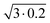 , which corresponds to a packing temperature of 0.2, because we set the mass of all the particles and the Boltzmann constant to unity. The initial compression rate is 10 and the termination compression rate is ≤10−4; we decrease the compression rate by a factor of two each time the reduced pressure (computed from 20 collisions per particle, 2 × 105 collisions for our packings comprised of 104 particles) reaches a value of 1012. This factor of two is referred to as the “compression rate decrease factor”. To avoid the immediate termination of the packing generation after the compression rate is updated (as far as the reduced pressure remains high) we perform equilibration with zero compression rate until the reduced pressure is below 1012 (also computed from 2 × 105 collisions). If the reduced pressure is still above 1012 after 50 cycles of 2 × 105 collisions, we assume that the packing is close to jamming and terminate the generation completely. The procedure above always terminates in nearly jammed configurations. We refer to this modification as the MLS algorithm.
, which corresponds to a packing temperature of 0.2, because we set the mass of all the particles and the Boltzmann constant to unity. The initial compression rate is 10 and the termination compression rate is ≤10−4; we decrease the compression rate by a factor of two each time the reduced pressure (computed from 20 collisions per particle, 2 × 105 collisions for our packings comprised of 104 particles) reaches a value of 1012. This factor of two is referred to as the “compression rate decrease factor”. To avoid the immediate termination of the packing generation after the compression rate is updated (as far as the reduced pressure remains high) we perform equilibration with zero compression rate until the reduced pressure is below 1012 (also computed from 2 × 105 collisions). If the reduced pressure is still above 1012 after 50 cycles of 2 × 105 collisions, we assume that the packing is close to jamming and terminate the generation completely. The procedure above always terminates in nearly jammed configurations. We refer to this modification as the MLS algorithm.
The code for this modification is available online.40 The MLS algorithm is validated in Section IV (Subsection B), after we provide an overview of the results that we obtained by applying this algorithm with the current parameters (Subsection A).
The idea of decreasing the compression rate has already been applied to the LS algorithm in order to produce nearly jammed configurations, as can be found in Torquato and Jiao42 (Section V A), Skoge et al.44 (Section II), Jiao et al.45 (Section II A), and Biazzo et al.46 These papers do not, in general, contain the requirement to start packing generation from fast compressions. To our knowledge, packing generation which starts from fast compressions has never been interpreted as searching for the closest jammed configuration.
IV. Results and discussion
Here, we present our packing generation results and the results of searching for the closest jammed configurations of the generated packings. We estimate the GCP limits φGCP for monodisperse and polydisperse packings on the basis of their densities obtained after slow compressions. We analyze packing densities for fast compressions, define the RCP limits φRCP and the lowest typical (LT) jamming densities φLT, and determine these densities for monodisperse and polydisperse packings. We provide an overview of our data in Subsection A. In Subsection B we validate the MLS algorithm; this validation relies on the data overview and therefore cannot be presented earlier. We analyze the data in Subsection C. This analysis leads us to definitions of the RCP limits, which we introduce in Subsection D. Subsection E presents concepts of typical and untypical basins of attraction, defined through the RCP limits. We discuss our results in Subsection F. Our findings are summarized in Fig. 5 and 6. To ease the reading of this section, we provide with Table 1 an overview of the symbols used below. Some of them have already been introduced, some will be introduced later.| Symbol | Short description | Key figures and tables | Values for σ = 0 |
|---|---|---|---|
| σ | Standard deviation of the log-normal particle radii distributions | ||
| γ | Compression rate for initial packing generation | X-axis in Fig. 2 | |
| φ | Initial packing density after LS or FB generation | Y-axis in Fig. 2a and c | |
| φ J | Closest jamming density of a packing | Y-axis in Fig. 2b and d | |
| φ fastmin | Minimum closest jamming density for packings produced with fast compressions | Fig. 4 and Table 3 | ∼0.635 (for packings in this study) |
| φ fastmax | Maximum closest jamming density for packings produced with fast compressions | Fig. 4 and Table 3 | ∼0.64 |
| φ LT | Lowest typical jamming density or its estimate, φLT = φfastmin | Fig. 5 and Table 4 | ∼0.635 (for packings in this study) |
| φ RCP | Random-close packing limit or its estimate, φRCP = φfastmax | Left sides of Fig. 2b and d and 5 and Table 4 | ∼0.64 |
| φ GCP | Glass close packing limit or its estimate | Right sides of Fig. 2 and 5 and Tables 2 and 4 | ∼0.65 |
| φ HCP | Crystalline packing density for monodisperse packings (FCC or HCP crystals) | ∼0.74 | |
| φ max | Highest packing density: φHCP for monodisperse packings, φGCP for sufficiently polydisperse packings | ∼0.74 | |
| φ L | Lowest possible jamming density, at least 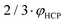 for monodisperse packings (density of tunnelled crystals43) for monodisperse packings (density of tunnelled crystals43) |
∼0.49 |
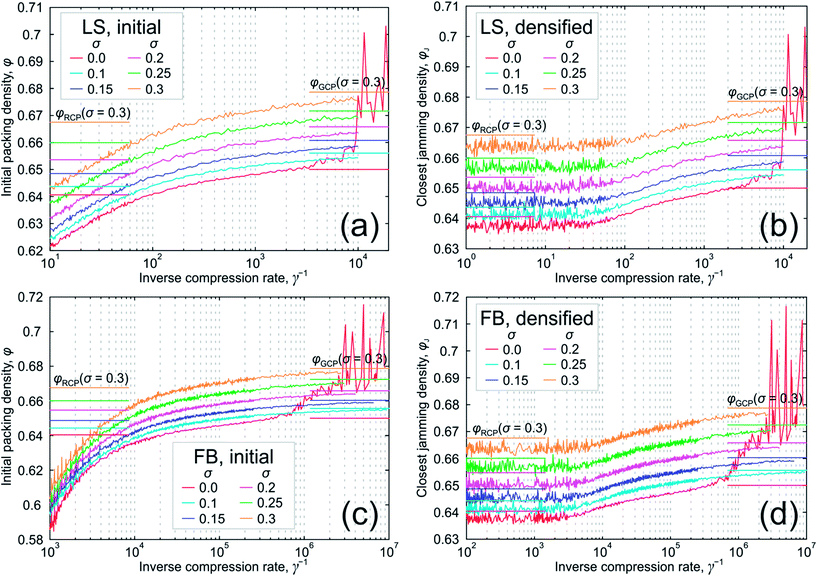
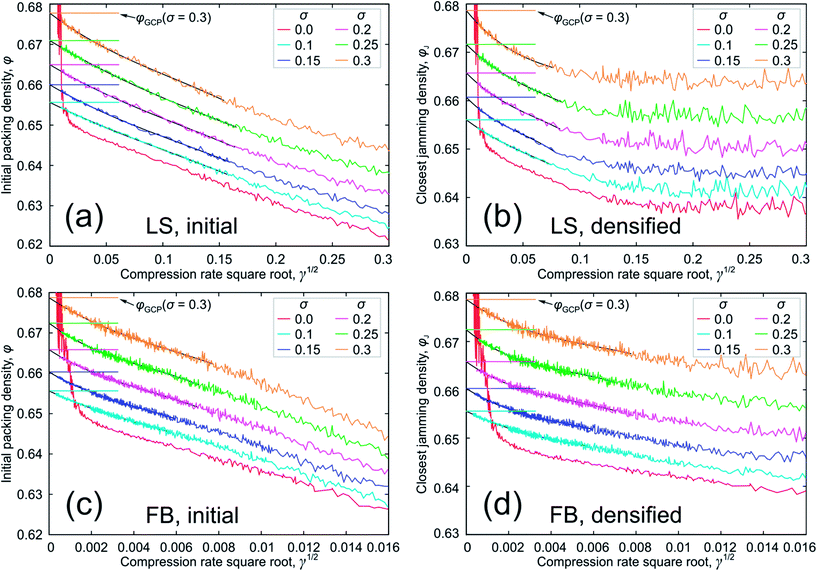
A. Data overview
The dependence of the packing densities φ on the inverse compression rates γ−1 for packings produced with the LS and FB algorithms is shown in Fig. 2a and c, respectively. The closest jamming densities φJ obtained with the MLS algorithm vs. the inverse compression rates γ−1 for the same LS and FB packings are shown in Fig. 2b and d, respectively. All packings in Fig. 2b and d are nearly isostatic and have very high equilibrium reduced pressure (1012).We did not average the data in Fig. 2; each point in these figures corresponds to a single packing. To guide the eye, points have been connected by straight lines. Averaging assumes that fluctuations in the data will disappear in the thermodynamic limit. This question is still unresolved and we do not discuss it here.5,19 Additionally, averaging would remove the information about the exact boundaries of jamming intervals for finite packings.
We distinguish between two packing generation regimes in Fig. 2: slow compressions (i.e., high inverse compression rates, long generation times) and fast compressions (i.e., low inverse compression rates, short generation times). We consider the generation as slow for the FB packings with γ−1 > 0.2 × 104 and for LS packings with γ−1 > 0.6 × 102. We consider the generation as fast for the FB packings with γ−1 < 103 and for LS packings with γ−1 < 5.
For slow compressions, the jamming densities in Fig. 2b and d remain close to the initial densities for all the packing types. This occurs because the packings are already trapped in closed or nearly closed bounding regions and are almost jammed. The search for the closest jammed configuration only slightly increases their densities. Though the plots for the LS and FB algorithms look similar, the inverse compression rates for the FB packings are shifted by two orders of magnitude with respect to the LS packings.
The obtained narrow horizontal bands for jamming densities after the fast initial compressions in Fig. 2b and d can be explained as follows. Fast generations do not allow the packings (with Poisson distribution of points as starting configuration) to leave the initial bounding regions, though the packings are not jammed at the end of the fast compressions. The search for the closest jamming density will also retain packings in their initial bounding regions, but will compress the regions into polytopes and finally into jammed configurations, slightly increasing the packing density. Therefore, the jamming density distribution for fast compressions should correspond to the closest jamming density distribution for Poisson packings, i.e., to the uniform sampling of the phase space.
B. Validation of the modified Lubachevsky–Stillinger (MLS) algorithm
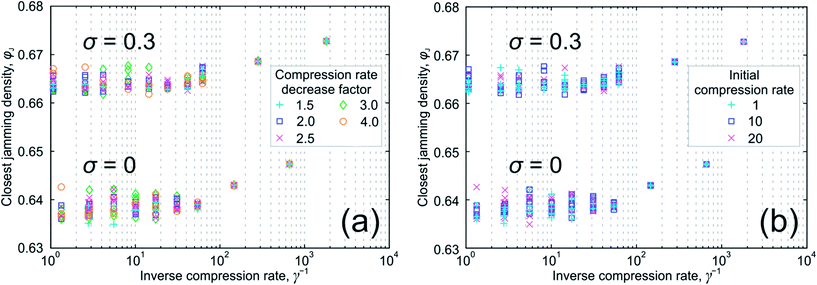
Prior to a detailed discussion of the data in Fig. 2, we analyze how the estimated closest jamming densities depend on algorithm parameters. For this purpose, we selected several LS packings with σ = 0 (monodisperse packings) and σ = 0.3 (widest particle size distribution in this work) and searched for their closest jamming densities with varied search parameters. We changed the compression rate decrease factor (i.e., the number we used to divide the compression rate as the pressure becomes high enough), the initial compression rate, and the final compression rate. For the compression rate decrease factor we used the values 1.5, 2, 2.5, 3, and 4; for the initial compression rate – 1, 10, and 20; and for the final compression rate – 10−4 and 10−5. This results in a total of 30 combinations.Fig. 3a shows how the final jamming densities depend on the compression rate decrease factor. The dependence on the initial compression rate is depicted in Fig. 3b. All 30 combinations are represented in each figure, but are coloured according to one of the varied parameters.
We found that with a compression rate decrease factor of 10 the jamming densities for fast compressions are systematically shifted upward. It means that the compression rate decreases too quickly. After several decreases it is so low that the packings have enough time (until pressure becomes high again) to leave the initial bounding region and travel to bounding regions with higher jamming densities.
C. Data analysis
We approximate the φJ(γ−1) plots by the least-squares method with an asymptotic expansion 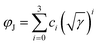 and extrapolate it to zero compression rate (infinite generation time). Estimates of the GCP limits are then found as φGCP = c0. We took the 80 last data points to the right in Fig. 2b to fit the LS data and 300 points to fit the FB data (Fig. 2d). Both numbers were selected to exclude points from the horizontal plateaus at short generation times. Estimates of φGCP along with 95% confidence intervals for the LS and FB packings are reported in Table 2 in the rows “LS, densified” and “FB, densified”. These estimates are displayed as horizontal lines to the right in Fig. 2b and d, respectively.
and extrapolate it to zero compression rate (infinite generation time). Estimates of the GCP limits are then found as φGCP = c0. We took the 80 last data points to the right in Fig. 2b to fit the LS data and 300 points to fit the FB data (Fig. 2d). Both numbers were selected to exclude points from the horizontal plateaus at short generation times. Estimates of φGCP along with 95% confidence intervals for the LS and FB packings are reported in Table 2 in the rows “LS, densified” and “FB, densified”. These estimates are displayed as horizontal lines to the right in Fig. 2b and d, respectively.
| σ | ||||||
|---|---|---|---|---|---|---|
| 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | |
| LS, initial | 0.6528 ± 1.8489 × 10−4 | 0.6557 ± 1.955 × 10−4 | 0.6600 ± 2.2824 × 10−4 | 0.6650 ± 2.8891 × 10−4 | 0.6711 ± 3.4862 × 10−4 | 0.6777 ± 4.5487 × 10−4 |
| FB, initial | 0.6528 ± 1.4523 × 10−3 | 0.6540 ± 1.9576 × 10−3 | 0.6608 ± 1.9004 × 10−3 | 0.6650 ± 1.7833 × 10−3 | 0.6711 ± 3.0192 × 10−3 | 0.6790 ± 3.8918 × 10−3 |
| LS, densified | 0.6530 ± 3.5721 × 10−4 | 0.6561 ± 3.4474 × 10−4 | 0.6607 ± 3.8526 × 10−4 | 0.6658 ± 5.2342 × 10−4 | 0.6716 ± 6.517 × 10−4 | 0.6786 ± 9.4406 × 10−4 |
| FB, densified | 0.6519 ± 1.5772 × 10−4 | 0.6556 ± 1.9659 × 10−4 | 0.6603 ± 2.4266 × 10−4 | 0.6658 ± 3.0977 × 10−4 | 0.6725 ± 4.2419 × 10−4 | 0.6787 ± 5.0797 × 10−4 |
As the packings generated by sufficiently slow compressions are almost jammed, we may use the densities of initially created packings for the same asymptotic expansion to estimate the GCP limits. We used 125 data points to the right in Fig. 2a to fit the LS data and 300 points to the right in Fig. 2c to fit the FB data. The GCP limit estimates along with 95% confidence intervals for the LS and FB packings are reported in Table 2 in the rows “LS, initial” and “FB, initial”. These estimates are displayed as horizontal lines to the right in Fig. 2a and c, respectively. Plots from Fig. 2 built vs.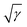 , along with their polynomial fits, can be found in Appendix G (asymptotic expansion of packing densities to the GCP limits).
, along with their polynomial fits, can be found in Appendix G (asymptotic expansion of packing densities to the GCP limits).
We do not estimate the GCP limit for monodisperse packings by asymptotic expansion, because the φ(γ−1) and φJ(γ−1) plots do not exhibit asymptotes for low compression rates. Instead, they start to grow rapidly as densities φ ≈ φJ ≈ 0.65 are reached. It is known that monodisperse packings demonstrate an entropy minimum and the onset of crystallization at φ ≈ 0.647–0.651.9–17 In our previous paper,17 we reproduced these features at φ ≈ 0.647–0.651 for the monodisperse FB packings shown in Fig. 2c (as well as for LS packings created with the code of Skoge et al.,44 not used in the present paper). We analyzed the Voronoi volumes standard deviation,1,47,48 Voronoi volumes entropy,9,14 pore-size entropy,17 and the local bond-orientational order Q6local.49 Here, we also applied these measures to the monodisperse LS packings (Fig. 2a) and to the monodisperse densified LS and FB packings (Fig. 2b and d). We confirm that the behaviour of the measures remains unchanged: entropy-like measures have a local minimum at φ ≈ φJ ≈ 0.647–0.651 and local order starts to increase rapidly at the same density (data not shown). Thus, we associate the growth in the φ(γ−1) and φJ(γ−1) plots at φ ≈ φJ ≈ 0.65 with the onset of crystallization; and interpret the entropy minimum for monodisperse packings as the GCP limit, φGCP ≈ 0.65. It is easy to show why the GCP limit implies the onset of crystallization. If φGCP ≈ 0.65 is the highest achievable density for monodisperse packings with suppressed crystallization (e.g., by pinning a certain fraction of particles50), the only way to reach still higher densities – for generation protocols that try to avoid crystallization as long as possible – is to prepare crystalline inclusions in the packings at φGCP. We assume that, if crystallization is artificially suppressed in monodisperse packings, the φ(γ−1) and φJ(γ−1) plots look similar to those for polydisperse packings, reaching asymptotes φ = φGCP or φJ = φGCP at γ−1 = ∞, with φGCP ≈ 0.65.
Closest jamming densities for fast compressions (horizontal density bands) have clear lower and upper bounds in Fig. 2b and d. We determine the horizontal parts of the plots visually, i.e., consider the plots of packing density vs. the inverse compression rate for the LS and FB algorithms as horizontal for γ−1 < 5 (Fig. 2b) and for γ−1 < 103 (Fig. 2d), respectively. The number distributions of the closest jamming densities for fast compressions by the LS and FB algorithms are presented in Fig. 4. These distributions are localized in narrow density bands. The maximum and minimum densities for LS and FB packings in these bands are provided in Table 3. The maximum achievable density for monodisperse packings is ∼0.64 for both algorithms.
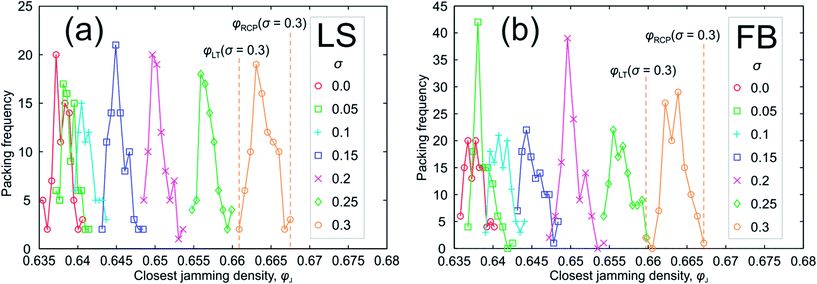 | ||
| Fig. 4 Closest jamming density distributions for sphere packings created with fast compressions. (a) Packings generated with the Lubachevsky–Stillinger (LS) algorithm. (b) Packings generated with the force-biased (FB) algorithm. The meaning of symbols for the different standard deviations σ of the log-normal sphere radii distributions is explained in the legends. φfastmax and φRCP are determined for each σ as the rightmost points of the distributions, φfastmin and φLT are determined for each σ as the leftmost points of the distributions. These values are summarized in Table 3. | ||
| σ | |||||||
|---|---|---|---|---|---|---|---|
| 0.0 | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | |
| φ fastmin, LS | 0.6349 | 0.6367 | 0.6391 | 0.6425 | 0.6480 | 0.6542 | 0.6601 |
| φ fastmin, FB | 0.6356 | 0.6364 | 0.6388 | 0.6428 | 0.6469 | 0.6540 | 0.6593 |
| φ fastmax, LS | 0.6406 | 0.6414 | 0.6437 | 0.6485 | 0.6536 | 0.6599 | 0.6675 |
| φ fastmax, FB | 0.6404 | 0.6428 | 0.6443 | 0.6487 | 0.6547 | 0.6601 | 0.6676 |
We denote these maximum and minimum densities from Table 3 as φfastmax and φfastmin, respectively. They depend on the particle radii distribution.
We assume that our results for the GCP limits and further discussion for the RCP limits are protocol-independent. We base our assumption on the following points: (i) the behaviour of φJ(γ−1) plots is qualitatively the same for both the FB and LS protocols; (ii) the differences between the corresponding values of φfastmin for different protocols are ≤10−3; (iii) the differences between the corresponding values of φfastmax for different protocols are ≤10−3; (iv) the differences between the corresponding φGCP estimates from Table 2 are ≤2 × 10−3.
D. Definition of the RCP limits φRCP through φfastmax
Fig. 4 and Table 3 show that φfastmax is the highest practically obtained closest jamming density for sufficiently large Poisson packings or packings created with fast compressions. It implies that basins of attraction with jamming densities φJ > φfastmax are practically impossible to sample for sufficiently large packings; in other words, basins of attraction with φJ ≤ φfastmax cover for such packings the fraction of the phase space that is close to unity. We associate φfastmax with the random close packing limit φRCP. We assume that in the thermodynamic limit the lowest density φ0, for which the basins of attraction with φJ ≤ φ0 still cover the almost entire phase space, is also close to φfastmax. Under this assumption, we define the random close packing limit φRCP for infinite packings as the minimum density for which basins of attraction with jamming densities ≤ φRCP cover the almost entire phase space. The RCP limit for sufficiently large packings is thus the highest practically obtained closest jamming density for Poisson configurations or packings created with fast compressions. When packings are relatively small and all basins of attraction can in practice be sampled by Poisson configurations, we have to select an arbitrary fraction α, e.g., α = 0.95, and define the RCP limit as the density for which basins of attraction with φJ ≤ φRCP cover the selected fraction α of the phase space.In the same manner we define for infinite packings another characteristic density φLT as the maximum density for which basins of attraction with jamming densities ≥ φLT cover the almost entire phase space. The LT limit for sufficiently large packings is the lowest practically obtained closest jamming density for Poisson configurations or packings created with fast compressions. Thus, for the packings under study φLT = φfastmin. Mathematical formulations for both finite and infinite packings are given in the Appendix (Subsection F).
We do not investigate the dependence of φLT, φRCP, and φGCP on the number of particles in the packings, but add the following remarks. As mentioned, monodisperse packings exhibit a structural transition and the onset of crystallization at φGCP ≈ 0.65.9–17 This density is reported even for packings of 105 particles,11 which suggests that φGCP is preserved in the thermodynamic limit. φLT and φRCP depend on the number of particles in a packing;5φLT increases and φRCP slightly decreases as the number of particles increases. There are two possible scenarios for their behaviour for infinite packings: they converge to a single J-point (at φ ≈ 0.64 for monodisperse packings),5 or φLT reaches an asymptote below φRCP.19 In both cases φGCP is different from φLT and φRCP in the thermodynamic limit.
Further below, under φLT and φRCP we will understand the corresponding densities for finite packings of 104 particles. It follows from Fig. 4 that φRCP = φfastmax and φLT = φfastmin. Now, we join all the characteristic points obtained so far for the different particle radii distributions in a single table and in a single plot (Table 4 and Fig. 5). φLT was estimated by averaging the minimum closest jamming densities after fast compressions φfastmin from Table 3 for both LS and FB packings; φRCP was estimated by averaging the maximum closest jamming densities after fast compressions φfastmax from Table 3 for both LS and FB packings; φGCP was estimated by averaging the columns in Table 2; and φGCP for monodisperse packings was taken at a conventional value of φ = 0.65.17 For monodisperse packings φLT ≈ 0.635 and φRCP ≈ 0.64.
| σ | |||||||
|---|---|---|---|---|---|---|---|
| 0.0 | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | |
| φ LT | 0.6353 | 0.6366 | 0.6390 | 0.6426 | 0.6475 | 0.6541 | 0.6597 |
| φ RCP | 0.6405 | 0.6421 | 0.6440 | 0.6486 | 0.6542 | 0.6600 | 0.6676 |
| φ GCP | 0.65 | 0.6526 | 0.6554 | 0.6606 | 0.6651 | 0.6716 | 0.6787 |
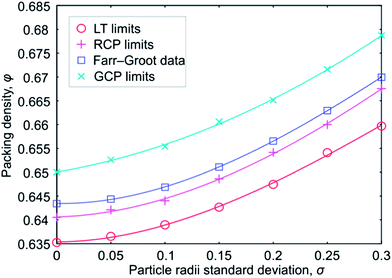 | ||
| Fig. 5 Characteristic densities for finite packings of 104 spheres with log-normal sphere diameter distribution: red circles (○) are lowest typical (LT) jamming densities φLT; magenta crosses (+) are RCP limits φRCP; blue squares (□) are φRCP estimates obtained by Farr and Groot;51 and cyan crosses (×) are GCP limits φGCP. All values (except the Farr–Groot data) can be found in Table 4. | ||
The plots in Fig. 5 demonstrate that all of the characteristic densities increase with the width of the particle size distribution. The increase of φGCP is natural, as far as polydisperse packings have more degrees of freedom (not only three coordinates per particle, but also a radius), and there are more possibilities to arrange the packings in order to achieve a desired density. The increase of φRCP can be explained in a similar way. While φLT, φRCP, and φGCP vary with the particle radii standard deviation, the differences between them do not change much, e.g., φGCP − φRCP ≈ 0.01 for all standard deviations. Such a small difference explains why it is hard to discern φRCP and φGCP experimentally. We also provide in Fig. 5 a plot for the semi-theoretical RCP limit estimates obtained by Farr and Groot.51 This plot has a very similar shape and is shifted slightly upward compared with our φRCP estimates.
E. Typical and untypical basins of attraction
We distinguish between typical basins of attraction and untypical ones. Basins of attraction with jamming densities in the range [φLT, φRCP] are typical by definition; the others are untypical. The probability to sample an untypical basin of attraction with Poisson packings or with packings produced by fast compressions tends to zero in the thermodynamic limit. It is close to zero already for packings of 104 particles. This happens because the phase space is dominated by typical basins; their total volume is almost equal to the total phase space volume in the thermodynamic limit.If there is a way to distinguish typical from untypical basins of attraction without relying on their jamming densities, it will be possible to provide another definition for φRCP: it is the highest jamming density for typical basins of attraction or the highest typical closest jamming density of Poisson packings. In the same manner we can define φLT: it is the lowest jamming density for typical basins of attraction or the lowest typical closest jamming density of Poisson packings. This is the reason for using LT (lowest typical) as subscript for φLT.
It was suggested that the RCP limit is a special density at which almost every infinite Poisson packing will jam in the process of infinitely fast compressions and was referred to as the J-point.5 In other words, it is the closest jamming density for almost every Poisson packing. We confirmed that this point is rather a segment [φLT, φRCP] for finite packings.5,19 It is sometimes argued that even in the thermodynamic limit this segment does not collapse to a single J-point.19 The estimate for φLT for monodisperse packings by Pica Ciamarra et al.19 (φ = 0.635–0.636) is in good agreement with our result (φLT ≈ 0.635). We note that φLT is referred to as the random-loose packing (RLP) density in these papers. We use a separate term, the “lowest typical” density, to avoid confusion with another definition and estimate for the RLP limit at φRLP = 0.536–0.55,1,52,53 as well as to emphasize that we are investigating frictionless particles.
Here we observed untypical jammed configurations only in the range (φRCP, φmax]. There should be another set of untypical jammed configurations with densities below φLT. Examples of such configurations for monodisperse particles are tunnelled crystals, discovered by Torquato and Stillinger.43 These tunnelled crystals form an uncountable set of untypical jammed configurations at 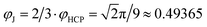 . Another special procedure has been proposed to systematically create untypical jammed configurations with jamming densities in the range [0.6, φLT) for monodisperse packings.42,45 One has to select a typical jammed packing, remove a certain fraction of particles and apply a special sequential linear programming generation algorithm,42 which is also believed to produce the closest jammed configurations. The untypical jamming densities below φLT should also have a lower limit, which we denote as φL, the lowest density of jammed configurations. Thus, for monodisperse packings φL is at least
. Another special procedure has been proposed to systematically create untypical jammed configurations with jamming densities in the range [0.6, φLT) for monodisperse packings.42,45 One has to select a typical jammed packing, remove a certain fraction of particles and apply a special sequential linear programming generation algorithm,42 which is also believed to produce the closest jammed configurations. The untypical jamming densities below φLT should also have a lower limit, which we denote as φL, the lowest density of jammed configurations. Thus, for monodisperse packings φL is at least 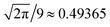 . The existence of untypical jammed configurations below φLT and a lower bound for their densities has been proposed by Pica Ciamarra et al.54,55 along with a special algorithm to generate jammed untypical two-dimensional packings below φLT. This lower bound is called the “random very loose packing” density in these papers. Since we want to avoid the mixing of “lowest typical” jamming density and “random loose packing” density, we use the term “lowest” jamming density in this paper.
. The existence of untypical jammed configurations below φLT and a lower bound for their densities has been proposed by Pica Ciamarra et al.54,55 along with a special algorithm to generate jammed untypical two-dimensional packings below φLT. This lower bound is called the “random very loose packing” density in these papers. Since we want to avoid the mixing of “lowest typical” jamming density and “random loose packing” density, we use the term “lowest” jamming density in this paper.
F. Discussion
The definition of the RCP limit for monodisperse packings shows excellent agreement with the recurring experimental value of φRCP ≈ 0.64.5–8 We suggest that the two common φRCP estimates for monodisperse packings (i.e., 0.64 and 0.65) actually correspond to two distinct characteristic points:(1.) φ ≈ 0.64.5–8 We interpret it as the RCP limit φRCP, the highest jamming density for typical basins of attraction.
(2.) φ ≈ 0.65.9–17 We interpret it as the GCP limit φGCP, the highest jamming density for polydisperse packings and the density above the RCP limit with a minimum number of jammed configurations for monodisperse packings.
For finite packings, even infinitely fast compressions of Poisson configurations produce jamming densities in the range [φLT, φRCP]. The lowest jamming density φLT for monodisperse packings of 104 particles under study is ∼0.635.
Chaudhuri et al.28 demonstrated that the jamming densities depend on preparation history and should exist in a certain range. This discovery complies very naturally with the picture we present. Indeed, the jamming densities should depend on the employed generation protocol and can be found at any density in the range [φL, φmax]; but searching for the closest jammed configuration for sufficiently large Poisson packings will in practice always produce a density in the range [φLT, φRCP].
Kamien and Liu56 showed that there may be an uncertainty in the range of densities where the reduced pressure reaches infinity during packing densification. We showed that the pressure can reach infinity during a single packing densification in the entire range of densities [φL, φmax]; again, searching for the closest jammed configuration for sufficiently large Poisson packings will in practice always produce a density in the range [φLT, φRCP]. Our definition of the RCP limit as the highest typical jamming density is also consistent with experimental observations, which state that φRCP is the jamming density maximally achievable in experiments.7
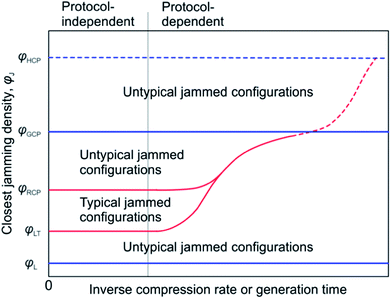
In Fig. 6 we schematically display how the closest jamming densities depend on the generation time for finite packings. We assume that algorithms start from Poisson packings and update the configuration continuously with generation time. The typical closest jamming densities were previously defined only for Poisson packings or for zero initial packing density. Under typical closest jamming densities for non-zero initial packing densities we understand the closest jamming densities that will be almost always found for packings created at a given density using a given algorithm. The right part of the plot (cf. vertical gray dividing line) depends on the packing generation protocol, and we depict it for protocols capable of approaching the GCP limit for polydisperse packings and reaching crystalline configurations for monodisperse packings. Other protocols may converge to lower densities instead, as low as φLT or even φL. Indeed, the protocol of Khirevich et al.2 produces packings with densities close to φLT for infinite generation times. The form of the plot φJ(γ−1) in Fig. 6, as well as in Fig. 2b and d, was conjectured by Parisi and Zamponi18 (see Fig. 2a in that paper). The major difference is the presence of the plateau at φGCP in the conjectured plot for monodisperse packings.
In the future we like to measure the characteristic densities φLT, φRCP, and φGCP for other particle radii distributions, e.g., Gaussian and bidisperse,57 and compare the results to predictions from other models.58,59 Our methodology provides a framework for investigating these densities for hard particles of arbitrary shape and dimensionality.
V. Summary and conclusions
We introduced a modification to the LS packing generation algorithm to directly produce the closest jammed configurations (inherent structures of hard spheres) for arbitrary packings. The application of this protocol to LS and FB packings consisting of 104 particles yields the following conclusions, independent from the employed packing generation protocol: closest jamming densities for Poisson packings and packings produced with fast compressions are located in narrow density bands depending on particle size distribution, from φ = 0.634–0.636 to φ ≈ 0.64 for monodisperse particles; closest jamming densities for packings created with slow compressions converge to certain asymptotic values (φ ≈ 0.65 for monodisperse particles).We attribute the asymptotic packing densities for infinitely slow compressions to lower bounds of the GCP limits.18 We attribute φ ≈ 0.64 (monodisperse packings) to the RCP limit and interpret φ = 0.634–0.636 and similar densities for polydisperse packings as another characteristic density φLT. Thus, we define the RCP limit φRCP for sufficiently large finite packings as the highest practically achievable closest jamming density of Poisson configurations. Similarly, φLT is the lowest practically achievable closest jamming density of Poisson configurations. In the thermodynamic limit, φRCP and φLT may coincide and thus form a J-point, but they are different for finite packings.
These definitions led us to the distinction between typical jammed configurations and corresponding basins of attraction, which have jamming densities in the range [φLT, φRCP] and in the thermodynamic limit occupy the almost entire phase space, and untypical ones, whose jamming densities reside in the ranges [φL, φLT) and (φRCP, φmax] and which in the thermodynamic limit occupy a portion of the phase space with zero probability measure. The RCP limit is thus the highest typical closest jamming density of Poisson packings and packings produced with sufficiently fast compressions; φLT is the lowest typical closest jamming density of Poisson packings and packings produced with sufficiently fast compressions.
The characteristic densities φLT, φRCP, and φGCP depend on the standard deviation of the employed log-normal particle radii distributions, but differences between them do not change much, e.g., φGCP − φRCP ≈ 0.01 for all standard deviations. This small difference explains why it is challenging to differentiate between φRCP and φGCP experimentally.
VI. Appendix
Here we present precise definitions for the closest jammed configuration (inherent structure of hard spheres), basin of attraction, and bounding region. We also give mathematical definitions for the random-close packing limit φRCP and the lowest typical density φLT.A. Mathematical difficulty with the definition in the main text
In the definition for the closest jammed configuration below (Subsection C) we will use an approach slightly different from that in the main text, but will show their equivalence. At first, we explain the mathematical difficulty with the definition in the main text.We defined the artificial potential energy for hard-sphere packings as the maximum density that can be specified for a given packing configuration (to avoid particle intersections) taken with the minus sign. This potential energy is a non-smooth function over particle coordinates. Indeed, this maximum density is controlled by the closest pair of particles. The potential energy is a smooth function in a certain range of coordinates of one of the particles in the closest pair (around its initial position). But for a sufficiently large displacement of this particle some other particle will form the closest pair with it. The potential energy will not be smooth at the position of the first particle where the closest pair changes. The gradient of the potential energy is undefined at this point.
The closest jammed configuration is specified in the main text as the local minimum in the potential energy that is reached through the gradient descent (steepest descent) in the potential energy landscape from the initial packing configuration. The steepest descent is undefined at the points with undefined gradient. Thus, we have to use a different approach.
B. Closest jammed configuration, general idea
Each packing configuration of N monodisperse or polydisperse particles (with predefined nominal radii) can be represented as a point in a 3N-dimensional packing phase space (3 coordinates per particle center). For packing box sides Lx, Ly, Lz, respectively, the total phase space volume equals Vtot = (LxLyLz)N. The actual particle radii are proportional to the nominal ones and thus are determined only by the proportionality ratio or by the actual packing density. If there is a particle pair in contact in a packing, the configuration point resides on the corresponding hypercylinder surface. If there are multiple pairs in contact, the configuration point resides on the intersection of the corresponding hypersurfaces.Packing contraction is equivalent to simultaneous particle radii growth so that all radii remain equally proportional to their nominal values. It is equivalent to hypercylinder radii growth in the phase space. We proportionally increase the particle radii and simultaneously drag the configuration point so that no particle intersections appear. At the same time we require that the configuration point moves as little as possible in the sense of the Euclidean distance. This condition ensures that the configuration point always remains on the initial hypercylinder surfaces, i.e., all the particle contacts are preserved and no intersections between particles in contact appear. Indeed, if one of the contacts is broken (a particle pair is split), it means that the configuration point has moved too far away from the corresponding hypersurface, which is not the minimal possible movement of the configuration. The minimal possible movement would be to preserve the point on the given hypersurface. If there is a single particle pair in contact, it will correspond to moving the point along the normal of the contact hypercylinder. If the packing is also monodisperse, it implies symmetric particle-pair spreading.
While growing, more hypersurfaces will approach the configuration point and some will cross it. The hypersurfaces will form a disjoint phase space region and finally collapse into a single infinitesimal point, a jammed configuration. As far as we required minimization of configuration displacement, we define this very jammed configuration as the closest (to the initial one) jammed configuration.
Until the configuration point resides in the infinitesimal limiting polytope (or a hyperinterval), it is always possible to contract a packing (increase particle radii) and update the configuration to avoid intersections. Thus, the closest jammed configuration is defined for any unjammed configuration. As far as we require minimization of configuration displacement, it is also defined uniquely.
We cannot simply define the closest jammed configuration as the jammed configuration with the minimum Euclidean distance to the current configuration, because this jammed configuration may be separated by regions of the phase space that correspond to particle intersections. In other words, this jammed configuration may be unreachable for any physical compression algorithm. Our definition automatically conforms to the requirement of physical accessibility for the closest jammed configuration.
This definition is equivalent to the definition from the main text (searching for a potential energy minimum with the steepest descent, where the potential energy is the maximum density at a given configuration taken with a minus sign). Indeed, (i) displacement minimization during the increase of particle radii is equivalent to the gradient descent in the landscape of our artificial potential energy at points where the gradient is defined; (ii) both definitions terminate at jammed configurations.
If a jammed packing contains rattler particles, there is only a subset of particles that is jammed; in other words, there is a subspace of the total phase space that has collapsed into a single point. Rattler particles are allowed to move and thus transform this point into a hyperline in the entire phase space. As far as rattler particles are usually trapped in cages formed by other particles, this hyperline is usually a hyperinterval. Such hyperlines (hyperintervals) have zero volume as their projection on the subspace of jammed particles has zero volume. Though Salsburg and Wood24 do not explicitly mention rattlers, their discussion can be amended to incorporate rattler particles. For example, predictions of the coordination number shall be formulated for a subset of jammed particles (for a subspace that collapses into a point). When we talk about limiting polytopes and infinitesimal points into which they collapse, we keep in mind that they are defined for jammed subsets of particles and should be expanded into hyperintervals if rattlers are taken into account.
If rattlers are considered, the closest jammed configuration is not a single point, but a hyperinterval of zero volume with the same density for each configuration. We combine all these configurations into a single equivalence class.
In the next subsection we provide a precise mathematical definition for the closest jammed configuration. We will not use this definition directly to search for such configurations; instead, we modify the LS algorithm.
C. Closest jammed configuration, definition
We introduce the following notations.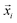 is a coordinate of the ith particle,
is a coordinate of the ith particle, 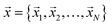 is the packing configuration vector in the phase space,
is the packing configuration vector in the phase space, 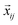 is the vector from the ith to the jth particle (accounting for boundary conditions, if necessary;
is the vector from the ith to the jth particle (accounting for boundary conditions, if necessary; 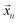 may thus be non-zero), and Di is the nominal diameter of the ith particle (its absolute value is unimportant, relative values matter in the current definition).
may thus be non-zero), and Di is the nominal diameter of the ith particle (its absolute value is unimportant, relative values matter in the current definition). 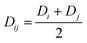 is the nominal distance between particles in contact. We also introduce time t and specify that the actual particle radii grow as Di(t) = tDi; the initial time is selected to avoid intersections (initially, there may be no contacts at all). The actual distance between particles in contact grows as Dij(t) = tDij. Let us also introduce particle velocities
is the nominal distance between particles in contact. We also introduce time t and specify that the actual particle radii grow as Di(t) = tDi; the initial time is selected to avoid intersections (initially, there may be no contacts at all). The actual distance between particles in contact grows as Dij(t) = tDij. Let us also introduce particle velocities 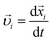 and a 3N-dimensional velocity vector for the configuration point
and a 3N-dimensional velocity vector for the configuration point 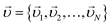 . We further introduce the concept of bonds, i.e., pairs of particles in contact. At each time there is a finite number of bonds K, which corresponds to a coordination number
. We further introduce the concept of bonds, i.e., pairs of particles in contact. At each time there is a finite number of bonds K, which corresponds to a coordination number 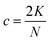 . We enumerate bonds by the index
. We enumerate bonds by the index 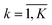 . We define
. We define 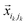 as the vector between particles in the kth bond and Dikjk(t) as the actual distance between these particles.
as the vector between particles in the kth bond and Dikjk(t) as the actual distance between these particles.
While contracting the packing (increasing particle radii) between new bond formations, we (i) avoid intersections between particles; and (ii) minimize particle velocities. As we have already found out, it is equivalent to (i) ensuring that the configuration point always resides at the initial hypercylinder surfaces; and (ii) minimizing 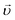 . The mathematical formulation is:
. The mathematical formulation is:
After differentiating the restrictions for bonds with respect to time we obtain a system of linear equations, which we supply in the complete definition:
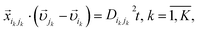 | (1) |
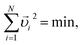 | (2) |
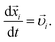 | (3) |
The search for the closest jammed configuration is defined as the integration of eqn (3) in time, with velocities determined from eqn (1) and (2), until the system is jammed. A general way to determine jamming is through the infinite stationary pressure produced by particles supplied with velocities.24
The definition by eqn (1)–(3) does not require that at least one pair of particles is initially in contact. If no particles are in contact, the trivial solution to the system is zero velocities for all particles, so that they grow without movement until the first contact is formed. Therefore, integration can always be formally started from zero time.
Eqn (1) and (2) form an operator acting on the hypervectors of the phase space, which we denote as C; it produces hypervelocity for a packing configuration, 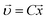 . Thus, the closest jammed configuration
. Thus, the closest jammed configuration 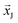 is defined mathematically for an arbitrary initial configuration
is defined mathematically for an arbitrary initial configuration 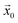 as
as
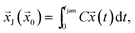 | (4) |
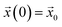 , and tjam denotes the time at which the packing jams.
, and tjam denotes the time at which the packing jams.
Eqn (1) and (2) pose a well-known problem of a minimum-norm solution to a linear system. Here, the particle velocities are unknown variables, and eqn (1) can be rewritten as 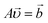 . It is known that if a linear system has at least one solution, then
. It is known that if a linear system has at least one solution, then 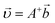 is one of its minimum-norm solutions. Here, A+ is a Moore–Penrose matrix pseudoinverse for A. To search for the closest jamming density, we select this solution by definition. As far as particle radii can always be increased for unjammed configurations, there is at least one solution to the system (1). It makes the closest jammed configuration uniquely defined for any unjammed packing.
is one of its minimum-norm solutions. Here, A+ is a Moore–Penrose matrix pseudoinverse for A. To search for the closest jamming density, we select this solution by definition. As far as particle radii can always be increased for unjammed configurations, there is at least one solution to the system (1). It makes the closest jammed configuration uniquely defined for any unjammed packing.
Because the probability to encounter linearly dependent rows in the matrix A tends to zero for packings in the thermodynamic limit, we assume that for such packings the linear system (1) will be of full rank. For such systems 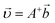 is the only minimum-norm solution, and A+ can be found explicitly as AT(AAT)−1. It means that in the thermodynamic limit the choice of
is the only minimum-norm solution, and A+ can be found explicitly as AT(AAT)−1. It means that in the thermodynamic limit the choice of 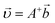 as a solution to (1) is unambiguous.
as a solution to (1) is unambiguous.
If rattler particles are present in the final jammed packing, the closest jammed configuration is still defined uniquely. But we would like to join all the configurations from the limiting hyperinterval into an equivalence class; i.e., consider this very packing with arbitrary positions of rattlers as the same jammed configuration. Mathematically, we define a projection operator J that selects coordinates of jammed particles from the entire configuration vector. Two jammed configurations 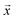 and
and 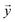 belong to the same equivalence class, if
belong to the same equivalence class, if
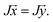 | (5) |
Each packing will jam at one and only one equivalence class of the closest jammed configurations.
The system (1)–(3) is a modified formulation of the packing generation algorithm by Zinchenko.3 The algorithm did not contain the requirement of the hypervelocity minimization, and the solution for the system (1), underdetermined at the initial stage, was searched for with the conjugate gradient algorithm using previous or random velocities as an initial conjugate gradient state.
D. Further definitions
Let Ω be the entire phase space, ΩP(t) be the phase space occupied at a given time by hypercylinders of particle contacts,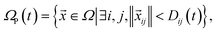 | (6) |
| ΩA(t) = Ω\ΩP(t). | (7) |
The basin of attraction 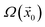 of the jammed configuration
of the jammed configuration 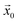 can then be defined as
can then be defined as
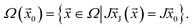 | (8) |
A bounding region for the given jammed configuration 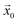 at a given time (equivalently, for a given density) is defined as
at a given time (equivalently, for a given density) is defined as
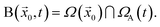 | (9) |
Let Γ be an operator that produces a surface of a set. Then the bounding surface for the given bounding region is 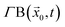 , and the bounding region is closed if the bounding surface is fully formed by hypercylinder surfaces:
, and the bounding region is closed if the bounding surface is fully formed by hypercylinder surfaces:
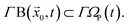 | (10) |
A state 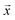 at a given density is called a glassy state,18 if it resides in a closed bounding region:
at a given density is called a glassy state,18 if it resides in a closed bounding region:
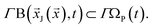 | (11) |
E. Additional properties of the closest jammed configurations
Here we investigate some additional properties of the closest jammed configurations.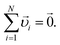 | (12) |
Let us assume that the solution to the system (1) and (2) has a non-zero total velocity, which gives an additional velocity per particle 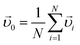 . We examine the solution
. We examine the solution 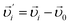 . It corresponds to changing the reference system and automatically complies with (1), which can be checked directly. The sum in eqn (2) will then be transformed into
. It corresponds to changing the reference system and automatically complies with (1), which can be checked directly. The sum in eqn (2) will then be transformed into
There is always a simple solution to the system (1) for a fully periodic packing: 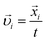 with simultaneous periodic box expansion (which can almost immediately be verified directly). If the number of bonds for any subset of N′ particles equals K0(N′), eqn (12) together with (1) form a linear system of 3N′ + 1 equations for 3N′ unknown velocity components and an unknown box expansion rate. As far as the matrix for the linear system (1) will be of full rank for random packings in the thermodynamic limit, the solution
with simultaneous periodic box expansion (which can almost immediately be verified directly). If the number of bonds for any subset of N′ particles equals K0(N′), eqn (12) together with (1) form a linear system of 3N′ + 1 equations for 3N′ unknown velocity components and an unknown box expansion rate. As far as the matrix for the linear system (1) will be of full rank for random packings in the thermodynamic limit, the solution 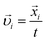 for this subset of particles will be unique and this subset of particles is jammed. Other particles (rattlers) may also be assigned velocities
for this subset of particles will be unique and this subset of particles is jammed. Other particles (rattlers) may also be assigned velocities 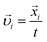 . This proves why K0 is not only the minimum number of bonds for non-rattlers to jam a packing, but also the only possible one in random packings, and thus would explain numerous experiments reproducing the coordination number ∼6 for non-rattler particles in jammed packings. This also leads to a convenient termination condition for the system (1)–(3): the integration in (4) should be stopped when the number of bonds for non-rattler particles is equal to K0 = 3(N′ − 1) + 1.
. This proves why K0 is not only the minimum number of bonds for non-rattlers to jam a packing, but also the only possible one in random packings, and thus would explain numerous experiments reproducing the coordination number ∼6 for non-rattler particles in jammed packings. This also leads to a convenient termination condition for the system (1)–(3): the integration in (4) should be stopped when the number of bonds for non-rattler particles is equal to K0 = 3(N′ − 1) + 1.
F. Definition of the RCP limit
We recall that by Vtot we understand the total volume of the phase space Ω and by N the number of particles,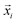 is a coordinate of the ith particle,
is a coordinate of the ith particle, 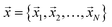 is the packing configuration vector in the phase space. Let us denote by
is the packing configuration vector in the phase space. Let us denote by 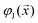 a function that produces a density for the closest jammed configuration if the packing generation is started at a configuration
a function that produces a density for the closest jammed configuration if the packing generation is started at a configuration 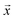 . Let us denote by Vpack = LxLyLz the packing box volume. Then
. Let us denote by Vpack = LxLyLz the packing box volume. Then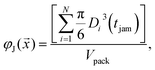 | (13) |
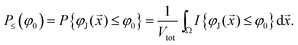 | (14) |
Now we can mathematically define the random close packing limit as
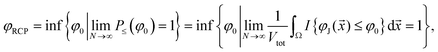 | (15) |
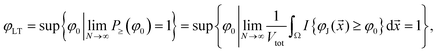 | (16) |
Now we transform these definitions for finite-size packings. For sufficiently large finite packings, untypical basins of attraction are still practically impossible to sample. Thus, we transform eqn (15) into
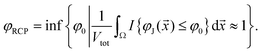 | (17) |
Eqn (16) can be transformed similarly. When packings are relatively small and all basins of attraction can in practice be sampled by Poisson packings, we have to select an arbitrary probability threshold α, e.g., α = 0.95, and define the RCP limit as
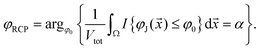 | (18) |
Eqn (16) can be transformed similarly. Eqn (17) and (18) can be regarded as definitions of the RCP limit for finite packings, or as estimates for the RCP limit of infinite packings.
G. Asymptotic expansion of packing densities to the GCP limits
In this subsection of the Appendix we present the plots from Fig. 2 built against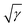 (Fig. 7). We fit the plots
(Fig. 7). We fit the plots 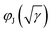 and
and 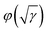 in the main text with third-degree polynomials and expand to γ = 0 (infinite generation time) to obtain GCP limit estimates. Polynomial fits are depicted as black lines under the actual data. The GCP limit estimates (fit values at γ = 0) are depicted as horizontal lines of corresponding colour to the left of the images. The plots for data from computer simulations have no drastic changes in behavior and are fitted well, except for monodisperse packings, where crystallization starts for very slow compressions. It suggests that our estimates of the highest jamming densities are close to the real GCP limits.
in the main text with third-degree polynomials and expand to γ = 0 (infinite generation time) to obtain GCP limit estimates. Polynomial fits are depicted as black lines under the actual data. The GCP limit estimates (fit values at γ = 0) are depicted as horizontal lines of corresponding colour to the left of the images. The plots for data from computer simulations have no drastic changes in behavior and are fitted well, except for monodisperse packings, where crystallization starts for very slow compressions. It suggests that our estimates of the highest jamming densities are close to the real GCP limits.
Acknowledgements
We are grateful to the John von Neumann Institute for Computing (NIC) and the Jülich Supercomputing Center (JSC), Forschungszentrum Jülich (FZJ, Jülich, Germany), for the allocation of special CPU-time grants (NIC project numbers: 5658 and 6550, JSC project ID: HMR10).References
- C. Song, P. Wang and H. A. Makse, Nature, 2008, 453, 629–632 CrossRef CAS PubMed.
- S. Khirevich, A. Höltzel and U. Tallarek, Comm. Comput. Phys., 2013, 13, 801–822 Search PubMed.
- A. Zinchenko, J. Comput. Phys., 1994, 114, 298–307 CrossRef.
- G. D. Scott and D. M. Kilgour, J. Phys. D: Appl. Phys., 1969, 2, 863–866 Search PubMed.
- C. S. O'Hern, L. E. Silbert, A. J. Liu and S. R. Nagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 011306 CrossRef.
- Y. Jin and H. A. Makse, Phys. Stat. Mech. Appl., 2010, 389, 5362–5379 CrossRef CAS PubMed.
- J. D. Bernal and J. Mason, Nature, 1960, 188, 910–911 CrossRef.
- J. G. Berryman, Phys. Rev. A, 1983, 27, 1053–1061 CrossRef CAS.
- A. V. Anikeenko, N. N. Medvedev and T. Aste, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 031101 CrossRef CAS.
- A. V. Anikeenko and N. N. Medvedev, Phys. Rev. Lett., 2007, 98, 235504 CrossRef CAS.
- S. C. Kapfer, W. Mickel, K. Mecke and G. E. Schröder-Turk, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 030301 CrossRef.
- B. A. Klumov, S. A. Khrapak and G. E. Morfill, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 184105 CrossRef.
- M. Bargieł and E. M. Tory, Adv. Powder Technol., 2001, 12, 533–557 CrossRef PubMed.
- T. Aste and T. Di Matteo, Eur. Phys. J. B, 2008, 64, 511–517 CrossRef CAS.
- T. Aste and A. Coniglio, Europhys. Lett., 2004, 67, 165–171 CrossRef CAS.
- K. Lochmann, A. Anikeenko, A. Elsner, N. Medvedev and D. Stoyan, Eur. Phys. J. B, 2006, 53, 67–76 CrossRef CAS.
- V. Baranau, D. Hlushkou, S. Khirevich and U. Tallarek, Soft Matter, 2013, 9, 3361–3372 RSC.
- G. Parisi and F. Zamponi, Rev. Mod. Phys., 2010, 82, 789–845 CrossRef.
- M. Pica Ciamarra, M. Nicodemi and A. Coniglio, Soft Matter, 2010, 6, 2871–2874 RSC.
- S. Torquato and F. H. Stillinger, Rev. Mod. Phys., 2010, 82, 2633–2672 CrossRef.
- S. Torquato, T. M. Truskett and P. G. Debenedetti, Phys. Rev. Lett., 2000, 84, 2064–2067 CrossRef CAS PubMed.
- A. Donev, J. Appl. Phys., 2004, 95, 989–999 CrossRef CAS PubMed.
- A. Donev, S. Torquato, F. H. Stillinger and R. Connelly, J. Comput. Phys., 2004, 197, 139–166 CrossRef PubMed.
- Z. W. Salsburg and W. W. Wood, J. Chem. Phys., 1962, 37, 798–804 CrossRef CAS PubMed.
- P. Wang, C. Song, Y. Jin and H. A. Makse, Phys. Stat. Mech. Appl., 2011, 390, 427–455 CrossRef CAS PubMed.
- C. S. O'Hern, S. A. Langer, A. J. Liu and S. R. Nagel, Phys. Rev. Lett., 2002, 88, 075507 CrossRef.
- N. Xu, J. Blawzdziewicz and C. S. O'Hern, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 061306 CrossRef.
- P. Chaudhuri, L. Berthier and S. Sastry, Phys. Rev. Lett., 2010, 104, 165701 CrossRef.
- N. Xu and E. S. C. Ching, Soft Matter, 2010, 6, 2944–2948 RSC.
- H. A. Makse, D. L. Johnson and L. M. Schwartz, Phys. Rev. Lett., 2000, 84, 4160–4163 CrossRef CAS.
- P. Wang, C. Song, Y. Jin, K. Wang and H. A. Makse, J. Stat. Mech.: Theory Exp., 2010, P12005 CrossRef CAS PubMed.
- A. Donev, S. Torquato and F. H. Stillinger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 011105 CrossRef.
- M. C. Vargas and G. Pérez-Ángel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 042313 CrossRef.
- E. Zaccarelli, C. Valeriani, E. Sanz, W. C. K. Poon, M. E. Cates and P. N. Pusey, Phys. Rev. Lett., 2009, 103, 135704 CrossRef CAS.
- F. H. Stillinger, Science, 1995, 267, 1935–1939 CAS.
- B. D. Lubachevsky and F. H. Stillinger, J. Stat. Phys., 1990, 60, 561–583 CrossRef.
- B. D. Lubachevsky, J. Comput. Phys., 1991, 94, 255–283 CrossRef.
- J. Mościński, M. Bargieł, Z. A. Rycerz and P. W. M. Jacobs, Mol. Simul., 1989, 3, 201–212 CrossRef.
- A. Bezrukov, M. Bargieł and D. Stoyan, Part. Part. Syst. Charact., 2002, 19, 111–118 CrossRef.
- 2013, https://code.google.com/p/packing-generation/.
- F. H. Stillinger, E. A. DiMarzio and R. L. Kornegay, J. Chem. Phys., 1964, 40, 1564–1576 CrossRef CAS PubMed.
- S. Torquato and Y. Jiao, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 061302 CrossRef CAS.
- S. Torquato and F. H. Stillinger, J. Appl. Phys., 2007, 102, 093511 CrossRef PubMed.
- M. Skoge, A. Donev, F. H. Stillinger and S. Torquato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 041127 CrossRef.
- Y. Jiao, F. H. Stillinger and S. Torquato, J. Appl. Phys., 2011, 109, 013508 CrossRef PubMed.
- I. Biazzo, F. Caltagirone, G. Parisi and F. Zamponi, Phys. Rev. Lett., 2009, 102, 195701 CrossRef.
- S. Khirevich, A. Daneyko, A. Höltzel, A. Seidel-Morgenstern and U. Tallarek, J. Chromatogr. A, 2010, 1217, 4713–4722 CrossRef CAS PubMed.
- S. Khirevich, A. Höltzel, A. Seidel-Morgenstern and U. Tallarek, J. Chromatogr. A, 2012, 1262, 77–91 CrossRef CAS PubMed.
- P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 784–805 CrossRef CAS.
- R. L. Jack and L. Berthier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 021120 CrossRef.
- R. S. Farr and R. D. Groot, J. Chem. Phys., 2009, 131, 244104 CrossRef PubMed.
- M. Jerkins, M. Schröter, H. L. Swinney, T. J. Senden, M. Saadatfar and T. Aste, Phys. Rev. Lett., 2008, 101, 018301 CrossRef.
- G. E. Schröder-Turk, W. Mickel, M. Schröter, G. W. Delaney, M. Saadatfar, T. J. Senden, K. Mecke and T. Aste, Europhys. Lett., 2010, 90, 34001 CrossRef.
- M. Pica Ciamarra and A. Coniglio, Phys. Rev. Lett., 2008, 101, 128001 CrossRef.
- M. Pica Ciamarra, P. Richard, M. Schröter and B. P. Tighe, Soft Matter, 2012, 8, 9731–9737 RSC.
- R. D. Kamien and A. J. Liu, Phys. Rev. Lett., 2007, 99, 155501 CrossRef.
- K. Lochmann, L. Oger and D. Stoyan, Solid State Sci., 2006, 8, 1397–1413 CrossRef CAS PubMed.
- M. Clusel, E. I. Corwin, A. O. N. Siemens and J. Brujic, Nature, 2009, 460, 611–615 CrossRef CAS.
- K. A. Newhall, I. Jorjadze, E. Vanden-Eijnden and J. Brujic, Soft Matter, 2011, 7, 11518–11525 RSC.
| This journal is © The Royal Society of Chemistry 2014 |

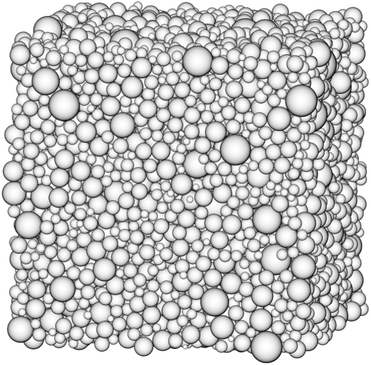
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 polydisperse spheres. The sphere radii distribution is log-normal and has a standard deviation
000 polydisperse spheres. The sphere radii distribution is log-normal and has a standard deviation