Pushing for particulate level models of adiabatic and isothermal processes in upper-level chemistry courses: a qualitative study

Abstract

In the past three decades, researchers have noted the limitations of a problem-solving approach that overemphasizes algorithms and quantitation and neglects student misconceptions and an otherwise qualitative, conceptual understanding of chemical phenomena. Since then, studies and lessons designed to improve student understanding of chemistry has overwhelmingly targeted introductory level, high school and first-year college students. In this article, we present a model-based learning cycle approach with upper-level undergraduate and beginning graduate students that investigated their ability to model the adiabatic and isothermal compression/expansion of a gas in a syringe. We were interested to observe, given the extent of their previous chemistry coursework, how students struggled to connect macroscopic observations with particulate representations. Analysis of laboratory reports, reflective journal entries, and classroom discourse transcripts indicate the learning experience was efficacious in uncovering and addressing student conceptual challenges with using models appropriately to describe gas behaviour under the experimental conditions for this investigation.

---

Introduction

In a study on student performance and factors leading to success in physical chemistry, Nicoll and Francisco (2001) found that most physical chemistry students, as a consequence of upper level math requirements, generally did not struggle with formula manipulation and derivation. The most important factor they found that was predictive of success in physical chemistry was the students' ability to solve word problems and to think logically. While the algorithmic approach to problem solving may still be the norm in chemistry classrooms (Stamovlasis et al., 2005), the pedagogy associated with this approach has been criticized on several counts (e.g.Nurrenbern and Pickering, 1987; Pickering, 1990; Sawrey, 1990; Nakhleh (1993); Nakhleh and Mitchell, 1993; Cohen et al., 2000; Cracolice et al., 2008), it is clearly in conflict with national science standards (NGSS Lead States, 2013a, 2013b), and its efficacy in preparing the future workforce is questionable (e.g. Kerr and Runquist, 2005). We do not advocate for a minimization of problem solving in the teaching of chemistry. Rather, we propose that the teaching of this problem solving is contextualized within a more comprehensive, holistic approach such as that described by Johnstone (1982) where the relationships between the worlds of abstract mathematics, macroscopic observables, and submicroscopic particles are well entrenched in students' understanding of chemical phenomena. Specifically, we contend that particulate-level modeling is a useful scaffold that can provide the qualitative context needed to more fully appreciate quantitative formulation (e.g., a mathematical equation or model). This approach is not without its challenges given that modeling, as suggested by Chittleborough and Treagust (2007) in this journal, is a scientific practice that takes much time to develop. Nevertheless, we contend that modeling lends itself to developing the critical thinking skills students will need whatever career paths they may ultimately choose.

Previous reports in this journal indicate that student misconceptions across educational levels (K-16) are prevalent and persistent (for examples, see Kousathana and Tsaparlis, 2002; Pinarbasi et al., 2009; Smith and Nakhleh, 2011; Naah and Sanger, 2012). Within the realm of physical chemistry topics such as gas pressure, kinetic energy, and collision theory, student ideas that conflict with those of canonical science have been reviewed and summarized elsewhere Goedhart and Kaper (2002). Lin and Cheng (2000) examined the difficulties high school students and teachers had at solving conceptual problems using particulate modeling. The students in particular showed poor conceptual knowledge of the tenets of the kinetic molecular theory and exhibited such misconceptions as “nature abhors vacuum”, gases have no weight, and gas molecules expand when heated. Similarly, Ashkenazi et al. (2008) found that students do not appreciate similarities and differences between different gases. To ameliorate these misconceptions, researchers have often turned to qualitative approaches in developing student mental models of internal energy, heat, work, pressure, etc. (see Waite, 1985) and of force, velocity, time, energy, and change (Toomey and Garafalo, 2003).

Others have developed lessons and demonstrations on gas compression and expansion. Gachic (1968) provided an early example of using the so-called “fire syringe” or “fire piston” in a lesson on gas compression, but offered no lesson on how to teach this to students. Mills et al. (2001) devised two workshops using the fire syringe to teach introductory students about adiabatic and isothermal compression/expansion. Based on descriptions of effective use of model-based inquiry (Windschitl et al., 2008), we feel that the inclusion of such could enrich Mill's original lesson by (1) taking into account student preconceptions and their mental models used to explain gas behavior during compression/expansion, (2) having students express (verbally and visually) these mental models by responding to prompts about the changes in the system through the construction of graphical representations, and (3) following up with students to assess their current models to see if they have undergone revision and are beginning to develop a submicroscopic/particulate understanding that accounts for the observations made. In our study, we examined the ideas of undergraduate and graduate pre-service chemistry teachers who had previously been exposed to these concepts of gas behavior. We hypothesized that they could have developed, through prior instruction, a particulate-level understanding of some chemical and physical processes. However, given the nature of traditional instruction, such a perspective may never have been conceptualized and internalized effectively. We propose that the experience described herein may facilitate the expression, consideration, and appropriate revision of student mental models with regards to adiabatic and isothermal gas expansion/compression that could promote a more sophisticated and scientifically accurate understanding of this phenomenon.

In this study, we sought to consider the following: (1) What preconceptions do advanced undergraduate and beginning graduate students have with regards to gas behavior during (pseudo) adiabatic compression and expansions? (2) What model(s) and rationale do students use to account for observables (e.g. temperature and pressure) during the adiabatic compression/expansion of a gas? (3) How well do students reconcile or revise those models based on their previous predictions when faced with experimental results that differ from what was predicted?

Lesson design

Materials

We used a PASCO XPlorer GLX as a measuring device. This device contains a USB port for which data collected can be exported to a computer for data processing and four ports for attachment to different sensors (pH, conductivity, temperature, pressure, etc.). To this device was connected a sensor via an electronic port. This sensor was connected to a 60 mL plastic syringe with a thermistor inside acting as a temperature probe similar to that described by Gachic (1968) and Mills (2001). The resistance of a thermistor is a function of temperature and can be used to produce a unique electrical output when the gas is compressed or expanded. In the plunger of the thermistor is a plastic guard that does not allow the syringe to be compressed to less than 20 mL (so as to prevent damage to the thermistor). The equipment just described can be purchased from popular probeware distributors.‡

Lesson structure

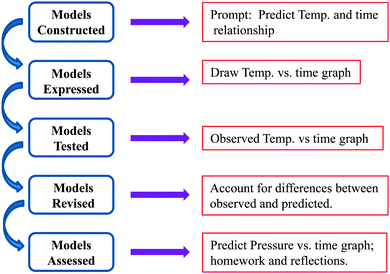
The investigation was designed to be similar to Justi's (2002) model-based learning approach, which begins with (1) constructing/accessing initial (mental) models, (2) expressing models, (3) testing models, (4) reconciling/revising models, and (5) re-expressing models. This we summarize in Fig. 1. The students are first asked to consider the following experiment. After setting the plunger of the syringe to 60 mL, imagine compressing the air in the syringe to 20 mL as fast as possible and then holding the plunger down at that position for ∼10 s. Then, as quickly as possible and without removing the plunger entirely, imagine pulling the plunger back out to 60 mL and holding it at that position for another ∼10 s. Students were then asked to predict the shape of the graph for the change in temperature (vertical axis) with respect to time (horizontal axis) and, separately, the change in pressure with respect to time during the rapid compression and expansion of the gas in the syringe. They were also prompted to provide a detailed rationale for the graphs they constructed. At this stage there was no mention of the nature of the compression/expansion process (i.e., whether the process was adiabatic or isothermal). After taking one to two minutes to consider this process individually, students discussed their graphs in small groups (3–5 participants) and as consensus was reached, recorded them in their lab notebooks and on the display at the front of the classroom. The instructor then led a whole-class discussion where the different graphs were considered to ensure that the preconceptions of each of the small groups were clear to everyone.

Fig. 1 Diagrammatic summary of model approach used in our lesson.

The students then conducted the compression/expansion procedure at least twice to confirm the outcome. For each trial, the students were asked to record their observations in a laboratory notebook, identify similarities and differences between their predictions and observations, and attempt to reconcile the two graphs (predicted vs. observed) through writing and discussion in their small groups. The instructor then prompted the small groups to develop an explanatory model that would account for the actual results, and after a few minutes to do so, led a discussion to consider the merits and weaknesses of what was proposed for the temperature vs. time and pressure vs. time graphs. We found, as will be discussed in the results, that students tended to use heuristics to make their predictions (specifically Boyle's Law to determine the change in pressure due to the change in volume). As an evaluation of whether this discussion was generative, we gave students, as an assessment prompt, the task of proposing a way in which compressing the gas in the syringe would follow Boyle's Law.

Study design

Participants

To increase the overall sample size and to determine how more experienced students might perform relative to a more novice population, three chemistry classes at a mid-size southeastern university in the U.S. where chosen. One group (n = 4) was of a junior/senior-level, calculus-based, physical chemistry laboratory required as part of an ACS-approved Bachelor's in Chemistry degree program. Another group (n = 13) consisted of undergraduates in a junior/senior-level course designed to improve pedagogical content knowledge of and conceptual understanding of chemical principles. A third group (n = 13) consisted of graduate students in a pre-service chemistry education teaching program with the same goals as the second group. As we observed no discernible differences in conceptual understanding amongst the groups, we report observations of all three groups in aggregate. An Institutional Review Board (IRB) exemption was granted for this study as it was deemed to fall within normal educational practices.

Data sources

We video recorded a whole class discussion (instructor and students) and audio recorded student only discussion. Copies of student-generated plots regarding the temperature vs. time and pressure vs. time were collected and analyzed. Additional data sources included student reflective journal entries, responses to an assigned homework problem set and formal laboratory reports related to this experiment.

Methods

We used a structural coding process for analysing the data collected (see Bogdan and Biklen, 2006; Saldaña, 2009 for an overview). As Saldaña, 2009 describes it, “Structural Coding applies a content-based or conceptual phrase representing a topic of inquiry to a segment of data that relates to a specific research question” (p. 66). Specifically within this study, one rater developed, through a constant comparative analysis, common themes that generated the structural codes. These initial codes were reviewed by a second rater and discussed until a consensus was reached regarding the code appropriate for the set of excerpts.

Results

Here, we report the models proposed by students as they went through the modeling cycle to answer the prompt concerning how the temperature will change with respect to time during the rapid compression and expansion of the gas in the syringe. First, we present the student models along with predictions and their rationale of how they initially believed the temperature vs. time graph should appear. Second, we show typical results observed of the compression/expansion of an ideal gas in the syringe. Third, we consider excerpts of instructor-led discussion aimed at assisting students in model revision. Fourth and finally, we discuss how well students internalized and used their revised models to simulate a slow (e.g. isothermal) compression and how they used such models to account for the pressure vs. time plots observed during the rapid (e.g. adiabatic) compression/expansion of the gas in the syringe. We also look at student responses to homework questions as another way of gauging students' abilities to extend their understanding to novel scenarios.

Predictions

From the structural coding analysis, the initial models of students were determined to be representative of three main perspectives. These three perspectives are illustrated by the group predictions of the temperature vs. time graphs, as summarized in Fig. 2a–c. Plot (a) follows the claim that the rapid compression/expansion of the gas in the syringe would be isothermal. Plot (b) was predicted by students who claimed that compression leads to increased temperature and expansion leads to decreased temperature. In general, these students tended to invoke a Boyle's law argument to note the pressure increase due to the volume decrease and then correlate this change in pressure to a change in temperature. Plot (c), was predicted by a single student who thought that the temperature would fall slightly below room temperature, but who otherwise had no explanation as to why the gas cooled down after compression or why the gas heated up during compression.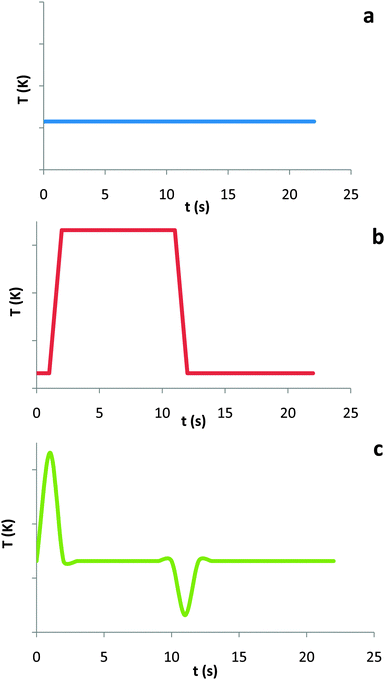

Fig. 2 Temperature vs. time plots predicted by students in response to the prompt of predicting the temperature change, if any, of the rapid compression/expansion of the syringe.

After displaying the graphs, students were asked to rationalize the shapes of their graphs. These arguments are summarized by how they characterized the experimental outcome (I, ‘no temperature change’, ΔT = 0; or II, ‘temperature change’, ΔT ≠ 0 during compression/expansion of the syringe). Groups invoking argument I used both Boyle's Law and work/energy principles in their reasoning. Groups adhering to stance II used justifications based on Boyle's/Amonton's Law, or on competing gas laws.

Prediction I. Some groups predicted that ΔT = 0 using a Boyle's law argument and so drew a horizontal line for the temperature vs. time plot (see Fig. 2a). This model envisioned the experiment as involving ONLY pressure and volume changes as no external heat sources or sinks were employed, so no temperature change would be expected. This conception sometimes included a work argument to claim that the work being done (via compression) on the gas adds only to the potential energy of the gas. It is interesting to note, in one student's post-laboratory reflective journal, that she discounted an appreciable change in temperature even though work was done:

“Prior to the syringe lab, I modeled my temperature graph with the temperature remaining constant throughout the experiment. I knew work was being done on the system but since the increase in pressure represented an increase in potential energy (as a result of that work) I assumed the temperature could be ignored. This is how physics was modeled for us as well. When dealing with friction (a place where a good deal of energy is converted to heat) we are taught to model the system ignoring the heat loss… I was not swayed by arguments about the increase in pressure naturally resulting in an increase in temperature because Boyle's law had already been taught to me. Surely I acknowledged, some temperature increase might occur due to a small amount of the work being converted to kinetic energy but how much could it really be?”

Prediction II. Some groups predicted that during the compression, the temperature would increase above room temperature and stabilize during the first 10 s hold. During the expansion phase, the temperature would decrease, return to room temperature and remain steady for the second 10 s interval (see Fig. 2b). From Boyle's Law, (PV = const.) students rationalized that the pressure would increase as the volume decreased. Then, they seemed to apply Amonton's Law (P/T = const.) to correlate the pressure change as causing the temperature change. Prediction II was the predominant argument used by most students. Excerpts from three students who support this argument read as follows:

“The molecule[s] would bang into each other more frequently and increase the temperature. And if we hold the plunger at that smaller volume, the temperature should hold.”

“It was predicted that the temperature and the pressure increase as the volume decreases. The temperature and the pressure were predicted to decrease as the volume increases. It was also predicted that…both parameters are constant at each 10 s rest…Each prediction was made according to everyday observations. For example, on a hot day the pressure is high and on a cold day the pressure is low or a dented ping-pong ball would inflate if it is put in hot water because the pressure inside increases due to the increase in temperature.”

“At the time though, I did not think much of the act of compression would heat the system up significantly nor did I think expansion would cool it down. I thought the temperature would go up but that it would stay constant when the plunger was held for ∼10 s and that it would decrease back to its original temperature after expansion…I always learned that the increase in pressure of a system which is compressed also leads to a temperature increase.”

Another group who also proposed the plot in Fig. 2b used what we coded as a “competing gas laws argument”. It was claimed that Boyle's Law (PV = k), was being followed. From there, two competing claims were made. In the first claim, after applying Boyle's Law, Charles' law (V/T = k) was applied to argue that the volume decrease leads to a temperature decrease. In the second claim, after applying Boyle's Law, Amonton's Law (P/T = k) was applied to argue that if pressure increases then temperature should also increase. It was as if the students were pitting Charles' Law against Amonton's Law:

“…This decrease in volume means that the temperature should go down. Yet, when you begin to push the plunger down, you increase the pressure which should lead to an increase in temperature…After talking for a while about it, we decided that the change in temperature would be more [a]ffected by the change in pressure than the change in volume. This led us to predict that the temperature would increase upon compression though we were uncertain about the shape of this change. We also predicted that the temperature would remain high if held at 20 cc.”

“We thought of Charles' Law which state[s] that volume is directly proportional to temperature so when one goes up the other goes up…since we were decreasing the volume the temperature of the gas should decrease. We also knew based off the Ideal Gas equation that pressure and temperature were also directly related. The pressure of the gas was increasing so based off of this we thought that the temperature would increase…We knew that to look at the individual laws, the other variables had to remain constant. However, we were having trouble initially with the idea that more than two variables were changing. In the end we predicted that the temperature would increase as the volume increased. We assumed that the increase in pressure would have a greater effect than the decrease in volume.”

Only one student predicted the graph depicted in Fig. 2c but could not cite a specific argument explaining why the temperature increased rapidly during the compression and, during the hold, decreased rapidly back to room temperature.

Experimental data

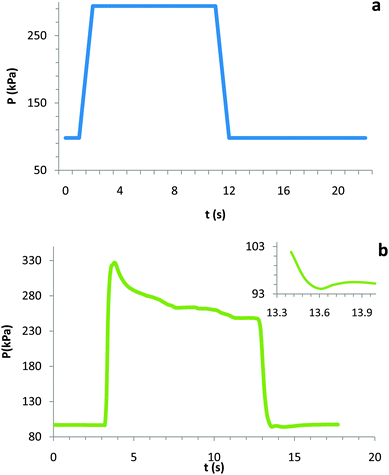
Students were generally surprised by the actual results achieved (see Fig. 3). The compression of the gas lead to a fairly dramatic temperature change relative to ambient conditions. Results varied slightly depending on the rapidity with which students compressed and expanded the syringe.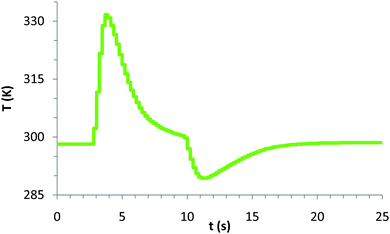

Fig. 3 Representative temperature vs. time plot that students observe during the rapid compression/expansion of the ideal gas in the syringe.

Quantitatively, typical results from the compression/expansion of the gas in the syringe (see Fig. 3) show a maximum temperature, T_max of 331.65 K (58.5 °C) where the change of temperature during the compression was ΔT₁ = 33.5 °C, and a T_min of 289.35 K (16.2 °C) during the compression where the change in temperature was ΔT₂ = −8.8 °C.

Model revision

Within the context of discussion with their classmates, students were prompted to develop a model for why the temperature increased occurred during the compression. From an analysis of the class discussions, the responses to this prompt were placed in three code groups. One argument claimed that the temperature increase was due to increased collisions (40 : 45–40 : 55; 43 : 10–43 : 18; 43 : 48–43 : 53; 47 : 45–48 : 50 of video). There was no explicit distinction by the students as to whether this pressure increase can be attributed to an increase in the number of particle–particle, particle–wall, or both types of collisions. Another argument proposed that external work or energy was being added to the system during compression (32 : 40–33 : 15; 42 : 10–42 : 35; 43 : 10–44 : 05; 49 : 07–49 : 37). A third argument suggested that there were increased intermolecular interactions and that these interactions acted to add internal energy through heat generation (41 : 37–41 : 40; 43 : 23–43 : 30; 44 : 14–44 : 20; 49 : 08–50 : 19). This third argument appeared to be an amalgamation of ideas of the particles coming within close contact with each other. In one variation, the heat was generated by “molecular friction” or rubbing of molecules against each other. In another, it was gas particles actually bonding or reacting with each other in a kind of exothermic reaction. In yet another interpretation, there was the suggestion that electron clouds “rub against each other”:

Instructor: Let's talk about this idea now—adding energy into the system. To me there are a couple of competing theories. Energy comes from without, without the system, because you are doing something to add energy to the system. Or, the energy comes from the system itself and basically, in the state it is in, when they [gas particles] are rubbing up against each other this friction that is caused generates heat. Right? Now, does someone want to argue…I mean…there's going to be different ideas. Repulsion was the one I thought that…I don't really have…do you have a better idea as to how this [the syringe] would get hotter.

Student: Yeah, a little bit. As you compress it [the syringe], the electron clouds [of the gas particles] get closer. They don't like each other because they are negative on the outside. As far as electron clouds are concerned, they are fairly negative on the outside; they don't like each other. So the energy that needs to be released is released somehow and it can't be released by expanding when you compress it so energy is released by other means…by molecular interactions.

Instructor: So repulsion is pushing them away and giving them energy?

Student: Yeah.

We were not, at this point satisfied with the students' arguments. With regards to the increased particle collisions, we asked students to clarify and elaborate on how these would lead to an increase in temperature (47 : 44–49 : 06). One student commented about knowing the effect (e.g., compression leads to an increase in temperature), but not how this heat is generated (48 : 08–48 : 51):

Instructor: Explain to me how that happens?

Student: Well I don't know how…I mean I can tell you that I,…from like something I've seen before.

Instructor: What did you see before?

Student: I've seen that when a gas comes from somewhere where its not compressed…it comes from being not compressed into more space, its not compressed anymore and it cools down so that would tell me that going the reverse direction [e.g. compression] it would heat up.

Instructor: Right, yes, and then, and the question is, is the heat coming out or heat going in due to the increasing number of collisions?

Student: It must be…I mean if you're going from its compressed in one place…its going…its compressed.

We also asked students to reconsider the argument concerning the internal production of heat through increased molecular interactions. Specifically, we pushed them to consider how, after the compression and during the hold, the syringe cools back down to room temperature (50 : 41–53 : 06), and whether that resulted from heat being lost by the system or from a decrease of molecular interactions perhaps due to condensing of the gas. Sensing that some additional guidance was needed, we intervened by prompting students to consider the definition of temperature as related to the kinetic energy of the gas particles and that this kinetic energy is related to the speed of the particles. From there we asked students to explain how the act of compression led to an increase in gas particle speed (53 : 31–55 : 06). When this failed to further the conversation, we then offered students an analogy (similar to that of Mills et al., 2001) of a ball hitting against a wall moving towards it, and how that ball would exhibit an increased recoil velocity (55 : 16–58 : 12). Following the analogy, we asked students to consider how the particle's speed is reduced (i.e., how the system cools) when the wall becomes stationary (during the 10 s hold). Again, students could not envision this and we had to use particulate-level models to assist them in visualizing this process.

Following the discussion of how the gas temperature in the syringe increased during compression and decreased during the 10 s hold, we prompted students to now explain how the particles move slower during the expansion. One student gave a reasonable answer of slower recoil velocity (61 : 31–61 : 39) and was later able to argue that the surroundings, during the expansion, transferred heat to the gas particles allowing the gas in the syringe to warm to room temperature.

Model assessment

Formative assessment. Students tended to be accepting of a particulate model proposed by the instructor via ‘just in time teaching’ (Marrs et al., 2003) wherein the change in speed of the gas particles depends on the particle–wall collision force during both the compression and expansion phases. This we evinced from student reflections such as this one:

“It was by consensus [within a group of four] that the temperature increase happened because of the speed that the plunger was forced into the syringe caused the molecules bouncing off of it to have higher velocities (kinetic energies) and thusly increasing the temperature of the gas. As the molecules continued to bounce around during the holding of the compression kinetic energy was transferred to the walls of the syringe and picked up by molecules colliding on the outside walls of the container. This caused the steady decrease in temperature. The dramatic decrease in temperature that took the temperature below room temp. was because the plunger was moving away from the molecules and increase volume inside the syringe. As molecules hit the receding plunger kinetic energy was lost to the plunger and the overall result was the lowering of the internal temperature in the syringe. Once the plunger was pulled fully out of the syringe, the temperature increased gradually to room temperature by the molecules gaining kinetic energy back from the walls of the container as the outside molecules collided with it.”

We then sought to lead students through a discussion of the pressure vs. time plot, both the predicted and observed (see Fig. 4a and b). Before the experiment, all students used a Boyle's law argument to predict the pressure change with respect to time (see Fig. 4a). According to this line of reasoning, if the volume decreased by three folds so then the pressure would increase (from 98 kPa) by the same factor (to 294 kPa) during the compression. The pressure would stabilize during the first 10 s hold and then, during the expansion and second 10 s hold, return and remain at ambient atmospheric pressure. As shown in Fig. 4b, this is not what was observed. During the compression, a maximum pressure P_max of 319 kPa (ΔP = 221 kPa) was reached. In general, a pressure of more than three times the initial pressure is reproducible. Much like the temperature, this maximum pressure decreased over time and stabilized around three times atmospheric pressure (∼294 kPa). While subtle, the pressure did, as depicted in the inset of Fig. 4b decrease below ambient pressure during the expansion.

Fig. 4 Pressure vs. time plots predicted (a) and observed (b) in response to the prompt of predicting the pressure change during the rapid compression/expansion of a gas in a syringe. Inset in (b) is intended to show decrease in pressure below ambient pressure (94 kPa)

We wanted to press students to see if they had in fact been able to accommodate the proposed particulate model by prompting them to explain why they observed the pressure vs. time plot shown in Fig. 4b. Students responded with ideas such as an improperly sealed syringe to failure to properly hold down the syringe to 20 mL during expansion of the syringe (66 : 16–67 : 00):

Instructor: That's the first time I ever heard that [responding to leaking syringe]. One argument for why the pressure would go down was that it wasn't sealed, right? So are there any other explanations we can entertain or are we going to leave here [with the idea]…with some gas escaping (but it only escapes for a little while?)…maybe this is where we completely expand it so we can't see it escaping.

Student 1: It could be the user not statically holding the plunger.

Instructor: Could be. Could be. But, I didn't see that. No one was shaking too bad.

Student 2: I think the syringe is actually expanding itself.

Instructor: [Inaudible].

Student 2: The syringe can expand itself which would increase the volume which would decrease

Instructor: Which would decrease the pressure, okay.

We responded with a more specific prompt of having students explain why a maximum pressure above ∼300 kPa was observed (68 : 16–68 : 26):

Instructor: How do we get above 300 [kPa]?

Student: Because the pressure is…because the temperature is high right? As the temperature goes up the pressure also goes up.

Students seemed to have used algorithmic understanding to explain the effect, but not how the effect was observed. That is, students again related how the pressure could increase because of a decrease in volume. However, few students noted that the force of collisions of the gas particles was also changing due to the change in temperature and the correlated change in kinetic energy and particle speeds.

We wanted to continue to challenge the students' understanding with a new prompt which asked students to devise a way in which one could compress or expand the syringe and observe little to no change in temperature with respect to time. That is, we were asking them, implicitly, to model the isothermal compression or expansion of the syringe. Most students quickly picked up on what we were asking and proposed very slowly compressing/expanding the syringe to allow for equilibration of temperature between the system and the surroundings (results of such are discussed in the Applications).

Summative assessment. We also sought to gauge student conceptions post-experiment to see if the lesson had a lasting impact on their mental models. Student answers to a homework assignment (see ESI†) indicate at some model revision and successful application of such to a different context. In a question regarding how a diesel engine operates, for example, one student gave the following response:

“I imagine that a diesel engine rapidly compresses the fuel in order to ignite it…As we observed in lab, compressing air increases its temperature dramatically, even over small changes in volume. Diesel engines take advantage of this by injecting fuel right as the air is compressed and heated. This increase in temperature ignites the fuel and the engine starts.”

In response to a question regarding why it might be unsafe to heat up a can of compressed gas this same student wrote the following:

“Raising the temperature of a constant volume of compressed gas can be dangerous because it will result in increased pressure, which would ultimately result in an explosion. As the gas particles are given more kinetic energy, they would like to expand, but the rigid container prevents such expansion. As a result, pressure builds and eventually exceeds the strength of the container, which explodes.”

Some of the ideas we wished to impress on students were conveyed, although not uniformly across classes. In the above, the student seemed to hypothesize that the gas molecules themselves were expanding. It was hoped, for this question, that students would cite an increase in the force of gas particle collisions against the container walls to account for the increased pressure.

In response to the question of how a diesel engine works, a student wrote

“A diesel engine takes in air and compresses it quickly. The compression of the air is followed by the release of fuel. As we've seen in our experiment, the quick compression of a gas increases the pressure, which increases the temperature by roughly the same degree.”

Similar to before, this student was claiming that pressure was the agent that was causing the gas particles to have increased kinetic energy (i.e. increased temperature). When students were asked to describe two commercial processes which make use of compression/expansion work, this same individual responded using similar logic as before to propose that a change in volume is causing a pressure and temperature change:

“Two other commercial processes that use thermal properties of gases expanding/compressing are refrigeration and cryogenics. We use refrigeration every day. The fridge uses a compressor to compress gas. Then, the pressurized gas goes through an expansion. This expansion causes the pressure to lower and the temperature to lower, as well. The cold gas (now condensed into a liquid) pulls in heat from the freezer compartment and then from the refrigerator compartment as it goes down. It gets recompressed and starts all over again. Cryogenics work using expansion much in the same way: gases are cooled until they are liquids from being at a high pressure and then suddenly releasing pressure to become very cold. Liquid oxygen and nitrogen are used in industry and are manufactured somewhat in this manner.”

In one more instance, a student reflection described the reason why the pressure rose to above the predicted threefold increase invoked macroscopic observables as the cause for change:

“From the ideal gas law formula, PV = n × R × T, the behavior of the pressure versus time can be explained. Since the volume decrease 3 : 1, the pressure had to increase 1 : 3 to maintain the formula equality. However, since the pressure did go slightly above the 3* original amount another explanation did need to be discussed. At the initial compression the temperature increase drastically as the volume decreased. The rise in temperature explains the pressure that goes above the 1 : 3 increases. As the temperature fell and volume stayed in a decreased amount during the holding of the compression, the pressure was able to gradually fall to the three atmosphere mark. If the compression was held for longer than ten seconds, the pressure would have stayed at the three atmospheres for as long as the compressed volume stayed at one third the original volume.”

Some students seem to again be reverting back to more heuristic descriptions and arguments with which they are all too familiar, rather than use a particulate understanding and explanation of gas behavior that we desired to engender in students' understandings.

Discussion

From our observations, we infer the following findings with regards to what preconceptions students had, what models students invoked, how they justified their models, and the extent to which they revised their models and applied these revised models under new contexts.

Findings

Algorithmic learning vs. rich modeling. As evidenced in a number of student reflections and in recorded conversations, students tended to invoke equations such as Boyle's Law or the Ideal Gas Law in response to the first prompt concerning the development of a model that would account for the temperature change with respect to time during the rapid compression/expansion of the gas in the syringe. This is problematic as such equations can be used only under a specific set of conditions. Boyle's Law holds when ΔT = Δn = 0. The Ideal Gas Law will tend not to hold at high pressure and low temperature. Mathematically, it does not hold when both (∂P/∂V)_T = (∂P²/∂V²)_T = 0, which is marked by an inflection point on the critical isotherm. One of the inherent flaws of a model comes from a model's oversimplification (typically in the form of assumptions made) of a complex phenomenon by the setting of specific conditions (e.g. constant temperature and number of moles for Boyle's Law). Models begin to fail when these conditions are not satisfied. If students understand and appreciate this, then they could be one step closer to moving past algorithmic learning—which researchers continue to note results in poor conceptual understanding by students (Nurrenbern and Pickering, 1987; Pickering, 1990; Sawrey, 1990; Nakhleh and Mitchell, 1993; Cohen et al., 2000; Cracolice et al., 2008)—and towards coherent, scientifically-accepted understandings.

Fragmented knowledge. The models all students invoked tended to be incomplete and/or incoherent. DiSessa (1982, 2004) noted that the separation between novice and expert learners was in the former's inability to display coherence of knowledge. Novice learners tend to exhibit knowledge in piecemeal, but struggle to make the needed connections between concepts. We see this evinced in the explanations students used to justify their temperature vs. time graphs. We observed students claim, during the prediction phase, that work/energy was being supplied to the system. The statement is accurate but incomplete; students could not explain how work being done on the gas during the compression led to an increase in kinetic energy of the gas particles resulting in the observed temperature increase. Several groups tried to use Charles' Law, Boyle's Law, and Amonton's Law as if they were mutually exclusive. Students tended not to consider that each law applies to a specific set of conditions in which such can be successfully applied. Some students appealed to either common experience or formal instruction that gas expansion leads to a temperature decrease while gas compression leads to a temperature increase, but could not explain why. Notwithstanding the misuse of equations, noted above, these students are not taking into account that P, V, and T are not independent of each other which we feel is evidence for a fragmented mindset that students came into this experiment. We feel that it is not entirely the students fault that they have this mindset, but a failure, on the part of their educational experience, to challenge student misconceptions more rigorously so as to make the more coherent connections that would move student understanding towards more expert-level knowledge.

Particulate modeling. The post-investigation prompt students were given (i.e., propose a model that would account for the temperature change during the rapid compression/expansion of the gas in the syringe) did not explicitly include a directive to use a particulate model to account for the temperature and pressure increase. This kind of modeling might be expected to be used at least by some students across the populations studied, but was not observed to be invoked by any without instructor intervention. A particulate model, if initially invoked, might have led students to consider the nature of the collisions and impact (force) of collisions between the particle and the container walls during the prediction phase.

Kinetic-molecular theory. Some students tried to invoke the ideal gas law and the kinetic molecular theory to inform their explanations.

However, the ‘increased intermolecular interactions’ model invoked by some students [which claims that the interactions between particles are significant because the distance between particles is now assumed to be small], is contrary to the kinetic-molecular theory. If particle–particle distance did decrease so significantly, the gas would be expected to condense (and thus ideal gas behavior could not be used). This finding seems to show that students have only a superficial understanding of the kinetic-molecular theory. It is noteworthy that the condensation of the gases into liquids would be consistent with the exothermic features of the adiabatic compression, however.

Pressure, temperature, and collision theory. We were interested to observe that some groups invoked the ‘increased collisions’ model (i.e., the increase in the frequency of particle–particle and particle–wall collisions) to account for both the temperature and pressure increases observed during the compression phase. This explanation seems to follow the commonly observed effect described above that gas expansion leads to a temperature decrease while gas compression leads to a temperature increase. What is of importance to note is that the pressure change, in of itself, does not cause the temperature change nor vice versa. The increase in particle–wall collisions (not particle–particle collisions), due to a decrease in surface area (e.g. via compression) is one mechanism to account for the pressure increase, but not for the increase in temperature. It is this notion of increased pressure for which most of students we observed were comfortable conceptualizing and articulating. The other conception of increased gas pressure through increased force of collisions was not invoked by any group in the three classes we observed. Students could have, using an algorithmic approach, arrived at this second conclusion by simply noting the mathematical definition of pressure (P = F/A). The students studied did not seem to be comfortable with applying fundamental physics concepts of elastic collisions, speed, force, or kinetic energy to properly explain gas behavior.

Implications

Physical chemistry is a critical course in the undergraduate chemistry program with regards to preparing the next generation of academics, researchers, industrial chemists, and chemistry teachers, among other professionals. It is critical because physical chemistry represents a pivotal nexus: the place where the conceptual background of chemistry forged in foundation courses meets the deeper mathematics underlying those conceptions, as well as the principles of physics that can help broaden them. The study presented in this paper raises questions, though, as to how well the potential of physical chemistry to serve in this capacity is being met. In this section, we will make several key points related to the concerns surfaced through the analysis of the text (notes, class discussion, and reflections) generated during the adiabatic/isothermal compression/expansion lesson. Further, we will review key pieces of the data presented which provide evidence for the validity of these concerns.

The first point to be made is that, despite a call by Johnstone (1982) over thirty years ago for specific attention to be given to helping students move fluently between the macro, micro, and symbolic ‘worlds’, the students involved in this study did not exhibit this ability. Evidence for this shortcoming was abundant when students made their initial predictions about the appearance of the temperature vs. time graphs. In all cases, they were prone to resort to either other symbolic pieces of knowledge (the equations of the gas laws) or to macroscopic relationships (temperature–volume, pressure–volume, etc.). In no case did they draw on a particulate perspective in these initial explanations. Even after prompting, the students showed difficulty evoking a particulate model that could account for the results they observed. If these were students in a freshmen general chemistry course, that outcome might be expected; given that all of these students were upperclassmen and had either completed physical chemistry or were taking it concurrently with the class in which the syringe activity was completed, this inability is problematic.

Our first point leads naturally to our next. A challenge with supporting the kind of understanding that Johnstone is advocating is that students must develop the propensity to move towards particulate models when the situation demands this. The data presented in this paper shows that the natural inclination of these students was to search first for algorithmic solutions that could be applied to the task they were given. Based on the research from cognitive psychology on problem solving (e.g.Novick and Bassok, 2005), this is not surprising. However, that propensity is all the more reason that a major focus of chemistry teaching at all levels needs to be on supporting students in forming mechanisms for searching deeper for conceptual and model-based schema to use in exploring a given problem space (Raghavan and Glaser, 1995). One of the encouraging things from this study is that the approach used encouraged students to employ such schema more and more as the investigation progressed.

Another challenge with assisting students in engaging in the kind of thinking commensurate with recent reform documents (National Research Council, 2012; NGSS Lead States, 2013a, 2013b) was brought to light in this study. When students' experiences related to a phenomenon under examination are strong and familiar, they are inclined to be unwilling to search for models which might bring into question predictions based on those experiences. This is in line with what a number of studies from the conceptual change literature indicate (e.g.Vosniadou, 2002; Inagaki and Hatano, 2008). An obvious example of this was the student who had had numerous prior experiences with syringes, had never felt a temperature increase (or decrease) during any of those experiences, and so was reluctant to consider a model from which such temperature changes might be predicted. While overcoming such cognitive biases in students exploring chemical phenomena represents a hurdle for those teaching physical chemistry, research has described pedagogical practices that make this possible (e.g. Mason, 2002). We believe that the model-based learning cycle outlined in this paper is illustrative of such an approach.

There is another form of scaffolding which students will need in order for a model-based inquiry approach (Windschitl et al., 2008) to be effective: helping them know how to contextualize the use of the models they invoke. Throughout the data presented (and in additional data not presented), students exhibited difficulty in terms of knowing when the use of a particular model was appropriate or inappropriate based on the conditions. This perhaps results from a lack of a systems thinking emphasis in the teaching of chemical principles (Thornton et al., 2004). The group of students who tried to use both Charles' Law and the Ideal Gas Law in their initial prediction of the compression graph were representative of this. They did not understand that the Ideal Gas Law contains all of the variables to describe a gaseous system and that Charles' Law makes assumptions about certain of those variables that limit the systems to which it can be applied. Additionally, numerous groups were unable to recognize the syringe surroundings as a possible heat sink/source within this investigation. For a model-based inquiry approach to succeed, students must be assisted in breaking from their routine of not considering the assumptions on which a model is based, of utilizing models that only encapsulate a single component of a system, and of isolating variables that clearly interact within the system (Mandinach and Thorpe, 1987).

Our last point discussed a form of ontological scaffolding this study suggests students will need to successfully participate in model-based inquiry (being helped to see the whole system); our fifth point relates to a form of epistemological scaffolding that is also necessary. It is related to the way that individuals respond when their predictions about a scientific investigation do not match the results. Johnson (2010) [citing the work of Dunbar (1997, 1999)] pointed out that, “More than half of the data collected by the [science] researchers [Dunbar observed] deviated significantly from what they predicted they would find. Dunbar found that the scientists tended to treat these surprising outcomes as the result of flaws in their experimental methods” (p. 138). In other words, given the choice of questioning their design or questioning their reasoning, the researchers predominantly were dubious of the design. We saw a similar epistemological stance adopted by the students in this study who explained the anomalous results of the expansion of the gas in terms of the syringe's plunger being pulled out of the body, rather than considering that the anomaly might cast doubt on the way they were conceptualizing the phenomenon. As Johnson notes, “transforming error into insight” requires seeing such data as ‘signal, not noise’ (p. 138). For students, being guided to entertain the possibility that data of this kind might indicate a deficiency in their model is essential to conceptual change and movement towards more sophisticated scientific understandings.

Finally, given that the approach described in the article did show efficacy in terms of allowing students to move more fluently between the macro, micro, and symbolic perspectives on the phenomenon, we want to identify the features we believe are crucial to achieving this outcome. The features that we have identified are (1) establishing an environment where being wrong is seen as a step on the pathway towards deeper learning, (2) supporting conceptualization as a foundation for mathematization, (3) promoting an epistemological stance of considering both the source of one's own justifications and the logic of others' perspectives, and (4) utilizing/highlighting discursive interactions which create spaces where the other features are realized through the thoughtful facilitation of the teacher.

Applications

Work

While our investigation focused on students preconceptions of adiabatic compression/expansion and their ability to accommodate a particulate-level model of this phenomenon, the lesson (see details in the Appendix) can be easily quantified for the determination of the work done on the gas during a quick, adiabatic compression and the slow, isothermal compression of the gas in the syringe. Adiabatic or isothermal expansion, is possible, but is not as facile as the compression given the experimental setup. Through student experience, a good isothermal compression where the change in temperature is small takes effort and time. However, one can generate a temperature vs. time graph shown in Fig. 5 where ΔT = 298.8 ± 0.1 K: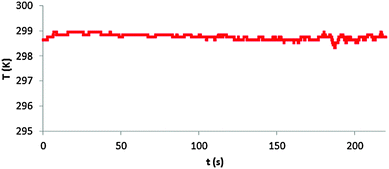

Fig. 5 Sample student temperature vs. time plot generated by a slow, near isothermal compression of the gas in the syringe.

Using the Ideal Gas Law, we can find the corresponding volume of the gas in the syringe at each pressure and create a PV plot given in Fig. 6. The black line represents a cubic best-fit§ polynomial function (P = −1.495 × 10¹⁸ Pa/(m³)³ + 2.741 × 10¹⁴ Pa/(m³)² − 1.854 × 10¹⁰ Pa/(m³) + 5.477 × 10⁵ Pa). Graphically, the area under the PV curve denotes the work done to compress the gas in the syringe. Integration of this best-fit function with the upper and lower bounds set as the initial and final volumes, respectively, gives the work. For the isothermal compression above from 60 mL to 30 mL, the work is computed to be 4.1 J. We can compare the work found through experimental results with what could be expected from a theoretical reversible compression of an ideal gas under isothermal conditions.¶ Doing so gives the same result, 4.1 J.

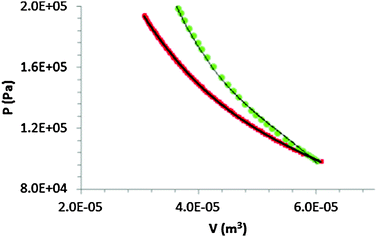Fig. 6 Student generated PV plot for the slow, isothermal compression (red) and quick, adiabatic compression (green) of the gas in the syringe. Black lines represent best-fit functions.

The calculation of the work for the adiabatic process is not as straightforward to do as we cannot use the ideal gas law to find the instantaneous volume of the syringe at an instantaneous pressure. We estimated this volume knowing the initial volume and pressure before the compression. We assumed γ, the ratio of the gas' (e.g. air) heat capacities at constant pressure (C_P) and constant volume (C_V) to be 1.4. At each time interval, we used the instantaneous pressure as the final pressure. From these values, we calculated the volume at a given instance|| and created the below PV plot (see Fig. 6).

Again, a best-fit function can be used to arrive at a function of P. Here, we used a cubic polynomial (P = −5.295 × 10¹⁸ Pa/(m³)³ + 8.600 × 10¹⁴ Pa/(m³)² − 4.954 × 10¹⁰ Pa/(m³) + 1.118 × 10¹⁰ Pa). Integrating this and using the same upper and lower limits as before (60 and 30 mL), the work done is 4.8 J. This is slightly more than what theory predicts for a reversible, adiabatic compression (4.7 J).** Instructors might use these results to facilitate a discussion on the work needed to compress a hot gas adiabatically or isothermally. Such could, under broader contexts, lead to a discussion of the conditions by which an isothermal compression/expansion would do more/less work than an adiabatic compression/expansion.

The Carnot cycle

This lesson does lend itself to modeling a reversible Carnot cycle. For example, one could ask students to go from 60 mL → 50 mL slowly (isothermally) and then from 50 mL → 40 mL quickly (adiabatically) during the expansion phase and then from 40 mL → 50 mL slowly and then from 50 mL → 60 mL quickly. The work done by the cycle can be found by finding the area enclosed within best-fit functions of each step-wise process. Instructors could use this lesson as a segue into related topics of engine efficiency, entropy, and the second law of thermodynamics as formulated by Kelvin and Planck.††

Heat engines

The Carnot cycle itself is useful in speaking of heat engines in general. Such heat engines are familiar to students in AC units and refrigerators which operate based on expansion and compression cycles.

Work processes

This lesson discusses two of the three processes by which a gas can undergo compression and expansion. Left out is the isobaric compression/expansion of a gas. Instructors could use this lesson to assess students on their knowledge of the similarities and differences of the three processes.

Conclusion

We challenged students to predict the outcome of a thermodynamic process (pseudo-adiabatic compression and expansion) as a way of assessing (1) their preconceptions and (2) their ability to model their conceptions. We were not troubled as much as to the shortcoming of our students to give the “right” answer, but more on their inability to, without instructor support, revise their models to account for observations counter to those anticipated. We feel that the ability of students to model could lead them to better conceptual understanding of chemical and physical phenomena. However, this skill set is, in our opinion, not a cornerstone of present-day curricula from the high-school level and up. Reform in education should include modeling as a fundamental skill to achieve the goals we have set for ourselves.

Acknowledgements

We would like to thank all participating students for agreeing to have their work included in this study and Y. Payton for proposing the lesson plan to this study. We would like to thank M. Mitchell, H. Abbott-Lyon for helpful and thoughtful conversation. We would like to acknowledge the reviewers and editorial staff for their insight and feedback. This work was supported in part by NSF awards DUE-1035451 and DRL-1316347.

References

1. Ashkenazi G., Gordon J. S. and Hofstein J. D., (2008), Similarity and Difference in the Behavior of Gases: An Interactive Demonstration, J. Chem. Educ., 85(1), 72–77.
2. Bogdan R. and Biklen S. K., (2006), Qualitative Research for Education: An Introduction to Theories and Methods, 5th edn, Upper Saddle River: Pearson.
3. Chittleborough G. and Treagust D. F., (2007), The modelling ability of non-major chemistry students and their understanding of the sub-microscopic level, Chem. Educ. Res. Pract., 8(3), 274–292.
4. Cohen J., Kennedy-Justice M., Pai S., Torres C., Toomey R., DePierro E. and Garafalo F., (2000), Encouraging Meaningful Quantitative Problem Solving, J. Chem. Educ., 77(9), 1166–1173.
5. Cracolice M. S., Deming J. C. and Ehlert B., (2008), Concept Learning versus Problem Solving: A Cognitive Difference, J. Chem. Educ., 85(6), 873–878.
6. DiSessa A. A., (1982), Unlearning Aristotelian Physics: A Study of Knowledge-Based Learning, Cognit. Sci., 6, 37–75.
7. DiSessa A. A., (2004), Coherence versus fragmentation in the development of the concept of force, Cognit. Sci., 28, 843–900.
8. Dunbar K., (1997), How scientists think: On-line creativity and conceptual change in science, in Ward T. B., Smith S. M. and Vaid J. (ed.), Creative Thought: An Investigation of Conceptual Structures and Processes, Washington, D.C.: American Psychological Association, pp. 461–493.
9. Dunbar K., (1999), How scientists build models: In vivo science as a window on the scientific mind, in Magnani L., Nersessian N. J. and Thagard P. (ed.), Model-Based Reasoning in Scientific Discovery, New York: Plenum Press, pp. 98–98.
10. Engel T. and Reid P., (2010), Thermodynamics, Statistical Thermodynamics, & Kinetics, 2nd edn, Upper Saddle River: Pearson.
11. Gachic L., (1968), The Heat of Compression, J. Chem. Educ., 45(7), A569.
12. Goedhart M. J. and Kaper W., (2002), From Chemical Energetics to Chemical Thermodynamics, in Gilbert J. K., de Jong O., Justi R., Treagust D. F. and van Driel J. (ed.), Chemical Education: Towards Research-based Practice, Dordrecht: Kluwer Academic Publishers, pp. 339–362.
13. Inagaki K. and Hatano G., (2008), Conceptual change in naïve biology, in Vosniadou S. (ed.), International Handbook of Research on Conceptual Change, New York: Routledge, pp. 240–262.
14. Johnson S., (2010), Where good ideas come from: The natural history of innovation, New York: Penguin.
15. Johnstone A. H., (1982), Macro- and micro-chemistry, School Sci. Rev., 64, 377–379.
16. Justi R. S. and Gilbert J. K., (2002), Modelling, teachers' views on the nature of modelling, and implications for the education of modellers, Int. J. Sci. Educ., 24(4), 369–387.
17. Kerr S. and Runquist O., (2005), Are We Serious about Preparing Chemists for the 21st Century Workplace or Are We Just Teaching Chemistry?, J. Chem. Educ., 82(2), 231–233.
18. Kousathana M. and Tsaparlis G., (2002), Students' Errors in Solving Numerical Chemical-Equilibrium Problems, Chem. Educ. Res. Pract., 13(1), 5–17.
19. Lin H.-S. and Cheng H.-J., (2000), The Assessment of Students and Teachers' Understanding of Gas Laws, J. Chem. Educ., 77(2), 235–238.
20. Mandinach E. B. and Thorpe M. E., (1987), The systems thinking and curriculum innovation project. Technical Report, Part 1. ED301146.
21. Marrs K. A., Blake R. and Gavrin A., (2003), Use of warm up exercises in just in time teaching: determining students' prior know-ledge and misconceptions in biology, chemistry, and physics, J. Coll. Sci. Teach., 33(7), 42–47.
22. Mills P. A., Sweeney W. V. and Cieniewicz W., (2001), Experiencing and Visualizing the First Law of Thermodynamics: An In-Class Workshop, J. Chem. Educ., 78(10), 1360–1361.
23. Naah B. M. and Sanger M. J., (2012), Student misconceptions in writing balanced equations for dissolving ionic compounds in water, Chem. Educ. Res. Pract., 13(1), 186–194.
24. Nakhleh M. M., (1993), Are Our Students Conceptual Thinkers or Algorithmic Problem Solvers? Identifying Conceptual Students in General Chemistry, J. Chem. Educ., 70(1), 52–55.
25. Nakhleh M. B. and Mitchell R. C., (1993), Concept Learning versus Problem Solving: There Is a Difference, J. Chem. Educ., 70(3), 190–192.
26. National Research Council [Committee on Conceptual Framework for the New K-12 Science Education Standards], (2012), A frame-work for K-12 science education: Practices, crosscutting concepts, and core ideas, Washington, DC: National Academies Press.
27. Nicholl G. and Francisco J. S., (2001), An Investigation of the Factors Influencing Student Performance in Physical Chemistry, J. Chem. Educ., 78(1), 99–102.
28. NGSS Lead States, (2013a), Next Generation Science Standards: For States, By States. Volume 1: The Standards, Washington, DC: The National Academies Press.
29. NGSS Lead States, (2013b), Next Generation Science Standards: For States, By States. Volume 2: Appendixes, Washington, DC: The National Academies Press.
30. Novick L. R. and Bassok M., (2005), Problem solving, in Holyoak K. J. and Morrison R. G. (ed.), The Cambridge Handbook of Thinking and Reasoning, New York: Cambridge University Press, pp. 321–349.
31. Nurrenbern S. C. and Pickering M., (1987), Concept learning vs. problem solving. Is there a difference?, J. Chem. Educ., 64(6), 508–510.
32. Pickering M., (1990), Further Studies on Concept Learning vs. Problem Solving, J. Chem. Educ., 67(3), 254–255.
33. Pinarbasi T., Sozbilir M. and Canpolat N., (2009), Prospective chemistry teachers' misconceptions about colligative proper-ties: boiling point elevation and freezing point depression, Chem. Educ. Res. Pract., 10(3), 273–280.
34. Raghavan K. and Glaser R., (1995), Model–based analysis and reasoning in science: the MARS curriculum, Sci. Educ., 79(1), 37–61.
35. Saldaña J., (2009), The coding manual for qualitative researchers, Thousand Oaks, CA: Sage.
36. Sawrey B. A., (1990), Concept Learning versus Problem Solving: Revisited, J. Chem. Educ., 67(3), 253–254.
37. Smith K. C. and Nakhleh M., (2011), University students' conceptions of bonding and melting in dissolving phenomena, Chem. Educ. Res. Pract., 12(2), 398–408.
38. Stamovlasis D., Tsaparlis G., Kamilatos C., Papaoikonomou D. and Zarotiadoui E., (2005), Conceptual understanding versus algorithmic problem solving: further evidence from a national chemistry examination, Chem. Educ. Res. Pract., 6(2), 104–118.
39. Thornton B., Peltier G. and Perreault G., (2004), Systems thinking: a skill to improve student achievement, Clearing House, 77(5), 222–227.
40. Toomey R. and Garafalo F., (2003), Linking Physics with Chemistry—Opportunities in a Constructivist Classroom, Chem. Educ. Res. Pract., 4(2), 189–204.
41. Vosniadou S. (2002), On the nature of naïve physics, in Limón M. and Mason L. (ed.), Reconsidering conceptual change: Issues in theory and practice, New York: Springer, pp. 61–76.
42. Waite B. A., (1985), A Gas Kinetic Explanation of Simple Thermodynamic Processes, J. Chem. Educ., 62(3), 224–227.
43. Windschitl M., Thompson J. and Braaten M., (2008), Beyond the scientific method: model-based inquiry as a new paradigm of preference for school science investigations, Sci. Educ., 92(5), 1–27.

---

Footnotes

† Electronic supplementary information (ESI) available: Lesson plans, instructor notes and sample assessment items are available. See DOI: 10.1039/c4rp00008k

‡ We used the equipment from PASCO entitled “Ideal Gas Experiment” (see http://pasco.com). Alternatively, equipment from Vernier may be used as an alternative (www.vernier.com).

§ The choice of function used for fitting (here polynomial and cubic) was one of convenience, and facilitated the calculation of the work done under each condition. We sought one that was a “best-fit” to the data obtained.

¶ Work done through a reversible compression of an ideal gas under isothermal conditions is derived from integration of the ideal gas law. This can be found in most physical chemistry textbooks. We simply report the results of such:

W_rev = −nRT ln(V_i/V_f).

|| As in Note 2, the derivation of the relation of the initial pressure and volume with that of the final pressure and volume for a reversible adiabatic expansion or compression of an ideal gas can be found in most physical chemistry textbooks. We simply report the results of such:

P_iV_i^γ = P_fV^γ_f.

** For a reversible adiabatic compression, the work done is given by.

W_rev = P_iV^γ_i[(V^1−γ_f − V^1−γ_i)/(1 − γ)].

†† In Engel and Reid's (2010) text, this statement reads as follows:“It is impossible for a system to undergo a cyclic process whose sole effects are the flow of heat into the system from a heat reservoir and the performance of an equivalent amount of work by the system on the surroundings.”

---