In search of new reconstructions of (001) α-quartz surface: a first principles study

Abstract

Using Born–Oppenheimer molecular dynamics (BOMD) simulations and “static” density functional theory (DFT) calculations, the stability of cleaved and reconstructed α-SiO₂(001) surfaces was studied. We found reconstructions (“dense”, 2 × 2 reoptimized “dense”, and 3 × 3 reoptimized “dense”) which minimize the surface energy. The analysis of the surface energies shows that the cleaved surface reconstructs to the 2 × 2 reoptimized “dense” surface having a surface energy around 10% smaller than the “dense” surface. The results suggest that the optimization of Si–Si and Si–O distances at top surface layers plays the key role in stabilizing the 2 × 2 “dense” surface over the well-known “dense” surface.

---

α-quartz (P3₁21 space group) is a stable silica (SiO₂) polymorph¹ and one of the most abundant minerals, having wide applications in construction, piezoelectric devices, glass production industries, etc. It is also one of the major parts of oil shales² and seems to play a significant role in their properties. A number of studies have been focused on the analysis of α-SiO₂ properties and formed the basic knowledge on phase stability,¹ electronic properties,^3–7 defects,^8–10 some surface properties,^3,11–16etc. Nevertheless, the understanding of α-SiO₂ surface properties is still weak. It is known that similar to other semiconductors/insulators, cleaved α-SiO₂ surfaces tend to minimize high energy dangling bonds by surface reconstructions.¹⁶ However, experimental investigations of α-SiO₂ surfaces (especially of reconstructions) are rare and do not provide sufficient details on atomic ordering at the surfaces. It is particularly due to difficulty to use atomic force microscopy (AFM) for the analysis of semiconductor and insulator surfaces. AFM studies reported that α-SiO₂ surface is flat.¹⁷ Low-energy electron diffraction (LEED) investigations showed that the α-SiO₂(001) surface has a (1 × 1) pattern.^18,19 However, both AFM and LEED studies did not provide any information on the reconstructions at low temperatures. To the best of our knowledge, only 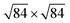reconstruction, which takes a place at the temperatures above 873 K, was reported so far.¹⁸ Nevertheless, this reconstruction can be attributed to the α–β quartz phase transition occurring at 846 K.¹⁸ Therefore, the use of computational studies for the understanding of α-SiO₂ surfaces is of significant interest.

During the last 15 years, a few fundamental studies^11,14,16 showed that α-SiO₂(001) surface has the lowest energy. In particular, Rignanese et al. reported first principles study of cleaved and reconstructed α-SiO₂(001) surfaces, and they suggested that a “dense” surface is the most favorable reconstruction.¹⁴ The properties of the same reconstructed surface were further studied by Rignanese et al.¹³ and Goumans et al.¹¹ Moreover, the “dense” surface was later used for the analysis of molecular adsorption on the SiO₂ surfaces^3,11,13 and SiO₂ interfaces with other materials.^20,21 Recently, using the mix of molecular dynamics (MD) and first principles calculations, Chen et al. showed that the “dense” surface may further reconstruct.²² Nevertheless, all previous studies of the reconstructions have some limitations such as small size of the studied systems, limited analysis of system stability, use of empirical interaction potentials for MD, etc. Because of this, in this work, using BOMD simulations and “static” DFT calculations, detailed analysis of the stability of reconstructed and cleaved α-SiO₂(001) surfaces was performed. We show that the well-known “dense” surface should be considered as metastable. Moreover, the electric and structural properties of the found reconstructed surfaces are analyzed and discussed in details.

All calculations were carried out using the Vienna ab initio simulation package (VASP) with the Perdew–Burke–Ernzerhof (PBE)²³ functional. Projector augmented wave (PAW) pseudopotentials^24,25 were used to model the effect of core electrons. The non-local parts of the pseudopotentials were treated in reciprocal and real space for the “static” DFT and BOMD calculations, respectively. The cutoff energies for the plane wave basis set were set to 400 and 300 eV for all “static” DFT and BOMD calculations, respectively. It should be noted that for BOMD, the increase of the cutoff energy to 400 eV did not affect the final (“static” DFT) energies of both the 27-layer unit cell and the 2 × 2 supercell slabs. The Brillouin-zone integrations were performed using Γ-centered Monkhorst–Pack²⁶ grids (see Table S1†).

SiO₂ surface was modelled as a periodic SiO₂ slab containing N (N = 27, 36, or 45) atomic layers and a vacuum region of about 12 Å. In this study, we used three slab sizes: unit cell, 2 × 2 supercell, and 3 × 3 supercell (only for 27-layer slab, see ESI†). For the studied systems, all atoms were relaxed until the internal forces were smaller than 0.01 eV Å⁻¹. The fixation of the central layers and its impact on the surface energy of the cleaved surface (for 27-layer slab) were also studied, but the effect was found to be insignificant.

To find possible reconstructions at α-SiO₂(001) surface, BOMD simulations with two different annealing/quenching temperature protocols were used. For the first temperature protocol, atomic velocities were initialized at 1 K using the Maxwell–Boltzmann distribution. Then, the system was heated to 1000 K during the period of 20 ps. Using canonical ensemble BOMD (number of atoms, volume, and temperature are conserved), the resulted system was annealed at 1000 K for a period of 20 ps. Finally, the resulted system was quenched to 1 K with a cooling rate of 0.033 K fs⁻¹. For the second temperature protocol, the velocities were initialized using the Maxwell–Boltzmann distribution at a few different initial temperatures: 500, 600 (for unit cell calculations only), 1000, and 1500 K. Then, canonical ensemble BOMD simulations were carried out for the period of 15–20 ps with a time step of 1.5–2 fs. To ensure that the increase of simulation time does not affect the structures and energetics, the key BOMD calculations were performed for the period of about 45 ps. Finally, the resulted systems were quenched to 1 K with the cooling rate of 0.033 K fs⁻¹, and the obtained configurations were further optimized using quasi-Newton algorithm. For all BOMD simulations, the system temperature was controlled using the Nose thermostat.^27–29 It should be noted that the results obtained from the first and the second temperature protocols were found to be similar (the largest energy difference was found to be about 0.02 eV), and hence, in this study, results only for the second temperature protocol are included. Moreover, the key results are presented only for the lowest energy structures predicted based on the mix of BOMD and “static” DFT calculations. Nevertheless, it should be noted that for the slab annealed at different temperatures, the largest difference of “static” DFT energies was found to be as much as 0.02 eV.

In α-SiO₂, each Si forms bonds with four O atoms with two slightly different bond lengths (in this study, 1.625 and 1.628 Å) and the average O–Si–O angle of about 109.5°. The formed Si–O bonds have the covalent polar nature (in some references,^30,31 the Si–O can be also treated as ionic bond). The analysis of computed Bader charges³² indicates that Si atoms have a charge reduction (electron density reduction) of about 3.23e (the Bader charge is 3.23e), while the O atoms have a charge increase of about 1.62e (the Bader charge is −1.62e). The computed Bader charges correlate well with the analysis of Si and O electronegativities³³ and previously reported results (from 3.26e to 3.33e and from −1.63 to −1.67 for Si and O, respectively).^34,35 For α-SiO₂, the computed PBE band gap is found to be 5.71 eV, and it is, as expected, smaller compared to experimental values (8.9 ± 0.2 eV for amorphous SiO₂ (ref. 36)), but it is comparable with other theoretical studies (from about 5.6 eV for local density approximation or PBE to 9.4 eV for GW).^5–7,14

To study surface stability, the surface energy (γ) was calculated as γ = (E_S − E_SiO2)/(2A), where E_S and E_SiO2 are the energies of the slab and of the bulk SiO₂, containing the same number of SiO₂ units as the slab; A is the surface area of one side of the slab. Considering the α-SiO₂ structure and taking into account the presence of two surfaces in the slab model, the stoichiometric (001) slab can be built as Si/O- or O/O-terminated slab (see Fig. S1†). However, since the Si/O-terminated α-SiO₂(001) slab is highly energetically unstable (the average surface energy was found to be 3.42 J m⁻² for the 27-layer slab), this study was limited to the analysis of O/O-terminated slabs. This is consistent with other studies of α-SiO₂ surface stability.^11,14

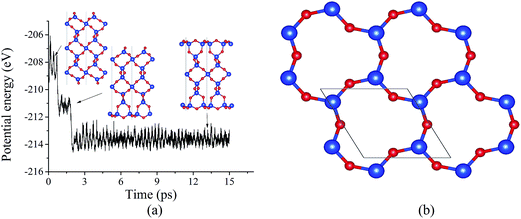
The surface energy of the cleaved α-SiO₂(001) surface is found to be 2.23 J m⁻² and does not depend on the slab thickness (number of SiO₂ layers). Due to the presence of dangling bonds, the cleaved surface tends to reconstruct. Using BOMD simulation, the evolution of the potential energy of 27-layer unit slab (Fig. 1a) was studied. It was found that the potential energy decreases with two steps ((1) reconstruction of one surface and (2) reconstruction of the second surface). As the result of the reconstruction, the under-coordinated Si surface atoms become four-coordinated. Moreover, the comparison of the cleaved and reconstructed structures indicates that the reconstructed system has significant atomic displacements for the top 6 surface atomic layers (see Fig. 1a). The atomic displacements lead to the formation of 3- and 6-member rings (named based on the number of Si–O pairs in the rings), which are not typical for bulk α-SiO₂ (see Fig. 1a and b). The same reconstruction was also observed for both 36- and 45-layer systems (see ESI†), and for all considered slab thicknesses, the surface energy was found to be 0.39 J m⁻².

Fig. 1 (a) Evolution of potential energy of cleaved α-SiO₂(001) surface at 600 K. (b) Top view on reconstructed α-SiO₂(001) surface generated from BOMD simulation of a unit cell. Here and for all other figures, red and blue circles are oxygen and silicon atoms, respectively.

The Bader charge analysis shows that atoms at the surface layers of the reconstructed and cleaved surfaces have a significant difference in the atomic charges. For the reconstructed surface, the average Bader changes for first-layer O and Si surface atoms are −1.60e and 3.20e, respectively, which are comparable to those (−1.62e and 3.23e) for the bulk α-SiO₂. In contrast, for the cleaved surface, the average Bader charges on surface O and Si atoms are −1.41e and 3.01e, respectively. This difference correlates well with that for the surface energies of cleaved surface and reconstructed surfaces.

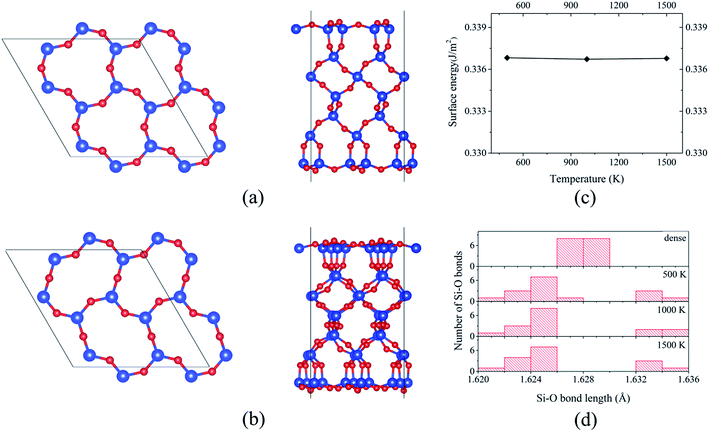
The formed 6-member ring has a triangle-like structure (named as “dense” surface, see Fig. 1b), which is the same as that reported based on MD simulations^11,12 and DFT calculations using the local density approximation.^13,14 Despite the previous studies, the possibility of the “dense” surface reconstruction is not well studied. To the best of our knowledge, only Rignanese et al.¹⁴ reported a first principles study of surface stability as a function of time, but that study was limited to a short MD simulation period of about 300–400 fs (which is believed to be too short for significant changes of the reconstruction). Other studies^11,12,22 used a classical MD to obtain the reconstructed surface, which is known to have limitations with describing SiO₂ properties.³⁷ Because of this, using “dense” prereconstructed 2 × 2 supercell slab (see Fig. 2a), BOMD simulations of 27-layer slab were performed. For all considered annealing temperatures (500, 1000, and 1500 K), the application of annealing/quenching temperature protocol leads to the transformation of 6-member triangle-like rings to 6-member ellipse-like rings (see Fig. 2a and b, the reconstruction is called as 2 × 2 reoptimized “dense” surface). This reconstruction is found to be similar to that reported based on classical MD simulations by Chen et al.²² This reconstruction reduces the surface energy from 0.39 to 0.34 J m⁻² for all considered temperatures, indicating that the annealing temperature does not affect the final energetics (see Fig. 2c). The transformation of 6-member ring induces the turning of the 3-member rings, resulting in atomic displacements at deeper atomic layers than those for the “dense” surface (see Fig. 2a and b). For instance, the analysis of Si–O bond length distributions for the central Si slab layer shows a significantly broadened distribution compared to that for the “dense” surface (see Fig. 2d). As illustration, for the “dense” 27-layer slab, Si atoms in central layer form two bonds of mostly identical bond lengths (about 1.628 Å; it should be noted that for the “dense” surface, the Si–O bond lengths formed by Si atoms within the central layers approaches to those for the bulk α-SiO₂ (1.625 and 1.628 Å) in 45-layer slab). For 2 × 2 reoptimized “dense” surface in 27-layer model, the Si–O bonds have bond lengths varying from 1.622 to 1.635 Å for all considered temperatures (see Fig. 2d). This broadening indicates the existence of indirect surface-surface interaction, which can be induced by overlapping of the atomic displacements. Because of this, it is rough to use the 27-layer model for the analysis of reconstruction at real α-SiO₂(001) surfaces. However, these results can be useful for the analysis of atomic structures of thin α-SiO₂(001) nanosheets.

Fig. 2 Top and lateral views on (a) prereconstructed (“dense” surface) 27-layer supercell slab and (b) 2 × 2 reoptimized “dense” slab. (c) Surface energy of 2 × 2 reoptimized “dense” 27-layer supercell slab as a function of annealing temperature. (d) Bond length distributions for the central layer of 27-layer supercell slab for “dense” and 2 × 2 reoptimized “dense” surfaces at different temperatures (500, 1000, and 1500 K).

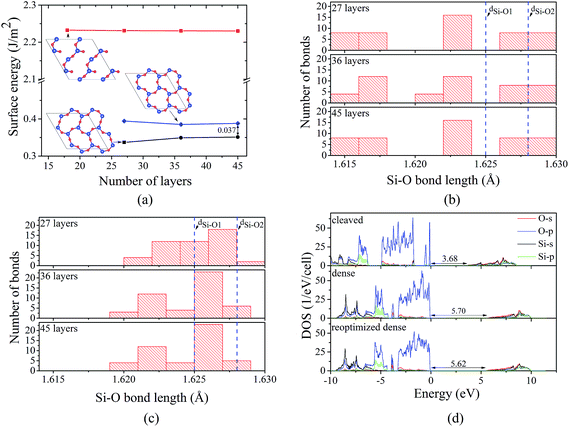
Application of annealing/quenching temperature protocol to 36- and 45-layer 2 × 2 supercell slabs leads to the transformation of 6-member triangle-like rings to 6-member ellipse-like rings for all considered temperatures (500, 1000, and 1500 K). The observed rings are structurally similar to those for the 27-layer model. Moreover, similar to the 27-layer model, the formation of the 6-member ellipse-like rings results in the turning of the 3-member rings and significant atomic displacements within at least 13 (for 45-layer model) atomic layers. Herewith, for the 45-layer model, the largest change of the Si–O bond length for the central layers are about 0.002 Å, indicating that the 45-layer slab can be used to represent the real α-SiO₂(001) surface. For both 36- and 45-layer supercell slabs, the surface energies were found to be 0.35 J m⁻², which are slightly larger compared to that for the 27-layer system (0.34 J m⁻²), but it is still about 0.04 J m⁻² lower than that for the “dense” surface (see Fig. 3a). The analysis of Si–O bond length distribution in 6-member rings for the “dense” and 2 × 2 reoptimized “dense” surfaces suggests that the reconstruction causes the reduction of the dispersion of the distribution (see Fig. 3b and c). As illustration, for the 6-member rings at the “dense” surface, the Si–O bond lengths vary from 1.616 to 1.629 Å, while for the 2 × 2 reoptimized “dense” surface, the variation is from 1.620 to 1.628 Å. Moreover, for 2 × 2 reoptimized “dense” surface, the number of Si–O bonds with bond lengths lying within those for bulk α-SiO₂ (1.625 and 1.628 Å) is found to be significantly larger compared to that for “dense” surface (see Fig. 3b and c). The ring transformation also induces the increase of the average nearest in-plane Si–Si distance (the average nearest in-plane O–O distance is not affected significantly by the transformation) by about 0.05 Å. Taking into account that the Bader charges for the surface atoms at the 2 × 2 reoptimized “dense” surface are the same as those for the “dense” surface (−1.60e and 3.20e for O and Si, respectively), the increase of Si–Si distance implies the reduction of repulsive electrostatic interaction between the ions. All these are the reasons why the 2 × 2 reoptimized “dense” surface has a smaller surface energy compared to that for the “dense” surface.

Fig. 3 (a) Computed surface energy as a function of the number of layers in the slab model for cleaved (red line), “dense” (blue line), and 2 × 2 reoptimized “dense” (black line) α-SiO₂(001) surfaces. (b) Computed Si–O bond length distribution for 6-member surface rings at “dense” surface. (c) Computed Si–O bond length distribution for 6-member surface rings at 2 × 2 reoptimized “dense” surface. Blue lines correspond to two Si–O bond lengths (d_Si–O1 = 1.625 and d_Si–O2 = 1.628 Å) in bulk α-SiO₂. (d) Density of states for cleaved, “dense”, and 2 × 2 reoptimized “dense” slabs. The Fermi level is set at VBM, and it refers to 0 eV.

Finally, electronic properties were calculated for the cleaved, “dense”, and the 2 × 2 reoptimized “dense” surfaces (all calculations were done for 45-layer slab supercells, see Fig. 3d). For the cleaved surface, the dangling bonds produce the occupied O-p states above the valence band maximum (VBM) of bulk α-SiO₂. These states reduce the band gap from 5.71 (for bulk) to 3.68 eV, which is consistent with the observation by Rignanese et al.¹⁴ In contrast, both “dense” and 2 × 2 reoptimized “dense” surfaces have a similar DOSs and do not provide O-p states above the VBM. The minor difference between the DOSs for the “dense” and 2 × 2 reoptimized “dense” surface comes from the difference in band gap (5.70 and 5.62 eV for “dense” and 2 × 2 reoptimized “dense” surface, respectively), indicating that the surface reconstruction can induce the minor reductions of the band gap (by 0.08 eV) due to the surface effects.

In summary, based on DFT calculations, a detailed analysis of possible reconstructions at α-SiO₂(001) surface was performed. It was found that the “dense” surface has a tendency to reconstruct; the 6-member triangle-like rings at the “dense” surface reconstruct to 6-member ellipse-like rings. This reconstruction is caused by the optimization of both Si–O bond length distribution and Si–Si interactions at the surface layer. The 2 × 2 reoptimized “dense” surface has the surface energy about 10% lower than the “dense” surface and atomic displacements for the top 13 surface atomic layers. The found lowest energy reconstruction can induce the minor change for the electronic properties (the reduction of band gap by about 0.08 eV).

Acknowledgements

This work was in part financially supported by the Research Council of Norway (project: 221469). We acknowledge access to HPC resources at NSC through SNIC/SNAC and at USIT through NORTUR.

References

1. V. Swamy, S. K. Saxena, B. Sundman and J. Zhang, J. Geophys. Res.: Solid Earth, 1994, 99, 11787–11794.
2. D.-M. Wang, Y.-M. Xu, D.-M. He, J. Guan and O.-M. Zhang, Asia-Pac. J. Chem. Eng., 2009, 4, 691–697.
3. N. I. Vakula, G. M. Kuramshina, L. G. Gorb, F. Hill and J. Leszczynski, Chem. Phys. Lett., 2013, 567, 27–33.
4. P. Labéguerie, M. Harb, I. Baraille and M. Rérat, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 045107.
5. N. Binggeli, N. Troullier, J. L. Martins and J. R. Chelikowsky, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 4771–4777.
6. L. Martin-Samos, G. Bussi, A. Ruini, E. Molinari and M. J. Caldas, Phys. Status Solidi B, 2011, 248, 1061–1066.
7. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
8. G. Roma, Y. Limoge and S. Baroni, Phys. Rev. Lett., 2001, 86, 4564–4567.
9. L. Martin-Samos, G. Roma, P. Rinke and Y. Limoge, Phys. Rev. Lett., 2010, 104, 075502.
10. W. L. Scopel, A. J. R. da Silva, W. Orellana and A. Fazzio, Appl. Phys. Lett., 2004, 84, 1492–1494.
11. T. P. M. Goumans, A. Wander, W. A. Brown and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2007, 9, 2146–2152.
12. M. V. Koudriachova, J. V. L. Beckers and S. W. de Leeuw, Comput. Mater. Sci., 2001, 20, 381–386.
13. G. M. Rignanese, J. C. Charlier and X. Gonze, Phys. Chem. Chem. Phys., 2004, 6, 1920–1925.
14. G. M. Rignanese, A. De Vita, J. C. Charlier, X. Gonze and R. Car, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 13250–13255.
15. F. Musso, P. Ugliengo, X. Solans-Monfort and M. Sodupe, J. Phys. Chem. C, 2010, 114, 16430–16438.
16. N. H. de Leeuw, F. M. Higgins and S. C. Parker, J. Phys. Chem. B, 1999, 103, 1270–1277.
17. N. Satoru, A. Nobushige, K. Kenji, S. Hiroji, S. Hideya and H. Kohji, Jpn. J. Appl. Phys., 1997, 36, 3081.
18. F. Bart and M. Gautier, Surf. Sci., 1994, 311, L671–L676.
19. W. Steurer, A. Apfolter, M. Koch, T. Sarlat, E. Søndergård, W. E. Ernst and B. Holst, Surf. Sci., 2007, 601, 4407–4411.
20. T. C. Nguyen, M. Otani and S. Okada, Phys. Rev. Lett., 2011, 106, 106801.
21. J. Lee, N. Lee, Y. Lansac and Y. H. Jang, R. Soc. Chem. Adv., 2014, 4, 37236–37243.
22. Y.-W. Chen, C. Cao and H.-P. Cheng, Appl. Phys. Lett., 2008, 93, 181911.
23. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
24. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
25. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
26. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
27. S. Nosé, Mol. Phys., 1984, 52, 255–268.
28. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
29. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
30. K. Teraishi, H. Takaba, A. Yamada, A. Endou, I. Gunji, A. Chatterjee, M. Kubo, A. Miyamoto, K. Nakamura and M. Kitajima, J. Chem. Phys., 1998, 109, 1495–1504.
31. S. Grabowsky, M. F. Hesse, C. Paulmann, P. Luger and J. Beckmann, Inorg. Chem., 2009, 48, 4384–4393.
32. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
33. A. L. Allred and E. G. Rochow, J. Inorg. Nucl. Chem., 1958, 5, 264–268.
34. A. Metsue and T. Tsuchiya, Phys. Chem. Miner., 2012, 39, 177–187.
35. N. Richard, S. Girard, L. Martin-Samos, V. Cuny, A. Boukenter, Y. Ouerdane and J. P. Meunier, J. Non-Cryst. Solids, 2011, 357, 1994–1999.
36. T. H. DiStefano and D. E. Eastman, Solid State Commun., 1971, 9, 2259–2261.
37. S. Munetoh, T. Motooka, K. Moriguchi and A. Shintani, Comput. Mater. Sci., 2007, 39, 334–339.

---

Footnote

† Electronic supplementary information (ESI) available: Computational details, structures, and calculations for 3 × 3 supercell (3 × 3 reoptimized “dense” surface). See DOI: 10.1039/c4ra10726h

---