Open Access Article
Open Access ArticleInspecting chiral molecules by Raman optical activity spectroscopy
Václav
Parchaňský
ab,
Josef
Kapitán
*c and
Petr
Bouř
*ab
aInstitute of Organic Chemistry and Biochemistry, Academy of Sciences, Flemingovo náměstí 2, 16610 Prague, Czech Republic. E-mail: bour@uochb.cas.cz
bDepartment of Analytical Chemistry, Institute of Chemical Technology, Technická 5, 16628 Prague, Czech Republic
cDepartment of Optics, Palacký University Olomouc, 17. listopadu 12, 77146 Olomouc, Czech Republic. E-mail: kapitan@optics.upol.cz
First published on 21st October 2014
Abstract
Raman optical activity (ROA) is a relatively new method combining the variability of scattering experiments with the structural sensitivity of chiral spectroscopy. Typically, ROA can be employed to determine absolute configuration (AC) of organic compounds, chiral metal complexes, and conformation of biologically relevant chiral molecules in solution. The present review covers the latest theoretical and experimental studies documenting the possibilities and limitations of the technique to probe molecular structure. The quantum-chemical apparatus necessary for spectral interpretation is introduced, and example applications provided, including recent data on possible extensions of the ROA spectroscopy to a more diverse systems.
I. Introduction
Molecular Raman optical activity (ROA), together with the other form of vibrational optical activity (VOA), vibrational circular dichroism (VCD), was developed in the early 1970s,1 in the hope that the vibrational region would provide more information about molecular structure than electronic spectra. Indeed, this goal has been achieved. The vibrational optical activity (VOA) revealed information on absolute configuration of compounds that could not have been obtained otherwise,2 and has been successfully applied to a broad range of organic and inorganic molecules, such as metal complexes3 and biologically-relevant systems,4 including whole virus particles.4d,5 Commercially, VCD has been available from about 1997, and ROA from 2003.Several fortuitous circumstances contributed to this development, such as the existence of suitable instrumentation (lasers, optical components, lock-in amplifiers), development of the light-scattering theory, computational techniques, and powerful computers allowing one to reliably interpret the experiment. The advantage of the vibrational spectral region consists of the availability of many bands exhibited by most molecules (up to 3N-6 of fundamental vibrations, where N is the number of atoms); these are usually much better resolved than for the electronic transitions. During a VOA experiment, typical molecule stays in its electronic ground state, which immensely facilitates quantum-chemical simulations of the spectra.
While VCD detects a difference in the absorption of left- and right circularly polarized light (L-, R-CPL), ROA measures a scattering difference between R- and L-CPL. The present review focuses on the latter technique, because it is still less common, more complex, and more variable in terms of instrumentation and applications. The aim is to provide the reader a guidance as to when is ROA relevant, and what kind of information about molecules can be extracted from the spectra.
II. Theoretical aspects
Theoretical considerations have always belonged to driving forces propelling the development of ROA spectroscopy. Additionally, quantum-chemical spectral simulations from the first principles provide the most accurate and universal way of interpreting the spectra. They interlink ROA (and Raman) band frequencies and intensities with molecular geometry, as described in detail in classical monographs by L. Nafie6 and L. Barron.7 Here, we summarize the most important points useful for perspective ROA users, and list contemporary theoretical procedures.To simulate Raman and ROA spectra, one needs to calculate vibrational frequencies and spectral intensities. In most cases, harmonic frequencies obtained by diagonalization of the Hessian, i.e., the matrix of energy second derivatives with respect to nuclear coordinates, are sufficient. The frequency computation is very efficiently implemented using the analytical gradient techniques8 available in a number of common software packages.9 When combined with the density functional theory (DFT), computations of sizable systems can be routinely performed. One should note, however, that the frequency estimation is in principle the most computer time and memory consuming part of the computations, although this very much depends on the implementation in the program code. For the Hartree–Fock and common DFT levels, the number of integrals needed to obtain the Hessian, i.e. the computational time, is in the worst possible case proportional to the fifth power of the number of atoms.10
In addition, because of its limited precision, the harmonic approximation may eventually become a bottleneck in such simulations. Fortunately, anharmonic corrections, including those based on analytical higher-energy11 and polarizability12 derivatives, are nowadays available as well. These are particularly needed for so-called anharmonic vibrations, such as C–H stretches vibrating at ∼3000 cm−1. So far, other errors than those stemming from the harmonic approximation, such as the solvent effects or functional inaccuracy appear to be more troublesome for typical ROA spectra measured within the spectral range of about 100–2000 cm−1.13
Several aspects of the intensity simulations are apparent from the general formula for the Stokes Raman/ROA spectrum originating from ith vibrational transition,14
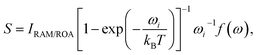 | (1) |
For a backscattering and scattered circular polarized (SCP) experiment,6,7
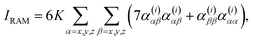 | (2) |
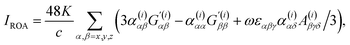 | (3) |
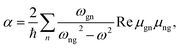 | (4) |
 | (5) |
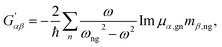 | (6) |
An important parameter is also the circular intensity difference, CID = IROA/IRAM, which can be directly compared to experiment. On the other hand, absolute intensities are very difficult to measure. For a typical sample, CID is as small as 10−4, which brings about many experimental difficulties, as outlined in the next section.
The polarizability derivatives are available via the response theory and analytical gradient techniques, much like the Hessian. These are normally computed using Cartesian derivatives,14,15 and a fully analytical implementation has appeared relatively recently.15b,16 Most of the modern ways of their computation are summarized in ref. 17. The direct summation over the electronic states (“SOS” method) is usually not practical for their enumeration, although the most recent studies on the magnetic circular dichroism18 suggest that SOS and time-dependent density functional theory (TD DFT) can be potentially useful in this context, as an alternative to the response (or “coupled-perturbed”) procedures. A third promising way of computing the molecular polarizabilities is represented by the time-dependent methods,19 although these are not readily available for everyday use, similarly as for SOS.
Clearly, when the laser light resonates with an electronic transition in the molecule (ωgn = ω), the formulae 4–6 are not usable. Proper theory for this case is explained in ref. 6. Sometimes the resonance may inhibit the measurement, e.g. due to sample decomposition or fluorescence masking the desired signal. In other cases, the resonant signal increase can make the measurement easier. The resonance or pre-resonance conditions are therefore currently being explored by one of the authors (J. K.) of the present review as a way of increasing ROA sensitivity.
Another extension of ROA theory is needed for inhomogeneous samples, in particular for the surface-enhanced ROA (SEROA). This technique has not matured yet, but SEROA is intensely investigated in several laboratories.20 It is based on the well-established surface-enhanced Raman scattering (SERS) or surface-enhanced resonance Raman scattering (SERRS), where the intensity of the scattered light increases by several orders (typically 108) when a molecule is in the vicinity of a noble metal surface, such as cupper, silver, or gold.21 If successful, SEROA on colloids or plates would thus combine the enormous sensitivity of SERS with the ability of ROA to better see details of system geometry. SERS/SERRS themselves are complicated phenomena; traditionally the enhancement is attributed to a combination of chemical, electromagnetic and plasmonic mechanisms.22 The key factor appears to be the local enhancement of electromagnetic field of the laser, e.g., in the contact region of two colloid particles (“hot spot”). Some studies suggest that ROA effects can be incorporated in the theory by adding the magnetic-dipole and electric-quadrupole components, e.g., via perturbation23 or matrix-based24 formalisms. In the matrix perturbation theory24 a generalized total polarizability Pt of the system (e.g., a colloid particle and the investigated molecule) containing all the polarizability contributions (eqn (4)–(6)) is obtained via matrix inversion as.
| Pt = P·(E − X·P)−1 | (7) |
The DFT computations of ROA intensities are available for fairly large molecules. However, because of the intrinsic scaling unfavourable to large systems, it is impractical and often even impossible to apply them directly to systems comprising hundreds of atoms. To overcome this limitation, we proposed the Cartesian coordinate tensor transfer (CCT);25 the force field and polarizability derivatives are computed for smaller fragments, and these “molecular property tensors” are then transferred back to the studied “big” system. The technique was extensively applied to VOA of biopolymers.26 Although one needs to be careful about its general applicability to ROA and to some compact chemical entities, such as peptide α-helices,27 we found it extremely convenient for extending the DFT simulations to proteins and other systems containing hundreds of atoms.
III. Experimental background
The experimental setup very much builds on the Raman technology. Let us recall that Raman scattering is a two photon process. The intensity of Raman scattering from a molecule is proportional to the irradiance of the excitation radiation and the differential Raman scattering cross-section of that molecule. The latter depends on the frequency of scattered radiation, scattering geometry, polarization of incident and scattered light, and molecular properties.28In laboratory conditions, the radiation is typically scattered from a small volume, and thus proportional to the concentration. The choice of the excitation frequency strongly affects the intensity and the signal to noise ratio (S/N). Raman intensity is proportional to the fourth power of the frequency, and Raman optical activity even to its fifth power. The additional frequency dependence of ROA enters through the optical activity tensor G′ (cf.eqn (3) and (6) above). Virtually all modern detectors in UV and VIS spectral range operate in a photon-counting mode, where the number of Raman and ROA scattered photons is third- and fourth-power dependent on the frequency, respectively.29
The choice of excitation wavelength is also important as unwanted signal from impurities should be minimized. Since their fluorescence is often by many orders of magnitude stronger than Raman scattering, mere noise associated with the fluorescence background can easily mask the desired signal. In practice, lasers emitting at 514 or 532 nm appear as a good compromise with respect to the intensity of Raman scattering and the signal from fluorescent impurities. Most modern ROA spectrometers use these wavelengths.6,30 However, ROA spectrometers operating at 785 nm were also constructed31 and an even wider choice is to be expected in the future.
The fluorescence problem can be avoided not only in the NIR (near infra-red) spectral region, but also by employing excitation wavelengths below ∼260 nm. For the latter, Raman and fluorescence signals become spectrally separated32 while the very high intensity of UV Raman scattering remains preserved. However, absorption and resonance effects have to be taken into account. There are also problems with availability and properties of the optical elements exposed to such high-energetic radiation. In UV, the Raman shift due to fundamental vibrations corresponds to few nm, whereas tens and hundreds of nanometers are available for visible and near-infrared measurements, respectively. Suppression of unwanted Rayleigh scattering from the sample is thus more difficult in UV. High quality UV edge filters are relatively expensive and their cut-off frequency is usually above 500 cm−1. Double or triple grating spectrographs have been successfully used in resonance Raman studies,33 but their application to UV ROA is not straightforward due to their detrimental effects to the detected signal.
Lasers are obviously ideal sources of radiation for Raman scattering. For ROA, their stability is of paramount importance. Today, high-quality diode-pumped solid-state lasers are readily available in VIS and NIR. This is clearly not the case in the UV range.
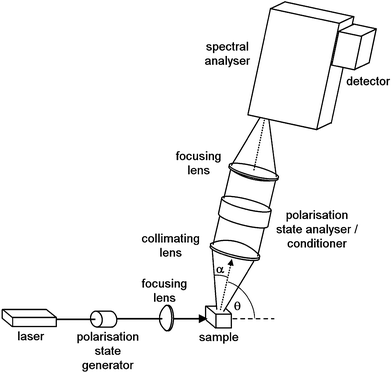
Scattering geometry, i.e., the angle between the incident and scattered radiation (θ in Fig. 1) is another critical experimental factor affecting the intensity and detectable S/N of Raman scattering and ROA. The right-angle scattering geometry is the easiest one to realize, and the first ROA spectra were obtained with it.1b,34 An ingenious double-lens collection optical system in the right angle scattering geometry was also developed.35 It was soon realized, however, that ROA is maximal in the back-scattering geometry. The ROA signal can then be increased by almost an order of magnitude,36 and the latest instruments predominantly use the back-scattering configuration.6
The forward-scattering geometry was thought to have the lowest ROA intensity. In fact, based on a simple two-group model it was predicted to be zero.7 Nevertheless, this scheme has been developed in W. Hug's group. The signal was smaller than in the backscattering geometry, but it still yielded a very interesting information about the studied systems.30b,37
From the optical design point of view, it is the right-angle scattering geometry which is optimal, since illuminated sample segment is parallel with the input plane of spectral analyzer, and its image can largely overlap and fill the elongated slit of a spectrograph. Sample volume can be kept small by using thin capillaries. Both collinear (back- and forward-) scattering geometries have to overcome problems arising from the fact that the illuminated sample segment is located along the optical axis and perpendicular to the spectrograph's input plane. A cross-section transformer has to be utilized so that the étendue of the optical system is conserved. Several solutions exist to this problem, such as precisely assembled bundles of multimode fibre optics.38
The ROA setups may also differ by so-called modulation scheme, i.e. a selection of the polarization states of the excitation and scattered radiation.6,39 The simplest and historically first was the incident circularity polarization (ICP) scheme. The sample is sequentially illuminated by right- and left-circularly polarized radiation, whereas the total scattered radiation is detected.1b,34 This scheme is still used in a few laboratories these days.31b,40 Nafie et al. developed so called in-phase and out-of-phase dual-circular polarization modulation schemes (DCPI, DCPII),39,41 where both the incident and scattered radiations are circularly polarized. Finally, in the scattered circular polarization (SCP) ROA scheme, the sample is irradiated by essentially unpolarized radiation, and the right- and left-circular component is detected in the scattered signal. The right- and left-circularly polarized components can thus be detected simultaneously.38 This is a great advantage over the other modulation schemes, as artefacts due to fluctuation in the laser power and sample absorption, otherwise causing a problematic flicker noise, can be reduced.
ROA measurement in all modulation schemes in the backscattering geometry was proposed38 and demonstrated.42 Reduced intensity of strongly polarized Raman bands in the DCP modulation schemes can be advantageous. Through a combination of several modulation schemes isolation of so-called optical invariants can be achieved.39
When applying the ROA spectroscopy, it is important to realize the possibility of “artifacts” in the recorded spectrum. Unfortunately, they may be encountered frequently; they are caused by residual stress in optical components such as sample cell walls or limited precision of polarization components. These false signals can be recognized by measuring both enantiomers of the studied molecules, and they can be identified by inspecting the sum of the two spectra. However, this method is not universal, since both enantiomers are rarely available. W. Hug discovered that it is possible to mimic the opposite enantiomer by purely optical means. He invented a very ingenious and effective way of automatic artifact elimination.43 This “virtual enantiomer” approach is described in detail in original literature and in excellent reviews.30,43 The virtual enantiomer approach was also developed for the ICP modulation scheme.40b None of such strategies eliminates the artifacts completely, but with careful utilization of the ROA spectrometer and sampling techniques, they can be reduced to acceptable levels.
ROA spectrometers were originally extremely sensitive to the alignment of optical and polarization elements, purity of the samples (which have to be fluorescence and dust free), and stability of laser power output.44 Fortunately, the above mentioned breakthroughs attributed to W. Hug38,43 somewhat changed the situation and opened up the possibility for commercialization of ROA spectrometers, which indeed happened in 2003.
IV. Examples of application
a. Absolute configuration of small molecules
For small molecules the ROA applications are often quite straightforward, as they are usually available in large amounts; concentrated solutions provide high-quality experimental spectra. At the same time, spectra can be simulated at a high level of approximation. In such case, ROA appears as one of the most reliable methods of determination of the absolute configuration (AC). The AC determination is a task important for the pharmaceutical industry, for example. Drug targets in living organisms may be chiral, and the AC is critical for biological activity and toxicity.Obviously, X-ray diffraction remains the standard for AC determinations. However, for everyday use, it is often too laborious. In addition, crystals of some compounds cannot be grown at all.
Although nuclear magnetic resonance (NMR) is nominally blind to chirality,45 complexes with standard chiral reagents may be routinely use for a chiral discrimination of compounds containing specific binding groups.46 AC studies using optical rotatory dispersion (ORD) and circular dichroism (CD) are also frequent and flexible in acceptable experimental conditions, but these methods provide only a limited number of spectral features, and their interpretation by computations is difficult.47 Finally, vibrational circular dichroism (VCD) should be mentioned here; it is comparable to ROA in reliability of AC determination48 but differs in some experimental and fundamental aspects.6
In a pioneering ROA study in 1993 by Polavarapu et al. successfully assigned AC of an organosulphuric compound, by comparing experimental and calculated spectra.49 As the technique remained confined to special laboratories, relatively few studies followed in the next decade.4h,50 A spectacular AC determination was published in 2007, where ROA distinguished enantiomers of chirally deuterated neopentane (Fig. 2).2a This feat was practically unachievable by any other analytical method.
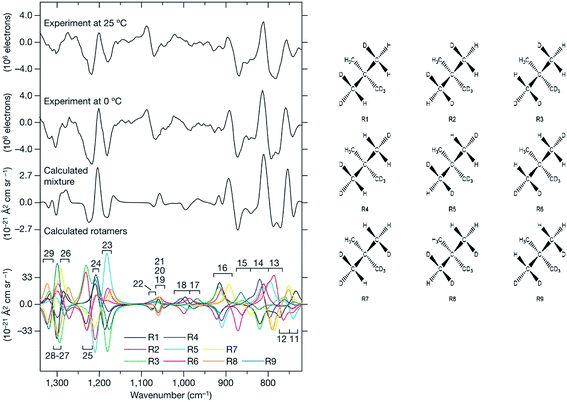 | ||
| Fig. 2 ROA spectra of (R)–[2H1, 2H2, 2H3]–neopentane measured at two temperatures, and a comparison with the simulations.2a The need to properly average all conformers94 (shown to the right) in the simulation is apparent. Reprinted from ref. 2a with permission from Macmillan Publishers Ltd: Nature Chemistry. | ||
An interesting ROA application appeared in a total synthesis: by comparison of the spectra of the original natural compound and its product the stereochemistry was verified.51 For the sake of reliability, it is obviously desirable to combine ROA with other spectroscopic methods, such as VCD.52 AC assignment and the reliability can be improved by a multivariate calibration.53 Even for smaller molecules, the interpretation based on computations may be significantly complicated by the need to consider multiple conformer equilibria, proper solvent model, and the dispersion interactions.52c,54
b. Chiral complexes
Chiral transition metal complexes posses certain specifics, which can be both favourable or inconvenient for ROA studies. For example, many of them strongly absorb the laser light, which can inhibit the measurement due to fluorescence or sample decomposition. On the other hand, resonance (between an electronic transition and impinging radiation) can enhance the ROA signal. This was found for a transition metal complex by Merten et al. in 2010.55 The observed enhanced CID ratio agreed with the theory. For other transition metal complex the spectrum was explained by an electronic–vibrational interaction involving two electronic states (Fig. 3).56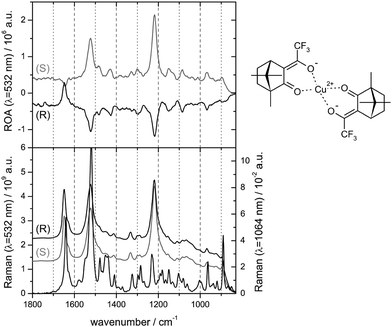 | ||
| Fig. 3 Pre-resonance experimental ROA (top) and Raman (bottom) spectra for two enantiomers of bis-(trifluoroacetylcamphorato) copper(II), measured with the excitation light of 532 nm; non-resonance Raman spectrum for 1064 nm excitation is added at the bottom.56 Note that the resonance often causes a nearly single-signed ROA signal. Redrawn from ref. 56, permission of the American Chemical Society. | ||
Complexes of alkali metals or alkali earth metals usually behave in the same way as most organic molecules. For a complex of the potassium ion with valinomycin, ROA revealed a new non-symmetric conformation, previously undetectable to NMR.57
In the past, we also observed so-called induced resonance ROA spectra in europium complexes with chiral alcohols or ketones. This effect may perhaps be more accurately referred to as a circularly polarized luminescence. The chiral component induces an ROA signal in the originally achiral complex, with participation of Eu electronic states. The signal is about 100× larger than for the organic molecule alone.58 This combination of the transfer of chirality and resonance is very promising for a sensitive chirality detection, at a timescale of minutes instead of hours or even days required in conventional ROA measurements. Currently, theoretical approaches are being developed in order to fully comprehend and predict this very effect.59
c. Peptides and proteins
Peptides and proteins are conveniently studied by ROA, as they are usually stable in the visible laser light and soluble in water. This was demonstrated already in 1990s by Barron et al., for both enantiomers of a dipeptide (L-Ala-L-Ala, D-Ala-D-Ala), and lysozyme and α-chymotrypsin proteins.60 Indeed, the dipeptide enantiomers provided nearly “mirror” images. ROA bands in the protein spectrum reflected differences in the secondary structure, and several bands were tentatively assigned.Reliable collection of the spectra and discovering their relation to the conformation stimulated many biomolecular applications. At the beginning, the interpretation of the spectra was somewhat hampered by limitations of the quantum-chemical simulation methods.61 Several empirical rules were thus proposed to aid spectral interpretation.62 Alternatively, a principle component analysis of 75 (mostly globular) proteins revealed specific ROA features, roughly assignable to their secondary and tertiary structure (Fig. 4).
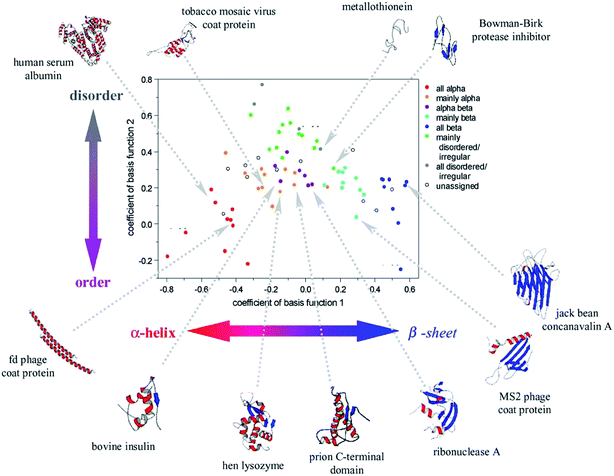 | ||
| Fig. 4 Coefficients obtained from a principal component analysis of ROA spectra of 75 proteins reveal the relation between their structure and spectral response. Reproduced with permission (Elsevier) from ref. 5d. | ||
Since then, experimental instrumentation and computational tools have undergone an extensive development.63 To list typical examples, ROA was employed to classify protein folding,64 dependence of polyproline folding on the peptide chain length,65 investigation of protonation of phosporylated proteins,66 and even analysis of the blood plasma.67 Several studies on shorter peptide model compounds enabled a more detailed spectral analysis based on extended computations.52c,54,68 By decomposing experimental ROA spectra into calculated spectra of individual conformers, whose populations were then converted to their relative energies, a large part of the two-dimensional potential energy surface (“Ramachandran plot”) could be constructed for the Ac-Ala-NHMe diamide (Fig. 5).68a
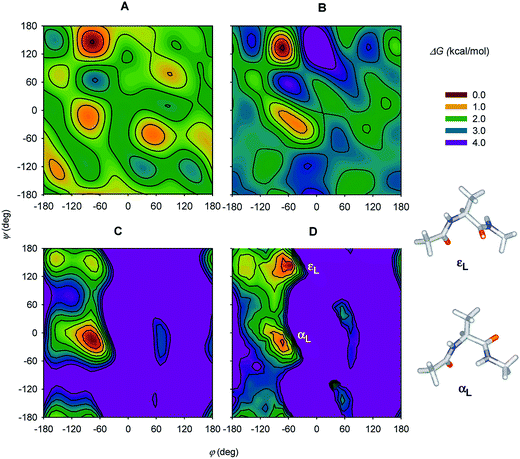 | ||
| Fig. 5 (A and B) Free-energy plots obtained by decomposing experimental Ac-Ala-NHMe ROA spectra obtained in H2O and D2O solutions, respectively, and (C) the molecular dynamics and (D) DFT theoretical free-energy surfaces. For D, the two lowest-energy conformers are indicated (εL and αL). Reprinted and adapted from ref. 68a, with permission of American Chemical Society. | ||
Theoretical spectral modeling also enabled detailed conformational studies of several larger systems.69 Indeed, ROA was proposed as suitable for an analysis of 310-helical peptides.70 For the valinomycine peptide, where the CCT transfer technique was used, populations of conformations “invisible” by NMR could be estimated.4j Remarkably, fully ab initio simulation of the β-domain of rat metallothionein protein provided ROA intensities well comparable with the experiment.4a The spectrum of the largest protein simulated using quantum chemical methodology so far, insulin, was obtained via the tensor transfer technique.4i
d. Saccharides and polysaccharides
Sugars and related compounds are important constituents of living organisms. They are also of interest because of their role in pharmaceutical, food and material industry. Typically, they do not possess a chromophore absorbing in a range accessible to commonly used electronic circular dichroism spectrometers (∼180–800 nm); VOA is thus the only way to study their chirality by optical spectroscopy.Extensive ROA studies have been conducted on monosaccharides,71 disaccharides,72 and polysaccharides71c including cyclodextrins73 and the glucosaminoglycan heparin.74 These observations led to identification of characteristic ROA bands for characteristic structural saccharides' features. In disaccharides and polysaccharides the ROA bands at ∼430 and ∼917 cm−1 are very sensitive to conformation, and were thus used for investigations of cyclodextrins.73
An empirical analysis of ROA spectra, as used e.g. to determine the structure of glycoproteins, is of limited reliability.75 Simulations from the first principles are thus highly desirable but enormously complicated by the saccharides' flexibility and their strong polar interactions with the environment. To determine a prevalent conformation of the sugar backbone or the OH groups, one has to take into account a large number of conformers. In a study on gluconate,76 molecular dynamics was used for the conformer sampling, and the spectra generation was speeded up by the Cartesian coordinate tensor transfer. A similar “multi-scale” (combined molecular mechanics/quantum mechanics) approach was used to simulate Raman and ROA spectra of methyl-β-D-glucose (Fig. 6).77 A simpler way is to compute the spectra for a selected conformer set, and carry out their Boltzmann weighting based on relative energies.78
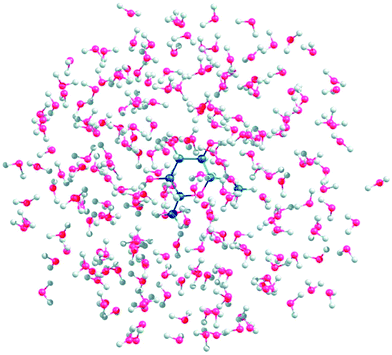 | ||
| Fig. 6 A snapshot of methyl-β-D-glucose gg conformer explicitly hydrated with 150 water molecules (reproduced from ref. 77, permission of American Chemical Society). Such multi-scale (i.e. combined molecular mechanics/quantum mechanics) simulations seem to be necessary to understand ROA spectra and other properties of sugars. | ||
ROA thus appears to be a promising technique to study secondary and tertiary structure not only of proteins69a but also polysaccharides.74,79 Its sensitivity to the tertiary structure is particularly appealing, and still rather unexplored. Perhaps the technique sensitively responds to changes in conformation and environment of the surface molecular parts. Lately, Johannessen et al. succeeded in analysing and interpreting the spectra of glycan and yeast external invertase,80 a system that would be very difficult to study by other techniques, such as X-ray diffraction or NMR. Complex matrices of biomolecules were studied on glycoproteins: the spectroscopy was found sensitive to entanglement-induced conformational changes in the oligosaccharide chains of mucin.81
e. Nucleic acids
One has to admit that nucleic acids are a difficult system to study by ROA, as they may decompose in the intense laser radiation, or exhibit solubility problems. Yet the first ROA study of single-stranded nucleotides in solution reported as early as 1997 (ref. 82) revealed many interesting spectral features for this class of compounds, and was followed by studies focusing on temperature-induced spectral changes of polynucleotides,83 DNA, and RNA.84 Notable spectral differences for individual DNA conformations were observed. Further spectroscopic investigations revealed new properties of polynucleotides, as related to their conformation and dynamics.85 The multi-level computational techniques, similar as for other systems, casted light on the link between the spectra and molecular structure, including the dynamical and environmental effects.86The measurement of virus particles represents an impressive chapter of ROA history. The first spectra of an intact virus were hampered by a limited resolution and high noise.87 Yet some spectral features could be identified, and advanced instrumentation soon yielded more complex studies.5b,5c,5e Oligonucleotide spectra revealed specific fingerprint patterns that could be assigned to the GNRA tetraloop, pyrimidine-rich asymmetric bulge and a base mismatch in ribosomal RNA of the encephalomyocarditis virus.88
f. Extensions of the technique
Although the above listed and other examples aim to document the benefits of the technique in molecular studies, one should be also aware of its limitations. The most serious one is the inherently low efficiency of Raman scattering as such, and then, on the top of it, the even smaller difference of the left- and right-circularly polarized scattered light (cf. CID). Many researchers including ourselves therefore experimented with various techniques leading to an enhanced signal, while often employing the resonance phenomena.The simplest option is probably the electronic resonance6 taking place when the energy corresponding to excitation frequency is equal to a difference of electronic energies. The ROA can be enhanced in an europium complex, providing low-lying electronic states.55 Simultaneous resonance involving two electronic states has been reported for a copper complex.56 A similar induced-resonance ROA was already mentioned above.59
Several laboratories perform ROA measurements with ultraviolet radiation (UV ROA), where the resonance is achieved “the other way”, by adjusting laser frequency to the molecular transitions, rather than looking for chromophores resonating with the light. Obviously, technical problems need to be overcome to enable a routine use of UV ROA, as most samples decompose in intense UV radiation.
As indicated in part II, Raman scattering can be significantly enhanced by placing the molecule of interest close to some materials, most often noble metals (Cu, Ag, Au). Enhancement factors between 104 and 1014, and even “single-molecule experiments” have been reported, although one has to be aware of the way the enhancement is estimated.89 This well-established modality was explored also in ROA experiments.90 Indeed, surface-enhanced ROA (SE ROA) may boost the intensities, and in some cases also CID. So far, however, SE ROA experimental data are scarce and not easily amendable to modelling.20 The key to the success seems to be proper conformational averaging providing an artefact-free experiment, and a controlled access of the investigated molecule to the metal surface, e.g. via a linker or coating.20c
Due to the low efficiency of Raman/ROA scattering the technique may not seem suitable for gas samples, where the concentration of the active compound is low by definition. While this may be generally true, we did measure ROA spectra in two special cases. For methyloxirane, the ROA spectrum was enhanced by the low (34 °C) boiling point, translating to a relatively high vapour pressure.91 The spectra could be reasonably well reproduced by computations including the rotational line broadening, and served as a benchmark for solvent models, anharmonic corrections, or coupled cluster methods.91,92
In paramagnetic NO2 molecule, Raman scattering at 532 nm was enhanced by a resonance with its electronic levels, and the chirality was induced by external magnetic field.93 This “paramagnetic” ROA was reasonably well reproduced by the angular momentum and time-dependent perturbation (Fermi golden rule) theories. In mixture of nitrogen oxides (“NOx”) we could show that the ROA technique can detect impurities in such gases.
V. Concluding remarks
By now, the ROA technique has matured in terms of instrumentation availability, and simulation and interpretation techniques. It can be recommended as a cheaper alternative to X-ray diffraction or nuclear magnetic resonance, while bearing in mind its specific drawbacks. Further development is certainly desirable, such as sensitivity improvement, and experimental noise reduction; higher accuracy and accounting of the fine effects (anharmonicity, resonances) in the simulated spectra have to be addressed as well. The examples shown in the present review demonstrate an enormous potential of the ROA technique, both in the classical field of biomolecular studies, and in new applications including heterogeneous and large-scale systems.Acknowledgements
This work was supported by the Czech Science Foundation (P208/11/0105, 13-03978S), Academy of Sciences (M200551205), and Ministry of Education (LH11033, 20/2014). We thank Dr Radek Pelc for the advice on the text.References
- (a) G. Holzwarth, E. C. Hsu, H. S. Mosher, T. R. Faulkner and A. Moscowitz, J. Am. Chem. Soc., 1974, 96, 251 CrossRef CAS; (b) L. D. Barron, M. P. Bogaard and A. D. Buckingham, J. Am. Chem. Soc., 1973, 95, 603 CrossRef CAS.
- (a) J. Haesler, I. Schindelholz, E. Riguet, C. G. Bochet and W. Hug, Nature, 2007, 446, 526 CrossRef CAS PubMed; (b) P. L. Polavarapu, Angew. Chem., Int. Ed., 2002, 41, 4544 CrossRef CAS.
- S. Luber and M. Reiher, Chem. Phys., 2008, 346, 212 CrossRef CAS PubMed.
- (a) S. Luber and M. Reiher, J. Phys. Chem. B, 2010, 114, 1057 CrossRef CAS PubMed; (b) E. Smyth, C. D. Syme, E. W. Blanch, L. Hecht, M. Vasak and L. D. Barron, Biopolymers, 2001, 58, 138 CrossRef CAS; (c) C. D. Syme, E. W. Blanch, C. Holt, R. Jakes, M. Goedert, L. Hecht and L. D. Barron, Eur. J. Biochem., 2002, 269, 148 CrossRef CAS; (d) E. W. Blanch, L. Hecht and L. D. Barron, Methods, 2003, 29, 196 CrossRef CAS; (e) I. H. McColl, E. W. Blanch, A. C. Gill, A. G. O. Rhie, M. A. Ritchie, L. Hecht, K. Nielsen and L. D. Barron, J. Am. Chem. Soc., 2003, 125, 10019 CrossRef CAS PubMed; (f) I. H. McColl, E. W. Blanch, L. Hecht, N. R. Kallenbach and L. D. Barron, J. Am. Chem. Soc., 2004, 126, 5076 CrossRef CAS PubMed; (g) E. W. Blanch, A. C. Gill, A. G. O. Rhie, J. Hope, L. Hecht, K. Nielsen and L. D. Barron, J. Mol. Biol., 2004, 343, 467 CrossRef CAS PubMed; (h) E. W. Blanch, L. Hecht, L. A. Day, D. M. Pederson and L. D. Barron, J. Am. Chem. Soc., 2001, 123, 4863 CrossRef CAS; (i) S. Yamamoto, J. Kaminský and P. Bouř, Anal. Chem., 2012, 84, 2440 CrossRef CAS PubMed; (j) S. Yamamoto, H. Watarai and P. Bouř, ChemPhysChem, 2011, 12, 1509 CrossRef CAS PubMed.
- (a) E. W. Blanch, A. F. Bell, L. Hecht, L. A. Day and L. D. Barron, J. Mol. Biol., 1999, 290, 1 CrossRef CAS PubMed; (b) E. W. Blanch, D. J. Robinson, L. Hecht and L. D. Barron, J. Gen. Virol., 2001, 82, 1499 CAS; (c) E. W. Blanch, L. Hecht, C. D. Syme, V. Volpetti, G. P. Lomonossoff, K. Nielsen and L. D. Barron, J. Gen. Virol., 2002, 83, 2593 CAS; (d) E. W. Blanch, I. H. McColl, L. Hecht, K. Nielsen and L. D. Barron, Vib. Spectrosc., 2004, 35, 87 CrossRef CAS PubMed; (e) E. W. Blanch, D. J. Robinson, L. Hecht, C. D. Syme, K. Nielsen and L. D. Barron, J. Gen. Virol., 2002, 83, 241 CAS.
- L. A. Nafie, Vibrational Optical Activity: Principles and Applications, Wiley-Blackwell, 2011 Search PubMed.
- L. D. Barron, Molecular Light Scattering and Optical Activity, Cambridge University Press, Cambridge, 2004 Search PubMed.
- (a) P. Pulay, in Modern electronic structure theory, ed. D. R. Yarkony, World Scientific, Singapore, 1995, pp. 1191–1240 Search PubMed; (b) Applications of electronic structure theory, ed. H. F. Schaefer III, Plenum Press, New York, 1977 Search PubMed; (c) P. Pulay, Mol. Phys., 1969, 17, 187 Search PubMed.
- (a) M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Gaussian, Inc., Wallingford CT, 2009 Search PubMed; (b) C. Angeli, K. L. Bak, V. Bakken, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, T. Enevoldsen, B. Fernandez, C. Haettig, K. Hald, A. Halkier, H. Heiberg, T. Helgaker, H. Hettema, H. J. A. Jensen, D. Jonsson, P. Joergensen, S. Kirpekar, W. Klopper, R. Kobayashi, H. Koch, O. B. Lutnaes, K. V. Mikkelsen, P. Norman, J. Olsen, M. J. Packer, T. B. Pedersen, Z. Rinkevicius, E. Rudberg, T. A. Ruden, K. Ruud, P. Salek, A. Sanchez de Meras, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. O. Sylvester-Hvid, P. R. Taylor, O. Vahtras, D. J. Wilson and H. Agren, Dalton, University of Oslo, Oslo, 2005–2009 Search PubMed; (c) R. Ahlrichs, M. Bar, H.-P. Baron, R. Bauernschmitt, S. Bocker, M. Ehrig, K. Eichkorn, S. Elliot, F. Furche, F. Haase, M. Haser, H. Horn, C. Huber, U. Huniar, M. Kattannek, C. Kolmel, M. Koolwitz, K. May, C. Ochsenfeld, H. Ohm, A. Schafer, U. Schneider, O. Treutler, M. von Arnim, F. Weigend, P. Weis and H. Weiss, Turbomole, University of Karlsruhe, Karlsruhe, 1998 Search PubMed.
- G. Scusseria, J. Phys. Chem. A, 1999, 103, 4782 CrossRef.
- M. Ringholm, D. Jonnsson, R. Bast, B. Gao, A. J. Thorvaldsen, U. Ekstrom, T. Helgaker and K. Ruud, J. Chem. Phys., 2014, 140, 034103 CrossRef PubMed.
- B. Gao, M. Ringholm, R. Bast, K. Ruud, A. J. Thorvaldsen and M. Jaszunski, J. Phys. Chem. A, 2014, 118, 748 CrossRef CAS PubMed.
- J. Hudecová, V. Profant, P. Novotná, V. Baumruk, M. Urbanová and P. Bouř, J. Chem. Theory Comput., 2013, 9, 3096 CrossRef.
- P. L. Polavarapu, Vibrational spectra: principles and applications with emphasis on optical activity, Elsevier, Amsterdam, 1998 Search PubMed.
- (a) P. Bouř, J. Comput. Chem., 2001, 22, 426 CrossRef; (b) K. Ruud, T. Helgaker and P. Bouř, J. Phys. Chem. A, 2002, 106, 7448 CrossRef CAS.
- V. Liegeois, K. Ruud and B. Champagne, J. Chem. Phys., 2007, 127, 204105 CrossRef PubMed.
- K. Ruud and J. Thorvaldsen, Chirality, 2009, 21, E54 CrossRef CAS PubMed.
- P. Štěpánek and P. Bouř, J. Comput. Chem., 2013, 34, 1531 CrossRef PubMed.
- A. Mohammed, H. Agren, M. Ringholm, A. J. Thorvaldsen and K. Ruud, Mol. Phys., 2012, 110, 2315 CrossRef CAS.
- (a) S. Abdali, J. Raman Spectrosc., 2006, 37, 1341 CrossRef CAS; (b) K. Osinska, M. Pecul and A. Kudelski, Chem. Phys. Lett., 2010, 496, 86 CrossRef CAS PubMed; (c) S. O. Pour, S. E. J. Bell and E. W. Blanch, Chem. Commun., 2011, 47, 4754 RSC.
- G. McNay, D. Eustace, W. E. Smith, K. Faulds and D. Graham, Appl. Spectrosc., 2011, 65, 825 CrossRef CAS PubMed.
- G. C. Schatz, M. A. Young and R. P. VanDuyne, in Surface-Enhanced Raman Scattering, ed. K. Kniepp, M. Moskovits and H. Kneipp, Springer, Germany, 2006, pp. 19–45 Search PubMed.
- B. G. Janesko and G. E. Scuseria, J. Chem. Phys., 2006, 125, 124704 CrossRef PubMed.
- (a) P. Bouř, J. Chem. Phys., 2007, 127, 136101 CrossRef PubMed; (b) V. Novák, J. Šebestík and P. Bouř, J. Chem. Theory Comput., 2012, 8, 1714 CrossRef.
- (a) P. Bouř, J. Sopková, L. Bednárová, P. Maloň and T. A. Keiderling, J. Comput. Chem., 1997, 18, 646 CrossRef; (b) S. Yamamoto, X. Li, K. Ruud and P. Bouř, J. Chem. Theory Comput., 2012, 8, 977 CrossRef CAS.
- (a) P. Bouř, J. Kubelka and T. A. Keiderling, Biopolymers, 2000, 53, 380 CrossRef; (b) P. Bouř and T. A. Keiderling, J. Mol. Struct.: THEOCHEM, 2004, 675, 95 CrossRef PubMed; (c) J. Kim, J. Kapitán, A. Lakhani, P. Bouř and T. A. Keiderling, Theor. Chem. Acc., 2008, 119, 81 CrossRef CAS PubMed; (d) V. Andrushchenko, H. Wieser and P. Bouř, J. Phys. Chem. B, 2002, 106, 12623 CrossRef CAS; (e) V. Andrushchenko and P. Bouř, J. Phys. Chem. A, 2007, 111, 9714 CrossRef CAS PubMed.
- N. S. Bieler, M. P. Haag, C. R. Jacob and M. Reiher, J. Chem. Theory Comput., 2011, 7, 1867 CrossRef CAS.
- D. A. Long, The Raman Effect: A Unified Treatment of the Theory of Raman Scattering by Molecules, Wiley-Blackwell, 2002 Search PubMed.
- R. L. McCreery, Raman Spectroscopy for Chemical Analysis, Wiley-Interscience, 2000 Search PubMed.
- (a) W. Hug, in Encyclopedia of Spectroscopy and Spectrometry, Academic Press, 2010, pp. 2387–2396 Search PubMed; (b) W. Hug, in Comprehensive Chiroptical Spectroscopy, ed. N. Berova, P. L. Polavarapu, K. Nakanishi and R. W. Woody, John Wiley & Sons, Inc., 2012, pp. 147–177 Search PubMed.
- (a) L. A. Nafie, Appl. Spectrosc., 2007, 61, 1103 CrossRef CAS PubMed; (b) M. Unno, T. Kikukawa, M. Kumauchi and N. Kamo, J. Phys. Chem. B, 2013, 117, 1321 CrossRef CAS PubMed.
- S. A. Oladepo, K. Xiong, Z. Hong, S. A. Asher, J. Handen and I. K. Lednev, Chem. Rev., 2012, 112, 2604 CrossRef CAS PubMed.
- (a) S. Bykov, I. Lednev, A. Ianoul, A. Mikhonin, C. Munro and S. A. Asher, Appl. Spectrosc., 2005, 59, 1541 CrossRef CAS PubMed; (b) S. V. Bykov, B. Sharma and S. A. Asher, Appl. Spectrosc., 2013, 67, 873 CrossRef CAS PubMed.
- W. Hug, S. Kint, G. F. Bailey and J. R. Scherer, J. Am. Chem. Soc., 1975, 97, 5589 CrossRef CAS.
- W. Hug, Appl. Spectrosc., 1981, 35, 115 CrossRef CAS.
- L. Hecht, L. D. Barron and W. Hug, Chem. Phys. Lett., 1989, 158, 341 CrossRef CAS.
- P. Oulevey, PhD Thesis, Departement für Chemie, University of Freiburg, 2011.
- W. Hug and G. Hangartner, J. Raman Spectrosc., 1999, 30, 841 CrossRef CAS.
- L. A. Nafie and D. Che, in Modern Nonlinear Optics, Part 3, 1994, pp. 106–149 Search PubMed.
- (a) J. Kapitán, V. Baumruk and P. Bouř, J. Am. Chem. Soc., 2006, 128, 2438 CrossRef PubMed; (b) S. Yamamoto and H. Watarai, J. Raman Spectrosc., 2010, 41, 1664 CrossRef.
- (a) L. A. Nafie, G.-S. Yu and T. B. Freedman, Vib. Spectrosc., 1995, 8, 231 CrossRef CAS; (b) M. Vargek, T. B. Freedman and L. A. Nafie, J. Raman Spectrosc., 1997, 28, 627 CrossRef CAS.
- H. Li and L. A. Nafie, J. Raman Spectrosc., 2012, 43, 89 CrossRef CAS.
- W. Hug, Appl. Spectrosc., 2003, 57, 1 CrossRef CAS.
- P. Bouř, V. Baumruk and J. Hanzlíková, Collect. Czech. Chem. Commun., 1997, 62, 1384 CrossRef.
- R. A. Harris and C. J. Jameson, J. Chem. Phys., 2006, 124, 096101 CrossRef CAS PubMed.
- (a) I. Ohtani, Y. Kusumi, Y. Kashman and H. Kakisawa, J. Am. Chem. Soc., 1991, 113, 4092 CrossRef CAS; (b) C. Tan, Y. Kobayashi and Y. Kishi, Angew. Chem., Int. Ed., 2000, 39, 4282 CrossRef CAS; (c) J. M. Seco, E. Quiñoá and R. Riguera, Chem. Rev., 2004, 104, 17 CrossRef CAS.
- D. M. McCann and P. J. Stephens, J. Org. Chem., 2006, 71, 6074 CrossRef CAS PubMed.
- (a) Y. He, W. Bo, R. K. Dukor and L. A. Nafie, Appl. Spectrosc., 2011, 65, 699 CrossRef CAS PubMed; (b) K. H. Hopmann, J. Šebestík, J. Novotná, W. Stensen, M. Urbanová, J. Svenson, J. S. Svendsen, P. Bouř and K. Ruud, J. Org. Chem., 2012, 77, 858 CrossRef CAS PubMed.
- P. L. Polavarapu, L. Hecht and L. D. Barron, J. Phys. Chem., 1993, 97, 1793 CrossRef CAS.
- J. Costante, L. Hecht, P. L. Polavarapu, A. Collet and L. D. Barron, Angew. Chem., Int. Ed., 1997, 36, 885 CrossRef CAS.
- M. A. Lovchik, G. Fráter, A. Goeke and W. Hug, Chem. Biodiversity, 2008, 5, 126 CAS.
- (a) P. L. Polavarapu, Chirality, 2008, 20, 664 CrossRef CAS PubMed; (b) M. Fedorovsky, H. Gerlach and W. Hug, Helv. Chim. Acta, 2009, 92, 1451 CrossRef CAS; (c) J. Hudecová, J. Horníček, M. Buděšínský, J. Šebestík, M. Šafařík, G. Zhang, T. A. Keiderling and P. Bouř, ChemPhysChem, 2012, 13, 2748 CrossRef PubMed.
- E. Debie, E. De Gussem, R. K. Dukor, W. Herrebout, L. A. Nafie and P. Bultinck, ChemPhysChem, 2011, 12, 1542 CrossRef CAS PubMed.
- X. Li, K. H. Hopmann, J. Hudecová, W. Stensen, J. Novotná, M. Urbanová, J. S. Svendsen, P. Bouř and K. Ruud, J. Phys. Chem. A, 2012, 116, 2554 CrossRef CAS PubMed.
- C. Merten, H. Li, X. Lu, A. Hartwig and L. A. Nafie, J. Raman Spectrosc., 2010, 41, 1563 CrossRef.
- C. Merten, H. Li and L. A. Nafie, J. Phys. Chem. A, 2012, 116, 7329 CrossRef CAS PubMed.
- S. Yamamoto, M. Straka, H. Watarai and P. Bouř, Phys. Chem. Chem. Phys., 2010, 12, 11021 RSC.
- S. Yamamoto and P. Bouř, Angew. Chem., Int. Ed., 2012, 51, 11058 CrossRef CAS PubMed.
- S. Yamamoto and P. Bouř, J. Comput. Chem., 2013, 34, 2152 CrossRef CAS PubMed.
- L. D. Barron, A. R. Gargaro and Z. Q. Wen, Chem. Commun., 1990, 1034 RSC.
- L. D. Barron, A. R. Gargaro, L. Hecht and P. L. Polavarapu, Spectrochim. Acta, Part A, 1991, 47, 1001 CrossRef.
- Z. Q. Wen, L. Hecht and L. D. Barron, Protein Sci., 1994, 3, 435 CrossRef CAS PubMed.
- (a) M. Pecul, Chirality, 2009, 21, E98 CrossRef CAS PubMed; (b) S. Yamamoto, Anal. Bioanal. Chem., 2012, 403, 2203 CrossRef CAS PubMed.
- M. Kinalwa, E. W. Blanch and A. J. Doig, Protein Sci., 2011, 20, 1668 CrossRef CAS PubMed.
- V. Profant, V. Baumruk, X. Li, M. Šafařík and P. Bouř, J. Phys. Chem. B, 2011, 115, 15079 CrossRef CAS PubMed.
- L. Ashton, C. Johannessen and R. Goodacre, Anal. Chem., 2011, 83, 7978 CrossRef CAS PubMed.
- M. Tatarkovič, Z. Fišar, J. Raboch, R. Jirák and V. Setnička, Chirality, 2012, 24, 951 CrossRef PubMed.
- (a) V. Parchaňský, J. Kapitán, J. Kaminský, J. Šebestík and P. Bouř, J. Phys. Chem. Lett., 2013, 4, 2763 CrossRef; (b) M. Quesada-Moreno, A. A. Márquez-García, J. R. Avilés-Moreno and J. J. López-González, Tetrahedron: Asymmetry, 2013, 24, 1537 CrossRef CAS PubMed; (c) M. M. Quesada-Moreno, J. R. Avilés-Moreno, A. A. Márquez-García, F. Partal-Ureña and J. J. López González, J. Mol. Struct., 2013, 1046, 136 CrossRef CAS PubMed; (d) K. Knapp, M. Gorecki, J. Frelek, R. Luboradzki, M. Hollosi, Z. Majer and E. Vass, Chirality, 2014, 26, 228 CrossRef CAS PubMed.
- (a) S. Yamamoto and H. Watarai, Chirality, 2012, 24, 97 CrossRef CAS PubMed; (b) S. Yamamoto, T. Furukawa, P. Bouř and Y. Ozaki, J. Phys. Chem. A, 2014, 118, 3655 CrossRef CAS PubMed; (c) B. Nieto-Ortega, J. M. Hierrezuelo, C. Carnero Ruiz, J. T. López Navarrete, J. Casado and F. J. Ramírez, J. Phys. Chem. Lett., 2013, 5, 8 CrossRef.
- C. R. Jacob, ChemPhysChem, 2011, 12, 3291 CrossRef CAS PubMed.
- (a) L. D. Barron, A. R. Gargaro and Z. Q. Wen, Carbohydr. Res., 1991, 210, 39 CrossRef CAS; (b) A. F. Bell, L. Hecht and L. D. Barron, J. Raman Spectrosc., 1993, 24, 633 CrossRef CAS; (c) A. F. Bell, L. Hecht and L. D. Barron, J. Raman Spectrosc., 1995, 26, 1071 Search PubMed; (d) Z. Q. Wen, L. D. Barron and L. Hecht, J. Am. Chem. Soc., 1993, 115, 285 CrossRef CAS.
- A. F. Bell, L. Hecht and L. D. Barron, J. Am. Chem. Soc., 1994, 116, 5155 CrossRef CAS.
- A. F. Bell, L. Hecht and L. D. Barron, Chem.–Eur. J., 1997, 3, 1292 Search PubMed.
- T. R. Rudd, R. Hussain, G. Siligardi and E. A. Yates, Chem. Commun., 2010, 46, 4124 RSC.
- F. Zhu, N. W. Isaacs, L. Hecht and L. D. Barron, J. Am. Chem. Soc., 2005, 127, 6142 CrossRef CAS PubMed.
- J. Kaminský, J. Kapitán, V. Baumruk, L. Bednárová and P. Bouř, J. Phys. Chem. A, 2009, 113, 3594 CrossRef PubMed.
- J. R. Cheeseman, M. S. Shaik, P. L. A. Popelier and E. W. Blanch, J. Am. Chem. Soc., 2011, 133, 4991 CrossRef CAS PubMed.
- S. Luber and M. Reiher, J. Phys. Chem. A, 2009, 113, 8268 CrossRef CAS PubMed.
- N. R. Yaffe, A. Almond and E. W. Blanch, J. Am. Chem. Soc., 2010, 132, 10654 CrossRef CAS PubMed.
- C. Johannessen, R. Pendrill, G. Widmalm, L. Hecht and L. D. Barron, Angew. Chem., Int. Ed., 2011, 50, 5349 CrossRef CAS PubMed.
- L. Ashton, P. D. Pudney, E. W. Blanch and G. E. Yakubov, Adv. Colloid Interface Sci., 2013, 199–200, 66 CrossRef CAS PubMed.
- A. F. Bell, L. Hecht and L. D. Barron, J. Am. Chem. Soc., 1997, 119, 6006 CrossRef CAS.
- A. F. Bell, L. Hecht and L. D. Barron, Biospectroscopy, 1998, 4, 107 CrossRef CAS.
- A. F. Bell, L. Hecht and L. D. Barron, J. Am. Chem. Soc., 1998, 120, 5820 CrossRef CAS.
- A. F. Bell, L. Hecht and L. D. Barron, J. Raman Spectrosc., 1999, 30, 651 CrossRef CAS.
- K. J. Jalkanen, V. Würtz Jürgensen, A. Claussen, A. Rahim, G. M. Jensen, R. C. Wade, F. Nardi, C. Jung, I. M. Degtyarenko, R. M. Nieminen, F. Herrmann, M. Knapp-Mohammady, T. A. Niehaus, K. Frimand and S. Suhai, Int. J. Quantum Chem., 2006, 106, 1160 CrossRef CAS.
- E. W. Blanch, A. F. Bell, L. Hecht, L. A. Day and L. D. Barron, J. Mol. Biol., 1999, 290, 1 CrossRef CAS PubMed.
- (a) A. J. Hobro, M. Rouhi, E. W. Blanch and G. L. Conn, Nucleic Acids Res., 2007, 35, 1169 CrossRef CAS PubMed; (b) A. J. Hobro, M. Rouhi, G. L. Conn and E. W. Blanch, Vib. Spectrosc., 2008, 48, 37 CrossRef CAS PubMed.
- (a) K. Kneipp, H. Kneipp, I. Itzkan, R. R. Dasar and M. S. Feld, Chem. Rev., 1999, 99, 2957 CrossRef CAS PubMed; (b) K. Kneipp, H. Kneipp, S. Abdali, R. W. Berg and H. Bohr, Spectroscopy, 2004, 18, 433 CrossRef CAS.
- Z. Q. Wen, X. Cao and A. Vance, J. Pharm. Sci., 2008, 97, 2228 CrossRef CAS PubMed.
- J. Šebestík and P. Bouř, J. Phys. Chem. Lett., 2011, 2, 498 CrossRef.
- T. D. Crawford and K. Ruud, ChemPhysChem, 2011, 12, 3442 CrossRef CAS PubMed.
- J. Šebestík and P. Bouř, Angew. Chem., Int. Ed., 2014, 53, 9236 CrossRef PubMed.
- W. Hug and J. Haesler, Int. J. Quantum Chem., 2005, 104, 695 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2014 |