Resonant detection of the signature of control of a resonance state lifetime using a pump–probe scheme
Abstract
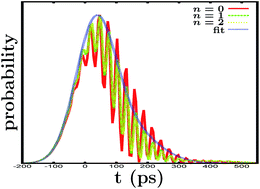
Realistic wave packet simulations demonstrate that the signature of control of the survival probability and lifetime of a specific resonance state can be observed and probed in typical time-resolved pump–probe experiments. The main condition required is the existence of a resonant state having enough oscillator strength and overlapping essentially only with the target resonance subject to control. By selecting different resonant states, the effects of control on the different specific target resonances can be probed.

 Please wait while we load your content...
Please wait while we load your content...