Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Action spectrum experiment for the measurement of incoherent photon upconversion efficiency under sun-like excitation†
Rowan W.
MacQueen
a,
Yuen Yap
Cheng
a,
Andrew N.
Danos
a,
Klaus
Lips
b and
Timothy W.
Schmidt
*a
aSchool of Chemistry, UNSW, Sydney, NSW 2052, Australia. E-mail: timothy.schmidt@unsw.edu.au
bHelmholtz-Zentrum Berlin für Materialien und Energie, Institut für Silizium-Photovoltaik, Kekuléstr. 5, 12489 Berlin, Germany
First published on 8th October 2014
Abstract
Photon upconversion (UC) processes result in the emission of photons at higher energies than those absorbed. Among the several recent novel applications of UC, the most widely studied is its use with photovoltaic (PV) cells. Photon UC can sensitize PV cells to portions of the solar spectrum at lower energy than the band gap, which are wasted in a normal single-junction cell, and so begins to address one of the major sources of PV cell efficiency loss. Developing a rigorous but practical method of quantifying upconversion efficiency is therefore an important objective. This task is complicated by the nonlinearity of upconversion efficiency at application-relevant light intensities, meaning the excitation conditions under which efficiency is measured must also be specified. A first-principles approach to determining upconversion efficiency, based on the quantum yields of the underlying photochemical processes, is rigorous in principle but difficult in practice. Absolute photometric measurements that treat the upconverter as a black box are similarly difficult, and measure optical losses alongside the photochemical performance. The widely-utilized relative actinometry method, based on comparisons to a known fluorescence standard, fails as a rigorous method without explicit consideration of the generation profile and reabsorption. In response to these issues, we report an upconverter action spectrum experiment, which is based on continuous-wave photoluminescence techniques. The experiment is used to determine the upconversion efficiency of a photochemical upconverter employing triplet–triplet annihilation (TTA). Full specification of the excitation conditions is made, allowing the efficiency measurement to be linked to well-defined solar excitation conditions. We measure the TTA–UC performance of the PQ4PdNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) rubrene system over a range of excitation conditions corresponding to 0.09–3.22 multiples of AM1.5G solar illumination. At 1 sun, we obtain a TTA yield of 1.1%.
rubrene system over a range of excitation conditions corresponding to 0.09–3.22 multiples of AM1.5G solar illumination. At 1 sun, we obtain a TTA yield of 1.1%.
Introduction
Incoherent photon upconversion (UC) is a process whereby a material absorbing uncorrelated photons of a given energy, re-emits photons at a higher energy. The process has generated considerable interest across a number of contemporary research fields, including photovoltaics (PV),1–3 water splitting,4 medical imaging,5in vivo drug activation,6 lighting,7 and displays.8 UC allows PV devices to harvest sub-band gap photons that are otherwise unusable;9 in medical applications, UC can locally generate wavelengths of light that cannot be effectively supplied from outside the body, and the anti-Stokes shifted emission is easily distinguishable from autofluorescence.10In all the applications of incoherent photon UC, but especially PV, the efficiency of the upconversion process is a key parameter. Normal Stokes-shifted fluorescence is a linear process, and the efficiency is represented by a single number, ΦPL. But all incoherent photon UC processes are non-linear, at least when unsaturated. Hence ΦUC, the quantum yield of photon UC, varies with excitation intensity, and can be meaningfully reported only alongside specification of the excitation conditions. Recording upconversion efficiency therefore entails the measurement of:
(1) ΦUC itself (or an analogue), and
(2) The excitation conditions under which the measurement was made.
In so-called relative actinometry measurements, the light output of an unknown material (the upconverter) is compared to a luminescent standard with known quantum yield, and the efficiency is inferred.11 Relative actinometry is a popular method of measuring UC performance. For example, in a recent review by Moth-Poulsen and coworkers of TTA–UC systems with reported efficiencies, it was the method used for 40 out of the 54 reported experiments.2
But central to the efficacy of relative actinometry must be a consideration of the generation profile – the distribution of photoexcited centers within the sample caused by propagation and attenuation of the excitation beam – and reabsorption. If no correction is made for differing generation profiles and reabsorption, relative actinometry can produce meaningful results only when the unknown and reference samples are excited with equivalent generation profiles, and both exhibit the same reabsorption behaviour.
These requirements alone make simple relative actinometry an uncertain prospect for accurately establishing upconversion efficiency. The non-linear response of upconverters at low light levels further compounds this. In a Stokes-shifted fluorescence sample, the distribution of photoexcited absorbers and the distribution of fluorescing sites both trivially match the generation profile of the excitation beam. But in an upconverting medium, the upconversion yield depends on the concentration of photoexcited centers. The distribution of sites emitting upconversion will therefore be a truncation of the generation profile, the extent of the truncation depending on the degree of nonlinearity – which itself is intensity-dependent. Given these compounding complications, the likelihood of an uncorrected measurement by relative actinometry yielding a meaningful upconversion quantum yield is low.
Further discussion of the problems associated with simple relative actinometry for upconversion can be found in the ESI.† But given the many pitfalls of the technique already propounded, we present a new and more rigorous photoluminescence method for quantifying upconverter performance.
The experiment reported herein generates excitation spectra of photon upconverters, which are then analysed to produce an accurate metric of UC efficiency. The experiment is performed by measuring the linear response of an upconverter to a low-intensity monochromatic modulated probe beam, while under excitation by a brighter continuous beam, which positively biases the upconverter efficiency. The generated spectra are supported by a comprehensive one-dimensional optical model, accounting for the generation profile of both excitation sources, the kinetic processes governing upconversion generation, and the reabsorption of emitted light.
The paper is arranged as follows: first, the experimental setup, measurement procedure, and concentration factor calculation are introduced. Then, an optical model for the action spectrum of an organic upconverter utilizing triplet–triplet annihilation (TTA) is derived, from which the upconversion efficiency is extracted. This is followed by the results from an action spectrum measurement of a previously-characterized TTA–UC system. Finally, we present a perspective of how this experiment can be applied to various upconversion experiments in the future.
Action spectrum experiment
Overview and setup
The action spectrum experiment is conceptually similar to a fluorescence excitation measurement, in that a low-intensity excitation beam is scanned in wavelength while a photoluminescence response at a fixed wavelength is measured. Here, the emission wavelength is within the upconversion band, and the excitation or ‘probe’ beam is scanned over all absorbing species to produce an excitation spectrum of the upconverter.The second-order nature of photon upconversion processes means that the response scales super-linearly with excitation intensity in the low-intensity regime.12–14 Thus a low-intensity beam produces essentially no upconversion. To counteract this, we illuminate the probed area with a second light source – the ‘bias’ – which is a broadband incoherent beam resonant with the upconverter, and much more intense than the probe. Lock-in amplification of the detector to the probe beam renders light generated by the bias beam undetected, so the bias affects the measurement only indirectly, by improving the response of the upconverter to the probe beam. As in the PV cell enhancement experiment reported by our group, this technique decouples the response measurement (linked to the probe) from the excitation conditions (determined by the bias), which greatly simplifies analysis.15
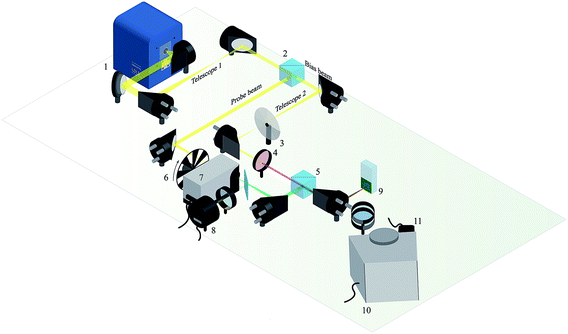
The experimental setup is shown in Fig. 1. Off-axis parabolic mirrors are used for all collimating and focusing optics throughout the setup, minimizing chromatic effects. The probe and bias beams of the action spectrum experiment originate in a high-brightness broadband incoherent light source (EQ1500, Energetiq). The output is collimated at 0.5 numerical aperture, passed through a telescope arrangement that halves the beam diameter, then split into the two beams by a polarising beam-splitter cube.
The transmitted beam constitutes the bias, which enters a second identical telescope, then passes through a variable neutral density filter wheel and a chromatic filter, producing a beam of variable brightness that is strongly absorbed by the upconverter in the low-energy (i.e. upconversion) wavelength range. The reflected beam forms the probe, which passes through a monochromator and chopper wheel. A low-reflectance beamsplitter positioned after the monochromator allows a reference silicon photodiode (918D-UV-OD3, Newport) to monitor the probe beam intensity, to track lamp stability.
The probe and bias beams are recombined in a second identical polarising beam splitter cube, forming a collinearly-propagating collimated beam pair. The diameter of the bias beam is half that of the probe. The two beams are focused onto the surface of the upconverter. The inverse relationship between beam diameter and spot size means the spot formed by the probe is wholly contained within that of the bias, an important condition of the two-beams method of biasing and probing. Upconverted emission from the photoexcited sample is collimated, then imaged into a second monochromator using a pair of lenses.
This detection monochromator passes a fixed narrow band, usually corresponding to the wavelengths of peak upconversion intensity, to a photomultiplier tube (PMT) attached to the monochromator output. The PMT produces current commensurate with the intensity of incident photons in the sub-saturation regime, which can be adjusted with the voltage applied across the PMT photodynodes. The PMT photocurrent is pre-amplified (Stanford Research Systems SR570) and read by a digital acquisition module, the output of which, in turn, is read by an in-house LabView routine. The amplified, digitized PMT signal is digitally phase-locked to the modulated probe beam frequency, thus rendering upconversion generated solely from the bias beam invisible to the measurement. During analysis, the phase-locked signal is normalised by the photon flux of the probe beam, correcting for the varying spectral intensity of the white light source.
Measurement procedure
Prior to the collection of an action spectrum, the following procedure is undertaken:(1) The detection wavelength λem is selected on the detection monochromator, usually by maximizing signal;
(2) Detector linearity is established by ensuring the maximum signal does not produce a saturated response from the PMT, the onset of which is checked using a calibrated detector with a known saturation threshold. The PMT sensitivity is adjusted as necessary; and
(3) The bias beam is long- or band-pass filtered to give resonant excitation in the upconverting region without flooding the PMT with scatter at the emission wavelength.
Then, an action spectrum is measured by scanning the probe beam over the entire absorption range of the upconverter, bracketing λem. Thus, upconversion processes are induced by excitation wavelengths λ > λem, and Stokes-shifted emission processes at wavelengths λ < λem. A series of spectra are collected for a range of bias intensities, allowing measurement of the upconverter performance under changing excitation conditions.
In order to normalize the phase-locked probe beam response, the reference photodiode with power meter (2936-C, Newport) is placed at the sample position after collection of the action spectra. The probe beam is scanned as per the action spectrum measurement while recording power, which is then converted to photon flux per wavelength increment. The power meter used in this work automatically compensates for the changing photodiode responsivity with wavelength using on-board calibration data.
The final additional measurements are those relating to the bias beam, described below. The excellent lamp stability means that the probe and bias beam measurements generally remain valid for as long as the experimental setup is unchanged. This allows a high throughput of samples, as the action spectra themselves are collected in a matter of minutes.
We quantify the excitation conditions provided by the bias beam by relating them to the effect of irradiation by the AM1.5G solar spectrum.16 Thus the efficiency values subsequently extracted from each action spectrum can be assigned accurate device-relevant excitation conditions. In a molecular system, we compare the excitation rates of the low-energy absorber under the bias (kΦb), and the AM1.5G spectrum (kΦe), yielding the solar concentration factor fc = kΦb/kΦe.
Calculating kΦ for a given excitation source is simple:
| kΦ = ∫ρ(λ)σ(λ)dλ, | (1) |
The bias spectrum is measured using a USB spectrometer (Ocean Optics HR4000), scattering the bias beam from a Spectralon slab. Bias beam power is determined in one of two ways: for bias spectra that are relatively narrow, such that the photodiode responsivity is flat across the spectrum, the power meter calibration wavelength is set to the flux-weighted central wavelength of the bias spectrum, and read off the power meter. For a broader bias spectrum, the obtained power reading is corrected by flux-weighting the responsivity then integrating over the bias spectrum, as per the responsivity correction procedure described by Rohwer and Martin.17 The bias spot size is determined by the following method: the spot is digitally photographed against a mask containing grid lines of known spacing. An in-house software procedure is used to flatten the image and crop around the spot at a known width, calibrated using the grid lines, and output a surface plot of the image intensity. The fringe of the spot corresponding to intensities <(2e)−1 of the brightest point are subtracted, then the remaining area is fit using a suitable model (e.g. an ellipse) to produce the spot size. The photograph is taken at low bias intensity to avoid saturation of the camera's sensor.
Model action spectrum: TTA–UC system
A comparison of gross height of the UC peak is sufficient to infer the relative UC efficiency of homologous samples measured under the same bias conditions (a larger UC peak implying commensurately more efficient UC). But, in order to obtain an absolute measure of the upconversion efficiency, modelling of the action spectrum is required. The key to modelling the action spectrum is consideration of the two modes available for exciting the same emitting center: through upconversion processes, and through direct photoexcitation. The latter then acts as a reference for the former, meaning the ratio becomes the quantity of interest that ultimately determines the UC efficiency. We expect the experiment to be compatible with any incoherent upconverter that can satisfy this condition of dual excitation modes.Our work thus far has concentrated on the investigation of organic upconverters harnessing triplet–triplet annihilation (TTA). These TTA–UC systems are currently the subject of intensive research efforts, and have made significant progress of late in fields such as solar cell enhancement and biological imaging.3,15,18,19
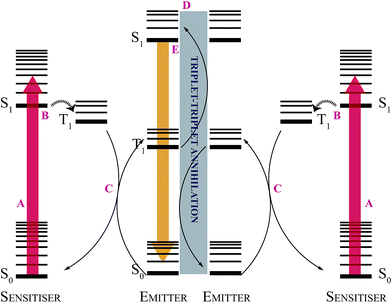
Standard TTA–UC systems consist of an organometallic triplet sensitizer, responsible for low-energy photon absorption, working in concert with a highly fluorescent emitter molecule, which accepts triplet excitations, undergoes TTA with other triplet-excited emitters, and produces a highly emissive singlet-excited state from which upconverted photons are generated. The general scheme for TTA–UC is presented in Fig. 2. In TTA–UC, the emitter S1 state can be produced via TTA, and also via photoexcitation of the emitter's S1 ← S0 transition, thereby satisfying the dual excitation condition.
The action spectrum is collected using front-face excitation and detection, with the collimating lens positioned at near-normal incidence to the illuminated spot. Relying on this near-symmetry, we use a one-dimensional model of the excitation and generation conditions within the upconverter to extract efficiency values from the spectrum. The TTA–UC model consists of two parts: emitter fluorescence generated through upconversion, and through direct photoexcitation. The full model derivation and the underlying assumptions can be found in the ESI;† key results are presented below.
Sensitizer photoexcitation
TTA–UC can be described using the following rate model for NT|z, the steady-state emitter triplet concentration at depth z: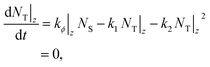 | (2) |
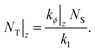 | (3) |
Hence NT, which directly affects the TTA rate, decreases with the attenuation of the excitation beam as it propagates into the sample, causing kΦ to drop. By accounting for the Beer–Lambert behaviour of the excitation beams, reabsorption of the emitter fluorescence, and the rate formulation of TTA–UC, then subtracting the contribution due solely to the unbiased probe beam, we arrive at a surprisingly simple expression for the upconversion intensity with respect to the probe beam:
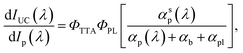 | (4) |
A similar treatment for direct excitation of the emitter is much simpler, owing to the linear response of the system and hence non-participation of the bias beam in the detected term. The following expression for probe beam response is obtained:
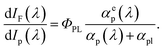 | (5) |
TTA–UC fitting function
Combining eqn (4) and (5) yields the following TTA–UC action spectrum fitting function: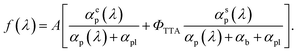 | (6) |
Of note is the fact that ΦPL has been subsumed into the scale factor A. Hence ΦTTA can be quantitatively determined without knowledge of the fluorescence quantum yield, a notoriously troublesome variable to determine accurately. The only assumption in combining eqn (4) and (5) is that the TTA and direct photoexcitation channels produce indistinguishable singlet-excited emitters. The formal upconversion quantum yield is given by ΦUC = ΦPLΦTTA/2, and can be produced from the action spectrum results with knowledge of the emitter fluorescence quantum yield. But the challenge in producing efficient TTA–UC systems lies almost entirely in boosting ΦTTA rather than ΦPL, since a large range of highly fluorescent emitters are readily available. Further, the ΦTTA term entirely shoulders the nonlinear characteristics of TTA–UC.
TTA–UC efficiency determined
The experiment
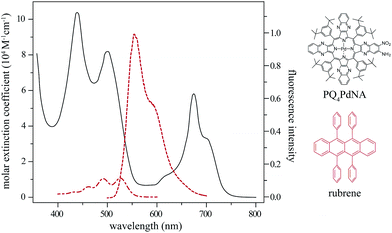
A TTA–UC system was prepared, consisting of the metalloporphyrin sensitiser PQ4PdNA (0.58 mM) and rubrene (11 mM) in toluene. The structures and relevant spectra of the two species are shown in Fig. 3. Solar cell figure of merit enhancements have been reported for this system,15 as have the TTA–UC kinetics of the closely-related PQ4Pd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) rubrene system.20,21 The toluene solution was de-aerated using three freeze–pump–thaw cycles, then permanently sealed within a 2 mm path-length quartz cuvette. Repeated measurements revealed no detectable degradation of the sample over the duration of the experiment.
rubrene system.20,21 The toluene solution was de-aerated using three freeze–pump–thaw cycles, then permanently sealed within a 2 mm path-length quartz cuvette. Repeated measurements revealed no detectable degradation of the sample over the duration of the experiment.
A 610 nm long-pass filter was added to the bias beam path, and the detector monochromator was set to 555 nm with a bandpass of approximately 5 nm. With the sample positioned at the focus of the collinear bias and probe beams, the PMT sensitivity was adjusted such that the PMT produced a large signal when the photoluminescence signal was greatest (full bias intensity, and direct photoexcitation of rubrene by the probe) without exceeding the linear response region. This ensured that the action spectrum was collected with a good signal-to-noise ratio while retaining comparability of the various spectral features (a photodetector with a high dynamic range is useful in this respect).
Two action spectra were then recorded over 400–780 nm, the full wavelength range of the sample: one with the maximum bias intensity, the other with the bias blocked. The bias-blocked spectrum was subtracted from the full bias spectrum over the upconversion range (600–780 nm), removing the unbiased probe contribution to the upconversion signal. The direct emitter photoexcitation range is largely insensitive to the bias, and yields much more intense photoluminescence; hence bias-blocked background subtraction is unnecessary there.
The PMT sensitivity was increased, and a series of 14 spectra were then recorded over the upconversion range, each at a different bias intensity. A background spectrum recorded with the bias blocked was subtracted from each. The use of increased PMT sensitivity in this range was possible since it was no longer necessary to maintain a linear response over the much more intense direct emitter photoexcitation range. Measurement of the upconversion performance under low-light conditions was thus made with an improved signal-to-noise ratio, compared to the same region of the spectrum collected as part of a full action spectrum. Mapping between this higher-sensitivity data series and the full range action spectrum using a constant of proportionality allowed for the determination of ΦTTA at all bias intensities used (0.09–3.22 suns).
Following collection of the action spectra, calibration measurements were carried out. The probe beam photon flux and bias beam solar concentration factor were found as per the procedures described earlier. All action spectra were flux-normalised, to account for the spectral intensity of the lamp. The background-corrected full-bias action spectrum was modeled using eqn (6), and the higher-sensitivity long-wavelength scans were scaled to the full bias, full-spectrum result.
Results and discussion
The two full-range action spectra are shown in Fig. 4A, and illustrate the importance of the bias beam to the measurement. The small feature in the red region corresponds to photoexcitation of the sensitiser, and the subsequent generation of upconverted emission by TTA–UC. This feature all but vanishes when the bias is blocked, demonstrating the nonlinear dependence of TTA–UC on excitation intensity and the necessity of biasing to produce well-resolved action spectra. By contrast, the larger feature toward the blue, corresponding to direct photoexcitation of the emitter and the production of prompt fluorescence, is much less sensitive to the bias intensity.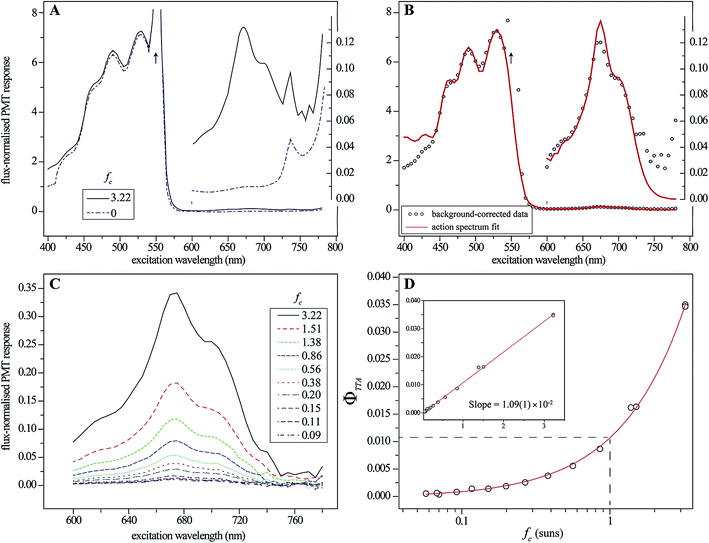 | ||
Fig. 4 Action spectrum results for the PQ4PdNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) rubrene system (detector monochromator set to 555 nm with a bandpass of approximately 5 nm). (A) Full action spectra for maximum and zero bias intensity, corresponding to concentration factors of 3.2 and zero, respectively. The arrow shows the location of the scatter peak, which was ignored during fitting. The inset shows the upconversion region scaled by 52 times on the same abscissa as the main plot; (B) fit of eqn (6) to the background-corrected full-bias spectrum, with the upconversion region similarly zoomed; (C) the upconversion region measured at higher sensitivity for a range of concentration factors; (D) ΦTTA values, extracted from the fit of eqn (6), plotted with respect to concentration factor. rubrene system (detector monochromator set to 555 nm with a bandpass of approximately 5 nm). (A) Full action spectra for maximum and zero bias intensity, corresponding to concentration factors of 3.2 and zero, respectively. The arrow shows the location of the scatter peak, which was ignored during fitting. The inset shows the upconversion region scaled by 52 times on the same abscissa as the main plot; (B) fit of eqn (6) to the background-corrected full-bias spectrum, with the upconversion region similarly zoomed; (C) the upconversion region measured at higher sensitivity for a range of concentration factors; (D) ΦTTA values, extracted from the fit of eqn (6), plotted with respect to concentration factor. | ||
This is true due to three mechanisms: the greater optical density of the emitter in the blue–green region (owing to the disparity in concentration), the difference in the quantum yields of prompt emitter fluorescence and upconversion, and the linear response of the prompt fluorescence. The small difference that is observed is due to absorption by the Soret band of PQ4PdNA, which adds to the upconversion channel through internal conversion and intersystem crossing to the T1 state.
The fit of eqn (6) to the background-corrected full-bias action spectrum is shown in Fig. 4B, the goodness of the fit indicating that the core photophysical processes of the TTA–UC system are well-represented. The fitting parameter ΦTTA comes from scaling the model in the upconversion region to match the measured response.
Fig. 4C shows action spectra of the upconversion region made at increased detector sensitivity for a range of bias intensities, corresponding to solar concentrations from 0.09 to 3.22 suns. The experiment demonstrably enables facile measurement of ΦTTA for this system at much less than one-sun illumination. To wit, Fig. 4D displays ΦTTA values as a function of solar concentration, obtained by scaling the data from Fig. 4C by the full-spectrum fit from Fig. 4B. The data is well-fit by a straight line, demonstrating the linear relationship between upconversion efficiency and intensity, and hence the quadratic scaling of generated upconversion, at low light intensity. A ΦTTA value of 1.09(1)% is determined for excitation at 1 sun intensity. Points on the plot in Fig. 4B can be used to estimate the upconversion yield by relative actinometry. The usual equation employed is
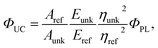 | (7) |
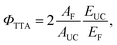 | (8) |
Naïve application of this equation to the relative photoluminescence generated at 675 nm and 530 nm in Fig. 4B yields ΦTTA = 0.111 at 3.22 suns, some three times the value obtained using the detailed model. Most of this difference is due to the experiment being performed on an optically dense sample. The incorporation of the absorbances in eqn (7) and (8) are only relevant to optically thin samples, where a substantial proportion of the input light is transmitted through the sample. In the present case, the probe beam is completely absorbed at both 675 nm and 530 nm, and so the sample absorbances of A675 = 34 and A530 = 113 can be ignored. Assuming complete absorption and ignoring subsequent reabsorption of photoluminescence, ΦTTA = 2EUC/EF yields 3.32%, which is much closer to the 3.51% calculated from the detailed model, which takes into consideration reabsorption. Indeed, the sample absorbance is 14 at the detection wavelength of 555 nm, which is somewhat less than those at 675 nm and 530 nm, and so much of the emitted photoluminescence will be detected in the front-face geometry. To apply eqn (7) with confidence would require an optical density approximately 10−3 lower than presently employed – a fluorescence cuvette of dimension 10 μm would be required.
Of note is the speed with which action spectra may be collected, particularly for coarse wavelength increments (5 nm in this work), the simplicity of the fitting function, and the ability to re-use calibration measurements across multiple trials (as long as the optical setup remains unchanged). Based on these positive attributes, the upconverter action spectrum technique should be a valuable tool for determining upconversion efficiency. Our development of the experiment thus far has focused on TTA–UC systems, but we anticipate that it will be generally applicable to all incoherent upconverter materials including rare earths.
Perspectives
The nonlinear response of upconversion efficiency to excitation intensity mandates particularly careful measurement of the upconversion performance. As described earlier, the use of relative actinometry as a ‘black box’ method of determining upconversion quantum yield is unlikely to yield trustworthy results.The action spectrum measurement expounded here is akin to a relative actinometry measurement in that the upconversion efficiency is measured by comparison to the fluorescence quantum yield of the TTA–UC emitter. But by using the same fluorescent molecule as the standard and the upconverter emitter, the fluorescence quantum yield cancels out in the evaluation, and the measurement becomes immune to substitution errors since no sample changing is necessary. Optical and kinetic modelling of the measured system account for differences in generation profile and reabsorption between the upconversion and prompt fluorescence pathways, and allow the extraction of ΦTTA, the key parameter underlying incoherent upconversion in organic materials. The model used in this work assumes the low-intensity regime, in which the intensity of upconverted emission scales quadratically with excitation intensity. The measured linear trend of ΦTTA with fc suggests that this assumption is sound for the range of bias intensities utilized.
In non-scattering solid TTA–UC materials, which often exhibit high optical densities, the present technique is equally valid as for solutions, since all optical characteristics of the material are taken into account. We also anticipate that the action spectrum experiment should be extensible to inorganic lanthanide-based upconverters, if sufficiently efficient materials can be developed. But a key assumption that underlies the relative simplicity of the TTA–UC action spectrum fitting function, eqn (6), must be noted. Currently we assume that the emitter fluorescence spectrum does not depend on excitation intensity, which is reasonable for fluorescent organic systems. But work by Fischer et al. shows that it is not the case with rare-earth upconverters, where features in the upconversion spectrum grow at different rates with respect to excitation conditions.22 This is due to the multiple pathways by which emitting states in the material are generated.22 Any optical model for the action spectrum of a lanthanide-based upconverter must take this into account.
Conclusion
The accurate determination of incoherent upconversion efficiency is an important part of the development of upconverters for energy, lighting and imaging applications. We have developed the upconverter action spectrum, an experimental technique combining the high throughput of relative actinometry methods with a detailed photochemical description of the upconverter, allowing the accurate determination of upconversion efficiency under well-quantified excitation conditions. Applied to a previously-reported TTA–UC system, we obtained a ΦTTA value of 1.09% at 1 sun. The action spectrum experiment allows for the high-throughput measurement and comparison of many upconverter samples, and should assist in the study and development of these emerging materials.Acknowledgements
This work was funded by the Australian Renewable Energy Agency (Project A-023), with contributions from The New South Wales Government and The University of Sydney. Aspects of the research were supported under Australian Research Council's Discovery Projects funding scheme (DP110103300). TWS acknowledges the Australian Research Council for a Future Fellowship (FT130100177). RWM acknowledges receipt of an Australian Postgraduate Award. KL is indebted to the Deutsche Forschungsgemeinschaft (DFG) for grant 583727 which initiated the German-Australian bilateral cooperation. We thank Dr Murad Tayebjee for his spot size measurement procedure and associated software.References
- J. de Wild, A. Meijerink, J. K. Rath, W. G. J. H. M. van Sark and R. E. I. Schropp, Energy Environ. Sci., 2011, 4, 4835–4848 CAS.
- V. Gray, D. Dzebo, M. Abrahamsson, B. Albinsson and K. Moth-Poulsen, Phys. Chem. Chem. Phys., 2014, 16, 10345–10352 RSC.
- T. F. Schulze and T. W. Schmidt, Energy Environ. Sci. Search PubMed in press.
- M. Zhang, Y. J. Lin, T. J. Mullen, W. F. Lin, L. D. Sun, C. H. Yan, T. E. Patten, D. W. Wang and G. Y. Liu, J. Phys. Chem. Lett., 2012, 3, 3188–3192 CrossRef CAS.
- C. Wohnhaas, V. Mailander, M. Droge, M. A. Filatov, D. Busko, Y. Avlasevich, S. Baluschev, T. Miteva, K. Landfester and A. Turshatov, Macromol. Biosci., 2013, 13, 1422–1430 CrossRef CAS PubMed.
- S. H. C. Askes, A. Bahreman and S. Bonnet, Angew. Chem., Int. Ed., 2014, 53, 1029–1033 CrossRef CAS PubMed.
- S. Sivakumar, F. C. J. M. van Veggel and M. Raudsepp, J. Am. Chem. Soc., 2005, 127, 12464–12465 CrossRef CAS PubMed.
- S. Baluschev, V. Yakutkin, T. Miteva, G. Wegner, T. Roberts, G. Nelles, A. Yasuda, S. Chernov, S. Aleshchenkov and A. Cheprakov, New J. Phys., 2008, 10, 013007 CrossRef.
- T. Trupke, A. Shalav, B. S. Richards, P. Würfel and M. A. Green, Sol. Energy Mater. Sol. Cells, 2006, 90, 3327–3338 CrossRef CAS PubMed.
- Q. Liu, T. S. Yang, W. Feng and F. Y. Li, J. Am. Chem. Soc., 2012, 134, 5390–5397 CrossRef CAS PubMed.
- T. N. Singh-Rachford and F. N. Castellano, J. Phys. Chem. Lett., 2010, 1, 195–200 CrossRef CAS.
- J. E. Auckett, Y. Cheng, T. Khoury, R. G. C. R. Clady, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, J. Phys.: Conf. Ser., 2009, 185, 012002 CrossRef.
- A. Haefele, J. Blumho, R. S. Khnayzer and F. N. Castellano, J. Phys. Chem. Lett., 2012, 3, 299–303 CrossRef CAS.
- A. Monguzzi, R. Tubino, S. Hoseinkhani, M. Campione and F. Meinardi, Phys. Chem. Chem. Phys., 2012, 14, 4322–4332 RSC.
- Y. Y. Cheng, B. Fuckel, R. W. MacQueen, T. Khoury, R. Clady, T. F. Schulze, N. J. Ekins-Daukes, M. J. Crossley, B. Stannowski, K. Lips and T. W. Schmidt, Energy Environ. Sci., 2012, 5, 6953–6959 CAS.
- T. F. Schulze, Y. Y. Cheng, B. Fueckel, R. W. MacQueen, A. Danos, N. J. L. K. Davis, M. J. Y. Tayebjee, T. Khoury, R. G. C. R. Clady, N. J. Ekins-Daukes, M. J. Crossley, B. Stannowski, K. Lips and T. W. Schmidt, Aust. J. Chem., 2012, 65, 480–485 CrossRef CAS.
- L. S. Rohwer and J. E. Martin, J. Lumin., 2005, 115, 77–90 CrossRef CAS PubMed.
- T. N. Singh-Rachford and F. N. Castellano, Coord. Chem. Rev., 2010, 254, 2560–2573 CrossRef CAS PubMed.
- J. H. Kim, F. Deng, F. N. Castellano and J. H. Kim, Chem. Mater., 2012, 24, 2250–2252 CrossRef CAS.
- Y. Y. Cheng, B. Fuckel, T. Khoury, R. Clady, M. J. Y. Tayebjee, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, J. Phys. Chem. Lett., 2010, 1, 1795–1799 CrossRef CAS.
- R. B. Piper, M. Yoshida, D. J. Farrell, T. Khoury, M. J. Crossley, T. W. Schmidt, S. A. Haque and N. J. Ekins-Daukes, RSC Adv., 2014, 4, 8059–8063 RSC.
- S. Fischer, J. C. Goldschmidt, P. Loper, G. H. Bauer, R. Bruggemann, K. Kramer, D. Biner, M. Hermle and S. W. Glunz, J. Appl. Phys., 2010, 108, 044912 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra08706b |
| This journal is © The Royal Society of Chemistry 2014 |