Monte Carlo simulation studies of cation selectivity in ion exchange of zeolites
Abstract
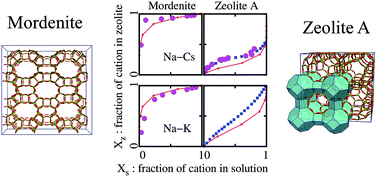
In order to evaluate the selectivity for specific cations in ion-exchange of zeolites, we calculate the ion-exchange isotherms in various zeolites using Monte Carlo simulation techniques. The calculation results agree well with experiments. Furthermore, we examine the dependence of the cation selectivity on the Si/Al ratio and find that the Cs selectivity initially increases with the Si/Al ratio but saturates above a certain value. These results reveal that the selectivity for Cs is enhanced cooperatively by the microporous structure and the Si/Al ratio of the zeolite framework. The present simulation scheme is promising in selecting useful materials for Cs decontamination in waste treatments.

 Please wait while we load your content...
Please wait while we load your content...