Processability, structural evolution and properties of melt processed biaxially stretched HDPE/MWCNT nanocomposites
Abstract
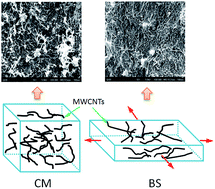
Biaxial stretching of melt mixed high density polyethylene (HDPE)/multiwalled carbon nanotube (MWCNT) nanocomposites was conducted in the melt state at different stretching ratios (SRs). The addition of MWCNTs leads to significant strain hardening in the HDPE, greatly improving the stability and thus processability of the stretching process. Scanning electron microscopy shows that the MWCNTs in the polymer matrix are gradually disentangled and randomly oriented in the stretching plane with increasing SRs. All the stretched samples exhibit an increase in crystallinity (about 10%) due to strain induced crystallization and a broadened distribution of crystallite size according to the XRD and DSC results. The mechanical properties of the composites improve with increasing SRs, while they drop off after a SR of 2.5 for the neat HDPE which is likely to be due to the relaxation of polymer chains prior to solidification. The presence of the MWCNTs appears to inhibit this relaxation thus helping to maintain the orientation and mechanical properties at high SRs. The modulus, yield strength and breaking strength of stretched composites with 8 wt% MWCNTs increase by approximately 54%, 85% and 193% respectively compared with the neat HDPE at a SR of 3. The electrical percolation threshold for the unstretched material occurs at 1.9 wt% MWCNTs. As SR increases, the values of critical concentration increase from 1.9 wt% to 4.9 wt% implying the destruction of conductive networks due to an increased inter-particle distance. A loading of 6 wt% MWCNTs is sufficient to ensure that the sheet conductivity is robust to changes in the SR. Decreased values of critical exponent from 1.9 to 1.1 and morphological investigation reveal a transformation of the system structure from three dimensional to two dimensional as SR increases.

 Please wait while we load your content...
Please wait while we load your content...