Theoretical study on molecular packing and electronic structure of bi-1,3,4-oxadiazole derivatives†
Abstract
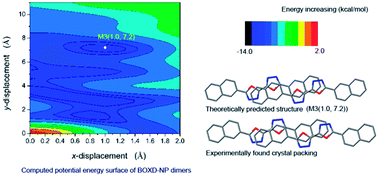
The molecular aggregation structure of 5,5′-bis(naphthalen-2-yl)-2,2′-bi(1,3,4-oxadiazole) (BOXD-NP) was studied by computing the intermolecular interaction potential energy surface (PES) at density functional theory level based on a dimer model. All B3LYP, CAM-B3LYP and M062x functionals can yield a reliable isolated molecular geometry. The conformation of BOXD-NP obtained with all methods is perfectly planar, indicating good conjugation ability between oxadiazole and naphthalene rings. The vibrational frequencies of BOXD-NP were also calculated using the B3LYP/6-311+G** method, which showed great consistency with the experimental observations and makes the assignments of the IR spectra more solid. It was revealed that the lowest excited state of BOXD-NP should be assigned as a highly allowed π–π* state by TD-DFT calculation. Considering the non-covalent interactions in molecular aggregates, the M062x functional was applied in the construction of the PES. Besides the packing structure found in the crystals, PES also predicted several stable structures, indicating that PES has great ability in guiding molecular self-assembly. Symmetry Adapted Perturbation Theory (SAPT) analysis on these energy-minimum molecular stacking structures revealed that London dispersion forces are the strongest attractive component in the binding.

 Please wait while we load your content...
Please wait while we load your content...