DOI:
10.1039/C4RA05409A
(Paper)
RSC Adv., 2014,
4, 45275-45285
Nucleation of charged droplets; an ion-atmosphere model
Received
6th June 2014
, Accepted 8th September 2014
First published on 8th September 2014
Abstract
We have explored the nucleation of charged droplets within the framework of Debye–Hückel ion-atmosphere model. In view of this the nucleation potential energy barrier has been appropriately modified. The Zeldovich–Becker–Döring–Frenkel theory (ZBDFT) and Boundary Layer Theory (BLT) have been exploited to understand the role of droplet charge on the steady state and transient nucleation rates. The time lag associated with the attainment of steady state cluster size distribution and the transient cluster flux have been analyzed in detail. The role played by the critical cluster size and the charge content of the droplets in modulating the transient nucleation rate have been explored. Also, a subtle analysis of the time lag has revealed the importance of diffusion of sub-critical clusters to attain the steady state. As interesting observations we have found complete confinement of droplet charge inside the inner region which is in close proximity with critical cluster size and sudden surge in nucleation rate as the droplet charge surpasses a threshold value. We demonstrate the enhancement of transient nucleation rate involving the charged droplets in comparison with their uncharged counterparts which runs in conformity with the earlier observations. The present work also highlights potential importance in the field of atmospheric physics research where the charged droplets are found as inalienable components.
I. Introduction
Nucleation is the commencement of a process that leads to the formation of a new phase from the metastable parent phase.1 The distinct domains of the new phase are created amidst the parent phase. It is a highly non-linear process with respect to the chemical driving force and occurs at nanoscale level where molecules attach and detach from the new phase clusters in a random way.2–4 The most common examples of metastable states are supersaturated vapor and supercooled liquids which are thermodynamically stable against small perturbations. However, in many important nucleation environments the nucleating droplets or clusters are found to be at a finite electric potential. This may be due to either the presence of electrons and ions in the gas phase or to the thermal ionization or photoionization of droplets. This potential modulates the physical properties of the vapor-droplet medium in numerous ways and modifies classical nucleation theory in a non-trivial way.
Researches on nucleation of charged droplets are going unabated nowadays because of its potential importance so far as understanding the atmospheric physics is concerned.5–12 Atmospheric nucleation also sheds light on various natural processes such as generation of cloud droplets, aerosol pollutants (e.g. acid rain), or the formation of tropospheric aerosol propelled by cosmic radiation,6 or by certain ion driven processes.13 A considerable proportion of total number of particles present in atmosphere is formed originally by nucleation from gas phase. Nucleation can be noticed in several places of atmosphere, e.g. in boundary layers in troposphere, in remote locations of coastal areas, in boreal forests14 as well as urban areas and pollution plumes. As a result of tremendous improvement in the instrumentation to observe and characterize nucleation process in last two decades,15 numerous observations on nucleation phenomenon have been made that include quantification of nucleation rate,16 characterization of growth processes and fast chemical characterization of newly formed particles. It is now quite well-known that free ions always exist in the atmosphere and they may be formed by radioactive emanations, lightning, corona discharge, combustion etc. These free ions, as soon as come into contact with water vapor, spontaneous formation of first critical nucleus takes place. The nucleus can grow further in two ways, either by subsequent fluctuational addition of water molecules, or by nuclei collision and coalescence processes.17 In absence of suitable nuclei, water particles may nucleate from water vapors directly. This is homogeneous nucleation (HON) and occurs when the saturation ratios are extremely high ( ), where pH2O is the partial pressure of water and p0(T) is equilibrium vapor pressure over a flat surface of a condensed phase at temperature T.18 Moreover, the primary ions formed initially in the atmosphere may rapidly react with common air ingredients to produce a series of increasingly stable terminal ions such as HSO4−. Depending on the availability of certain vapors such as H2SO4, H2O, NH3 and numerous other organic species, the core terminal ions quickly collect ligands and form a continuous distribution of charged clusters. Once a ligand vapor gets overwhelmingly supersaturated with respect to its condensed phase, a considerable fraction of ion clusters can undergo nucleation and we envisage a proliferation of ultrafine particles.19 The condensing vapor may exhibit dipole nature and thus gets electrostatically attracted to charged particles.20 It needs to be mentioned that there are also some important quantum chemical calculations that deal with role of amine and ammonia in ion-induced H2SO4–H2O nucleation in atmosphere.21,22
), where pH2O is the partial pressure of water and p0(T) is equilibrium vapor pressure over a flat surface of a condensed phase at temperature T.18 Moreover, the primary ions formed initially in the atmosphere may rapidly react with common air ingredients to produce a series of increasingly stable terminal ions such as HSO4−. Depending on the availability of certain vapors such as H2SO4, H2O, NH3 and numerous other organic species, the core terminal ions quickly collect ligands and form a continuous distribution of charged clusters. Once a ligand vapor gets overwhelmingly supersaturated with respect to its condensed phase, a considerable fraction of ion clusters can undergo nucleation and we envisage a proliferation of ultrafine particles.19 The condensing vapor may exhibit dipole nature and thus gets electrostatically attracted to charged particles.20 It needs to be mentioned that there are also some important quantum chemical calculations that deal with role of amine and ammonia in ion-induced H2SO4–H2O nucleation in atmosphere.21,22
In addition to this, charged droplets can also be generated in the atmosphere as a result of transfer of space charge concentrations formed at the cloud top (because of flow of current density between ionosphere and surface) to these droplets. Many of these droplets may evaporate at cloud–air interface. This charge remains attached to the residual evaporation nuclei which mingle quite well with more droplets in many types of clouds.23,24 Furthermore, since, in the atmosphere, there is a continuous production of ions by galactic cosmic rays, the nucleation of charged droplets could serve as a link between cosmic radiation and global cloud cover.25 In their important works Yu and Turco,6 and Andreae et al.26 have illustrated that background ionization can play an important role in generation and evolution of ultrafine particles in marine boundary layer. These tropospheric aerosols influence the earth's radiation budget directly by serving as cloud condensation center, thereby affecting the optical properties and lifetimes of clouds. It has been also found that electrical forces play prominent role in the initial stages of aerosol formation especially for very small cluster sizes under a variety of conditions. A thorough analysis of atmospheric aerosol nucleation process comes out to be highly important since the freshly formed particles directly influence the number density and size distribution of atmospheric aerosols and affect earth's atmosphere.27–29
Charges and charge induced processes have frequently been reported to enhance nucleation30 by enhancing activation probability and also growth rates of droplets20 in comparison with the neutral clusters. Thus, the charged clusters can preferentially accomplish stable, observables dimensions.19 The charge assists to stabilize the cluster as the electrostatic interaction impedes the cluster molecules from evaporating off the cluster as readily as in the neutral case.27 The electrostatic increment in the kinetics of vapor condensation onto charged clusters appears as the key factor in the formation of new condensation nuclei.31,32 The nucleation barrier thus gets considerably lowered and critical cluster becomes smaller in size. Neutral clusters, on the other hand, in general fail to surpass a critical size because of their low stability and slow growth rate. In fact, the reason behind the large amount of time required to assemble a neutral critical embryo in comparison with that of a charged embryo has been explained by Yu and Turco.19 There are also some notable works that give enough evidence of acceleration of nucleation rate because of charging.33 Shchekin et al. investigated the work of droplet formation on a charged condensation nucleus exposed to an external electric field.34 Warshavsky et al. investigated the influence of external field on thermodynamic characteristics and shape of dielectric liquid droplet.35 Gamero-Castaño and Fernández de la Mora, have presented a detailed account of enhancement of nucleation rate because of charge on the basis of critical supersaturation ratio between charged condensation embryos and vapor molecules.36 In the ongoing discussion the fundamental works on the thermodynamics and kinetics of condensation on charged particles, such as the pioneering work by Russell37 and fundamental series of papers by Kuni and co-workers38–42 deserve proper mention.
Above discussion amply reveals the importance of studying the nuances of nucleation kinetics of charged droplets. The focus of the present work is the determination of cluster size distribution [f(g, t)] for nucleation using boundary layer theory (BLT).43 Based on a Debye–Hückel ion-cloud model (DHICM) under realistic initial and boundary conditions with special attention to transient nucleation kinetics and time lag, we have addressed the problem of nucleation of charged particles. In order to make the present investigation a self-contained one, we have exploited both Zeldovich–Becker–Döring–Frenkel Theory (ZBDFT)44,45 and BLT to analyze the steady state and transient nucleation kinetics, respectively. Exploiting BLT for atmospheric nucleation one could have a vivid picture of the complexity of the process. BLT also helps us study in more detail the inner region in the vicinity of critical cluster size where the droplet charge is solely confined. Moreover, the time-lag and the dependence of the kinetics on the cluster size and charge content can also be well explored.
It goes without saying that the robustness of our theoretical derivations and importance of new findings can only be judged on comparison with realistic case study. In view of this we have gone through some important works on H2O unary nucleation and H2SO4–H2O binary nucleation.46–50 Apart from these binary homogeneous nucleation (BHN) of H2SO4 and H2O is the cornerstone of nucleation mechanism involving additional species such as NH3, ions and organic compounds that may have recognizable signature on atmospheric nucleation under certain conditions. In fact, the atmospheric ions undergo strong dipole–charge interactions with dipolar precursors (H2SO4, H2O, NH3) and assist to surmount the potential barrier that leads to a substantial enhancement of nucleation rate.50–52 In their important works Yu has substituted BHN by quasi unary nucleation (QUN) process that includes H2SO4 at equilibrium with H2O vapor. The predicted nucleation rate based on extended QUN model has been found to agree well with experimental data with some uncertainty.50,53 The studies are really important in the field of atmospheric research since in atmosphere neutral H2SO4–H2O clusters are continuously formed by recombination or neutralization of charged clusters. A prudent use of evaporation process of neutral H2SO4–H2O clusters can predict ion-mediated nucleation rates.54 However, it will be an entirely new investigation to apply BLT to such unary and binary nucleation problems and needs fresh investigation.
II. The model and the theoretical scheme
A. Transient kinetics of nucleation of charged droplets: the DHICM framework
The DHICM framework is a well-known model belonging to electrochemistry. It deals with distribution of ions in an electrolyte solution mostly based on electrostatic interactions.55 Here we consider a sea of charged vapor molecules (CVM). A single CVM is arbitrarily selected out of the assembly and called a reference CVM or central CVM. The remaining CVMs are looked upon as a continuous dielectric medium. The remaining CVMs lapse into anonymity, their charges being smeared out into a continuous spatial distribution of charge. The total charge in the atmosphere must be of opposite sign and exactly equal to the charge on the reference CVM. Thus, the sea of CVMs comprises of a central CVM standing alone in a continuum and the continuum acquires a dielectric constant (same as that of bulk vapor phase). The charge in the neighborhood of central CVM gradually smoothes out and contributes to the dielectric a net charge density (ρ).
In the present framework we do not consider heterogeneous condensation of neutral (non-charged) vapor molecules on an ensemble of charged nucleating centers (which is a classical statement of problem on the heterogeneous condensation on charged centers) uniformly distributed within the vapor phase (consisting of neutral vapor molecules). We actually consider the homogeneous condensation of charged vapor molecules of which one is selected to be a central CVM due to regular electrostatic attraction. The application of expressions from the classical nucleation theory (including the kinetic equation and an expression for its steady-state solution) has no conflict with our model. The potential for the nucleation process [cf. eqn (13)] is a consequence of classical nucleation theory considering nucleation as a fluctuational process.44 The DHICM model simply modifies the potential [cf. eqn (14)] by adding an extra term that accounts for the electrostatic interaction (Δϕadd).
1. Basic equations. Let's now make a brief discussion on the basic equations of classical nucleation theory (CNT) that describe the nucleation phenomenon.56,57 These equations could be derived based on Zeldovich–Becker–Dösring–Frenkel theory (ZBDFT). The subsequent discussion is relevant in order to develop appropriate perspective for the application of BLT in the present problem. It is assumed that the clusters do not interact and coalescence of large nuclei is neglected. Then, from a Markovian approach (no memory effects) the relaxation of the metastable parent phase to a stable one is described by a continuous cluster size distribution function f(g, t), where g represents the cluster size. From f(g, t) other characteristics of the nucleating system (e.g. nucleation rate, integrated flux, time lag etc.) can be determined. The time-evolution of this distribution, at the kinetic level, is given by.| |
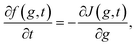 | (1) |
where J(g, t) is the cluster flux defined in the continuous cluster size space| |
 | (2) |
β(g, t) represents the rate of collision between monomers at concentration f(1, t) and a g-mer.
| |
 | (3) |
n(g, t) stands for the cluster size distribution and with respect to the monomer concentration n(1, t) can be written as.
| |
 | (4) |
where
s1 and
m1 are the surface area and the mass of monomer, respectively.
g* represents the critical size of the cluster that corresponds to maximum free energy of cluster formation
| |
 | (5) |
And the free energy of cluster formation can be written as.
| |
 | (6) |
where
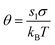
, and

is the saturation ratio.
θ comes out to be the total surface energy relative to the thermal energy.
neq(1) is the saturation monomer concentration. The critical region spreads around
g* over a range restricted by the following condition
| | |
|W(g) − W(g*)| ≤ kBT,
| (7) |
so that the spread becomes
| |
 | (8) |
The spread is related to the Zeldovich factor (Z, a measure of departure of steady state from equilibrium concentration of critical nuclei) by.
| |
 | (9) |
Thus, the critical region becomes the region of clusters g* − δ ≤ g* + δ and comprises of a left region, g* − δ ≤ g ≤ g*, and a right region, g* ≤ g ≤ g* + δ. There exists a left outer region to the left of critical region (1 ≤ g < g* − δ) and a right outer region (g > g* + δ) to the right of it. The critical region is endowed with the steepest variation of cluster concentration with size and is regarded as transition layer.58 Solution of eqn (1) to determine the dynamic cluster size distribution requires setting up of appropriate boundary and initial conditions. The boundary conditions are imposed at both ends of cluster size distribution. At g = 1 it is logical to assume the monomer number concentration to be the same as in the equilibrium distribution.
| |
 | (10) |
For large g, n(g) defined by eqn (4) bounces absurdly beyond the critical region though the true cluster size distribution f(g, t) remains finite. Thus, the second boundary condition becomes.
| |
 | (11) |
The transient nucleation kinetics is usually studied as the saturation ratio S is raised to a specified value at t = 0. Since at equilibrium the cluster concentrations for g ≥ 2 becomes much smaller than that of the monomer, the initial condition could reasonably be written as
| | |
f(g, 0) = n(1)δ(g − 1),
| (12) |
where
δ(
g − 1) is the Dirac delta function.
eqn (1), along with the proper initial and boundary conditions [
eqn (10)–(12)], adequately describe the constant temperature nucleation at the kinetic level. The solution demands either application of suitable numerical method or an approximate analytical method.
2. Steady state nucleation rate: the ZBDFT approach. The potential energy function describing the nucleation process in the cluster size space (g) can be written as44| |
 | (13) |
where ϕA and ϕB are the thermodynamic potentials per molecule of distinct phases A and B and  represents the surface free energy between the phases A and B (μ being a constant proportional to surface energy). In presence of charged droplets there comes an extra term in eqn (13) that accounts for the electrostatic interaction (Δϕadd). Thus, Δϕ(g) becomes
represents the surface free energy between the phases A and B (μ being a constant proportional to surface energy). In presence of charged droplets there comes an extra term in eqn (13) that accounts for the electrostatic interaction (Δϕadd). Thus, Δϕ(g) becomes| |
 | (14) |
In view of Debye–Hückel theory Δϕadd can be written as55
| |
 | (15) |
where
ψ is the electrostatic potential of a particular droplet by the surrounding droplet cloud,
q being the charge of the particular droplet, and
Ng stands for the number of charged droplets. The electrostatic potential is given by

where
ε is the dielectric constant of the medium, and
κ−1 is the thickness of the droplet cloud formally known as Debye–Hückel screening length. Introduction of Δ
ϕadd to incorporate the influence of charging is a standard procedure in the light of DHICM. The derivation of Δ
ϕadd involves introduction of potential of average force, (
U), which is linked with time-average forces between ions.
U finally turns out to be Coulombic potential energy of ions and absorbs within it the long-range interaction term

.
55
Following Frenkel's work44 we could write  where F is the total number of molecules in the generalized sense. To be specific, F represents total number of individual molecules by considering number of molecules contained in a cluster of size g and there are Ng number of such clusters. And η is a small parameter which accounts for the relative preponderance of charged droplets in a sea of vapor phase. Thus, in the present model, the potential energy function describing the nucleation process in the cluster size space (g) can be written as
where F is the total number of molecules in the generalized sense. To be specific, F represents total number of individual molecules by considering number of molecules contained in a cluster of size g and there are Ng number of such clusters. And η is a small parameter which accounts for the relative preponderance of charged droplets in a sea of vapor phase. Thus, in the present model, the potential energy function describing the nucleation process in the cluster size space (g) can be written as
| |
 | (16) |
where, the third term is actually a new addition to the present theory where
Λ is a parameter that takes care of the charge on the droplets and is given by
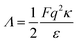
, the function
ϕ(
g) inside the exponential part of
eqn (16) reads
A straightforward application of ZBDFT44 ultimately gives the steady state relative nucleation rate that can be written as
| |
 | (17) |
where

and

.
r*,
p, and
m being the radius of critical droplet, the vapor pressure, and the mass of the droplet, respectively. Based on
eqn (17), a plot of ln(
Jg*)
vs. 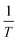
for different
Λ's reveals the enhancement in the steady state nucleation rate with increase in the extent of charging [
Fig. 1]. The observation indeed runs in conformity with the observations of other workers.
33,35,36 Tripathi and Harrison have showed that modest charges on aerosol particles (APs) arising from natural asymmetries in ion concentration are sufficient to increase collision rates with suitable freezing nuclei.
33 Warshavsky and Shchekin have shown that the uniform external electric field enhances nucleation for a fixed vapor chemical potential due to decrease in the chemical potential per molecule in droplet and the work of droplet formation.
35 Gamero-Castaño and de la Mora, have presented a detailed account of enhancement of nucleation rate because of charge on the basis of critical supersaturation ratio between charged condensation embryos and vapor molecules.
36
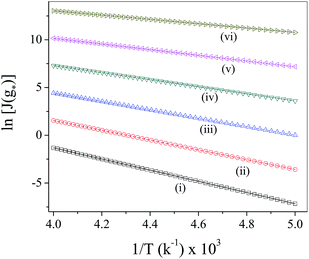 |
| | Fig. 1 Plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Js vs. 1/T at different Λ values based on ZBDFT (i) Λ = 0.0, (ii) Λ = 5.0 × 10−8, (iii) Λ = 1.0 × 10−7, (iv) Λ = 2.0 × 10−7, (v) Λ = 3.0 × 10−7, (vi) Λ = 4.0 × 10−7. Js vs. 1/T at different Λ values based on ZBDFT (i) Λ = 0.0, (ii) Λ = 5.0 × 10−8, (iii) Λ = 1.0 × 10−7, (iv) Λ = 2.0 × 10−7, (v) Λ = 3.0 × 10−7, (vi) Λ = 4.0 × 10−7. | |
3. Transient kinetics of nucleation: the BLT approach. BLT is a perturbative method for solving a differential equation whose highest derivative is multiplied by the perturbing parameter ε. A boundary layer is a narrow region where the solution of a differential equation changes rapidly. By definition, the thickness of a boundary layer must approach 0 as ε → 0.Let's define  and
and 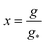 to represent the normalized cluster size distribution and normalized cluster size respectively. By means of above change of variables and with the help of eqn (2), (4), (6) and (9) and the fact that f(1, t) = n(1), eqn (1) can be transformed into
to represent the normalized cluster size distribution and normalized cluster size respectively. By means of above change of variables and with the help of eqn (2), (4), (6) and (9) and the fact that f(1, t) = n(1), eqn (1) can be transformed into
| |
 | (18) |
where we have replaced
W(
g) of
eqn (6) by Δ
ϕ(
g) of
eqn (14). Letting

, where
ε is a small parameter related to the width of the critical region
δ,
eqn (18) becomes
| |
 | (19) |
Laplace transformation of eqn (19) gives
| |
 | (20) |
where

.
Eqn (20) governs the cluster distribution and the small parameter
ε gets attached to the term containing the highest derivative. The modified boundary conditions become
| |
 | (21) |
We have tried to solve eqn (20) together with the boundary conditions using BLT. The dominant term of eqn (20) attached to  is
is  which changes sign at x = 1 in the interval
which changes sign at x = 1 in the interval  . Hence there is a single localized region of rapid change of y(x, s) in the ε neighborhood of x = 1. Thus, we expect a boundary layer (transition layer) at x = 1. According to BLT the complete solution of eqn (20) can be thought of as combination of three component solutions: the left outer solution ylout(x,s) that satisfies the left boundary condition at
. Hence there is a single localized region of rapid change of y(x, s) in the ε neighborhood of x = 1. Thus, we expect a boundary layer (transition layer) at x = 1. According to BLT the complete solution of eqn (20) can be thought of as combination of three component solutions: the left outer solution ylout(x,s) that satisfies the left boundary condition at  and far below the ε vicinity of the critical region (inner region) at x = 1, the inner solution yin(x, s) valid inside the ε vicinity of critical region, and the right outer solution yrout(x,s) that satisfies the right boundary condition at x → ∞ and far above the ε vicinity of the said critical region.43
and far below the ε vicinity of the critical region (inner region) at x = 1, the inner solution yin(x, s) valid inside the ε vicinity of critical region, and the right outer solution yrout(x,s) that satisfies the right boundary condition at x → ∞ and far above the ε vicinity of the said critical region.43
The boundary conditions relevant to the outer solutions become
| |
 | (22) |
To the leading order in ε the outer equation reads.
| |
 | (23) |
Keeping in mind that y(x, 0) = 1 (in view of eqn (10) and (12) and the substitution 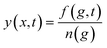 ), the outer solutions to eqn (20) can be obtained from eqn (23) which read
), the outer solutions to eqn (20) can be obtained from eqn (23) which read
| |
 | (24) |
where we have used the boundary conditions [
cf. eqn (22)]. In
eqn (24) 
. Since the growth of the cluster in the vicinity of
g* can be considered to be a diffusion process,
τ simply acts as a measure of the time required to traverse the critical region whence
β(
g*) playing the role of an equivalent diffusion coefficient. We now turn our attention towards the inner solution to
eqn (20). We have already discussed that outer solutions are no longer valid near
x = 1 where the boundary layer exists having a thickness
ε. We therefore introduce the
inner variables 
and
Yin(
X,
s) ≡
yin(
x,
s). Using these inner variables and letting
η ∼
ε2 eqn (20) becomes
| |
 | (26) |
We now assume a perturbation series of the form
| |
 | (27) |
and restate the boundary condition
y(∞,
s) = 0 as
| | |
Yn(∞, s) = 0, n ≥ 0.
| (28) |
Substituting eqn (27) into (26) and collecting the terms corresponding to ε0 we get the leading order inner differential equation
| |
 | (29) |
where

and

. Using the scaling variables
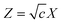
,
U =
cYin, where
c = 1 − 2
ηF we get the
scaled inner equation| |
 | (30) |
where
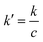
.
eqn (30) is the co-error function differential equation whose general solution is given by
59| | |
U = A(s)ik′erfc(Z) + B(s)ik′erfc(−Z).
| (31) |
inerfc(x) is called the repeated integral of co-error function erfc(x) and is defined as
| |
 | (32) |
In terms of our original inner variables Yin(X, s) and X we write, from eqn (31)
| |
 | (33) |
where

and

. The constants
A′(
s) and
B′(
s) in
eqn (33) are determined by asymptotic matching of inner and outer solutions. The matching requires that the inner and outer solutions should agree in both left intermediate limit (LIL) and right intermediate limit (RIL) characterized by (
x → 1−,
X → − ∞) and (
x → 1+,
X → + ∞), respectively. The said matching at RIL gives
B′(
s) = 0, whereas at LIL it gives
| |
 | (34) |
The terms inside the left and right square brackets of eqn (34) represent the uncharged and charged parts, absorbed in the coefficient A′(s), respectively. The derivation of eqn (34) was a bit involved where we have used the fact that η is a small parameter and a property of repeated integral of co-error function59 viz.
The inner solution thus takes the form
| |
 | (35) |
Returning to our original inner variables yin(x, s) and x together with the fact that η is a small parameter we arrive at the inner solution that gives the cluster size distribution near the critical size
| |
 | (36) |
where
ε′ = 2
2ηF(T)ε.
III. Results and discussion
We now summarize the main results.
A. Cluster size distribution
The cluster size distribution near critical size can now be obtained after an inverse Laplace transform of inner solution [cf. eqn (36)] which gives56| |
 | (37) |
where 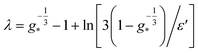 . This distribution plays an important role to determine the nucleation rate. However, the transient cluster distribution well away from the critical region can be obtained after taking the inverse Laplace transforms of outer solutions eqn (24) and (25),56
. This distribution plays an important role to determine the nucleation rate. However, the transient cluster distribution well away from the critical region can be obtained after taking the inverse Laplace transforms of outer solutions eqn (24) and (25),56| | |
ylout(g, t) = Θ(t − μ(g)τ),
| (38) |
andwhere  and Θ is the Heaviside step function: Θ(z) = 1 for z > 0,
and Θ is the Heaviside step function: Θ(z) = 1 for z > 0,  for z = 0, and Θ(z) = 0 for z < 0.
for z = 0, and Θ(z) = 0 for z < 0.
B. Time lag
Along with a careful analysis of critical cluster size regime the analysis of sub-critical cluster size domain also merits importance because of its close link with the problem of time lag. In nucleation process the time required for the growth of droplets of appreciable size is considered to be an important aspect. ZBDFT provides us with a rate of nucleation that varies extremely rapidly with the degree of supersaturation. Thus, in a situation when the supersaturation is increasing rapidly with time, the formation and growth of new nuclei will promote condensation of vapor much more than the continued growth of old nuclei. In the early stage of nucleation, the process is controlled by the highly variable nucleation rate. A persistent increase in the extent of condensation then reduces supersaturation to a negligible value and nucleation disappears. Now, the droplet growth process governs the return to equilibrium. Thus, the commencement of condensation is switched on by nucleation and the nucleation process requires an appreciable time during which it exhibits a non-steady state character. The time lag is the time required by the sub-critical clusters to reach the steady state.56 And within this time the nucleation rate is far below than that predicted by steady state theory [cf. eqn (17)]. Thus, in the early moments of this time lag we can ignore the thermodynamic barrier and diffusion process becomes important for the formation of system of embryos.
As we have mentioned earlier, τ of eqn (24) represents the characteristic time for a cluster to diffuse over the free energy barrier (the critical region) of length scale δ whereas μ(g)τ of eqn (38) reflects the true time-lag with which the sub-critical clusters approach a steady state one by one. The combined appearance of μ(g) and τ in eqn (38) indicates that determination of time needed to reach a steady state cluster size distribution involves serious consideration of the diffusion of the sub-critical clusters over a width δ. Fig. 2 depicts the dependence of the coefficient μ(g) attached to the time-lag on critical cluster size g*. The plot reveals a rather low sensitivity of μ(g) on g*. The plot also exhibits an increase in μ(g) with g. Since we have come to know that the sub-critical clusters attain steady state one by one from the smaller clusters to the larger ones, the aforesaid enhancement of μ(g) with g indicates a continually delayed period of time for the onset of steady state for each g-mers as the size increases; starting from somewhat smaller clusters or more primarily monomers. Since the formation of large clusters demands crossing of a higher Gibbs energy barrier, the time needed to arrive at a steady state cluster distribution becomes greater for large clusters in comparison with the smaller ones. On the other hand, eqn (39) indicates complete disappearance of any cluster size distribution beyond the critical region yrout.
 |
| | Fig. 2 Plot of coefficient μ(g) associated with time-lag against normalized cluster size  for (i) g* = 10 and (ii) g* = 50. for (i) g* = 10 and (ii) g* = 50. | |
C. Domain of droplet charge
A look at the outer solutions [cf. eqn (24) and (25)] reveals that there is no role of droplet charges (Λ) in the outer region. The influence of droplet charge is solely confined in the inner region in the neighborhood of critical cluster size g*.
D. Transient nucleation rate
In view of eqn (2) and (37) the transient cluster flux at some cluster size g is given by.| |
 | (40) |
and the transient nucleation rate at g = g* is given by| |
 | (41) |
where Jss represents the steady state nucleation of the charged droplets and can be written as| | |
Jss = Z(g*)β(g*)n(g*).
| (42) |
In the long time limit (t → ∞), J(g*, t) → Jss.
Based on the equations derived above we are now ready to monitor the normalized transient nucleation rate J(g, t)/Jss as a function of normalized time t/τ. It seems quite relevant now to inspect the roles played by critical cluster size and droplet charge on the said nucleation rate. Fig. 3 displays the plot of J(g, t)/Jss against t/τ for different values of g* based on eqn (41). From the figure we find that time lag associated with the nucleation of charged droplets is of the order of 5τ. Moreover, the nucleation rate has been found to decrease with increase in the critical cluster size as we have increased g* from 10 to 40. Beyond g* = 50, however, the nucleation rate attains saturation. Fig. 4, more importantly, depicts the influence of droplet charge parameter Λ on the transient nucleation rate. Starting from an assembly of uncharged droplets (Λ = 0), no significant change is observed in the nucleation rate with increase in Λ initially, however, the scenario changes dramatically as soon as Λ exceeds a threshold value of Λth = 2.0 × 10−7 whence a sudden jump in the transient nucleation rate is observed. The observation is difficult to explain. However, we feel that at this threshold value the interaction between the charged droplets takes place in such a way that nucleation free energy is suddenly depleted causing noticeable enhancement in nucleation rate. The rate goes on increasing persistently with further increase in Λ values thereby corroborating the findings of earlier workers which invariably demonstrated charge induced enhancement in the transient nucleation rate.6,7,20,30,33–36
 |
| | Fig. 3 Plot of normalized transient nucleation rate J(g, t)/Jss as a function of normalized time t/τ at T = 200k for different g* values: (i) g* = 10, (ii) g* = 20, (iii) g* = 30, (iv) g* = 40, and (v) g* = 50. | |
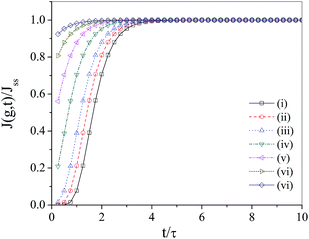 |
| | Fig. 4 Plot of normalized transient nucleation rate J(g, t)/Jss as a function of normalized time t/τ at T = 200k for different Λ values: (i) Λ = 0.0, (ii) Λ = 5.0 × 10−8, (iii) Λ = 1.0 × 10−7, (iv) Λ = 2.0 × 10−7, (v) Λ = 3.0 × 10−7, (vi) Λ = 4.0 × 10−7, (vii) Λ = 5.0 × 10−7 s. | |
It needs to be mentioned that the role of sign of the charge on binary atmospheric nucleation is an important issue.12,14,60–62 In the present investigation we did not find any dependence of our result on the sign of the charge of nucleating center (or a central CVM). Actually, in DHICM theory the sign of charge of central ion is immaterial, the distribution of charge in space is of fundamental importance. If the central ion is considered to be positively charged, the surrounding ion-atmosphere gains an overall negative charge and vice versa preserving the electroneutrality of the entire system. The absence of role of sign of the charge on nucleation thus appears to be a limitation of DsHICM. Since the negatively charged droplets contain more charge within them (compared with the positively charged droplets) their behavior is expected to be different. It therefore comes out that some different model needs to be conceived in order to appreciate the role of sign of droplet charge on nucleation kinetics.
IV. Conclusions
The nucleation of charged droplets within the framework of Debye–Hückel ion-atmosphere model reveals intriguing features. Both the ZBDFT and BLT approaches proclaim enhancement of steady state and transient nucleation rate, respectively, in comparison with the uncharged droplets. The said enhancement occurs since the charge on the droplets reduces the height of the nucleation barrier considerably. It has been found that the influence of droplet charge is solely confined within the inner region in the vicinity of critical cluster size. However, the investigation has also revealed that the time-lag required to attain the steady state cluster size distribution is intimately mingled with the diffusion of sub-critical clusters over a width δ. The normalized transient nucleation rate exhibits saturation when steady state is reached and the rate decreases with increase in the size of the critical cluster up to a certain extent. Beyond that extent there is no change in the transient nucleation rate as g* is increased further. On the other hand, the transient nucleation rate exhibits a different behavior as the charge content of the droplet increases. As soon as the charge content surpasses a threshold value there occurs a sudden hike in the nucleation rate followed by a consistent increase with further enhancement of the charge content.
Although the conclusion that nucleation rate enhances because of the charges on the droplet is not new per se, the present approach deals with the problem in a newer perspective. The ZBDFT is an old theory based solely on CNT. However, we have shown that an appropriate modification of ZBDFT (because of involvement of charge) could well predict the enhancement in the nucleation kinetics. The present BLT approach helps us realize the intricacies of the nucleation kinetics of charged droplets which remains outside the scope of standard ZBDFT. It needs to be mentioned that, in practice, nucleation in the atmosphere involves multiple species. In that case the form of Δϕadd requires to be appropriately modified incorporating other interactions. This will surely enhance complexity of the problem immensely. The pertinent differential equations (inner and outer) can prove to be challenging ones.
The notable work of Shi et al.56 has given us the guideline to carry out the present work. However, we have extrapolated their work to study the nucleation kinetics of charged vapor droplets by modifying ZBDFT inspired by DHICM model of electrochemistry. The modifications are rigorous and effectively highlight the intricacies of the nucleation kinetics of charged vapor droplets. In our present study we have examined various important aspects of nucleation such as cluster size distribution, time lag, domain of droplet charge, and the transient nucleation rate. We would like to explore now nucleation of charged droplets in the presence of scavengers present in the atmosphere which happens to be a field of extreme importance. We would like to explore the aforesaid topic in near future. We anticipate that the data obtained from that and their analysis will further enrich the results of present investigation.
We, therefore, believe that the present investigation would have potential contribution in understanding various nucleation processes that involve charge droplets particularly in the field of atmospheric physics research. The findings could also consolidate the earlier ones on a more rational basis.
Acknowledgements
The author sincerely expresses his gratitude to Prof. Deb Shankar Ray, Department of Physical Chemistry, Indian Association for the Cultivation of Science for helpful discussions.
References
- D. Kashchiev, in Nucleation – Basic Theory with Applications, Butterworth-Heinemann, Oxford, UK, 2000 Search PubMed
 .
. - J. H. ter Horst, D. Bedeaux and S. Kjelstrup, The role of temperature in nucleation process, J. Chem. Phys., 2011, 134, 054703 CrossRef CAS PubMed
 .
. - E. Ruckenstein and Y. S. Djikaev, Recent developments in the kinetic theory of nucleation, Adv. Colloid Interface Sci., 2005, 118, 51–72 CrossRef CAS PubMed
 .
. - B. Nowakowski and E. Ruckenstein, A kinetic approach to the theory of nucleation in gases, J. Chem. Phys., 1991, 94, 1397–1402 CrossRef CAS PubMed
 .
. - D. R. Warren, K. Okuyama, Y. Kousaka, J. H. Seinfeld and R. C. Flagan, Homogeneous nucleation in supersaturated vapor containing foreign seed aerosol, J. Colloid Interface Sci., 1987, 116, 563–581 CrossRef CAS
 .
. - F. Yu and R. P. Turco, From molecular clusters to nanoparticles: role of ambient ionization in tropospheric aerosol formation, J. Geophys. Res., 2001, 106, 4797–4814 CrossRef CAS
 .
. - J. Curtius, E. R. Lovejoy and K. D. Froyd, Atmospheric ion-induced aerosol nucleation, Space Sci. Rev., 2006, 125, 159–167 CrossRef CAS PubMed
 .
. - J. H. Seinfeld and S. N. Pandis, in Atmospheric Chemistry and Physics – From Air Pollution to Climate Change, John Wiley and Sons Inc., New York, 1998 Search PubMed
 .
. - A. Laaksonen, A. Talanquer and D. W. Oxtoby, Nucleation – measurements, theory, and atmospheric applications, Ann. Rev. Phys. Chem., 1995, 46, 489–524 CrossRef CAS PubMed
 .
. - V.-M. Kerminen, T. Anttila, T. Petäjä, L. Laakso, S. Gagné, K. E. J. Lehtinen and M. Kulmala, Charging state of the atmospheric nucleation mode: implications for separating neutral and ion-induced nucleation, J. Geophys. Res., 2007, 112, D21205 CrossRef
 .
. - M. Kulmala and V.-M. Kerminen, On the formation and growth of atmospheric nanoparticles, Atmos. Res., 2008, 90, 132–150 CrossRef CAS PubMed
 .
. - L. Laakso, J. M. Mäkelä, L. Pirjola and M. Kulmala, Model studies on ion-induced nucleation in the atmosphere, J. Geophys. Res., 2002, 107, AACS-1–AACS-19 CrossRef
 .
. - A. Luts, T.-E. Parts and M. Vana, New aerosol particle formation via certain ion driven processes, Atmos. Res., 2006, 82, 547–553 CrossRef CAS PubMed
 .
. - A. Hirsikko, T. Bergman, L. Laakso, M. Dal Maso, I. Riipinen, U. Hōrrak and M. Kulmala, Identification and classification of the formation of intermediate ions measured in boreal forest, Atmos. Chem. Phys., 2007, 7, 201–210 CrossRef CAS
 .
. - L. Laakso, S. Gagné, T. Petäjä, A. Hirsikko, P. P. Aalto, M. Kulmala and V.-M. Kerminen, Detecting charging state of ultra-fine particles: instrumental development and ambient measurements, Atmos. Chem. Phys., 2007, 7, 1333–1345 CrossRef CAS
 .
. - M. Kulmala, Dynamic atmospheric cluster model, Atmos. Res., 2010, 98, 201–206 CrossRef CAS PubMed
 .
. - A. I. Rusanov, Thermodynamic theory of nucleation of charged particles, J. Colloid Interface Sci., 1979, 1, 32–47 CrossRef
 .
. - B. J. Murray and E. J. Jensen, Heterogeneous nucleation of amorphous solid water particles in the upper mesosphere, J. Atmos. Sol.-Terr. Phys., 2010, 72, 51–61 CrossRef CAS PubMed
 .
. - F. Yu and R. P. Turco, Ultrafine aerosol formation via ion-mediated nucleation, Geophys. Res. Lett., 2000, 27, 883–886 CrossRef CAS
 .
. - P. M. Winkler, G. Steiner, A. Vrtala, H. Vehkamäki, M. Noppel, K. E. J. Lehtinen, G. P. Reischl, P. E. Wagner and M. Kulmala, Heterogeneous Nucleation Experiments Bridging the Scale from Molecular Ion Clusters to Nanoparticles, Science, 2008, 319, 1374–1377 CrossRef CAS PubMed
 .
. - T. Kurtén, V. Loukonen, H. Vehkamäki and M. Kulmala, Amines are likely to enhance neutral and ion-induced sulfuric acid-water nucleation in the atmosphere more effectively than ammonia, Atmos. Chem. Phys., 2008, 8, 40954103 Search PubMed
 .
. - I. K. Ortega, T. Kurtén, H. Vehkamäki and M. Kulmala, The role of ammonia in sulfuric acid ion induced nucleation, Atmos. Chem. Phys., 2008, 8, 2859–2867 CrossRef CAS
 .
. - B. A. Tinsley, Influence of solar wind on the global electric circuit, and inferred effects on cloud microphysics, temperature, and dynamics in the troposphere, Space Sci. Rev., 2000, 94, 231–258 CrossRef CAS
 .
. - B. A. Tinsley, R. P. Rohrbaugh, M. Hei and K. V. Beard, Effects of image charges on the scavenging of aerosol particles by cloud droplets and on droplet charging and possible ice nucleation processes, J. Atmos. Sci., 2000, 57, 2118–2134 CrossRef
 .
. - K. S. Carslaw, R. G. Harrison and J. Kirkby, Cosmic rays, clouds, and climate, Science, 2002, 298, 1732–1737 CrossRef CAS PubMed
 .
. - M. O. Andreae, C. D. Jones and P. M. Cox, Strong present-day aerosol cooling implies a hot future, Nature, 2005, 435, 1187–1190 CrossRef CAS PubMed
 .
. - J. Curtius, Nucleation of atmospheric aerosol particles, C. R. Phys., 2006, 7, 1027–1045 CrossRef CAS PubMed
 .
. - K. A. Koehler, P. J. Demott, S. M. Kreidenwis, O. B. Popovicheva, M. D. Petters, C. M. Carrico, E. D. Kireeva, T. D. Khokhlova and N. K. Shonija, Cloud condensation nuclei and ice nucleation activity of hydrophobic and hydrophillic soot particles, Phys. Chem. Chem. Phys., 2009, 11, 7906–7920 RSC
 .
. - H. Vortisch, B. Krämer, I. Weidinger, L. Wöste, T. Leisner, M. Schwell, H. Baumgärtel and E. Rühl, Research on aerosol particles in connection with Earth's atmosphere, Phys. Chem. Chem. Phys., 2000, 2, 1407–1413 RSC
 .
. - D. Rzesanke, J. Nadolny, D. Duft, R. Müller, A. Kiselev and T. Leisner, On the role of surface charges for homogeneous freezing of supercooled water microdroplets, Phys. Chem. Chem. Phys., 2012, 14, 9359–9363 RSC
 .
. - J. L. Katz, J. A. Fisk and V. M. Chakarov, Condensation of a supersaturated vapor IX. Nucleation on ions, J. Chem. Phys., 1994, 101, 2309–2318 CrossRef PubMed
 .
. - G. T. Gao, K. J. Oh and X. C. Zeng, Effect of uniform electric field on homogeneous vapor-liquid nucleation and phase equilibria. II. Extended simple point charge model water, J. Chem. Phys., 1999, 110, 2533–2538 CrossRef CAS PubMed
 .
. - S. N. Tripathi and R. G. Harrison, Enhancement of contact nucleation by scavenging of charged aerosol particles, Atmos. Res., 2002, 62, 57–70 CrossRef CAS
 .
. - A. K. Shchekin, M. S. Kshevetskiy and V. B. Warshavsky, The work of droplet formation on a charged condensation nucleus exposed to an external electric field, Colloids Surf., A, 2003, 223, 277–285 CrossRef CAS
 .
. - V. B. Warshavsky and A. K. Shchekin, The effects of external electric field in thermodynamics of formation of dielectric droplet, Colloids Surf., A, 1999, 148, 283–290 CrossRef CAS
 .
. - M. Gamero-Castaño and J. Fernández de la Mora, Ion-induced nucleation: measurement of the effect of embryos size and charge state on the critical supersaturation, J. Chem. Phys., 2002, 117, 3345 CrossRef PubMed
 .
. - K. C. Russell, Nucleation on gaseous ions, J. Chem. Phys., 1969, 50, 1809 CrossRef CAS PubMed
 .
. - F. M. Kuni and A. I. Rusanov, Theory of nucleation on charged nuclei. 1. General thermodynamic relationships, Colloid J., 1982, 44, 824–830 Search PubMed
 .
. - F. M. Kuni, A. K. Shchekin and A. I. Rusanov, Theory of nucleation on charged cores: 2. Thermodynamic parameters of an equilibrium nucleus, Colloid J., 1982, 44, 935–941 Search PubMed
 .
. - F. M. Kuni, A. K. Shchekin and A. I. Rusanov, Theory of nucleation on charged nuclei. 3. Expansion in the curvature parameter of a drop in a strong, field of charged nucleus, Colloid J., 1983, 45, 598–604 Search PubMed
 .
. - F. M. Kuni, A. K. Shchekin and A. I. Rusanov, Theory of nucleation on charged nuclei. 4. Calculation of the work of formation for a droplet in the strong field of a charged nucleus, Colloid J., 1983, 45, 801–807 Search PubMed
 .
. - F. M. Kuni, A. K. Shchekin and A. I. Rusanov, Theory of nucleation on charged nuclei. 5. Chemical potential of vapor on threshold of barrierless nucleation, and asymmetry of chemical potential relative to sign of nuclear charge, Colloid J., 1983, 45, 951–957 Search PubMed
 .
. - C. M. Bender and S. A. Orszag, in Advanced Mathematical Methods for Scientists and Engineers, McGraw-Hill, New York, 1978 Search PubMed
 .
. - J. Frenkel, in Kinetic Theory of Liquids, Dover, New York, 1946 Search PubMed
 .
. - D. Kashchiev, Analysis of experimental data for the nucleation rate of water droplets, J. Chem. Phys., 2006, 125, 044505 CrossRef PubMed
 .
. - M. Kulmala, A. Laaksonen and L. Pirjola, Parametrization for H2SO4/H2O nucleation rates, J. Geophys. Res., 1998, 103, 8301–8307 CrossRef CAS
 .
. - H. Vehkamäki, M. Kulmala, I. Napari, K. E. J. Lehtinen, C. Timmreck, M. Noppel and A. Laaksonen, An improved parametrization for H2SO4–H2O nucleation rates for tropospheric and stratospheric conditions, J. Geophys. Res., 2002, 107, AAC31–AAC310 CrossRef
 .
. - E. R. Lovejoy, J. Curtius and K. D. Froyd, Atmospheric ion-induced nucleation of sulfuric acid and water, J. Geophys. Res., 2004, 109, D08204 Search PubMed
 .
. - A. A. Natsheh, A. B. Nadykto, K. V. Mikkelsen, F. Yu and R. Ruuskanen, Sulfuric acid and sulfuric acid hydrates in the gas Phase: a DFT Investigation, J. Phys. Chem. A, 2004, 108, 8914–8929 CrossRef CAS
 .
. - F. Yu, Quasi-unary homogeneous nucleation of H2SO4 − H2O, J. Chem. Phys., 2005, 122, 074501 CrossRef PubMed
 .
. - A. B. Nadykto and F. Yu, Dipole moment of condensing monomers: a new parameter controlling the ion-induced nucleation, Phys. Rev. Lett., 2004, 93, 016101 CrossRef
 .
. - A. B. Nadykto, J. M. Mäkelä, F. Yu, M. Kulmala and A. Laaksonen, Comparison of the experimental mobility equivalent diameter for small cluster ions with theoretical particle diameter corrected by effect of vapour polarity, Chem. Phys. Lett., 2003, 382, 6–11 CrossRef CAS PubMed
 .
. - F. Yu, Improved quasi-unary nucleation model for binary H2SO4 − H2O homogeneous nucleation, J. Chem. Phys., 2007, 127, 054301 CrossRef PubMed
 .
. - F. Yu and R. P. Turco, The formation and evolution of aerosols in stratospheric aircraft plumes: numerical simulations and comparisons with observations, J. Geophys. Res., 1998, 103, 25915–25934 CrossRef CAS
 .
. - J. O'M Bockris and A. K. N. Reddy, in Modern Electrochemistry 1, Plenum Publishing Corporation, New York, 1998 Search PubMed
 .
. - G. Shi, J. H. Seinfeld and K. Okuyama, Transient kinetics of nucleation, Phys. Rev. A, 1990, 41, 2101–2108 CrossRef CAS
 .
. - P. Demo and Z. Kožĩseks, Homogeneous nucleation processes: analytical approach, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 3620–3625 CrossRef CAS
 .
. - G. Shi and J. H. Seinfeld, Transient kinetics of nucleation and crystallization: Part I. Nucleation, J. Mater. Res., 1991, 6, 2091–2096 CrossRef CAS
 .
. - M. Abramowitz and I. Stegun, in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Dover Publications, USA, 1964 Search PubMed
 .
. - A. B. Nadykto, F. Yu and J. Herb, Towards understanding the sign preference in binary atmospheric nucleation, Phys. Chem. Chem. Phys., 2008, 10, 7073–7078 RSC
 .
. - A. B. Nadykto, A. A. Natsheh, F. Yu, K. V. Mikkelsen and R. Ruuskanen, Quantum nature of the sign preference in ion-Induced nucleation, Phys. Rev. Lett., 2006, 96, 125701 CrossRef
 .
. - M. Vana, E. Tamm, U. Hõrrak, A. Mirme, H. Tammet, L. Laakso, P. P. Aalto and M. Kulmala, Charging state of atmospheric nanoparticles during the nucleation burst events, Atmos. Res., 2006, 82, 536–546 CrossRef CAS PubMed
 .
.
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.  ), where pH2O is the partial pressure of water and p0(T) is equilibrium vapor pressure over a flat surface of a condensed phase at temperature T.18 Moreover, the primary ions formed initially in the atmosphere may rapidly react with common air ingredients to produce a series of increasingly stable terminal ions such as HSO4−. Depending on the availability of certain vapors such as H2SO4, H2O, NH3 and numerous other organic species, the core terminal ions quickly collect ligands and form a continuous distribution of charged clusters. Once a ligand vapor gets overwhelmingly supersaturated with respect to its condensed phase, a considerable fraction of ion clusters can undergo nucleation and we envisage a proliferation of ultrafine particles.19 The condensing vapor may exhibit dipole nature and thus gets electrostatically attracted to charged particles.20 It needs to be mentioned that there are also some important quantum chemical calculations that deal with role of amine and ammonia in ion-induced H2SO4–H2O nucleation in atmosphere.21,22
), where pH2O is the partial pressure of water and p0(T) is equilibrium vapor pressure over a flat surface of a condensed phase at temperature T.18 Moreover, the primary ions formed initially in the atmosphere may rapidly react with common air ingredients to produce a series of increasingly stable terminal ions such as HSO4−. Depending on the availability of certain vapors such as H2SO4, H2O, NH3 and numerous other organic species, the core terminal ions quickly collect ligands and form a continuous distribution of charged clusters. Once a ligand vapor gets overwhelmingly supersaturated with respect to its condensed phase, a considerable fraction of ion clusters can undergo nucleation and we envisage a proliferation of ultrafine particles.19 The condensing vapor may exhibit dipole nature and thus gets electrostatically attracted to charged particles.20 It needs to be mentioned that there are also some important quantum chemical calculations that deal with role of amine and ammonia in ion-induced H2SO4–H2O nucleation in atmosphere.21,22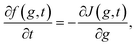





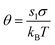 , and
, and  is the saturation ratio. θ comes out to be the total surface energy relative to the thermal energy. neq(1) is the saturation monomer concentration. The critical region spreads around g* over a range restricted by the following condition
is the saturation ratio. θ comes out to be the total surface energy relative to the thermal energy. neq(1) is the saturation monomer concentration. The critical region spreads around g* over a range restricted by the following condition




 represents the surface free energy between the phases A and B (μ being a constant proportional to surface energy). In presence of charged droplets there comes an extra term in eqn (13) that accounts for the electrostatic interaction (Δϕadd). Thus, Δϕ(g) becomes
represents the surface free energy between the phases A and B (μ being a constant proportional to surface energy). In presence of charged droplets there comes an extra term in eqn (13) that accounts for the electrostatic interaction (Δϕadd). Thus, Δϕ(g) becomes

 where ε is the dielectric constant of the medium, and κ−1 is the thickness of the droplet cloud formally known as Debye–Hückel screening length. Introduction of Δϕadd to incorporate the influence of charging is a standard procedure in the light of DHICM. The derivation of Δϕadd involves introduction of potential of average force, (U), which is linked with time-average forces between ions. U finally turns out to be Coulombic potential energy of ions and absorbs within it the long-range interaction term
where ε is the dielectric constant of the medium, and κ−1 is the thickness of the droplet cloud formally known as Debye–Hückel screening length. Introduction of Δϕadd to incorporate the influence of charging is a standard procedure in the light of DHICM. The derivation of Δϕadd involves introduction of potential of average force, (U), which is linked with time-average forces between ions. U finally turns out to be Coulombic potential energy of ions and absorbs within it the long-range interaction term  .55
.55
 where F is the total number of molecules in the generalized sense. To be specific, F represents total number of individual molecules by considering number of molecules contained in a cluster of size g and there are Ng number of such clusters. And η is a small parameter which accounts for the relative preponderance of charged droplets in a sea of vapor phase. Thus, in the present model, the potential energy function describing the nucleation process in the cluster size space (g) can be written as
where F is the total number of molecules in the generalized sense. To be specific, F represents total number of individual molecules by considering number of molecules contained in a cluster of size g and there are Ng number of such clusters. And η is a small parameter which accounts for the relative preponderance of charged droplets in a sea of vapor phase. Thus, in the present model, the potential energy function describing the nucleation process in the cluster size space (g) can be written as
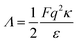 , the function ϕ(g) inside the exponential part of eqn (16) reads
, the function ϕ(g) inside the exponential part of eqn (16) reads
 and
and  . r*, p, and m being the radius of critical droplet, the vapor pressure, and the mass of the droplet, respectively. Based on eqn (17), a plot of ln(Jg*) vs.
. r*, p, and m being the radius of critical droplet, the vapor pressure, and the mass of the droplet, respectively. Based on eqn (17), a plot of ln(Jg*) vs. 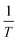 for different Λ's reveals the enhancement in the steady state nucleation rate with increase in the extent of charging [Fig. 1]. The observation indeed runs in conformity with the observations of other workers.33,35,36 Tripathi and Harrison have showed that modest charges on aerosol particles (APs) arising from natural asymmetries in ion concentration are sufficient to increase collision rates with suitable freezing nuclei.33 Warshavsky and Shchekin have shown that the uniform external electric field enhances nucleation for a fixed vapor chemical potential due to decrease in the chemical potential per molecule in droplet and the work of droplet formation.35 Gamero-Castaño and de la Mora, have presented a detailed account of enhancement of nucleation rate because of charge on the basis of critical supersaturation ratio between charged condensation embryos and vapor molecules.36
for different Λ's reveals the enhancement in the steady state nucleation rate with increase in the extent of charging [Fig. 1]. The observation indeed runs in conformity with the observations of other workers.33,35,36 Tripathi and Harrison have showed that modest charges on aerosol particles (APs) arising from natural asymmetries in ion concentration are sufficient to increase collision rates with suitable freezing nuclei.33 Warshavsky and Shchekin have shown that the uniform external electric field enhances nucleation for a fixed vapor chemical potential due to decrease in the chemical potential per molecule in droplet and the work of droplet formation.35 Gamero-Castaño and de la Mora, have presented a detailed account of enhancement of nucleation rate because of charge on the basis of critical supersaturation ratio between charged condensation embryos and vapor molecules.36
 and
and 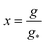 to represent the normalized cluster size distribution and normalized cluster size respectively. By means of above change of variables and with the help of eqn (2), (4), (6) and (9) and the fact that f(1, t) = n(1), eqn (1) can be transformed into
to represent the normalized cluster size distribution and normalized cluster size respectively. By means of above change of variables and with the help of eqn (2), (4), (6) and (9) and the fact that f(1, t) = n(1), eqn (1) can be transformed into
 , where ε is a small parameter related to the width of the critical region δ, eqn (18) becomes
, where ε is a small parameter related to the width of the critical region δ, eqn (18) becomes

 . Eqn (20) governs the cluster distribution and the small parameter ε gets attached to the term containing the highest derivative. The modified boundary conditions become
. Eqn (20) governs the cluster distribution and the small parameter ε gets attached to the term containing the highest derivative. The modified boundary conditions become
 is
is  which changes sign at x = 1 in the interval
which changes sign at x = 1 in the interval  . Hence there is a single localized region of rapid change of y(x, s) in the ε neighborhood of x = 1. Thus, we expect a boundary layer (transition layer) at x = 1. According to BLT the complete solution of eqn (20) can be thought of as combination of three component solutions: the left outer solution ylout(x,s) that satisfies the left boundary condition at
. Hence there is a single localized region of rapid change of y(x, s) in the ε neighborhood of x = 1. Thus, we expect a boundary layer (transition layer) at x = 1. According to BLT the complete solution of eqn (20) can be thought of as combination of three component solutions: the left outer solution ylout(x,s) that satisfies the left boundary condition at  and far below the ε vicinity of the critical region (inner region) at x = 1, the inner solution yin(x, s) valid inside the ε vicinity of critical region, and the right outer solution yrout(x,s) that satisfies the right boundary condition at x → ∞ and far above the ε vicinity of the said critical region.43
and far below the ε vicinity of the critical region (inner region) at x = 1, the inner solution yin(x, s) valid inside the ε vicinity of critical region, and the right outer solution yrout(x,s) that satisfies the right boundary condition at x → ∞ and far above the ε vicinity of the said critical region.43

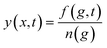 ), the outer solutions to eqn (20) can be obtained from eqn (23) which read
), the outer solutions to eqn (20) can be obtained from eqn (23) which read
 . Since the growth of the cluster in the vicinity of g* can be considered to be a diffusion process, τ simply acts as a measure of the time required to traverse the critical region whence β(g*) playing the role of an equivalent diffusion coefficient. We now turn our attention towards the inner solution to eqn (20). We have already discussed that outer solutions are no longer valid near x = 1 where the boundary layer exists having a thickness ε. We therefore introduce the inner variables
. Since the growth of the cluster in the vicinity of g* can be considered to be a diffusion process, τ simply acts as a measure of the time required to traverse the critical region whence β(g*) playing the role of an equivalent diffusion coefficient. We now turn our attention towards the inner solution to eqn (20). We have already discussed that outer solutions are no longer valid near x = 1 where the boundary layer exists having a thickness ε. We therefore introduce the inner variables  and Yin(X, s) ≡ yin(x, s). Using these inner variables and letting η ∼ ε2 eqn (20) becomes
and Yin(X, s) ≡ yin(x, s). Using these inner variables and letting η ∼ ε2 eqn (20) becomes


 and
and  . Using the scaling variables
. Using the scaling variables 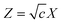 , U = cYin, where c = 1 − 2ηF we get the scaled inner equation
, U = cYin, where c = 1 − 2ηF we get the scaled inner equation
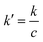 . eqn (30) is the co-error function differential equation whose general solution is given by59
. eqn (30) is the co-error function differential equation whose general solution is given by59

 and
and  . The constants A′(s) and B′(s) in eqn (33) are determined by asymptotic matching of inner and outer solutions. The matching requires that the inner and outer solutions should agree in both left intermediate limit (LIL) and right intermediate limit (RIL) characterized by (x → 1−, X → − ∞) and (x → 1+, X → + ∞), respectively. The said matching at RIL gives B′(s) = 0, whereas at LIL it gives
. The constants A′(s) and B′(s) in eqn (33) are determined by asymptotic matching of inner and outer solutions. The matching requires that the inner and outer solutions should agree in both left intermediate limit (LIL) and right intermediate limit (RIL) characterized by (x → 1−, X → − ∞) and (x → 1+, X → + ∞), respectively. The said matching at RIL gives B′(s) = 0, whereas at LIL it gives



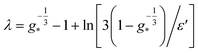 . This distribution plays an important role to determine the nucleation rate. However, the transient cluster distribution well away from the critical region can be obtained after taking the inverse Laplace transforms of outer solutions eqn (24) and (25),56
. This distribution plays an important role to determine the nucleation rate. However, the transient cluster distribution well away from the critical region can be obtained after taking the inverse Laplace transforms of outer solutions eqn (24) and (25),56 and Θ is the Heaviside step function: Θ(z) = 1 for z > 0,
and Θ is the Heaviside step function: Θ(z) = 1 for z > 0,  for z = 0, and Θ(z) = 0 for z < 0.
for z = 0, and Θ(z) = 0 for z < 0.

 for (i) g* = 10 and (ii) g* = 50.
for (i) g* = 10 and (ii) g* = 50.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)


