A theoretical study on ionic liquid endohedral C540 fullerene

Abstract

The effect of the confinement of ionic liquid (choline benzoate) cluster inside C540 fullerene has been studied through both molecular dynamic and density functional theory simulations. The solvation of the fullerene by the ionic liquid is also analysed and compared with pristine fullerene cages. The mobility of the studied endohedral fullerenes under external electric fields is simulated as a function of the intensity of applied fields. Density functional calculations allowed inferring both the changes in the electronic structure of C540 because of the ionic liquid and the interactions between the molecules forming the ionic liquid inside C540. This is the first available study on endohedral fullerenes with confined ionic liquids published in open literature. More importantly, theoretical simulations carried out in this work could be used both in the prediction of the properties and as a guide to experimentalist for the rational designing of new materials based on ionic liquids confined in fullerenes for specific applications.

---

1. Introduction

Endohedral fullerenes (EHFs) are composed of fullerenes of different size encapsulating atoms, ions, molecules or molecular clusters.^1–3 The unconventional properties of these systems have attracted significant attention in academia not only in physics and chemistry but also in interdisciplinary areas such as materials and biological sciences.^4–7 The possibility of isolating different atoms or molecules (e.g. metal atoms, nitrides, carbides, noble gases or non-metallic atoms) through their confinement in fullerene cages leads to the development of new platforms in searching novel functionalities and applications.^8–10 The main properties of all these types of EHFs and the state-of-the-art of the problem were recently reviewed by Popov et al.³ The novel properties of most of the studied EHFs make them suitable options in fields, such as biomedicine,^11,12 or photovoltaics,¹³ and possible applications in other fields, such as lasers or superconductors, have been considered.³

Studies on the encapsulation of molecules in fullerenes are lesser in comparison with metallofullerenes. Dodziuk et al.¹⁴ reported a broad molecular mechanics study on EHFs formed by the encapsulation of small molecules (H₂, water), hydrocarbons, ketones, amines @C60, C70, C76, C80 and C82 fullerenes, reporting the stabilization energy upon encapsulation and analysing the host–guest sizes in relationship with stabilization upon confinement. Despite the simplicity of the computational approach used, Dodziuk et al.¹⁴ reported the development of weak host–guest interactions for most of the studied compounds. The confinement of H₂ clusters in C60 were studied theoretically by Ren et al.¹⁵ and Barajas-Barraza et al.,¹⁶ by analysing the molecular arrangement as a function of the dihydrogen cluster sizing. The encapsulation of water molecules led to several studies considering the incarceration of a single water molecule^17–19 and water clusters.^20,21 Charkin et al.²² analysed the properties of several guest molecules (e.g. benzene) in fullerenes using methods based on the density functional theory (DFT). DFT methods were also used by Ganji et al.²³ for the study of NH₃ confined in C60, considering not only single ammonia molecules but also the confinement of ammonia clusters. Despite the attraction of using fullerene cages to isolate single molecules or molecular clusters of fixed size, studies on the confinement of more complex molecules have not been reported.

Ionic liquids (ILs) have attracted considerable attention in the scientific community because of their remarkable physical and chemical properties,²⁴ the possibility of tuning these properties through a suitable combination of involved ions,^25,26 and their applications in very different technologies.^27,28 Therefore their behaviour with respect to carbon nanostructures,^29,30 graphene,^31–36 carbon flakes,³⁷ graphene nanoribbons,^38,39 or nanopores arrays^29,40 has been the subject of several studies. The scarce literature on the behavior of fullerenes with ILs systems is mainly devoted to empty fullerene cages solvated in ILs.^39,41–43 Our research group used molecular dynamics simulations for the study of C60 solvated in the N-methylpiperazinium IL.³⁹ Nevertheless, according to our knowledge regarding the studies of ILs, or more complex molecules in general, confined inside fullerene cages (ionic liquid – EHFs) are absent in the literature.

To focus on the rational design of new materials based on ILs confined in endohedral fullerenes for determinate tasks, a deeper knowledge on the influence of encapsulated molecules (guest) on the fullerene (host) features and vice versa is required. Unfortunately, it is difficult to define a priori which molecules lead to concrete features. Up to now, a trial and error approach has been widely used in experiments. This is a typical context wherein theoretical simulations can provide new insights to experimentalists regarding the suitability of new systems. Thus, here, we propose a computational study through both classical molecular dynamics (DM) and density functional theory (DFT) simulations on the characteristics of IL molecules confined inside endohedral fullerenes. For this purpose, choline benzoate IL (CH_BE, Fig. 1) confined inside C540 fullerene was selected as a first case study. Discarding classical ILs, choline-based cation ((2-hydroxyethyl)trimethylammonium) is among the most suitable new options for developing ILs because of the environmental, toxicological and economical aspects^44–46 and the aromatic character of the selected anion. Moreover, our group reported a recent study on the behaviour of CH_BE with regard to graphene and single-walled carbon nanotubes.³⁶ To study the confinement of a single ion or a single IL molecule inside a fullerene cage, we decided to study the confinement of several IL molecules. Therefore, the selected system for this study was an IL cluster composed of 6 ion pairs confined inside a C540 cage (6_CH_BE@C540) with the objective of checking the suitability of isolating small IL clusters inside fullerene cages. The fullerene cage was selected to allow the proper fit of the IL cluster.

Fig. 1 Molecular structure of choline, CH, and benzoate (BE) ions considered in this work.

Therefore, the main goal of this work is to the study the energetic, structural and dynamic properties of 6_CH_BE@C540 in comparison with the pristine C540. Properties of CH_BE@C540 and C540 were studied in vacuum and CH_BE was also used as the surrounding solvent. In addition, considering the recent results by Xu et al.¹⁹ on the electrically driven transport of endohedral fullerenes encapsulating water molecules, the behaviour of 6_CH_BE@C540 (in vacuum and when surrounded by CH_BE solvent) was also analyzed as a function of EEF intensity under external electric fields (EEFs). To our knowledge, this is the first available study on endohedral fullerenes with confined ionic liquids published in open literature.

2. Computational details

2.1 Molecular dynamics simulations

Ionic liquids were modeled according to a force field parameterization previously reported;³⁶ the parameters for C540 were also previously considered.³⁹ Classical molecular dynamics simulations were carried out using the MDynaMix v.5.0 molecular modelling package.⁴⁷ Six CH_BE ion pairs were extracted from the central region of a cubic simulation box containing 200 ion pairs, which was simulated in the NPT ensemble at 0.1 MPa and 303 K for 5 ns, and were placed inside a C540 cage to form the endohedral fullerene. The studied systems together with the labelling are reported in Table 1. Simulations considering one C540 cage, for both empty (pristine) and filled with 6 ion pairs, were carried out for comparison. Initial boxes for systems containing one C540 cage in CH_BE were built from rectangular boxes of 41 × 41 × 41 ų size, in which C540 was initially placed in a central spherical hole with a radius of 3 Å, which is larger than the outer radius of C540 cage.

Table 1 Systems considered in this work for molecular dynamics simulations. N is the number of C540 fullerene cages considered in the simulation and ILpairs@C540 is the number of ion pairs confined inside the C540 cage

Label	N	Medium	IL pairs @C540	IL pairs outside C540
1 × PRIST_C540_VAC	1	Vacuum	0	0
1 × PRIST_C540_IL	1	CH_BE	0	185
1 × 6_CH_BE@C540_VAC	1	Vacuum	6	0
1 × 6_CH_BE@C540_IL	1	CH_BE	6	185

---

Molecular dynamics simulations for all the studied systems were performed at 303 K in the NVT ensemble using the box size reported in the previous paragraph, and with the temperature controlled using the Nosé–Hoover thermostat. Coulombic interactions were handled with the Ewald summation method⁴⁸ with a cut-off radius of 15 Å. Tuckerman–Berne double time step algorithm,⁴⁹ with long and short time steps of 1 and 0.1 fs, was considered for solving the equations of motion. Lorentz–Berthelot mixing rules were used for Lennard-Jones terms. Simulations extending up to 10 ns were performed.

Simulations under EEFs were performed for static fields applied in the z-direction with 0.02, 0.04, 0.06, 0.08 and 0.10 V × Å⁻¹ intensities. These non-equilibrium simulations were also performed using a Nosé–Hoover kinetic thermostat. Using kinetic thermostats for non-equilibrium simulations may lead to problems because of the EEF-induced drift motion contributing to the total kinetic energy, which is not separated by the thermostat from purely thermal effects, thus leading to an overestimation of kinetic energy. Nevertheless, the contribution of the drift motion is strongly dependent on the intensity of the applied field; results previously reported by our group showed that in the case of CH_BE this contribution is almost negligible for fields lower than 0.10 V × Å⁻¹.⁵⁰ Therefore, using kinetic thermostats for the studied systems should lead to reliable results, which is in agreement with the simulations of ILs under moderate EEFs available in the literature.^51–54 Similarly, kinetic thermostats were also used for the simulation on EHFs under EEFs.¹⁹

2.2 DFT calculations

Because of the large size of the systems under study (C540, 6_CH_BE and 6_CH_BE@C540 have 540, 210 and 750 atoms, respectively), only single point calculations over structures obtained from 10 ns long molecular dynamic simulations were carried out. Moreover, to reduce computational costs, DFT calculations were carried out using a pure functional such as the Perdew–Burke–Ernzerhof parameterized generalized gradient approximation (PBE).⁵⁵ First, we studied the effect of the confined IL on the electronic structure of the cage. For this, band structure (BS) diagrams and density of states (DOS) of pristine C540 and 6_CH_BE@C540 systems were computed considering an fcc unit cell along a set of symmetry lines within the Brillouin zone. Partial density of states (PDOS) was obtained using the program developed by A. Postnikov.⁵⁶ These DFT calculations were performed with the SIESTA 3.1 code⁵⁷ using the PBE functional along double-ζ polarized (DZP) basis set and the norm-conserving Troullier–Martins pseudopotentials.⁵⁸ Prior to computing BS, the lattice constant parameter for the fcc C540 crystal was estimated by assessing the minimum of the total energy as a function of the lattice constant.^59,60

Second, the Gaussian 09 (Revision D.01) package⁶¹ was used to compute the binding energy and study the interaction network of the confined CH_BE cluster. These calculations were carried out at the PBE/6-31G* theoretical level. Interactions between different molecules forming the confined IL cluster were analyzed by atoms in molecules (AIM)⁶² and natural bond orbital (NBO)⁶³ theories. Interacting molecules were localized by analyzing NBO charge transfers between different units. Previously, the effect of a C540 cage on intermolecular interactions between ions was tested. First, this analysis was carried out taking into account the C540 cage. Then, NBO calculations were performed for the 6_CH_BE cluster, with cluster geometry obtained upon confinement in C540, but the C540 surrounding cage was not considered. After comparing both analyses, our calculations showed that the surrounding cage leads to negligible effects on the calculation of the charge transfer interactions between confined molecules. Therefore, for the sake of simplicity, the C540 cage was not considered in NBO and AIM studies. Then, we carried out a topological analysis of electronic density over different interacting ion pairs using the AIM2000 program.⁶⁴

3. Results and discussion

The studied systems, as shown in Table 1, led the analysis of several relevant issues: (i) changes in the C540 geometrical structure and properties upon encaging IL molecules and because of IL solvation; (ii) the structure and properties of confined IL molecules, (iii) the characteristics of the C540 external solvation sphere, and (iv) the behaviour of endohedral C540 fullerenes under external electric fields. Therefore, the results reported in this work are analysed and discussed separately according to abovementioned issues.

3.1 Properties of C540 molecules upon IL encaging and salvation

Molecular dynamics simulations of the systems reported in Table 1 were carried out considering C540 molecules as non-rigid, and thus encaging IL pairs; surrounding the fullerene with IL should lead to changes in C540 structure in comparison with the empty and isolated C540, which are analysed in this section. The calculated average C–C bond distance, d_C–C, in C540 is reported in Table 2. Dunlap and Zope⁶⁵ reported d_C–C = 1.4264 Å obtained from quantum chemistry calculations of empty and isolated C540; this value is 2.7% lower than the one reported in Table 1 for the same system. Although considering different computational approaches, values reported in Table 1 may be considered as reasonable. Results reported in Table 2 show that neither confining CH_BE molecules inside C540 nor surrounding it with the IL lead to remarkable changes in d_C–C from no IL case to IL case in/out of the C540 structure. In Table 2, the average C540 radius, R_C540, is also reported, which is defined as the average distance between the C540 center-of-mass and the C atoms in C540. The R_C540 value for empty and isolated fullerene reported in Table 2 (10.7399 Å) is larger than the ones reported by Dunlap and Zoe (10.5528 Å)⁶⁵ and Itoh et al. (10.53 Å),⁶⁶ obtained through quantum chemistry and tight-binding methods, respectively. R_C540 also suffers negligible changes upon confining IL molecules and after solvation with IL, leading to shrinkage percentage of roughly 0.15%. These results indicate that C540 remains almost unchanged with CH_BE inside or outside its structure; nevertheless, we have calculated radial distribution functions, g(r), between the center-of-mass of the C540 and the C540 carbon atoms to quantify structural properties (Fig. 2). Results for empty fullerene in vacuum (1 × PRIST_C540_VAC) show the appearance of four peaks in g(r), Fig. 2a; the structure around one of the twelve pentagonal sites is reported in Fig. 2c and d, showing the atoms corresponding to the peaks in Fig. 2a. Encaging CH_BE in C540 (1 × 6_CH_BE@C540_VAC) leads to a small weakening in the g(r) peaks corresponding to atoms closer to C atoms in pentagonal sites (yellow and gray dots in Fig. 2a, c and d), but the positions of the maxima for the remaining C do not change. The solvation of C540 (both empty and endohedral) leads to remarkable changes in g(r) (Fig. 2a); peaks corresponding to C atoms close to the pentagonal site vanish and only two peaks in g(r) are obtained, showing that although d_C–C and R_C540 do not change upon IL solvation, the structure of the cage suffers subtle changes in the vicinity of the pentagonal sites. This is also confirmed by the corresponding running integrals reported in Fig. 2b. Planarity around the pentagonal sites, ϕ, is defined as ϕ = 360 − (θ₁ + θ₂ + θ₃)⁶⁶ with θ_i being the angles formed by the three bonds between each C pentagonal atoms and its nearest neighbors. Values reported in Table 2 for ϕ are larger than those reported by Itoh et al.⁶⁶ for empty and isolated C540 (9.92°). The subtle changes in C540 structure inferred from g(r) values in Fig. 2 may be justified by considering the changes in ϕ, as shown in Table 2. Both encaging CH_BE molecules inside C540 and solvating the fullerene with CH_BE decrease ϕ for the pentagonal sites and increase planarity for those sites (ϕ = 0° would point to a fully planar site), which could justify the vanishing maxima in g(r) reported in Fig. 2 for the sites marked with yellow and gray symbols in the vicinity of the pentagonal carbons.

Table 2 Average C–C bond distance, d_C–C, for atoms in C540 fullerene, average C540 fullerene radius, R_C540, and average planarity, ϕ, and average intramolecular Lennard-Jones energy for C540, E_LJ(C540). Systems defined as in Table 1. All the values are obtained from molecular dynamics simulations at 303 K

System	dC–C/Å	RC540/Å	ϕ/deg	ELJ(C540)/eV per atom
1 × PRIST_C540_VAC	1.4530 ± 0.0184	10.7399 ± 0.3804	11.04 ± 3.23	50.92 ± 0.00
1 × PRIST_C540_IL	1.4529 ± 0.0174	10.7311 ± 0.3984	8.89 ± 3.37	51.88 ± 0.01
1 × 6_CH_BE@C540_VAC	1.4522 ± 0.0173	10.7340 ± 0.3889	9.42 ± 2.08	51.40 ± 0.01
1 × 6_CH_BE@C540_IL	1.4509 ± 0.0180	10.7224 ± 0.3964	8.08 ± 4.25	52.31 ± 0.01

---

Fig. 2 (a) Radial distribution function, g(r), and (b) the corresponding running integrals of g(r), N, between the center of mass of C540 and the C540 carbon atoms for the reported systems with system labelling as in Table 1. In panels (c) and (d), carbon atoms around a pentagonal site in C540 are reported (top and side views), with atoms color code used to define atoms corresponding to the maxima in g(r) shown in panel (a). In panels (c) and (d), only the pentagonal site is shown for the sake of visibility, and in panel (d) the remaining atoms of C540 are also omitted. Dashed gray vertical lines in panel (b) show the position of maxima in g(r) reported in panel (a). All the values were obtained from molecular dynamics simulations at 303 K.

The energetics of C540 fullerene upon CH_BE confinement and solvation is reported in Table 2, in which intramolecular Lennard-Jones energy for C540, E_LJ(C540), is reported for the studied systems. Reported results show that encaging CH_BE molecules leads to an increment in E_LJ(C540) of roughly 0.5 eV (∼0.5%) for both C540 in vacuum and surrounded by IL, whereas the solvation of C540 with CH_BE molecules increases E_LJ(C540) by roughly 0.93 eV (∼1%) for both pristine and endohedral C540. These results are in agreement with increasing planarity around the pentagonal sites in C540 upon both CH_BE encaging and solvation.

3.2 Properties of CH_BE confined in C540

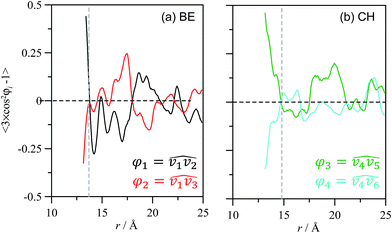
The properties of CH_BE ions confined inside C540 fullerene should change in comparison with CH_BE ions in the bulk liquid. Radial distribution functions between the center of mass of C540 fullerene and those for ions confined inside C540 and for the systems in which the endohedral fullerene is in vacuum and solvated by CH_BE ions are shown in Fig. 3. Fig. 3 show that the structure of confined ions varies from 1 × 6_CH_BE@C540_VAC to 1 × 6_CH_BE@C540_IL, and thus the IL molecules in the external C540 solvation shell also affect the structure of confined ions, especially for CH cation, whereas the effect on BE anion is weaker. Three peaks in g(r) for CH are inferred (with maxima at 2.9, 5.7 and 6.5 Å) when endohedral C540 is in vacuum, whereas a single peak at 6.5 Å is obtained when solvated by IL. On the contrary, for BE, although some subtle changes in g(r) appear on going from vacuum to IL solvation, a well-defined peak at roughly 7.5 Å is obtained. Therefore, solvating CH_BE@C540 endohedral fullerene with CH_BE moves CH ions from the inner spaces of the C540 toward the C540 surface. Similarly, BE ions remain 1 Å closer to the C540 carbon atoms than the CH ions, which is clearly inferred from the behaviour of the running integrals reported in Fig. 3b. Site-site radial distribution functions between the ions of selected atoms and carbon atoms in C540 are reported in Fig. 4 for the 1 × 6_CH_BE@C540_IL system. In the case of confined BE anions, a strong peak close to C540 inner surface is obtained, whereas head COO groups are placed in inner layers roughly 2 Å further into C540 inner surface. For CH cations, hydroxyl oxygen is placed closer than nitrogen atoms to C540 surface. Once the radial arrangement of confined ions is defined, the ion orientation and spatial configuration are also inferred from molecular dynamics simulations. Results reported in Fig. 5 show that BE ions remain closer to the C540 inner surface (roughly at 3.2 Å, Fig. 3) than CH cations with the anion aromatic cycles almost parallel to the C540 surface (although slightly skewed as inferred from Fig. 4 results) because of the disruption of π–π stacking by the curvature of the C540 inner surface. Similarly, spatial distribution functions reported in Fig. 5b show alternating layers of anion and cations with caps corresponding to BE anions in the vicinity of C540 surface, whereas CH cations occupy empty spaces resulting from the arrangement of BE anions to interact with C540 π-system. To characterize the structure of confined ions, several vectors were defined both for BE and CH, and the angles between them were used to quantify spatial orientation with respect to the C540 surface (Fig. 6). For BE anion, φ₁ and φ₂ angles tend to be 90° for a perfect parallel orientation of BE aromatic cycle with regard to C540 surface; results reported in Fig. 6a and b show slight deviation from this 90° reference value, but the obtained preferential orientation allows efficient π–π stacking with fullerene. In the case of CH cation, results reported in Fig. 6b show that the cation is skewed with the hydroxyl group pointing toward the interior of the C540, which is in agreement with the g(r) reported in Fig. 4.

Fig. 3 (a) Radial distribution functions, g(r), and (b) the corresponding running integrals, N, between the center of mass of C540 and the center of mass of CH cation and BE anion for ions confined inside C540 with system labelling as in Table 1. r = 0 Å corresponds to the C540 center of mass, and the vertical gray dashed line shows the position of C540 carbon atoms, defined as the average C540 radius reported in Table 2. All the values obtained from molecular dynamics simulations at 303 K. In the case of 1 × 6_CH_BE@C540_IL system only g(r) inside the C540 is reported.

Fig. 4 Radial distribution functions, g(r), between the carbon atoms in C540 (C) fullerene and selected atoms in CH and BE ions, for 1 endohedral C540 fullerene encaging 6 CH_BE ion pairs surrounded by CH_BE ionic liquid (1 × 6_CH_BE@C540_IL in Table 1). Atoms' code as in Fig. 1. All the values obtained from molecular dynamics simulations at 303 K. Only ions inside the C540 fullerene are considered in the calculation of g(r).

Fig. 5 (a) Representative snapshot and (b) spatial distribution function for CH and BE ions confined inside C540 for 1 endohedral C540 fullerene encaging 6 CH_BE ion pairs surrounded by CH_BE ionic liquid (1 × 6_CH_BE@C540_IL in Table 1). All the values obtained from molecular dynamics simulations at 303 K. Color code: (blue) CH cation and (green) BE anion. In panel (b), dashed red line show the position of C540 surface, defined with the average C540 radius reported in Table 2.

Fig. 6 Orientation of ions confined inside C540 fullerene. All the values calculated for 1 endohedral C540 fullerene encaging 6 CH_BE ion pairs surrounded by CH_BE ionic liquid (1 × 6_CH_BE@C540_IL in Table 1). All the values obtained from molecular dynamics simulations at 303 K.

The energetics of endohedral systems was also analysed from molecular dynamics simulations. Intermolecular Lennard-Jones energy, E_inter(LJ), between the ions and C540 atoms was calculated for 1 × 6_CH_BE@C540_VAC and 1 × 6_CH_BE@C540_IL to infer the effects of external solvation shell ions on the confined ones. E_inter(LJ) between confined ions and C540 atoms changes for BE from −3.61 ± 0.01 eV to −4.92 ± 0.01 eV, and for CH from −2.80 ± 0.01 eV to −3.28 ± 0.01 eV from 1 × 6_CH_BE@C540_VAC to 1 × 6_CH_BE@C540_IL. Therefore, it may be concluded that BE–C540 interaction is remarkably stronger than the CH–C540 interaction when the endohedral fullerene is in vacuum or is surrounded by IL. Similarly, the external solvation of the endohedral fullerene with IL leads to an improvement in the interaction between the confined ions and the internal fullerene surface, most remarkably for BE ions (increasing Lennard-Jones interaction 1.31 eV) but also for CH cations (increasing 0.48 eV), which is in agreement with the structural changes reported in the previous sections.

The effects of host–guest interactions upon ions confinement inside C540 have been also studied thoroughly by analysing the changes in the electronic structure of the 1 × 6_CH_BE@C540_VAC system using density functional theory methods for complementing the information inferred from the molecular dynamics simulations in previous sections. In a first step, the lattice constant parameter for C540 has been optimized; the minimal energy as a function of lattice constant was found for a value of 35.20 Å (Fig. 7). There are no comparison data obtained experimentally for lattice constant.

Fig. 7 Energy convergence as a function of the lattice constant parameter for C540 cage.

Band diagrams for C540 and 1 × 6_CH_BE@C540_VAC along the symmetry directions of the fcc cubic Brillouin zone are plotted in Fig. 8. At the Γ point, a change in the energy gap is inferred, which is increased roughly 0.3 eV due to the confined ionic liquid. Although the lowest unoccupied level (LUMO) practically remains constant, the highest occupied orbital (HOMO) is stabilized by 0.28 eV, whereas the Fermi level (E_F) suffers destabilization of 0.37 eV. Such increase in the E_F level leads to the lowest unoccupied levels to cross with Fermi level. Unoccupied levels whose energy is lower than E_F are evident along all the directions of the Brillouin zone, suggesting long-range interactions between the guest and the C540 cage.⁶⁰ Six unoccupied states whose energies are lower than E_F were found. One of each band would be related with those levels from the cations, which have lost one electron. Changes in the BS diagram have been analyzed with partial density of states (PDOS). Because of the π-electronic structure of C540, the guest PDOS were obtained considering only the contribution of p-orbitals of the atoms (see Fig. 9). As expected, in the case of the C540 cage, total DOS and p-orbital PDOS show a very similar behaviour. For the host–guest system, PDOS due to the atoms of the confined liquid have also been calculated. Total DOS and p-orbital PDOS show very similar profiles, indicating that the band structure is mainly due to the C540 cage. IL confined cluster atoms show slight contributions to the total DOS. In contrast, both HOMO and LUMO levels show an important contribution from the oxygen atoms of the anions. The energy stabilization of the HOMO states could be related with the allocation of the anion negative charge.

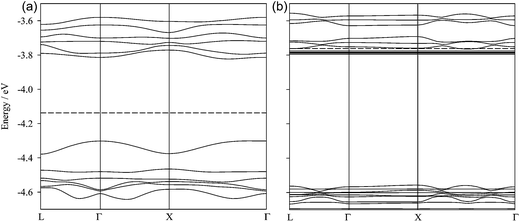Fig. 8 Electronic band structure for (a) pristine C540 and (b) 6_CH_BE@C540 systems. Dotted lines represent Fermi level.

Fig. 9 Total and PDOS of (a) pristine C540 cage and (b) 6_CH_BE@C540 systems.

A binding energy value of −14.01 eV has been estimated for the confined IL cluster and C540 cage at PBE-D/6-31G* level. To our knowledge, binding energies for ILs confined in fullerenes are not reported yet. However, this large binding energy value is indicative of an energetically favoured confinement process for CH_BE IL. The interaction network of ions confined in C540 has been studied through NBO and AIM theories. In the context of AIM theory, the localization of the critical points (CP) is a very suitable tool for the characterization of intermolecular interactions. Although there are four types of critical points, only bond critical points (BCP) were considered to analyze the intermolecular interactions of confined ions. BCPs are characterized through the charge density (ρ), its Laplacian (∇²ρ), and the ellipticity (ε), defined as |(λ₁/λ₂) − 1|, wherein λ_i is the largest/smallest (i = 1/i = 2) curvature of the charge density in a direction perpendicular to the bond path. Ellipticity could be used to measure the extent to which charge is preferentially accumulated, and provides a criterion for structural stability. Thus, large ellipticity values are related with weak bonds. NBO and AIM parameters for those interactions having AIM parameters fulfilling the criteria to be considered intermolecular interactions are reported in Table S1 (ESI†), being plotted in Fig. 10. Almost all the inferred intermolecular interactions arise from the lone pair of both the oxygen atoms in the anion acting as donors and the hydrogen atoms in the cation acting as acceptors. Only NBO charge transfers whose values are larger than 0.05 eV satisfy AIM criteria. As noted in Fig. 10, the confined IL cluster adopts a spherical configuration. As expected, the largest NBO charge transfer correspond with large ρ and small ε, and also with the shortest donor–acceptor distances. Moreover, the strongest interactions are those wherein the phenyl motif of the benzoate anion tends to be parallel to C540 aromatic rings with a typical π–π stacking distance, which is indicative of a π-stacking interaction.

Fig. 10 Different views for the schematic representation of the interaction network for CH_BE confined inside the C540 cage. For clarity, C540 cage and non-interacting H atoms are omitted. C, O, N and H are represented in grey, red, blue and green respectively.

NBO charge distribution for the confined IL molecules has been also analysed (Table 3). All the equivalent atoms show similar charge values, independent of their position in the confined cluster. According to the molecular structure of the cation, a positive charge should be allocated to N atoms, which yield a charge of −0.29 a.u. The calculated total charge of the cation is 1.16 a.u. On the other hand, a negative charge in the anion should be allocated to both the O atoms, which show a charge of −0.73 a.u. with the total anion charge being −0.85 a.u. This effect is related to a charge transfer of around 0.3 eV between the cation and the anion. This charge transfer energy is very similar to the change in the HOMO state due to confined IL. Then, a relationship between the stabilization of the HOMO state and charge transfer between IL ions could be established.

Table 3 NBO charge distribution for atoms in CH_BE confined inside C540 (1 × 6_CH_BE@C540_VAC). See Fig. 1 for atom labelling

Atom	NBO charge^a/a. u.
a Reported data are average values over all the CH_BE atoms confined inside C540.b Alkyl hydrogen atoms in CH cation.c Aromatic hydrogen atoms in BE anion.
N1	−0.29
C1	−0.50
Hal^b	0.28
C2	−0.28
C3	−0.14
O1	−0.77
H4	0.50
C6/C7	−0.23
C5	−0.15
C4	0.72
O2	−0.73
Har^c	0.24

---

HOMO and LUMO states for the 1 × 6_CH_BE@C540_VAC system also show an important contribution from the confined IL cluster (Fig. 11). As expected from PDOS results, HOMO and LUMO orbitals are mainly located on anions. LUMO orbitals are mainly delocalized over all the anion, whereas HOMO is mainly located over COO⁻ motifs. Although Fig. 11 only plots the HOMO and LUMO orbital, an analogous behaviour was inferred for six orbitals below and above.

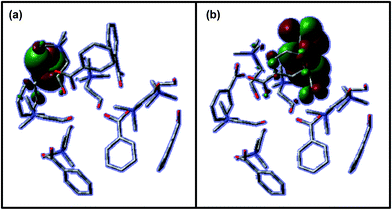Fig. 11 Isovalues of (a) HOMO and (b) LUMO molecular orbitals for 6_CH_BE cluster confined in C540. Values were calculated at PBE-D/6-31G* level.

3.3 Properties of C540 external solvation by CH_BE

The effect of external solvation shells on the properties of ions confined inside C540 fullerene was analysed in a previous section; in the following section, the structure of CH_BE ions externally solvating C540 fullerene will be analysed. Fig. 12 shows g(r) for the systems formed by one C540 fullerene surrounded by the ionic liquid for both empty (1 × PRIST_C540_IL, Fig. 12a) and filled with IL (1 × 6_CH_BE@C540_IL, Fig. 12b) fullerene. g(r) for BE and CH ions show strong peaks for the first external solvation shell, for both empty and endohedral C540. BE anions are roughly 1 Å closer to the C540 external surface than CH anions, which is parallel with the behaviour of confined ions with regard to the internal C540 surface (Fig. 12b). The distance between the center of mass for externally solvating BE anions and the C540 surface is 3.2 Å, whereas it is 4.2 Å in the case of CH cations for 1 × PRIST_C540_IL. The external solvation of the fullerene by IL is weakly affected by the presence of confined ions inside the C540 (1 × 6_CH_BE@C540_IL); nevertheless, results reported in Fig. 12 show that confining CH_BE ions inside C540 leads to an approaching of the first CH_BE external solvation shell to the C540 surface by roughly 0.1 Å, which is in agreement with the effect of the external shell on internal confined ions. Site–site g(r) between C540 carbon atoms and selected ion sites for externally solvating ions are reported in Fig. 13 for empty and endohedral C540. A comparison between results reported in Fig. 4 and 13 shows similar structuring on the C540 surface both for CH_BE ions inside and outside the fullerene. Similarly, the effect of confined ions on the structuring of the external ionic solvation shell is very weak, as can be inferred from the comparison of Fig. 13a and b; nevertheless, to quantify this effect, the differences between the running integrals obtained from g(r) for the solvation of empty and endohedral C540 are reported in Fig. 14. The first external solvation shell (r ∼ <10 Å) is slightly richer in BE ions for empty fullerene than for the endohedral one, whereas the opposite effect is obtained for the CH cation. Spatial arrangement around C540 for ions externally solvating the fullerene are reported in Fig. 15. The image showed in Fig. 15a probes BE ions lying almost parallel to the C540 external surface, with a slight skew in agreement with g(r) reported in Fig. 13. Spatial distribution function reported in Fig. 15b shows alternating layers of anions and cations with BE anions closer to the C540 surface and CH cations occupying the available space. Orientations of ions in the external shell are also analysed through the order parameters defined for the molecular vectors reported in Fig. 16, showing a strong preferential orientation for CH and BE ions with almost parallel arrangements of both the ions in the first external shell.

Fig. 12 Radial distribution functions, g(r), between the center of mass of C540 and the center of mass of CH cation and BE anion for (a) 1 empty C540 fullerene surrounded by CH_BE ionic liquid (1 × PRIST_C540_IL in Table 1), and (b) 1 endohedral C540 fullerene encaging 6 CH_BE ion pairs surrounded by CH_BE ionic liquid (1 × 6_CH_BE@C540_IL in Table 1). All the values obtained from molecular dynamics simulations at 303 K. r = 0 Å correspond to C540 center of mass, and the vertical gray dashed line shows the position of C540 carbon atoms, defined as the average C540 radius reported in Table 2.

Fig. 13 Radial distribution functions, g(r), between the carbon atoms in C540 (C) fullerene and selected atoms in CH and BE ions, for (a) 1 empty C540 fullerene surrounded by CH_BE ionic liquid (1 × PRIST_C540_IL in Table 1), and (b) 1 endohedral C540 fullerene encaging 6 CH_BE ion pairs surrounded by CH_BE ionic liquid (1 × 6_CH_BE@C540_IL in Table 1). Atoms code as in Fig. 1. All the values obtained from molecular dynamics simulations at 303 K. In panel b, only ions outside the C540 fullerene are considered in the calculation of g(r). r = 0 Å corresponds to the position of C540 carbon atoms.

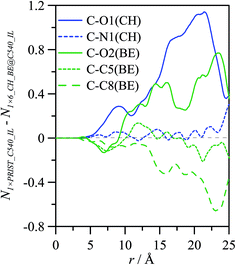Fig. 14 Running integrals, N, differences obtained from the corresponding radial distribution functions reported in Fig. 13 between values for 1 empty C540 fullerene surrounded by CH_BE ionic liquid (N_{1×PRIST_C540_IL}, defined as in Table 1), and 1 endohedral C540 fullerene encaging 6 CH_BE ion pairs surrounded by CH_BE ionic liquid (N_{1×6_CH_BE@C540_IL}, defined as in Table 1). Atoms' code as in Fig. 1. For N_{1×6_CH_BE@C540_IL} only ions outside C540 were considered, as in Fig. 13.

Fig. 15 (a) Representative snapshot and (b) spatial distribution function for CH and BE ions in the first external solvation shell of C540 for 1 endohedral C540 fullerene encaging 6 CH_BE ion pairs surrounded by CH_BE ionic liquid (1 × 6_CH_BE@C540_IL in Table 1). All the values obtained from molecular dynamics simulations at 303 K. Color code: (blue) CH cation and (green) BE anion. In panel (b), dashed red line show the position of C540 surface, defined with the average C540 radius reported in Table 2.

Fig. 16 Orientation of ions outside C540 fullerene. All values calculated for 1 endohedral C540 fullerene encaging 6 CH_BE ion pairs surrounded by CH_BE ionic liquid (1 × 6_CH_BE@C540_IL in Table 1). All values obtained from molecular dynamics simulations at 303 K. Vectors defined as in Fig. 6. Vertical gray dashed lines stand for the position of the first external solvation shell defined according to g(r) in Fig. 12.

The energetics for the interaction between the externally solvating ions and C540 is reported in Table 4. The reported results show stronger BE–C540 than CH–C540 interactions (roughly 2 eV stronger), which may be justified considering that BE anions are closer to the C540 external surface than CH cations, as reported in previous sections. Moreover, putting C540 inside the IL weakens CH–BE interactions, both for Coulombic and Lennard-Jones contributions, in comparison with those in pure CH_IL (with no C540).⁶⁷ Nevertheless, this decrease in anion–cation interaction strength upon C540 solvation evolves in parallel with a decrease in anion–anion and cation–cation Coulombic repulsive energies. Therefore, the total balance of interionic energy, defined as the difference between the anion–cation interaction energy minus the sum of anion–anion and cation–cation contributions, is −5.49 eV for pure CH_BE whereas it is −5.79 and −5.56 eV, for 1 × PRIST_C540_IL and 1 × 6_CH_BE@C540_IL, respectively. Similarly, the total ion–C540 interactions are −19.19 and −27.39 eV for 1 × PRIST_C540_IL and 1 × 6_CH_BE@C540_IL, respectively. Therefore, placing C540 fullerene into CH_BE is strongly energetically favoured.

Table 4 Interaction energies, E_inter, between the reported constituents in the systems 1 × PRIST_C540_IL, 1 × 6_CH_BE@C540_IL and in the pure ionic liquid (CH_BE, ionic liquid in absence of C540 fullerene). All the values are obtained from molecular dynamics simulations at 303 K. Coul and LJ stand for Coulombic and van der Waals components of the total interaction energy. All values are in eV

	CH_BE^a		1 × PRIST_C540_IL		1 × 6_CH_BE@C540_IL
	Einter(Coul)	Einter(LJ)	Einter(Coul)	Einter(LJ)	Einter(Coul)	Einter(LJ)
a Values for pure CH_BE obtained at 298 K (ref. 67).
BE–C540	—	—	—	−10.61	—	−15.53
CH–C540	—	—	—	−8.59	—	−11.87
BE–CH	−27.68	−0.38	−27.15	−0.35	−26.77	−0.34
BE–BE	11.34	−0.16	10.87	−0.16	10.78	−0.15
CH–CH	11.55	−0.15	11.15	−0.16	11.07	−0.15

---

The dynamic properties of the studied endohedral fullerene are of importance to characterize the studied systems. Self-diffusion coefficients, D, were obtained using molecular dynamics simulation trajectories from mean square displacements and Einstein's equation. Diffusion properties for the 1 × 6_CH_BE@C540_IL system were calculated for ions confined inside the fullerene, in the first external solvation shell (defined according to the first minima in g(r) reported in Fig. 12), and the remaining fluid layers (Table 5). Ions confined inside C540 fullerene show very low D values, two orders of magnitude lower than those for bulk CH_BE in the absence of fullerene, and show a solid-like behaviour of confined ions. This slow dynamics of ionic liquids upon confinement has also been reported in carbon nanotubes^39,68 and may be explained considering the formation of a crystal-like phase of ions when confined inside carbon nanostructures.⁶⁹ Nevertheless, this effect is strongly dependent on the size of ions and the width of the carbon nanotube. Ohba and Chaban⁷⁰ have recently reported that for 1-ethyl-3-methylimidazolium chloride confinement in (10,10) carbon nanotubes leads to an increase of 1.5 orders of magnitude for the diffusion rates in comparison with the bulk fluid, whereas in the case of (22,22) carbon nanotube, diffusion rates are similar to or slightly lower than that in bulk fluid, depending on temperature. This behaviour is justified considering the disruption of the ionic liquid network upon confinement, and thus nanotubes with large diameter can maintain the most relevant features of the bulk fluid when ions are confined. In the case of confinement in large fullerenes, when the cage is fully filled with ions, similar to this work, the mobility of the ions is very low and anion–cation intermolecular forces are very strong, which would justify the poor diffusion rates obtained from molecular dynamics simulations.

Table 5 Center-of-mass self-diffusion coefficients, D, in the system 1 × 6_CH_BE@C540_IL. All the values obtained from molecular dynamics simulations at 303 K. Values calculated for ions confined inside the C540 fullerene, r < R_C540, for ions in the first external solvation shell of C540 fullerene, R_C540 < r < 17 Å, and for ions in outer C540 fullerenes solvation shells, r > 17 Å, where r is the distance between the center of mass of C540 and the center of mass of the corresponding ion, and R_C540 is C540 average radius reported in Table 2. The definition of solvation shells is according to radial distribution functions reported in Fig. 12b

Shell	r/Å	10^11 × D/m^2 s^−1
		BE	CH
a Values calculated for pure CH_BE in the absence of C540.
CH_BE^a	—	0.1107 ± 0.0051	0.0983 ± 0.0049
Ions inside C540	r < RC540	0.0024 ± 0.0006	0.0035 ± 0.0004
Ions in the first external solvation shell of C540	RC540 < r < 17	0.0015 ± 0.0008	0.0017 ± 0.0008
Ions in outer external solvation shell of C540	r > 17	0.0963 ± 0.0039	0.0900 ± 0.0040

---

Similarly, ions in the first external solvation shell also show very low D values, even lower than those of confined, which may be justified considering the strong interaction with the C540 surface as inferred from the energetics reported in Table 4. D values for confined BE anions and in the first external solvation shell are lower than those for CH cations, which is in contrast with the behaviour of more external ions or in the bulk CH_BE. This may be justified considering the stronger BE–C540 interaction in comparison with CH–C540 because of the π–π stacking of BE ions. Banerjee⁷¹ reported the solvation of fullerenes by water, toluene and acetone, in which it was shown that molecules in the first external solvation shell had reduced mobility in comparison with bulk molecules. For example, results from Banerjee⁷¹ in water–C540 system showed D values of 2.1 × 10⁻⁹ and 2.4 × 10⁻⁹ m² s⁻¹ for water molecules in the first solvation shell and in the bulk phase, respectively. Viscosity of CH_BE IL and the self-diffusion coefficients are three orders of magnitude larger than that of water, but in addition to this effect, water molecules decrease their mobility roughly up to 12% on going from bulk water to C540 solvation layer, whereas the mobility of BE ions is 60 times lower in the solvation layer than in the bulk IL. Banerjee⁷¹ also reported studies on toluene–C60 showing that toluene mobility decreases up to 25% on going to fullerene solvation shells, which is almost double the effect than that for water molecules, showing the importance of π–π interaction with the fullerene. Nevertheless, changes in ionic mobility on ILs going to fullerene solvation shells are remarkably larger than those for organic solvents. The diffusion of CH_BE ions placed further into the first C540 external solvation shell approaches that of pure CH_BE, although D values are lower for 1 × 6_CH_BE@C540_IL than for pure CH_BE, showing that the disrupting effect of C540 on IL structure extends to large distances of the fullerene, which is in agreement with the behaviour of g(r) showed in Fig. 12. Similarly, the self-diffusion coefficient of C540 in CH_BE was also calculated to be (0.0004 ± 0.0002) × 10⁻¹¹ m² s⁻¹; the very low D value should be considered with caution because of the length of the simulations (obviously fully diffusive regime was not reached for C540 in the applied simulation time), but it shows, at least qualitatively, the low mobility of the studied giant fullerene in CH_BE.

3.4 Endohedral fullerenes under external electric fields

In a recent work, Xu and Chen proposed to control the direction and rate of transport of endohedral C60 fullerenes containing a single water molecule using external electric fields,¹⁹ and thus, encouraged by their results, the behaviour of 1 × 6_CH_BE@C540_IL under EEFs was studied as a method to control the slow diffusion of the studied C540 endohedral fullerene in CH_BE. For comparison, the behaviour of an empty C540 fullerene, 1 × PRIST_C540_IL, under EEFs was also studied. In a recent work,⁷² our group reported a study on the behaviour of bulk CH_BE (among other ILs) under EEFs. These previous results showed that CH_BE has an intrinsic electric field of 0.36 V Å⁻¹ and 0.31 V Å⁻¹ for BE and CH ions, respectively. Therefore, considering that EEFs applied in this work were lower than 0.10 V Å⁻¹, the effect of EEFs on the studied systems should be moderate. Nevertheless, the possible application of stronger EEFs was discarded considering the common range of applied fields for technical applications. The molecular dynamics simulations carried out in this work under EEFs were performed using fields applied along the z-direction, and thus the z-component of the total dipole moment, μ_z, was calculated for the studied systems. Fig. 17 shows μ_z values for BE anions under EEFs for the first ns of simulations, and for ions confined inside the fullerene, in the first external shell and in outer regions. Results in Fig. 17a show that ions confined inside C540 are not affected by the applied EEFs (for E ≤ 0.10 V Å⁻¹), and thus the fullerene acts as a screening cage for the confined ions. These results may seem puzzling, Amusia and Baltenkov⁷³ showed that C60 fullerene under a static electric field behaves as a set of separate atoms instead of a conducting sphere, and thus the fullerene cage would not be able to fully screen the external electric field. Nevertheless, Connerade et al.⁷⁴ and Lo et al.⁷⁵ analyzed the dynamical screening of fullerenes and showed that in the static limit confined atoms are completely shielded from the external field; moreover, this screening effect against electromagnetic radiation stands for frequencies lower than 20 eV. Therefore, in the case of the endohedral systems studied in this work (ionic liquid@C540), we have to consider several factors that justify the strong screening of the C540 cage: (i) the studied ionic liquids have a strong intrinsic electric field, as mentioned above, (ii) the applied external fields are lower than 0.10 V Å⁻¹, (iii) strong ion–C540 interactions because the cage is fully filled with ions instead of placing a single molecule inside.

Fig. 17 Total dipole moment along the z-direction for BE anions, μ_Z, for 1 endohedral C540 fullerene encaging 6 CH_BE ion pairs surrounded by CH_BE ionic liquid (1 × 6_CH_BE@C540_IL in Table 1) under EEFs. BE anions (a) confined inside C540, (b) in the first external C540 solvation shell, and (c) in outer shells.

For ions solvating C540 in the first layer (Fig. 17b) the reported results also show an almost negligible effect of the applied fields, which is in agreement with the strength of the ions–C540 interactions reported in previous sections. Ions in regions further than the first C540 shell are only affected by the field for the stronger cases studied. Analogous results were inferred for CH cations and for the behaviour of empty fullerenes under EEFs.

4. Conclusions

A combined DFT and molecular modelling study of the properties of choline benzoate ionic liquid encapsulated in endohedral C540 fullerene is reported in this work. The behaviour of ions confined inside the fullerene is characterized by the strong π–π stacking of BE anions on C540 walls, which determine the structure of the confined ion pairs, with CH cations occupying the available empty spaces in more internal regions, but also being able to interact with the fullerene. The structure of the confined ions is affected by the presence or absence of ions solvating outside the C540, which improves the ion–C540 interactions for confined ions. DFT studies on the electronic properties of CH_BE@C540 fullerene show changes in the band structures and density of states of C540 upon confinement of ions, which arise from the ions–C540 interactions, which are characterized by AIM and NBO analysis. The results of EEF applications for the studied endohedral fullerenes show that C540 acts as a perfect chemical Faraday cage for the confined ions, but very strong interaction between the ions in the first external C540 solvation layer and C540 surface lead to negligible effects of applied EEFs on these ions. Only when large EEFs are applied, some effects are obtained on the structuring of ions in regions further than the first solvation layers of C540.

In general, theoretical simulations carried out in this work could be used in both the prediction of the properties and the rational design of new materials based on IL cluster confined in fullerenes for technological applications.

Acknowledgements

Gregorio García acknowledges the funding by Junta de Castilla y León and cofunding by European Social Fund for a postdoctoral contract. We also acknowledge the Computing and Advanced Technologies Foundation of Extremadura (CénitS, LUSITANIA Supercomputer, Spain) and the Foundation of Supercomputing Center of Castile and León (FCSCL, CALÉNDULA Supercomputer, Spain) for providing supercomputing facilities. The statements made herein are solely the responsibility of the authors.

References

1. H. Shinohara, Rep. Prog. Phys., 2000, 63, 843–892.
2. T. Akasaka and S. Nagase, Endofullerenes: A New Family of Carbon Clusters, Kluwer, Dordretch, 2002.
3. A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989–6113.
4. A. Rodríguez-Fortea, A. L. Balch and J. M. Poblet, Chem. Soc. Rev., 2011, 40, 3551–3563.
5. S. Osuna, M. Swart and M. Solá, Phys. Chem. Chem. Phys., 2011, 13, 3585–3603.
6. D. M. Rivera-Nazario, J. R. Pinzón, S. Stevenson and L. A. Echegoyen, J. Phys. Org. Chem., 2013, 26, 194–205.
7. T. Akasaka and X. Lu, Chem. Rec., 2011, 12, 256–269.
8. N. J. Turro, J. Y. C. Chen, E. Sartori, M. Ruzzi, A. Marti, R. Lawler, S. Jockusch, J. López-Gejo, K. Komatsu and Y. Murata, Acc. Chem. Res., 2010, 43, 335–345.
9. M. Rudolf, S. Wolfrum, M. Guldi, L. Feng, T. Tsuchiya, T. Akasaka and L. Echegoyen, Chem.–Eur. J., 2012, 18, 5136–5148.
10. L. Feng, M. Rudolf, S. Wolfrum, A. Troeger, Z. Slanina, T. Akasaka, S. Nagase, N. Martín, T. Ameri, C. Brabec and D. M. Guldi, J. Am. Chem. Soc., 2012, 134, 12190–12197.
11. F. P. atouros and M. D. Shultz, Nanomedicine, 2013, 8, 1853–1864.
12. M. Carini, L. Dordevic, T. Da Ros, Fullerenes in Biology and Medicine, in. Handbook of Carbon Nanomaterials. Vol. 3, Medicinal and Bio-related Applications, ed. D'Souza F. and Kadish K. M., World Scientific, 2012, pp. 1–47.
13. R. B. Ross, C. M. Cardona, D. M. Gauldi, S. G. Sankaranarayanan, M. O. Reese, N. Kopidakis, J. Peet, B. Walker, G. C. Bazan, E. V. van Keuren, B. C. Holloway and M. Drees, Nat. Mater., 2009, 8, 208–212.
14. H. Dodziuk, G. Dolgonos and O. Lukin, Carbon, 2001, 39, 1907–1911.
15. Y. X. Ren, T. Y. Ng and K. M. Liew, Carbon, 2006, 44, 397–406.
16. R. E. Barajas-Barraza and R. A. Guirado-López, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155426.
17. Q. Zhang, T. Pankewitz, S. Liu, W. Klopper and L. Gan, Angew. Chem., Int. Ed., 2010, 49, 9935–9938.
18. L. Shi and L. Gan, J. Phys. Org. Chem., 2013, 26, 766–772.
19. B. Xu and X. Chen, Phys. Rev. Lett., 2013, 110, 156103.
20. C. N. Ramachandran and N. Sathyamurthy, Chem. Phys. Lett., 2005, 410, 348–351.
21. J. Hernández-Rojas, V. Monteseguro, J. Bretón and J. M. Gómez-Llorente, Chem. Phys., 2012, 399, 240–244.
22. O. P. Charkin and N. M. Klimenko, Adv. Quantum Chem., 2009, 58, 69–114.
23. M. D. Ganji, M. Mohseni and O. Goli, J. Mol. Struct.: THEOCHEM, 2009, 913, 54–57.
24. C. A. Angell, Y. Ansari and Z. Zhao, Faraday Discuss., 2012, 154, 9–27.
25. E. T. Fox, E. F. Weaver and W. A. Henderson, J. Phys. Chem. C, 2012, 116, 5270–5274.
26. A. T. Kurananithi and A. Mehrkesh, AIChE J., 2013, 59, 4627–4640.
27. N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123–150.
28. S. Werner, M. Haumann and P. Wasserscheid, Annu. Rev. Chem. Biomol. Eng., 2010, 1, 203–230.
29. T. Fukushima, A. Kosaka, Y. Ishimura, T. Yamamoto, T. Takigawa, N. Ishii and T. Aida, Science, 2003, 300, 2072–2074.
30. T. Fukushima and T. Aida, Chem.–Eur. J., 2007, 13, 5048–5058.
31. M. Sha, G. Wu, Y. Liu, Z. Tang and H. Fang, J. Phys. Chem. C, 2009, 113, 4618–4622.
32. S. Maolin, Z. Fuchun, W. Guozhong, F. Haiping, W. Chunlei, C. Shimou, Z. Yi and H. Jun, J. Chem. Phys., 2008, 128, 134504.
33. S. Wang, S. Li, Z. Cao and T. Yan, J. Phys. Chem. C, 2010, 114, 990–995.
34. Q. Dou, M. L. Sha, H. Y. Fu and G. Wu, J. Phys.: Condens. Matter, 2011, 23, 175001–175009.
35. S. A. Kislenko, I. S. Samoylov and R. H. Amirov, Phys. Chem. Chem. Phys., 2009, 11, 5584–5590.
36. M. Atilhan and S. Aparicio, J. Phys. Chem. C, 2012, 116, 12055–12065.
37. E. Soolo, D. Brandell, A. Liivat, H. Kasemägi, T. Tamm and A. Aablo, J. Mol. Model., 2012, 18, 1541–1552.
38. N. D. Patra, Y. Song and P. Kral, ACS Nano, 2011, 5, 1798–1804.
39. M. Atilhan and S. Aparicio, J. Phys. Chem. C, 2013, 117, 22046–22059.
40. P. Wu, J. Huang, V. Meunier, B. G. Sumpter and R. Qiao, ACS Nano, 2011, 11, 9044–9051.
41. B. Qi and X. Xang, Mater. Lett., 2008, 62, 980–983.
42. C. M. Maciel and E. E. Fileti, Chem. Phys. Lett., 2013, 568, 75–79.
43. V. V. Chaban, C. Maciel and E. E. Fileti, J. Solution Chem., 2014, 43, 1010–1031.
44. P. Nockemann, B. Thijs, K. Driesen, C. R. Jansenn, K. van Hecke, L. van Meervelt, S. Kossmann, B. Kirchner and K. Binnemans, J. Phys. Chem. B, 2007, 111, 5254–5263.
45. D. J. Couling, R. J. Bernot, K. M. Docherty, J. K. Dixon and E. J. Maginn, Green Chem., 2006, 8, 82–90.
46. J. Pernak, A. Syguda, I. Mirska, J. Nawrot, A. Pradzynska, S. T. Griffin and R. Rogers, Choline-Derivative-Based Ionic Liquids, Chem.–Eur. J., 2007, 13, 6817–6827.
47. A. P. Lyubartsev and A. Laaksonen, Comput. Phys. Commun., 2000, 128, 565–589.
48. U. L. Essmann, M. L. Perera, T. Berkowitz, H. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
49. M. Tuckerman, B. J. Berne and G. J. Martyna, J. Chem. Phys., 1992, 97, 1990–2001.
50. S. Aparicio, M. Atilhan and N. Pala, J. Chem. Phys., 2013, 139, 224502.
51. N. J. English, D. A. Mooney and S. O’Brien, Mol. Phys., 2011, 109, 625–638.
52. Y. Zhao, K. Dong, X. Liu, S. Zhang, J. Zhu and J. Wang, Mol. Simul., 2012, 38, 172–178.
53. N. J. English and D. A. Mooney, J. Phys. Chem. B, 2009, 113, 10128–10134.
54. N. J. English and D. A. Mooney, Phys. Chem. Chem. Phys., 2009, 11, 9370–9374.
55. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
56. http://www.home.uni-osnabrueck.de/apostnik/download.html, Accesed on January 16, 2014.
57. J. M Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779.
58. N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006.
59. J. Kürti, J. Koltaik, V. Zólyomi and S. Pekker, Phys. Status Solidi B, 2009, 246, 2618–2621.
60. A. Z. Alzanrani, ISRN Condens. Matter Phys., 2012, 2012, 208234.
61. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. M. Nakatsuji, H. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. T. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2010.
62. R. F. W. Bader, Atoms in Molecules: a Quantum Theory, Oxford University Press, Oxford, 1990.
63. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
64. F. Biegler-König, J. Schönbohm and D. Bayles, J. Comput. Chem., 2001, 22, 545–559.
65. B. E. Dunlap and R. J. Zope, Chem. Phys. Lett., 2006, 422, 451–454.
66. S. Itoh, P. Ordejón, D. A. Drabold and R. M. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 2132–2140.
67. S. Aparicio and M. Atilhan, J. Phys. Chem. B, 2012, 116, 9171–9185.
68. R. Singh, J. Monk and F. R. Hung, J. Phys. Chem. C, 2010, 114, 15478.
69. S. Chen, G. Wu, M. Sha and S. Huang, J. Am. Chem. Soc., 2007, 129, 2416–2417.
70. T. Ohba and V. V. Chaban, J. Phys. Chem. B, 2014, 118, 6234.
71. S. Banerjee, J. Chem. Phys., 2013, 138, 044318.
72. S. Aparicio, M. Atilhan and N. Pala, J. Chem. Phys., 2013, 139, 224502.
73. M. Y. Amusia and A. S. Baltenkov, Phys. Lett. A, 2006, 360, 294–298.
74. J. P. Connerade and A. V. Slov'yov, J. Phys. B: At., Mol. Opt. Phys., 2005, 38, 807.
75. S. Lo, A. V. Korol and A. V. Slov'yov, J. Phys. B: At., Mol. Opt. Phys., 2007, 40, 3973.

---

Footnote

† Electronic supplementary information (ESI) available: NBO and AIM results (Table S1). See DOI: 10.1039/c4ra07239a

---