Theoretical analyses of the fluorescence lifetimes of the D-amino acid oxidase–benzoate complex dimer from porcine kidney: molecular dynamics simulation and photoinduced electron transfer†
Arthit Nueangaudoma,
Kiattisak Lugsanangarma,
Somsak Pianwanita,
Sirirat Kokpol*a,
Nadtanet Nunthabootb,
Fumio Tanaka*ac,
Seiji Taniguchic and
Haik Chosrowjanc
aDepartment of Chemistry, Faculty of Science, Chulalongkorn University, 254 Phayathai Road, Bangkok 10330, Thailand. E-mail: Somsak.t@chula.ac.th
bDepartment of Chemistry, Faculty of Science, Mahasarakham University, Mahasarakham 44150, Thailand
cDivision of Laser Biochemistry, Institute for Laser Technology, Utsubo-Honmachi, 1-8-4, Nishiku, Osaka 550-0004, Japan. E-mail: fumio.tanaka@yahoo.com
First published on 8th October 2014
Abstract
The mechanism of photoinduced electron transfer (ET) from benzoate (Bz) and aromatic amino acids to the excited isoalloxazine (Iso*) in the D-amino acid oxidase–benzoate complex (DAOB) dimer from porcine kidney was studied using molecular dynamics simulation (MDS) and an electron transfer theory, and compared with that in the DAOB monomer. The DAOB dimer displayed two fluorescent lifetime components of 0.85 ps and 4.8 ps, as reported. The ET parameters contained in the Kakitani and Mataga (KM) model were determined so as to reproduce these lifetimes with MDS atomic coordinates. The Bz–isoalloxazine (Iso) distances were 0.66 nm in subunit A (Sub A), 0.68 nm in subunit B (Sub B) and 0.61 nm in the monomer. The fluorescent lifetimes of 4.8 ps and 0.85 ps were found to originate from Sub A and Sub B, respectively. In Sub A, Tyr228 was the fastest ET donor followed by Bz and Tyr55, while Bz was followed by Tyr228 and Tyr314 in Sub B. The ET rate from Bz was fastest in Sub B, followed by that in Sub A and the DAOB monomer. The static dielectric constants obtained near Iso were 2.4–2.6 in the DAOB dimer and monomer and 5.8–5.9 in holo D-amino oxidase (DAAO). The different dielectric constants could account for the experimental fluorescence peak observed for DAOB (524 nm) and DAAO (530 nm). Logarithmic ET rates decreased linearly with the donor–acceptor distance expressed by both center to center distance (Rc) and edge to edge distance (Re) in Sub A and Sub B of DAOB dimer and monomer, which reveals that the conventional Dutton rule holds in the ET processes in DAOB. The logarithmic ET rates were decomposed into the electronic coupling (EC), square root (SQ) and exponential (GTRAM) terms. It was found that both the EC term and the GTRAM term also decreased linearly with Rc. The sum of the slopes in the EC and GTRAM vs. Rc plots coincided with the slopes in the logarithmic ET rate vs. Rc functions, suggesting that the GTRAM term makes a significant contribution to the linear relations between logarithmic ET rate and Rc.
I. Introduction
D-Amino acid oxidase (DAAO) from porcine kidney contains flavin adenine dinucleotide (FAD) as a cofactor,1,2 and exists in a wide range of species from yeasts to humans.3–5 Its function is to oxidize D-amino acids to the corresponding imino acids, producing ammonia and hydrogen peroxide. Recently, mammalian DAAO has been demonstrated to be involved in D-serine metabolism in the brain and to regulate glutamatergic neurotransmission.6,7 Various novel inhibitors to human DAAO have been found by means of in silico screening.8DAAO from porcine kidney exists in a monomer (Mw 39 kDa)–dimer equilibrium state at relatively low concentrations,9–12 and may be in a dimer–tetramer equilibrium at higher concentrations.13–15 The crystal structures of the DAAO–benzoate (Bz) complex (DAOB) dimer have been determined.16,17 Each subunit of the DAOB dimer contains Iso as the ET acceptor, and one Bz, 10 Trp and 14 Tyr residues as potential ET donors.
The fluorescence of flavins in many flavoproteins is strongly quenched, which is ascribed to photoinduced electron transfer (ET) from tryptophans (Trp) and/or tyrosines (Tyr) to the excited isoalloxazine (Iso*).18–20 Fluorescence dynamics of flavoproteins have been worked in the picoseconds domain by Visser et al.,21,22 by means of photon-counting method. Ultrafast fluorescence dynamics of some flavoproteins in the time domain of femtoseconds to picoseconds have been studied by means of fluorescence up-conversion,23–27 and theoretically by molecular dynamics simulation (MDS) and an electron transfer theory28–32 using the available protein structures.16,17
The structural basis for the temperature-induced transition of the DAAO monomer has been analyzed by MDS with the Kakitani and Mataga (KM) equation based ET theory.33 The conformational change was characterized with the ET rates from Tyr224, Tyr228 and Tyr314 to the Iso*. The fluorescence lifetimes of flavin in DAAO and DAOB monomer have been reported to be 160 and 60 ps, respectively, with the decreased lifetime upon the binding of Bz to DAAO being ascribed to the fast ET from Bz to Iso*.34,35 The fluorescence dynamics of the DAOB dimer has been reported by means of the up-conversion,23 whilst it was recently reported that the DAAO dimer displays non-equivalent conformations between the two subunits.36 In the present work we have demonstrated by means of MDS structures and KM-theory based ET analysis that not only the structure of the DAOB dimer is quite different from the DAOB monomer, but also the conformations of subunit A (Sub A) and Sub B of the DAOB dimer are non-equivalent.
II. Methods of analyses
MDS calculation
The starting structure of DAOB was obtained from the X-ray structure in the protein data bank (PDB code: 1VE9).16 The MDS and all calculations were performed using the AMBER 10 suite of programs.37 The parm99 force field38 was used to describe the protein atoms the general Amber force field with the restrained electrostatic potential37 charges was used for the FAD and Bz, and all missing hydrogen atoms of the protein were added using the LEaP module.39 The simulated systems were subsequently solvated with a cubic box of 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 390 TIP3P water molecules, and the electroneutrality of the system was attained by adding 10 sodium counter-ions. The systems were set up under the isobaric–isothermal ensemble with a constant pressure (1 atm) and temperature (293 K). Electrostatic interactions were corrected by the Particle Mesh Ewald method.40 The SHAKE algorithm41 was used to constrain all bonds involving hydrogen atoms. All MDS based calculations were performed with a time steps of 2 fs and a non-bond-interaction cut off radius of 10 Å. The coordinates of the MDS snapshots were collected every 0.1 ps. Equilibrium, attained after 20 ns of the MDS calculation, was ascertained by monitoring the global root mean square deviation (RMSD). The calculation was then continued for up to a further 30 ns, and the last 5 ns data were used for the analyses.
390 TIP3P water molecules, and the electroneutrality of the system was attained by adding 10 sodium counter-ions. The systems were set up under the isobaric–isothermal ensemble with a constant pressure (1 atm) and temperature (293 K). Electrostatic interactions were corrected by the Particle Mesh Ewald method.40 The SHAKE algorithm41 was used to constrain all bonds involving hydrogen atoms. All MDS based calculations were performed with a time steps of 2 fs and a non-bond-interaction cut off radius of 10 Å. The coordinates of the MDS snapshots were collected every 0.1 ps. Equilibrium, attained after 20 ns of the MDS calculation, was ascertained by monitoring the global root mean square deviation (RMSD). The calculation was then continued for up to a further 30 ns, and the last 5 ns data were used for the analyses.
ET rates from Trp and Tyr
The original Marcus theory42,43 has been modified in various ways.44–48 In the present analysis, KM theory47 was used, because it is applicable for both non-adiabatic ET processes and adiabatic ET processes, and has been found to give satisfactory results for both static,27,33,35,36 and dynamic ET analyses.28–32 When the donor is Trp or Tyr, the ET rate described by the KM theory is expressed by eqn (1).
 | (1) |
λqjS is the solvent reorganization energy42,43 of the ET donor q and j, and is expressed as eqn (2);
 | (2) |
| Donor | Sub A | Sub B | Monomer |
|---|---|---|---|
| a The centre-to-centre distances (Rc) between the Iso acceptor and each donor of Sub A and Sub B in the dimer and in the monomer are shown as the mean values (nm) obtained from 5000 snapshots with 1 ps time intervals. Temperature was 20 °C. Bz denotes benzoate; Sub denotes subunit. | |||
| Bz | 0.66 | 0.68 | 0.61 |
| Tyr55 | 0.95 | 1.05 | 1.31 |
| Tyr144 | 1.32 | 1.38 | 1.43 |
| Trp185 | 1.10 | 1.31 | 1.39 |
| Tyr224 | 1.32 | 1.04 | 0.97 |
| Tyr228 | 0.96 | 0.99 | 0.81 |
| Tyr279 | 1.36 | 1.45 | 1.24 |
| Tyr314 | 1.06 | 1.02 | 1.07 |
The standard free energy change was expressed with the ionization potential of the ET donor (EqIP) as eqn (3);
| ΔGq0 = EqIP − GIsop0, | (3) |
ET rate from Bz
When the donor is Bz, the ET rate may be expressed by eqn (4);
 | (4) |
 | (5) |
| ΔGBz0 = EBzIP − GIsop0, | (6) |
Electrostatic energy in the DAOB dimer
Protein systems contain many charged/polar moieties which may influence the ET rate. Ionic groups in each subunit of DAOB are the negatively charged pyrophosphate (−2) in FAD, Bz (−1), 22 Glu (−1) and 13 Asp (−1), plus the positively charged 12 Lys (+1) and 21 Arg (+1) residues, resulting in a net charge of −5. In the dimer, the total number of point charges are double that of the monomer and was counterbalanced in the MDS by 10 sodium ions.When the donor is Trp or Tyr, the ES energy between the donor cation j ≥ 1 and all other ionic groups in the protein is expressed by eqn (7);
 | (7) |
The ES energy between the Iso anion and the ionic groups was obtained by eqn (8);
 | (8) |
ESj in eqn (1) was expressed as eqn (9);
| ESj = EIso + E(j), | (9) |
When the donor is Bz, the ES energies have to be considered separately from Trp and Tyr, since the photoproduct of Bz is neutral, which is in contrast to that for Trp and Tyr which are cations. In the point charge approximate utilized above, the ES energies between the neutral radical of Bz produced by ET and all other ionic species totals to zero. Accordingly, these ES energies were calculated using the charge densities of atoms in neutral Bz by eqn (10);
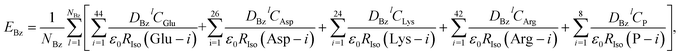 | (10) |
 holds. The ES energies between the Iso anion and the neutral Bz were also calculated from their respective charge densities using eqn (11),
holds. The ES energies between the Iso anion and the neutral Bz were also calculated from their respective charge densities using eqn (11),
 | (11) |
The charge density of atom i in the Iso anion is denoted as DIsoi.  holds. NIso is number of atoms of lumiflavin and is equal to 31. DBzl and DIsoi were used as obtained and reported previously.35 The NetES energy for Bz is given by eqn (12),
holds. NIso is number of atoms of lumiflavin and is equal to 31. DBzl and DIsoi were used as obtained and reported previously.35 The NetES energy for Bz is given by eqn (12),
| ESBz = EBz + EBzIso. | (12) |
Determination of the ET parameters
The fluorescence spectrum of the DAOB dimer showed an emission peak at 524 nm (Fig. S1, ESI†). The fluorescence decays of the DAOB dimer with two-exponential decay functions have been reported previously by Mataga et al.23 and the decay functions at the emission wavelength (λ) are expressed by eqn (13);| F(λt) = α1(λ)exp{−t/τ1(λ)} + α2(λ)exp{−t/τ2(λ)}, | (13) |
Some of the ET parameters contained in eqn (1)–(11) have been reported previously,28–33,35,36 whilst the parameters used in the present work are listed in Table 2. First we tried to reproduce the experimental lifetimes with the previously obtained ET parameters, but the agreements between the calculated and observed lifetimes were not satisfactory (not shown). Accordingly, in the present ET analysis GIsoA0, GIsoB0, RBz0, εDA0, and εDB0 were chosen as adjustable parameters to obtain a best-fit between the observed and calculated lifetimes. GIsoA0 and GIsoB0 are the free energies related to electron affinities of Iso* in Sub A and Sub B, respectively, while εDA0 and εDB0 are the static dielectric constants between Iso and the donors (Bz, Tyr55 and Tyr228) in Sub A and between Iso and the donors (Bz and Tyr228) in Sub B, respectively (see below eqn (2)). RBz0 is the critical ET distance for Bz in eqn (4). The other ET parameters are common to both subunits. The unknown ET parameters were determined by two methods, where the minimum chi-squared values (χ12 or χ22) were derived from eqn (14) and (15) in methods 1 and 2, respectively:
 | (14) |
 | (15) |
| νTrp0a (ps−1) | νTyr0a (ps−1) | βTrpa (nm−1) | βTyra (nm−1) | RTrp0a (nm) | RTyr0a (nm) | ε0b | τ1c (ps) | τ2c (ps) | νBz0d (ps−1) | βBzd (nm−1) | EBzIPd (eV) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a Data taken from Nunthaboot et al. (2011).29b Data taken from Table S2, ESI.c Mean shorter (τ1) and longer (τ2) lifetimes over ten decays with different emission wavelengths. Data taken from Mataga et al. (2000)23 and listed in Table S1, ESI.d Data taken from Nueangaudom et al. (2012).35 | |||||||||||
| 1016 | 197 | 21 | 6.25 | 0.663 | 0.499 | 5.78 | 0.848 | 4.77 | 2001 | 15.0 | 7.25 |
The observed lifetimes, τobs1 (0.848 ps) and τobs2 (4.77 ps), are the mean lifetimes of τ1(λ) and τ2(λ) in eqn (13), respectively, over 10 emission wavelengths (λ). In method 1 (χ12) it was assumed that the fluorescent component with τobs1 and τobs2 were from Sub A and Sub B, respectively, whilst in method 2 (χ22) it was assumed that the fluorescent component with τobs1 and τobs2 were from Sub B and Sub A, respectively. The obtained values of χ12 and χ22 were then compared to determine the likely ET mechanism in the DAOB dimer.
Molecular orbital study of charge densities of Iso and hydrogen bonding amino acids
The charge densities were obtained by a semi-empirical MO method with the software package of MOPAC2009. The keywords, EF (geometrical optimization), PRECISE (accurate calculation), PM6 (semi-empirical Hamiltonians), XYZ (geometry expressed by (x,y,z) coordinates), GEO-OK (neglect check on abnormal access of atoms), EPS (dielectric constant for COSMO solvation energy) were used. The details of these keywords are found on the website: http://openmopac.net. In addition to these keywords, the keyword EXCITED was used for Iso*. The values of EPS were 2.6 both for Sub A and Sub B, because εDA0 and εDB0 were close to 2.6 (see Table 3). Sub A formed hydrogen bondings (H-bond) with Ala49, Leu51 and Thr317 in Sub A, and with Ala49 and Leu51 in Sub B. The charge densities of Iso and Iso* were calculated with and without H-bond clusters.| Methodb | Modelc | GIsoA0d (eV) | GIsoB0e (eV) | εDA0f | εDB0g | RBz0h (nm) | χA2i | χB2j | χT2k | |
|---|---|---|---|---|---|---|---|---|---|---|
| a The five parameters listed here were varied until χT2 became the minimum. Other ET parameters used are listed in Table 2.b Total chi-squared values for methods 1 and 2 are given by eqn (14) and (15), respectively.c The calculated fluorescence lifetimes for Sub A and Sub B are indicated as τAcalc and τBcalc, respectively. In method 1 τAcalc was fit with τobs1, and τBcalc with τobs2. In method 2, τAcalc was fit with τobs2 and τBcalc with τobs1. The calculated lifetimes, τAcalc and τBcalc were 0.848 ps and 4.77 ps, respectively, which completely agreed with those of the observed lifetimes.d Standard free energy related to electron affinity of Iso* in Sub A.e Standard free energy related to electron affinity of Iso* in Sub B.f Static dielectric constant around Iso, Bz, Tyr55 and Tyr228 in Sub A, of which mean Rc values were within 1 nm.g Static dielectric constant around Iso, Bz and Tyr228 in Sub B, of which mean Rc values were within 1 nm.h Critical ET distance of Bz as a donor.i Chi-squared value for Sub A.j Chi-squared value for Sub B.k Total chi-squared value for method 1(χ12) and for method 2 (χ22). | ||||||||||
| 1 | τobs1 (τAcalc) | τobs2 (τBcalc) | 8.34 | 8.48 | 2.65 | 2.56 | 0.417 | 1.79 × 10−19 | 1.96 × 10−30 | 8.76 × 10−20 |
| 2 | τobs1 (τBcalc) | τobs2 (τAcalc) | 8.42 | 8.43 | 2.53 | 2.64 | 0.462 | 2.72 × 10−21 | 2.23 × 10−30 | 1.36 × 10−21 |
III. Results
Comparisons between MDS snapshot and crystal structure and between the two subunits in the DAOB dimer
Fig. 1 shows the MDS snapshot of the two subunits of the DAOB dimer superimposed on the crystal structure. In Fig. 1A, the crystal structure of Sub A was superimposed on that of Sub B and in Fig. 1B MDS snapshot of Sub A was superimposed on that of Sub B. In crystal the local structures of Sub A and Sub B (ref. 16) are almost equivalent. However, in the MDS snapshots the both structures displayed considerable difference between Sub A and Sub B, especially in the aromatic amino acids of Tyr224, Tyr55 and Tyr314 among the chromophores were quite different between Sub A and Sub B. The structures were compared between the crystal and MDS for Sub A in Fig. 1C, and for Sub B in Fig. 1D. It is obvious that the crystal and MDS structures are quite different both in Sub A and Sub B, not only near Iso binding site, but also in the entire protein (Fig. 1E). This may be ascribed to the presence of freely mobile water molecules near the protein in MDS snapshots. | ||
| Fig. 1 Comparison of the protein structures between Sub A and Sub B in DAOB dimer. The structures were shown in yellow for Sub A and in cyan for Sub B in the crystal structures, and in green for Sub A and in magenta for Sub B in the MD snapshots. The crystal structure was taken from Mizutani et al.16 The MDS calculation was performed at 20 °C. All figures superimposed using Discovery Studio program, alignment by 100% steric and align to consensus of protein. | ||
Time-evolutions of the Rc between the potential donors and Iso are shown in Fig. S2, ESI,† whilst the Rc distributions of potential ET donors including Bz are shown in Fig. 2, where large differences were evident in the Rc distributions of Tyr55 and Trp185 between Sub A and Sub B, whilst Tyr144 and Tyr224 were present only in Sub A or Sub B, respectively. The mean Rc values between Iso and these donors, derived from 5000 snapshots with 1 ps time intervals, are listed in Table 1. The Rc distance for Bz was shortest among the monomer and the dimer subunits, and slightly shorter in Sub A than Sub B. The Rc values were higher by 0.05 and 0.07 nm respectively in Sub A and Sub B compared to that in the monomer. Within the dimer subunits, the Rc for Trp185 was shorter in Sub A (1.10 nm) than in Sub B (1.31 nm), while it was 1.39 nm in the monomer. The Rc values of Tyr55 were slightly (1.1-fold) smaller in Sub A (0.95 nm) than Sub B (1.05 nm), but much larger in the monomer (1.31 nm) with only that in Sub A being <1 nm. The Rc values of Tyr228 were similar in Sub A and Sub B (0.96 and 0.99 nm), but markedly smaller in the monomer (0.81 nm) and with all three being shorter than 1 nm. The Rc value for Tyr224 in sub B (1.04 nm) was closer to that of the monomer (0.97 nm) but was much larger in Sub A (1.32 nm). In contrast, the Rc values for Tyr314 were similar in all three systems. Thus, the protein conformations near Iso were quite different between Sub A and Sub B in the dimer, and in the monomer.
Root of mean square deviation and root of mean square fluctuation
Root of mean square deviation (RMSD) and root of mean square fluctuation (RMSF) were obtained using the AMBER10 software. Time-evolutions of RMSD of the entire protein (Sub A and Sub B), FAD and Bz are shown in Fig. S3, ESI.† The RMSDs of all components attained equilibrium between 25–30 ns of MDS calculations. The RMSF is considered to be a useful index for protein fluctuation, and the RMSF for the amino acid residues is shown in Fig. S4† along with those from the literature for the DAOB monomer,35 holoDAAO monomer,33 and Sub A and Sub B of the holoDAAO dimer36 for comparison. The mean RMSF values over all the amino acids were small in Sub A and Sub B of the DAOB dimer (0.191 and 0.171, respectively), but much larger in the DAOB monomer (0.522), and in Sub A and Sub B of the holoDAAO dimer (0.347 and 0.344), respectively, and largest in the holoDAAO monomer (0.701). The lowest mean RMSF values were hence found in the DAOB dimer and the highest in the holoDAAO monomer, whilst the mean RMSF value of the DAOB monomer was higher than those of the holoDAAO dimer. It is well known that Bz binding to holoDAAO from porcine kidney greatly stabilizes the protein, and indeed this trait is used in the purification of holoDAAO.12 It is also recognized that the holoDAAO monomer is the most unstable of the protein species. Thus, the mean RMSD may be related to protein stability in general.Best-fit ET parameters
In holoDAAO dimer the static dielectric constant (εDA0) was introduced between Iso and the donors only when the mean Rc is shorter than 1 nm.36 This model was also used in the present work (see below eqn (2)). However, in DAOB monomer εDA0 was introduced for all donors.33 To compare the ET parameters in the DAOB dimer with those in the DAOB monomer, first the fluorescence lifetime of the DAOB monomer34 (60 ps) was analyzed with the same model as the present work, introducing εDA0 only for the donors with the mean Rc shorter than 1 nm. The ET parameters of the monomer obtained with this model are listed in Table S2, ESI.† The values of νBz0, βBz and EBzIP (ionization potential of the Bz anion) were the same as those previously reported.35 The obtained value of ε0 was 5.78, which was similar to that previously reported, but the values of RBz0 (0.384 nm) and εDA0 (2.45) were a little larger (0.116 and 2.22 respectively).35 The calculated lifetime of the DAOB monomer completely coincided with one of the observed lifetimes (that at 60 ps).34The unknown ET parameters for the DAOB dimer were GIsoA0, GIsoB0, εDA0, εDB0, ε0 and RBz0. These best-fit parameters, obtained with methods 1 and 2 (see Determination of the ET parameters section), are listed in Table 4. The total chi-squared values were 64-fold larger with method 1 than with method 2, and so method 2 seems to be a better method. The best-fit parameters (from method 2) were GIsoA0 = 8.42 eV, GIsoB0 = 8.43 eV, εDA0 = 2.53, εDB0 = 2.64 and RBz0 = 0.462 nm.
| Protein | Donor | kwET (ps−1) | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kwETb kwETb |
Rcc (nm) | λwjSd (eV) | ESj(k)e (eV) | ESDAf (eV) |
|---|---|---|---|---|---|---|---|
| a Mean values over 5000 snapshots are listed for the DAOB dimer obtained with the ET parameters listed in Table 4, whilst for the monomer the ET parameters listed in Table S2, ESI were used.b Logarithmic ET rate of eqn (1).c Centre-to-centre distance (Rc) between Iso and the ET donors.d Solvent reorganization energy, derived from eqn (2).e NetES energies for Tyr and Trp derived from eqn (9), and for Bz from eqn (12).f ES energy between Iso anion and an aromatic amino acid cation or Bz neutral radical. | |||||||
| Sub A | Tyr228 | 1.17 × 10−1 | −2.15 | 0.957 | 0.619 | 0.0750 | −0.594 |
| Bz | 7.50 × 10−2 | −2.59 | 0.659 | 0.811 | −0.0852 | −0.0198 | |
| Tyr55 | 1.14 × 10−2 | −4.48 | 0.946 | 0.617 | −0.103 | −0.601 | |
| Trp185 | 4.65 × 10−3 | −5.37 | 1.10 | 1.83 | −0.434 | −0.226 | |
| Tyr314 | 1.58 × 10−3 | −6.45 | 1.06 | 1.97 | −0.323 | −0.234 | |
| Trp52 | 1.68 × 10−5 | −11.0 | 1.33 | 1.90 | −0.113 | −0.187 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Sub B | Bz | 8.92 × 10−1 | −0.114 | 0.683 | 0.939 | −0.0944 | −0.0217 |
| Tyr228 | 2.80 × 10−1 | −1.27 | 0.987 | 0.715 | 0.0698 | −0.553 | |
| Tyr314 | 6.56 × 10−3 | −5.03 | 1.02 | 1.95 | −0.442 | −0.243 | |
| Tyr55 | 2.64 × 10−4 | −8.24 | 1.05 | 1.97 | −0.159 | −0.236 | |
| Tyr224 | 5.38 × 10−5 | −9.83 | 1.04 | 1.96 | −0.0099 | −0.239 | |
| Trp185 | 3.72 × 10−5 | −10.2 | 1.31 | 1.89 | −0.183 | −0.190 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Monomer | Bz | 9.92 × 10−3 | −4.61 | 0.611 | 0.687 | 0.898 | 0.140 |
| Tyr228 | 4.23 × 10−3 | −5.46 | 0.812 | 0.512 | 0.172 | −0.725 | |
| Tyr224 | 1.93 × 10−3 | −6.25 | 0.970 | 0.538 | 0.0221 | −0.607 | |
| Tyr314 | 5.05 × 10−4 | −7.59 | 1.07 | 1.97 | −0.130 | −0.232 | |
| Tyr55 | 6.59 × 10−5 | −9.63 | 1.31 | 2.05 | −0.171 | −0.191 | |
| Trp185 | 1.37 × 10−5 | −11.2 | 1.36 | 1.90 | −0.0953 | −0.184 | |
ET rates in DAOB dimer
The ET rates from all Tyr and Trp residues in addition to Bz were obtained with the ET parameters described above. Fig. S5, ESI† shows the time-evolutions of the logarithmic ET rates of the six fastest donors, including Bz. Fig. 3 shows the distributions of the logarithmic ET rates, with the distributions in the DAOB monomer, obtained with the ET parameters listed in Table S2, ESI,† also shown for comparison. The distributions of logarithmic ET rate in Tyr314 of Sub A displayed a double maxima, and Trp185 displayed a broad shoulder. The distributions for each donor were markedly different between the two subunits and in the monomer. Table 5 lists the mean ET rates over 5000 snapshots with 1 ps time intervals, together with the physical quantities related to ET. In Sub A the fastest rate was from Tyr228, then followed by Bz, Tyr55, Trp185, Tyr314 and Trp52. However, in Sub B the fastest donor was Bz (11.8-fold faster than in Sub A, and 7.62-fold faster than Tyr228 in Sub A), and then followed by Tyr228, Tyr314, Tyr55, Tyr224 and Trp185. In the monomer, the fastest donor was also Bz and then followed by Tyr228, Tyr224, Tyr314, Tyr55 and Trp185, but the mean ET rates in each case were more than 10-fold slower than in the dimer subunits.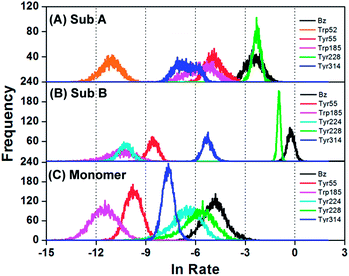 | ||
| Fig. 3 Distribution of the logarithmic ET rates in the DAOB subunits for the six fastest ET donors. The observed fluorescence lifetime τobs1 (0.848 ps) was from Sub B and τobs2 (4.77 ps) from Sub A. | ||
| Protein | Donor | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ECwb ECwb |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SQwc SQwc |
GTRAMwd | GTwe (eV) | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ratef ratef |
|---|---|---|---|---|---|---|
a ET rates given by eqn (1) and (4) were decomposed into the ECw, SQw and GTRAM terms. The quantities were expressed as means over 5000 snapshots with 1 ps time intervals.b ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ECw is the logarithmic electronic coupling term (ps−1), derived from eqn (16).c Explicit form of ln ECw is the logarithmic electronic coupling term (ps−1), derived from eqn (16).c Explicit form of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SQw, derived from eqn (17).d Explicit form of GTRAM, derived from eqn (19).e GT is total free energy gap, derived from eqn (18).f Logarithmic rate, derived from eqn (20). SQw, derived from eqn (17).d Explicit form of GTRAM, derived from eqn (19).e GT is total free energy gap, derived from eqn (18).f Logarithmic rate, derived from eqn (20). |
||||||
| Sub A | Tyr228 | 2.37 | −2.87 | −1.67 | −0.322 | −2.15 |
| Bz | 4.62 | −3.00 | −2.68 | −0.466 | −2.59 | |
| Tyr55 | 2.45 | −2.86 | −4.18 | −0.509 | −4.48 | |
| Trp185 | −1.88 | −3.41 | −0.0663 | −0.0573 | −5.37 | |
| Tyr314 | 1.76 | −3.44 | −4.96 | 0.991 | −6.45 | |
| Trp52 | −6.84 | −3.43 | −0.748 | 0.378 | −11.0 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Sub B | Bz | 4.28 | −3.07 | −1.32 | −0.353 | −0.11 |
| Tyr228 | 2.19 | −2.94 | −0.531 | −0.194 | −1.27 | |
| Tyr314 | 1.98 | −3.44 | −3.61 | 0.843 | −5.03 | |
| Tyr55 | 1.80 | −3.44 | −6.63 | 1.15 | −8.24 | |
| Tyr224 | 1.89 | −3.44 | −8.36 | 1.29 | −9.83 | |
| Trp185 | −6.37 | −3.42 | −0.480 | 0.295 | −10.2 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Monomer | Bz | 4.20 | −2.92 | −6.12 | 0.651 | −4.61 |
| Tyr228 | 3.20 | −2.77 | −6.32 | −0.569 | −5.46 | |
| Tyr224 | 2.30 | −2.80 | −6.10 | −0.574 | −6.25 | |
| Tyr314 | 1.68 | −3.44 | −5.89 | 1.08 | −7.59 | |
| Tyr55 | 0.25 | −3.46 | −6.53 | 1.16 | −9.63 | |
| Trp185 | −7.36 | −3.43 | −0.482 | 0.297 | −11.2 | |
NetES energy
The time-evolutions of NetES energies between the photoproducts and ionic groups in the DAOB dimer are shown in Fig. S6, ESI,† with the distributions of the NetES energies shown in Fig. 4 along with those in the monomer for comparison. The NetES energies in the dimer ranged from −0.5 eV to 0.2 eV, while those in monomer ranged from −0.3–1.0 eV. The mean NetES energies are listed in Table 4. Tyr228 had the fastest ET rate and the highest NetES energy in Sub A, but in Sub B whilst Bz had the fastest ET rate, its NetES energy was 1.7 fold lesser than that for Tyr228. Thus, the NetES energy was highest in Tyr228 in both Sub A and Sub B. The lowest NetES energy was found in Trp185 in Sub A (followed by Tyr314) and in Tyr314 in Sub B (followed by Trp185), whilst the NetES energies of Bz were similar in both subunits. Note that the NetES energies of Tyr314 in Sub A displayed a double maximum at around −0.3 eV and −0.4 eV. | ||
| Fig. 4 Distribution of the NetES energy in the DAOB subunits for the six fastest ET donors, with that in the monomer for comparison. NetES energies are given by eqn (9) for Tyr and Trp, and by eqn (12) for Bz. Upper, middle and lower panels show the NetES energy of the DAOB Sub A, Sub B and the monomer, respectively. | ||
The NetES energy of Bz in the monomer was much higher (11-fold) than those in either subunits of the dimer, and the same trend was noted for all of the other five donors (Table 4). This revealed that in the dimer the NetES energies in each subunit were influenced by those in the other subunit.34 The mean values of NetES energies in the aromatic amino acids of the monomer were also higher than in the dimer subunits.
The other physical quantities related to ET
The time-evolution of the ESDA between the Iso anion and donor cation (aromatic amino acids) or neutral radical (Bz) are shown in Fig. S7, ESI,† and the ESDA distributions and mean values are shown in Fig. 5 and Table 4, respectively. The ESDA of the Bz neutral radical in the dimer fluctuated around zero (slightly negative) with appreciable portions of the ESDA distributions being negative in both Sub A and Sub B. The mean Bz ESDA values were the lowest in Sub B and the highest in the monomer. The distribution pattern of Tyr55 was quite different between Sub A and Sub B. In Sub A the distribution peak was highly negative (mean −0.601 eV; see Table 4), while in Sub B it was similar with those of Tyr224 and Tyr314 (mean −0.236 eV), and with one in the monomer (mean −0.191 eV). The mean ESDA values for Tyr228 were somewhat similar in Sub A and Sub B, but were significantly lower in the monomer. | ||
| Fig. 5 Distribution of the ESDA between the photo-products in the DAOB subunits, with that in the monomer for comparison. The ESDA, the electrostatic energy (eV) between the photo-products, is expressed as −e2/εp0Rj in eqn (1), using the static dielectric constants εADA for Sub A and εBDA for Sub B. The acceptor was the Iso anion, and the donors were Trp cations or Tyr cations for aromatic amino acid donors. For Bz, the ESDA was obtained from eqn (11). | ||
The solvent reorganization energies (λwjS) (Table 4) for Bz and Tyr228 were highest in Sub B (slightly more than in Sub A at 1.16- and 1.03-fold, respectively) but much lower in the monomer at 1.18- to 1.37-fold and 1.2- to 1.4-fold, respectively, whilst that for Tyr314 was essentially equally high in all three forms (Sub A, Sub B and the monomer).
Polarity around Iso
The polarity around Iso may be related to number of water molecules near it. The radial distribution functions of water molecules (G(r)) near the heteroatoms of Iso, which is considered to represent water molecules steadily located near the heteroatoms of Iso, is shown in Fig. S8, ESI.† The G(r) functions of Sub A and Sub B in the DAOB dimer are shown in red and blue respectively, whilst that for the monomer is shown in black and is taken from previous work35 for comparison. In Sub B an average of 1.1 water molecules were located near O2 and N3 (see Chart 1 for atom notations), one molecule near O4, and approximately two molecules were located near N5. However, in Sub A no water molecule existed near these heteroatoms in Iso as in the monomer.These results, and the G(r) functions in Fig. S8, ESI,† suggest that the polarity near Iso was higher in Sub B than in Sub A. This is in accordance with the results of the dielectric constants εDA0 and εDB0 (2.53 and 2.64 respectively, Table 3) in the DAOB dimer, which suggests polarity near Iso, Bz, Tyr55 and Tyr228 in Sub A is a little lower than that near Iso, Bz and Tyr228 in Sub B (see descriptions on εDA0 and εDB0 below eqn (2)). In the monomer the value of εDA0 near Iso, Bz, Tyr224 and Tyr228 was 2.45 Table S2, ESI† and no water molecule was also found near heteroatoms of Iso. It should be noted that molecules other than water may also influence the polarity, such as any ionic groups near Iso.
Fig. S9, ESI† shows water molecules existing 0.7 nm from IsoN5. In Sub A Iso, Bz, Tyr55 and Tyr228 are shown, and in Sub B Iso, Bz and Tyr228 in a snapshot. The static dielectric constant in these domains are εDA0 for Sub A and εDB0 for Sub B. In Sub A there exist three water molecules, but no water molecule near Iso within 0.5 nm, as predicted by G(r) function in Fig. S8.† In Sub B some water molecules exist near Iso within 0.5 nm. These results are in accordance with the interpretation about the polarity near Iso described above.
Emission peak of fluorescence spectrum of a flavoprotein may be related to the static dielectric constant near Iso (εDA0 for Sub A and εDB0 for Sub B). Fluorescence spectrum of DAOB dimer is shown in Fig. S1, ESI.† The emission peak was 524 nm, while the peak of holoDAAO dimer is around 530 nm.52 The static dielectric constants near Iso were 2.4–2.7 in DAOB dimer and monomer, while it is 5.8–5.9 in holoDAAO dimer and monomer.33,36 These results are in accordance with those of the static dielectric constant near Iso obtained by the present ET analyses. Similar result with respect to the relationship between the static dielectric constant near the donor and Iso, and emission peak of Iso was obtained in flavodoxins.32 However, it should be noted that the fluorescence spectrum of Iso depends on two factors, polarity around Iso, (Stokes Shift) and hydrogen bond (H-bond) structure between Iso* and nearby amino acids. Iso contains five hydrogen bonding acceptors and one donor (see Chart 1). The energy shift of Iso upon H-bond formations has been studied by a MO method for the ground state of Iso.54 It is well known that H-bond or proton transfer phenomena are different between the ground and excited states in general. Accordingly, the modifications of the transition energies of Iso by H-bond formations should be examined for Iso* by MO method.
Difference in the charge densities Iso and Iso* between sub A and sub B with and without H-bonds
Charge densities of atoms in free Iso and Iso with H-bond cluster were shown in Table S3, ESI.† Numbering of atoms in Iso and H-bonded amino acids are shown in Fig. S11, ESI.† The charge densities were not much different between Sub A and Sub B. The charge densities with the differences greater than 0.01 are indicated in green in Table S3.† In the ground state of Iso the atom O7 (O4 in the Chart 1), H19 and H21 displayed the differences greater than 0.01 between Sub A and Sub B. In the excited state many more atoms displayed the greater differences. Atom N1 (N1 in Chart 1) displayed quite large difference by 0.03 between Sub A and Sub B. The differences were 0.25 in C8 (C4a in Chart 1), 0.24 in C11 (C6 in Chart 1), 0.28 in H29 (H connected to N10 in Chart 1), and 0.34 in H31 (H connected to N10 in Chart 1). H-bond cluster considerably modified the charge densities of Iso in the excited state, for example, by 0.027 in C10 (C5a in Chart 1) of Sub A, by 0.041 in C11 (C6 in Chart 1) of Sub A and by 0.017 in C11 of Sub B, by 0.05 in N27 (N10 in Chart 1) of Sub A. These differences in the charge densities between Sub A and Sub B in the excited state may be related to the difference in the ET rates between Sub A and Sub B. Fig. S12† shows molecular orbitals of HOMO and LUMO of Iso in the ground and excited states without H-bond clusters. The LUMO and HOMO displayed considerable difference between the ground and excited states.Relationship between logarithmic ET rate and Rc
The dependence of the logarithmic ET rate on the donor–acceptor distance (edge to edge distance, Re) is called as Dutton ruler.44 The relationship between logarithmic ET rates and the donor–acceptor distances is shown in the DAOB dimer and the monomer in Fig. 6, where Rc was used as the donor–acceptor distance. The relationship should be examined separately with each kind of ET donor, otherwise linear relations of the logarithmic ET rates with Rc cannot be expected. It has been noted that the Rc rather than the Re is responsible for the relationship between logarithmic ET rate and Rc in flavoproteins50,51 in contrast to photosynthetic systems where Re was used as the donor–acceptor distance.44 In all three DAOB systems excellent linear relations were obtained, including in the monomer. The slopes for Trp were similar in the two dimer subunits (−22.1 and −22.2 in Sub A and Sub B, respectively), and a little higher in the monomer (−24.7), and likewise for Tyr they were −13.0, −13.2 and −14.6 in Sub A, Sub B and the monomer, respectively. Thus, the slopes for both Trp and Tyr were quite similar between Sub A and Sub B, but a little higher in the monomer than those in the dimer. The relationship between logarithmic ET rate and the donor–acceptor distances was also examined with Re as shown in Fig. 7. The ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) rate vs. Re relationship also displayed linear functions. The slopes of the approximate functions of Trp were −19.1 in Sub A, −19.8 in Sub B and −19.7 in monomer, while those of Tyr were −14.2 in Sub A, −14.4 in Sub B, and −15.0 in monomer. These values were quite different from those with Rc as the donor–acceptor distance, which suggests that Rc and Re are proportional.
rate vs. Re relationship also displayed linear functions. The slopes of the approximate functions of Trp were −19.1 in Sub A, −19.8 in Sub B and −19.7 in monomer, while those of Tyr were −14.2 in Sub A, −14.4 in Sub B, and −15.0 in monomer. These values were quite different from those with Rc as the donor–acceptor distance, which suggests that Rc and Re are proportional.
 | ||
| Fig. 7 Relationship between logarithmic ET rates and Re in DAOB. The logarithmic ET rates are taken from Fig. 6. Re represents edge to edge distance. | ||
The Re values should be dependent on inter-planar angles between Iso and donors. Fig. S10, ESI† shows the relationship between Iso and main donors, Tyr228 and Bz. In this figure the logarithmic ET rates did not display any clear relations with the inter-planar angles. This should be ascribed that any theories including KM rate do not explicitly include the angular-dependence between the donor and acceptor as Förster-type energy transfer rate.
Numerical elucidation of differences in the fluorescence lifetimes between two subunits in the DAOB dimer and between the dimer and monomer
The observed fluorescent lifetimes of DAOB were 4.77 ps in Sub A and 0.848 ps in Sub B in the dimer. It is then of interest to elucidate the difference in the lifetimes (ET rates) between the two subunits in the DAOB dimer. The logarithmic ET rate expressed by eqn (1) or (4) may be rewritten as eqn (16)–(19):
 | (16) |
 | (17) |
| GTw = ΔGw0 − e2/εp0Rj + λwjS + ESj(k), | (18) |
 | (19) |
The logarithmic ET rate can then be obtained from eqn (20),
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kwET = ln kwET = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ECw + ln ECw + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SQw + GTRAMw. SQw + GTRAMw.
| (20) |
In these equations, q is Trp, Tyr or Bz, while ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kwET is the logarithm of the ET rate given by eqn (1) for Trp and Tyr, and by eqn (4) for Bz. The meanings of each term in these equations are described below eqn (1) and (4), where ECw is the electronic coupling term, and GTw is the total free energy gap and appeared in exponential functions of the rates. These values for several donors are listed in Table 5.
kwET is the logarithm of the ET rate given by eqn (1) for Trp and Tyr, and by eqn (4) for Bz. The meanings of each term in these equations are described below eqn (1) and (4), where ECw is the electronic coupling term, and GTw is the total free energy gap and appeared in exponential functions of the rates. These values for several donors are listed in Table 5.
The contributions of the Bz and Tyr228 ET rates to the total rates (inverse of the fluorescence lifetime) were ca. 90% in all the systems. Given that the values of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kwET in Bz were −2.59 in Sub A and −0.114 in Sub B, this raises the question as to why the rate of Bz was some 22.7-fold slower in Sub A than in Sub B. The values of ln
kwET in Bz were −2.59 in Sub A and −0.114 in Sub B, this raises the question as to why the rate of Bz was some 22.7-fold slower in Sub A than in Sub B. The values of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ECw for Bz were slightly higher in Sub A than in Sub B. The values of ln
ECw for Bz were slightly higher in Sub A than in Sub B. The values of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SQw were similar between Sub A and Sub B, but the absolute value of GTRAMw for Bz was 2.1-fold higher in Sub A than in Sub B. The ln
SQw were similar between Sub A and Sub B, but the absolute value of GTRAMw for Bz was 2.1-fold higher in Sub A than in Sub B. The ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kwET (Table 5) was obtained as sum of these values, according to eqn (20), and these were found to agree well with the ln
kwET (Table 5) was obtained as sum of these values, according to eqn (20), and these were found to agree well with the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kwET values (Table 5). That the value of ln
kwET values (Table 5). That the value of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kwET was smaller in Sub A (slower ET rate) than in Sub B was hence ascribed to the two-fold larger absolute value of GTRAMw in Sub A than in Sub B. GTRAMw is mainly determined by GTw eqn (16), because there was very little variation in SQ between the subunits. The values of ΔGw0 (given by eqn (6)) were similar in the two subunits, whilst the ESDA (−e2/εp0Rj), solvent reorganization energy (λwjS from eqn (5)) and ESBz (from eqn (12)) were all quite similar (1.01- to 1.16-fold difference) in the two subunits (Table 4). The values of GTw for Bz, obtained by the sum of each term according to eqn (18), were 1.32 fold higher in Sub A than in Sub. This is the reason why the absolute value of GTRAMw from eqn (19) was larger in Sub A than in Sub B, and so that the lifetime of Sub A is much longer than Sub B (ET rate of Sub A is much slower than Sub B, and note that GTRAMw is always negative, see eqn (19) and (20)). The reason why the absolute value of GTw was greater in Sub A than in Sub B is due to the smaller value of λwjS in Sub A than in Sub B, which in turn was due to the shorter Rc in Sub A than in Sub B and to the smaller dielectric constant of εDA0 than of εDB0, as revealed by eqn (5).
kwET was smaller in Sub A (slower ET rate) than in Sub B was hence ascribed to the two-fold larger absolute value of GTRAMw in Sub A than in Sub B. GTRAMw is mainly determined by GTw eqn (16), because there was very little variation in SQ between the subunits. The values of ΔGw0 (given by eqn (6)) were similar in the two subunits, whilst the ESDA (−e2/εp0Rj), solvent reorganization energy (λwjS from eqn (5)) and ESBz (from eqn (12)) were all quite similar (1.01- to 1.16-fold difference) in the two subunits (Table 4). The values of GTw for Bz, obtained by the sum of each term according to eqn (18), were 1.32 fold higher in Sub A than in Sub. This is the reason why the absolute value of GTRAMw from eqn (19) was larger in Sub A than in Sub B, and so that the lifetime of Sub A is much longer than Sub B (ET rate of Sub A is much slower than Sub B, and note that GTRAMw is always negative, see eqn (19) and (20)). The reason why the absolute value of GTw was greater in Sub A than in Sub B is due to the smaller value of λwjS in Sub A than in Sub B, which in turn was due to the shorter Rc in Sub A than in Sub B and to the smaller dielectric constant of εDA0 than of εDB0, as revealed by eqn (5).
It is also of interest why the fluorescent lifetime of the monomer is much longer than in the DAOB dimer, that is 12.6- and 70.8-fold longer than that for Sub A and Sub B, respectively.34 The ET rate from Bz was the fastest among the donors in the monomer. The values of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ECw and GTRAMw for Bz in the monomer were 1.1- and 2.3-fold lower than in Sub A and 1.02- and 4.64-fold lower than in Sub B, respectively, although ln
ECw and GTRAMw for Bz in the monomer were 1.1- and 2.3-fold lower than in Sub A and 1.02- and 4.64-fold lower than in Sub B, respectively, although ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SQw was only 1.03- and 1.05-fold higher than in Sub A and Sub B, respectively. Thus, the GTRAMw in the monomer was markedly smaller than those in Sub A and Sub B and this is likely to be the principal reason why the value of ln
SQw was only 1.03- and 1.05-fold higher than in Sub A and Sub B, respectively. Thus, the GTRAMw in the monomer was markedly smaller than those in Sub A and Sub B and this is likely to be the principal reason why the value of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kwET in the monomer was much smaller, and so the fluorescence lifetime was much longer, than those in the dimer subunits. GTRAMw is mainly dependent on GTw (eqn (19)), which is itself derived from the summation of the ΔGw0, ESDA, λwjS and ESBz values (eqn (18)). The values of ΔGw0, ESDA and λwjS in Bz were not dramatically different (1.1- to 1.55-fold difference) between the monomer and the dimer subunits (Table 5). However, the NetES energy (ESBz) was markedly higher in the monomer than in the dimer subunits. Thus, the main reason why the fluorescent lifetime is much longer (slower ET rate) in the monomer than those in the dimer is due to greater NetES energy (ESBz) in the monomer compared to in the dimer. This was ascribed to the inter-subunit interactions in terms of the Rc and dielectric constant, as stated above.
kwET in the monomer was much smaller, and so the fluorescence lifetime was much longer, than those in the dimer subunits. GTRAMw is mainly dependent on GTw (eqn (19)), which is itself derived from the summation of the ΔGw0, ESDA, λwjS and ESBz values (eqn (18)). The values of ΔGw0, ESDA and λwjS in Bz were not dramatically different (1.1- to 1.55-fold difference) between the monomer and the dimer subunits (Table 5). However, the NetES energy (ESBz) was markedly higher in the monomer than in the dimer subunits. Thus, the main reason why the fluorescent lifetime is much longer (slower ET rate) in the monomer than those in the dimer is due to greater NetES energy (ESBz) in the monomer compared to in the dimer. This was ascribed to the inter-subunit interactions in terms of the Rc and dielectric constant, as stated above.
The ET rate from Tyr228 to Iso* was 2.4-fold slower in Sub A than in Sub B, but some 660-fold faster than that in the monomer. That the ET rates from Tyr228 were much faster in the dimer subunits than in the monomer, despite that the donor–acceptor Rc distances of the dimer were ∼1.2-fold longer than that in the monomer, is because the absolute values of GTRAMw in the dimer were much smaller than that in the monomer. The greater absolute GTRAMw value in the monomer was mainly ascribed to the low λqjS with a shorter Rc and a low εDA0 Table S2, ESI.†
IV. Discussion
During 1980–2000 a number of workers have reported on ET and dark electron transfer in small molecules and in proteins.55–60 In these works, however, it was difficult to determine theoretically and experimentally individual ET parameters contained in the ET rates. Our approach to analyze ET rate quantitatively is that (1) fluorescence decays or lifetimes of flavoproteins are obtained from experimental results, (2) atomic coordinates of a flavoprotein are determined by MDS methods, (3) ET rates are evaluated with an analytical theory like KM rate or sometimes Marcus rate, (4) the several unknown ET parameters are determined by a non-linear least squares method according to Marquardt algorithm. By using the above described strategy, we have reported on ET mechanisms on several flavoproteins.28–33,35,36Experimentally, the DAOB dimer displays two fluorescent species with lifetimes of 0.85 ps and 4.8 ps, which have been identified as being derived from Sub B and Sub A, respectively. The structural basis for the heterogeneity has been studied by means of MDS and ET analysis. The contributions of the ET rates from Bz and Tyr228 to the total rates were ∼90% in all systems, including in the monomer. The Rc distances of the main donors in Sub A and Sub B respectively, were 0.66 and 0.68 for Bz, compared to 0.96 and 0.99 nm for Tyr228, which did not correlate with the differences in the ET rates. This is in contrast to that for the DAAO holodimer,36 where the difference in the fluorescence lifetime between the monomer and dimer was attributed to the difference in Rc. The ET rates of Bz were significantly different between Sub A and Sub B, being the second fastest in Sub A and the fastest in Sub B.
Decomposing the ET rate into the electronic coupling (ECw), square root (SQw) and exponential (GTRAMw) terms revealed that the main reason for the faster ET rate of Bz in Sub B was the two-fold larger absolute GTRAMw value in Sub A than in Sub B. This in turn was ascribed to the greater λwjS in Sub B than in Sub A, because the Rc was longer and the dielectric constant was smaller in Sub B than in Sub A. That the fluorescence lifetime was 12.6- and 70.8-fold shorter (much faster ET rate) in the dimer than in the monomer was explained by the 2.3- and 4.64-fold larger GTRAMw values in the dimer compared to the monomer, which in turn was due to the much higher NetES energy (ESBz) in the monomer compared to the dimer.
Original Marcus theory42,43 was derived assuming that the donor and acceptor are spherical (also KM rate). It is not unreasonable to use Rc as the donor–acceptor distance for the ET analyses. If the molecules are spherical, Rc and Re should be identical. Firstly the relationship between logarithmic ET rate and the donor–acceptor distances has been experimentally obtained with Re in photosynthetic systems.44 In these systems ET rates were slower (longer than 0.63 ps in the lifetimes), and so the distances were longer, comparing to in flavoproteins. When the distance is quite long, and so the ET rate is relatively slow, the effects of the difference between Rc and Re on the theoretical ET rates or the logarithmic rates vs. the donor–acceptor distance relationship may not be significant. When the donor–acceptor distances become shorter, and so ET rates are faster than ca. 0.5 ps in lifetimes, the behavior of logarithmic ET rates vs. the donor–acceptor distances are quite different. The logarithmic ET rates deviates from a linear function of Rc which was obtained at relatively longer distances.50,51
The relationship between logarithmic ET rate and Rc in DAOB was analyzed with the ECw, SQw and GTRAMw terms. If it can be explained by the ECw term alone (or principally) then the slopes should equate to or be close to −βw (w; Trp, Tyr and Bz; see Table 2). However, there were considerable discrepancies between the slope of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) rate vs. Rc function and −βw in Tyr. The logarithmic ET rate could be decomposed into its constitutive three terms (eqn (20)), where the dependence of the logarithmic ET rate on Rc could be expressed as a sum of those for ECw and GTRAMw, since the variation in ln
rate vs. Rc function and −βw in Tyr. The logarithmic ET rate could be decomposed into its constitutive three terms (eqn (20)), where the dependence of the logarithmic ET rate on Rc could be expressed as a sum of those for ECw and GTRAMw, since the variation in ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SQw between Sub A, Sub B and the monomer was essentially negligible compared to the two other terms. Fig. 8 shows relationship between GTRAMw and Rc in Tyr. The slopes were −6.98 in Sub A, −7.31 in Sub B and −8.44 in monomer. Sums of these slopes and −βTyr were −13.2 in Sub A, −13.6 in Sub B and −14.7 in monomer, which are compared to the slopes in Fig. 6, −13.0 in Sub A, −13.2 in Sub B and −14.6 in monomer. The slope calculated based on logarithmic ET rate vs. Rc function was practically identical to the sum of the slope in Fig. 8 and −βTyr in each system. This implies that the slope in the GTRAMw vs. Rc relationship considerably contributes to the slope in the relationship between logarithmic ET rate and Rc. Further it is concluded that a linear relationship between the logarithmic ET rates and Rc is obtained only when GTRAMw linearly depends on Rc.
SQw between Sub A, Sub B and the monomer was essentially negligible compared to the two other terms. Fig. 8 shows relationship between GTRAMw and Rc in Tyr. The slopes were −6.98 in Sub A, −7.31 in Sub B and −8.44 in monomer. Sums of these slopes and −βTyr were −13.2 in Sub A, −13.6 in Sub B and −14.7 in monomer, which are compared to the slopes in Fig. 6, −13.0 in Sub A, −13.2 in Sub B and −14.6 in monomer. The slope calculated based on logarithmic ET rate vs. Rc function was practically identical to the sum of the slope in Fig. 8 and −βTyr in each system. This implies that the slope in the GTRAMw vs. Rc relationship considerably contributes to the slope in the relationship between logarithmic ET rate and Rc. Further it is concluded that a linear relationship between the logarithmic ET rates and Rc is obtained only when GTRAMw linearly depends on Rc.
 | ||
| Fig. 8 Relationship between GTRAMw and Rc of Tyr in Sub A and Sub B in the DAOB dimer and the DAOB monomer. GTRAMw is defined by eqn (19). Inserts show approximate linear functions of Y (GTRAMw) with X (Rc). | ||
It has been reported that the relationship between logarithmic ET rate and Rc in flavin mononucleotide (FMN) binding proteins displays a bell-shaped (not linear) function in the ET processes from Trp to Iso* when the ET rates are ultrafast (10–15 ps−1).53 This work emphasized that the GTRAMw term plays the main role determining the bell-shaped behaviour. However, a bell-shape was not observed in the ET from Tyr to Iso* in the flavodoxin from Helocobactor pylori,32 even though the ET rate was ultrafast at 6–23 ps−1. Thus, the bell-shape behaviour can only be observed when GTw linearly depends on Rc, and so GTRAMw becomes a parabolic function of Rc. In DAOB, the rates (0.01–0.9 ps−1) were much slower than those in the FMN binding proteins and the flavodoxins, and in addition the GTRAMw was a linear function of Rc, not parabolic.
V. Conclusion
Experimental fluorescence dynamics of DAOB dimer displays two lifetime components, 0.85 ps and 4.8 ps. It was identified that the fluorescence with the shorter lifetime is from Sub B and one with the longer lifetime from Sub A. The difference in the lifetimes was mainly ascribed to differences in the ET rates from Bz to Iso*in the two subunits. This is because the absolute value of GTw for ET from Bz in Sub A is greater than that in Sub B.Relationship between logarithmic ET rate and Rc displayed linear functions both for Tyrs and for Trps as ET donors. Sum of the slopes of the GTRAMw vs. Rc functions and of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ECw vs. Rc functions were almost identical with the slopes of ln
ECw vs. Rc functions were almost identical with the slopes of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kwET vs. Rc functions, which reveals that the GTRAMw term considerably contributes to the slope of the ln
kwET vs. Rc functions, which reveals that the GTRAMw term considerably contributes to the slope of the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kwET vs. Rc function.
kwET vs. Rc function.
Acknowledgements
This work was financially supported by The Chulalongkorn University Dutsidi Phiphat Scholarship. Thanks are also given to The National e-Science Infrastructure Consortium Project for computing facilities.References
- R. Miura, C. Setoyama, Y. Nishina, K. Shiga, I. Miyahara, H. Mizutani and K. Hirotsu, J. Mol. Catal. B: Enzym., 2001, 12, 43–52 CrossRef CAS.
- V. I. Tishkov and S. V. Khoronenkova, Biochemistry (Moscow), 2005, 70, 40–54 CrossRef CAS PubMed.
- L. Pollegioni, L. Piubelli, S. Sacchi, M. S. Pilone and G. Molla, Cell. Mol. Life Sci., 2007, 64, 1373–1394 CrossRef CAS PubMed.
- T. Kawazoe, H. K. Park, S. Iwana, H. Tsuge and K. Fukui, Chem. Rec., 2007, 7, 305–315 CrossRef CAS PubMed.
- S. Sacchi, L. Caldinelli, P. Cappelletti, L. Pollegioni and G. Molla, Amino Acids, 2012, 43, 1833–1850 CrossRef CAS PubMed.
- C. Madeira, M. E. Freitas, C. Vargas-Lopes, H. Wolosker and R. Panizzutti, Schizophr. Res., 2008, 101, 76–83 CrossRef PubMed.
- M. P. M. Boks, T. Rietkerk, M. H. van de Beek, I. E. Sommer, T. J. de Koning and R. S. Kahn, Eur. Neuropsychopharmacol., 2007, 17, 567–572 CrossRef CAS PubMed.
- M. Katane, N. Osaka, S. Matsuda, K. Maeda, T. Kawata, Y. Saitoh, M. Sekine, T. Furuchi, I. Doi, S. Hirono and H. Homma, J. Med. Chem., 2013, 56, 1894–1907 CrossRef CAS PubMed.
- M. L. Fonda and B. M. Anderson, J. Biol. Chem., 1968, 243, 5635–5643 CAS.
- S. W. Henn and G. K. Ackers, Biochemistry, 1969, 8, 3829–3838 CrossRef CAS.
- S. W. Henn and G. K. Ackers, J. Biol. Chem., 1969, 244, 465–470 CAS.
- K. Yagi and N. Ohishi, J. Biochem., 1972, 71, 993–998 CAS.
- E. Antonini, M. Brunori, M. R. Bruzzesi, E. Chiancone and V. Massey, J. Biol. Chem., 1966, 241, 2358–2366 CAS.
- H. Tojo, K. Horiike, K. Shiga, Y. Nishina, H. Watari and T. Yamano, J. Biol. Chem., 1985, 260, 12607–12614 CAS.
- H. Tojo, K. Horiike, K. Shiga, Y. Nishina, H. Watari and T. Yamano, J. Biol. Chem., 1985, 260, 12615–12621 CAS.
- H. Mizutani, I. Miyahara, K. Hirotsu, Y. Nishina, K. Shiga, C. Setoyama and R. Miura, J. Biochem., 1996, 120, 14–17 CrossRef CAS.
- A. Mattevi, M. A. Vanoni, F. Todone, M. Rizzi, A. Teplyakov, A. Coda, M. Bolognesi and B. Curti, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 7496–7501 CrossRef CAS.
- A. Karen, N. Ikeda, N. Mataga and F. Tanaka, Photochem. Photobiol., 1983, 37, 495–502 CrossRef CAS PubMed.
- A. Karen, M. T. Sawada, F. Tanaka and N. Mataga, Photochem. Photobiol., 1987, 45, 49–53 CrossRef CAS PubMed.
- D. Zhong and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 11867–11872 CrossRef CAS PubMed.
- P. A. van den Berg, A. van Hoek, C. D. Walentas, R. N. Perham and A. J. Visser, Biophys. J., 1998, 74, 2046–2058 CrossRef CAS.
- P. A. van der Berg and A. J. W. G. Visser, New Trends in Fluorescence Spectroscopy. Applications to Chemical and Life Sciences, Springer, Berlin, 2001 Search PubMed.
- N. Mataga, H. Chosrowjan, Y. Shibata, F. Tanaka, Y. Nishina and K. Shiga, J. Phys. Chem. B, 2000, 104, 10667–10677 CrossRef CAS.
- N. Mataga, H. Chosrowjan, S. Taniguchi, F. Tanaka, N. Kido and M. Kitamura, J. Phys. Chem. B, 2002, 106, 8917–8920 CrossRef CAS.
- H. Chosrowjan, S. Taniguchi, N. Mataga, F. Tanaka, D. Todoroki and M. Kitamura, J. Phys. Chem. B, 2007, 111, 8695–8697 CrossRef CAS PubMed.
- H. Chosrowjan, S. Taniguchi, N. Mataga, F. Tanaka, D. Todoroki and M. Kitamura, Chem. Phys. Lett., 2008, 462, 121–124 CrossRef CAS PubMed.
- H. Chosrowjan, S. Taniguchi, N. Mataga, T. Nakanishi, Y. Haruyama, S. Sato, M. Kitamura and F. Tanaka, J. Phys. Chem. B, 2010, 114, 6175–6182 CrossRef CAS PubMed.
- N. Nunthaboot, F. Tanaka, S. Kokpol, H. Chosrowjan, S. Taniguchi and N. Mataga, J. Phys. Chem. B, 2008, 112, 13121–13127 CrossRef CAS PubMed.
- N. Nunthaboot, S. Pianwanit, S. Kokpol and F. Tanaka, Phys. Chem. Chem. Phys., 2011, 13, 6085–6097 RSC.
- K. Lugsanangarm, S. Pianwanit, S. Kokpol, F. Tanaka, H. Chosrowjan, S. Taniguchi and N. Mataga, J. Photochem. Photobiol., A, 2011, 219, 32–41 CrossRef CAS PubMed.
- N. Nunthaboot, N. Kido, F. Tanaka, K. Lugsanangarm, A. Nueangaudom, S. Pianwanit and S. Kokpol, J. Photochem. Photobiol., A, 2013, 252, 14–24 CrossRef CAS PubMed.
- K. Lugsanangarm, S. Pianwanit, A. Nueangaudom, S. Kokpol, F. Tanaka, N. Nunthaboot, K. Ogino, R. Takagi, T. Nakanishi, M. Kitamura, S. Taniguchi and H. Chosrowjan, J. Photochem. Photobiol., A, 2013, 268, 58–66 CrossRef CAS PubMed.
- A. Nueangaudom, K. Lugsanangarm, S. Pianwanit, S. Kokpol, N. Nunthaboot and F. Tanaka, Phys. Chem. Chem. Phys., 2012, 14, 2567–2578 RSC.
- K. Yagi, F. Tanaka, N. Nakashima and K. Yoshihara, J. Biol. Chem., 1983, 258, 3799–3802 CAS.
- A. Nueangaudom, K. Lugsanangarm, S. Pianwanit, S. Kokpol, N. Nunthaboot and F. Tanaka, J. Photochem. Photobiol., A, 2012, 250, 6–17 CrossRef CAS PubMed.
- A. Nueangaudom, K. Lugsanangarm, S. Pianwanit, S. Kokpol, N. Nunthaboot and F. Tanaka, Phys. Chem. Chem. Phys., 2014, 16, 1930–1944 RSC.
- D. A. Case, T. A. Darden, I. T. E. Cheatham, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, M. Crowley, R. C. Walker, W. Zhang, K. M. Merz, B. Wang, S. Hayik, A. Roitberg, G. Seabra, I. Kolossváry, K. F. Wong, F. Paesani, J. Vanicek, X. Wu, S. R. Brozell, T. Steinbrecher, H. Gohlke, L. Yang, C. Tan, J. Mongan, V. Hornak, G. Cui, D. H. Mathews, M. G. Seetin, C. Sagui, V. Babin and P. A. Kollman, AMBER 10, University of California, San Francisco, 2008 Search PubMed.
- J. Wang, P. Cieplak and P. A. Kollman, J. Comput. Chem., 2000, 21, 1049–1074 CrossRef CAS.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS PubMed.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS PubMed.
- R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155–196 CrossRef CAS.
- C. C. Moser, J. M. Keske, K. Warncke, R. S. Farid and P. L. Dutton, Nature, 1992, 355, 796–802 CrossRef CAS PubMed.
- T. Kakitani and N. Mataga, J. Phys. Chem., 1985, 89, 8–10 CrossRef CAS.
- A. Yoshimori, T. Kakitani, Y. Enomoto and N. Mataga, J. Phys. Chem., 1989, 93, 8316–8323 CrossRef CAS.
- N. Matsuda, T. Kakitani, T. Denda and N. Mataga, Chem. Phys., 1995, 190, 83–95 CrossRef CAS.
- H. B. Gray and J. R. Winkler, Pure Appl. Chem., 1992, 64, 1257–1262 CrossRef CAS.
- V. Vorsa, T. Kono, K. F. Willey and N. Winograd, J. Phys. Chem. B, 1999, 103, 7889–7895 CrossRef CAS.
- F. Tanaka, H. Chosrowjan, S. Taniguchi, N. Mataga, K. Sato, Y. Nishina and K. Shiga, J. Phys. Chem. B, 2007, 111, 5694–5699 CrossRef CAS PubMed.
- F. Tanaka, R. Rujkorakarn, H. Chosrowjan, S. Taniguchi and N. Mataga, Chem. Phys., 2008, 348, 237–241 CrossRef CAS PubMed.
- N. Nunthaboot, K. Lugsanangarm, S. Pianwanit, S. Kokpol, F. Tanaka, S. Taniguchi, H. Chosrowjan, T. Nakanishi and M. Kitamura, Comput. Theor. Chem., 2014, 1030, 9–16 CrossRef CAS PubMed.
- V. Massey, B. Culti and H. Ganther, J. Biol. Chem., 1966, 241, 2347–2357 CAS.
- K. Nishimoto, Y. Watanabe and K. Yagi, Biochim. Biophys. Acta, 1978, 526, 34–41 CrossRef CAS.
- D. N. Beratan, J. N. Betts and J. N. Ounchic, Science, 1991, 252, 1285–1288 CAS.
- D. S. Bendall, Protein Electron Transfer, BIOS Scientific Publishers Ltd., Oxford, UK, 1996 Search PubMed.
- H. B. Gray and J. R. Winkler, Annu. Rev. Biochem., 1996, 65, 537–561 CrossRef CAS PubMed.
- Biophysics of Electron Transfer and Molecular Bioelectronics (Electronics and Biotechnology Advanced (Elba) Forum Series), ed. NicoliniC., Springer, 1999 Search PubMed.
- M. Bixon and J. Jortner, Electron transfer—from isolated molecules to biomolecules, biomolecules, in Advances in Chemical Physics: Electron Transfer-from Isolated Molecules to Biomolecules Isolated Molecules to Biomolecules, John Wiley & Sons Inc, Hoboken, NJ, USA, 1999, part 1 Search PubMed.
- A. Warshel and W. W. Parson, Q. Rev. Biophys., 2001, 34, 563–679 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra05211k |
| This journal is © The Royal Society of Chemistry 2014 |



