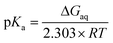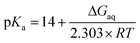Metal-induced histidine deprotonation in biocatalysis? Experimental and theoretical insights into superoxide reductase

Abstract

Metal-induced histidine deprotonation may have tremendous effects on metalloprotein catalysis. Here, we explore protonation states of all active site histidines in superoxide reductase (SOR), a non-heme iron enzyme catalysing the reduction of superoxide to hydrogen peroxide. Using experimental and theoretical techniques, we show that these amino acids remain in their neutral state under physiological conditions, excluding deprotonation. Based on our findings, alternative explanations for lack of H/D exchange of SOR histidines are discussed, including high barriers for acid/base reactions of coordinated ligands.

---

Superoxide O₂˙⁻ is a reactive oxygen species (ROS) that is deleterious to biological systems. Therefore, both ageing and numerous diseases in humans have been related to oxidative stress from increased levels of superoxide and other ROS.¹ To minimize these effects, most living species employ enzymatic systems that detoxify ROS. In anaerobic and microaerophilic organisms, superoxide reductase (SOR)² allows casual exposure to oxygen and growth under low levels of oxygen, respectively, by catalysing the reduction of superoxide to hydrogen peroxide via the following reaction:³

SOR_red + O₂˙⁻ + 2H⁺ → SOR_ox + H₂O₂

Superoxide reductases form a group of non-heme iron enzymes (Fig. 1A) that supply one electron during substrate reduction. In the ferrous state, the active site iron is coordinated by four equatorial histidines and an axial cysteinate, forming a square pyramidal geometry with a vacant site for substrate binding. In the octahedral ferric state, coordination of the active site is not uniform: during turnover, the sixth coordination site is supposedly occupied by dioxygen species in different protonation and oxidation states.^2–5 In contrast, the ferric resting state comprises an additional glutamate as a ligand in most,^6–8 but not all,⁹ cases. Based on the number of metal centres, superoxide reductases can be divided into two major subclasses:² neelaredoxins (Nlr)¹⁰ solely contain the active site (1Fe-SOR), while desulfoferrodoxins (Dfx)¹¹ harbour an additional rubredoxin-like iron centre (2Fe-SOR), the function of which remains elusive.

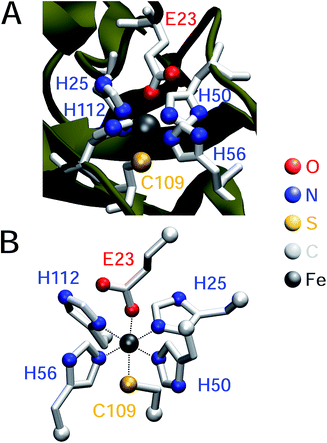Fig. 1 (A) Crystal structure of a single monomer of the superoxide reductase from I. hospitalis (PDB 4BK8).⁸ (B) Model compound of the superoxide reductase active site chosen for pK_a computation.⁸ In both cases, amino acids coordinated to the active site iron are highlighted in red (E), blue (H), and yellow (C) and listed in one-letter code according to the numbering of I. hospitalis SOR.

In a recent infrared (IR) study,⁸ we have identified ν(C=C) and ν(C–N) stretching vibrations of the active site histidines in the 1Fe-SORs from Ignicoccus (I.) hospitalis and Archaeoglobus fulgidus. In line with previous IR studies on SOR from Desulfoarculus baarsii (2Fe-SOR) and Treponema pallidum (1Fe-SOR),⁷ frequencies of both normal modes were found to be nearly insensitive towards H/D exchange, contrary to expectations for neutral histidine (Fig. 2).¹² Metal-induced histidine deprotonation due to pronounced pK_a lowering¹³ might be a possible explanation since the imidazolate anion represents the only form of the imidazole side chain of histidine that lacks exchangeable protons (Fig. 2).^12,14 Consistently, histidine deprotonation has also been suggested for other metalloenzymes, but no systematic studies are available so far.^15,16

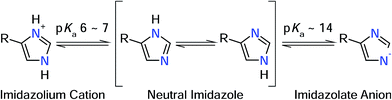Fig. 2 Protonation equilibria and tautomeric forms of the imidazole side chain of histidine. R refers to the NH₂–C_αH–CH₂–COOH moiety (in its respective protonation states).¹⁹

Notably, knowledge of the protonation state of histidine ligands is essential to understand the catalytic process of metalloenzymes. Specifically, the protonation state affects the imidazole donor/acceptor capabilities, which are key determinants for redox properties and reactivity. Moreover, in case of SOR histidine deprotonation could also influence catalysis by tuning the proton-supplying water-network around the active site.⁴ Therefore, we discuss the possibility of metal-induced histidine deprotonation together with alternative scenarios based on spectro-electrochemical and theoretical studies on SOR and model systems.

Numerous normal mode frequencies of the imidazole side chain are sensitive to the protonation state and, thus, valuable markers for this property (vide infra).¹² Analysis of absolute wavenumbers alone, however, might be ambiguous, especially in proteins and coordination compounds, where vibrational frequencies are also perturbed by metal binding and electrostatic interactions. Nonetheless, IR spectroscopy can be applied to probe pH dependent changes of these modes, thereby identifying transformations between the different forms.

In case of metal-bound imidazole, the number of acid–base equilibria is reduced to one, since protonation of both nitrogen atoms results in a dissociation of the complex. Consequently, pH dependent changes in histidine normal modes can be clearly ascribed to the transition between neutral imidazole and the imidazolate anion. A transition below pH = 7.5 would be indicative of histidine in the anionic form under physiological conditions, while a transition above pH 7.5 would indicate that the physiological state involves the neutral form. To probe this transition, we have recorded redox-dependent IR difference spectra over the pH range (6–9), at which I. hospitalis SOR is stable (Fig. 3I). Signals in these spectra are restricted to those modes sensing the redox transition of the active site,^7,8 where positive (negative) bands correspond to the ferrous (ferric) form of the enzyme. Clearly, the overall spectral appearance as well as the histidine marker bands, ν(C=C) and ν(C–N), are essentially unaffected by pH variations. This shows that amino acids at the SOR active site titrate far from physiological pH, supporting that protons required in superoxide reduction are derived from water.² Specifically, our findings indicate that the acid–base equilibrium for imidazolate formation lies outside the stable pH range of SOR.

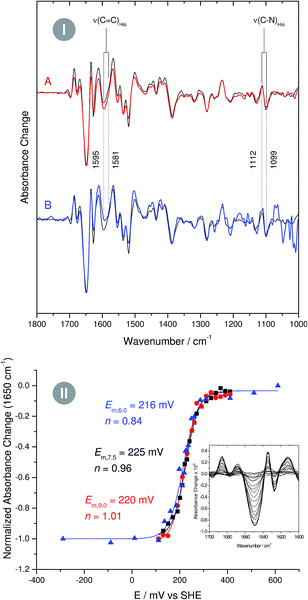Fig. 3 (I) Infrared difference spectra of the superoxide reductase (SOR) from I. hospitalis recorded at pH 9 (A, red line) and pH 6 (B, blue line). A spectrum recorded at pH 7.5 is shown as a reference in the background of both traces (black line). Spectra are normalized with respect to the difference band at 1650 cm⁻¹ (rearrangement of helices).⁸ (II) pH dependent reduction potentials of the I. hospitalis SOR, determined from potentiometric titrations at pH 6 (), pH 7.5 (), and pH 9 (). Relative amounts of the redox species were quantified by using the 1650 cm⁻¹ band as a marker for the ferrous enzyme (see inset).

As the impact of this equilibrium on non-imidazole modes is not known, this conclusion is, strictly speaking, limited to histidines, which undergo redox-dependent changes. To check if this finding can be extended to all histidines at the active site, we have performed pH dependent potentiometric titrations, using the most intense difference band at 1650 cm⁻¹ (rearrangement of helices)⁸ as a marker for the redox state of the iron. Since a change of the protonation state alters the donor/acceptor properties of imidazole,¹² the reduction potential of a histidine-coordinated metal ion is expected to be a function of the pH. However, examination of the Nernst curves reveals no significant variation of the reduction potential between pH 6 and 9, confirming that for all active site histidines of SOR the pK_a for imidazolate formation resides above or below this range (Fig. 3II).

A moderately lowered pK_a between 9 and 14 represents a likely scenario for coordinated imidazole,¹³ suggesting that all active site histidines in SOR reside in their neutral, protonated form. In contrast, a pK_a below 6 is unlikely from a fundamental Lewis acid point of view (vide infra) and, to the best of our knowledge, unprecedented for both biological and synthetic imidazole complexes. Nonetheless, we have also considered this experimentally inaccessible scenario to explore the eventuality of extraordinary strong pK_a lowering due to the specific ligand sphere conserved in all SORs. For this aim, we have calculated microscopic imidazole pK_a values of a consensus model compound of the SOR active site (Fig. 1B),⁸ using a quantum mechanical approach and thermodynamic cycles (Scheme 1) as described in the Experimental section. Neglecting influences of the protein matrix, this approach is insufficient to precisely determine absolute pK_a values of a specific SOR, but appropriate to estimate the general impact of metal binding on histidine acidity in this class of enzymes. The model complex has been treated as dissolved in water, since the SOR active site is largely solvent exposed.^2,3 Those parts interacting with the protein matrix primarily face a hydrophobic environment in I. hospitalis SOR,⁸i.e. the calculated quantities represent a lower limit of the real pK_a values. Using the above approach, we have estimated pK_a values of 9.3, 7.0, 8.3, and 9.3 for H25, H50, H56, and H112, respectively (I. hospitalis SOR numbering). As expected, all values are lower compared to histidine in aqueous solution, but clearly incompatible with an acid–base equilibrium below pH 6 for the active site histidines.

Scheme 1 Extended thermodynamic cycle for the calculation of pK_a values from ΔG in aqueous solution. The first cycle (shown in black) represents the deprotonation of an acid of interest, yielding its conjugate base. In the present study, this acid–base couple refers to the SOR active site model with each one ethylimidazole ligand in its neutral (EtImH) and anionic (EtIm⁻) form, respectively. The reference acid–base couple of the second cycle, free neutral imidazole (ImH) and imidazolate (Im⁻), is depicted in blue. Indices g, aq, and sol indicate gas phase, aqueous phase, and solvation Gibbs energies.

In this context, we have to emphasize that metal-induced pK_a lowering in histidine is governed by electron donation to a Lewis acid¹⁷ and, consistently, acidification is also observed upon adding a second proton to imidazole, yielding the imidazolium cation (pK_a 6–7, Fig. 2). Taking into account charge, ionic radius, and electronegativity, H⁺ appears to be a stronger Lewis acid than Fe³⁺.¹⁸ Therefore, electron affinity is likely to be higher for the proton, especially in case of SOR, where the acidity of the ferric iron is reduced by electron donation from six basic ligands. Consequently, the observed results are in line with the expectation that the pK_a of coordinated neutral histidine is generally higher than that of the imidazolium cation.

Nonetheless, it should be stressed that calculations for H50 yield an apparent pK_a close to physiological pH. The conjugate base of the corresponding model, however, reveals a dissociation of the trans oriented H112 (Table 1). As indicated by a shortening of the Fe–N_H50 bond, this dissociation is accompanied by an increased electron donation from H50 (as well as the other histidines) and, thus, a more pronounced acidification of the respective N_H50-bound proton. This effect is overestimated in the model, i.e. the real pK_a is expected to be considerably higher, since histidine dissociation from the iron is not observed in SOR crystal structures. Moreover, deprotonation of H50 is particularly unlikely as its N-bound proton is H-bonded to the backbone-carbonyl of P51 (the same holds for the respective histidine in SOR from other organisms).⁸

Table 1 Fe–N bond lengths (Å) for all imidazole ligands of the SOR model compounds in comparison to those experimentally determined in crystal structures^a

Coordinated histidine	X-ray data		Computed SOR model complex
	Tm	Ih	ImH	Im^−
				H112	H25	H50	H56
a Crystal structure data of SORs from Thermotoga maritima (Tm, PDB 3QZB, Joint Centre for Structural Genomics, unpublished results) and Ignicoccus hospitalis (Ih, PDB 4BK8)^8 were solved at 1.1 and 2.5 Å resolution, respectively. Ethylimidazole/histidine ligands are termed according to the Ih SOR numbering.
H112	2.18	2.20	2.23	2.08	2.22	3.64	2.36
H25	2.16	2.20	2.19	2.23	2.02	2.16	2.29
H50	2.23	2.27	2.21	2.44	2.23	2.00	2.27
H56	2.16	2.23	2.17	2.21	2.27	2.16	2.03

---

Thus, we exclude metal-induced deprotonation for all active site histidines at physiologically relevant pH, in line with experimental pK_a values observed for other histidine/imidazole complexes of transition metal ions.¹³ This conclusion is also confirmed by the observed high C=C stretching frequencies in SOR (1600–1580 cm⁻¹),^7,8 suggesting metal bound neutral (1605–1575 cm⁻¹) rather than anionic (1565–1555 cm⁻¹) imidazole.¹⁴ Furthermore, this normal mode is expected to exhibit very low IR intensity for imidazolate,¹⁹ in contrast to experimental findings for SOR, where ν(C=C) difference bands are among the most pronounced amino acid side chain features.^7,8

In the light of these findings, an alternative model is required to explain the observed H/D exchange insensitivity of the histidine C=C and C–N stretching vibrations. In principle, metal binding could alter the composition of these normal modes, and this may involve decoupling of the δ(N–H) deformation coordinate, which is responsible for H/D exchange sensitivity. However, both ν(C=C) and ν(C–N) exhibit a normal H/D exchange behaviour in the computed SOR model complex.⁸ Thermodynamic reasons can also be excluded on the basis of the present data, indicating that H/D exchange is retarded by kinetic effects. In this respect, solvent accessibility is a negligible factor as the active site is highly solvent exposed (vide supra). Thus, the lack of any detectable H/D exchange must root in the specific kinetics of proton abstraction from the iron-bound histidines and subsequent deuteron binding.

In the model compound studied in this work, dissociation of any nitrogen-bound proton involves a geometric rearrangement of the complex such that the Fe–N bond length of the deprotonated histidine is shortened, while those of the remaining neutral histidines are generally elongated (Table 1). This observation can be explained by the increased donor strength of the anionic imidazolate, which reduces the acidity of the iron (the deprotonation of H50 is an exception, because the resulting dissociation of H112 acidifies the iron). We propose that this rearrangement raises the reorganization energy associated with H(D)⁺ abstraction and attachment. Assuming that N–H bond cleavage, N–D bond formation, and the geometric rearrangement in the iron–histidine complex proceed asynchronous, even an imbalanced transition state with a high barrier ΔG^‡ could be expected.^20,21 Such a scenario could well account for the observed H/D exchange insensitivity in SOR. It may also represent a general determinant for proton exchange kinetics of coordinated imidazole in related complexes, and this may affect the dynamics of the proton supplying water network around the SOR active site. Furthermore, the geometric rearrangement predicted to accompany proton abstraction represent a further argument against metal-induced histidine deprotonation, since comparable distortions of the active site geometry have not been observed in the highest resolution SOR crystal structures (Table 1). In addition, H/D exchange of non-coordinated histidine in aqueous solution is likely to proceed via the imidazolium cation (pK_a 6–7) rather than the imidazolate anion (pK_a ∼ 14). As the imidazolium cation is inaccessible for metal-bound histidine, H/D exchange is forced to take place via the alternative, kinetically less favourable pathway.

Conclusions

Metal-induced histidine deprotonation in SOR can be excluded; all active site histidines reside in their neutral form. This is an important finding, which provides a sound structural basis for future mechanistic studies. Furthermore, we propose that structural reorganization might lead to high barriers for acid/base reactions of coordinated amino acids. This scenario is potentially relevant for proton-coupled reactions in metalloenzymes and the behaviour of dibasic ligands in general.

Experimental section

Sample preparation

I. hospitalis SOR was purified as described previously,²² concentrated to 2 mM and buffered in 20 mM Tris (pH 7.5) and 50 mM Bis-tris propane/MES, pH 6 and 9, respectively. To ensure proper electron transfer in solution, samples were incubated with 150 mM NaCl and a mixture of redox mediators, as described in ref. 8.

IR spectro-electrochemistry

Redox-dependent IR difference spectra of I. hospitalis SOR were recorded and processed as exemplified in ref. 8. Here, the most pronounced band at 1650 cm⁻¹ relates to the redox-dependent rearrangement of up to three helices close to the active site.⁸ Considering this feature as a marker for the relative amount of ferrous SOR, reduction potentials were determined by fitting Nernst curves to the resulting data sets. Interfering difference bands arising from the mediator mixture at pH 6 were subtracted from the spectra.

Computation of pK_a values

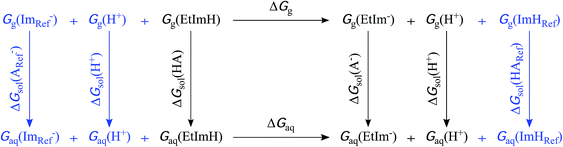
Microscopic pK_a values for heterolytic N–H bond dissociation were computed quantum-mechanically for all four ethylimidazole (EtIm) ligands of a previously described model compound of the SOR active site (Fig. 1B)⁸ by using the general relation between pK_a and the change in Gibbs energy of an acid/base reaction in aqueous phase (ΔG_aq):

A thermodynamic cycle (scheme 1, black)²³ was set-up to estimate ΔG_aq for the deprotonation of each EtIm ligand from gas phase and solvation Gibbs energies of the involved compounds. This first cycle was extended by a second one (see e.g.ref. 24) comprising free imidazole (Im, pK_a = 14) as a reference system (in blue). In such a way, systematic errors of the theoretic method are minimized and an increased accuracy is achieved, since calculations are independent from error-prone empiric values for solvation Gibbs energies of the proton. Using this extended cycle, pK_a values of the EtIm ligands relate to the resulting overall change of Gibbs energy ΔG_aq by:

All computations were performed on the BP86 level of theory^25,26 in Gaussian 03,²⁷ using the 6-31g* and tzvp basis sets²⁸ for H, C, N, O, S atoms and the Fe atom, respectively. To determine electronic, zero point vibrational, and thermal contributions (298 K) to gas phase Gibbs energies (G_g), geometry optimization and frequency calculations were performed as described previously.⁸ Solvation effects (ΔG_sol) were estimated from a polarizable continuum model,²⁹ using the default parameters implemented in Gaussian 03.

Notes and references

1. M. Valko, D. Leibfritz, J. Moncol, M. T. D. Cronin, M. Mazur and J. Telser, Int. J. Biochem. Cell Biol., 2007, 39, 44.
2. Y. Sheng, I. A. Abreu, D. E. Cabelli, M. J. Maroney, A. F. Miller, M. Teixeira and J. S. Valentine, Chem. Rev., 2014, 114, 3854.
3. A. F. Pinto, J. V. Rodrigues and M. Teixeira, Biochim. Biophys. Acta, 2010, 1804, 285.
4. G. Katona, P. Carpentier, V. Niviere, P. Amara, V. Adam, J. Ohana, N. Tsanov and D. Bourgeois, Science, 2007, 316, 449.
5. F. Bonnot, T. Molle, S. P. Menage, Y. Moreau, S. Duval, V. Favaudon, C. Houee-Levin and V. Niviere, J. Am. Chem. Soc., 2012, 134, 5120.
6. A. P. Yeh, Y. Hu, F. E. Jenney, M. W. Adams and D. C. Rees, Biochemistry, 2000, 39, 2499.
7. C. Berthomieu, F. Dupeyrat, M. Fontecave, A. Vermeglio and V. Niviere, Biochemistry, 2002, 41, 10360.
8. M. Horch, A. F. Pinto, T. Utesch, M. A. Mroginski, C. V. Romao, M. Teixeira, P. Hildebrandt and I. Zebger, Phys. Chem. Chem. Phys., 2014, 16, 14220.
9. J. V. Rodrigues, B. L. Victor, H. Huber, L. M. Saraiva, C. Soares, D. E. Cabelli and M. Teixeira, J. Biol. Inorg. Chem., 2008, 13, 219.
10. L. Chen, P. Sharma, G. J. Le, A. M. Mariano, M. Teixeira and A. V. Xavier, Eur. J. Biochem., 1994, 226, 613.
11. I. Moura, M. Bruschi, G. J. Le, J. J. Moura and A. V. Xavier, Biochem. Biophys. Res. Commun., 1977, 75, 1037.
12. K. Hasegawa, T. A. Ono and T. Noguchi, J. Phys. Chem. B, 2000, 104, 4253.
13. R. J. Sundberg and R. B. Martin, Chem. Rev., 1974, 74, 471.
14. K. Hasegawa, T. A. Ono and T. Noguchi, J. Phys. Chem. A, 2001, 106, 3377.
15. G. Smulevich, J. M. Mauro, L. A. Fishel, A. M. English, J. Kraut and T. G. Spiro, Biochemistry, 1988, 27, 5477.
16. R. Hienerwadel and C. Berthomieu, Biochemistry, 1995, 34, 16288.
17. A. Blackman, Advances in Heterocyclic Chemistry: Volume 58, Academic Press, San Diego, 1993.
18. Y. Zhang, Inorg. Chem., 1982, 21, 3886.
19. A. Barth, Prog. Biophys. Mol. Biol., 2000, 74, 141.
20. W. P. Jencks, Chem. Rev., 1985, 85, 511.
21. C. F. Bernasconi, Acc. Chem. Res., 1987, 20, 301.
22. F. G. Pinho, C. V. Romao, A. F. Pinto, L. M. Saraiva, H. Huber, P. M. Matias, M. Teixeira and T. M. Bandeiras, Acta Crystallogr., Sect. F: Struct. Biol. Cryst. Commun., 2010, 66, 605.
23. M. D. Liptak and G. C. Shields, J. Am. Chem. Soc., 2001, 123, 7314.
24. J. Ali-Torres, L. Rodriguez-Santiago and M. Sodupe, Phys. Chem. Chem. Phys., 2011, 13, 7852.
25. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
26. J. P. Perdew, Phys. Rev. B, 1986, 33, 8822.
27. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, and J. A. Pople, Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford CT, 2004.
28. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
29. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999.

---

Footnote

† Present address: Department of Medical Biochemistry and Biophysics, Karolinska Institutet, Scheeles Väg 2, 17177 Stockholm, Sweden.

---