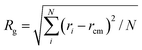Interaction of fullerene chains and a lipid membrane via computer simulations

Abstract

Coarse-grained molecular dynamics simulations were applied to investigate the interaction of fullerene polymers with a lipid membrane. It was found that the average center-of-mass distance between the polymer and membrane becomes larger with an increase of functionalization degree of the fullerene polymer. Free energy calculation shows the functionalization is energetically helpful to the adsorption of polymers on the membrane. For polymers with functionalized fullerenes, we found that the penetration of hydrophobic part into the lipid bilayer is realized by the thermally activated turnover of polymers.

---

Introduction

The rapid development of nanotechnology and synthesis methods have led to exciting innovations in many fields including the biomedical science and technology.¹ Nanomaterials are of great interest for application in the areas of specific targeting, drug delivery, and enhanced bioimaging.^2,3 An important example receiving considerable attention is the buckminsterfullerene (C₆₀). Possible uses of C₆₀ and its derivatives as X-ray contrast agents, antioxidant drugs for neurodegenerative diseases, and inhibitors of the allergic response have been suggested.⁴ However, chemical treatments are generally required for their potential biological applications in order to improve the solubility of C₆₀. For instance, functionalizations with –OH and –NH₂ have been used to increase its hydrophilicity.⁵ Recently, fullerenes were used as building blocks to construct novel materials such as the side-chain fullerene polymers, main-chain fullerene polymers, and star-shaped fullerene polymers.⁶ The introduction of fullerenes can enhance the properties of polymers such as photoconductivity. Meanwhile, the polymers can overcome the drawbacks of fullerenes (e.g., poor solubility) for large-scale applications. For example, amphiphilic fullerene polymers have been used for drug delivery via self-assembled supramolecular structures, which nearly can not realized by a single C₆₀.⁷ Main-chain fullerene polymers are a type of polymer characterized by the presence of the fullerene spheres in the polymer backbone. Water-soluble poly(fullerocyclodextrin)s prepared by Geckeler and coworkers showed an excellent DNA-cleaving activity in photodynamic cancer therapy.⁸ For biomedical applications, it is of significantly importance to characterize the interactions of fullerene polymers with cellular components such as DNA, proteins, especially, the plasma membrane, by which cells respond to extracellular environment.

Molecular dynamics (MD) simulations have played important roles in understanding the molecular mechanism of biosystems.^9–11 All atom molecular dynamics (AAMD) simulations have been used to study the interaction of a C₆₀ and its derivatives with lipid membranes.¹² Bedrov et al.¹³ focused on the passive transport of C₆₀ fullerene via atomistic simulations in the framework of CHARMM force field, and found that there is no free energy barrier for transport of the fullerene from the aqueous phase into the lipid core of membrane. Qiao et al.¹⁴ reported that the C₆₀(OH)₂₀ molecule is excluded by a dipalmitoylphosphatidylcholine (DPPC) bilayer but causes the area per neighboring lipid molecule reduced by 25%. The interactions of cationic amino functionalized C₆₀ with a palmitoyl-oleyl-phosphatidyl-choline (POPC) membrane has also been studied by the CHARMM force field.¹⁵ However, it is difficult to study the interactions of fullerene polymers with membranes by atomistic models due to the limitation of system size and time scale.¹⁶ Therefore coarse-grained models have been applied to study the related systems.¹⁷ Wong-Ekkabut et al.¹⁸ simulated the translocation of fullerene clusters through a lipid membrane employing MARTINI force field, and suggested that high concentrations of fullerene are unlikely to cause mechanical damage to the membrane. Fundamental studies are still required to understand the interactions of fullerene–polymeric materials with biological membranes.¹⁹

In the present paper, we study the interactions of fullerene chains composed of eight C₆₀s, some of which are surface-modified, with a DPPC membrane through coarse grained molecular dynamics simulations (CGMD) within the framework of the MARTINI force field.^21,22 The surface properties of fullerenes play an important role in determining their cell uptake and translocation. It becomes more and more difficult for the polymer penetrating into the membrane with the increase of functionalization degree of the fullerene polymer. However, the PMF calculation shows that the adsorption of functionalized fullerene polymers on the membrane is energetically favorable. In addition, we also found that the thermal fluctuation may assist the turnover of functionalized fullerene polymer for penetrating into a membrane. The paper is organized as follows. We first introduce the CG model and give an overview of the simulation settings. Then we discuss on the results of structures, dynamics, and free energies of the interacting systems. Finally, a short summary is concluded.

Model and methods

Five types of main-chain fullerene polymers (see Fig. 1) are considered to interact with a DPPC bilayer. Polymers consist of eight C₆₀s and/or its derivatives. The C₆₀ was modeled as a hydrophobic particle while its derivative as a hydrophilic particle. The eight fullerenes were connected via a bond without bond angle constraint which was modeled by a harmonic potential with K = 1250 kJ mol⁻¹ nm⁻² and R₀ = 0.47 nm to represent a simple fullerene polymer chain. The relative toxicity of fullerene-based polymers is mostly attributed to the ratio of the hydrophilic/hydrophobic fullerenes, which can lead to cell membrane disruption and subsequent cellular death.²⁰ We change the ratio of C₆₀ on the polymers from 1 to 0 so as to explore how the degree of functionalization of C₆₀–polymer might influence the interaction of the polymers with a lipid bilayer (Fig. 1). The CG simulations were on the basis of the MARTINI force field²¹ in which 4 to 1 mapping strategy was used. The force field and the topologies for C₆₀ and DPPC lipid were downloaded from the website of Marrink group (http://md.chem.rug.nl/marrink/coarsegrain.html), where four bead types (Q₀⁺, Q_a⁻, N_a, and C₁) were used for DPPC and CNP bead type was used for C₆₀. In order to model the C₆₀'s derivative with hydrophilicity, the bead type of C₆₀ was replaced with P4. The detailed description of our model was given in the ESI.†

Fig. 1 Five types of main-chain fullerene polymers were studied. The ratio of functionalized (hydrophilic) fullerene was increased from system 1 (S1) to system 5 (S5). Green and blue beads represent the C₆₀ and its derivative, respectively. The eight fullerenes were connected via a bond which was modeled by a harmonic potential to represent a simple fullerene polymer chain.

In each unbiased simulation, one polymer molecule interacts with a pre-equilibrated bilayer of 512 DPPC lipids. The polymer was initially placed 4 nm away from the center of mass (c.o.m.) of the bilayer. The system was then solvated with CG waters and energy-minimized for up to 1000 steps using a steepest-descent algorithm to remove any steric conflicts. Typically, each system was simulated for 1.0 μs. The data of the last 400 ns was used for analysis.

The umbrella sampling method²³ was used to calculate the potential of mean force (PMF). Twenty-seven independent windows (spaced by 0.2 nm) along the normal direction, z, of bilayer (z = 5.0 to 0.0 nm from the bilayer center) were allocated for sampling. The z coordinate of the c.o.m. of each polymer was restrained relative to the z coordinate of the c.o.m. of the bilayer with a harmonic biasing potential with a force constant of 1000 kJ mol⁻¹ nm⁻². For each window, 1.0 μs CGMD simulation was carried out. Data was analyzed with the WHAM method.²⁴

A Berendsen thermostat/barostat²⁵ was used to maintain a constant temperature of 310 K and a constant pressure of 1 atm with compressibility of 5.0 × 10⁻⁵ bar⁻¹ in the NP_zP_‖T ensemble. The time step of integration was 0.025 ps. A cutoff of 1.2 nm was used for electrostatic interactions and van der Waals interactions. The Lennard-Jones potential was smoothly shifted to zero between 0.9 and 1.2 nm and the Coulomb potential was smoothly shifted to zero between 0 and 1.2 nm. The relative dielectric constant is 15 for explicit water screening.²² All simulations were implemented with GROMACS package of version 4.5 (ref. 26) and visualized by VMD.²⁷

Results and discussion

In this section, we present the structural information such as number-density distribution, dynamics, and thermodynamics of the fullerene polymers interacting with a lipid membrane. Some analytical methods were given in ESI.†

Structure

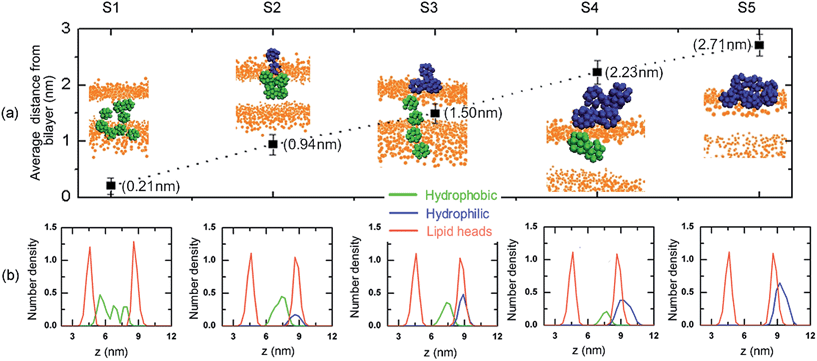
The average distance between the c.o.m of fullerene polymer and the c.o.m of bilayer are shown in Fig. 2a. It is about 0.21 nm for S1, which means that the polymer consisting of pristine C₆₀ fully penetrates into the lipid bilayer. The snapshot shows that the C₆₀ chain swells its configuration as in a good solution. The result is consistent with the finding of Li et al.,²⁸ who suggested that the bilayer was less able to accommodate the aggregated C₆₀ pair. For the totally functionalized fullerene chain (S5), the polymer adheres to the lipid bilayer, where the distance is about 2.71 nm. It demonstrates that the polymer can not penetrate into the bilayer as displayed by the equilibrated configuration. The average distances are 0.94 nm, 1.50 nm, and 2.23 nm for the S2, S3, and S4, respectively. The snapshots reveal that the hydrophobic part of the fullerene polymers enters the bilayer and makes contact with the lipid tails. The structure resembles the lipid-anchored proteins which are anchored to one leaflet of cell membrane. The average distance increases with the increase of the ratio of functionalized C₆₀, which implies that the functionalization is a pathway to control the penetration of fullerene polymers.

Fig. 2 (a) Average positions of fullerene polymers for various systems from the center of mass (c.o.m) of the DPPC bilayer. Insets are representative snapshots of final configurations for five systems. Green beads represent the hydrophobic fullerenes, while blue beads represent the hydrophilic fullerenes. Orange points represent the lipid head groups. Water are not shown for clarity. (b) Number density of hydrophobic fullerenes, hydrophilic fullerenes, and lipid head groups as a function of z distance.

Fig. 2b shows the corresponding density profiles of hydrophobic part and hydrophilic part of polymers as well as the lipid head groups of five systems. It can be seen that the distribution of fullerene in S1 is between the lipid head groups of two leaflets of bilayer, while the distribution of fullerene polymer in S5 is above the top leaflet of bilayer around the lipid head groups. For the other three systems, the hydrophilic and hydrophobic parts of the polymer distribute on the two sides of lipid head groups. And, the c.o.m distance between the two parts is about 1.5 nm. As expected, the simulations showed that more polar derivatives prefer to the water phase while less polar ones end up in the bilayer interior.²⁹ The above results suggest that the more surface-modified the fullerene polymer is, the larger the average c.o.m distance is and the harder it is to penetrate into the membrane.

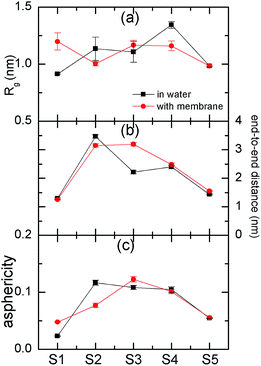
Further, the structures of fullerene polymers in water solution and after interacting with membrane were shown in Fig. 3. For S1 and S3, we find that the radius of gyration, R_g, in membrane is slightly larger than that in water, while the R_g for S2 and S4 in membrane is smaller than that in water. The profiles of end-to-end distance and asphericity as a function of functionalization degree seems like a horse-saddle. This maybe because the amphiphilic fullerene polymers for S2, S3, and S4 were split into two parts; one part is in water and the other part is in membrane. Here the asphericity, a, is equal to 1 − 3〈(I_xI_y +I_yI_z + I_zI_x)/(I_x + I_y + I_z)²〉, where I_x, I_y, and I_z are the three eigenvalues of the radius of gyration tensor. The R_g, the end-to-end distance, and the asphericity for the S5 seems not to be changed after interacting with membrane because the fully functionalized fullerene polymer does not penetrate into the membrane (i.e., it is still in water solution). In addition, we also calculated the order parameter of lipid tail, s = 0.5〈3 cos² θ − 1〉, where θ is the angle between the C1A–C4A bond vector of acl chain and the bilayer normal, and the angular brackets indicate averaging over time and lipid molecules. The order parameter of lipids around the polymer was weakly disturbed for all cases (see Fig. S2 in ESI†). Moreover, we find the polymers can make the local thinning of membrane, especially, for S1–S3 (Fig. 4). For S5, the polymer slightly change the membrane thickness due to its non-penetration.

Fig. 3 (a) Radii of gyration, R_gs, of the five types of fullerene chain in water and when interacting with membrane. Radius of gyration, R_g, was calculated by the equation , where N is the number of beads on the chain. r_i is the position vector of the ith bead and r_cm is the center of mass of the chain. (b) The end to end distances of the five types of fullerene chain in water and when interacting with membrane. The end-to-end distance is the norm of the end-to-end vector defined by a vector from the center of mass of C₆₀ at one end of the chain to the center of mass of C₆₀ at the other end of the chain. (c) Average relative shape anisotropy, a, of the five fullerene chains.

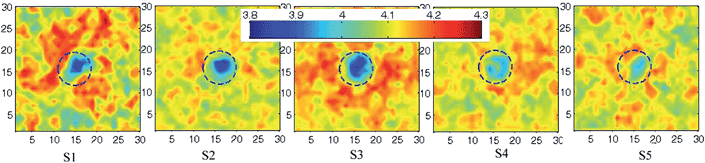Fig. 4 Thickness fluctuations across the bilayer in the x–y plane (grid resolution: 30 × 30) after the membrane interacting with the fullerene polymer for the five cases. The legend in units of nanometer shows the bilayer thickness values mapped to a rainbow color gradient. Grid-based membrane analysis tool³⁰ was used for averaging the coordinates of last 100 ns of our simulations.

Dynamics

The dynamics of how the fullerene polymer penetrates into the membrane was given in Fig. 5 for S1 and S3. It can be seen that the C₆₀ polymer diffuses randomly in the water solution at the beginning. It reaches the down leaflet of bilayer at about 400 ns. After a while, the polymer enters the membrane and stays between the two leaflet of lipid bilayer (Fig. 5a). The time evolution of the z-distance between polymer center and bilayer center also manifests the above process (the inset of Fig. 5b). It has been suggested that the binding of apolar molecules to lipid membranes is often enthalpy-driven, with an unfavorable entropic contribution.³¹ When the polymer contacts with the bilayer, the potential energy between the polymer and lipid heads deceases firstly, accompanied with the slight increase of that between the polymer and water molecules (Fig. 5b). Then, the potential energy between the polymer and lipid tail groups decreases sharply. The potential energy decrease between the polymer and lipids is more than the energy increase between the polymer and water. To evaluate the penetration time of C₆₀s, simulations were performed additionally ten times for each system. The average penetration time for the system is about 137 ns as the polymer was placed 3.4 nm about the center of mass of membrane (see Table S2 in ESI†). However, the polymer does not adsorb on the membrane over half of ten simulations of 1.0 μs due to the existence of energy barrier. Longer simulations are needed for capturing more penetration phenomena.

Fig. 5 (a) Time sequences of the polymer-bilayer interactions for S1. (b) Potential energies (between fullerene polymer and water; between polymer and lipid tail groups; between polymer and lipid head groups) as a function of simulation time for S1. The inset is the distance between the c.o.m of polymer and the c.o.m of bilayer in the z direction as a function of time for S1. (c) Time sequences of the polymer-bilayer interactions for S3. (d) The distance between the c.o.m of polymer and the c.o.m of bilayer in the z direction as a function of time for S3, and the order parameter of polymer defined by the direction from the c.o.m of hydrophilic part to the c.o.m of hydrophobic part of the polymer relative to the z-axis of box.

In addition, we capture a typical penetration process for S3 (Fig. 5c). The polymer waits a long time, about 1 μs, to insert into the bilayer. Under the influence of thermal fluctuation, the hydrophobic part of polymer begins to contact with the bilayer, and then turn over into the interior of bilayer. During this process, the hydrophilic part of polymer acts as a cupule attached on the bilayer that ensures the polymer not to diffuse away. The time evolutions of c.o.m distance between the fullerene polymer and lipid bilayer, and the order parameter of the polymer relative to the bilayer norm show that the process of turnover of the polymer is very short, about 25 ns (Fig. 5d). This behavior is similar to the thermally activated barrier hopping process. The conclusion is consistent with the finding of Qiao et al.,¹⁴ who suggest a single pristine C₆₀ molecule can “jump” into the DPPC bilayer. The polymer can rapidly penetrate into the membrane as long as it finds a suitable way with the help of thermal motion. Similar behaviors are also found in the S2 and S4. This may imply that the turnover behavior for penetration may be a general phenomenon for the amphiphilic polymers when interacting with cell membranes. Additionally we found that the polymer of S5 just adsorb on the membrane without penetration for the total simulations.

Potential of mean force

The potential of mean force was calculated to obtain the free energy profiles (as a function of the position of the fullerene polymer along the z axis normal to the bilayer) from bulk water to the core of the bilayer (Fig. 6a). The PMF profile of S1 displays a weak barrier of 1–2 K_BT near 3.75 nm due to the hydrophobic interactions as the polymer approaches the membrane. This barrier pushes the polymer to diffuse away as shown in the subsection of dynamics. If the barrier is overcome by thermal activation, the free energy decreases till the center of bilayer, and the polymer is pulled into the bilayer core. For S2, the PMF profiles decrease as the polymers approach the membrane from 5.0 nm to 3.0 nm. The functionalization of two C₆₀s on the polymer seems to have ability to eliminate the barrier of pure C₆₀ polymer for penetration. For S3–S5, there is a minimum in the PMF at the water/membrane interface. That's why the partly functionalized fullerene polymer prefers adsorbing on the membrane. The position of minimal energy is about 2` nm from the c.o.m of bilayer in S5, which is similar to that of the unbiased simulation.

Fig. 6 (a) Potentials of mean force (PMFs) as a function of position along the bilayer normal for five systems. (b) Well depth (blue/square; left-hand scale) of the energy minima (derived from the PMFs in Fig. 4a) for various systems. Also shown is the value of the PMFs at the center of the bilayer (red/circles, right-hand scale). (c) Distance between the energy minima (derived from the PMFs in Fig. 4a) and the c.o.m of lipid bilayer. Error bars are shown.

The energy minima is −110 K_BT, −75 K_BT, −50 K_BT, −40 K_BT, and −20 K_BT for the S1, S2, S3, S4, and S5, respectively (Fig. 6b). This means that the adsorption or penetration of polymers is strongly energetically favorable. However, the free energies in the center of bilayer are about −60 K_BT, −25 K_BT, 30 K_BT, and 105 K_BT for S2, S3, S4, and S5, respectively (Fig. 6c). Compared with the energy minima, it suggests that the polymers can hardly penetrate across the bilayer. The positions of energy minima for five systems is shown in Fig. S3.† It can be found that the distance is corresponding to the value of average distance in Fig. 2a, which is in accordance with that of our unbiased simulations.

Conclusion

In conclusion, the interactions of main-chain fullerene polymers with a DPPC membrane were firstly investigated by coarse-grained molecular dynamics simulations. We found that the C₆₀ polymer chain can fully partition into the lipid bilayer. The more surface-modified the fullerene polymer is, the farther away the center-of-mass position of polymer is from the bilayer, implying the harder for the polymer to penetrate into the membrane. In addition, The PMF calculations indicate that the free energy is in favor of the adsorption of functionalized fullerene polymers on the membrane. The adsorption provides enough time for the partly functionalized polymers to find a path to penetrate into the membrane via the polymer turnover with the help of thermal fluctuation. Furthermore, we found that the passive penetration of fullerene polymers through the membrane is difficult although the adsorption is energetically favorable. It should be pointed out, however, that a recent paper³² suggested it is an artifact barrier of the CG model as a single C₆₀ approaches the POPC membrane. For DPPC membrane, whether the barrier really exists or not should be checked via atomistic simulations although we found there has a small barrier in S1 system within the framework of CG model. Fullerene polymers, the fundamental unit of which is fullerene, combine the properties of polymer and fullerene, a type of nanoparticles. It is interesting to study their physicochemical properties when interacting with biomembrane. Our findings is valuable in designing new materials for bio-applications.

Acknowledgements

The work was supported by the National Natural Science Foundation of China (nos 91027040, 21104056, 1174180, and 10974080.) and the National Basic Research Program of China (973 program of no. 2012CB821500).

References

1. A. E. Nel, L. Madler, D. Velegol, T. Xia, E. M. V. Hoek, P. Somasundaran, F. Klaessig, V. Castranova and M. Thompson, Nat. Mater., 2009, 8, 543.
2. W. Tian and Y. Ma, Chem. Soc. Rev., 2013, 42, 705.
3. K. Yang and Y. Ma, Nat. Nanotechnol., 2010, 5, 579.
4. R. Partha and J. L. Conyers, Int. J. Nanomed., 2009, 4, 261.
5. T. Ros and M. Prato, Chem. Commun., 1999, 663.
6. C. Wang, Z. Guo, S. Fu, W. Wu and D. Zhu, Prog. Polym. Sci., 2004, 29, 1079.
7. R. Partha, M. Lackey, A. Hirsch, S. Casscells and J. L. Conyers, J. Nanobiotechnol., 2007, 5, 6.
8. S. Samal, B. J. Choi and K. E. Geckeler, Chem. Commun., 2000, 1373.
9. W. Tian and Y. Ma, Soft Matter, 2012, 8, 2627.
10. W. Tian and Y. Ma, Soft Matter, 2012, 8, 6378.
11. A. Jusufi, R. H. DeVane, W. Shinoda and M. L. Klein, Soft Matter, 2011, 7, 1139.
12. P. Ke and M. Lamm, Phys. Chem. Chem. Phys., 2011, 13, 7273.
13. D. Bedrov, G. D. Smith and H. Davandeand, J. Phys. Chem. B, 2008, 112, 2078.
14. R. Qiao, A. P. Roberts, A. S. Mount, S. J. Klaineand and P. Ke, Nano Lett., 2007, 7, 614.
15. S. Kraszewski, M. Tarek and C. Ramseyer, ACS Nano, 2011, 5, 8571.
16. C. Ren, W. Tian, I. Szleifer and Y. Ma, Macromolecules, 2011, 44, 1719.
17. L. Monticelli, E. Salonen, P. C. Ke and I. Vattulainen, Soft Matter, 2009, 5, 4433.
18. J. Wong-Ekkabut, S. Baoukina, W. Triampo, I. M. Tang, D. P. Tieleman and L. Monticelli, Nat. Nanotechnol., 2008, 3, 363.
19. M. Schulz, A. Olubummo and W. H. Binder, Soft Matter, 2012, 8, 4849.
20. C. M. Sayes, J. D. Fortner, W. Guo, D. Lyon, A. M. Boyd, K. D. Ausman, Y. J. Tao, B. Sitharaman, L. J. Wilson, J. B. Hughes, J. L. West and V. L. Colvin, Nano Lett., 2004, 4, 1881–1887.
21. S. J. Marrink, A. H. de Vries and A. E. Mark, J. Phys. Chem. B, 2004, 108, 750.
22. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812.
23. G. M. Torrie and J. P. Valleau, J. Comput. Chem., 1992, 13, 187.
24. S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, J. Comput. Chem., 1992, 13, 1011.
25. H. J. C. Berendsen, J. P. M. Postma, W. F. Van Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684.
26. D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701.
27. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33.
28. L. W. Li, H. Davande, D. Bedrov and G. D. Smith, J. Phys. Chem. B, 2007, 111, 4067.
29. R. S. G. D'Rozario, C. L. Wee, E. J. Wallace and M. S. P. Sansom, Nanotechnology, 2009, 20, 115102.
30. W. J. Allen, J. A. Lemkul and D. R. Bevan, J. Comput. Chem., 2009, 30, 1952–1958.
31. J. Seelig, Biochim. Biophys. Acta, 1997, 1331, 103.
32. L. Monticelli, J. Chem. Theory Comput., 2012, 8, 1370–1378.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra04593a

---