Influence of vortex domain switching on the electrocaloric property of a ferroelectric nanoparticle

Abstract

The influence of vortex domain switching on the electrocaloric (EC) property of a PbTiO₃ nanoparticle is studied using the phase field method combined with thermodynamics analysis. The calculation results reveal that both a very large negative adiabatic temperature change (ΔT = −6.34 K) and a positive adiabatic temperature change (ΔT = 4.16 K) appear in the PbTiO₃ nanoparticle when the vortex domain switches from the clockwise state to the counterclockwise state under a curled electric field. The obtained results will be of help in understanding the EC property in ferroelectrics with multidomain structure.

---

The electrocaloric (EC) effect has been widely studied recently because it can be used in solid-state refrigeration with the features of being environmentally friendly and of high efficiency.^1–7 The EC effect in a ferroelectric material involves the change of entropy and temperature when an external electric field is applied or withdrawn. According to the Maxwell relation, the magnitudes of the adiabatic temperature change and the isothermal entropy change depend on the magnitude of the polarization change.⁸ In a ferroelectric material, the homogeneous zones with the same polarization direction are named as domains, with domain walls existing between different polarization directions. It has been proved that these domains have a large influence on the EC property of a ferroelectric material. Neese et al. reported that the poly(vinylidene fluoride-co-trifluoroethylene) copolymer has an adiabatic temperature change of more than 12 K and an isothermal entropy change of more than 55 J kg⁻¹ K⁻¹, attributed to the contribution of the nanopolar domain.⁹ The EC effect in an epitaxial BaTiO₃ thin film with the polydomain ca₁/ca₂/ca₁/ca₂ phase at room temperature was found to be larger than that in the monodomain c phase using the Ginzburg–Landau–Devonshire thermodynamic theory.¹⁰ Wang et al. showed that the extrinsic contribution from the multidomain to monodomain transition driven by temperature significantly enhances the EC response using a phase field model.¹¹ In addition, Prosandeev et al. found that there is a 30% increase of the EC coefficient in a PbZr_0.4Ti_0.6O₃ nanodot with vortex domain structure compared with that in the monodomain structure by using first-principles investigation.¹² These works indicate that the ferroelectric nanostructure with multidomain structures, especially with the vortex domain structure, may provide an effective way for achieving a large EC effect.

In these works, the domain of the ferroelectric material is fixed without motion during the study of the EC property. Note that the ferroelectric domain could move or switch under a sufficiently large or changed electric field, respectively.¹⁰ Recently, a theoretical study showed that the domain displacement can enhance the EC response of an epitaxial Pb(Zr_1−x,Ti_x)O₃ thin film with multidomain structure.¹³ In an experimental study, the heat generation in single cycle of domain switching was found in a PZT ceramic using a 50 Hz infrared thermal camera.¹⁴ These works suggest a strong influence of the domain switching on the EC property, while the exact type of domain switching is not reported. The properties of a ferroelectric material with different types of domain switching may be different.¹⁵ In fact, the physical properties of a ferroelectric nanostructure with the vortex domain structure are largely different from those of other kinds of domain structures.¹⁶

To understand the mechanism of the influence of vortex domain switching on the EC effect for application in future solid-state refrigeration, it is necessary to develop a model to analyze the EC effect of the ferroelectric nanostructure with vortex domain switching. In addition, it is difficult to simultaneously measure the EC property and the vortex domain switching in experiments due to the small size of the ferroelectric nanostructure. In this work, the adiabatic temperature change (ΔT) of a PbTiO₃ (PTO) ferroelectric nanoparticle with vortex domain switching is studied. The vortex domain switching of PTO is obtained by using the phase field method. Then, ΔT of the PTO nanoparticle during the vortex domain switching is calculated by thermodynamics analysis.

In the phase field model, the temporal evolution of the spontaneous polarization P = (P₁, P₂, P₃) which is chosen as the order parameter is obtained using the time-dependent Ginzburg–Landau equation

where r represents the spatial vector, L is a kinetic coefficient, and F is the total energy of the ferroelectric material. The total energy of the PTO nanoparticle can be expressed as , where F_GL is the Ginzburg–Landau energy density, F_grad is the gradient energy density, F_elec is the electric energy density, F_elas is the elastic energy density and F_surf is the surface energy density. The Ginzburg–Landau energy density of PTO is described as¹⁷

F_GL(P_i) = α₁(P₁² + P₂² + P₃²) + α₁₁(P₁⁴ + P₂⁴ + P₃⁴) + α₁₂(P₁²P₂² + P₂²P₃² + P₁²P₃²) + α₁₁₁(P₁⁶ + P₂⁶ + P₃⁶) + α₁₁₂[P₁⁴(P₂² + P₃²) + P₂⁴(P₁² + P₃²) + P₃⁴(P₁² + P₂²)] + α₁₂₃P₁²P₂²P₃², (2)

where α_i, α_ij, α_ijk and α_ijkl are phenomenological coefficients. α₁ = (T − T₀)/2ε₀c₀ is a function of temperature, where T and T₀ are the temperature and the Curie temperature, respectively, ε₀ is the dielectric constant of the vacuum and c₀ is the Curie constant. The lowest order of the gradient energy density which is compatible with the cubic symmetry is taken as , where g_ijkl is the gradient energy coefficient. The elastic energy density is written as , where c_ijkl is the elastic modulus and ε_ij and ε⁰_kl are the total strain and the spontaneous strain, respectively. The electric energy density is dependent on the electrostatic field E^d_i and the external curled field E^cul_i. The E^d_i caused by the depolarization field is obtained by the negative gradient of the electrostatic potential E^d_i = −φ_i, where the electrostatic potential φ is obtained by solving the electrostatic equilibrium equation ∇·(−ε₀κ∇φ + P) = 0. The surface energy density has the form , where D₁₁ and D₄₄ relate to the gradient energy coefficients and δ_eff is the extrapolation length.^18,19

The PTO nanoparticle is represented by using a model of 20 × 20 discrete grids with a cell size of Δx* = Δy* = 1. Then, an extrapolative polarization boundary condition is adopted along the x and y directions of the PTO nanoparticle which indicate the [100] and [010] directions, respectively. For convenience, the normalized variables described in ref. 20 are used. The mechanical and electrical boundary conditions of the free-standing PTO nanoparticle are σ_ijn_j = 0 and D_in_i = 0, respectively. To solve eqn (1), the finite difference method for spatial derivatives and the Runge–Kutta method of order four for temporal derivatives are employed. The toroidal moment of polarization G is obtained from , where N is the number of cells and P_i is the polarization located at r_i.²¹ A curled electric field 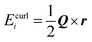is employed.²² The vorticity vector of the curled electric field Q is assumed as Q = Qn₃, where n₃ represents the unit-direction vector along the c-axis.²³ The change of toroidal moment caused by the change of vorticity vector related to the polarization induces a temperature change in the ferroelectric nanostructure with the vortex domain structure under the curled electric field.²⁴ The toroidal moment changes correspondingly with the change of the vorticity vector because Q is the thermodynamically conjugated field to G.²⁵ Then, the adiabatic temperature change (ΔT) of the PTO nanoparticle is defined as

where C is the heat capacity.²⁶

Firstly, the simulation is started from the paraelectric phase and a Gaussian random noise fluctuation of polarization field is introduced as the initial value of polarization. Then, the time interval is Δt* = 0.006. The total number of time steps is set to 2000 to ensure the domain structure of the PTO nanoparticle reaches a stable state. Fig. 1(a) shows the domain structure of the PTO nanoparticle at 25 °C. The direction and length of the arrows denote the direction and magnitude of the polarization, respectively. It reveals that the PTO nanoparticle forms a clockwise vortex domain structure with a head-to-tail arrangement. Then, an anticlockwise electric field with Q = −0.2 mV Å⁻² is applied on the PTO nanoparticle to study the EC effect. Fig. 1(b)–(f) show the distribution of ΔT and polarization in the PTO nanoparticle at the different normalized evolution time steps (t*) at 25 °C. The color denotes the magnitude of ΔT. Fig. 1(b) shows the distribution of polarization and ΔT of the PTO nanoparticle at t* = 100. It can be seen that a negative ΔT appears in the PTO nanoparticle because of the increase of entropy related to the decrease of toroidal moment. On further increasing the time step, the surface's polarization begins to switch through four vortices, as shown in Fig. 1(c). After that, the four vortices move to the inside of the PTO nanoparticle (Fig. 1(d)). At t* = 700, the direction of polarization located at the center of the PTO nanoparticle begins to reverse, as shown in Fig. 1(e). And ΔT at the surface of the PTO nanoparticle is positive, while ΔT at the center is negative. At t* = 1000, the switching process has completed. After that, the magnitude and direction of the polarization will not change, as shown in Fig. 1(f). Then, ΔT of the PTO nanoparticle are positive due to the decrease of the entropy. The magnitude of ΔT at the surface of the PTO nanoparticle is larger than that in the center.

Fig. 1 The domain structure of the PTO nanoparticle at different normalized evolution time steps t*: (a) t* = 0, (b) t* = 300, (c) t* = 500, (d) t* = 600, (e) t* = 700, (f) t* = 1000.

Fig. 2 shows the toroidal moment and the corresponding ΔT of the PTO nanoparticle as a function of Q at room temperature, where Q = 0.4 sin(2πf*t*) mV Å⁻² and f* = 0.001. The adiabatic temperature change–curled electric field (ΔT–Q) hysteresis loop of the PTO nanoparticle has the shape of a butterfly. From point A₁ to B₁ in Fig. 2, it can be seen that the magnitude of ΔT in the PTO nanoparticle decreases from 4.16 to 0 K when Q decreases from 0.4 to 0 mV Å⁻², respectively. Meanwhile, the toroidal moment of the PTO nanoparticle show a decreasing tendency, as shown from point A₂ to B₂. According to eqn (3), the decrease of Q would give rise to the magnitude of ΔT decreasing. The magnitude of ΔT (4.16 K) in the PTO nanoparticle (20 nm) with the vortex domain structure at Q = 0.4 mV Å⁻² is larger than that of a BaTiO₃ nanoceramic (15 nm) with a monodomain structure under E = 200 kV cm⁻¹ (ΔT = 1.6 K).²⁷ When Q decreases from 0 to −0.25 mV Å⁻², ΔT sharply decreases from 0 to −6.34 K, as shown from point B₁ to C₁ in Fig. 2. The sharp decrease of ΔT results from the large toroidal moment change which is caused by the vortex domain structure switching. After that, ΔT increases from −6.34 to 4.16 K when Q decreases from −0.25 to −0.4 mV Å⁻², as shown from point C₁ to D₁ in Fig. 2. This is because the magnitude of the toroidal moment change increases in this process.

Fig. 2 The toroidal moment and the adiabatic temperature change of the PTO nanoparticle as a function of vorticity Q.

Note that the polarization–electric field hysteresis loop is also observed in ferroelectrics with a monodomain structure. Therefore, the hysteresis loop between the adiabatic temperature change and electric field may have the shape of a butterfly in monodomain ferroelectrics. To confirm this, this model is applied to a ferroelectric thin film with monodomain structure to study the influence of the monodomain switching on the EC effect. Fig. 3(a) shows the domain morphologies of a PbZr_0.2Ti_0.8O₃ ferroelectric thin film without applied electric field at 25 °C. A dimensionless applied electric field E* = 3 sin(2πf*t*) is applied along the x axis of the PbZr_0.2Ti_0.8O₃, where f * = 0.0025 is the frequency of the electric field. Fig. 3(b) shows the polarization and the adiabatic temperature change of the PbZr_0.2Ti_0.8O₃ ferroelectric thin film as a function of E*. As shown in Fig. 3(b), the temperature change–electric field hysteresis loop of the PbZr_0.2Ti_0.8O₃ ferroelectric thin film with monodomain structure has the shape of a butterfly. Note that in an experiment it was observed that adiabatic temperature change–electric field hysteresis loop of PZT-5 ceramics displays the shape of a butterfly.²⁸ Meanwhile, a temperature change was found in PZT-5 ceramics under the different driving voltage using the infrared thermal camera.¹⁴ The simulation result of this work is in good agreement with the experimental observations, which confirms the validity of this model. Therefore, we believe that the butterfly curve of the temperature change–electric field hysteresis originates from the nonlinear relationship between the polarization and the electric field.

Fig. 3 The polarization and the adiabatic temperature change of a PbZr_0.2Ti_0.8O₃ ferroelectric thin film as a function of dimensionless applied electric field E*.

In conclusion, the EC effect of a PTO nanoparticle with vortex domain switching under a curled electric field is investigated using the phase field method combined with thermodynamics analysis. The calculation results show that the adiabatic temperature change–electric field hysteresis loop which has the shape of a butterfly is caused by the nonlinear relationship between the polarization and the electric field. The PTO nanoparticle has a positive adiabatic temperature change of 4.16 K and a negative adiabatic temperature change of −6.34 K during the vortex domain switching. We believe that this model can also be used to study the influence of multidomain or monodomain switching on the EC effect of ferroelectric materials.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (nos 11072208, 11272274, 11372266 and 11032010), the Hunan Provincial Natural Science Foundation of China (no. 12JJ1007), the Specialized Research Fund for the Doctoral Program of Higher Education (no. 20114301110004), the Foundation for the Author of National Excellent Doctoral Dissertation of PR China (201143) and the Scientific Research Fund of Hunan Provincial Education Department (14C1092).

References

1. J. F. Scott, Annu. Rev. Mater. Res., 2011, 41, 1.
2. X. Li, S. Lu, X. Chen, H. Gu, X. Qian and Q. M. Zhang, J. Mater. Chem., 2013, 1, 23.
3. E. Defay, S. Crossley, S. Kar-Narayan, X. Moya and N. D. Mathur, Adv. Mater., 2013, 25, 3337.
4. L. Luo, M. Dietze, C. Solterbeck, M. Es-Souni and H. Luo, Appl. Phys. Lett., 2012, 101, 62907.
5. Y. Bai, G. Zheng and S. Shi, Mater. Res. Bull., 2011, 46, 1866.
6. Y. P. Shi and A. K. Soh, Acta Mater., 2011, 59, 5574.
7. Y. Liu, J. Wei, P. Janolin, I. C. Infante, X. Lou and B. Dkhil, Appl. Phys. Lett., 2014, 104, 082901.
8. S. Lu and Q. Zhang, Adv. Mater., 2009, 21, 1983.
9. B. Neese, B. J. Chu, S. G. Lu, Y. Wang, E. Furman and Q. M. Zhang, Science, 2008, 321, 821.
10. Q. Jian-Hua, D. Jian-Ning, Y. Ning-Yi and W. Xiu-Qin, Chin. Phys. B, 2012, 21, 97701.
11. J. Wang, M. Liu, Y. Zhang, T. Shimada, S. Shi and T. Kitamura, J. Appl. Phys., 2014, 115, 164102.
12. S. Prosandeev, I. Ponomareva and L. Bellaiche, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 52103.
13. J. Karthik and L. W. Martin, Appl. Phys. Lett., 2011, 99, 32904.
14. H. Chen, Y. Pei, B. Liu and D. Fang, Appl. Phys. Lett., 2013, 102, 242912.
15. F. Xu, S. Trolier-McKinstry, W. Ren, B. Xu, Z. L. Xie and K. J. Hemker, J. Appl. Phys., 2001, 89, 1336.
16. Y. Ivry, D. P. Chu, J. F. Scott and C. Durkan, Phys. Rev. Lett., 2010, 104, 207602.
17. L. E. Cross and R. C. Pohanka, Mater. Res. Bull., 1971, 6, 939.
18. D. C. Ma, Y. Zheng, B. Wang and C. H. Woo, Appl. Phys. Lett., 2011, 99, 142908.
19. R. K. Vasudevan, Y. Chen, H. Tai, N. Balke, P. Wu, S. Bhattacharya, L. Q. Chen, Y. Chu, I. Lin, S. V. Kalinin and A. V. Nagarajan, ACS Nano, 2011, 5, 879.
20. Y. Zhang, J. Y. Li and D. N. Fang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 64103.
21. I. I. Naumov, L. Bellaiche and H. Fu, Nature, 2004, 432, 737.
22. S. Prosandeev, I. Ponomareva, I. Naumov, I. Kornev and L. Bellaiche, J. Phys.: Condens. Matter, 2008, 20, 193201.
23. W. J. Chen, Y. Zheng, B. Wang, D. C. Ma and F. R. Ling, Phys. Chem. Chem. Phys., 2013, 15, 7277.
24. B. Li, J. B. Wang, X. L. Zhong, F. Wang, Y. K. Zeng and Y. C. Zhou, RSC Adv., 2013, 3, 7928.
25. T. Cast An, A. Planes and A. Saxena, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 144429.
26. Y. Shen, D. R. Clarke and P. A. Fuierer, Appl. Phys. Lett., 2008, 93, 102907.
27. J. H. Qiu and Q. Jiang, J. Appl. Phys., 2009, 105, 34110.
28. J. Wang, T. Yang, K. Wei and X. Yao, Appl. Phys. Lett., 2013, 102, 152907.

---