Investigation of plasma electrolytic oxidation on valve metals by means of molecular spectroscopy – a review
Abstract
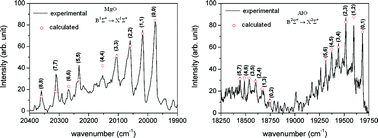
A review of results of molecular spectroscopic investigations during plasma electrolytic oxidation of valve metals is presented. Particular attention is paid to three spectral systems, B1Σ+ → X1Σ+ of MgO, and B2Σ+ → X2Σ+, and C2Π–X2Σ+ of AlO. It was shown that a reliable assignment of the observed spectral features can only be carried out by critical comparison with the data obtained from high-resolution spectroscopy, and by using the results of quantum mechanical structure calculations. Assuming the existence of partial local thermal equilibrium, we used our spectroscopic results to determine the plasma temperature. Although limited in quality, the obtained spectra are very rich, they cover large wavelength regions, and are used to obtain information about physical and chemical processes that take place in the course of plasma electrolytic oxidation of light metals and their alloys.

 Please wait while we load your content...
Please wait while we load your content...