Simulation of conformational properties of end-grafted diblock copolymers

Abstract

Conformational properties of end-grafted flexible diblock copolymers were studied by using Monte Carlo simulation. The copolymers, XA_nB_n and XB_nA_n, are grafted with the end X to a flat surface which attracts monomers A but repulses monomers B. Results show that the blocks A in XA_nB_n and XB_nA_n are adsorbed upon the surface at low temperature, and the adsorption of blocks A takes place roughly at the same temperature. However, the conformational size and instantaneous shape of the blocks A and B in XA_nB_n and XB_nA_n are different. The possible reasons were discussed and they were interpreted by different properties and grafting locations of the two blocks.

---

1. Introduction

Adsorption of polymers on attractive surfaces or interfaces plays an important role in various areas of technological applications and biological processes.^1–6 The conformation of adsorbed polymers can be classified into distinct types according to the adsorption strength.^7,8 It is relevant to many applications, such as gel permeation chromatography,^1,2 compatibilization by copolymer,^3,4 copolymer separation,⁵ medical implants and bioaffinity sensors.⁶ The behavior of polymers near an attractive surface has been numerous studied by theory and computer simulation.^8–11

The adsorption of end-grafted homogeneous polymers on a flat attracting surface was intensively investigated.^12–17 Every monomer contacting with the surface is assigned an attraction energy E. There is a phase transition from a desorbed state at high temperatures to an adsorbed state at low temperatures beyond a critical value T_c, which is named as the critical adsorption point (CAP). The conformation of an adsorbed polymer changes from three dimensional to a quasi two dimensional conformation at CAP. The properties of adsorption, conformational size and shape of the polymer show different behaviors at the temperature below, above, and near the CAP. At CAP, it was found that the conformational sizes, such as mean square end-to-end distance 〈R²〉 and mean square radius of gyration 〈R_G²〉, reach minimum.¹⁶ But it is difficult to directly measure the conformational properties of a single polymer.¹⁸ Theoretical study of a single polymer chain is important as it provides a tool for understanding the properties of polymer aggregates.

The critical adsorption and conformational properties of end-grafted AB copolymers has also been investigated.^19–21 The critical adsorption point, statistical conformational size and shape of the copolymer are the key factors to understand the behavior of copolymer, since these properties are dependent on the chain length and polymer-surface attraction.^19–21 The AB copolymer is composed of two types of monomers A and B that have different properties. Therefore AB copolymer can be modeled as a synthetic protein or DNA.²² The properties of copolymer tethered to surface are more complex. The copolymer is usually modeled as having attractive monomers A and non-attractive monomers B. It was found that copolymer's properties depend not only on the whole chain length but also on the block size of the attractive monomers and the interaction strength.^20,21 Copolymers tend to adsorb with the attractive blocks rather flat on the surface, whereas the non-attractive block in one dangling tail (or loop) protrudes into the solution.¹⁹ Besides, for end-grafted diblock copolymer A_nB_n, the adsorption and conformational properties will be also dependent on the position of non-attractive block B, i.e. on the grafted end which is near B or near A. Study the adsorption of end-grafted diblock copolymers is helpful to understand the macroscopic behaviors and structures of block-copolymer on surface.^23–25

In the present paper, we study the adsorption of two simple flexible diblock copolymers XA_nB_n and XB_nA_n with the end monomer X grafted to a flat surface. The conformational size and instantaneous shape of the whole copolymer and that of the blocks A or B in XA_nB_n and XB_nA_n are studied. We find that the adsorption property of the blocks A in both copolymers is similar, but the conformational properties are quite different for the block A and block B. As a result, properties of diblock copolymer XA_nB_n are different from XB_nA_n. Our results show that the conformational properties of the whole copolymer as well as that of each block are dependent on the position of the non-attractive block B.

2. Model and calculation method

We use self-avoiding walk (SAW) copolymers on the simple cubic lattice with one end grafted to a flat surface. The flat surface located at z = 0 is assumed infinitely large and impenetrable to copolymer chain. The copolymer XA_nB_n or XB_nA_n has equal block length for the blocks A and B. The polymer length is defined as N = 2n. The graft monomer X is fixed at position (0, 0, 1), and copolymer is restricted to lie in the upper half space (z > 0). Each monomer occupies one site of the lattice. The bond length in copolymer can fluctuate from 1, and 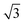lattice unit.^26–28 We consider that two types of monomers are different in the interaction with the surface. The interaction between the monomer A and the surface is attractive, whereas that between the monomer B and the surface is pure repulsive. Especially, every monomer locating at layer z = 1, namely contacting with the surface, is assigned an interaction energy E_AS = −1 for monomer A and E_BS = 0 for monomer B. We consider the case that the interaction between two non-bonded monomers are pure repulsive and is assigned as E_AA = E_BB = E_AB = 0 in the simulation. Here, we only consider a simple flat surface with short-range interactions, which is widely used in theory and simulation.^11–17 Whereas long-range interactions, such as electrostatic interactions which might be exist in real surface, are ignored in the present work.

Fluctuation of bond in polymer is due to random Brownian motion resulted from random collisions between monomers and solvent molecules. In the dynamic model, a monomer is chosen randomly and attempts to jump one lattice spacing selected randomly from one of the six directions. This jump will be accepted if the following five conditions are satisfied: (1) the new site locates at z > 0, (2) the new bond vector still belong to the allowed bond set, (3) self-avoidance is obeyed, (4) two bonds do not intersect, and (5) the Boltzmann factor exp(−ΔE/k_BT) > p, where 0 < p < 1 is a random number in (0, 1) and ΔE is the energy shift due to the change of monomer sites. The Boltzmann constant k_B is set unity in the simulation. In one Monte Carlo step (MCS) all monomers except the grafted end in the chain attempt to move once.

Annealing method is adopted to simulate the temperature dependence of polymer properties. Starting at a high temperature T = 8, we slowly decrease T with a small step ΔT. The step is chosen as small as 0.05 near T_c, while a slightly big value is chosen away from T_c. The chain changed its configurations with time. At each T, the copolymer is first equilibrated for about 2.5N^2.13MCS.¹⁵ Then we record the conformations of polymer at every 0.1N^2.13MCS in the next 100 N^2.13MCS. The results are averaged over 1000 conformations for one independent run. And our final results are further averaged over 1000 independent runs. The simulation codes are written in Fortran 90 with MPI.

In this work we have simulated the adsorption and conformation properties of copolymer A_nB_n with different grafted points and with different block length n varied from n = 5 to n = 200. We find that the conformational properties of three representative copolymers A₅₀B₅₀, A₁₀₀B₁₀₀, and A₂₀₀B₂₀₀ present the similar behaviors. However the difference in the conformational properties between XA_nB_n and XB_nA_n increases slightly with the increase in the block length n. Therefore, in this work we take XA₂₀₀B₂₀₀ and XB₂₀₀A₂₀₀ as the main samples.

3. Results and discussions

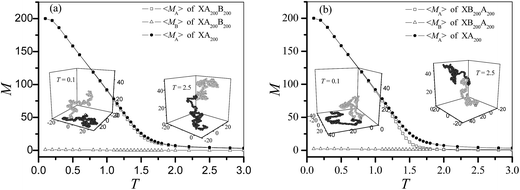
Fig. 1 shows the mean number of surface contacts for blocks A and B at different temperatures for the diblock copolymers XA₂₀₀B₂₀₀ and XB₂₀₀A₂₀₀. The block B almost does not contact with the surface since E_B = 0, whereas the block A begins to be adsorbed at about T = 1.5 which is close to the CAP of homogeneous polymer.¹⁷ It means that the CAPs of XA₂₀₀B₂₀₀ and XB₂₀₀A₂₀₀ are about T = 1.5 and the non-attractive block B has little influence on the CAP of diblock copolymers A_nB_n. The difference between XA₂₀₀B₂₀₀ and XA₂₀₀ is smaller than that between XB₂₀₀A₂₀₀ and XA₂₀₀, indicating that the influence of the end-grafted block B is slightly more obvious than the dangled block B. At T > 1.7, the block A in XB₂₀₀A₂₀₀ does not contact the surface anymore. The insets show the snapshots of polymer configurations at high temperature T = 2.5 and at low temperature T = 0.1. The configurations of XA₂₀₀B₂₀₀ and XB₂₀₀A₂₀₀ at T = 2.5 are similar. Both copolymers fully extend in the solution. But at T = 0.1, large difference can be found for the block B: block B in XA₂₀₀B₂₀₀ behaves like an end-grafted chain whereas it in XB₂₀₀A₂₀₀ behaves like a ring with two end monomers B contacting with the surface. The block B stretches in the solution for XA₂₀₀B₂₀₀, whereas the middle part extends in solution for XB₂₀₀A₂₀₀. At T = 0.1, the contact number is M = 200 for both copolymers, indicating that all the monomers A lie on the surface and thus the conformation of block A is two-dimensional.

Fig. 1 The mean number of surface contacts 〈M〉 at different temperatures T for diblock copolymers XA₂₀₀B₂₀₀ (a) and XB₂₀₀A₂₀₀ (b). The dark circles present monomers A, while the gray circles present monomers B.

The square end-to-end distances R² and the square radius of gyration R_G² of a chain with length N are defined as:

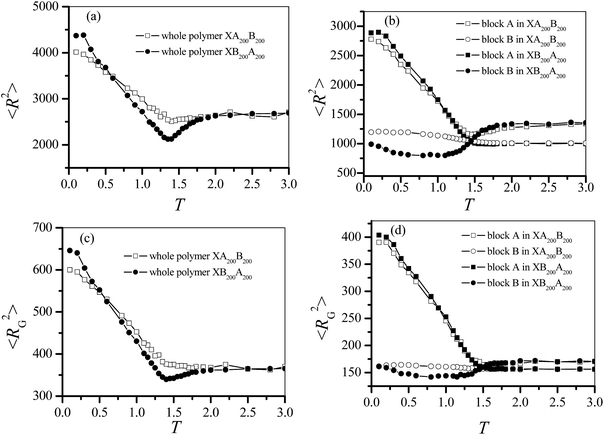
where r⃑_i and are the position vectors of the i^th monomer and the center of mass of the chain, respectively. The mean square end-to-end distances 〈R²〉 and the mean square radius of gyration 〈R_G²〉 are calculated at different temperatures. At the same time, the mean square end-to-end distances and the mean square radius of gyration for the block A (〈R_A²〉 and 〈R_GA²〉) and the block B (〈R_B²〉 and 〈R_GB²〉) are also calculated. The results are presented in Fig. 2 for XA₂₀₀B₂₀₀ and XB₂₀₀A₂₀₀. The location T = 1.5 at which both 〈R_A²〉 and 〈R_GA²〉 are minima is defined as the CAP of the copolymer XA₂₀₀B₂₀₀ as the method adopted for homogeneous polymers.¹⁶ We find that both 〈R²〉s and 〈R_G²〉s of XA₂₀₀B₂₀₀ and XB₂₀₀A₂₀₀ show the same behaviors. And difference between the two copolymers is only at low temperatures below CAP. The behavior of polymer conformation can be understood from the behaviors of blocks A and B.

Fig. 2 The dependence of mean square end-to-end distances 〈R²〉 and mean square radius of gyration 〈R_G²〉 on the temperature T for diblock copolymer XA₂₀₀B₂₀₀ and XB₂₀₀A₂₀₀. 〈R²〉 of whole copolymer chain (a), the block A and the block B (b), while 〈R_G²〉 of whole copolymer chain (c), the block A and the block B (d).

〈R_A²〉 of XA₂₀₀B₂₀₀ decreases with the decrease in T at high temperatures but increases with the decrease in T at low temperatures, which is consistent with the behavior of a homogeneous polymer.¹⁷ That implies that the dangled block B has little influence on the properties of XA₂₀₀B₂₀₀. 〈R_A²〉 of XB₂₀₀A₂₀₀ however increases monotonically with the decrease in T. Such a difference results from that the block A of XA₂₀₀B₂₀₀ is initially end-grafted whereas the block A of XB₂₀₀A₂₀₀ is initially roughly free in the solution. At high temperature, 〈R_A²〉 of XA₂₀₀B₂₀₀ is bigger than 〈R_A²〉 of XB₂₀₀A₂₀₀. On the other hand, with the decrease of T, the block B of XA₂₀₀B₂₀₀ changes from a free conformation with small 〈R_B²〉 at high T to an end-grafted conformation with a slightly larger 〈R_B²〉 at low T. 〈R_B²〉 of XA₂₀₀B₂₀₀ at T = 0.1 is roughly the same as 〈R_A²〉 of XA₂₀₀B₂₀₀ at high temperatures. While the block B of XB₂₀₀A₂₀₀ changes from an end-grafted conformation at high T to a double end-grafted conformation at low T. We find 〈R_B²〉 of XB₂₀₀A₂₀₀ changes nonmonotonically with T. A minimum of 〈R_B²〉 is found when the polymer changes from an end-grafted conformation to a double end-grafted conformation. The properties of 〈R_G²〉 are similar to those of 〈R²〉 for these two end-grafted diblock copolymers A_nB_n. The different conformational properties of block A or block B are due to their different surface interactions and their different positions in chain.

The dependence of 〈R²〉 and 〈R_G²〉 on the chain length N of homogenous polymer is in scaling laws as 〈R²〉 ∝ N^2ν and 〈R_G²〉 ∝ N^2ν.^16,26,27 Here the exponent ν is dependent on polymer model and space dimension.^29–31 For SAW chain, ν = 0.588 for a three-dimensional (3D) chain and 0.75 for two-dimensional (2D) one, respectively.²⁹ While in a melt of poly(ethylene terephthalate) (PET), ν is dependent on chain length.^30,31 It was found that the exponent changes from about 0.6 for short chains to about 0.5 for longer chain.^30,31 We here examine whether the scaling laws are still valid for the end-grafted diblock copolymer chain. We calculate 〈R²〉 and 〈R_G²〉 of copolymers XA_nB_n and XB_nA_n for different block lengths n = 5, 10, 20, 25, 40, 50, 75, 100, 150, and 200. We find that the scaling relation is still applicable for the copolymers XA_nB_n and XB_nA_n at different temperatures above, below or near CAP. For example, the dependence of 〈R²〉 and 〈R_G²〉 on N in is presented in Fig. 3a for copolymers at low temperature T = 0.5 and at T = 1.4 near CAP. The dependence of the scaling exponent ν on the temperature T is plotted in Fig. 3b for the scaling law of 〈R_G²〉 ∝ N^2ν. We find that there is a transition for the value of ν with the decrease of T. The location of the transition point is near CAP. At the temperature T above CAP, the value of ν is close to the Flory exponent 0.588 of 3D SAW chain. At T below CAP, the value of ν increases with the decrease of T. At the temperature T = 0.5 or below, the scaling exponent ν = 0.675 is located between ν = 0.6 of three dimension and ν = 0.75 of two dimension, which is due to two dimensional conformation of block A adsorbed on the surface and three dimensional conformation of block B dangled in the solution. At T near CAP, the value ν of XB_nA_n is slightly smaller than that of XA_nB_n because the block B changes from an end-grafted conformation to a double end-grafted one. We find that the scaling exponent ν of 〈R²〉 ∝ N^2ν is also similar to that of 〈R_G²〉∝ N^2ν.

Fig. 3 The dependence of mean square end-to-end distances 〈R²〉 and mean square radius of gyration 〈R_G²〉 on chain length N (a) and the dependence of the scaling exponent ν on the temperature T (b) for two end-grafted diblock copolymers XA_nB_n and XB_nA_n.

The instantaneous shape of polymer can be expressed by the mean asphericity parameter 〈A〉 which is defined as

in three-dimension space. Here, L₁², L₂², and L₃² (L₁² ≤ L₂² ≤ L₃²) are the eigenvalues of the radius of gyration tensorwhere s_i = col(x_i,y_i,z_i) is the position of monomer i in a frame of reference with its origin at the center of mass. This parameter ranges from 0 for spherically symmetric chain conformations, to 0.25 for circular ones, and to 1 for rod-shaped ones. For a long SAW chain, the instantaneous shape is an ellipsoid with 〈A_free〉 ≈ 0.44 for polymer in dilute solution³² and 〈A_grafted〉 ≈ 0.45 for end-grafted polymer.¹⁷

Fig. 4 shows the dependence of 〈A〉 on T for copolymers XA₂₀₀B₂₀₀ and XB₂₀₀A₂₀₀. Values of the mean asphericity parameter 〈A〉 are calculated for the whole copolymer 〈A〉, block A 〈A_A〉 and block B 〈A_B〉, respectively. We find that the variation of 〈A〉 is similar to that of 〈R²〉 and 〈R_G²〉, indicating that there are correlations between shape and size for each block in the copolymers as that found in homogeneous polymer.³³ 〈A_A〉 of the blocks A increases fast below T = 1.5, indicating the transition from 3D to 2D takes place roughly at the same temperature for both copolymers. The value of 〈A_A〉 is about 0.62 at low temperatures, indicating that the 2D conformation of block A is elliptical. The increase of 〈A_B〉 with decreasing temperature for the block B of XA₂₀₀B₂₀₀ shows that the block B changes to end-grafted conformation at low temperature. Whereas for the block B in XB₂₀₀A₂₀₀, it changes from an end-grafted conformation to a double end-grafted one. We find that 〈A_B〉 decreases at first and then increases with the decrease in temperature.

Fig. 4 The mean asphericity parameter 〈A〉 at different temperatures T for whole copolymer chain (a) and for the block A and the block B (b) in copolymers XA₂₀₀B₂₀₀ and XB₂₀₀A₂₀₀.

4. Conclusion

Dynamic Monte Carlo methods are carried out for the investigation of adsorption and conformational properties of diblock copolymers XA_nB_n and XB_nA_n. The conformational properties, the mean square end-to-end distance 〈R²〉, the mean square radius of gyration 〈R_G²〉 and the mean asphericity parameter 〈A〉, are dependent on temperature and the property of block. We found that at high temperature (above CAP), the conformations of the whole diblock copolymer XA_nB_n and XB_nA_n are almost the same, whereas that of block A or block B in XA_nB_n and XB_nA_n exist difference due to the different positions of A and B in the end-grafted polymer. At low temperature (below CAP), the block A is attracted to the surface, whereas the block B in XA_nB_n is an end-grafted coil and that in XB_nA_n is a loop with two ends contacted with the surface. At the intermediate temperature (near CAP), the conformational size and instantaneous shape of the whole copolymer reach a minimum, especially in XB_nA_n. Our results show that one could distinguish different types of blocks in copolymer by measuring their temperature dependence of size and shape.

Our results show that the difference in conformational properties of XA_nB_n and XB_nA_n is due to the different properties between two blocks and different positions of B. Therefore the difference will be reduced if the difference between two blocks is reduced. The cases of different block length between block A and block B are also considered for diblock copolymers XA_mB_n and XB_nA_m. However, the effect of block length A on the behavior of block B is quite interesting. If the block B is the dangled block as in XA_mB_n, the behavior of block B is roughly independent of the length of block A. Whereas if the block B is the end-grafted block as in XB_nA_m, the behavior of block B is strongly dependent on the length of block A. In this case, the block B changes from one end grafted chain at high temperature to a loop with two ends grafted. The behavior can be also observed but the transition temperature (close to CAP) is dependent on the length of block A, since CAP increases with the length of block A.⁸ Therefore, the general trend is that the effect of block A is reduced when the length of block A is decreased.

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grant Nos. 11304231, 11374255, and 21171145 and by the Zhejiang Natural Science Foundation of China under Grant No. LY14B040004.

References

1. E. Uliyanchenko, S. Wal and P. J. Schoenmakers, Polym. Chem., 2012, 3, 2313–2335.
2. B. Trathnigg, Prog. Polym. Sci., 1995, 20, 615–650.
3. N. Zgheib, J. L. Putaux, A. Thill, E. Bourgeat-Lami, F. D'Agosto and M. Lansalot, Polym. Chem., 2013, 4, 607–614.
4. G. Pu, Y. Luo, A. Wang and B. Li, Macromolecules, 2011, 44, 2934–2943.
5. Y. S. Lipatov, A. E. Nesterov, T. D. Ignatova and D. A. Nesterov, Polymer, 2002, 43, 875–880.
6. L. A. Ruiz-Taylor, T. L. Martin, F. G. Zaugg, K. Witte, P. Indermuhle, S. Nock and P. Wagner, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 852–857.
7. R. J. Roe, J. Chem. Phys., 1965, 43, 1591–1598.
8. E. Eisenriegler, K. Kremer and K. Binder, J. Chem. Phys., 1982, 77, 6296–6320.
9. F. Wang and D. P. Landau, Phys. Rev. Lett., 2001, 86, 2050–2053.
10. D. P. Landau and F. Wang, Comput. Phys. Commun., 2002, 147, 674–677.
11. D. T. Seaton, T. Wüst and D. P. Landau, Comput. Phys. Commun., 2009, 180, 587–589.
12. H. Zhang, J. Zhu, J. He, F. Qiu, H. Zhang, Y. Yang, H. Lee and T. Chang, Polym. Chem., 2013, 4, 830–839.
13. R. Decase, J. U. Sommer and A. Blumen, J. Chem. Phys., 2004, 120, 8831–8840.
14. E. J. J. van Rensburg and A. R. Rechnitzer, J. Phys. A: Math. Gen., 2004, 37, 6875–6898.
15. M. B. Luo, J. Chem. Phys., 2008, 128, 044912.
16. H. Li, C. J. Qian and M. B. Luo, Polymer J., 2010, 42, 383–385.
17. H. Li, C. J. Qian, L. Z. Sun and M. B. Luo, J. Appl. Polym. Sci., 2012, 124, 282–287.
18. M. Vacha and S. Habuchi, NPG Asia Mater., 2010, 2, 134–142.
19. O. A. Evers, J. M. H. M. Scheutjens and G. J. Fleer, Macromolecules, 1990, 23, 5221–5233.
20. Y. Tan, L. Fang, J. Xiao, Y. Song and Q. Zheng, Polym. Chem., 2013, 4, 2939–2944.
21. S. Bhattacharya, H.-P. Hsu, A. Milchev, V. G. Rostiashvili and T. A. Vilgis, Macromolecules, 2008, 41, 2920–2930.
22. A. Meller, L. Nivon, E. Brandin, J. Golovchenko and D. Branton, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 1079–1084.
23. G. Srinivas, D. E. Discher and M. L. Klein, Nat. Mater., 2004, 3, 638–644.
24. S. Egli, H. Schlaad, N. Bruns and W. Meier, Polymers, 2011, 3, 252–280.
25. J. N. L. Albert and T. H. Epps III, Mater. Today, 2010, 13, 24–33.
26. J. S. Shaffer, J. Chem. Phys., 1994, 101, 4205–4213.
27. H. Li, C. J. Qian, C. Wang and M. B. Luo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 012602.
28. H. Li, C. J. Qian, C. Wang and M. B. Luo, Polym. Polym. Compos., 2012, 20, 107–110.
29. A. Yethiraj, Macromolecules, 2003, 36, 5854–5862.
30. Q. Wang, D. J. Keffer, S. Petrovan and J. B. Thomas, J. Phys. Chem. B, 2010, 114, 786–795.
31. Q. Wang, D. J. Keffer, D. M. Nicholson and J. B. Thomas, Macromolecules, 2010, 43, 10722–10734.
32. M. B. Luo and J. H. Huang, J. Chem. Phys., 2003, 119, 2439–2443.
33. M. B. Luo, J. H. Huang, Y. C. Chen and J. M. Xu, Eur. Polym. J., 2001, 37, 1587–1590.

---