Conformational complexity of morphine and morphinum in the gas phase and in water. A DFT and MP2 study

Abstract

The structural and conformational properties of morphine and protonated morphine (morphinum) in the gas phase and in water solution have been explored with quantum calculations. Fully optimized calculations using the cc-pVTZ basis set, with various methods (MP2, B3LYP, and PBE0) for the species in the gas phase and with B3LYP with simulation of the solvent effect as a continuum with the SMD method were conducted. The study focuses on the determination of the relative energies of the 12 possible conformers that arise from the orientation of the two OH groups and the equatorial vs. axial position of the methyl group on the nitrogen and the energy barriers that separate these minima. The calculations indicate a preference for conformers having the methyl group equatorial, but corresponding axial conformers are not significantly higher in energy. Only 8 of the 12 possible conformers of gaseous morphine were found to be minima on the potential energy hypersurface. All 12 conformers of morphinum are minima according to MP2 computations. B3LYP/SMD (water) calculations predict the coexistence of 12 conformers for both morphine and morphinum with energy ranges of 17 kJ mol⁻¹ for morphine, and as low as 13 kJ mol⁻¹ for morphinum. In morphinum, energy differences of less than 8 kJ mol⁻¹ are computed for 8 conformers, including axial forms. The inversion at nitrogen is calculated to be energetically accessible at room temperature since the activation barrier is less than 30 kJ mol⁻¹ in the gas phase and only around 40 kJ mol⁻¹ with simulated water solvation. The many conformers within a small energy span, the fact that a thermodynamic equilibrium exists between morphine and morphinum in water, and the rapid nitrogen inversion show that morphine and morphinum have a large conformational diversity in water, and thus in the physiological media, which could be a clue to the interaction of this drug with receptors.

---

1 Introduction

Morphine is a highly potent opiate analgesic drug that acts directly on the central nervous system, the peripheral nervous system, and the gastrointestinal tract. It is used as an analgesic (relieves or eliminates pain) and as a narcotic. Morphine has many undesirable side effects such as addiction, constipation, abdominal cramps, diarrhoea, vomiting, drowsiness, etc. Properties of this much investigated prototypical opioid have been reviewed extensively.^1–12

The numerous physiological properties of morphine ultimately depend on the structural (in large part conformational) properties of this compound and on its N-protonated analogue, the morphinum cation, but the relations between structures and functions are still unclear. Furthermore, the diversity of the possible conformations has not yet been fully understood. Studies, such as the present one, should therefore not only lead to a better understanding of the conformational properties of morphine and morphinum, but could help understanding their physiological behaviour and be helpful for the efforts of synthesizing drugs free of unwanted side effects.

Morphine (C₁₇H₁₉NO₃) is composed of five condensed rings (A–E; see Fig. 1) in a rigid quasi diamond-like structure. The labelling of the nitrogen and carbon atoms is shown in Fig. 1. The protonated N17-form morphinum (C₁₇H₂₀NO₃⁺), is a two-protic acid with pK_a1 = 8.31 (N17, ring D) and pK_a2 = 9.51 (phenol function, ring A).¹³ At physiological pH (7.365), the concentration of the morphinum cation is about 9 times larger than that of morphine. At this pH, there is also an insignificant concentration of the phenoxidic anion (C₁₇H₁₈NO₃⁻), which is therefore not considered further.

Fig. 1 Morphine and morphinum (left) with atom numbering and the X-ray structure of morphine (right). The conformation of morphine found in the X-ray work is denoted M_equ-3anti-6g⁺. Hydrogen atoms, other than those of interest for the conformational properties, have been omitted for clarity.

The conformational properties of morphine and morphinum are associated with the equatorial and axial positions of the methyl group at N17, as well as the rotational isomerism about the C3–O and C6–O bonds (Fig. 1). For convenience, the conformers with equatorial and axial methyl group in the morphine and morphinum are denoted as M_equ, M_ax, M⁺_equ, and M⁺_ax, respectively.

Microwave studies have shown that the phenol OH group lies in the aromatic plane,¹⁴ which indicates that the dihedral angle C4–C3–O–H is either ≈0° (synperiplanar) or 180° (antiperiplanar). These two conformations will be noted 3syn and 3anti. The other hydroxyl group is bonded to a sp³ carbon C6 and it is well established that three rotamer forms could exist. In the antiperiplanar rotamer, the C5–C6–O–H dihedral angle is ≈180°, whereas it is about +60° in the +synclinal form and −60° in the −synclinal conformer. The three rotamer forms of the hydroxyl group at C6 are referred to as 6anti, 6g⁺, and 6g⁻, respectively. Combining the conformational possibilities for the two OH groups leads to 6 possible conformers for morphine for a given position of the methyl group at nitrogen. Since this methyl group at N17 can be either equatorial or axial (isomers referred as equatorial or axial in this work), there are 12 possible conformers for morphine. A similar reasoning applies to morphinum, which also has 12 possible conformers.

There are several recent experimental and theoretical investigations of the conformational and structural properties related to morphine and morphinum. The ¹³C NMR studies show that the equatorial to axial inversion at N in morphine analogues, codeine and sinomenine, in aprotic solvents is relatively fast with an energy barrier of 25–27 kJ mol⁻¹.¹⁵ A MM3 calculation of morphine yield a value of 27.6 kJ mol⁻¹,¹⁶ which agree well with the experimental values.¹⁵

Crystalline morphine exists in two polymorphic forms.¹⁷ Very recently, the X-ray structure of the stable polymorph was reported.¹⁸ The heavy-atom skeleton of this compound is drawn in Fig. 1 (right). It has an equatorial methyl group, the hydroxyl group attached to C6 is engaged in an intramolecular hydrogen bond with the ether oxygen atom of the E ring (6g⁺ conformation), and the phenolic OH group of C3 has an 3anti conformation and forms an intermolecular hydrogen bond with a neighbour morphine molecule. A recent X-ray determination of the structure of morphine hydrochloride anhydrate¹⁹ reveals that the morphinum cation has the same conformation as morphine¹⁸ with one exception, namely, the phenolic OH, which now has a 3syn conformation forming a second hydrogen bond with oxygen of the E ring.

It is typical that only one conformer is present in the crystalline state of both morphine and its hydrochloride. However, relatively small energy differences are expected between several conformers of morphine and morphinum in the gas phase and in water solution. Unfortunately, no experimental methods are presently able to map the full conformational landscape of such relatively complicated compounds. Consequently, a computational study is an attractive alternative method. Computations with quantum methods restricted to equatorial conformations of morphine have recently been reported for the gas phase,^20–22 as well as for aqueous solution.²⁰ In this work, state-of-the-art quantum calculations are carried out to investigate the full conformational landscape of morphine and morphinum in the gas phase and in water solution. The study includes calculations for equatorial morphine to a higher methodological level than previously^20–22 using a choice of several DFT functionals and a wave-function method, MP2. The axial conformations of morphine, not considered in previous works, were included.^20–22 This study reveals that axial conformers are not much higher in energies than their equatorial counterparts and should definitely be taken into consideration. No similar calculations have previously been reported for morphinum, the predominating species in water solutions at physiological pH and the first results are therefore reported herein. The energies of transition states of nitrogen inversion of morphine derivatives reported previously¹⁵ were obtained in aprotic solvents and do not consider the various individual conformers involved in this motion. This is also the case for the MM3 calculations, which refer to the gas phase.¹⁶ In the present study, the equatorial to axial transition states of several conformers are calculated for the first time both for the gas phase and water solution and it is shown that solvation modifies the barrier heights.

2 Computational details

The calculations were carried out with the Gaussian 09 program²³ running on the Abel cluster of the University of Oslo. DFT and wave-function based methods were used in order to detect small energy variations originating from weak interactions within certain conformations of morphine/morphinum. For the DFT methods, the B3LYP^24,25 and PBE0,²⁶ functionals were employed. Selected calculations were carried out using the M06-2X²⁷ functional. The MP2 method was used as a wave-function based procedure. The influence of the solvent (water) was modelled using the SMD continuum solvation method of Marenich et al.²⁸ only in the case of B3LYP calculations. The modeling by a continuum was selected over the introduction of explicit water molecules because it was considered that a large number of water molecules would have been needed to treat in an equal manner the solvation of the two OH and the amine/ammonium groups. The cc-pVTZ basis set of Peterson and Dunning is used for all atoms and with all methods.^29,30 All minima, including those obtained in the MP2 and B3LYP/SMD calculations, were fully optimized without any constraints. To explore the potential energy surfaces associated with the rotation of the OH groups, a large number of relaxed scans were conducted at the B3LYP level in which the position of one of the two OH groups was varied via a dihedral angle (10° steps) defined relative to the carbon skeleton, while all other structural parameters are optimized. The information obtained from this exploration was used for carrying out full optimization of minima and transition states. The nature of each extremum (minimum or transition state) was assigned by analytical calculations of frequencies in the case of the B3LYP and PBE0 functionals. The MP2 energies of the transition states were carried out as single point calculations on B3LYP geometries. The Gibbs energies and enthalpies were calculated from the harmonic approximation of frequencies at 298 K and P = 1 atm only with the B3LYP and PBE0 functionals. The trends in electronic energies and Gibbs energies and enthalpies are similar and for this reason the electronic energies available for all methods are used to present the results.

3 Results and discussion

3.1 Rotational energy profiles of morphine and morphinum

A series of B3LYP scans about either the C3–O or the C6–O bond were undertaken for the isomer with the equatorial and axial methyl group at nitrogen, M_equ and M_ax, respectively. The corresponding calculations were carried out for the morphinum form (M⁺_equ, and M⁺_ax). This first set of calculations was carried out for systems in the gas phase. The phenol OH was held in either the 3syn or 3anti conformation for the study of the rotation about the C6–O bond (ω = dihedral angle C5–C8–O–H). Likewise, the rotation about the C3–O bond was performed while holding the alcohol C6–OH in either the 6g⁺, 6g⁻, or in the 6anti position.

A typical example is the potential curve of isolated M_equ (black line in Fig. 2) for the rotation about the C6–O bond (ω) with phenolic OH in the 3syn conformation (ω′ = 0°). There are only two minima on this curve, one corresponding to 6g⁺ (ω ≈ 50°) and the other one to 6anti (ω ≈ 180°), 15.9 kJ mol⁻¹ higher in energy than 6g⁺. Interestingly, the expected g⁻-minimum for ω ≈ 300° (−60°) is missing. However, an inflexion in the curve is seen for ω ≈ 300°. The maxima for ω appear at approximately 130 and 250°. Their energies are 18.9 and 18.0 kJ mol⁻¹ above 6g⁺.

Fig. 2 Potential energy (B3LYP) curves for rotation about the C6–O bond (ω) of equatorial morphine with C4–C3–O–H dihedral angle (ω′ = 0°) in the 3syn position. The black curve refers to calculations in gas phase and the red curve to calculations including the solvation effect (water).

The corresponding B3LYP/SMD energies obtained for M_equ in water are shown as the red curve in Fig. 2. Comparison with the calculations for M_equ in the gas phase (black curve) shows that the solvation modifies the conformational properties significantly. The energies of the maxima for ω ≈ 130° (10.5 kJ mol⁻¹ above the energy of 6g⁺), at ca. 240° (8.3 kJ mol⁻¹), and at about 340° (7.8 kJ mol⁻¹), are significantly lower than for the gas phase (black curve). 6g⁻ is now suggested to be a possible secondary minimum in contrast to the gas-phase results.

The B3LYP energy for rotation about C3–O bond of M_equ (ω′ = C4–C3–O–H) with the C₅C₆OH in the 6g⁺ conformation is shown as the black curve in Fig. 3. There are the two expected minima on this potential energy curve corresponding to 3syn and 3anti, respectively, with 3syn being more stable than 3anti by 6.7 kJ mol⁻¹. The two maxima are located at ω′ ≈ 100 and 270°, at 16.8 and 17.8 kJ mol⁻¹ above the 3syn minimum. This is in good agreement with the experimental value of the barrier to internal rotation of the OH group of phenol, which is 16.3(6) kJ mol⁻¹.³¹ Related computations for M_equ in water with the alcohol OH group held in the 6g⁺ position resulted in the curve shown in red in Fig. 3. The solvent lowers the energy of the maxima (12.5 and 12.6 kJ mol⁻¹) and essentially equalizes the energy of 3syn and 3anti (difference of 0.7 kJ mol⁻¹).

Fig. 3 Potential energy (B3LYP) curves for rotation about the C3–O bond (ω′) of equatorial morphine with C5–C6–O–H dihedral angle (ω = +60°) in the 6g⁺ position. The black curve refers to calculations in gas phase and the red curve to calculations including the solvation effect (water).

Related curves for morphinum are shown in Fig. 4 (rotation about the C6–O bond described by ω) and Fig. 5 (rotation about the C3–O bond described by ω′), where the black and red graphs represent the gas phase and the water solution, respectively. The variations of the energies as a function of ω or ω′ are smaller when the solvent effect is included. An exception appears for values of ω larger than 320°, where the values of energies including solvation are higher (Fig. 4). The maxima of the black curve of Fig. 4 (gas phase) occur at ω = 140, 240, and 340° with energies 12.8, 10.0, and 6.6 kJ mol⁻¹ higher than that of the 6g⁺ minimum. The maxima of the water–solution graph (red curve) occur nearly for the same values of ω as for the gas phase with energy values that are 10.6, 8.2, and 7.8 kJ mol⁻¹ higher than that of the 6g⁺ minimum. The potential energy curve for rotation about C3–O (Fig. 5) shows that the gas barrier heights are about 16.9 and 18.7 kJ mol⁻¹ for ω′ = 100 and 270°, respectively, relative to the 3syn minimum. The corresponding values are 12.5 (93°) and 12.6 kJ mol⁻¹ (273°) for water solution.

Fig. 4 Potential energy (B3LYP) curves for rotation about the C6–O bond (ω) of equatorial morphinum with C4–C3–O–H dihedral angle (ω′ = 0°) in the 3syn position. The black curve refers to calculations in gas phase and the red curve to calculations including the solvation effect (water).

Fig. 5 Potential energy (B3LYP) curves for rotation about the C3–O bond (ω′) of equatorial morphinum with C5–C6–O–H dihedral angle (ω = +60) in the 6g⁺ position. The black curve refers to calculations in gas phase and the red curve to calculations including the solvation effect (water) by a continuum (SMD) method.

3.2 Optimized structures of morphine and morphinum conformers

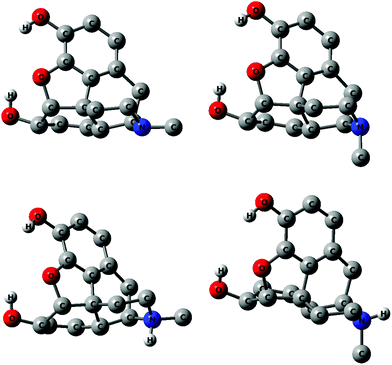
Many additional scans similar to those described above reveal that several rotamers exist within a relatively small energy span and that the energy barriers separating them are relatively low. This information was used to carry out a full optimization of minima at the B3LYP, B3LYP/SMD, PBE0 and MP2 levels. As mentioned in the Computational details section the vibrational frequencies were calculated only with the B3LYP and PBE0 methods. The relative energies of minima are listed in Tables 1 and 2 for morphine and Tables 3 and 4 for morphinum. The Cartesian coordinates of all extrema are listed in the ESI, Tables 1S–90S.† Enthalpies and Gibbs energies calculated using the harmonic vibrational frequencies obtained in B3LYP and PBE0 calculations are listed in Tables 91S and 92S of the ESI.† MP2 bond distances are given in Table 93S of the ESI† for the conformers of morphine and morphinum observed in the solid-state by the X-ray diffraction studies.^18,19 Dipole moments could play a role for the relative stability in water and are therefore included in Tables 1 and 3. Selected conformers of equatorial and axial morphine and their morphinum counterparts are shown in Fig. 6.

Table 1 B3LYP relative energies^a,b and dipole moments of conformers of morphine in the gas phase and in water solution

Method	B3LYP (gas)		B3LYP/SMD (water)
	ΔE/kJ mol^−1	Dipole moment/D	ΔE/kJ mol^−1	Dipole moment/D
a The cc-pVTZ basis set was used in all calculations; see text. b Absolute energies and structures in Cartesian coordinates are given in the ESI.† c This form was not found as a minimum on the conformational energy hypersurface; see text.
Max-3anti-6anti	39.6	2.73	16.6	4.75
Mequ-3anti-6anti	29.4	2.85	8.1	4.95
Max-3syn-6anti	26.3	4.07	15.4	6.67
Max-3anti-6g^−	—^c		14.7	3.67
Max-3syn-6g^−	—^c		13.6	6.22
Max-3anti-6g^+	16.8	2.72	9.1	3.87
Mequ-3syn-6anti	15.9	3.61	6.7	5.60
Max-3syn-6g^+	10.3	2.65	8.6	4.09
Mequ-3anti-6g^−	—^c		6.3	3.94
Mequ-3syn-6g^−	—^c		5.0	5.13
Mequ-3anti-6g^+	6.6	3.48	0.8	5.32
Mequ-3syn-6g^+	0.0	2.73	0.0	3.94

---

Table 2 MP2 and PBE0 relative energies^a,b of conformers of morphine in the gas phase

Method	MP2	PBE0
Relative energy	ΔE/kJ mol^−1	ΔE/kJ mol^−1
a The cc-pVTZ basis set was used in all calculations; see text. b Absolute energies and structures in Cartesian coordinates are given in the ESI.† c This form was not found as a minimum on the conformational energy hypersurface; see text.
Max-3anti-6anti	37.6	38.5
Mequ-3anti-6anti	29.4	28.9
Max-3syn-6anti	23.9	25.5
Max-3anti-6g^−	—^c	—^c
Max-3syn-6g^−	—^c	—^c
Max-3anti-6g^+	14.8	15.7
Mequ-3syn-6anti	15.4	15.8
Max-3syn-6g^+	8.3	9.8
Mequ-3anti-6g^−	—^c	—^c
Mequ-3syn-6g^−	—^c	—^c
Mequ-3anti-6g^+	6.7	6.1
Mequ-3syn-6g^+	0.0	0.0

---

Table 3 B3LYP relative energies^a,b and dipole moments conformers of morphinum in the gas phase and in water solution

Method	B3LYP (gas)		B3LYP/SMD (water)
	ΔE/kJ mol^−1	Dipole moment/D	ΔE/kJ mol^−1	Dipole moment/D
a The cc-pVTZ basis set was used in all calculations; see text. b Absolute energies and structures in Cartesian coordinates are given in the ESI.† c This form was not found as a minimum on the conformational energy hypersurface; see text.
M^+ax-3anti-6anti	23.6	11.59	13.2	17.92
M^+equ-3anti-6anti	18.0	11.63	7.7	17.90
M^+ax-3syn-6anti	14.5	12.28	12.3	18.68
M^+ax-3anti-6g^−	—^c		11.3	17.71
M^+ax-3syn-6g^−	11.5	11.88	10.6	18.58
M^+equ-3syn-6anti	9.0	12.30	6.5	18.70
M^+ax-3anti-6g^+	7.7	11.99	5.9	17.73
M^+equ-3anti-6g^−	—^c		5.9	17.72
M^+equ-3syn-6g^−	5.9	11.97	4.8	18.63
M^+ax-3syn-6g^+	5.6	12.23	5.6	17.91
M^+equ-3anti-6g^+	2.2	12.02	0.6	17.59
M^+equ-3syn-6g^+	0.0	12.23	0.0	17.86

---

Table 4 MP2 and PBE0 relative energies^a,b of conformers of morphinum in the gas phase

Method	MP2	PBE0
Relative energy	ΔE/kJ mol^−1	ΔE/kJ mol^−1
a The cc-pVTZ basis set was used in all calculations; see text. b Absolute energies and structures in Cartesian coordinates are given in the ESI.† c This form was not found as a minimum on the conformational energy hypersurface; see text.
M^+ax-3anti-6anti	21.9	23.2
M^+equ-3anti-6anti	18.0	17.6
M^+ax-3syn-6anti	12.5	14.5
M^+ax-3anti-6g^−	9.9	—^c
M^+ax-3syn-6g^−	9.3	12.0
M^+equ-3syn-6anti	8.7	9.0
M^+ax-3anti-6g^+	5.9	7.8
M^+equ-3anti-6g^−	5.3	—^c
M^+equ-3syn-6g^−	4.6	6.3
M^+ax-3syn-6g^+	3.9	5.6
M^+equ-3anti-6g^+	2.1	1.6
M^+equ-3syn-6g^+	0.0	0.0

---

Fig. 6 The two lowest energy conformers both in the gas phase and in water solution of equatorial (upper left) and axial morphine (upper right) and the corresponding two conformers with equatorial methyl group (lower left) and axial methyl group in morphinum (lower right). Hydrogen atoms attached to carbon atoms have been omitted for clarity.

Inspection of the structures of the many conformers reveals few unusual or unexpected features. The C4C3OH (ω′) and C₅C₆OH (ω) dihedral angles are the parameters to consider to describe the conformational properties. The values of ω′ and ω at the MP2 level are +5 and +42°, respectively, in M_equ-3syn-6g⁺, while +6 and +45° were obtained for its morphinum analogue M⁺_equ-3syn-6g⁺. The significant deviation from +60° for ω is probably caused largely by hydrogen bonding with the oxygen atom of the E ring (Fig. 1). A rotation of the ω dihedral angle to less than +60° brings the hydrogen atom of the hydroxyl group and the oxygen atom of the E ring into closer proximity strengthening the intramolecular hydrogen bond. Typical values of ω for 6anti conformers were about −170°, while the g⁻ angles of morphinum conformers were approximately −60°.

Several interesting features emerge from Tables 1–4. The isomers with the equatorial methyl group at nitrogen, M_equ-3syn-6g⁺ and M⁺_equ-3syn-6g⁺, indeed have the lowest energies in both the gas phase and in water presumably because the phenol and alcohol hydroxyl groups are involved in bifurcated intramolecular hydrogen bonding with the oxygen atom of the E ring (Fig. 1). The non-bonded hydrogen to oxygen distance, taken at the MP2 level, is 2.10 Å for the alcohol hydrogen case, and 2.45 Å for the phenol part, which are less than the sum of the Pauling van der Waals radii of oxygen and hydrogen, 2.60 Å.³² The first hydrogen bonds is therefore of intermediate strength, while that with the phenol group is probably marginal. An estimate of the combined strength of these two intramolecular hydrogen bonds may be obtained by comparing the MP2 internal energies of M_equ-3syn-6g⁺ and M_equ-3anti-6anti, which differ by 29.4 kJ mol⁻¹ (Table 1). The energies of the corresponding isomers with axial methyl group differ by 29.3 kJ mol⁻¹, which indicates that the position of the methyl group at N has no influence.

No g⁻ forms were located for gaseous morphine both by B3LYP, PBE0, and MP2 methods (Tables 1 and 2). Additional attempts using the M06-2X method^27,33 gave the same results. In most cases, hypothetical g⁻ forms used as the starting point converged to the corresponding g⁺ conformers. It is therefore most likely that g⁻ forms do not exist for morphine in the gas phase. One possible rational is that the interatomic distance between the hydroxyl hydrogen atom and the hydrogen atom at C6 of 2.30 Å is marginally below 2.40 Å, which is the sum of the vdW radii of two hydrogen atoms.³⁴ Repulsion between the lone pairs of the alcohol oxygen atom and the oxygen atom of the E ring may also contribute. However, other factors could be responsible since in the case of morphinum calculated in the gas phase, all g⁻ rotamers are found as minima at the MP2 level. These results are method-dependent since M⁺_equ-3anti-6g⁻ and M⁺_ax-3anti-6g⁻ are not found as minima with the DFT methods (Tables 3 and 4). A reason for this could be that dispersion forces, which are treated differently at the DFT and MP2 levels, play a key role in the weak interactions stabilizing these conformers.

The gas-phase energy differences obtained with two different functionals and the MP2 method are remarkably similar, apart from the problematic g⁻ conformers discussed above. This validates the energetic pattern found for most conformers with the exceptions for some of the g⁻ forms.

The present calculations point out that the number of conformers and their relative order in energies for morphine and morphinum are different in gas phase and in water solution. In addition, all twelve minima are closer in energy in water solution, (energy span of less than 17 kJ mol⁻¹ for morphine and 13 kJ mol⁻¹ for morphinum) suggesting that they all could be present in a physiological environment. This is in particular the case of the two lowest isomers, M_equ-3syn-6g⁺ and M_equ-3anti-6g⁺, which are essentially at the same energy in water. These results suggest that the OH groups can assume more orientations in aqueous media than in the gas phase. Similar results have been found in a theoretical study of the effect of water on competing intra- and intermolecular hydrogen bonds of selected alcohols and phenols.³⁵

The four g⁻ conformers of morphine, which are not energy minima in gas phase, become minima in water solution. In addition, M_equ-3anti-6anti which is 29 kJ mol⁻¹ in the gas phase above the global minimum M_equ-3syn-6g⁺, is only 8.1 kJ mol⁻¹ above it in water solution. The polarity of water decreases the intramolecular H bonds and if water was explicitly represented it would mean that the two OH groups in M_equ-3anti-6anti could get involved in H bonding with water. A similar result is found for the corresponding morphinum pair (Table 3).

Tables 1 and 2 reveal that all computational methods show that the energy differences between corresponding axial and equatorial conformers of morphine are fairly constant (8–10 kJ mol⁻¹) both in gas phase and in water solution. The same is seen for morphinum (Tables 2 and 3), but the energy differences are somewhat smaller (5–8 kJ mol⁻¹). These comparatively small energy differences imply that axial forms contribute significantly to the equilibrium conformational mixture of morphine and morphinum.

In order to get further insight into why the water solution modifies the difference in energy between the isomers the way it does, the dipole moments of the molecules in their various conformations are reported in Tables 1 and 3. However, there is apparently no parallel between the magnitude in the dipole moment and the modification of the energy differences between the conformers and the magnitude of the dipole moment will not be considered further.

Baranska and Kaczor²¹ have carried out a search of the conformational space of morphine in the gas phase at the B3LYP level with an extended basis set and identified only four stable conformers. Rincón et al.²⁰ carried out a B3LYP(6-31G)(d,p) study of morphinum but also explored the conformational space only in the gas phase. This limited exploration of the conformational space followed by single point PCM calculations resulted in the identification of only 3 conformers out of the 12 identified in this work. Thus, this work shows that many more conformations of morphine and specially morphinum are accessible than earlier found, especially when aqueous solvation is included.

3.3 Transition states of N17 inversion

The energies of the transition states of inversion at nitrogen, which is associated with an equatorial to axial site change of the N17 methyl group in morphine are crucial for the conformational flexibility. There is no similar process in morphinum where the N17 lone pair is protonated.

The transition states for N inversion were located at the B3LYP level for the preferred morphine conformers (3syn-6g⁺, 3anti-6g⁺, 3syn-6anti, and 3anti-6anti) in the gas phase with energy of 27.6, 27.6, 28.1, and 28.1 kJ mol⁻¹ above the corresponding stable equatorial form. At the MP2/B3LYP level, the corresponding values are 36.9, 36.9, 37.3, and 37.3 kJ mol⁻¹. B3LYP/SMD calculations of the transition states were also performed for all six morphine species 3syn-6g⁺, 3anti-6g⁺, 3syn-6anti, 3anti-6anti, 3syn-6g⁻, and 3anti-6g⁻. The transition-state energies relative to the corresponding equatorial conformers were 41.1, 40.1, 41.5, 41.0, 39.6, and 40.9 kJ mol⁻¹, respectively. As expected, a polar solvent increased the energy barrier for N inversion. However, even in water the energy barriers for inversion at N is small and a rapid conversion between the equatorial and axial conformers should occur at room temperature. These results are in agreement with the experimental value of 25–27 kJ mol⁻¹ reported for the morphine derivatives codeine and sinomenine in aprotic solvents,¹⁵ and the MM3 barrier of morphine (27.6 kJ mol⁻¹).¹⁶

4 Conclusions

These calculations show that the two OH groups in morphine and morphinum can take a large number of orientations especially in water solution where many isomers are almost at the same energy. The calculations also show that nitrogen inversion is not energetically difficult and that exchange between the forms where the methyl is equatorial and axial should not be excluded. The differences in energy between the various isomers are even smaller in morphinum. This large conformational diversity in water, and thus in the physiological media, could be a clue to the interaction of this drug with receptors.

Acknowledgements

The authors thank Anne Horn for her skilful assistance. This work has been supported by the Research Council of Norway through a Centre of Excellence Grant (Grant no. 179568/V30). It has also received support from the Norwegian Supercomputing Program (NOTUR) through a grant of computer time (Grant no. NN4654K). OE and DB thank the CTCC for adjunct professor and researcher positions, respectively. MRS thanks the Faculty of Health Sciences, Pharmacy, Oslo and Akershus University College of Applied Sciences (Grant no. 13175).

References

1. M. Filizola and L. A. Devi, Nature, 2012, 485, 314–317.
2. H. Ueda and M. Ueda, Front. Biosci., Landmark Ed., 2009, 14, 5260–5272.
3. G. M. Rishton, Am. J. Cardiol., 2008, 101, 43D–49D.
4. J. Mika, Pharmacol. Rep., 2008, 60, 297–307.
5. A. A. Somogyi, D. T. Barratt and J. K. Coller, Clin. Pharmacol. Ther., 2007, 81, 429–444.
6. L. Martini and J. L. Whistler, Curr. Opin. Neurobiol., 2007, 17, 556–564.
7. B. H. Novak, T. Hudlicky, J. W. Reed, J. Mulzer and D. Trauner, Curr. Org. Chem., 2000, 4, 343–362.
8. T. Hudlicky, G. Butora, S. P. Fearnley, A. G. Gum and M. R. Stabile, Stud. Nat. Prod. Chem., 1996, 18, 43.
9. C. Stein, M. Schaefer and H. Machelska, Nat. Med., 2003, 9, 1003–1008.
10. A. M. Trescot, S. Helm, H. Hansen, R. Benyamin, S. E. Glaser, R. Adlaka, S. Patel and L. Manchikanti, Pain Physician, 2008, 11, S5–S62.
11. R. Benyamin, A. M. Trescot, S. Datta, R. Buenaventura, R. Adlaka, N. Sehgal, S. E. Glaser and R. Vallejo, Pain Physician, 2008, 11, S105–S120.
12. F. A. Casy and R. T. Parfitt, Opioid Analgetics: Chemistry and Receptors, Plenum Press, New York, 1986.
13. G. Schill and K. Gustavii, Acta Pharm. Suec., 1964, 1, 24–35.
14. N. W. Larsen, E. Mathier, A. Bauder and H. H. Guenthard, J. Mol. Spectrosc., 1973, 47, 183–188.
15. A. M. Belostotskii, Z. Goren and H. E. Gottlieb, J. Nat. Prod., 2004, 67, 1842–1849.
16. A. M. Belostotskii, H. E. Gottlieb and M. Shokhen, J. Org. Chem., 2002, 67, 9257–9266.
17. L. Kofler, Pharm. Monatsh., 1933, 14, 220–222.
18. T. Gelbrich, D. E. Braun and U. J. Griesser, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2013, 69, o2.
19. T. Gelbrich, D. E. Braun and U. J. Griesser, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2012, 68, o3358–o3359.
20. D. A. Rincón, M. N. D. S. Cordeiro and R. A. Mosquera, Int. J. Quantum Chem., 2010, 110, 2472–2482.
21. M. Baranska and A. Kaczor, J. Raman Spectrosc., 2012, 43, 102–107.
22. J. M. P. J. Garrido, M. P. M. Marques, A. M. S. Silva, T. R. A. Macedo, A. M. Oliveira-Brett and F. Borges, Anal. Bioanal. Chem., 2007, 388, 1799–1808.
23. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. Cioslowski and D. J. Fox, Gaussian, Inc, Wallingford CT, 2010.
24. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
25. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
27. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
28. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
29. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023.
30. K. A. Peterson and T. H. Dunning Jr, J. Chem. Phys., 2002, 117, 10548–10560.
31. N. W. Larsen and L. Schulz, J. Mol. Struct., 2009, 920, 30–39.
32. L. Pauling, The Nature of the Chemical Bond, Cornell University Press, New York, 3rd edn, 1959.
33. Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382.
34. L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, New York, 1960.
35. P. I. Nagy, J. Phys. Chem. A, 2012, 116, 7726–7741.

---

Footnote

† Electronic supplementary information (ESI) available: Fully optimized MP2, B3LYP, PBE0, and B3LYP/SMD structures in Cartesian coordinates of all extrema (minima and transition states) and electronic energies obtained using the cc-pVTZ basis set. Tables with relative electronic energies, enthalpies, and Gibbs energies. X-ray and MP2 structures of one conformer of each of morphine and morphinum. See DOI: 10.1039/c4ra02992e

---