Ring-annelated corannulenes as fullerene receptors. A DFT-D study

Abstract

Stacking π⋯π interactions of ring-annelated corannulenes with fullerenes C₆₀ and C₇₀ were studied at the B97-D level. For this purpose three-, four-, and five-membered rings (saturated and unsaturated) were annelated to the five rim bonds of corannulene. Substitution effects with NH, O and S units on each one of the five saturated five-membered rings annelated to the rim of corannulene were also evaluated. In all cases, complexation energies were larger than that for the parent compound, corannulene C₂₀H₁₀; in the best case an increase of almost 90% is found. According to our results, the increase of complexation energy is directly related to the increase of the dispersion contribution, where CH⋯π interactions play a very important role. This kind of interaction has special relevance for compounds with saturated annelated rings, where the spatial disposition favours the interaction between hydrogen atoms of CH₂ groups and the π cloud of fullerene. For compounds with unsaturated annelated rings the increase of dispersion is not so pronounced; however, this is fairly offset by the increase of the electrostatic interaction. Finally, stacking interactions between ring-annelated corannulenes and fullerene C₇₀ show complexation energy values quite similar to those obtained with fullerene C₆₀.

---

1. Introduction

Since the discovery of fullerenes by Kroto et al. in 1985 (ref. 1) the interest in buckybowls, bowl-shaped polycyclic aromatic hydrocarbons (PAHs) has increased. Buckybowls show a unique bowl-shaped architecture that provides two different faces, one concave and one convex, which significantly increases its potential with respect to standard PAHs. Thus, buckybowls can exhibit intermolecular interactions with a wide range of different species, such as transition metals,^2–5 metal cations^6–9 and anions.¹⁰ Also, the interaction with other curved surfaces can lead to an interesting type of interaction known as concave–convex π⋯π interaction. This interaction may have a huge practical value as in the case of molecular tweezers for trapping species of interest, such as fullerene, in which case buckybowls can be used as one the most efficient buckycatchers.¹¹

The two most popular fullerenes, C₆₀ and C₇₀ are quite similar but show unique properties.^12–14 It would be interesting to know how to separate these similar structures, and some findings suggest strategies to do this task through molecular tweezers with corannulene pincers.^15,16 The idea is to find molecular tweezers capable to discriminate C₆₀ from C₇₀. However, recent research shows that binding energies of C₆₀ complexes are very similar to those of C₇₀ ones.^15,17 In this context, understanding the factors that govern the concave–convex π⋯π interactions has become an attractive field of research. In the last years, several theoretical studies have been performed to investigate the curved π systems, mainly using the smallest buckybowl, corannulene C₂₀H₁₀ (compound 1, Fig. 1).^17–21 Undoubtedly, the knowledge of curvature and substituent effects of buckybowls could give an important insight into the design of more effective and/or selective fullerene receptors. Recently, Kennedy et al.²¹ have explored the effects of curvature on π⋯π interactions. Their results indicated that curvature affects to all four major components of non-covalent interactions (dispersion, electrostatics, exchange and induction) and that an increase of curvature in concave–convex π⋯π interactions leads to more favourable interaction energies, except at short distances where the most highly curved systems are less favourable as exchange repulsion terms begin to dominate the interaction.

Fig. 1 Ring-annelated corannulenes studied. Bonds (h = hub, s = spoke, f = flank, r = rim). C atom types (hs = hub-spoke, fs = flank-spoke, r = rim).

In order to evaluate the effect of substitution on concave–convex π⋯π interactions, our group has studied a series of corannulene dimers substituted with five alternating Br, Cl, CH₃, C₂H and CN units.¹⁹ The results showed that all substituted corannulenes evaluated behave as a better catcher than the unsubstituted corannulene as a consequence of the contribution of electrostatic and dispersive effects. However, not clear relationship between the curvature of bowls and the interaction energy was observed. Corannulene shows a noticeable rigidity, so that inclusion of up to five substituents has a small effect on its structure, and only a slight flattening of the bowl was observed.¹⁹

Nowadays, ring-annelated corannulenes have attracted the attention of researches because the correlation between the bowl depth and the bowl-to-bowl inversion barrier.^22,23 Ring annelation to the rim of corannulene gradually flattens the bowl and, moreover, it introduces CH₂ groups in the bowl structure that can interact with fullerenes through CH⋯π interactions. Undoubtedly, the introduction of CH₂ groups in the bowl structure seems a good strategy to enhance concave-convex π⋯π interactions. So, according to Denis results, the three CH₂ groups in sumanene structure are the great responsible for the stronger sumanene dimer interaction compared to that of corannulene dimer.¹⁷ In addition, a recent study performed by Mahesh Kumar et al.²⁴ reveals that CH⋯π interaction from methylene (–CH₂) group of adamantane molecule with benzene is stronger than that of methine (–CH) group.

For the above reasons, ring-annelated corannulenes seem suitable structures for the further study of the interaction ability of corannulenes in the recognition of fullerenes, by concave–convex π⋯π interactions. Therefore, the aim of this work is to evaluate the stacking interactions between ring-annelated corannulenes with fullerenes C₆₀ and C₇₀. In addition, for the ring-annelated corannulene with five saturated five-membered rings, the substitution effect of NH, O and S units was also evaluated.

2. Computational details

Since dispersion effects are crucial to study π⋯π interactions, dispersion-corrected DFT methods seem mandatory. Among them, perhaps the Grimme's empirical dispersion correction is the most popular. His original version (DFT-D),²⁵ was modified in 2006 (DFT-D2),²⁶ and further corrected in 2010 (DFT-D3),²⁷ and 2011 (DFT-D3(BJ)).²⁸

Recently, for the corannulene dimer, Kennedy et al.²¹ showed that the best results (compared with the benchmark performed at the QCISD(T)/aug-cc-pVTZ level²⁹) correspond to B3LYP-D3(BJ), but with a very small advantage over B3LYP-D2, M06-2X and B97-D2. Of these DFT methods, B97-D2 is the best to take advantage of the noticeable reduction of computational cost that allows the resolution of identity approximation (RI) implemented in Turbomole program suite,³⁰ since for non-hybrid functionals the RI procedure speeds up calculations by a factor 10 at least (as compared to conventional treatments) without sacrificing accuracy. In addition, calculations using B97-D2 method also provide very good results as can be observed in several previous works.^{15,19,26,31,32} Taking into account the above comments, the size of the studied systems and the software used (Turbomole), the choice of the B97-D2/TZVP (henceforth B97-D for simplicity) and the RI approximation seems appropriate. All the complexes were fully optimized at this level.

Counterpoise corrections, CP, were applied to all reported interaction energies to avoid basis set superposition error, BSSE.³³ According to this method, the interaction energy of a system A⋯B is calculated according to:

E_int = E^AB_AB(AB) − (E^AB_A(AB) + E^AB_B(AB))

where superscript refers to the geometry (that of the system AB) and the parenthesis indicates the basis set used (the full basis set of the system A⋯B). If, in addition, the energy cost involved in the deformation of each monomer to adopt the geometry of the dimer is considered:

E_def = (E^AB_A(A) − E^A_A(A)) + (E^AB_B(B) − E^B_B(B))

then, the full complexation energy is obtained as follows:

E_complex = E_int + E_def

Finally, to quantify the curvature of curved structures, POAV angle is an efficient tool. POAV is the pyramidalization angle proposed by Haddon;³⁴ it allows the description of local curvature of a conjugated system and is defined as the angle between de C–C bond and the vector perpendicular to the pyramidal base of three idealized C–C bonds (see ESI†).

3. Results and discussion

Stacking interactions between ring-annelated corannulenes with fullerenes C₆₀ and C₇₀ were studied at the B97-D level. Fig. 1 shows all ring-annelated corannulenes used: three-membered rings were annelated in 2, four-membered rings were annelated in 3 and 4 (saturated and unsaturated), and five-membered rings were annelated in 5 and 6 (saturated and unsaturated). Finally, bowls 7, 8, and 9 were added to the study to analyse the effect of including heteroatoms (for this purpose bowl 5 was chosen since in this case the effect of the heteroatom is more isolated from other possible effects).

The complexes were built by stacking the ring-annelated corannulenes with the corannulene face of fullerenes. Although for the corannulene dimer it is known that eclipsed conformation is the most favourable one,²⁹ both eclipsed and staggered conformations were studied. For the eclipsed conformation, the five spoke C–C bonds of corannulenes 1–9 were eclipsed with analogue bonds of the corannulene face of fullerenes C₆₀/C₇₀. For the staggered conformation, one of the monomers was rotated 36° around the axis defined by the centre of both hub five-membered rings. So, all complexes evaluated have C_5v symmetry.

Table 1 summarizes interaction energies for eclipsed and staggered conformations. First, it is worth noting that all the annelated corannulenes led to an important increase of the interaction energy (ranging from about 5 to 16 kcal mol⁻¹) relative to that of the C₂₀H₁₀ corannulene (compound 1). Second, the difference of interaction between C₆₀ and C₇₀ is very small: it does not reach 1 kcal mol⁻¹ at best, always in favour of C₇₀ except for the staggered complex with compound 4. Given the huge similarity between the geometric and electronic characteristics (both without dipole moment) of C₆₀ and C₇₀ it is reasonable to think that the small energy advantage of C₇₀ is justified by the fact that it has a non-zero quadrupole moment, which favours the electrostatic contribution of interaction. On the contrary, for C₆₀ the first nonvanishing multipole moment is the 64-pole moment. Unfortunately, the complexation energy for complexes with C₆₀ and C₇₀ are very similar. Therefore, it is not expected that the substituted buckybowls to specifically bind one of the fullerenes when exposed to the C₆₀/C₇₀ mixture.

Table 1 Interaction energies in kcal mol⁻¹ obtained at the B97-D2/TZVP level calculation for complexes in eclipsed conformations (staggered conformations results in parentheses)

	X = C60	X = C70
1⋯X	−17.03 (−14.57)	−17.16 (−14.72)
2⋯X	−22.20 (−22.22)	−22.48 (−22.37)
3⋯X	−28.45 (−27.65)	−28.84 (−27.97)
4⋯X	−24.09 (−28.22)	−24.84 (−28.09)
5⋯X	−32.01 (−30.69)	−32.54 (−31.19)
6⋯X	−30.05 (−26.76)	−30.15 (−26.98)
7⋯X	−30.04 (−28.51)	−30.46 (−28.77)
8⋯X	−33.27 (−30.41)	−33.78 (−30.99)
9⋯X	−32.02 (−29.89)	−32.36 (−30.09)

---

In all cases the preferred conformation is the eclipsed one (with differences ranging from about 1 to 3 kcal mol⁻¹), with two exceptions: complex 2⋯X where both conformations are virtually isoenergetic, and complex 4⋯X where unexpectedly the staggered conformation is about 4 kcal mol⁻¹ more favourable than the eclipsed one. Clearly, there is an effect that substantially favours the staggered conformation of 4⋯X. Although there are not conclusive evidences, that effect could be explained as follows: in the staggered conformation of complex 4⋯X both π bonds of the cyclobutadiene (which owns an extremely localized π clouds) are directly facing the spoke bond of fullerene, which is precisely the bond with the largest π character of fullerene (the largest bond order, the shortest bond length, the largest double-bond character). Thus, this additional π⋯π interaction, that takes place in the staggered conformation in a more appropriate way, not only offsets the advantage of the general trend favouring the eclipsed conformation, but it also overcomes it (ESI† includes several calculations for supporting the previous hypothesis). On the other hand, it seems that this effect is somewhat less pronounced with C₇₀, since only for the staggered conformation of complex 4⋯X the interaction energy with C₇₀ is smaller than that with C₆₀.³⁵

Complexation energies given in Table 2 represent the value of interaction energy taking into account the fragment deformation (for each complex the preferred conformation, eclipsed or staggered, was chosen). Except for compound 6, deformation energies are rather modest. The deformation energy must be directly related with the geometric changes suffered by corannulenes derivatives upon complexation with C₆₀ and C₇₀. Two main geometrical parameters provide a measure of the curvature of the corannulene bowls: h represents the bowl depth (taken as the distance between the plane of the hub carbons and that of the rim carbons) and POAV is the pyramidalization angle (POAV angle of the hub-spoke carbons of the bowl was used for our purposes). Table 3 shows the geometrical parameters of the isolated corannulenes, and Table 4 shows the values of these parameters after complexation. As can it be seen in Table 3, ring-annelated corannulenes optimized at the B97-D level show more curved structures (which is reflected in higher values of POAV and bowl depth h) than those obtained previously by Dinadayalane et al.²² at the B3LYP/6-31G* level. The largest difference is observed for compound 6 that show a virtually flat structure at the B3LYP/6-31G* level while our calculations at the B97-D level indicate a slightly curved structure with POAV angle of 4.17° and a bowl depth of 0.447 Å. In order to check the discrepancy between both calculations, a MP2/TZVP optimization of compound 6 was performed: the results were very similar to those obtained at the B97-D level, with POAV angle of 4.09° and bowl depth of 0.436 Å. The failure of the B3LYP calculations comes mainly from the inadequate description of the intramolecular van der Waals interactions.³⁶ In any case, our goal is not to rigorously obtain the absolute curvature of the isolated corannulenes.

Table 2 Complexation energy (E_comp) and deformation energy (E_def) in kcal mol⁻¹. Calculations were performed at the B97-D2/TZVP level

	X = C60		X = C70
	Edef	Ecomp	Edef	Ecomp
1⋯X	0.20	−16.83	0.16	−17.00
2⋯X	0.28	−21.94	0.12	−22.36
3⋯X	0.45	−28.00	0.46	−28.38
4⋯X	0.63	−27.59	0.60	−27.49
5⋯X	0.60	−31.41	0.55	−31.99
6⋯X	1.95	−28.10	1.95	−28.20
7⋯X	0.62	−29.42	0.60	−29.86
8⋯X	1.29	−31.98	1.38	−32.40
9⋯X	1.13	−30.89	1.17	−31.19

---

Table 3 POAV angle (in degrees) and bowl depth (Å) for the isolated ring-annelated corannulenes studied in this work at the B97-D2/TZVP level and at the B3LYP/6-31G* previously obtained²²

	B97-D2/TZVP		B3LYP/6-31G*
	POAV	h	POAV	h
1	8.63	0.928	8.1	0.864
2	7.60	0.838	6.6	0.674
3	6.67	0.725	5.3	0.572
4	7.53	0.808	6.5	0.678
5	8.04	0.855	7.1	0.738
6	4.17	0.447	0.0	0.093
7	8.15	0.873
8	8.08	0.866
9	7.50	0.784

---

Table 4 Equilibrium distance (D_eq) (Å), POAV angle (in degrees) and bowl depth (Å) for complexes in the eclipsed conformations (staggered conformations results in parentheses). Calculations were performed at the B97-D2/TZVP level

	X = C60			X = C70
	Deq	POAV	h	Deq	POAV	h
1⋯X	3.456 (3.535)	8.38 (8.09)	0.902 (0.868)	3.453 (3.543)	8.42 (8.11)	0.909 (0.870)
2⋯X	3.364 (3.396)	7.29 (7.18)	0.753 (0.740)	3.352 (3.384)	7.35 (7.22)	0.760 (0.744)
3⋯X	3.242 (3.315)	6.91 (6.90)	0.764 (0.763)	3.242 (3.301)	7.02 (7.01)	0.776 (0.776)
4⋯X	3.350 (3.365)	7.40 (8.07)	0.808 (0.880)	3.419 (3.374)	7.94 (8.15)	0.866 (0.889)
5⋯X	3.329 (3.404)	8.10 (8.13)	0.871 (0.880)	3.363 (3.397)	8.35 (8.20)	0.876 (0.937)
6⋯X	3.123 (3.181)	6.02 (5.72)	0.673 (0.637)	3.112 (3.170)	6.03 (5.73)	0.674 (0.639)
7⋯X	3.363 (3.433)	8.28 (8.21)	0.895 (0.891)	3.353 (3.429)	8.32 (8.30)	0.899 (0.901)
8⋯X	3.351 (3.410)	8.29 (8.20)	0.900 (0.896)	3.360 (3.409)	8.42 (8.28)	0.916 (0.905)
9⋯X	3.286 (3.337)	7.95 (7.71)	0.846 (0.825)	3.274 (3.328)	7.97 (7.77)	0.849 (0.832)

---

As expected from deformation energies, compound 6 undergoes the largest deformation of the bowl after complexation. So it substantially increases its curvature, which is reflected in an increase of about of 2 degrees in POAV and about of 2 tenths of Å in depth h. In the other cases the change of curvature of the bowl is rather small.

Table 4 also includes the equilibrium distance in the complex, D_eq, taken as the distance between the centres of the five membered rings of corannulene and fullerene. In all cases ring annelation to the rim of corannulene decreases the equilibrium distances compared to unsubstituted corannulene 1; however, the trend is very vague, so there is no clear relationship between the complexation energy and the decrease of equilibrium distance. A relationship between the curvature of bowls and the changes on complexation energy generated by ring annelation to the rim of corannulene does not exist either.

In order to analyse in more detail the balance of energy contribution to the stability of the complexes, the interaction energy was decomposed according to a simple method. So, the two contributions of the model employed were taken into account: the pure B97 interaction energy and the empirical dispersion contribution to the interaction energy. As it can be seen from Table 5, dispersion is mainly responsible for the attraction of the complexes evaluated, being clearly repulsive the contribution of the pure B97 functional. The annelation of corannulene led in all cases to an increase of the repulsive contribution, which is amply offset by the increase of the dispersive attraction, so the final balance is always favourable to ring annelation. Table 5 also shows that dispersion is responsible for the advantage of the eclipsed conformations, in all cases except for the above commented case of compound 4: in this case, dispersion is also responsible for preference but it clearly favours the staggered conformation.

Table 5 B97 interaction energy and dispersion contribution of the complexes obtained at the B97-D2/TZVP level (kcal mol⁻¹) for complexes in eclipsed conformations (staggered conformations results in parentheses)

	X = C60		X = C70
	B97	Dispersion	B97	Dispersion
1⋯X	16.17 (14.94)	−33.20 (−29.51)	16.21 (14.23)	−33.37 (−28.95)
2⋯X	20.32 (18.40)	−42.52 (−40.60)	20.54 (18.53)	−43.02 (−40.90)
3⋯X	25.34 (23.07)	−53.79 (−50.72)	25.13 (23.99)	−53.97 (−51.96)
4⋯X	21.31 (21.82)	−45.40 (−50.04)	20.14 (21.28)	−44.98 (−49.37)
5⋯X	28.18 (26.86)	−60.19 (−57.55)	28.00 (26.73)	−60.54 (−57.92)
6⋯X	21.33 (20.49)	−51.38 (−47.25)	21.27 (20.46)	−51.42 (−47.44)
7⋯X	27.96 (26.18)	−58.00 (−54.69)	27.77 (26.74)	−58.23 (−55.51)
8⋯X	28.40 (28.04)	−61.67 (−58.45)	27.88 (27.54)	−61.66 (−58.53)
9⋯X	27.30 (24.80)	−59.32 (−54.69)	27.28 (25.97)	−59.64 (−56.06)

---

Table 5 also shows that in terms of dispersion, annelation with saturated rings is more favourable that annelation with unsaturated ones: differences about of 8–10 kcal mol⁻¹ appear when the behaviour of compound 3 is compared with that of compound 4, and that of compound 5 with that of compound 6. In the final balance, the difference is much less noticeable, since compounds 4 and 6 partly offset their dispersive disadvantage with a more favourable behaviour in the contribution of the pure functional.

As regard inclusion of heteroatoms, a rather small effect is observed. So, values from Table 5 for compounds 7, 8, and 9, are not very different of those for compound 5, both for dispersion contribution and for that of the pure functional: differences are smaller than 2 kcal mol⁻¹.

The relationship between the dispersive contribution and the total complexation energy can be clearly visualized in Fig. 2. Undoubtedly, the increase of the complexation energy is related to the increase of the dispersion energy, being the correlation excellent, with r² = 0.98. Only compounds 4 and 6, and to a lesser extent compound 7, deviate very slightly of the linear behaviour. In order to explain these minimum discrepancies, a qualitative analysis of the contribution of electrostatic energy to interaction energy has been carried out. Obviously, that contribution cannot be too large since compounds 1–9 have a substantial dipole moment but, however, as commented above, the first nonvanishing multipole moment is the 64-pole one for C₆₀ and the quadrupole one for C₇₀. Therefore, the interaction must be negligible at a certain distance, especially in the case of C₆₀. However, the multipolar expansion does not work satisfactorily at short distances and local effects must be taken into account. In order to analyse that question, Fig. 3 shows maps of molecular electrostatic potential, MEP, of C₆₀ and the concave side of compounds 1–9. C₆₀ (C₇₀ virtually has the same map) shows an almost neutral MEP, but slightly positive on top of the five-membered rings. In the complexes studied, these five-membered rings face the central five-membered ring of corannulenes 1–9. Consequently, a negative MEP above the central ring of corannulenes will favour a larger electrostatic interaction between corannulene and fullerene. Examining Fig. 3 and taking as reference the MEP of the central region of compound 5 (compound that shows the best fitting in Fig. 2), it can be observed that compounds 4 and 6 clearly show a more favourable MEP (more negative) for interacting with C₆₀. This fact agrees with Fig. 2, where these two compounds obtain larger complexation energy than that predicted by its dispersion contribution. On the contrary, compounds 1, 2, 7, 8, and 9 show a less favourable MEP (more positive) in the central region; all of them are found over the straight line of Fig. 2 (this conclusion is especially adequate for compound 7, and in a much lesser extent for the other four compounds). That is to say, these five compounds obtain a smaller complexation energy than that predicted by its dispersion contribution. In summary, MEP maps can help to explain (in a rather qualitative way) the small deviations of Fig. 2.

Fig. 2 Dispersion contribution vs. complexation energy (in kcal mol⁻¹): E_complex = 0.522E_disp − 0.08256. r² = 0.98.

Fig. 3 Molecular electrostatic potential, MEP, onto an electron density isosurface of 0.001 a.u.

Obviously, the above discussion is rather limited since the electrostatic is not the only contribution to the pure B97 interaction energy; it also includes repulsion and induction components. However, it seems that the electrostatic contribution constitutes an important differentiating factor inside the B97 interaction since the two larger deviations in Fig. 2 (compounds 4 and 6) correspond to the most favourable MEPs; it clearly gives rise to a smaller repulsion in the B97 term (4–7 kcal mol⁻¹ lower than the similar structures 3, 5, 7, 8, and 9).

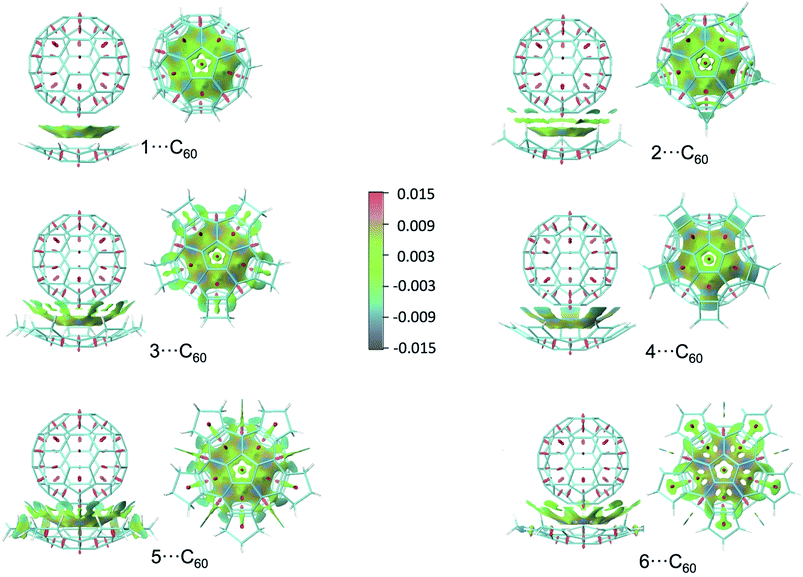
In order to obtain more information about the π⋯π interaction in the corannulene⋯fullerene complexes, the plotting of non-covalent interaction regions was performed using the recently developed NCIPLOT program.^37,38 This method enables identification of non-covalent interactions and it is based on the peaks that appear in the reduced density gradient (RDG) at low densities. Plotting an RDG isosurface for a low value of RDG, the non-covalent regions clearly appear in the supramolecular complex. These interactions correspond to both favourable and unfavourable interactions. In order to differentiate between them, the sign of the second density Hessian eigenvalue times the density is color-mapped onto the isosurface: bonding interactions can be identified by the negative sign. Fig. 4 shows the NCI plots for the interaction between C₆₀ and compounds 1–6 (figures for compounds 7–9 are almost the same that for compound 5) using an isosurface of 0.4 a.u.; blue, green an red indicate strongly attractive, weak and strongly repulsive interactions, respectively (with a scale running from −0.015 to 0.015 a.u.). In all cases a rather strong π⋯π interaction takes place between the spokes of corannulene and fullerene (except for compound 4, where the favourable conformation is the staggered one). Moreover, in complexes with compounds 2, 3, and 5, an additional important interaction takes place: that between the CH₂ groups and the π cloud of fullerene. Specifically, these are the so called C–H⋯π interactions, found in different molecular systems including organic crystals, proteins and nucleic acids.³⁹ They can be either electrostatic- or dispersion-dominated depending upon the acidity of the C–H group; dispersion energy is the most important in typical cases where an aliphatic or aromatic CH is the hydrogen donor.⁴⁰ Moreover, the proportion of electrostatic energy decreases on going from sp²-CH to sp³-CH. Thus, according to values of Table 5, C–H⋯π interactions of compound 2, and especially those of 3, 5, 7, 8, and 9, are mainly of dispersive character. In this six compounds an important interaction of the internal hydrogen atoms of the CH₂ groups belonging to the annelated ring, is the main responsible for the increase of complexation energy with fullerene, relative to what happens with compound 1. For compound 4 (the only one with a favourable staggered conformation) the increase of complexation energy comes from the additional π⋯π interaction that takes place with the π bonds of the annelated cyclobutadiene rings, as commented above. Finally, compound 6 has CH₂ groups, but too far from the π cloud of fullerene (as it happens for the external CH₂ group of compound 5). However, an additional weak interaction arises between the external π bonds of cyclopentadiene and the π cloud of fullerene, which partially offsets the lack of strong C–H⋯π interactions. Thus, compound 6 shows the smaller complexation energy of corannulene compounds with annelated five-membered rings.

Fig. 4 Front and bottom views of the NCIPLOT gradient isosurface (0.4 a.u.). The surfaces are colored on a blue-green-red scale according to the strength and type (attractive or repulsive) of interaction. Blue indicates strong attractive interactions, green indicate weak VdW interactions, and red indicates strong nonbonded overlap. Nonbonding regions only appear at the centre of all the rings, but they are irrelevant for the intermolecular analysis.

Finally, an attempt to confirm that interactions between corannulenes and fullerenes really come from π⋯π interactions is carried out. For this purpose a Natural Bond Analysis (NBO) was performed.⁴¹ Effectively, the results of the second order perturbation analysis confirm that the main contribution for all corannulene⋯C₆₀ complexes (except for 4⋯C₆₀, staggered) corresponds to the interaction between the π orbitals of the spokes of both monomers. However, that is not the only relevant contribution (see ESI†).

Conclusions

According to our results, ring annelation to the rim bonds of corannulene looks a good strategy to enhance the interaction with fullerenes C₆₀ and C₇₀. The increase of complexation energy is linearly correlated to the increase of dispersion energy. The very small deviations of this behaviour can be explained by electrostatic considerations. In all the complexes the eclipsed conformation is the more favourable since it maximizes the π⋯π interaction between the spoke bonds of corannulenes and fullerene. Compound 4 constitutes the only exception; in this case the staggered conformation offsets (and overcomes) that trend by an additional π⋯π interaction that emerges between the double bonds of the cyclobutadiene annelated rings and the spoke bonds of fullerene; this interaction takes place in the staggered conformation in a more suitable way.

NCI calculations allow us showing that C–H⋯π interactions play a fundamental role in the increase of dispersion. This kind of interaction takes place especially for compounds with saturated annelated rings, where the internal hydrogen atom of the CH₂ groups points directly to the π cloud of fullerene, establishing a strong contact which is pretty evident in the NCI maps. Compounds 4 and 6, with unsaturated annelated rings, offset the lack of strong C–H⋯π interactions by better electrostatic characteristics: their hubs show an enhanced negative MEP that give rise to a better interaction with the slightly positive MEP of the bottom of fullerenes.

Inclusion of heteroatoms in the structure 5 has a rather small effect, so that C–H⋯π interactions remain as the main feature.

Stacking interactions between ring-annelated corannulenes and fullerene C₇₀ show interaction energy values quite similar to that obtained for fullerene C₆₀: only slightly larger, but 1 kcal mol⁻¹ at best. Therefore, it is not expected that the substituted buckybowls to specifically bind one of the fullerenes when exposed to the C₆₀/C₇₀ mixture.

In summary, our results show that CH⋯π interactions can contribute significantly to enhance the interaction with fullerenes. So, the design of new molecular receptors that take into account the increase (and the proper orientation) of these interactions, could provide a considerable improvement in the task of fullerene recognition.

Acknowledgements

This research has been supported by the Xunta de Galicia (project INCITE09209103PR). The authors want to express their gratitude to the CESGA (Centro de Supercomputación de Galicia) for the use of their computers. D. J. thanks the Spanish Ministry of Education for FPU scholarship.

References

1. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162.
2. M. A. Petrukhina and L. T. Scott, Dalton Trans., 2005, 2969.
3. P. A. Vecchi, C. M. Alvarez, A. Ellern, R. J. Angelici, A. Sygula, R. Sygula and P. W. Rabideau, Organometallics, 2005, 24, 4543.
4. H. Sakane, T. Amaya, T. Moriuchi and T. Hirao, Angew. Chem., 2009, 48, 1640.
5. A. S. Filatov and M. A. Petrukhina, Coord. Chem. Rev., 2010, 254, 2234.
6. U. D. Priyakumar and G. N. Sastry, Tetrahedron Lett., 2003, 44, 6043.
7. J. R. Green and R. C. Dunbar, J. Phys. Chem. A, 2011, 115, 4968.
8. J. A. Carrazana-García, J. Rodríguez-Otero and E. M. Cabaleiro-Lago, J. Phys. Chem. B, 2011, 115, 2774.
9. M. Rellán-Piñero, J. Rodríguez-Otero, E. M. Cabaleiro-Lago and D. Josa, J. Mol. Model., 2012, 19, 2049.
10. P. García-Novo, A. Campo-Cacharrón, E. M. Cabaleiro-Lago and J. Rodríguez-Otero, Phys. Chem. Chem. Phys., 2012, 14, 104.
11. A. Sygula, F. R. Fronczek, R. Sygula, P. W. Rabideau and M. M. Olmstead, J. Am. Chem. Soc., 2007, 129, 3842.
12. W. Zha, D. Chen and W. Fei, J. Liq. Chromatogr. Relat. Technol., 1999, 22, 2443.
13. T. C. Wu, M. K. Chen, Y. W. Lee, M. Y. Kuo and Y. T. Wu, Angew. Chem., 2013, 52, 1289.
14. N. Martin, Chem. Commun., 2013, 49, 1039.
15. C. Mück-Lichtenfeld, S. Grimme, L. Kobryn and A. Sygula, Phys. Chem. Chem. Phys., 2010, 12, 7091.
16. A. Sygula and W. E. Collier, Molecular Clips and Tweezers with Corannulene Pincers, in Fragments of Fullerenes and Carbon Nanotubes: Designed Synthesis, Unusual Reactions, and Coordination Chemistry, ed M. A. Petrukhina and L. T. Scott, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2011.
17. P. A. Denis, Chem. Phys. Lett., 2011, 516, 82.
18. A. Sygula and S. Saebø, Int. J. Quantum Chem., 2009, 109, 65.
19. D. Josa, J. Rodríguez-Otero and E. M. Cabaleiro-Lago, Phys. Chem. Chem. Phys., 2011, 13, 21139.
20. G. Casella and G. Saielli, New J. Chem., 2011, 35, 1453.
21. M. R. Kennedy, L. A. Burns and C. D. Sherrill, J. Phys. Chem. A, 2012, 116, 11920.
22. T. C. Dinadayalane, S. Deepa and G. N. Sastry, Tetrahedron Lett., 2003, 44, 4527.
23. T. C. Dinadayalane, S. Deepa, A. S. Reddy and G. N. Sastry, J. Org. Chem., 2004, 69, 8111.
24. R. M. Kumar, M. Elango, R. Parthasarathi, D. Vijay and V. Subramanian, J. Chem. Sci., 2012, 124, 193.
25. S. Grimme, J. Comput. Chem., 2004, 25, 1463.
26. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
27. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
28. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
29. T. Janowski, P. Pulay, A. A. Sasith Karunarathna, A. Sygula and S. Saebø, Chem. Phys. Lett., 2011, 512, 155.
30. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165.
31. D. Josa, J. Rodríguez-Otero, E. M. Cabaleiro-Lago and M. Rellán-Piñeiro, Chem. Phys. Lett., 2013, 557, 170.
32. S. Grimme, C. Mück-Lichtenfeld and J. Antony, J. Phys. Chem. C, 2007, 111, 11199.
33. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
34. R. C. Haddon, J. Am. Chem. Soc., 1990, 112, 3385.
35. In order to explain this fact, geometric reasons could be argued: the corannulene face of both fullerenes is very similar; however, in the case of C₇₀ this face shows a slightly more pronounced curvature. This fact causes that π bonds of cyclobutadiene rings of 4 (especially, the outer ones) are more distant from the spokes of fullerene, and thus, π⋯π contacts are weakened. To quantify the difference in curvature of the corannulene face of C₆₀ and C₇₀, POAV is an efficient tool. So, POAV angle of the hub-spoke carbons of the corannulene face (the carbons of the five-membered ring) is 11.64° and 11.84° for C₆₀ and C₇₀, respectively. This difference may seem insignificant, but it is enough to increase the distance between the outer double bonds of cyclobutadiene and the flank-spoke carbons of fullerene from 3.217 to 3.230 Å (this small increase takes place in five contacts and it seems plausible to explain the decrease of a few tenths of kcal mol⁻¹ in the interaction energy).
36. When the Grimme's empirical dispersion correction is added to B3LYP calculations (B3LYP-D), the geometry of compound 6 becomes no fully planar, with a curvature rather similar to that obtained with B97-D2 and MP2: POAV = 3.33°.
37. E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. T. Yang, J. Am. Chem. Soc., 2010, 132, 6498.
38. J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. T. Yang, J. Chem. Theory Comput., 2011, 7, 625.
39. M. Nishio, Phys. Chem. Chem. Phys., 2011, 13, 13873.
40. M. Nishio, J. Mol. Struct., 2012, 1018, 2.
41. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra02744b

---