Interactions and structure of ionic liquids on graphene and carbon nanotubes surfaces

Abstract

Using quantum methods it was possible to build an atomistic force field for ionic liquids interacting with a graphene surface. Density functional calculations of 1-ethyl-3-methylimidazolium cation and thiocyanate anion interacting with a cluster of carbon atoms representing a graphene surface were performed, at a series of distances and orientations, using the BLYP-D functional. The DFT interaction energies were successfully fitted to a site–site potential function. The developed force field accounts also for the polarization of the graphene surface, therefore the use of induced dipoles to reproduce the interaction energy between charges and a conductor surface is not required. We report molecular dynamics results on the structure of the interfacial layer of the ionic liquid 1-ethyl-3-methylimidazolium thiocyanate at a flat graphene surface and inside single-wall carbon nanotubes of different diameters, including analyses of the positional and orientational ordering of the ions near the surface, and charge density profiles. Both anions and cations are found in the first ordered layer of ions near the surface, with the interfacial layer being essentially one ion thick.

---

Introduction

The fast-growing market for portable electronic devices, the development of hybrid vehicles and the use of renewable energy sources demand new energy storage devices with high energy density and high power density.¹ Supercapacitors store charge in electrochemical double layers (EDLs) at the electrode–electrolyte interface, they can deliver high power densities but exhibit much lower energy densities than batteries.^2–4 Supercapacitors have a long shelf and cycle life, and usually require low maintenance, but their moderate energy density is a drawback for their widespread deployment. Supercapacitors require an electrode with higher and more accessible surface area than that of a conventional electrode, while maintaining high conductivity. Carbon-based materials, including activated carbon,^5,6 carbon nanotubes^7,8 (CNTs), and graphene,^2–4,9–15 have been widely used in electrochemical double-layer supercapacitors, owing to their excellent physical and chemical properties. Graphene-based materials have a great attraction, due to their mechanical and electrical properties, an their high surface area. Electrochemical capacitors based on graphene materials could achieve a theoretical specific capacitance of 526 F g⁻¹, at most in an aqueous electrolyte (the specific capacitance is lower with organic electrolytes), if their entire surface area could be used.

Graphene-based materials can be easily obtained by simple chemical processing of graphite. Zhu et al.⁴ have synthesized, using chemical activation of exfoliated graphite oxide, a porous carbon with a Brunauer–Emmett–Teller surface of up to 3100 m² g⁻¹ and a high electrical conductivity. Cheng et al.¹¹ described a graphene and single-walled carbon nanotubes composite film prepared by a blending process for their use as electrodes in high energy density supercapacitors, achieving high specific capacities and energy densities with aqueous and organic electrolytes, but lower than the theoretical limit. The low capacitance is related with the reduction of the specific surface area of graphene, due to the restacking of graphene sheets during its processing as a result of the strong sheet-to-sheet van der Waals interactions. El-Kady et al.² developed a new strategy for the production of graphene-based electrodes, through an all-solid-state approach based on the use of infrared laser, to avoid the restacking of graphene sheets.

Another important fact that influences the properties of a supercapacitor is the selected electrolyte. Aqueous solutions are the more common choice,^16–20 even if they display a narrow cell voltage and low energy density. The future development of multifunctional flexible electronics such as roll-up displays, photo-voltaic cells, and even wearable devices presents new challenges for designing and fabricating light-weight, flexible energy storage devices.^2,21 Commercially available electrocapacitors consist of a separator sandwiched between two electrodes with liquid electrolyte. Unfortunately, these device architectures not only suffer from the possible harmful leakage of electrolytes, but their design makes difficult to use them for practical flexible electronics. The use of gelled electrolytes will reduce the device thickness and weight as well as simplify the fabrication process, as no special packing material is needed.

Ionic liquids, organic molten salts with melting points below 373.15 K,²² have a high potentiality as electrolyte,^23,24 as they have an intrinsic high electrical conductivity.^25–27 The properties of ionic liquids can be tuned by selecting different combinations of cation and anion. The number of available ILs can be easily and significantly increased by considering their binary (yielding over 10¹² combinations) or ternary mixtures (yielding over 10¹⁸ combinations). The properties of these mixtures should be easily predictable once information regarding their pure components is available. Giving the large number of ionic liquids that can be used as electrolytes in supercapacitors, it is not possible to experimentally test the performance of all of them. Information at a molecular level of the interaction of ionic liquids with graphene electrodes will provide useful hints on the behavior of particular ionic liquids. Theoretical chemistry tools play a very important role in allowing a better understanding of the interactions present in complex media as ionic liquids near of graphene electrode surfaces. Solvation of graphene electrodes in ionic liquids is governed by three kinds of molecular interaction: ion–ion, graphene, and graphene–ion, all non-trivial and each offering its own difficulties to description. Cummings and coworkers²⁸ highlight three different requirements of the force field needed to describe the interactions between the graphene surface and imidazolium-based ionic liquid: the conductive nature of the graphene sheets, the potentially strong π–π interactions between the imidazolium cation and the graphene, and the nanometer-sized heterogeneities observed in the bulk ionic liquid of imidazolium-based ILs due to agglomeration of the non-polar alkyl chains. Several studies^29–33 considered a simple Lennard-Jones potential to describe the interactions between the graphene (or graphite) electrode and the ionic liquid. Borodin and coworkers^34–38 introduce an important refinement in the force field, modeling the electrode polarizability using flexible Gaussian distributed charges on the electrode, that were calculated iteratively subject to the condition of electrostatic energy minimization at the imposed potential on electrodes. Using this approach, the authors were able to model the capacitance enhancement observed in subnanometer slit-geometry nanopores. Salanne and coworkers^39–41 model the ionic liquid using a coarse-grain force field. For the electrodes the authors use the method developed by Reed et al.,⁴² following the idea of Siepmann and Sprik,⁴³ which consists of determining the charge on each electrode atom at each MD step by requiring that the potential on this atom is constant and equal to a specified value, meaning that the electrode will polarize in the same way as a metal.

In the present work, an atomistic description for both the graphene surface and the ionic liquid was considered, providing a high level of detail regarding the interactions and conformations, and a specific model was developed to describe the interactions of the ionic liquid with the graphene surface, based on static quantum chemical calculations. Using this model it was possible to simulate both graphene surfaces and single-walled carbon nanotubes in contact with the ionic liquid [C₂C₁im][SCN] 1-ethyl-3-methylimidazolium thiocyanate (Fig. 1), an ionic liquid with a good performance as electrolyte for solar cells applications.^44–46

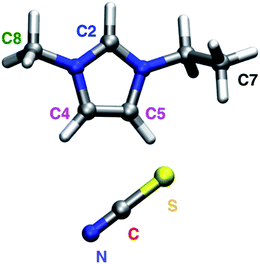Fig. 1 Molecular structure and labeling of the [C₂C₁im][SCN] ionic liquid. Please note that the colors associated to each atom correspond to the colors used in other Figures.

Results

Interaction model

Interactions within the ionic liquid were described by a classical, all-atom force field⁴⁷ specifically parameterized for the ionic liquid studied here. This model uses fixed electrostatic charges; therefore polarization of the ionic liquid is not specifically included. When calculating dynamic properties of ionic liquids the lack of polarization is an identified drawback, although for equilibrium properties and liquid-state structure the effect of inclusion of explicit polarizability is less significant. Graphene surfaces can be accurately described with a Tersoff–Brenner covalent potential,^48,49 that have been successfully used to describe mechanical properties of carbon nanotubes.⁵⁰ Nevertheless, for simplicity we have kept in a first step the surfaces of graphene rigid.

We have developed in this work a specific model to describe the interactions of the ionic liquid with the graphene surface, based on quantum chemical calculations, using a similar procedure to that considered to describe the interactions of ionic liquids and metallic surfaces (ruthenium nanoparticles⁵¹ and iron surfaces^52,53). Polarization of the graphene surface by the ions was also taken into account, using a model originally developed for metal surfaces.⁵⁴ The interaction model graphene–ionic liquid is one of the main original contributions of the present work and will be described in some detail. We have used Density Functional Theory (DFT) to determine the interaction energy of the ionic liquid and a cluster of graphene, containing 216 carbon atoms, and terminated at the border with hydrogen atoms. The hybridization state of all carbon atoms is sp², and the presence of the hydrogen atoms at the border was necessary to keep the cluster neutral. The size of the cluster was considered large enough to avoid border effects. We consider two different fragments of the ionic liquid, the 1-ethyl-3-methylimidazolium cation [C₂C₁im]⁺ and the thiocyanate anion [SCN]⁻. Dispersion-corrected density functional theory performs well to describe the interactions in systems containing ionic liquids,^55–57 and also dispersion interactions are important in π-systems. We have used in this work the BLYP-D^58,59 functional which includes the empirical dispersion correction D2 from Grimme.⁶⁰ A GGA functional was considered for the sake of feasibility.

We carried our calculations using TURBOMOLE 6.0,⁶¹ with the TZVP basis set^62,63 and the RI approximation.^64,65 The basis set superposition error was corrected via the counterpoise technique.⁶⁶ For a given orientation, the interaction energy at a given distance of the closest atom of the molecular fragment from the graphene cluster is the difference between the energy of the pair minus that of the isolated fragment and graphene cluster. The potential energy surfaces are depicted in Fig. 2 and 3 for the cation and anion respectively. It is possible to observe the strong adsorption energy of the anion and cation ranging from −30 kJ mol⁻¹ for the [SCN]⁻ anion (see Fig. 3) and it can reach values up to −100 kJ mol⁻¹ for the cation (see Fig. 2). For the cation, the preferred orientation occurs when the cation lays flat at the graphene surface, reflecting a strong π–π interaction. We present in Fig. S1 and S2 of the ESI† a comparison of the interaction energies between the fragments of the ionic liquid and the graphene cluster calculated by BLYP-D/TZVP (symbols) and those calculated using a Lennard-Jones potential extensively used in the literature,^30–33,67 observing the important discrepancies. It is immediately apparent that the use of a simple (and incorrect) interaction model will lead to erroneous results. We have fitted, using a self-developed program, the results of the DFT calculations to an empirical n − m (n = 9, m = 6) atom–atom interaction potential to be used in classical molecular dynamics simulations on systems containing graphene surfaces and the ionic liquid. The hydrogen atoms in the cation were, for simplicity, not explicitly considered; therefore our interaction model relies on the united-atom scheme, where several representative atoms of the cation describe the interactions of the ion with the graphene cluster. The interaction model represents correctly the potential energy landscape (Fig. 2 and 3), and the parameters obtained are given in the ESI.† This model is expected to describe accurately the interactions of the ionic liquid and graphene-based surfaces, independently of the geometry, since it is essentially an atom–atom model, so it could be applied to flat graphene surfaces, nanometer-size pores or carbon nanotubes. To account for the polarization of the graphene surface by the ions we consider a Drude-rod model,^54,68 where the polarizable atom is modeled by adding to each polarizable atom a freely rotating dipole composed of two opposite charges, q and −q, constrained at a given distance l₀, and having a mass m. We have considered in this work the values proposed by Iori and Corni.⁵⁴

Fig. 2 Interaction energies [C₂C₁im]⁺ – graphene as a function of separation z, for several orientations of the cation. Lines represent the fit of the interaction energies to a classical n − m analytical form (n = 9, m = 6) of the intermolecular potential between each atom of the graphene cluster and representative sites in the cation.

Fig. 3 Interaction energies [SCN]⁻ – graphene as a function of separation z, for several orientations of the anion. Lines represent the fit of the interaction energies to a classical n − m analytical form (n = 9, m = 6) of the intermolecular potential between each atom of the graphene cluster and representative sites in the anion.

Structure of the ionic liquid at a flat surface

We were interested in a first step on the structure of the ionic liquid at a flat graphene electrode that corresponds to an example of a supercapacitor, therefore, we have simulated a slab of the ionic liquid 1-ethyl-3-methylimidazolium thiocyanate placed between two flat graphene surfaces (Fig. S3†). The simulation box is a rectangular parallelepiped of dimensions L_xL_yL_z containing 1400 ion pairs of the studied ionic liquid, for a total of around 30 000 atoms in the simulated system. Periodic boundary conditions were applied in the three directions of space. The direction normal to the surface of the ionic liquid was elongated (250 Å) so that the liquid slab occupies around 120 Å in the middle with two equivalent graphene–ionic liquid interfaces. The systems were simulated via molecular dynamics using the DL_POLY classic⁶⁹ program at 423 K. Once the system was equilibrated for 2 ns, molecular dynamics runs of 2 ns were performed from which several thousand configurations were sampled, yielding representative averages of structural quantities.

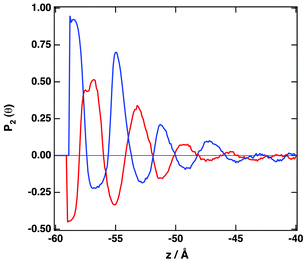
Fig. 4 depicts the number density profiles of several representative atoms of both cation and anion. The structural picture of Fig. 4 corresponds with a strong layering of the profiles of molecular density, charge, and electrostatic potential near of the graphene surface in agreement with recent simulation^{28,30,33,36,41,42,67} and experimental studies.⁷⁰ We observe the existence of a strong adsorption layer of ionic liquid with a thickness of ∼4 to 5 Å close to the graphene surface, where both cations and anions are present. A second and a third adsorption layer are also observed, but the density profiles correspond to an isotropic liquid at distances around 20 Å from the graphene surface. Interestingly, such periodicity can be correlated with the results reported by Atkin, Endres and coworkers^71–73 that have produced solvation force profiles for different ionic liquids confined between the tips of an atomic-force microscope (AFM) and mica, silica, graphite and metallic surfaces. Near of the surface there is an excess of positive charge, followed by a region of negative charge and a new region of positive charge. These fluctuations on the charge density confirm that both cations and anions are located close to the graphene surface. Another quantity that can be determined from the charge density plot is the potential of zero charge, defined as the potential drop within the double layer for uncharged surfaces being for the IL [C₂C₁im][SCN] around −0.35 V. We observe that the representative atoms of the cation's imidazolium ring, and the side methyl and ethyl groups are present in the same region (see also Fig. S4 of the ESI†). A clearer picture of the orientation of the ions can be obtained using the second Legendre polynomial:

in eqn (1), θ is the angle between a specific direction vector in the molecule-fixed frame and the direction normal to the surface, z. The Legendre polynomial functions enable us to investigate the range and extent of orientation preferences at the interface. P₂(θ) ranges from 1 to −0.5. A value of 1 implies that the two considered vectors are parallel, whereas a value of −0.5 indicates that they are perpendicular. We have selected the direction normal to the imidazolium ring and the vector connecting the nitrogen and sulfur atom of the anion; we observe in Fig. 5 that the imidazolium cation and the thiocyanate anion prefer to lie flat on the graphene surface, a result consistent with the density profiles presented in Fig. 4.

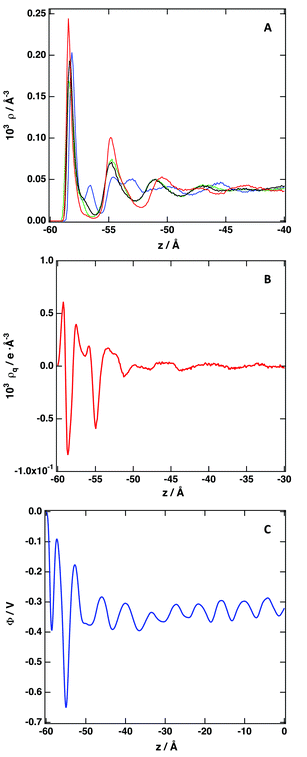Fig. 4 (A) Number density profile of individual atoms: C2 cation (blue), C7 cation (black), C8 cation (green) and C anion (red). See Fig. 1 for labeling. (B) Variation of the charge density along the direction normal to the graphene surface. (C) Electrostatic potential. The surface is located at z = −60 Å; z = 0 Å represents the bulk IL.

Fig. 5 Orientational ordering parameter. θ is defined by the angle between the direction vectors and the surface normal. Blue line: normal vector to the imidazolium ring; red line: vector NS in the [SCN]⁻ anion.

We have checked the effect of including or neglecting the polarization of the graphene surface, equivalent simulations were performed using the specific interaction model presented in this work to describe the interactions between the ionic liquid and the graphene, without considering the Drude-rod model.^54,68 The density profiles are presented in Fig. S5 of the ESI,† being the differences with the density profiles presented in Fig. 4 negligible. This result suggests that the specific interaction model presented in this work is able to account until some extent for the polarization of the surface when a charge entity approaches the surface. This fact leads to the conclusion that the development of a sophisticated interaction model using ab inito methods accounts for all kind of interactions present in the system. The use of ad-hoc techniques constructed to represent specific effects, as in this particular case is the polarization of the graphene surface on the simulated systems, is not necessary.

Structure of the ionic liquid inside of a carbon nanotube

In a second step we are interested in the structure of the ionic liquid near of the inner surface of a single walled carbon nanotube. Shim et al.⁷⁴ showed that the external solvation of CNTs by benzene is unaffected by the diameter of the nanotube. The structure of the liquid near of the outer surface is expected to be similar to that close to a flat surface. A total different picture can be expected when referred to the inner solvation, mainly when the diameter of the CNT decreases. We have considered three different CNTs: (10, 0), (15, 0) and (20, 0), with diameters ranging from 14 to 27 Å. The carbon nanotubes have a length of 300 Å. The CNT was placed inside of a parallelepiped box with dimensions L_x = L_y = 80 Å. Periodic boundary conditions on the three directions were considered to use the Ewald 3D method, a much more efficient method in terms of computational cost than other methods to treat the long-range coulombic interactions. The number of ion pairs inside of each nanotube was calculated from the density of the ionic liquid at the temperature of the simulations. For each CNT three different systems were settled:

(i) The average mass density of the IL inside of the CNT is the same as the bulk density of the IL.

(ii) The average mass density inside of the CNT is 0.5 times the bulk ionic liquid density.

(iii) The average mass density is 1.2 times the density of the bulk phase.

Each system was equilibrated for around 2 ns, after then production runs of 2 ns were obtained, and the structure of the ionic liquid inside of the CNT was characterized.

The structural picture is presented in Fig. 6 to 8 and also in Fig. S6 and S7 of the ESI.† The structure of the studied ionic liquid inside of the CNT of larger diameter is similar to the results presented in Fig. 4 regarding the solvation of a flat graphene surface. In the case of the (20, 0) CNT, we observe clearly the presence of strong adsorption layer at the surface of the nanotube, followed by a region of low density and a second solvation layer. The structure of the IL in the center of the nanotube resembles that of an isotropic liquid. In the (15, 0) CNT there are two solvation layers, one near to the surface and the second one close to the center of the nanotube. When the diameter of the nanotube is reduced, we observe only a strong layer of ions near of the interface, and a region of low density in the center of the nanotube. The presence of the CNT modifies strongly the structure of the ionic liquid, the free volume in the IL is redistributed, and in the region near of the surface of the CNT there is a strong local density of the IL, whereas a void region appears in the center of the nanotube. This picture, with a strong adsorbed layer of ionic liquid at the inner surface of the CNT, is more evident when the number of ion pairs inside of the CNT decrease (see Fig. 6). This situation can be achieved when the CNT is embedded in a mixture of the ionic liquid and a volatile solvent, and the later is removed, leading to the presence of a layer of IL near of the surface and a void in the center of the nanotube. When the mixture of the IL and the CNT is placed in a reservoir, and given the redistribution of the free volume in the ionic liquid, it seems possible that an excess of IL will enter the CNT, being the density inside larger than the density of the bulk liquid. Therefore, we have placed an excess of ionic liquid inside of the different CNTs (Fig. 8), to analyze how the possible structure of the IL inside of the CNT is modified. We observe that the main feature, also observed previously, a strong adsorbed layer near of the inner surface, is kept. For the (10, 0) CNT, we observe that IL is packed more compactly close to the surface, and a second region of high density appears in the center of the CNT. Therefore, even if the size of the IL studied here is small, we observe a region where the local density is low. Increasing the size of the CNT makes it easy to accommodate the excess of ionic liquid. For the (15, 0) CNT we observe that the second dense region placed in the center of the CNT is enlarged, being the structure of the IL more disorder. A similar effect is observed in the case of the (20, 0) CNT, the central region presents a lower level of ordering, but still there are regions with low local density. This result can have a large impact on the use of ILs as media for gas sequestration, since a mayor problem for the efficient use of ionic liquids is the low size of the cavities present. Placing the IL inside of a CNT will redistribute the free volume, and it will favor the solubility of different gases. We observe from the density profiles that for the different CNTs, the ionic liquids tend to stick to the surface, and also the local density of the different atoms of the IL present a maximum in the same region.

Fig. 6 Number density profile of individual atoms inside of (A) (10, 0) CNT; (B) (15, 0) CNT and (C) (20, 0) CNT: C2 cation (blue), C7 cation (black), C8 cation (green) and C anion (red). ρ_CNT = 0.5ρ_bulk. See Fig. 1 for labeling.

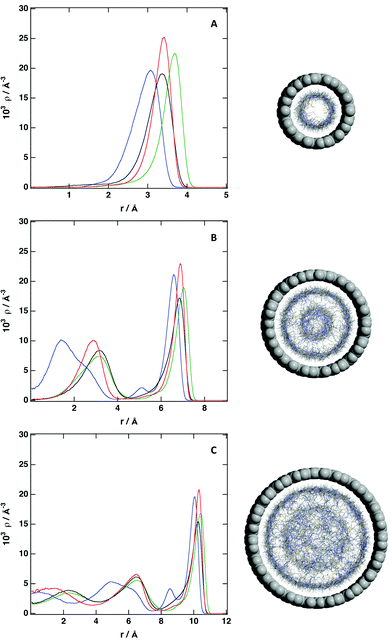Fig. 7 Number density profile of individual atoms inside of (A) (10, 0) CNT; (B) (15, 0) CNT and (C) (20, 0) CNT: C2 cation (blue), C7 cation (black), C8 cation (green) and C anion (red). ρ_CNT = 1.0ρ_bulk. See Fig. 1 for labeling.

Fig. 8 Number density profile of individual atoms inside of (A) (10, 0) CNT; (B) (15, 0) CNT and (C) (20, 0) CNT: C2 cation (blue), C7 cation (black), C8 cation (green) and C anion (red). ρ_CNT = 1.2ρ_bulk. See Fig. 1 for labeling.

Conclusions

As a conclusion, we have developed an interaction model between an ionic liquid and a graphene surface, being a mayor result of this work, as this model is generally applicable independent of the shape of the surface. We observe that the ionic liquid is strongly adsorbed at the graphene surface, independently of the geometry of the surface. We observe the presence of several solvation layers near of the interface, in good agreement with previous experimental results using AFM techniques.^72,75,76 The ions adopt a flat conformation at the surface, with both cations and anions near of the surface, even if the results of the DFT calculations show stronger adsorption energy of the cation. Structural effects appear when the IL is confined inside of a CNT. For nanotubes of large diameter, we observe a region in the center that can resemble an isotropic liquid phase, when the diameter decreases, the strong adsorption of the IL near of the surface lead to a region of low density in the middle of the CNT.

Acknowledgements

This work was supported by the Spanish Science and Technology Ministry (CTQ2011-23925 project) and the DFG, in particular by the projects KI-768/7-1 and KI-768/5-3 from the SPP-IL program. The participation of ASP was made possible by a post-doctoral fellowship granted by the DFG through the SPP-IL program. Computer time from the “Centro de Supercomputación de Galicia” (CESGA) is acknowledged gratefully.

References

1. Energy Storage. A key Technology for Decentralised Power, Power Quality and Clean Transport, European Commission, 2001.
2. M. F. El-Kady, V. Strong, S. Dubin and R. B. Kaner, Science, 2012, 335, 1326–1330.
3. P. Wu, J. Huang, V. Meunier, B. G. Sumpter and R. Qiao, ACS Nano, 2011, 5, 9044–9051.
4. Y. Zhu, S. Murali, M. D. Stoller, K. J. Ganesh, W. Cai, P. J. Ferreira, A. Pirkle, R. M. Wallace, K. A. Cychosz, M. Thommes, D. Su, E. A. Stach and R. S. Ruoff, Science, 2011, 332, 1537–1541.
5. E. Frackowiak and F. Beguin, Carbon, 2001, 39, 937–950.
6. E. Frackowiak and F. Beguin, Carbon, 2002, 40, 1775–1787.
7. D. N. Futaba, K. Hata, T. Yamada, T. Hiraoka, Y. Hayamizu, Y. Kakudate, O. Tanaike, H. Hatori, M. Yumura and S. Iijima, Nat. Mater., 2006, 5, 987–994.
8. A. Izadi-Najafabadi, S. Yasuda, K. Kobashi, T. Yamada, D. N. Futaba, H. Hatori, M. Yumura, S. Iijima and K. Hata, Adv. Mater., 2010, 22, E235–E241.
9. D. W. Wang, F. Li, J. Zhao, W. Ren, Z. G. Chen, J. Tan, Z. S. Wu, I. Gentle, G. Q. Lu and H. M. Cheng, ACS Nano, 2009, 3, 1745–1752.
10. Y. Wang, Z. Shi, Y. Huang, Y. Ma, C. Wang, M. Chen and Y. Chen, J. Phys. Chem. C, 2009, 113, 13103–13107.
11. Q. Cheng, J. Tang, J. Ma, H. Zhang, N. Shinya and L. C. Qin, Carbon, 2011, 49, 2917–2925.
12. C. Peng, S. Zhang, X. Zhou and G. Z. Chen, Energy Environ. Sci., 2010, 3, 1499–1502.
13. M. Pumera, Energy Environ. Sci., 2011, 4, 668–674.
14. M. D. Stoller, S. Park, Y. Zhu, J. An and R. S. Ruoff, Nano Lett., 2008, 8, 3498–3502.
15. C. Qian, J. Tang, J. Ma, H. Zhang, N. Shinya and L. C. Qin, Phys. Chem. Chem. Phys., 2011, 13, 17615–17624.
16. L. Demarconnay, E. Raymundo-Pinero and F. Beguin, Electrochem. Commun., 2010, 12, 1275–1278.
17. L. Trimperman, P. Skowron, A. Boisset, H. Galiano, D. Lemordant, E. Frackowiak, F. Beguin and M. Anouti, Phys. Chem. Chem. Phys., 2012, 14, 8199–8207.
18. M. Muller and B. Kastening, J. Electroanal. Chem., 1994, 374, 149–158.
19. M. Toupin, T. Brousse and D. Belanger, Chem. Mater., 2004, 16, 3184–3190.
20. J.-K. Chang, M.-T. Lee and W.-T. Tsai, J. Power Sources, 2007, 166, 590–594.
21. H. Nishide and K. Oyaizu, Science, 2008, 319, 737–738.
22. T. Welton, Green Chem., 2011, 13, 225.
23. N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123–150.
24. P. Wassercheid and T. Welton, Ionic Liquids in Synthesis, Wiley-VCH, 2nd edn, 2008.
25. V. Armel, M. Forsyth, D. R. MacFarlane and J. M. Pringle, Energy Environ. Sci., 2011, 4, 2234–2239.
26. E. I. Izgorodina, R. Maganti, V. Armel, P. M. Dean, J. M. Pringle, K. R. Seddon and D. R. MacFarlane, J. Phys. Chem. B, 2011, 115, 14688–14697.
27. U. A. Rana, R. Vijayaraghavan, D. R. MacFarlane and M. Forsyth, Chem. Commun., 2011, 47, 6401–6403.
28. H. Zhou, M. Rouha, G. Feng, S. S. Lee, H. Docherty, P. Fenter, P. T. Cummings, P. F. Fulvio, S. Dai, J. McDonough, V. Presser and Y. Gogotsi, ACS Nano, 2012, 6, 9818–9827.
29. Q. Dou, M. L. Sha, H. Y. Fu and G. Z. Wu, J. Phys.: Condens. Matter, 2011, 23, 175001.
30. M. Sha, G. Wu, Q. Dou, Z. Tang and H. Fang, Langmuir, 2010, 26, 12667–12672.
31. M. Sha, G. Wu, H. Fang, G. Zhu and Y. Liu, J. Phys. Chem. C, 2008, 112, 18584–18587.
32. M. Sha, G. Wu, Y. Liu, Z. Tang and H. Fang, J. Phys. Chem. C, 2009, 113, 4618–4622.
33. M. Sha, F. Zhang, G. Wu, H. Fang, C. Wang, S. Chen, Y. Zhang and J. Hu, J. Chem. Phys., 2008, 128, 134504.
34. L. Xing, J. Vatamanu, O. Borodin and D. Bedrov, J. Phys. Chem. Lett., 2013, 4, 132–140.
35. J. Vatamanu, O. Borodin, D. Bedrov and G. D. Smith, J. Phys. Chem. C, 2012, 116, 7940–7951.
36. J. Vatamanu, O. Borodin and G. D. Smith, Phys. Chem. Chem. Phys., 2010, 12, 170–182.
37. J. Vatamanu, O. Borodin and G. D. Smith, J. Phys. Chem. C, 2012, 116, 1114–1121.
38. L. Xing, J. Vatamanu, O. Borodin, G. D. Smith and D. Bedrov, J. Phys. Chem. C, 2012, 116, 23871–23881.
39. C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, P. Simon, Y. Gogotsi and M. Salanne, Nat. Mater., 2012, 11, 306–310.
40. C. Merlet, M. Salanne and B. Rotenberg, J. Phys. Chem. C, 2012, 116, 7687–7693.
41. C. Merlet, M. Salanne, B. Rotenberg and P. A. Madden, J. Phys. Chem. C, 2011, 115, 16613–16618.
42. S. K. Reed, O. J. Lanning and P. A. Madden, J. Chem. Phys., 2007, 126, 084704.
43. J. I. Siepmann and M. Sprik, J. Chem. Phys., 1995, 102, 511–524.
44. V. Armel, J. M. Pringle, M. Forsyth, D. R. Macfarlane, D. L. Officer and P. Wagner, Chem. Commun., 2010, 46, 3146–3148.
45. V. Armel, D. Velayutham, J. Sun, P. C. Howlett, M. Forsyth, D. R. Macfarlane and J. M. Pringle, J. Mater. Chem., 2011, 21, 7640–7650.
46. Y. Bai, Y. Cao, J. Zhang, M. Wang, R. Li, P. Wang, S. M. Zakeeruddin and M. Graetzel, Nat. Mater., 2008, 7, 626–630.
47. J. N. Canongia Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2006, 110, 19586–19592.
48. D. W. Brenner, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 9458–9471.
49. J. Tersoff, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 5538–5566.
50. B. Faria, N. Silvestre and J. N. Canongia Lopes, Compos. Sci. Technol., 2011, 71, 1811–1818.
51. A. S. Pensado and A. A. H. Padua, Angew. Chem., Int. Ed., 2012, 50, 8683–8687.
52. A. C. F. Mendonça, P. Malfreyt and A. A. H. Padua, J. Chem. Theory Comput., 2012, 8, 3348–3355.
53. A. C. F. Mendonça, P. Malfreyt and A. A. H. Padua, J. Chem. Theory Comput., 2012, 9, 1600–1610.
54. F. Iori and S. Corni, J. Comput. Chem., 2008, 29, 1656–1666.
55. E. I. Izgorodina, U. L. Bernard and D. R. MacFarlane, J. Phys. Chem. A, 2009, 113, 7064–7072.
56. S. Zahn and B. Kirchner, J. Phys. Chem. A, 2008, 112, 8430–8435.
57. S. Grimme, W. Hujo and B. Kirchner, Phys. Chem. Chem. Phys., 2012, 14, 4875–4883.
58. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
59. C. Lee, Y. Wang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
60. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
61. TURBOMOLE V6.0 2010, A Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, http://www.turbomole.com, 2010.
62. A. Schaefer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
63. A. Schaefer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
64. O. Vahtras, J. Almlöf and M. W. Feyereisen, Chem. Phys. Lett., 1993, 213, 514–518.
65. F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152.
66. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
67. M. V. Fedorov and R. M. Lynden-Bell, Phys. Chem. Chem. Phys., 2012, 14, 2552–2556.
68. B. G. Dick Jr and W. W. Overhauser, Phys. Rev., 1958, 112, 90–103.
69. DL_POLY Classic Molecular Simulation Package, 2011.
70. S. Baldelli, J. Bao, W. Wu and S.-S. Pei, Chem. Phys. Lett., 2011, 516, 171–173.
71. R. Atkin and G. G. Warr, J. Phys. Chem. C, 2007, 111, 5162–5168.
72. F. Endres, N. Borisenko, S. Z. El Abedin, R. Hayes and R. Atkin, Faraday Discuss., 2012, 154, 221–233.
73. J. J. Segura, A. Elbourne, E. J. Wanless, G. G. Warr, K. Voitchovsky and R. Atkin, Phys. Chem. Chem. Phys., 2013, 15, 3320–3328.
74. Y. Shim, Y. J. Jung and H. J. Kim, Phys. Chem. Chem. Phys., 2011, 13, 3969–3978.
75. R. Hayes, N. Borisenko, M. K. Tam, P. C. Howlett, F. Endres and R. Atkin, J. Phys. Chem. C, 2011, 115, 6855–6863.
76. R. Atkin, S. Z. El Abedin, R. Hayes, L. H. S. Gasparotto, N. Borisenko and F. Endres, J. Phys. Chem. C, 2009, 113, 13266–13272.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra02059f

---