Ab initio study of electronic effects in the ZnO/TiO2 core/shell interface: application in dye sensitized solar cells
Meysam
Pazoki
ab,
Nasser
Nafari
*c and
Nima
Taghavinia
a
aDepartment of Physics, Sharif University of Technology, Tehran, 11155-9161, Iran
bDepartment of Chemistry, Ångström Laboratory, Uppsala University, Box 532, SE 75120 Uppsala, Sweden
cSchool of Physics, Institute for Fundamental Sciences (IPM), Tehran, 19395-5531, Iran. E-mail: nafari@theory.ipm.ac.ir
First published on 5th November 2013
Abstract
Core/shell structure of ZnO nanowires coated with a monolayer of TiO2 is investigated using Density Functional Theory (DFT). The electronic states of the semiconductor is calculated and compared before and after coating of the TiO2 monolayer on a ZnO [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] surface. The effect of TiO2 coating induce surface states changes and shifts the conduction and valence band edges to higher energies. Our results, in qualitative agreement with the experimental work of Matt Law et al. (J. Phys. Chem. B, 110, 22652), show an increase in open circuit voltage and a decrease in short circuit current in ZnO/TiO2 core shell dye sensitized solar cells. Regarding the semiconductor density of states (DOS), TiO2 coated ZnO have more conduction band acceptor states and lower electronic back recombination in agreement with experimental results. Surface dipoles are attributed to changes of the local density of states of the surface. This method can be used for more investigation of starting effects of semiconductor interface and helps the study of surface states and their physical origin in dye sensitized solar cells.
0] surface. The effect of TiO2 coating induce surface states changes and shifts the conduction and valence band edges to higher energies. Our results, in qualitative agreement with the experimental work of Matt Law et al. (J. Phys. Chem. B, 110, 22652), show an increase in open circuit voltage and a decrease in short circuit current in ZnO/TiO2 core shell dye sensitized solar cells. Regarding the semiconductor density of states (DOS), TiO2 coated ZnO have more conduction band acceptor states and lower electronic back recombination in agreement with experimental results. Surface dipoles are attributed to changes of the local density of states of the surface. This method can be used for more investigation of starting effects of semiconductor interface and helps the study of surface states and their physical origin in dye sensitized solar cells.
Introduction
Dye sensitized solar cells (DSSCs) representing the third generation of solar cells, are environmentally friendly, of lower cost and have higher indoor efficiencies compared to conventional silicon solar cells.1,2 Their commercialization started with coming into the market for indoor-use conditions and keyboard chargers. Generally, DSSC working electrode consists of mesoporous TiO2 (or ZnO) structure coated on FTO substrate and dye molecules are adsorbed on the interface between semiconductor and electrolyte. The counter electrode is Pt coated FTO glass substrate. Incident photons excite the dye molecules; electrons of excited dyes are injected into the semiconductor and diffuse to the FTO, and its holes are injected to and diffused in the electrolyte. These holes also diffuse in the Pt layer which is regenerated by electrons of external circuit.2One of the fundamental questions of DSSCs is the interface in semiconductor/dye/electrolyte2 which has great influence on the electron injection and back recombination and its overall efficiency. The position of semiconductor energy levels which are determinant for the cell open circuit voltage (Voc) and short circuit current density (Jsc) strongly depends on the interface properties and several research groups have investigated the changes of these energy levels both experimentally and theoretically.3–11 The change in the position of semiconductor energy levels can occur by co-adsorbed molecules,10,11 electrolyte ions3,9 and by coating a thin insulator or semiconductor shell on the working electrode semiconductor.4–8 Also the semiconductor density of states (DOS) and its distribution of traps affect the electron transport and recombination resulting in different cell Voc and fill factor (FF).2,12,13 Core/shell structures are among structures for decreasing the electronic recombination, and thereby, increasing the efficiency of DSSCs.4–8 The properties of the shell affecting the DSSC performance, depend upon the physical separation of electrons and ions, the energy levels shifting, the creation of a barrier potential at interface, the passivity of the surface traps and the changes of the dye adsorption on the surface.4–8 Matt Law et al. have introduced ZnO nanowire/TiO2 shell as efficient DSSC with higher Voc and FF and lower Jsc compared to bare ZnO nanowire based DSSCs.5 They explained the changes of Jsc by different injection rate of different shell thicknesses and increase of Voc and FF by lower recombination rate and possible band shift. ZnO/TiO2 core shell structures have been used as DSSC working electrode in different morphologies including nanowires and nanoparticles, also in ultraviolet detectors and photocatalysis.14–18 In ZnO nanowire/TiO2 core/shell based DSSCs a small decrease in Jsc and an increase in FF and Voc of the cell have been reported.5,14
There are ab initio studies of DSSC semiconductor electronic states and their contribution to the cell performance.3,19–22 For the hetero-structured semiconductors in the DSSC, however, there are substantially less theoretical studies. Conesa have reported the position of conduction and valence bands in the anatase/wurtzite interface for the bulk TiO2/ZnO slabs,22 but there is no discussion about mono-layer coating of the shell, surface dipoles changes and the way band positions can be related to DSSC performance in terms of device voltage, current and recombination current.
In this paper we investigate the electronic properties of ZnO surface with a mono-layer of TiO2 coated on it and use our results to study the effects of core/shell DSSC qualitatively in comparison to the experimental data of ref. 5. The paper is organized as follows: In Sec. I we introduce the subject of ZnO/TiO2 core/shell DSSC and in Sec. II we present the method of our calculations using the Kohn Sham formalism in the framework of density functional theory (KS-DFT). The results and discussions are presented in Sec. III. First the [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] surface of ZnO has been studied. Then, we have studied the ZnO [10
0] surface of ZnO has been studied. Then, we have studied the ZnO [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] surface with TiO2 coating, and have calculated the density of states (DOS), surface dipoles, electric fields, position of Fermi energy, surface charge and relaxed positions and compared our results to bare ZnO surface. Furthermore according to our theoretical results, we discuss the possible effects of the TiO2 shell coating on our DSSC performance and its Voc, Jsc and FF. Finally, in Sec. IV we talk about the concluding remarks.
0] surface with TiO2 coating, and have calculated the density of states (DOS), surface dipoles, electric fields, position of Fermi energy, surface charge and relaxed positions and compared our results to bare ZnO surface. Furthermore according to our theoretical results, we discuss the possible effects of the TiO2 shell coating on our DSSC performance and its Voc, Jsc and FF. Finally, in Sec. IV we talk about the concluding remarks.
Theoretical methods
First principle calculations were performed by Quantum ESPRESSO23 package using density functional theory (DFT). Moreover, in this theory we have employed the Perdew–Burke–Ernzerhof pseudo-potential24 along with the generalized gradient approximation (GGA) for exchange correlation functional. We employed ultra-soft pseudo-potential in which the Zn 1s/2s/2p, Ti 1s/2s/2p and O 1s electrons considered as core electrons and the rest of electrons considered as valence electrons. Coordinates of all atoms were relaxed by bfgs (Broyden–Fletcher–Goldfarb–Shanno) algorithm,25 until the force acting on each atom is less than 0.002 Ry per a.u and we used the Davidson method for diagonalization of the Hamiltonian. The Kohn-Sham orbitals are expanded in a plane-wave basis set and the optimum cut-off energy for wave function and charge density are 30 and 320 Ry respectively. Self-consistency in total energy is achieved with a tolerance of less than 10−6 Ry. Brillouin zone sampling was carried out by a 4 × 1 × 2 Monkhorst-Pack grid for relaxation procedure, and by 5 × 2 × 3 Monkhorst-Pack grid for self-consistent procedures.The unit cell of ZnO surface consists of 8 layers of 2 × 2 ZnO unit cells with the wurtzite structure (Fig. 1(a)). The super-cell is constructed from atomic coordinates and lattice constants obtained via the minimization of ZnO bulk energy. The vacuum layer is 10.0 Angstrom, i.e., it is chosen to be sufficiently large so that the interaction between adjacent cells is negligible. The ZnO/TiO2 interface includes 8 layers of 2 × 2 ZnO unit cell plus 12 additional Ti and O atoms, forming a monolayer of TiO2 on the ZnO slab (Fig. 1(b)). The lattice constants of ZnO surface (a = 3.23 Å, c = 5.21 Å) and TiO2 rutile [100] surface (a = 2.95 Å, c = 4.60 Å) are roughly equal to their corresponding bulk values with differences of 7% and 11% respectively.
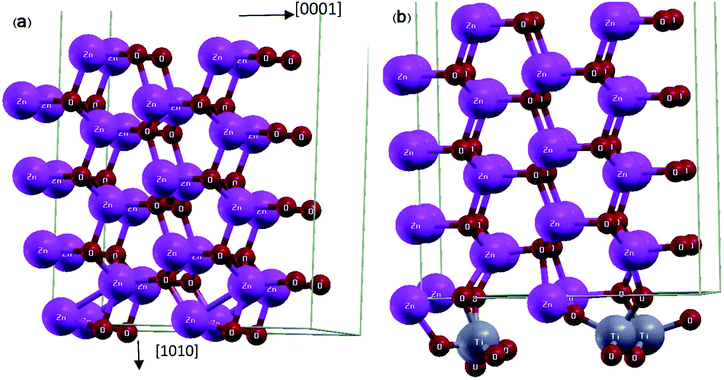 | ||
Fig. 1 Schematic representation of relaxed super-cells: (a) ZnO [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] slab and (b) ZnO [10 0] slab and (b) ZnO [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] slab coated with a monolayer of TiO2. 0] slab coated with a monolayer of TiO2. | ||
The experimental preparation of the coating has been done by atomic layer deposition with the rate of one-half mono-layer per cycle.26 Therefore, because of lattice mismatch at the interface, the appearance of defects might be possible. For both ZnO and ZnO/TiO2 slabs, the atomic coordinates of two bottom layers are fixed to the bulk coordinates and the other atoms were relaxed. The DOS of these two layers are subtracted from the total DOS to simulate the DOS of surface layers.
The structure is relaxed for several configurations with different positions of Ti and O atoms relative to ZnO surface atoms, all of which converge to the final positions where Ti atoms have moved closer to the oxygen surface atoms of ZnO slab and each Ti atom with its four adjacent O atoms forms a tetrapod (Fig. 1(b)).
The electric charge profile in the entire unit cell is obtained from our self-consistent calculations and also by integrating the local density of states of atomic orbitals, and by considering the contribution of nuclei and core electrons. The surface charge and surface dipoles can be calculated from the charge profile. Surface dipole electric fields and potentials were calculated according to the eqn (1) and (2), having in mind the first neighbour super-cell surface dipoles:
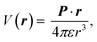 | (1) |
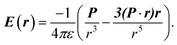 | (2) |
V(r) and E(r) denote potential and electric field at point r. ε is the permittivity of medium and P is the dipole moment. For calculating the work function, the bare potential of unit cell with extended vacuum layer is calculated and averaged over the entire volume of unit cell. The limiting value of bare potential at far distances is set to be the energy reference, i.e., the zero energy of vacuum.
Results and discussions
I. ZnO [10![[1 with combining macron]](https://www.rsc.org/images/entities/h3_char_0031_0304.gif) 0] surface
0] surface
Table 1 and Fig. 2 show the relaxation parameters of ZnO [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] slab. The results are in good agreement with previous DFT calculations and experimental results.27,28
0] slab. The results are in good agreement with previous DFT calculations and experimental results.27,28
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] surface.
0] surface.
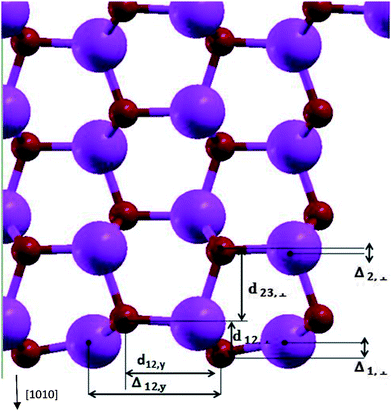 | ||
Fig. 2 The relaxation parameters for ZnO [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] slab. The big and small spheres are representatives of Zn and O atoms. 0] slab. The big and small spheres are representatives of Zn and O atoms. | ||
Calculated Zn–O bond length for the surface atoms is 1.86 Å which has about 7% contraction relative to the corresponding bulk bond lengths, and the calculated tilt of Zn–O bond-angle of surface atoms was 10.1 degrees-being in agreement to previous results.27,29,30 By calculating the Mulliken charges of atoms, the bond of relaxed surface atoms in comparison to inner layer atoms tend to show up their covalent nature. Comparison of relaxed and un-relaxed ZnO [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] slab shows slight change of states at the top of valence band (VB) and at the bottom of the conduction band (CB) in agreement with ref. 30. Oxygen vacancies in ZnO lead to the presence of intra-gap states31 which could be responsible for trap states distribution present in DSSCs. Also in TiO2 nanoparticles, uncoordinated Ti surface atoms leads to the unoccupied states 0.3–0.4 eV lower than CB.32 The calculated value of the work function of ZnO [10
0] slab shows slight change of states at the top of valence band (VB) and at the bottom of the conduction band (CB) in agreement with ref. 30. Oxygen vacancies in ZnO lead to the presence of intra-gap states31 which could be responsible for trap states distribution present in DSSCs. Also in TiO2 nanoparticles, uncoordinated Ti surface atoms leads to the unoccupied states 0.3–0.4 eV lower than CB.32 The calculated value of the work function of ZnO [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] surface is −4.76 eV relative to vacuum which is in good agreement with the experimental result of −4.65 eV of Moormann et al.34 Finally, our surface energy of [10
0] surface is −4.76 eV relative to vacuum which is in good agreement with the experimental result of −4.65 eV of Moormann et al.34 Finally, our surface energy of [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] surface, defined as the difference between the bulk and the slab energies is 1.27 J m−2 which is comparable to 1.3 J m−2 of ref. 30.
0] surface, defined as the difference between the bulk and the slab energies is 1.27 J m−2 which is comparable to 1.3 J m−2 of ref. 30.
In our calculations, band gap of ZnO is underestimated (Fig. 3) which is a well known error for DFT based band structure calculations of wide band gap semiconductors.33 But DFT can predict the work function, relaxation parameters and surface charges of the semiconductors well enough and comparable to experimental results.22,27,29–31,33 We have calculated the band gap of bare ZnO surface as 0.88 eV in agreement with ref. 27 and 41.
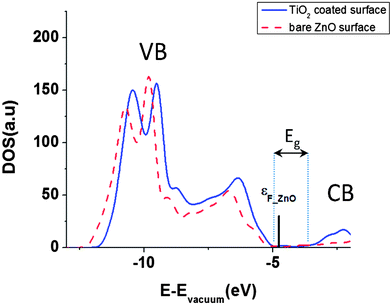 | ||
Fig. 3 Total DOS of bare and TiO2 coated ZnO [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] surface. The bar indicates the Fermi level of bare ZnO [10 0] surface. The bar indicates the Fermi level of bare ZnO [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] surface. 0] surface. | ||
II. TiO2 coated on ZnO [10![[1 with combining macron]](https://www.rsc.org/images/entities/h3_char_0031_0304.gif) 0] surface
0] surface
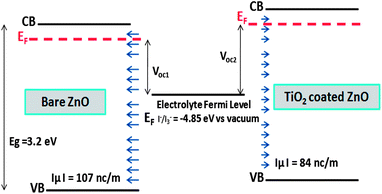
Fig. 3 shows the total density of states for the bare ZnO [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] slab and the TiO2 coated ZnO slab. After the coating, the CB and the VB are shifted to higher energies by approximately 210 meV. This way, we can qualitatively explain the experimentally verified results of decrease in short circuit current, Jsc, after TiO2 coating on ZnO nanowire.5 When the CB of semiconductor is shifted upward, then the injection efficiency and short circuit current would decrease because of lower driving force for electron transfer between the excited dye and the semiconductor.2,35 Since Voc in DSSCs is the difference between Fermi energies of electrolyte and semiconductor, by shifting the CB and VB to higher energies, the Fermi level is shifted correspondingly and the Voc of the cell will have the same increase.2,11
0] slab and the TiO2 coated ZnO slab. After the coating, the CB and the VB are shifted to higher energies by approximately 210 meV. This way, we can qualitatively explain the experimentally verified results of decrease in short circuit current, Jsc, after TiO2 coating on ZnO nanowire.5 When the CB of semiconductor is shifted upward, then the injection efficiency and short circuit current would decrease because of lower driving force for electron transfer between the excited dye and the semiconductor.2,35 Since Voc in DSSCs is the difference between Fermi energies of electrolyte and semiconductor, by shifting the CB and VB to higher energies, the Fermi level is shifted correspondingly and the Voc of the cell will have the same increase.2,11
These computational results are in qualitative agreement with the experimental data of Matt Law et al.5 They relate the increase of Voc to the reduction of dark current, but for thinnest shell of 0.5 nm TiO2, dark current reduction itself is not sufficient for explanation of their experimental data. Based on our calculations, the recombination resistance should also be enhanced after TiO2 coating. However, it seems that our calculations are in good agreement with data of thinnest shell of ref. 5 in which increase of Voc is due to both band shifts and dark current changes and it can explain the changes of injection rate and Jsc.
In order to examine the total DOS shifts, we have investigated the surface charge and surface dipole of the ZnO surface before and after the TiO2 coating. After the coating of TiO2 layer, some negative charge is transferred to the ZnO [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] surface, causing the Zn–O bonds to show higher ionic nature and to decrease the magnitude of normal component of the surface dipole. This charge transfer and distribution of surface dipoles can be responsible for energy shifts of CB and VB of ZnO. Normal component of dipole moment to the ZnO surface decreases by the TiO2 coating, resulting in the band shifts to the higher energies. Calculated normal component of surface dipole layer density is −107 and −84 nC m−1 for bare and TiO2 coated surfaces respectively. Considering the dielectric constant of wurtzite ZnO as 8, the resulting electric potential difference is 750 − 585 = 165 meV which is of the order of the calculated band shifts and could be, in part, responsible for the band shift. Zaban et al. (an experimental study) and Kusama et al. (a theoretical study) have used co-adsorbed molecules of different dipole moment and relate the CB shift of TiO2 to the changes of the co-adsorbed molecule dipole moment, which is in agreement with our assumptions and results.3,11
0] surface, causing the Zn–O bonds to show higher ionic nature and to decrease the magnitude of normal component of the surface dipole. This charge transfer and distribution of surface dipoles can be responsible for energy shifts of CB and VB of ZnO. Normal component of dipole moment to the ZnO surface decreases by the TiO2 coating, resulting in the band shifts to the higher energies. Calculated normal component of surface dipole layer density is −107 and −84 nC m−1 for bare and TiO2 coated surfaces respectively. Considering the dielectric constant of wurtzite ZnO as 8, the resulting electric potential difference is 750 − 585 = 165 meV which is of the order of the calculated band shifts and could be, in part, responsible for the band shift. Zaban et al. (an experimental study) and Kusama et al. (a theoretical study) have used co-adsorbed molecules of different dipole moment and relate the CB shift of TiO2 to the changes of the co-adsorbed molecule dipole moment, which is in agreement with our assumptions and results.3,11
External electric fields of ZnO/TiO2 core/shell surface dipoles is calculated at 2.0 nm distance from the surface, the average electric field was 15.0 mV nm−1 which is in fair agreement with the measured electric fields of ref. 36 (23.0 mV nm−1) causing Stark effect to occur in DSSCs.36 Due to surface electric fields, energy levels of adsorbed dye will be splitted and its absorption spectra will be shifted (Stark effect). The order of magnitude of the calculated surface dipoles are the same as the experimental values. It should be emphasized that the presence of dye and electrolyte ions will affect the surface electric fields considerably. Consideration of electrolyte, thicker TiO2 shells, attachment of dyes to TiO2 coating on ZnO, and inclusion of defects due to lattice mismatch in an ab-initio study can increase the accuracy of our results of real DSSCs.
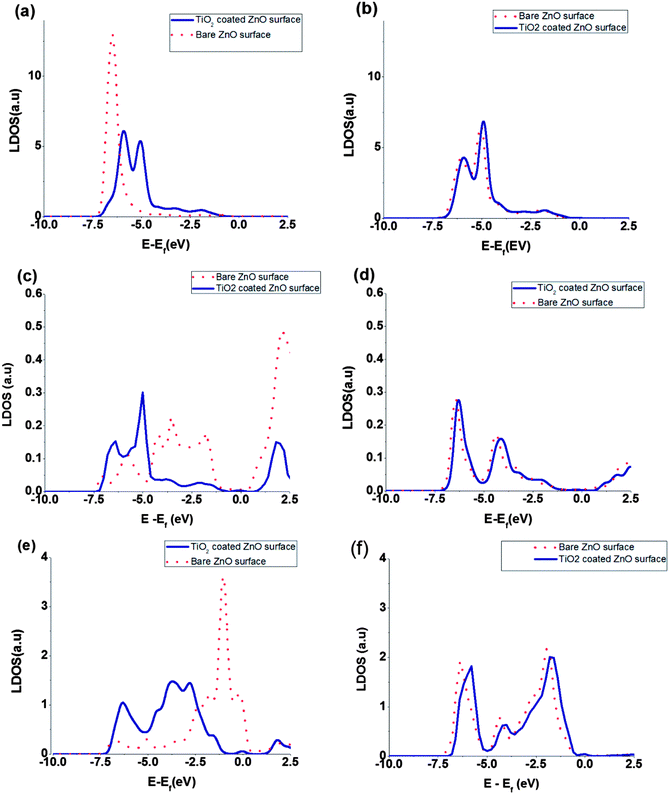
The local density of states (LDOS) of surface atoms and bulk, namely inner, atoms are plotted in Fig. 4. Also the calculated LDOS for the bare ZnO and the coated ZnO are shown in the figure. The effect of TiO2 coating on the LDOS of surface and bulk atoms is obvious in the Fig. 4. Because of the changes in the surface electric fields, we expect that the LDOS of surface atoms change their shape and position but the LDOS of bulk atoms keep their shape and shift the position of peaks only. Moreover, comparison of the total DOS shifts and LDOS shifts of ZnO bulk atoms shows that the order of magnitude of the peak shifts are almost the same (for the bulk atoms, LDOS shifts due to coating are from 150 to 300 meV but for the surface atoms, it is hard to define the peak shifts because of changes in peak shape. For the surface atoms, different peaks have different shifts from 600 to 1000 eV (Fig. 4)). The nearest neighbour interacting atoms and chemical environment surrounding the bulk atoms, will not changed by the coating of TiO2 and they just experience a shift induced by surface dipoles to the total DOS. But chemical environment of surface atoms will be changed by the coating, and we expect changes of peak shape as well as its position.
Fig. 5 shows a schematic representation of band positions and dipole layers for bare and TiO2 coated on ZnO surface. Voc1 and Voc2 represent the open circuit voltage of bare and TiO2 coated on ZnO nanowire based solar cells. Shift of TiO2 coated ZnO energy levels toward higher energies due to the coating, leads to its higher open circuit voltage compared to bare ZnO surface.
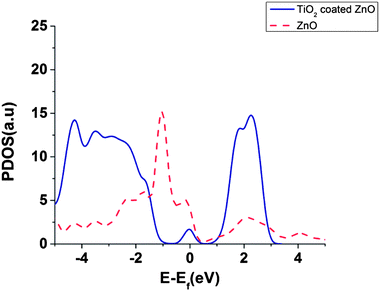
Partial density of states (PDOS) of surface atoms is shown for bare ZnO surface and for the TiO2 coated surface (Fig. 6). There is a small peak in the energy gap of TiO2 coated on ZnO which belongs to the TiO2 layer (Fig. 6). It seems that this intra-gap state is a consequence of configuration of oxygen and titanium uncoordinated surface atoms and could be changed for a thicker shell of TiO2. This small peak introduces surface trap states in the gap which act as trapping centres.
Our results, in agreement with ref. 39 and 40, show that the DOS of acceptor states for the TiO2 is much higher than ZnO which can result in higher injection efficiencies for TiO2 compared to ZnO.39,40
Surface recombination of electrons to the electrolyte acceptor states and electron injection from dye to the semiconductor can be described by the Marcus theory of electron transfer and strongly depends on the DOS of empty acceptor states and energy level difference of acceptor and donor states.37,38 Distribution of traps affects the electronic transport and lifetimes.12 For surface recombination, the TiO2 coated surface has much larger DOS in the CB, and the injected electrons lie near the CB minimum, but for bare ZnO surface, electrons fill the low density CB states and may fill the higher energies above the CB minimum. Shifting the energy levels of ZnO slab to the higher energies by TiO2 coating, results in a shift of intra-gap trap states and decrease the overlap of semiconductor exponential trap distribution by the density of acceptor states of electrolyte.11 This fact results in higher electron lifetime of TiO2 coated surface.37
Concluding remarks
In summary, we have investigated the electronic states of ZnO/TiO2 interface and have calculated the effect of TiO2 shell coating on the semiconductor band structure of ZnO as well as the surface charge. TiO2 shell changes the surface dipole distribution of ZnO nanowire causing a shift in the CB and VB of ZnO to higher energies. Calculated electric potential difference caused by surface dipole changes is in the order of the calculated band shifts and could be, in part, responsible for the band shift. This result is in qualitative agreement with the trend of experimental data of Matt Law et al. explaining the increase in Voc and decrease of Jsc using a mono-layer of TiO2 shell.5 Our results show that TiO2 shell decreases the overlap of ZnO surface trap density of states with electrolyte density of acceptor states, and in this way it can reduce the surface recombination of semiconductor electrons to the electrolyte oxidized states and increase the filling factor of the cell.External electric fields due to surface dipoles of TiO2 coated on ZnO is calculated, and the average electric field is found to be 15.0 mV nm−1 which is in fair agreement with the measured electric fields (23.0 mV nm−1) causing the Stark effect in DSSCs. This method can be used for studying the semiconductor surface states in the core/shell DSSCs in terms of surface local DOS, surface dipoles and possible band shifts and estimation/provision of different shell and core materials for improving the DSSC performance.
Acknowledgements
We wish to thank R. Asgari, R. Imani and T. Edvinson for their helpful discussions. We are also grateful to the Institute of fundamental sciences (IPM), Tehran for allowing us to use their computational cluster facilities.Notes and references
- B. O'Regan and M. Gratzel, Nature, 1991, 737, 3535 Search PubMed.
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595 CrossRef CAS PubMed.
- H. Kusamaa, H. Oritab and H. Sugihara, Sol. Energy Mater. Sol. Cells, 2008, 92, 84 CrossRef PubMed.
- Y. Diamant, S. Chappel, S. G. Chen, D. Melamed and A. Zaban, Coord. Chem. Rev., 2004, 248, 1271 CrossRef CAS PubMed.
- M. Law, A. Radenovic, T. Kuykendall, J. Liphardt and P. D. Yang, J. Phys. Chem. B, 2006, 110, 22652 CrossRef CAS PubMed.
- E. Palomares, J. N. Clifford, S. Haque, T. Lutz and J. Durrant, J. Am. Chem. Soc., 2003, 125, 475 CrossRef CAS PubMed.
- M. H. Kim and Y. U. Kwon, J. Phys. Chem. C, 2009, 113, 17176 CAS.
- T. C. Li, M. Goes, F. Santiago, J. Bisquert, P. Bueno, C. Prasittichai, J. Hupp and T. Marks, J. Phys. Chem. C, 2009, 113, 18385 CAS.
- G. Boschloo, L. Haggman and A. Hagfeldt, J. Phys. Chem. C, 2006, 110, 13144 CAS.
- X. Ren, Q. Feng, G. Zhou, C. Huang and Z. Wang, J. Phys. Chem. C, 2010, 114, 7190 CAS.
- S. Ruhle, M. Greenshtein, S. G. Chen, A. Merson, H. Pizem, S. Sukenik, D. Cahen and A. Zaban, J. Phys. Chem. B, 2005, 109, 18907 CrossRef PubMed.
- M. Pazoki, N. Taghavinia, Y. Abdi, F. Tajabadi, G. Boschloo and A. Hagfeldt, RSC Adv., 2012, 2, 12278 RSC.
- J. Bisquert, A. Zaban, M. Greenshtein and I. Mora-Sero, J. Am. Chem. Soc., 2004, 126, 13550 CrossRef CAS PubMed.
- R. Zhao, L. Zhu, F. Cai, Z. Yang, X. Gu, J. Huang and L. Cao, Appl. Phys. A: Mater. Sci. Process., 2013, 113, 67 CrossRef CAS.
- K. Park, Q. Zhang, B. Garcia, X. Zhou, Y. Jeong and G. Cao, Adv. Mater., 2010, 22, 2329 CrossRef CAS PubMed.
- K. Park, Q. Zhang, B. Garcia and G. Cao, J. Phys. Chem. C, 2011, 115, 4927 CAS.
- S. Panigrahi and D. Basak, Nanoscale, 2011, 3, 2336 RSC.
- A. Sartori, et al. , Cryst. Res. Technol., 2011, 46, 885 CrossRef CAS.
- E. Mosconi, et al. , J. Am. Chem. Soc., 2012, 134, 19438 CrossRef CAS PubMed.
- D. Cakir, O. Gulseren, E. Mete and S. Ellialtioglu, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 035431 CrossRef.
- C. E. Patrick and F. Giustino, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 085330 CrossRef.
- J. Conesa, J. Phys. Chem. C, 2012, 116, 18884 CAS.
- P. Giannozzi, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- S. R. Billeter, A. J. Turner and W. Thiel, Phys. Chem. Chem. Phys., 2000, 2, 2177 RSC.
- J. Arik, A. Aidla, T. Uustare and V. Sammelselg, J. Cryst. Growth, 1995, 148, 268 CrossRef.
- B. Meyer and D. Marx, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 035403 CrossRef.
- C. B. Duke, A. R. Lubinsky, S. C. Chang, B. W. Lee and P. Mark, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 15, 4865 CrossRef.
- P. Schroer, P. Kruger and J. Pollmann, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 17092 CrossRef.
- N. L. Marana, V. M. Longo, E. Longo, J. B. Martins and J. R. Sambrano, J. Phys. Chem. A, 2008, 112, 8958 CrossRef CAS PubMed.
- S. J. Clark, J. Robertson, S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 115311 CrossRef.
- N. Francesca, E. Mosconi, L. Storchi, E. Ronca, A. Selloni, M. Gratzel and F. De Angelis, Energy Environ. Sci., 2013, 6, 1221 Search PubMed.
- P. Erhart, K. Albe and A. Klein, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205203 CrossRef.
- H. Moormann, D. Kohl and G. Heiland, Surf. Sci., 1979, 80, 261 CrossRef CAS; H. Moormann, D. Kohl and G. Heiland, Surf. Sci., 1980, 100, 302 CrossRef.
- H. S. Wang and G. Zhou, J. Phys. Chem. C, 2009, 113, 15417 Search PubMed.
- U. B. Cappel, S. M. Feldt, J. Schoneboom, A. Hagfeldt and G. Boschloo, J. Am. Chem. Soc., 2011, 132, 9096 CrossRef PubMed.
- J. Bisquert, F. Fabregat-Santiago, I. Mora-Sero, G. Garcia-Belmonte and S. Gimenez, J. Phys. Chem. C, 2009, 113, 17278 CAS.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265 CrossRef CAS.
- J. A. Anta, E. Guillen and R. Tena-Zaera, J. Phys. Chem. C, 2012, 116, 11413 CAS.
- G. Boschloo, T. Edvinsson and A. Hagfeldt, Nanostructured Materials for Solar Energy Conversion, Elsevier, Amestrdam, 2006, ch. 8, p. 244 Search PubMed.
- C. Yong-hua, W. Un-hong and W. Jhi-gu, J. Inn. Mong. Norm. Univ., Nat. Sci. Ed., 2008, 37, 624 Search PubMed.
| This journal is © The Royal Society of Chemistry 2014 |