Improvement of the energy transfer from Ca3SnSi2O9 host to rare-earth ions with the assistance of oxygen vacancies
Xue Yua,
Ting Wangb,
Xuhui Xuc,
Tingming Jiangb,
Hongling Yub,
Qing Jiaob,
Dacheng Zhouc and
Jianbei Qiu*b
aKunming University of Science and Technology, Kunming, Yunnan, China
bCollege of Materials Science and Engineering, Kunming University of Science and Technology, Xuefu Road 253, Kunming, China. E-mail: Qiu@kmust.edu.cn
cKey Laboratory of Advanced Materials of Yunnan Province, College of Materials Science and Engineering, Kunming University of Science and Technology, Kunming, China
First published on 10th October 2013
Abstract
The blue emission of Ca3SnSi2O9 was identified to arise from the recombination of electrons and holes via intrinsic oxygen vacancy defects using photoluminescence spectra measurements, density functional theory calculations, and thermoluminescence analysis. A significant enhancement in the photoluminescence intensity of the blue emission was observed in samples of Ca3SnSi2O9 co-doped with fluorine, which was attributed to the increased number of oxygen vacancy defects produced in Ca3SnSi2O9. Most importantly, the improvement of the photoluminescence intensity of Dy3+ demonstrated that energy transfer from the Ca3SnSi2O9 host to the activators became more effective when fluorine was co-doped. It indicates that fluorine could be introduced into the Ca3SnSi2O9 host by this approach, which produced more oxygen vacancies and contributed to the improved photoluminescence performance of the activators.
Introduction
Continuing improvement in the efficiency of light emitting diodes (LEDs) has provided the potential for tremendous energy saving in general lighting applications. LEDs can therefore play a significant role in combating global warming through reducing energy consumption.1 Recent efforts to develop new LED phosphors include oxide,2–7 oxyfluoride,8–12 nitride,12–15 oxynitride,16–18 and sulfide hosts.19 Despite many successes, continued efforts are required to address issues of higher efficiencies, better color rendition, and better thermal quenching characteristics.20 Although numerous phosphors have been proposed in the last few years, these studies have focused primarily on the synthesis of compositional variants, to optimize known properties within classes of materials with previously known structure types. Recently, Danielson et al. identified that a new oxide-based blue phosphor (Sr2CeO4) exhibited a bright blue-white emission due to the charge transfer (CT) mechanism, which possessed an unusual one-dimensional chain structure type.20 These interesting results have encouraged us to exploit phosphors with unique crystal structures which could provide high chemical stability and excellent optical properties, which are essential to improve the performance of lighting and display devices.Blasse et al. have reported that isolated d10 ion complexes were able to show self-excitation emission, such as Zn4O compounds,21 Ba2ZnF6,22 Ca4ZrGe3O12,23 and Ca3SnSi2O9.24 Nowadays there also exists strong evidence for the observation of photoluminescence (PL) from transition-metal oxides. Examples are SrTiO3,25 SrZrO3,26,27 Sr2V2O7,28 and La0.825Sr0.175MnO3 nanowires,29 the Stokes shifts of which are very large. Several reports in the literature explain the conditions that favor PL emission in materials presenting a degree of order–disorder.29–31 The authors attribute the radiative decay process to distorted octahedra,30 self-trapped excitons, oxygen vacancies, surface states29 and charge transfer via intrinsic defects inside an oxygen octahedron.31 Although there is no general consensus in the literature about why and how radiative decay takes place in these compounds and the nature of this emission is not yet completely clear, it is a very interesting phenomenon to study especially when these materials act as the host matrix of potential single-component phosphors, which could provide unique emission to be combined with activators to achieve white light. Single-component white-light phosphors can overcome many of the problems associated with multiple emitting components, such as intrinsic color balance, device complications and high cost.28 Therefore, in this study, the focus of our research is on the rare earth doped Ca3SnSi2O9 with d10 configuration to pursue excellent PL performance.
In addition, as is well known, energy transfer plays an important role in the optical properties of luminescent materials, and their illumination performance is related to the local structures around activated ion centers.28 A new experimental design is therefore required to determine the origin of the emission transitions of Ca3SnSi2O9, and to achieve a fundamental mechanistic understanding of the relationship between the crystal structures and the luminescent properties of these phosphors. Hence, the effect of the change in crystal environment on the PL performance was studied with a distorted Sn–O bond in this work. Halo-containing oxides are generally obtained by introducing halogen ions (F−, Cl−, Br−, I−) into some conventional inorganic oxides to partially substitute for O2− ions, upon which the cation coordination environments are changed. These phosphors doped with rare earth activators usually exhibit high efficiencies, and other superior luminescent properties.32,33 In this work, F− ions were selected to substitute for O2− ions in Ca3SnSi2O9. Moreover, when the SnO6 octahedron becomes distorted in such a way that one Sn–O bond becomes shorter and more covalent whereas the remaining Sn–O bonds become longer and more ionic, the luminescence properties could be expected to change drastically. Finally, the effects of oxygen vacancies on the optical properties of the Dy3+ activators in Ca3SnSi2O9 were investigated.
Experimental section
A high-temperature solid-state synthesis procedure was employed to synthesize the Eu3+ doped Ca3SnSi2O9 phosphors. Analytical reagent grade CaCO3 (99.9%), CaF2 (99.9%), SnO2 (99.9%), SiO2 (99.9%), Eu2O3 (99.99%), and Dy2O3 (99.99%) were employed as raw materials. Small quantities of H3BO3 (5 mol%) were added as a flux. Stoichiometric amounts of the raw materials were mixed together with a small amount of ethanol (analytical reagent) homogeneously in an agate mortar for 30 min, and then the mixtures were first preheated at 900 °C in air for 2 h. After cooling to room temperature, the sample was reground and then sintered at 1400 °C for 4 h in an ambient atmosphere. After that, the as-obtained powders were cooled to room temperature naturally to yield the final product.The phases of samples were identified by X-ray powder diffraction (XRD) with Ni-filtered Cu Kα radiation at a scanning step of 0.02 in the 2θ range from 10° to 80°. A Hitachi F-7000 fluorescence spectrophotometer was used to record excitation and emission spectra. The weight of all powder samples was kept constant (0.5 g). The powder samples were compacted and excited under 45° incidence and emitted fluorescence was detected perpendicular to the excitation beam. All the measurements were carried out at room temperature. We take advantage of density functional theory (DFT) calculations that provide a detailed picture of the local atomistic structure and the electronic structure. The local-density approximations based on density functional theory were chosen for the theoretical basis of the density function. First, the crystallographic data from the Inorganic Crystal Structure Database no. 80466 were used to optimize the crystal structure. The second step was to calculate the density of states for the optimized structure. The convergences were set as 5 × 10−4 for maximum displacement tolerances, 0.1 eV nm−1 for maximum force, 0.02 GPa for maximum stress and 5 × 10−6 eV per atom for total energy change in the geometry optimization. The convergence criteria for the electronic wave function and for the geometry were 10−5 and 10−4 eV, respectively. The plane-wave energy cutoff was 380 eV.
Results and discussion
Fig. 1 shows the XRD pattern of the synthesized Ca3SnSi2O9 host matrix. The XRD pattern was found to be in good agreement with the literature (JCPDS no. 46-0812).24 This observation implies that the as-synthesized Ca3SnSi2O9 is chemically and structurally single-phase Ca3SnSi2O9, and agrees well with results from previous literature.24 The crystal structure of Ca3SnSi2O9 contains ribbons of edge-sharing CaO6 and SnO6 octahedra as shown in the inset of Fig. 1. The long direction of the ribbons is parallel to [100] and the width spans four octahedra. The SnO6 octahedra are in the middle of the ribbons and alternate with CaO6 octahedra parallel to [100]. The SnO6 octahedra have a common edge almost parallel to (010) and are related by an inversion center. A given ribbon touches (and shares oxygen with) two other ribbons at either end of its width, and the touching ribbons diverge at an angle of approximately 48°.The excitation and emission spectra of Ca3SnSi2O9 with different fluorine concentrations are depicted in Fig. 2. Although it has been reported that Ca3SnSi2O9 is one of the very few stannates which shows luminescence of reasonable intensity at room temperature under 220 nm excitation,24 the PL spectra yielded some interesting results which are presented in this work. The emission spectrum of Ca3SnSi2O9 displays a broad band extending from 350 to 550 nm, and the excitation spectrum consists of three broad bands between 200 and 350 nm which has not yet been reported. The emission was described in the literature as a charge transfer transition involving Sn(IV) and oxygen in the Sn2O10 group, which will be discussed subsequently. A particularly impressive result exhibited in Fig. 2 is that the intensity of the charge transfer transition located at 417 nm was significantly improved with increasing concentrations of fluorine. It is clearly shown that the emission intensity located at 417 nm is greatly enhanced when the concentration of fluorine increased from 1% to 2.2%. Meanwhile, the shape and the central frequency of the PL spectrum do not show appreciable changes between the Ca3SnSi2O9 host matrix and the fluorine doped samples, which indicates that the radiative processes giving rise to blue-light luminescence at room temperature have the same mechanism. The excitation spectrum corresponding to this emission consists of three bands, a strong one with a maximum at 311 nm and two weak ones at 220 and 244 nm. Although the central frequencies remain unchanged between the Ca3SnSi2O9 host matrix and Ca3SnSi2O9 doped with fluorine samples in the PL and PLE spectra, the great enhancement of the PL intensity indicates that the charge transfer transition of the host could be improved by co-doping with fluorine.
 | ||
| Fig. 2 Excitation and emission spectra of Ca3SnSi2O9 co-doped with different concentrations of fluorine. | ||
The density functional theory calculations of Ca3SnSi2O9 based on crystal structure refinement were employed and are shown in Fig. 3. The local density approximation (LDA) was chosen for the theoretical basis of the density function. Ca3SnSi2O9 possessed an indirect band-gap of about 3.936 eV (315 nm) with the valence band (VB) maximum at the B point and the conduction band (CB) minimum at the G point of the Brillouin zone. The electronic structure of the VB originates predominantly from Ca, O 2p states, whereas the CB is composed mostly of Sn 4s and Ca 3d states. It is expected that the value of the calculated band-gap of Ca3SnSi2O9, about 3.936 eV, will be smaller than the experimental one as the LDA underestimates the size of the band-gap.34 The calculation results provide evidence that the broad band peaks from 200–350 nm originate from the absorption of the host crystal Ca3SnSi2O9, which is predominantly ascribed to the charge transfer of Sn(IV)–O and Ca–O. The 417 nm (2.973 eV) emission band can be assigned to the recombination of the excited electrons with holes in an in-gap defect state, which results in the blue emission. In this work, oxygen vacancy defects are speculated to be electron traps contributing to the blue emission, which were produced during the high temperature synthesis processes.
To further illustrate the origin of the blue emission, the thermoluminescence (TL) technique was employed in this study. TL measurement is a main research tool as it has been proven to be a very useful means to reveal valuable information about the traps.35,36 Although the vast majority of the created free electrons and holes (electron deficient centers) in the crystalline materials recombine at room temperature, a few electrons diffuse away from their point of formation and become stabilized by being trapped at some defect in the structure. When the material is heated, the trapped electrons escape from the traps and a proportion of them recombine with holes at luminescence centers, emitting their excess energy in the form of light.37 Therefore, the TL measurements provide evidence for the existence of trapping centers. The TL glow curve of the Ca3SnSi2O9 was shown in Fig. 4; three TL peaks located at 326.3, 429.5, and 486.1 K were detected according to Gaussian fitting. The three TL peaks are labeled as TA, TB, and TC corresponding to traps with different depths. On the basis of TL results the trapping parameters were calculated by Chen's half width method. The activation energy (E) can be calculated by eqn (1) and (2).38,39
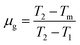 | (1) |
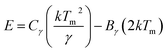 | (2) |
 | ||
| Fig. 4 TL glow curve of the Ca3SnSi2O9 host matrix. Inset: the decay curves monitored at the blue emission of 417 nm of Ca3SnSi2O9 and the Ca3SnSi2O9 sample co-doped with fluorine. | ||
| T1 (K) | Tm (K) | T2 (K) | τ (K) | δ (K) | ω (K) | μg | Trap depth | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Eτ (eV) | Eδ (eV) | Eω (eV) | E (eV) mean value | ||||||||
| TA | 288.4 | 326.3 | 364.3 | 37.9 | 38.0 | 75.9 | 0.501 | 0.316 | 0.378 | 0.348 | 0.347 |
| TB | 407.1 | 429.5 | 452.3 | 22.4 | 22.8 | 45.2 | 0.504 | 1.107 | 1.108 | 1.114 | 1.110 |
| TC | 474.2 | 486.1 | 498.1 | 11.9 | 12.0 | 23.9 | 0.502 | 2.843 | 2.672 | 2.776 | 2.764 |
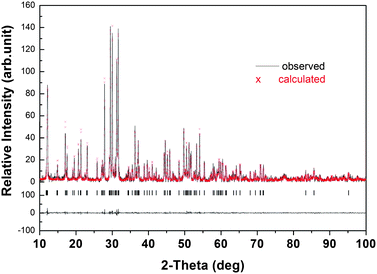
Fig. 5 exhibited the refinement of XRD patterns of Ca3SnSi2O9 when the fluorine doping concentration reached 2.2%. The black line and red crosses depict the observed and calculated patterns, respectively. The as-obtained fit parameter χ2 = 1.05 and Rwp = 9.1% ensure phase purity in the sample of Ca3SnSi2O9 with 2.2% fluorine doping. From the XRD refinement of Fig. 5, we could see that all the diffraction peaks could be indexed to Ca3SnSi2O9, which indicates that the pure phase could be derived when fluorine was doped. Samples were well crystallized, and the diffraction patterns could all be recognized as single phase in line with JCPDF 46-0812. No impurity phase was observed when fluorine was doped into Ca3SnSi2O9, which clearly indicates that the increase of PL emission in Ca3SnSi2O9 could be ascribed to the improved crystallization or the change in crystal environmental with the doping of fluorine.
To further illustrate the effect of co-doping fluorine on the Ca3SnSi2O9 crystal, hypersensitive PL spectra of Ca3SnSi2O9: Eu with different fluorine doping concentrations were measured and are shown in Fig. 6. Emission lines of the Eu3+ ion correspond to transitions from the excited 5D0 level to 7FJ (J = 1, 2, 3). We observe three main emissions: first, the emission in the vicinity of 590–600 nm is due to the magnetic dipole (MD) transition 5D0–7F1; second, the red emission around 610–630 nm is due to the hypersensitive electric dipole (ED) transition 5D0–7F2. The change in ratio of IED/IMD is a good measure of the symmetry of the Eu3+ site and is related to the Judd–Ofelt parameter Ω2.40 As the ratio of IED/IMD becomes larger with increasing fluorine concentration, the electric dipole transition is enhanced and quickly increases the crystal field strength. This increase could be related to an increase in the covalence or the distortion of the bonds surrounding the active ion. The 5D0–7F1 transition dominates in sites with inversion symmetry, whereas the 5D0–7F2 transition is the strongest in sites without inversion symmetry.41 Thus, it could be understood that the crystal field is significantly higher with increasing fluorine concentration. This ratio of intensities is related to the short average distance between Eu–O in the C2 sites and to the high distortion in the short order range (the degree of distortion in the CaO6 octahedra) with fluorine co-doping. It produces a strong crystal field around the Eu3+ ion with a high covalence in the Eu–O/Eu–F bond. This demonstrates that the crystal environment indeed changed with fluorine co-doping. The location of fluorine in Ca3SnSi2O9 is crucial to understand the optical properties of the phosphors. However, O2− and F− have no contrast in X-ray scattering, and crystallographic studies of O/F ordering are difficult to undertake. Because oxygen and fluorine are neighboring atoms in the periodic table, we propose that F− substitutes O2− in this study. This could be consistent with the fact that no impurity was observed in the X-ray Rietveld refinement.
In principle, the Ca3SnSi2O9 contains ribbons of edge-sharing CaO6 and SnO6 octahedra, which formed a low dimensional structure as discussed above. In this kind of low dimensional structure, it is very easy to implant other ions into the host lattice and create an energy transfer process between them if these ions show an absorption peak in the range of 400–500 nm. Here, we adopted Dy3+ as the activator in Ca3SnSi2O9, co-doping of which with different concentrations of fluorine then further increased the oxygen vacancies and enhanced the blue emission. As we expected, a significant improvement of the PL performance was observed in the Ca3SnSi2O9: Dy3+ samples. Fig. 7 shows the PL spectra of Ca3SnSi2O9: Dy3+ with different fluorine doping concentrations. The characteristic emission of Dy3+ (482, 574 nm) was observed under 310 nm excitation, which is ascribed to the 4F9/2–6H15/2, 4F9/2–6H13/2 transitions of Dy3+ respectively.42 The red emission (4F9/2–6H11/2) is too weak to be checked. Both the PL emission intensity of Ca3SnSi2O9 and Dy3+ was drastically improved with increasing fluorine concentration, although the doping concentration of Dy3+ is fixed. On one hand, the electric dipole transition was enhanced and the crystal field strength was quickly increased as well. On the other hand, more oxygen vacancies were formed. It was established that energy transfer from Ca3SnSi2O9 host to Dy3+ ions became more effective upon introducing fluorine ions, which was the main reason for the enhancement in the characteristic emission of the activators.
Conclusions
In summary, a Ca3SnSi2O9 host matrix was prepared by a solid state reaction. Ca3SnSi2O9 exhibited a blue emission which was ascribed to the recombination of electrons and holes via the intrinsic defects of oxygen vacancies under UV excitation. The emission intensity could be greatly improved by co-doping with fluorine due to the increase in the oxygen vacancies and the crystal field strength. The PL properties of Dy3+ as an activator could be improved by the enhancement of energy transfer efficiency from the host to the activators with the assistance of oxygen vacancies.Acknowledgements
We are thankful for financial support from the National Nature Science Foundation of China (11204113, 61308091, 61265004 and 51272097), Specialized Research Fund for the Doctoral Program of Higher Education of China (20115314120001), and the Foundation of Natural Science of Yunnan Province (2011FB022).Notes and references
- P. Waltereit, O. Brandt, A. Trampert, H. T. Grahn, J. Menniger, M. Ramsteiner, M. Reiche and K. H. Ploog, Nature, 2000, 406, 865 CrossRef CAS PubMed.
- W. B. Im, N. N. Fellows, S. P. DenBaars and R. Seshadri, J. Mater. Chem., 2009, 19, 1325 RSC.
- H. S. Jang, H. Y. Kim, Y. S. Kim, H. M. Lee and D. Y. Jeon, Opt. Express, 2012, 20, 2761 CrossRef CAS PubMed.
- W. R. Liu, C. H. Huang, C. W. Yeh, J. C. Tsai, Y. C. Chiu, Y. T. Yeh and R. S. Liu, Inorg. Chem., 2012, 51, 9636 CrossRef CAS PubMed.
- G. Lee, J. Y. Han, W. B. Im, S. H. Cheong and D. Y. Jeon, Inorg. Chem., 2012, 51, 10688 CrossRef CAS PubMed.
- M. L. Debasu, D. Ananias, J. Rocha, O. L. Malta and L. A. D. Carlos, Phys. Chem. Chem. Phys., 2013, 15, 15565 RSC.
- A. A. Reddy, S. Das, S. Ahmad, S. S. Babu, J. M. F. Ferreira and G. V. Prakash, RSC Adv., 2012, 2, 8768 RSC.
- W. B. Im, S. Brinkley, J. Hu, A. Mikhailovsky, S. P. DenBaars and R. Seshadri, Chem. Mater., 2010, 22, 2842 CrossRef CAS.
- Z. Xia and R. S. Liu, J. Phys. Chem. C, 2012, 116, 15604 CAS.
- A. A. Setlur, E. V. Radkov, C. S. Henderson, J. H. Her, A. M. Srivastava, N. Karkada, M. S. Kishore, N. P. Kumar, D. Aesram, A. Deshpande, B. Kolodin, L. S. Grigorov and U. Happek, Chem. Mater., 2010, 22, 4076 CrossRef CAS.
- K. W. Huang, W. T. Chen, C. I. Chu, S. F. Hu, H. S. Sheu, B. M. Cheng, J. M. Chen and R. S. Liu, Chem. Mater., 2012, 24, 2220 CrossRef CAS.
- M. Shang, D. Geng, X. Kang, D. Yang, Y. Zhang and J. Lin, Inorg. Chem., 2012, 51, 11106 CrossRef CAS PubMed.
- C. W. Yeh, W. T. Chen, R. S. Liu, S. F. Hu, H. S. Sheu, J. M. Chen and H. T. Hintzen, J. Am. Chem. Soc., 2012, 134, 14108 CrossRef CAS PubMed.
- M. Zeuner, P. J. Schmidt and W. Schnick, Chem. Mater., 2009, 21, 2467 CrossRef CAS.
- F. Hintze, F. Hummel, P. J. Schmidt, D. Wiechert and W. Schnick, Chem. Mater., 2012, 24, 402 CrossRef CAS.
- W. T. Chen, H. S. Sheu, R. S. Liu and J. P. Attfield, J. Am. Chem. Soc., 2012, 134, 8022 CrossRef CAS PubMed.
- J. Qiao, J. Zhang, X. Zhang, Z. Hao, W. Deng, Y. Liu, L. Zhang, L. Zhang, H. Zhao and J. Lin, Opt. Lett., 2013, 38, 884 CrossRef CAS PubMed.
- K. H. Lee and W. B. Im, J. Am. Chem. Soc., 2013, 96, 503 CAS.
- K. Feng, Y. Shi, W. Yin, W. Wang, J. Yao and Y. Wu, Inorg. Chem., 2012, 51, 11144 CrossRef CAS PubMed.
- E. Danielson, M. Devenney, D. M. Giaquinta, J. H. Golden, R. C. Haushalter, E. W. McFarland, D. M. Poojary, C. M. Reaves, W. H. Weinberg and X. D. Wu, Science, 1998, 279, 837 CrossRef CAS.
- G. Blasse, Chem. Phys. Lett., 1990, 175, 237 CrossRef CAS.
- H. Matthies, K. Recker, F. Wallrafen, G. J. Dirksen and G. Blasse, Chem. Phys. Lett., 1988, 149, 167 CrossRef CAS.
- G. Blasse, J. de Blank and D. J. W. IJdo, Mater. Res. Bull., 1995, 30, 845 CrossRef CAS.
- G. Blasse, M. A. Hamstra, D. J. W. IJdo and J. R. Plaisier, Mater. Res. Bull., 1995, 30, 967 CrossRef CAS.
- D. Kan, T. Terashima, R. Kanda, A. Masuno, K. Tanaka, S. Chu, H. Kan, A. Ishizumi, Y. Kanemitsu, Y. Shimakawa and M. Takano, Nat. Mater., 2005, 4, 816 CrossRef CAS.
- V. M. Longo, L. S. Cavalcante, A. T. de Figueiredo, L. P. S. Santos, E. Longo, J. A. Varela, J. R. Sambrano, C. A. Paskocimas, F. S. De Vicente and A. C. Hernandes, Appl. Phys. Lett., 2007, 90, 091906 CrossRef.
- V. M. Longo, L. S. Cavalcante, R. Erlo, V. R. Mastelaro, A. T. de Figueiredo, J. R. Sambrano, S. de Lάzaro, A. Z. Freitas, L. Gomes, N. D. Vieira Jr, J. A. Varela and E. Longo, Acta Mater., 2008, 56, 2191 CrossRef CAS PubMed.
- W. Q. Yang, H. G. Liu, M. Gao, Y. Bai, J. T. Zhao, X. D. Xu, B. Wu, W. C. Zheng, G. K. Liu and Y. Lin, Acta Mater., 2013, 61, 5096 CrossRef CAS PubMed.
- F. Chen, H. W. Liu, K. F. Wang, H. Yu, S. Dong, X. Y. Chen, X. P. Jiang, Z. F. Ren and J. M. Liu, J. Phys.: Condens. Matter, 2005, 17, L467 CrossRef CAS.
- W. F. Zhang, J. W. Tang and J. H. Ye, Chem. Phys. Lett., 2006, 418, 174 CrossRef CAS PubMed.
- M. S. Zhang, J. Yu, J. H. Chu, Q. Chen and W. C. Chen, J. Mater. Process. Technol., 2003, 137, 78 CrossRef CAS.
- H. Jing, C. Guo, G. Zhang, X. Su, Z. Yang and J. H. Jeong, J. Mater. Chem., 2012, 22, 13612 RSC.
- J. Wang, X. Jing, C. Yan, J. Lin and F. Liao, J. Lumin., 2006, 121, 57 CrossRef CAS PubMed.
- X. Zhu and S. G. Louie, Phys. Rev. B: Condens. Matter, 1991, 43, 14142 CrossRef CAS.
- J. Trojan-Piegza, J. Niittykoski, J. Hölsä and E. Zych, Chem. Mater., 2008, 20, 2252 CrossRef CAS.
- X. Xu, Y. Wang, W. Zeng, Y. Gong and B. Liu, J. Am. Ceram. Soc., 2011, 94, 3632 CrossRef CAS.
- A. J. J. Bos, Radiat. Meas., 2006, 41, S45 CrossRef PubMed.
- R. Chen, J. Electrochem. Soc., 1969, 116, 1254 CrossRef PubMed.
- R. Chen, J. Appl. Phys., 1969, 40, 570 CrossRef CAS.
- M. C. Pujol, J. J. Carvajal, X. Mateos, R. Solé, J. Massons, M. Aguiló and F. Díaz, J. Lumin., 2013, 138, 77 CrossRef CAS PubMed.
- J. W. Stouwdam and F. C. J. M. van Veggel, Nano Lett., 2002, 2, 733 CrossRef CAS.
- J. Gou, Y. Wang and F. Li, Electrochem. Solid-State Lett., 2007, 10, F31 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |