Catalytic oxidation of NO by Au₂⁻ dimers: a DFT study

Abstract

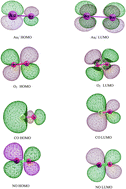
Density functional theory (DFT) calculations are performed to study the mechanistic details of NO oxidation promoted by gold dimer anions. Furthermore, we studied a full catalytic cycle producing two NO₂ molecules. The reaction is explored along three possible pathways. Our theoretical results show that anionic gold dimers present catalytic activity towards NO oxidation, as indicated by the calculated low energy barriers and high exothermicities. The present results enrich our understanding of the catalytic oxidation of NO by Au-cluster based catalysts. For the first time, we have presented a systematic study on the structure and energetics of various reaction intermediates involved in NO oxidation by Au₂⁻ clusters using density functional theory (DFT).

---

Introduction

The removal of poisonous NO gas, emitted mainly in automobile exhaust, is a major challenge in catalysis research and has been the subject of many investigations. Thus, understanding the adsorption mechanisms, dissociation of oxygen, and oxidation of NO at the molecular level is of great importance in designing suitable catalysts. As a new kind of catalyst to reduce air pollution, nano-sized gold clusters have attracted considerable interest recently from both the industrial and scientific communities.^1–5 Experimental and theoretical studies have proved that free and supported nano-sized gold clusters can efficiently catalyze CO, NO and H₂ oxidation reactions at low temperatures.^6,7 Nitrogen oxides exhibit rich chemistry on gold surfaces, particularly on oxygen covered gold surfaces.^8,9 Endou et al.¹⁰ have studied the adsorption and activation properties of precious metals (Ir, Pt and Au) towards NO by using the cluster model. McClure et al.¹¹ studied the adsorption and reaction of NO with atomic oxygen covered Au(111) surfaces, using collision induced desorption and temperature programmed desorption spectra. They suggested that nitric oxide may react with chemisorbed oxygen atoms at low temperatures. Torres et al.¹² theoretically studied the adsorption and oxidation of NO molecules with O on Au(111) surfaces at the low-coverage limit. They suggested that adsorbed NO reacts with pre-adsorbed oxygen by the Langmuir–Hinshelwood (LH) mechanism, in which the reaction occurs between chemisorbed oxygen atoms and NO molecules. The main route to nitrogen dioxide (NO₂) formation in combustion systems is through the oxidation of nitric oxide (NO). This process was originally investigated in order to explain the high proportion of NO₂ found in NO_x emissions from the exhaust of some gas turbine engines.¹¹ Ding et al.¹³ have used the density functional theory to investigate NO molecule adsorption on the gold clusters, observing a strong ability to adsorb NO molecules for the majority of gold clusters. Hao et al.¹⁴ studied the catalytic oxidation of NO over TiO₂ supported Pt clusters by in situ FTIR spectroscopy and proposed that the direct oxidation of gaseous NO to NO₂ is the main pathway for NO₂ formation. If one considers that Au₂⁻ promotes CO oxidation in the gas phase,^15,16 it is both natural and promising to investigate the catalytic activity of Au₂⁻ towards NO oxidation. Xu et al.¹⁷ reported density functional theory calculations (GGA-PW91) that probed the relationship between particle size, intermediate structures, and the energetics of CO and NO oxidation by molecular and atomic oxygen on Pt_x clusters (x = 1–5 and 10). Very recently, Xie et al.¹⁸ have investigated the reaction mechanism of NO reduction on the Rh₇⁺ cluster by means of DFT calculations and show that the first NO molecule which dissociates on the Rh₇⁺ cluster has an activation barrier of 39.6 kcal mol⁻¹, which is the rate-determining step of the whole catalytic cycle. In recent years, zeolites have been one of the most studied catalysts for NO_x decomposition. Kikuchi et al.¹⁹ showed that the NO reduction with methane on In/H-ZSM-5 could be improved by adding a transition metal such as Pt, Ir or Rh for enhancing the oxidation of NO to NO₂ at the early stage of the reaction, which is a necessary step for NO reduction by methane. Recently, Morpurgo et al.²⁰ investigated the mechanism of NO decomposition catalyzed by Cu-ZSM-5 by means of computational methods. Metkar et al.²¹ performed a comprehensive experimental and kinetic modeling study on NO oxidation reactions using Fe-ZSM-5, Cu-ZSM-5 and Cu-chabazite catalysts. Izquierdo et al.²² analyzed NO_x decomposition reactions over a Cu-ZSM-5 catalyst by ONIOM-DFT methods. Silver and proton-exchanged zeolites are also promising catalysts for the reduction of NO₂ with hydrocarbons.²³ It has been stated by Zeng et al.²⁴ that carbonaceous material supported metal oxides can remove NO effectively at room temperature. Since NO is easily oxidized to NO₂ at room temperature, and since NO₂ is easily removed by water, the catalytic oxidation of NO to NO₂ at room temperature is a promising method for the removal of NO. Therefore we restrict our attention to studying the mechanism of the title reaction at room temperature only. Recently, Gao et al.²⁵ systematically studied CO oxidation on subnanometer anionic gold clusters and their neutral counterparts by using ab initio calculations. Their study reveals that compared to the neutral clusters, the extra negative charge on the anionic clusters can enhance not only O₂ adsorption but also the strength of the co-adsorption of CO and O₂, which leads to a lower reaction barrier in the oxidation step. Thus, it may be concluded that in general, the anionic clusters are more efficient catalysts than their neutral counterparts. The catalytic reduction of NO by CO has also been studied extensively since both are present in exhaust gases.²⁶ Recently, supported Ir particles have shown unusually high reactivity for the reduction of NO by CO in the presence of oxygen.²⁷ NO oxidation has also been catalyzed by Rh and Co clusters.²⁸

To the best of our knowledge, no detailed theoretical or experimental studies have been reported for this reaction. In view of the potential importance and the rather limited information available, we carried out a detailed theoretical study on the potential energy surfaces of the title reaction to (1) explore elaborate oxidation processes; (2) investigate the products of the title reaction to assist in further experimental identification; and (3) give deep insights into the mechanism of the reaction of gold anionic dimers with nitric oxide. Therefore, to get a more complete picture of the oxidation processes of NO on the anionic Au dimers, it is pertinent to perform a comprehensive theoretical study to determine the energetics involved in the NO oxidation by considering a full structure optimization. The three most plausible pathways for the oxidation of NO are investigated during the present study and are given by pathways (1–3), as shown in Scheme 1.

Au₂⁻ + O₂ + NO → Au₂⁻–O + NO₂ (pathway 1)

Au₂⁻ + 1/2O₂ + NO → Au₂⁻ + NO₂ (pathway 2)

Au₂⁻ + O₂ + 2NO → Au₂⁻ + 2NO₂ (pathway 3)

Scheme 1 Reaction pathways for the oxidation of NO to NO₂ by Au₂⁻ dimers.

In recent years, density functional theory (DFT) has become a valuable tool for studying the properties of molecules and materials^29,30 and for identifying reaction mechanisms.^31,32 In this communication, for the first time, we have presented a systematic study on the structure and energetics of various reaction intermediates involved in NO oxidation by Au₂⁻ dimers using density functional theory (DFT).

Computational methods

All calculations have been performed using the GAUSSIAN 09 suite of programs.³³ In the framework of density functional theory (DFT), we employ the hybrid B3LYP^34,35 functional to explore the stationary points on the potential energy surfaces. Considering the strong relativistic effects of Au, we used the Los Alamos LANL2DZ^36,37 Effective Core Pseudopotentials (ECP) and valence double-ζ basis sets for Au atoms. The C, N and O atoms were treated with the 6-311G(d,p) basis sets. No symmetric constraints were imposed during geometry optimization. In order to determine the nature of different stationary points on the potential energy surface, vibrational frequency calculations were also performed using the same level of theory at which the optimization was made. All the stationary points have been characterized as either minima (the number of imaginary frequencies (NIMAG) = 0) or transition structures (NIMAG = 1). To ensure the reliability of the reaction path, the connections between the transition state and the corresponding minima were verified using intrinsic reaction coordinate (IRC) calculations developed by Gonzalez and Schlegel in the mass-weighted internal coordinate system.³⁸ Previous investigations^39–41 showed that the B3LYP/LANL2DZ combinations are sufficiently accurate for describing noble-metal systems. To further clarify the reliability of our calculations, we calculated the geometries and binding energies for Au₂⁻–O₂, Au₂⁻–CO, and Au₂⁻–NO. Our calculated values for the binding energies of O₂, CO and NO over Au₂⁻ are 19.29, 7.16 and 16.50 kcal mol⁻¹, respectively. The binding energy of CO is in good agreement with the reported value of Liu et al.⁴² It is clear from Fig. 1 that the HOMO and LUMO isosurfaces of Au₂⁻, O₂, CO and NO have matched shapes and symmetries. This further explains the binding orientations of NO with Au₂⁻, which are similar to O₂ and CO.

Fig. 1 The HOMO and LUMO isosurfaces for Au₂⁻ dimers and O₂, CO and NO molecules (isosurface value = 0.02).

The thermochemical parameters like standard reaction enthalpy (ΔH_r) and Gibbs free energy (ΔG_r) at a temperature T were estimated from the differences of H and G values of products and reactants at that temperature:

where E₀ is the total electronic energy including ZPE and H_corr and G_corr are the factors to be added to E₀ to obtain the enthalpy and Gibbs free energy, respectively, at a temperature T for taking into account the contribution of the translational, rotational and vibrational motion of a molecule. The H_corr and G_corr are defined as:

H_corr = H_trans + H_rot + H_vib + RT

G_corr = H_corr − T − S_total where entropy; S_total = S_trans + S_rot + S_vib + S_el

The thermal zero point energy correction (TZPE) is the thermal correction to the internal energy at 298 K and is given as a sum over four components for contributions from electronic, vibrational, rotational and translational degrees of freedom. The zero point vibrational energy ZPVE (or ZPE) results from the vibrational motion of molecular systems even at 0 K and is calculated for a harmonic oscillator model as a sum of the contributions from all vibrational modes of the system. The heat of adsorption (−ΔH_ads) is defined as:

−ΔH_ads = (E_cluster + H_adsorbate) − E_{cluster/adsorbate},

where E_{cluster/adsorbate}, is the total energy of the adsorbate on the cluster, E_cluster is the total energy of the bare cluster and H_adsorbate is the enthalpy of the adsorbate.

Results and discussion

The detailed thermodynamic calculations performed at the DFT level of theory for the free energies, reaction enthalpies and entropies with thermal zero-point energy corrections (TZPE) associated with pathways (1–3) are listed in Table 1. The optimized geometries of the reactants, intermediates, transition states and products obtained at the DFT level are shown in Fig. 2. Transition states found through a search on the potential energy surfaces of pathways (1–3) are characterized by TS1, TS2 and TS3, respectively. The search was made along the minimum energy path on a relaxed potential energy surface.

Table 1 Thermochemical data for the oxidation pathways of NO calculated at the DFT level of theory with TZPE corrections

Reaction channels	ΔGr (298 K) (kcal mol^−1)	ΔHr (298 K) (kcal mol^−1)	ΔS° (298 K) (cal mol^−1 K^−1)
Pathway 1	18.08	9.90	−33.29
Pathway 2	−24.16	−22.79	−16.20
Pathway 3	−48.32	−45.59	−32.40

---

Fig. 2 Optimized geometries of reactants, intermediates, transition states and products involved in the oxidative pathways of NO at B3LYP level.

Harmonic vibrational frequencies of the stationary points were calculated at the B3LYP level of theory and are given in Table 2. These results show that the reactant and products have stable minima on their potential energy surface characterized by the occurrence of only real and positive vibrational frequencies. On the other hand, transition states are characterized by the occurrence of only one imaginary frequency obtained at 390i, 246i and 534i cm⁻¹ for TS1, TS2 and TS3, respectively. These frequencies were analyzed using the ChemCraft⁴³ visualization program. Visualization of the imaginary frequency gives a qualitative confirmation of the existence of transition states connecting reactants and products. Intrinsic reaction coordinate (IRC) calculations³⁸ have also been performed for each transition state. The IRC plots for the transition states reveal that the transition state structure smoothly connects the reactant and the product sides. The energies of the reactants, transition states and products obtained in the IRC calculations are in excellent agreement with the individually optimized values at the B3LYP/LANL2DZ level of theory. The formation of complexes of Au₂⁻ with O₂ and NO molecules is expected to be the initial step of NO oxidation. Pathway 1 starts from the adsorption of O₂ on Au₂⁻ to form the superoxo-like complex Au₂⁻–O₂. After the adsorption of O₂, the incoming NO attacks the adsorbed O₂ to form a three species meta-stable complex IM1 which lies below the reactants by 39.31 kcal mol⁻¹. Then, the NO adsorbs the O atom to produce a NO₂ molecule via the transition state TS1. The calculated geometrical parameters of TS1 clearly indicate that the O–O bond is weakening and the N–O bond is forming. Visualization of the optimized structure of TS1 further reveals the elongation of the O–O bond (O1–O2) bond length from 1.257 to 1.436 Å (14%) with a simultaneous shrinkage of the N–O (N1–O1) bond from 1.378 to 1.192 Å (13%). In the optimized geometry of TS1, NO abstracts an O atom to produce NO₂ and complete the cycle. Thermodynamic calculations reveal that this pathway proceeds with an endothermicity of 9.90 kcal mol⁻¹ along with an energy barrier of 16.18 kcal mol⁻¹. The calculated heat of adsorption for this path is found to be 48.33 kcal mol⁻¹.

Table 2 Harmonic vibrational frequencies of reactants, intermediates, transition states and products

Species	Vibrational frequencies (cm^−1)
Au2^−	114
O2	1641
Au2^−–O	119, 295, 296, 311
Au2^−–O2	45, 60, 136, 216, 408, 1176
IM1	28, 56, 61, 137, 158, 228, 367, 465, 613, 808, 1006, 1647
IM2	12, 49, 137, 141, 185, 299, 820, 1067, 1557
IM3	42, 45, 73, 123, 132, 171, 172, 260, 379, 509, 1280, 1758
IM4	18, 30, 40, 47, 55, 68, 119, 139, 208, 231, 248, 437, 740, 825, 1329, 1499, 1647
TS1	390i, 27, 60, 88, 138, 191, 245, 435, 502, 728, 846, 1753
TS2	246i, 46, 57, 137, 141, 219, 785, 1223, 1505
TS3	534i, 27, 45, 53, 63, 138, 171, 176, 217, 242, 329, 397, 592, 638, 720, 953, 1453, 1699
NO	1988
NO2	766, 1399, 1706

---

In the case of pathway 2, the initial complex of Au₂⁻ with O and NO is denoted as IM2. The results given in Table 1 reveal that pathway 2 is exergonic (ΔG < 0) and exothermic in nature and thus, thermodynamically facile. The heat of adsorption for this pathway is found to be 128.97 kcal mol⁻¹. Our calculation shows that this complex is more stable (by 58.59 kcal mol⁻¹) than the reactants. The transition state involved along this path is TS2, where the transition vector is related to the imaginary frequency of 246 cm⁻¹ giving rise to the formation of the product-like intermediate IM2. The barrier along this path is calculated to be 11.91 kcal mol⁻¹. The calculated geometrical parameters of TS2 indicate that the Au–O bond is weakening and the O–N bond is forming. A similar analysis made on the optimized structure of TS2 reveals the elongation of the Au–O (Au₂⁻–O1) bond length from 2.164 to 2.462 Å, an increase of about 14%.

Considering the strong interaction of Au clusters with NO (with a binding energy of 16.50 kcal mol⁻¹), we explored another reaction channel (pathway 3) which can be described as the O–N–O–O–N–O group involved pathway with the participation of two NO molecules. Since the ΔG_r value for this pathway is significantly negative at 298 K, it should be a spontaneous process at lower temperatures. Interestingly, ΔH_r and ΔG_r values indicate that this should be the more thermodynamically favored pathway. Pathway 3 involves the simultaneous formation of two NO₂ molecules with a heat of adsorption value of 164.24 kcal mol⁻¹. Similar to pathway 1, by attaching the first NO molecule to IM1 we locate another meta-stable complex IM3 which lies below the reactants by 53.76 kcal mol⁻¹. By subsequent attachment of a second NO molecule to IM3, we locate IM4. Visualization of IM4 reveals that the N atom binds to Au₂⁻ and associates with one O of O₂ to form an O–N–O–O–N–O group which lies below the reactants by 43.58 kcal mol⁻¹, with the simultaneous formation of two NO₂ molecules via TS3 with a barrier of 8.92 kcal mol⁻¹. A schematic of the potential energy surface of the titled reaction obtained at the B3LYP + ZPE level of theory is plotted in Fig. 3. In the construction of the energy diagram, zero-point corrected total energies of the species are utilized. These energies are plotted with respect to the ground state energy of Au₂⁻ + O₂/O arbitrarily taken as zero. From Fig. 3, it is clear that path 3 (the O–N–O–O–N–O group) is the dominant path, having a lower barrier height for NO oxidation promoted by the Au₂⁻ dimer. Our calculated barrier heights for all the plausible pathways are comparable with the barrier height calculated by Liu et al.⁴² for CO oxidation promoted by the Au₂⁻ dimer. This result strongly suggests that like with CO oxidation, the Au₂⁻ dimer shows catalytic activity towards NO oxidation at low temperatures.

Fig. 3 Potential energy profile of NO oxidation by the Au₂⁻ dimer. The relative energies (in kcal mol⁻¹) were calculated with ZPE corrections at the B3LYP/LANL2DZ level of theory.

Conclusion

We present here the potential energy profile (including geometries, energies and vibrational frequencies of the reactants, intermediates, transition states and products) and thermochemical data for the oxidation of NO to NO₂ promoted by gold anionic dimers investigated at the DFT level of theory. Energetic calculations reveal that the most dominant oxidation pathway is path 3 (Au₂⁻ + O₂ + 2NO) that occurs with a barrier height of 8.92 kcal mol⁻¹. The present theoretical study may give useful information on the reaction mechanism and can provide powerful guidelines for future experimental studies for the title reaction.

Acknowledgements

The authors are thankful to DST, New Delhi for financial support. BKM is thankful to University Grants Commission, New Delhi for providing a Dr D. S. K. Post doctoral fellowship. The financial support in the form of a Junior Research Fellowship to DB from CSIR, New Delhi is also acknowledged.

References

1. M. Okumura, S. Nakamura, S. Tsubota, T. Nakamura, M. Azuma and M. Haruta, Catal. Lett., 1998, 51, 53.
2. G. C. Bond and D. Thompson, Catal. Rev. Sci. Eng., 1999, 41, 319.
3. M. Valden, X. Lai and D. W. Goodman, Science, 1998, 281, 1647.
4. M. Haruta, Chem. Rec., 2003, 3, 75.
5. M. C. Daniel and D. Astruct, Chem. Rev., 2004, 104, 293.
6. N. Lopez and J. K. Norskov, J. Am. Chem. Soc., 2002, 124, 11262.
7. H. Hakkinen and U. Landman, J. Am. Chem. Soc., 2001, 123, 9704.
8. N. Saliba, D. H. Parker and B. E. Koel, Surf. Sci., 1998, 410, 270.
9. J. Wang and B. E. Koel, J. Phys. Chem. A, 1998, 102, 8573.
10. A. Endou, N. Ohashi, S. Takami, M. Kubo, A. Miyamoto and E. Broclawik, Top. Catal., 2000, 11/12, 271.
11. S. M. McClure, T. S. Kim, J. D. Stiehl, P. L. Tanaka and C. B. Mullins, J. Phys. Chem. B, 2004, 108, 17952.
12. D. Torres, S. Gonzalez, K. M. Neyman and F. Illas, Chem. Phys. Lett., 2006, 422, 412.
13. X. L. Ding, Z. Y. Li, J. L. Yang, J. G. Hou and Q. S. Zhu, J. Chem. Phys., 2004, 121, 2558.
14. L. Li, Q. Shen, J. Cheng and Z. Hao, Catal. Today, 2010, 158, 361.
15. L. D. Socaciu, J. Hagen, T. M. Bernhardt, L. Woste, U. Heiz, H. Hakkinen and U. Landman, J. Am. Chem. Soc., 2003, 125, 10437.
16. M. L. Kimble, A. W. Castleman, R. Mitric Jr, C. Burgel and V. B. Koutecky, J. Am. Chem. Soc., 2004, 126, 2526.
17. Y. Xu, R. B. Getman, W. A. Shelton and W. F. Schneider, Phys. Chem. Chem. Phys., 2008, 10, 6009.
18. H. Xie, M. Ren, Q. Lei and W. Fang, J. Phys. Chem. A, 2011, 115, 14203.
19. E. Kikuchi, M. Ogura, N. Aratani, Y. Sugiura, S. Hiromoto and K. Yogo, Catal. Today, 1996, 27, 35.
20. S. Morpurgo, G. Moretti and M. Bossa, J. Mol. Catal. A: Chem., 2012, 358, 134.
21. P. S. Metkar, V. Balakotaiah and M. P. Harold, Catal. Today, 2012, 184, 115.
22. R. Izquierdo, L. J. Rodriguez, R. Anez and A. Sierraalta, J. Mol. Catal. A: Chem., 2011, 348, 55.
23. J. A. Martens, A. Cauvel, A. Francis, C. Hermans, F. Jayat, M. Remy, M. Keung, J. Lievens and P. A. Jacobs, Angew. Chem., Int. Ed., 1998, 37, 1901.
24. Z. Zeng, P. Lu, C. Li, L. Mai, Z. Li and Y. Zhang, Catal. Sci. Technol., 2012, 2, 2188.
25. Y. Gao, N. Shao, Y. Pei, Z. F. Chen and X. C. Zeng, ACS Nano, 2011, 5, 7818.
26. V. I. Parvulescu, P. Grange and B. Delmon, Catal. Today, 1998, 46, 233.
27. W. Chen, Q. Shen, R. A. Bartynski, P. Kaghazchi and T. Jacob, Langmuir, 2013, 29, 1113.
28. M. M. Yung, E. M. Holmgreen and U. S. Ozkan, J. Catal., 2007, 247, 356.
29. V. Stamenkovic, B. S. Mun, K. J. J. Mayrhofer, P. N. Ross, N. M. Markovic, J. Rossmeisl, J. Greeley and J. K. Norskov, Angew. Chem., Int. Ed., 2006, 45, 2897.
30. B. Kalita and R. C. Deka, J. Am. Chem. Soc., 2009, 131, 13252.
31. R. Valero, J. R. B. Gomes, D. G. Truhlar and F. Illas, J. Chem. Phys., 2010, 132, 104701.
32. W. Song and E. J. M. Hensen, Catal. Sci. Technol., 2013, 3, 3020.
33. M. J. Frisch, et al., Gaussian 09, Revision B. 01, Gaussian, Pittsburgh, PA, 2009.
34. A. D. Becke, J. Chem. Phys., 1992, 96, 2155.
35. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
36. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270.
37. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299.
38. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154.
39. A. M. Joshi, M. H. Tucker, W. N. Delgass and K. T. Thomson, J. Chem. Phys., 2006, 125, 194707.
40. A. M. Joshi, W. N. Delgass and K. T. Thomson, J. Phys. Chem. B, 2006, 110, 23373.
41. D. Y. Wu, B. Ren, Y. X. Jiang, X. Xu and Z. Q. Tian, J. Phys. Chem. A, 2002, 106, 9042.
42. P. Liu, K. Song, D. Zhang and C. Liu, J. Mol. Model., 2012, 18, 1809.
43. G. Zhurko and D. Zhurko, ChemCraft 1.6, 2011.

---