On the linear and non-linear electronic spectroscopy of chlorophylls: a computational study†
Alicja
Graczyk
,
Justyna M.
Żurek
and
Martin J.
Paterson
*
Institute of Chemical Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, UK. E-mail: m.j.paterson@hw.ac.uk
First published on 8th November 2013
Abstract
A theoretical analysis of linear and non-linear (two-photon absorption) electronic spectroscopy of all known porphyrinic pigments has been performed using linear and quadratic density functional response theory, with the long-range corrected CAM-B3LYP functional. We found that higher Soret transitions often contain non-Gouterman contributions and that each chlorophyll has the possibility for resonance enhanced TPA in the Soret region, although there is also significant TPA in the Q region.
Introduction
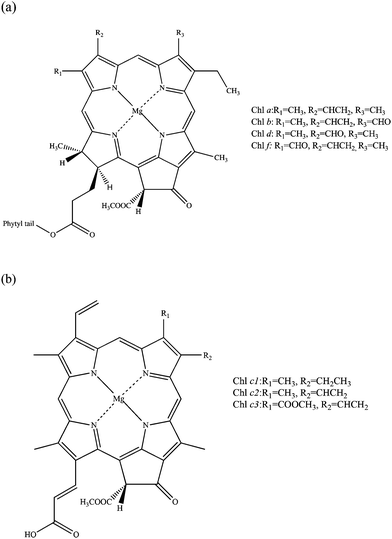
The spectroscopic properties of porphyrins and their structural analogues have attracted significant attention from both experimental and theoretical chemists, and have been comprehensively studied since the middle of the twentieth century. The initial purpose of such research was to acquire knowledge of the roles of porphyrins in fundamental biochemical processes including photosynthesis and respiration.1 In more recent times it has been discovered that porphyrins and their derivatives can be successfully used in many modern technologies; for example, they can be employed as agents for increasing the efficiency of solar cells,2 charge generation materials for laser printers,3 photosensitizers for use in photodynamic therapy4 (PDT) and potential artificial blood components.5 The effectiveness of processes involving the family of porphyrins is often related to both linear and non-linear optical properties of these molecules. This paper will focus on studies of linear and non-linear optical properties of known types of chlorophylls. Most chlorophylls are based on a reduced porphyrin macrocycle called chlorin.1,6,7 Currently five types of chlorophylls are known: chlorophylls a, b, c, d and f, which display small structural differences from each other. Chlorophyll c exists in three forms (c1, c2 and c3) and it is the only known chlorophyll which is porphyrin rather than chlorin based (Fig. 1).8–10Chlorophylls participate in the most fundamental reaction for living organisms, photosynthesis.1,11 Through the production of carbohydrates and molecular oxygen, photosynthesis, directly or indirectly, supports most life on our planet. Chlorophylls form part of the photosynthetic apparatus and contribute to its stabilisation. They are collected in chloroplasts in plants, which are one of the building blocks of the photosynthetic antenna.12 They participate in the first stage of photosynthesis, so-called light reactions. Their role can be briefly described as capturing photons of light and transferring the excitation energy to nearby reaction centres in the process of Förster resonance energy transfer.13
The most abundant type of photosynthetic pigment is chlorophyll a, which was the first one isolated (in 1817) and has been the most frequently studied. Chlorophyll f, on the other hand, is a very recent discovery. It was first recognized and described in the second half of 2010.14 As a consequence, very little research has been done on this molecule.
The family of chlorophyll molecules covers most of the photosynthetically useful spectra with extremely intense absorption in the blue region – the Soret band (330–480 nm), also called the B band, and less intense red regions – Q bands (620–1050 nm).7 Such a long absorption range makes chlorophylls good systems for OPA and TPA studies with potential applications in ecophysiology, biochemistry, biophysics and also medicine. TPA studies have gained increasing importance in recent years. This is due to their wide applications in fluorescence imaging, photonics, optical data storage, and most importantly production of singlet oxygen with applications in photodynamic anticancer therapy.15–20 Anticancer photodynamic therapy is a relatively new branch of medical technology which requires a photosensitizer, light of a wavelength suitable for absorption by the photosensitizer, and molecular oxygen.21 The absorption properties of a photosensitizer are clearly very important. A PDT drug must be able to absorb in the therapeutic window, which ranges from 600 to 800 nm. Light absorption and scattering in tissue depend on the wavelength of the electromagnetic radiation. The optical window for tissue penetration lies in the range of 600–1300 nm. Its lower limit is set by principal tissue chromophores, such as melanin, haemoglobin and cytochromes, which have high absorption bands below 600 nm. The upper limit is set by the water absorption of near infrared light.22 The other important aspect is that light of a wavelength exceeding 800 nm is unable to activate the photosensitizer. Therefore the search for ideal photosensitizers concentrates on ones absorbing in the red, which possess a high tissue penetration power and are energetic enough to produce singlet oxygen. In a TPA process the electronic transition of a molecule can be thought of as the simultaneous absorption of two photons. The use of this non-linear technique in PDT has been an attractive alternative to OPA since the development of high-power femtosecond lasers.23 One of the advantages of TPA over OPA includes the fact that the population of the excited state is quadratically proportional to the incident light intensity; therefore the maximum absorption occurs at the focal point of the laser beam.24 Because of this, there is potential to provide highly targeted treatment for tumours, since excitation can be pinpointed to small volumes at the focus of a laser.17 Another advantage of TPA is the possibility to use pulses of light in the near-infrared region (750–900 nm). Because light with this wavelength penetrates tissue more deeply than visible light, PDT therapy can be more effective. Also TPA opens the possibility of excitations forbidden in OPA.25 Non-linear spectroscopy is however very challenging to study both experimentally and theoretically. There have been a few experimental studies on TPA spectroscopy of chlorophylls and other organic pigments26–30 but very few on their computational modelling.31,32 There is however much more computational research on OPA spectroscopy of chlorophylls.33–42 In 1960 the American theoretical chemist Gouterman developed a theory of metal-free porphyrin UV-Vis spectra, the so-called four-orbital model, which describes the positions and character of main electronic transitions in such systems.1,43 Later this theory was extended to porphyrins containing metal ions. According to this model, the Soret and the Q bands are the result of the electronic transitions between four orbitals, i.e., HOMO and HOMO−1 π orbitals to LUMO and LUMO+1 π* orbitals. These orbitals are centered on the porphyrin core. In a metal-containing D4h porphyrin, the LUMO and LUMO+1 π* orbitals are degenerate by symmetry, while the HOMO and HOMO−1 π orbitals are nearly degenerate. Gouterman labeled the HOMO orbitals as a1u and a2u, while LUMO orbitals were designated as egy and egx. Therefore the possible transitions between these orbitals are a1u → egy and a2u → egx, having x polarization, and a1u → egx and a2u → egx, having y polarization. The x and y polarized excited states are further mixed and split in energy by configuration interaction and form two transitions of low intensity and energy (Qx and Qy, with Qy being a lower energy transition than Qx and also of higher intensity), and two high intensity and higher energy transitions (Bx and By).1 Some recent studies of OPA of chlorophylls and similar systems will now be presented. Linnanto et al. performed studies on spectroscopic properties of a, b, c1, c2, c3, and d chlorophylls using semi-empirical ZINDO/S CIS (15,15) and PM3 CISD (5,5) methods and also the ab initio CIS (5,5)/6-31G(d) method.37Ab initio CIS(5,5) methods turned out to overestimate the transition energies of the lowest excited states of the studied chlorophylls while the obtained energies when using semi-empirical methods were very close to experiments. This is not surprising as semi-empirical methods use experimental parametrisation. The semi-empirical PM3 CISD (5,5) method had problems with predicting the oscillator strengths of studied transitions. Vokáčová and Burda used TD-DFT to study the spectroscopy of chlorophylls a, b, c1, c2, c3, and d, different bacteriochlorophylls, phycobilins and carotenoids.35 In the case of (bacterio)-chlorophylls the phytyl chain was removed from the structure and replaced by a methyl group. TD-DFT with the B3PW91 functional and the 6-31+G(d) basis set were used. The authors have obtained qualitatively good agreement with experimental spectra. The calculated values for the Qy band were blue-shifted in comparison with experimental values by about 60–80 nm and about 20–30 nm for the Qx and Soret (B) bands. The four-orbital model of Gouterman turned out to be a reasonably good approximation within TD-DFT. The main electronic transitions were based mainly on four Gouterman MOs. Other studies by the Amos group include TD-DFT, CASPT2 and SAC-CI (symmetry-adapted cluster-configuration interaction) calculations on chlorophyll a, porphyrin and two oligoporphyrins of charge transfer N-band transitions located between Q and Soret bands.38 For TD-DFT studies different functionals with a 6-31G(d) basis set were used. Due to the poor description of charge transfer processes by standard DFT functionals the authors used long-range corrected TD-CAM-B3LYP and compared the results against the current-density functional (CDFT) of van Faassen, de Boeij, van Leeuwen, Berger, and Snijders which was found to provide a good description of long-range interactions of some conjugated systems. SAOP GGA, B3LYP and BP86 functionals were also used for completeness. They have found that amongst all DFT methods used, only CAM-B3LYP properly predicts HOMO–LUMO energy gaps and the positions and character of charge transfer bands between Q and Soret bands in chlorophyll a and other systems. In general, CASPT2 results with a (16,15) active space were the most qualitatively accurate and the reason for this could be a contribution from double or higher excitations. However, this is also the most expensive method, which requires a lot of computational and chemical insight. SAC-CI and CAM-B3LYP results were found to overestimate the Q-Soret splitting but overall they were also in reasonable agreement with experimental values. Due to the large computational scaling of the SAC-CI method it was concluded that CAM-B3LYP, amongst all, is the easiest and at the same time cost-effective method, which gives applicable accuracy for systems where charge-transfer states may be of importance.
Due to the important chlorophyll applications mentioned above, understanding the interaction of light with chlorophylls is crucial. This paper will focus on studies of the OPA and TPA spectra of all known chlorophylls a–f using time-dependent response density functional theory with the CAM-B3LYP functional which was previously found to give very reliable results for OPA and TPA studies, in a wide range of systems, due to its correct asymptotic behaviour.31,44–46 Such full linear and non-linear spectroscopic studies on all known chlorophylls have not been performed to date.
Methods
Theory and computational details
Linear and quadratic density functional response theory (commonly known as Time-Dependent Density Functional Theory, TD-DFT)47 has been used to study linear and non-linear spectroscopy of chlorophylls. TD-DFT uses the stationary density and instantaneously switches on a time dependent field as a perturbation, and then determines the response of the density to the perturbation. Excitation energies are given by the poles of the linear response function, while OPA and TPA transition strengths are obtained as residues of the linear and quadratic response functions respectively. To determine the transition strength of a given state for a TPA, the first residue of the quadratic response function needs to be considered. This gives the two-photon transition tensor T (which can be written in a sum over states (SOS) formalism):0 represents the ground state, j an intermediate state and f the final state, while ωj shows the excitation frequency of the jth state, ω the frequency of the irradiating light, and μα and μβ denote the spatially dependent components of the electric dipole operator (with α and β indicating the Cartesian coordinates x, y and z). Thus, the virtual state in TPA is written as a sum over all intermediates (real eigenstates) of the system. This SOS expression is not calculated explicitly in response theory, as it calculates the TPA transition directly without constructing each state.48 Nevertheless the SOS expression is very useful for analysis. Using T one can then calculate the two-photon absorption transition strength δ, which is determined by
| δTP = FδF + GδG + HδH |
The coefficients F, G and H are based on the polarisation of the incident photons and in this paper they will be used for the conditions of parallel linearly polarised light beams; thus F = G = H = 2. Experimentally the two-photon absorption cross-sections of molecules are reported in Goeppert-Mayer (GM) units, where 1 GM equals 10−50 cm4 s photon−1 molecule−1. However, in this work the TPA cross-sections (here directly transition strengths) are shown in atomic units.48
The structure of chlorophyll a found in the Chemical Entities of Biological Interest (ChEBI) database was chosen for initial studies.49 The influence of the phytyl tail on spectroscopic properties of chlorophyll a was examined and found to be minimal and so for further studies it was replaced with a methyl group to reduce the computational cost. This is presented in Fig. S1 of ESI.† Other conformers of chlorophyll a with a methyl instead of a phytyl tail were built based on the ChEBI structure and their total free energies were compared. Similarly conformers of other chlorophylls were built by changing appropriate ligands as shown in Fig. 1. The effect of the basis set on the (geometrical) structure of a simple chlorophyll model was examined using 6-31G(d), cc-pVDZ, cc-pVTZ, and aug-cc-pVDZ basis sets, and on the spectral properties using 6-31G(d), cc-pVDZ, and cc-pVTZ basis sets, and it was found to be of minor importance. Thus for our studies the 6-31G(d) basis set was used as a cost-effective choice. The influence of different DFT functionals on the structure of the same chlorophyll model gave only minimal changes in bond lengths (∼0.01–0.02 Å) and angles (<1°). The geometries of all studied chlorophylls a–f and their conformers were optimised using the CAM-B3LYP functional and the 6-31G(d) basis set. The structures of each chlorophyll having the lowest total free energy were chosen for further spectroscopic studies. The effect of the DFT functional on the spectroscopic features of chlorophyll a was examined using B3PW91, B3LYP, CAM-B3LYP, and BP86. These results are presented in ESI Fig. S2 and S3.† The qualitative spectral features of chlorophyll a calculated with these functionals are very similar. The positions of the Q bands with B3PW91, B3LYP and CAM-B3LYP were almost identical, and only differed slightly in intensity. An approximately 20 nm red-shift was observed for BP86 compared to other functionals. The positions of the B bands slightly differ between the different functionals used, with the CAM-B3LYP obtained B band being the most blue-shifted compared to experiments and BP86 the least. As mentioned in the introduction the CAM-B3LYP functional is known to properly describe the HOMO–LUMO energy gaps, positions and character of charge transfer bands between Q and B bands in such systems; thus TD-CAM-B3LYP with the 6-31G(d) basis set was used for further study of OPA spectra. In the computed spectra two different phenomenological broadening factors were considered. A 20 nm Gaussian broadening factor was chosen to compare the computed spectra with the experimental ones. The stick spectrum, produced by applying the broadening factor of 0.5 nm, was generated in order to illustrate the electronic transitions. The effect of solvents on spectra was examined using the SMD model50 with diethyl ether as a solvent for chlorophylls a–d and methanol for chlorophyll f for better comparison of calculated UV-Vis spectra with experiments. The first 15 excited states were considered for both OPA and TPA spectroscopic properties of all studied chlorophylls. The Gaussian 09c program was used for all geometry optimisations and OPA calculations, whereas TPA CAM-B3LYP studies were performed using the Dalton 2011 program.
Results and discussion
One-photon absorption (OPA)
Experimental and theoretical bands in the gas phase have been plotted against each other in order to determine systematic shifts for these types of systems. A reasonably systematic correlation between theory and experiment of the spectral features is achieved here; this is presented in Fig. S4 of ESI.† All theoretical spectra are systematically blue-shifted compared to the experimental ones. Table 1 presents the main calculated OPA transitions in the gas phase and in the solution as well as spectral bands determined experimentally. Fig. S5–S7 in ESI† present a visual comparison of theoretical and experimental spectra for chlorophylls a, b and f. The calculated spectra of all studied chlorophylls compare qualitatively with experimental studies. Three main spectroscopic bands Qy, Qx and B have been localised. The intensity of the calculated Soret band B, as experimentally expected, is much larger than the intensity of Q bands; also the Qy band is more intense than the Qx band. The generated pictures of the OPA spectra in the gas phase and the character of main transitions involved in these bands are also presented in Table 1. A more detailed analysis of single-particle hole transitions is presented in Fig. S8–S14 of ESI.† As mentioned above it is evident that all peaks in the computed spectra are blue-shifted in comparison with the experimental spectrum. There is a blue shift of around 90 nm to 110 nm for Qy bands of chlorophylls a, b and f. The smallest blue shift here for Qy bands of around 90 nm is observed for chlorophyll a and the biggest for chlorophyll f, 110 nm. For Qx bands of these systems, the smallest blue shift is observed for chlorophyll a (around 80 nm) and the largest blue shift is observed for chlorophyll f (around 140 nm). Chlorophylls c1, c2, c3 and d show around 60–70 nm blue shift for Qy bands and 25–40 nm blue shift for Qx bands, which is in better agreement with experimental studies. All the chlorophylls studied show a blue shift of around 70–80 nm for the Soret B bands. Since it has been reported that the presence of the solvent shifts porphyrin spectra to the red region,51 the difference in position of the computed and experimental peaks could be attributed to this phenomenon. Looking at the spectral bands calculated using the SMD solvent model50 with an appropriate solvent, it could be noticed that indeed this is the case. Including a solvent in the calculation moves the position of the peaks to the red region of around 5–20 nm for Q and B bands of all chlorophylls.| Method | TD-CAM-B3LYP (gas phase)a | TD-CAM-B3LYP (SMD model) | Experimentb |
|---|---|---|---|
| a TD-CAM-B3LYP computed spectra in the gas phase with two different Gaussian broadening factors of 20 and 0.5 nm, the character of main transitions, and their contribution in % for canonical orbitals or 1-particle transition density matrix eigenvalues for natural transition orbitals (NTOs). b Experimental bands for chlorophylls a–d recorded in diethyl ether solvent7 and chlorophyll f in methanol.14 | |||
| Chlorophyll a | |||

|
|||
| λ [nm] Qy | 570 | 581 | 662 |
| Osc. str. | 0.2281 | 0.3243 | — |
| λ [nm] Qx | 484 | 488 | 578 |
| Osc. str. | 0.0273 | 0.0602 | — |
| λ [nm] B | 355 | 370 | 430 |
| Osc. str. | 0.9272 | 1.1871 | — |
| 337 | 345 | ||
| 0.2517 | 0.7728 | ||
| 331 | 341 | ||
| 0.8331 | 0.4852 | ||
| Chlorophyll b | |||

|
|||
| λ [nm] Qy | 545 | 552 | 644 |
| Osc. str. | 0.1456 | 0.2045 | — |
| λ [nm] Qx | 472 | 475 | 549 |
| Osc. str. | 0.0062 | 0.0127 | — |
| λ [nm] B | 371 | 390 | 455 |
| Osc. str. | 0.9995 | 1.3133 | — |
| 355 | 369 | ||
| 0.8721 | 0.9854 | ||
| Chlorophyll c1 | |||
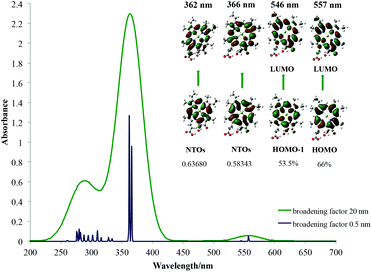
|
|||
| λ [nm] Qy | 557 | 562 | 628 |
| Osc. str. | 0.0538 | 0.0827 | — |
| λ [nm] Qx | 546 | 549 | 578 |
| Osc. str. | 0.0011 | 0.0024 | — |
| λ [nm] B | 366 | 384 | 444 |
| Osc. str. | 1.0082 | 1.4998 | — |
| 362 | 381 | ||
| 1.2758 | 1.3679 | ||
| Chlorophyll c2 | |||

|
|||
| λ [nm] Qy | 562 | 566 | 628 |
| Osc. str. | 0.0284 | 0.0421 | — |
| λ [nm] Qx | 552 | 556 | 579 |
| Osc. str. | 0.0029 | 0.0016 | — |
| λ [nm] B | 375 | 392 | 448 |
| Osc. str. | 0.9328 | 1.366 | — |
| 370 | 390 | ||
| 1.1987 | 1.411 | ||
| Chlorophyll c3 | |||

|
|||
| λ [nm] Qy | 559 | 562 | 626 |
| Osc. str. | 0.0035 | 0.0019 | — |
| λ [nm] Qx | 552 | 555 | 586 |
| Osc. str. | 0.0279 | 0.0402 | — |
| λ [nm] B | 380 | 397 | 452 |
| Osc. str. | 0.9088 | 1.4682 | — |
| 377 | 396 | ||
| 1.3752 | 1.3897 | ||
| Chlorophyll d | |||
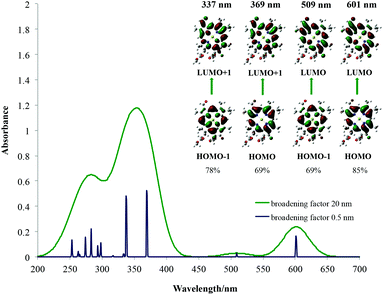
|
|||
| λ [nm] Qy | 601 | 616 | 668 |
| Osc. Str. | 0.2383 | 0.3302 | — |
| λ [nm] Qx | 509 | 516 | — |
| Osc. str. | 0.0296 | 0.058 | — |
| λ [nm] B | 369 | 386 | 447 |
| Osc. str. | 0.8243 | 1.0409 | — |
| 342 | 349 | ||
| 0.0004 | 0.9564 | ||
| 337 | |||
| 0.7563 | |||
| Chlorophyll f | |||

|
|||
| λ [nm] Qy | 600 | 620 | 712 |
| Osc. str. | 0.2801 | 0.4228 | — |
| λ [nm] Qx | 511 | 518 | 654 |
| Osc. str. | 0.0413 | 0.0965 | — |
| λ [nm] B | 363 | 375 | 444 |
| Osc. str. | 0.7866 | 0.9062 | — |
| 345 | 346 | 408 | |
| 0.0579 | 1.1823 | — | |
| 338 | |||
| 0.1443 | |||
| 337 | |||
| 0.7992 | |||
The average red shift for Qx bands here of around 5 nm is observed for chlorophylls a–c3 and f. The smallest influence of the solvent on the Qy bands is observed for chlorophyll c3 (3 nm) and the largest for chlorophyll f (20 nm). The chemical nature of the main spectroscopic bands has been shown in the right part of each spectrum and is determined by studying the canonical Kohn–Sham orbitals that take part in the main electronic transitions present. From this it can be seen that the two main transitions in the Soret band as well as transitions in the Qy and Qx bands are all between the frontier molecular orbitals located on the chlorophyll core, as predicted by Gouterman. Due to some orbital mixing present for chlorophylls c1, c2 and c3, natural transition orbitals (NTOs)52 were used to determine their main excitations, which in the end also resembled Gouterman orbitals. For the Soret band of chlorophyll a it has been noticed that the HOMO−2 orbital becomes significant and for chlorophyll b, the LUMO+2 orbital. This has already been seen for spectroscopy of porphycene core based systems and may imply that the Gouterman model should be treated with caution when discussing Soret bands of these systems.45,53 No charge transfer transitions have been observed. In Table 1 only the largest contributions to transitions have been shown. A detailed analysis of the spectral character of the studied chlorophylls is presented in ESI Fig. S8–S14.† From these results it can be concluded that calculated spectra are qualitatively very well comparable with experimental ones and can be used to help rationalise and assign experimental spectra of porphyrins and derivatives based on general trends, although quantitative spectral data are still problematic with TD-DFT.
Two-photon absorption (TPA)
TPA calculations were conducted for the first fifteen excited states of each chlorophyll using the CAM-B3LYP functional with a 6-31G(d) basis set in the gas phase. It has been shown before that this method gives reliable results for TPA spectroscopic properties of porphyrin systems compared with experimental studies.44 TPA computed results for chlorophylls a, b, d and f are presented in Table 2 and for chlorophylls c1, c2 and c3 in Table 3. Since in TPA both photons are absorbed simultaneously (in this case two equal energy photons, i.e., resonant absorption), the photon wavelength is twice the wavelength presented (i.e., at the eigenstate energy). Some of the large numbers of TPA transition strengths for some excitations in chlorophyll molecules can be explained by the so-called resonance enhancement effect.44,54 The intensity of the absorption depends on the position of the virtual state (i.e., at half the excitation energy for two equal photons being absorbed). The phenomenon can be explained using the sum-over-states expression mentioned in the theory section. Thus, the virtual state is written as a linear combination of all real eigenstates of the molecule. If the frequency of light is close to the frequency between the initial state and a real eigenstate, then the denominator will cause the transition moment to tend to infinity. Therefore, the species with potentially very large δ will have the TPA absorption maxima equal to or very close to half of the wavelength of Qy in OPA.| Chlorophyll a | Chlorophyll b | ||
|---|---|---|---|
| λ [nm] | δ [a.u.] | λ [nm] | δ [a.u.] |
| 571 | 519 | 544 | 760 |
| 484 | 3220 | 473 | 3560 |
| 334 | 9080 | 371 | 4230 |
| 337 | 5850 | 355 | 460 |
| 332 | 676 | 341 | 2020 |
| 327 | 14.1 | 330 | 1.99 |
| 322 | 1460 | 323 | 3.04 |
| 299 | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
308 | 1160 |
| 279 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
287 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
| 275 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410 410![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
272 | 3.62 × 1011 |
| 262 | 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
271 | 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 259 | 241![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
266 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 580 580![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 247 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
263 | 306![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 246 | 188![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
257 | 7780 |
| 240 | 303![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
257 | 8620 |
| Chlorophyll d | Chlorophyll f | ||
|---|---|---|---|
| λ [nm] | δ [a.u.] | λ [nm] | δ [a.u.] |
| 602 | 473 | 599 | 478 |
| 508 | 3170 | 510 | 2820 |
| 369 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
364 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
| 342 | 1.78 | 345 | 2120 |
| 338 | 1500 | 339 | 295 |
| 334 | 49.9 | 337 | 3040 |
| 333 | 4030 | 330 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
| 316 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
323 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
| 298 | 179![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
305 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 293 | 9500 | 297 | 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 283 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050 050![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
287 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 480![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 274 | 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
286 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
| 263 | 148![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
271 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
| 253 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280 280![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
254 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 251 | 576![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
252 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 750![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Chlorophyll c1 | Chlorophyll c2 | Chlorophyll c3 | |||
|---|---|---|---|---|---|
| λ [nm] | δ [a.u.] | λ [nm] | δ [a.u.] | λ [nm] | δ [a.u.] |
| 558 | 191 | 561 | 202 | 558 | 47.2 |
| 546 | 148 | 554 | 256 | 551 | 457 |
| 366 | 230 | 376 | 305 | 379 | 282 |
| 363 | 439 | 370 | 269 | 377 | 243 |
| 333 | 828 | 335 | 325 | 337 | 1890 |
| 329 | 93.8 | 331 | 185 | 331 | 536 |
| 316 | 247 | 329 | 188 | 329 | 338 |
| 310 | 2050 | 325 | 1810 | 313 | 2440 |
| 302 | 951 | 309 | 3770 | 307 | 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
| 294 | 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
303 | 6480 | 300 | 2950 |
| 288 | 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
295 | 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
297 | 4320 |
| 282 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
290 | 8680 | 296 | 4790 |
| 280 | 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460 460![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
286 | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
280 | 571![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 277 | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280 280![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
284 | 259![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
276 | 6.5 × 1012 |
| 253 | 9030 | 263 | 4770 | 274 | 914![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
Problems of standard molecular response theory can occur near the resonance region Soret because the excited states have infinite lifetimes when standard molecular functions are derived.55 Thus, damped response theory methods have been developed to sort out this problem, which remove the singularities of the response functions at the resonance frequencies.55,56 Even without using damped response theory, standard methods inform that there will be very large TPA cross-sections in certain chlorophylls due to accidental degeneracy between Soret and Q states (Table 4). Thus for example each chlorophyll has states in the Soret region with very large TPA cross-sections but these are shifted relative to each other by the specific nature of the chlorophyll. This is similar to what is observed with electronic fine tuning of macrocyclic cores.46 Also of interest here is the significant TPA in the Q region itself; although orders of magnitude less than the resonance enhanced Soret TPA, it is still intense enough to be of interest in PDT as discussed above.
| System | Q region in OPA [nm] | Soret region in TPA [nm] |
|---|---|---|
| Chlorophyll a | 570 | 275 |
| Chlorophyll b | 545 | 272 |
| Chlorophyll c1 | 557 | 280 |
| Chlorophyll c2 | 562 | 284 |
| Chlorophyll c3 | 559 | 276 |
| Chlorophyll d | 601 | 298 |
| 509 | 253 | |
| Chlorophyll f | 600 | 297 |
| 511 | 254 |
Conclusions
Theoretical OPA and TPA spectra of chlorophylls were calculated using the TD-CAM-B3LYP functional with the 6-31G(d) basis set. It has been shown that this method to a good approximation describes the structural and spectroscopic properties of chlorophylls at a reasonable computational cost. Calculated OPA spectra were in good qualitative agreement with their experimental equivalents and the electronic transitions were studied in a more in-depth manner by examining the nature of the orbitals involved in the transitions. The positions of linear electronic transition bands are blue-shifted in comparison to experiments but their relative intensities and chemical nature modelled quite well experimental findings. In general the Gouterman four-orbital model, which is frequently used to determine the character of main electronic transitions in porphyrins and similar systems, turned out to be a good approximation for the red-region of the chlorophyll spectra. However, it has been found that for the Soret bands of some chlorophylls, some crucial electronic contributions from higher lying orbitals are missing; thus, this model needs to be treated with caution when used for such systems. Using a solvent model, specifically the SMD model, in the calculation of the OPA spectroscopic properties had only a small red-shift effect. A more advanced model could be used, treating the solvent with discrete molecules in the first solvation sphere, using for example a QM/MM approach, which can be a perspective for future studies. It would be interesting to see whether a better solvent model caused a larger red-shift closer to absolute experimental values. The maximum TPA absorption values of calculated chlorophylls are between 550 and 600 nm, showing large transition strengths; all studied chlorophylls could be potential candidates for use in photodynamic therapy. Also of interest here would be comparing Q band TPA with resonance enhanced Soret TPA. Engineering of new systems based on chlorophylls d and f, which look especially promising because their spectra are the most red-shifted amongst all chlorophylls, may be important for future TPA studies in the context of phototherapy. Other important areas of further research could include the spectroscopy of chlorophyll dimers and larger aggregates and examination of how their spectra differ from those of single molecules. That research would be especially beneficial for PDT, as the concentration of the photosensitizer often has to be quite high to use this form of treatment effectively.Acknowledgements
We thank the European Research Council (ERC) for funding under the European Union's Seventh Framework Programme (FP7/2007-2013)/ERC Grant no. 258990, and the EPSRC for funding through grant EP/J006602.Notes and references
- L. R. Milgrom, The colours of life: An introduction to the Chemistry of Porphyrins and Related Compounds, Oxford University Press, Oxford, New York, 1997, p. VI Search PubMed.
- A. J. Mozer, M. J. Griffith, G. Tsekouras, P. Wagner, G. G. Wallace, S. Mori, K. Sunahara, M. Miyashita, J. C. Earles, K. C. Gordon, L. C. Du, R. Katoh, A. Furube and D. L. Officer, J. Am. Chem. Soc., 2009, 131(43), 15621 CrossRef CAS PubMed.
- D. Wöhrle, G. Schnurpfeil, S. G. Makarov, A. Kazarin and O. N. Suvorova, Macroheterocycles, 2012, 5(3), 191 CrossRef.
- E. D. Sternberg, D. Dolphin and C. Bruckner, Tetrahedron, 1998, 54(17), 4151 CrossRef CAS.
- L. J. Twyman and Y. Ge, Chem. Commun., 2006,(15), 1658 RSC.
- K. M. Kadish, K. M. Smith and R. Guilard, Chlorophylls and Bilins: Biosynthesis, Synthesis, and Degradation, in The Porphyrin Handbook, Academic Press, San Diego, 2000, vol. 13 Search PubMed.
- H. Scheer, Chapter 3 Chlorophylls, in Primary Processes of Photosynthesis, Part 1: Principles and Apparatus, The Royal Society of Chemistry, 2008, vol. 8, p. 101 Search PubMed.
- R. C. Dougherty, H. H. Strain, W. A. Svec, R. A. Uphaus and J. J. Katz, J. Am. Chem. Soc., 1966, 88(21), 5037 CrossRef CAS.
- C. J. R. Fookes and S. W. Jeffrey, J. Chem. Soc., Chem. Commun., 1989, 1827 RSC.
- N. Withers and F. T. Haxo, Plant Sci. Lett., 1975, 5(1), 7 CrossRef CAS.
- M. D. Archer and J. Barber, Molecular to Global Photosynthesis, Imperial College Press, River Edge, NJ, 2004 Search PubMed.
- B. R. Green and W. W. Parson, Light-harvesting antennas in photosynthesis, Kluwer Academic, Dordrecht, Boston, 2003, p. xx Search PubMed.
- V. L. Gunderson, T. M. Wilson and M. R. Wasielewski, J. Phys. Chem. C, 2009, 113(27), 11936 CAS.
- M. Chen, M. Schliep, R. D. Willows, Z. L. Cai, B. A. Neilan and H. Scheer, Science, 2010, 329(5997), 1318 CrossRef CAS PubMed.
- D. A. Parthenopoulos and P. M. Rentzepis, Science, 1989, 245(4920), 843 CAS.
- Q. D. Zheng, G. X. Xu and P. N. Prasad, Chem.–Eur. J., 2008, 14(19), 5812 CrossRef CAS PubMed.
- K. Ogawa and Y. Kobuke, Org. Biomol. Chem., 2009, 7(11), 2241 CAS.
- P. D. Zhao, P. Chen, G. Q. Tang, J. W. Liu, L. Lin, P. Guo, Q. Yu, J. Yao, D. M. Ma, G. L. Zhang and W. Chen, Sci. China, Ser. B, 2008, 51(6), 529 CrossRef CAS.
- G. S. He, L.-S. Tan, Q. Zheng and P. N. Prasad, Chem. Rev., 2008, 108(4), 1245 CrossRef CAS PubMed.
- L. Copley, P. van der Watt, K. W. Wirtz, M. I. Parker and V. D. Leaner, Int. J. Biochem. Cell Biol., 2008, 40(2), 227 CrossRef CAS PubMed.
- M. C. DeRosa and R. J. Crutchley, Coord. Chem. Rev., 2002, 233, 351 CrossRef.
- B. Fuchs, H.-P. Berlien and C. M. Philipp, The Laser's Position in Medicine, in Applied Laser Medicine, ed. H.-P. Berlien and G. J. Müller, Springer-Verlag, Berlin, Heidelberg, New York, 2003 Search PubMed.
- D. Meshulach and Y. Silberberg, Nature, 1998, 396(6708), 239 CrossRef CAS PubMed.
- K. D. Belfield, K. J. Schafer, Y. U. Liu, J. Liu, X. B. Ren and E. W. Van Stryland, J. Phys. Org. Chem., 2000, 13(12), 837 CrossRef CAS.
- P. W. Atkins, J. De Paula and R. Friedman, Quanta, Matter, and Change: A molecular approach to Physical Chemistry, Oxford University Press, Oxford, New York, 2009, p. xxi Search PubMed.
- D. Leupold, K. Teuchner, J. Ehlert, K. D. Irrgang, G. Renger and H. Lokstein, Biophys. J., 2002, 82(3), 1580 CrossRef CAS.
- J. Zimmermann, P. A. Linden, H. M. Vaswani, R. G. Hiller and G. R. Fleming, J. Phys. Chem. B, 2002, 106(36), 9418 CrossRef CAS.
- P. A. Linden, J. Zimmermann, T. Brixner, N. E. Holt, H. M. Vaswani, R. G. Hiller and G. R. Fleming, J. Phys. Chem. B, 2004, 108(29), 10340 CrossRef CAS.
- Y. Zeng, Y. Wu, D. Li, W. Zheng, W. X. Wang and J. N. Y. Qu, Planta, 2012, 236(5), 1653 CrossRef CAS PubMed.
- S. Shima, R. P. Ilagan, N. Gillespie, B. J. Sommer, R. G. Hiller, F. P. Sharples, H. A. Frank and R. R. Birge, J. Phys. Chem. A, 2003, 107(40), 8052 CrossRef CAS.
- M. G. Vivas, D. L. Silva, L. de Boni, R. Zalesny, W. Bartkowiak and C. R. Mendonca, J. Appl. Phys., 2011, 109(10), 103529 CrossRef.
- K. Susumu, J. A. N. Fisher, J. R. Zheng, D. N. Beratan, A. G. Yodh and M. J. Therien, J. Phys. Chem. A, 2011, 115(22), 5525 CrossRef CAS PubMed.
- C. Konig and J. Neugebauer, Phys. Chem. Chem. Phys., 2011, 13(22), 10475 RSC.
- D. Sundholm, Chem. Phys. Lett., 1999, 302(5–6), 480 CrossRef CAS.
- Z. Vokáčová and J. V. Burda, J. Phys. Chem. A, 2007, 111(26), 5864 CrossRef PubMed.
- L. L. Shipman, T. M. Cotton, J. R. Norris and J. J. Katz, J. Am. Chem. Soc., 1976, 98(25), 8222 CrossRef CAS.
- J. Linnanto and J. Korppi-Tommola, Phys. Chem. Chem. Phys., 2000, 2(21), 4962 RSC.
- Z. L. Cai, M. J. Crossley, J. R. Reimers, R. Kobayashi and R. D. Amos, J. Phys. Chem. B, 2006, 110(31), 15624 CrossRef CAS PubMed.
- M. Alvarado-Gonzalez, N. Flores-Holguin and D. Glossman-Mitnik, Int. J. Photoenergy, 2013, 424620 CAS.
- Y. Li, Z.-L. Cai and M. Chen, J. Phys. Chem. B, 2013, 117(38), 11309 CrossRef CAS PubMed.
- J. Linnanto and J. Korppi-Tommola, J. Phys. Chem. A, 2001, 105(15), 3855 CrossRef CAS.
- G. Zucchelli, R. C. Jennings, F. M. Garlaschi, G. Cinque, R. Bassi and O. Cremonesi, Biophys. J., 2002, 82(1), 378 CrossRef CAS.
- M. Gouterman, J. Mol. Spectrosc., 1961, 6, 138 CrossRef CAS.
- J. Arnbjerg, A. Jimenez-Banzo, M. J. Paterson, S. Nonell, J. I. Borrell, O. Christiansen and P. R. Ogilby, J. Am. Chem. Soc., 2007, 129(16), 5188 CrossRef CAS PubMed.
- L. T. Bergendahl and M. J. Paterson, J. Phys. Chem. B, 2012, 116(39), 11818 CrossRef CAS PubMed.
- L. T. Bergendahl and M. J. Paterson, RSC Adv., 2013, 3(24), 9247 RSC.
- M. E. Casida, Recent Advances in Density Functional Methods, Part I, World Scientific, Singapore, 1995 Search PubMed.
- T. D. Poulsen, P. K. Frederiksen, M. Jorgensen, K. V. Mikkelsen and P. R. Ogilby, J. Phys. Chem. A, 2001, 105(51), 11488 CrossRef CAS.
- http://www.ebi.ac.uk/chebi .
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113(18), 6378 CrossRef CAS PubMed.
- M. Sankar, C. Arunkumar and P. Bhyrappa, J. Porphyrins Phthalocyanines, 2004, 08(12), 1343 CrossRef CAS.
- R. L. Martin, J. Chem. Phys., 2003, 118(11), 4775 CrossRef CAS.
- J.-y. Hasegawa, K. Takata, T. Miyahara, S. Neya, M. J. Frisch and H. Nakatsuji, J. Phys. Chem. A, 2005, 109(14), 3187 CrossRef CAS PubMed.
- M. Drobizhev, Y. Stepanenko, Y. Dzenis, A. Karotki, A. Rebane, P. N. Taylor and H. L. Anderson, J. Am. Chem. Soc., 2004, 126(47), 15352 CrossRef CAS PubMed.
- K. Kristensen, J. Kauczor, T. Kjaergaard and P. Jorgensen, J. Chem. Phys., 2009, 131(4), 044112 CrossRef PubMed.
- P. Norman, Phys. Chem. Chem. Phys., 2011, 13(46), 20519 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: The effect of phytyl tail presence on one-photon absorption spectra of chlorophyll a; TD-DFT functional comparison; comparison with experimental spectra; detailed transition analysis; Cartesian coordinates for all species studied. See DOI: 10.1039/c3pp50262g |
| This journal is © The Royal Society of Chemistry and Owner Societies 2014 |