Effect of 1O2 quencher depletion on the efficiency of photodynamic therapy
Mark A.
Weston
*ab and
Michael S.
Patterson
ab
aDepartment of Medical Physics and Applied Radiation Sciences, McMaster University, 1280 Main Street West, Hamilton, Ontario, Canada L8S 4K1. E-mail: mark.weston@jcc.hhsc.ca
bDepartment of Medical Physics, Juravinski Cancer Centre, 699 Concession Street, Hamilton, Ontario, Canada L8 V 5C2
First published on 2nd December 2013
Abstract
Al(III) phthalocyanine chloride tetrasulfonic acid (AlPcS4) fluorescence and photodynamic oxygen consumption were monitored during AlPcS4-photodynamic therapy (PDT) of Mat LyLu cells in suspension. These measurements were used to calculate the PDT efficiency, which is defined as the oxygen consumption rate divided by the sensitizer concentration. As a function of the intracellular oxygen concentration consumed by PDT, the normalized PDT efficiency fell off more quickly at lower photosensitizer concentrations. The changes in PDT efficiency were compared to models of PDT in which the photosensitizer (PS) and singlet oxygen quencher (A) were either free to diffuse or were fixed. The model in which PS and A are free to diffuse did not agree with the experimental data because this model predicts that the reduction in PDT efficiency is independent of [PS]. A Monte Carlo model was written to simulate PDT when both PS and A are stationary. This model was found to describe the experimental data when the initial intracellular [A] = 90 mM and when the initial and final (i.e. after all A has been depleted) singlet oxygen lifetimes were 0.4 and 1.2 μs respectively.
Introduction
Singlet oxygen (1O2) generated during photodynamic therapy (PDT) is the primary agent responsible for biological damage.1–4 As a consequence, the objective of modern PDT dosimetry is to monitor the [1O2] generated during the treatment.5,6 In principle, this can be accomplished using explicit,7 implicit8 or direct9 methods.6 Although many in vitro and pre-clinical studies have investigated each of these techniques,10–13 relatively little clinical work has been reported. Continued understanding and refinement of these techniques is required if PDT is to become a more useful and widespread treatment.14For each of the aforementioned dosimetry techniques it is usually assumed that all of the 1O2 generated is consumed in reactions with 1O2 quenchers (A). This assumption is based on the short 1O2 lifetimes (τΔ) (in comparison to τΔ in water) that have been calculated or measured both in vitro and in vivo (0.01 to 0.6 μs).8,9,15,16 In addition, it is also implicitly assumed that [A] is much larger then the cumulative [1O2] generated during the PDT treatment so that depletion of A does not significantly alter the reaction kinetics (i.e. [A] remains constant).17–19
Recent work by Hackbarth and colleagues20,21 has shown that τΔ increases during PDT as biological targets are consumed. The lifetime increased rapidly and reached a stable value during experiments in which large amounts of [1O2] were generated. The depletion of A and the increase in τΔ imply that a larger fraction of the 1O2 generated during the treatment is physically quenched. Since the biological damage invoked by PDT is caused by the reaction of 1O2 with A, an increase in physical quenching results in a less efficient treatment. Consequently PDT dosimetry may be overestimating the [1O2] that actually reacts with biological targets. The significance of this overestimation depends on the initial fraction of 1O2 that reacts within the cell. For example, if at the start of treatment 99% of the singlet oxygen generated reacts within the cell, then an increase in lifetime by a factor of 3 would only reduce this fraction to 97%.
The objective of this study is to estimate the total concentration of singlet oxygen quenchers ([A]0) in Mat-LyLu (MLL) cells and to monitor changes in PDT efficiency during PDT with Al(III) phthalocyanine chloride tetrasulfonic acid (AlPcS4). PDT efficiency is defined as the PDT induced oxygen consumption rate divided by the sensitizer concentration. In this study PDT efficiency was monitored by measuring both the ground state oxygen (3O2) consumption rate and AlPcS4 fluorescence during AlPcS4-PDT of MLL cells in suspension. AlPcS4 was chosen because its photostability22,23 makes it possible to generate large [1O2] at low [PS]. Sensitizers such as BPD-MA, HPPH, mTHPC, ALA-PpIX, and Photofrin photobleach rapidly during PDT8,10,13,19,24 thereby limiting the cumulative [1O2] that can be produced. In addition, AlPcS4 has a large fluorescence yield23 which makes it easy to differentiate from background autofluorescence.
When all the 1O2 quenchers within the cells have been depleted, the photodynamic consumption of oxygen should stop and 1O2 will only be physically quenched. At this point the total [3O2] consumed by PDT is equal to [A]0. Since complete quencher depletion was not attained in this study, the experimental data were compared to 2 simple models of PDT in an attempt to estimate [A]0. In the first model it is assumed that both A and the photosensitizer (PS) are free to diffuse within the cell, while in the second model they are stationary and only 1O2 can diffuse. For the free diffusion model an analytical solution was derived in which the normalized (to the initial value) PDT efficiency is independent of [PS]. For the stationary (bound) model a Monte Carlo simulation was used to study the spatially dependent consumption of A around a single PS molecule.
Theory
A summary of symbols and constants used throughout the paper can be found in Table 1.| Symbol | Definition | Units |
|---|---|---|
| [3O2] | Concentration of ground state oxygen | M |
| [1O2] | Concentration of singlet oxygen | M |
| [PS] | Concentration of photosensitizer | M |
| [T1] | Concentration of triplet excited-state photosensitizer | M |
| [A] | Concentration of 1O2 quencher | M |
| k ot | Bimolecular rate constant for the reaction between 3O2 and T1 | M−1 s−1 |
| k oa | Bimolecular rate constant for the reaction between 1O2 and A | M−1 s−1 |
| k d | Rate constant for the decay of 1O2 to 3O2 | s−1 |
| S Δ | Fraction of T1–3O2 interactions that yield 1O2 | |
| D cell | Diffusion coefficient of oxygen in cells | m2 s−1 |
| D water | Diffusion coefficient of oxygen in water | m2 s−1 |
| τ Δ | 1O2 lifetime | s |
Model 1: free diffusion model
In the first model PS, A, and 1O2 are able to diffuse freely through the cell. This assumption is implicit in most theoretical treatments of PDT reported in the literature.5,25–27 Under this assumption, the differential equations describing [A] and [1O2] are shown in eqn (1) and (2) respectively.5,25–27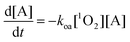 | (1) |
 | (2) |
Since the generation and de-excitation of 1O2 is rapid, [1O2] quickly approaches the steady state shown in eqn (3).
 | (3) |
 | (4) |
Under well oxygenated conditions (where C/[PS] is constant) normalizing eqn (4) to the initial PDT efficiency yields eqn (5).
 | (5) |
Therefore, under well oxygenated conditions the normalized rate of [A] depletion or, equivalently, the normalized rate of [3O2] depletion, is independent of [PS]. Furthermore, the parameters which dictate PDT efficiency are kd, koa, and [A]. Assuming that kd and koa are constant during the treatment, the efficiency of the treatment will depend on [A] and should be reduced as A is consumed. For example, if [A] = 90 mM the changes in normalized PDT efficiency as a function of [A] depleted for several different kd(koa)−1 is shown in Fig. 1.
 | ||
| Fig. 1 Normalized PDT efficiency as a function of depleted [A] for a model in which both PS and A freely diffuse. Plots were calculated using eqn (5) for [A]0 = 90 mM and for different values of kd/koa. | ||
Model 2. Stationary model
In the second model the photosensitizer and quenchers are fixed to intracellular structures and only 1O2 is able to diffuse. Under these circumstances a simple analytic solution describing the normalized rate of quencher depletion (similar to eqn (5)) cannot be derived. As an alternative, a Monte Carlo program was written to simulate three dimensional 1O2 diffusion and reaction. In the model the 1O2 molecule starts in the centre of a cubic lattice where a PS molecule is located. The physical dimensions of the lattice depend on the photosensitizer concentration ([PS]) and a quencher molecule is located at each lattice node. Hence the total number of nodes in the lattice is [A]/[PS]. Only [A] and [PS] combinations which yield odd value integer lattice dimensions (lattice dimensions = ([A]/[PS])1/3) can be simulated in this simple representation. The 1O2 molecule moves in discrete steps in the positive or negative x, y, or z directions. The length of this step (Δd) is equal to the average initial quencher separation, which is shown in eqn (6). | (6) |
The direction that the 1O2 molecule moves during each time step is chosen using a random number.
The time required to travel Δd will be denoted as Δt and is shown in eqn (7).
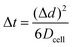 | (7) |
The probability that 1O2 undergoes physical or chemical quenching after each time interval was calculated using 1O2 lifetimes reported by Hackbarth et al. In experiments with several different cell lines and photosensitizers, Hackbarth et al. showed that 1O2 lifetime varies from about 0.3 to 0.5 μs at the start of treatment (τΔ(start)) to between 1 and 1.6 μs at the end of treatment (τΔ(end)).20,21 For simplicity we assume that τΔ(start) and τΔ(end) are equal to 0.4 and 1.2 μs respectively. As previously discussed, after a rapid increase in τΔ Hackbarth et al. observed that the lifetime remains stable during long exposures. In our model we assume that this final lifetime corresponds to physical quenching only (i.e. all the 1O2 quenchers have been consumed).20,21 Hence, the probability of a 1O2 molecule undergoing physical quenching after a time step of Δt is equal to 1 − exp(−Δt/τend). For example, if [A] and Dcell are equal to 90 mM and 1.6 × 10−10 m2 s−1 respectively then Δd and Δt are approximately 2.6 nm and 7.3 ns respectively. The probability that the 1O2 molecule will be physically quenched after 1 time step (7.3 ns for this example) is approximately 6 × 10−3.
Given the assumed values of τΔ(start) and τΔ(end), the probability that a 1O2 molecule undergoes chemical quenching (i.e. reacts with A) is twice the probability of physical quenching. If 1O2 has been chemically quenched, the quencher is removed from the system (i.e. all subsequent 1O2 molecules that arrive at this node cannot be chemically quenched). The outcome after each time interval (no quenching, chemical quenching (if a quencher was at the node), or physical quenching) was determined using a random number.
During the simulation it is possible for the 1O2 molecule to diffuse to the boundary of the lattice. In this case there is a chance that the next time step takes the molecule into the “domain” of the adjacent photosensitizer molecule. In this case the molecule is positioned at the opposite side of the unit cell. For example, if the lattice extends from x = −10 to x = 10 and the next step is from x = 10 to x = 11, the position is set to x = −9.
Materials and methods
Drug preparation
Al(III) phthalocyanine chloride tetrasulfonic acid (AlPcS4) was purchased from Frontier Scientific (Logan, Utah) and dissolved in distilled water. All procedures involving AlPcS4 were performed under low background light conditions.Cell culture
MAT-LyLu (MLL) rat prostate adenocarcinoma cells were cultured in RPMI medium 1640 (Gibco-BRL) supplemented with 10% FBS (Gibco-BRL) and 2% antibiotic–antimycotic (GIBCO-BRL). Cells were incubated for 24 hours in medium with AlPcS4 concentrations of 3, 12, or 30 μM. After incubation, the medium was removed and the cells were washed 3 times with cold phosphate buffered saline (PBS) and then exposed to trypsin. After 5 minutes, medium was added and the solution was centrifuged for 5 minutes at 208 g. The supernatant was removed and the cells were suspended in room temperature PBS to a concentration of 5 × 105 cells per mL.PDT treatments
For PDT treatments 3 mL of the cell suspension was placed in a 4 mL cuvette on top of a magnetic stirrer. A custom lid was placed on top of the suspension to minimize the amount of air that leaks into the system. A 8 mm stir bar was placed in the cuvette to keep the cells suspended during the experiment. The cells were treated with a collimated 400 nm LED (Mightex, Toronto, Ontario) at average fluence rates between 65 and 130 mW cm−2. To increase the fluence within the cuvette a mirror was placed behind the cuvette to reflect transmitted treatment light back into the sample.Oxygen consumption
Oxygen consumption was measured throughout each experiment using a Clark style oxygen electrode (Instech Laboratories, Inc., Plymouth Meeting, PA) controlled by a chemical microsensor (Diamond General Corp, Ann Arbor, MI). During each experiment the light fluence was alternated between off and on so that both the background oxygen consumption rate and the PDT induced oxygen consumption rate could be measured. We refer to oxygen consumption rate in the absence of treatment light as “background” rather than “metabolic” because the observed consumption is also affected by the slow leakage of oxygen into the cuvette.Fluorescence analysis
Fluorescence was collected by a lens-coupled fiber perpendicular to the excitation light. Fluorescence spectra were acquired (acquisition times ranged from 100 to 1500 ms) at set time intervals using a USB2000 Ocean Optics spectrometer (Ocean Optics Inc. Dunedin, FL) with a spectral range of 600 to 890 nm. Fluorescence spectra were analyzed as linear combinations of previously acquired basis spectra using a singular value decomposition (SVD) program written in Matlab (V 7.04).10,13,19 The basis spectra used in the SVD program were those for MLL cells autofluorescence, AlPcS4 and a spectrum equal to the first derivative of the AlPcS4 basis spectrum (to account for small wavelength shifts10).Intracellular AlPcS4 concentration
The intracellular concentration was obtained by incubating the cells in the tissue solubilizer Solvable™ (Perkin Elmer, Boston, MA) for 90 minutes and then acquiring the fluorescence signal. For each sample 1 mL of the cell suspension was added to 4 mL of Solvable. The fluorescence signal was compared to a calibration curve, which was constructed by dissolving known [AlPcS4] in Solvable with 20% PBS. The average intracellular [AlPcS4] concentration was then estimated by considering the total volume occupied by the cells in the suspension using the reported MLL cell diameter of 15 μm.8Extracellular AlPcS4 concentration
Before and after treatment the cell suspension was passed through a 0.45 μm filter. The fluorescence from the cell-free PBS was compared with the fluorescence observed during the treatment.Results
Oxygen consumption measurements
The extracellular [3O2] during an experiment in which the cells had been incubated with 12 μM of AlPcS4 is shown in Fig. 2. The treatment light was cycled on and off (this is shown by the dashed line in Fig. 2) so that measurements of background 3O2 consumption could be made.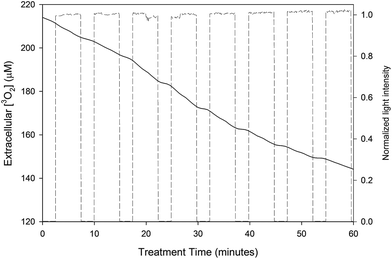 | ||
| Fig. 2 Extracellular [3O2] during PDT treatment of MLL cells incubated with 12 μM of AlPcS4. The intensity of the treatment light during the experiment (dashed line) is also shown. Note that the PDT consumption rate actually increases over the initial rate from about 10 to 50 minutes. This increase is accompanied by an increase in the sensitizer fluorescence, which is shown in Fig. 4. | ||
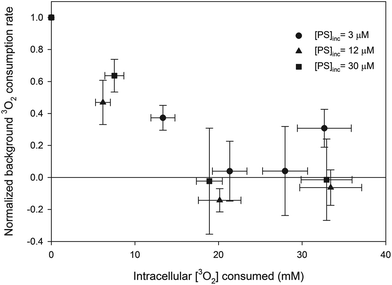
The 3O2 consumption rate induced by PDT was calculated by subtracting the background oxygen consumption rate from the measured consumption rate during PDT. The intracellular [3O2] consumed during each treatment fraction was obtained by multiplying the PDT 3O2 consumption rate by the duration of the fraction and then dividing this product by the fraction of the cell suspension that consists of MLL cells, which are assumed to be spherical with a diameter of 15 μm.8 The change in normalized background oxygen consumption rate (i.e. the data are normalized to the initial measurement of background oxygen consumption rate) as a function of the intracellular [3O2] consumed by PDT is shown in Fig. 3. Since a small concentration of cells was used (0.5 million cells per mL) the background oxygen consumption rates were small. Presumably the negative normalized [3O2] consumption rates observed at the larger consumed intracellular [3O2] is caused by a reduction in metabolic 3O2 rate and the leakage of oxygen into the system.
Changes in AlPcS4 fluorescence during PDT
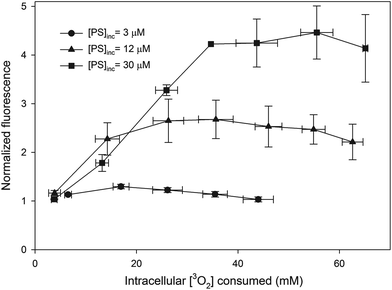
The AlPcS4 fluorescence as a function of the intracellular [3O2] consumed by PDT is shown in Fig. 4. In this figure each measurement is normalized to the initial fluorescence intensity. The data shown in the figure are the average of each quantity within consumed intracellular [3O2] bins that are 10 mM in width (i.e. 0–10, 10–20, etc.). The error bars are the standard deviations of all the measurements taken within these bins.Extracellular AlPcS4
As shown in Table 2, the percent contribution of extracellular AlPcS4 fluorescence to the total fluorescence collected at the start of the treatment was within error of the percentage at the end of the treatment for all concentrations studied. Given this, in the preceding analysis the extracellular fluorescence contribution is assumed to remain constant throughout the treatment for all [AlPcS4] studied.| % Contribution | 3 μM | 12 μM | 30 μM |
|---|---|---|---|
| Start | 40 ± 10 | 30 ± 10 | 33 ± 7 |
| End | 50 ± 10 | 40 ± 10 | 26 ± 6 |
The oxygen consumption rate due to extracellular AlPcS4 was estimated by measuring the rate of oxygen consumption in PBS with a known concentration of AlPcS4. From this measurement and the extracellular AlPcS4 fluorescence signals, it is estimated that greater than 94% of oxygen is consumed within the cells for all [AlPcS4] studied. Given the short mean free path of 1O2 in PBS (less than 200 nm) and the average distance between the cells (approximately 150 μm), it is unlikely that a significant fraction of extracellular 1O2 generated interacted with the cells.
Intracellular concentration
The intracellular [AlPcS4] for all incubation concentrations ([AlPcS4]inc) is shown in Table 3. On average, the fluorescence intensity of AlPcS4 in cells in PBS was 27 ± 1% of the intensity of cells in Solvable. If the sensitizer is disaggregated in Solvable and the reduction in intensity is caused by a large fraction of the AlPcS4 molecules in the cells being photodynamically inactive (i.e. these AlPcS4 molecules don't yield 1O2), the active [AlPcS4] can be calculated and is shown in the last column of Table 3.| [AlPcS4]inc (μM) | Intracellular [AlPcS4] (μM) | Average active [AlPcS4] (μM) |
|---|---|---|
| 3 | 8 ± 2 | 2.2 ± 0.6 |
| 12 | 40 ± 10 | 10 ± 3 |
| 30 | 90 ± 20 | 23 ± 6 |
Normalized PDT efficiency
PDT efficiency was calculated by dividing the amount of oxygen consumed by PDT in each treatment fraction by the fluence delivered and by the average fluorescence signal. The PDT efficiencies for each experiment were normalized to the first PDT efficiency measured. The normalized PDT efficiency as a function of the intracellular [3O2] consumed by PDT is shown in Fig. 5. The data shown in the figure are the average of each quantity within consumed intracellular [3O2] bins that are 10 mM in width.Monte Carlo simulations of PDT
The dependence of PDT efficiency on sensitizer concentration is accounted for by the stationary model of PDT. Good fits (shown in Fig. 6) were achieved with Dcell = 1.6 × 10−10 m2 s−1, [A]0 = 90 mM, and when [PS] was set to values close to the calculated active [AlPcS4] (shown in Table 3). In addition, the predicted PDT efficiency for the free diffusion model is shown when kd(koa[A])−1 = 0.5 (the same value used in the Monte Carlo simulations) and [A]0 = 90 mM. As shown in Fig. 6, at higher [PS] the efficiencies predicted by the stationary model approach the results of the analytic diffusion PDT model.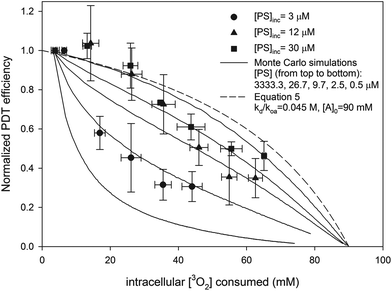 | ||
| Fig. 6 Predicted normalized PDT efficiency of different PDT models as a function of intracellular [3O2] consumed. Solid lines represent outputs of Monte Carlo simulations at different [PS] for the stationary PDT model. The values of Dcell, τΔ(start), τΔ(end), and [A]0 in the simulations were 1.6 × 10−10 m2 s−1, 0.4 μs, 1.2 μs and 90 mM respectively. The dashed line is the predicted PDT efficiency for the analytic diffusion model (eqn (5)) in which kd/koa[A] = 0.5. The experimental data are also shown. | ||
The change in 1O2 lifetime during PDT as calculated by the Monte Carlo simulation is shown in Fig. 7 for the case [PS] = 26.7 μM. The distribution of 1O2 quenchers (small circles) around a photosensitizer molecule (large square) is shown in Fig. 8 at four different stages of the treatment. An alternative view of the quencher distribution at τΔ = 0.6 and 0.9 μs is provided in Fig. 9. In Fig. 9 only the x plane in the middle of the lattice is shown. At τΔ = 1.05 and 1.15 μs, only 15 and 5 1O2 quenchers remained (out of the initial 225) in the x plane shown in Fig. 9.
Discussion
Challenges in using AlPcS4 to measure PDT efficiency
A drawback of using AlPcS4 is that a large fraction of the fluorescence signal is generated from extracellular sensitizer. Based on initial and final measurements of extracellular fluorescence it was assumed that the fraction of the fluorescence signal contributed from extracellular AlPcS4 remains constant during the treatment. In addition, the contribution of extracellular oxygen consumption was determined to be small (<6%) in comparison to the amount consumed within the cell. Given the increases in fluorescence observed during treatment (especially for cells incubated with the two highest [AlPcS4]) and the increased fluorescence signal in Solvable, the average concentration of AlPcS4 which is photodynamically active within the cell is difficult to determine. While it is possible that the fluorescence yield of AlPcS4 is reduced in cells (in comparison to Solvable), several reports have shown that AlPcS4 forms aggregates23,28 and that the aggregates have reduced fluorescence and photodynamic activity.29,30 A crude estimate of the active [AlPcS4] is shown in Table 3 and is equal to the ratio of the AlPcS4 fluorescence intensity of cells in PBS (averaged over the entire experiment) to Solvable multiplied by the intracellular [AlPcS4]. The fraction of AlPcS4 that is actually active within the cells can only be estimated because the florescence yields and the degree of aggregation in Solvable and in cells is not known. Increased AlPcS4 fluorescence during PDT has been observed in several studies and has been attributed to the photoinduced disaggregation and re-localization of the sensitizer.31,32 PDT efficiency was calculated by dividing the amount of oxygen consumed by PDT in a given treatment interval by the average fluorescence signal. Given that at the start of treatment the fluorescence signals for the 2 highest [AlPcS4] roughly doubled (see Fig. 4) while the calculated PDT efficiency remained constant (see Fig. 5), this approach seems reasonable.Metabolic oxygen consumption rate reduction during PDT
As shown in Fig. 3, the background oxygen consumption rate was reduced substantially during PDT for all concentrations studied. This reduction is caused by decreased metabolic consumption. In a study with the photosensitizer BPD-MA, Pogue et al. found the reduction in metabolic consumption rate correlated with the loss of mitochondrial function.33 This mechanism would explain the results shown in Fig. 3 as well.Stationary versus free photosensitizer and 1O2 quencher models
The dependence of normalized PDT efficiency on sensitizer concentration suggests that conventional PDT kinetics are inadequate for describing AlPcS4-PDT. As an alternative, a simple model was used in which both PS and A are stationary within the cell during treatment. Such a model is reasonable considering that sensitizers are known to localize to specific sites in cells34,35 and that 1O2 quenchers are typically proteins15,36,37 found close to these sites. Using Monte Carlo simulations it was shown that the stationary model was a good predictor of the measured AlPcS4-PDT efficiencies when Dcell = 1.58 × 10−10 m2 s−1, kd/koa = 0.045 M, and [A]0 = 90 mM. The concentration dependence is the result of the short lifetime of 1O2 within cells. As the [PS] is reduced, the distance that 1O2 must travel to deliver the same dose increases as does the probability that the molecule will be physically quenched. Conversely, at higher [PS] the difference in predicted PDT efficiencies between the stationary and diffusion models diminishes (as shown in Fig. 6) because the distance that the 1O2 has to travel is reduced. Fixed PS is consistent with photobleaching and dosimetry work done by our group and others.8,11,19,24 By modifying the bleaching kinetics to account for the short diffusion distance of 1O2, the photobleaching and 1O2 generation of several photosensitizers has been described.The intracellular distribution of AlPcS4 is complicated by the relocalization that likely occurs during the treatment. Our simple model assumes that the photosensitizer environment does not depend on [PS]. It is possible that observed changes in PDT efficiency were caused by the movement of sensitizer to different regions and that the observed concentration dependence is just a coincidence. However, the changes in 1O2 lifetime predicted by the model (see Fig. 7) are similar to experimental results reported by Hackbarth et al. for several different photosensitizers.20,21 Furthermore, the reduction in the background consumption rate as function of intracellular [3O2] consumed was similar for all [AlPcS4] studied (see Fig. 3) which suggests that the localization to at least one site (the mitochondria) is similar at all [AlPcS4].
1O2 lifetime in cells
In the Monte Carlo model it is assumed that the 1O2 lifetime changes from 0.4 to 1.2 μs. These values correspond to the average values reported by Hackbarth et al. for several different sensitizers in two different cell lines.20,21 The results and analysis by Hackbarth et al. estimate that the 1O2 lifetime in cells stabilizes after 100 to 200 mM of 1O2 has been generated. For example, Hackbarth et al. showed that during PDT with the photosensitizer Pheophorbide-a, in which roughly 700 mM21 of 1O2 was generated, that the 1O2 lifetime stabilized after roughly 100 mM of 1O2 had been generated.20 It is currently unknown whether chemical quenching significantly contributes to the final 1O2 lifetime. The final 1O2 lifetimes reported by Hackbarth et al. in cells are roughly a third of the value in water.9,20 Given that the effective diffusion coefficient of oxygen in cells has been estimated to be between 3 to 5 times less than the diffusion coefficient in water,38–40 it seems reasonable that the final lifetime reported by Hackbarth et al. corresponds to physical quenching. If chemical quenching is still occurring after the 1O2 lifetime has stabilized then the system must contain at least two generic quenchers. The first type would react rapidly with 1O2 and have a concentration in the 10's of mM range (similar to quencher used in our model) while the second type of quencher would have a much lower reaction rate and would have concentrations in the 100's if not 1000's of mM range. Incorporation of secondary quenchers would only complicate the Monte Carlo model and most likely not alter the results, i.e. the change in lifetime/PDT efficiency would still be caused by the depletion of quenchers that react rapidly with 1O2.Uncertainty associated with Dcell
The experimental results were well described using the Monte Carlo model when Dcell is equal to 1/12 of Dwater. Although lower Dcell values have been reported,41 generally Dcell is believed to between 20 and 33% of Dwater.38–40 The difference in the value used in the model and those reported could be the result of the relatively simple model used for the Monte Carlo simulations. In the model it is assumed that the PS is homogenously distributed throughout the cell and that [AlPcS4] is equal to the estimated active concentration (see Table 1). Numerous reports have suggested that sensitizers preferentially localize to preferred sites within the cell.34,35 If the sensitizer is more highly localized within the cell then the quenchers around the sensitizers are depleted more rapidly and 1O2 must travel larger distances to deliver the same dose. If the sensitizer is found in only a fraction of cell given by 1/L then the system can be modeled by placing L sensitizers at the origin of the cubic lattice and increasing the volume of the lattice by L. If the diffusion coefficient remains the same, the time required to deliver the same dose increases (because the 1O2 must travel farther) and as a consequence the PDT efficiency falls off faster. Hence, as the drug localization increases, the diffusion coefficient must be increased (by a factor of L2/3) to generate the same PDT efficiency curves. For example, if the PS was found in only a quarter of the cell (L = 4) then the diffusion coefficient must be increased by 42/3 = 2.52 (from 1/12 to 1/4.76 of Dwater) to generate the same curves shown in Fig. 6. Hence, the Monte Carlo simulations yield good fits to the experimental results (the same as those shown in Fig. 6) at Dcell values of 0.2 Dwater and Dwater if the drug is localized to 26.8 and 2.4% of the cell respectively. A similar correction is required if the fraction of PS molecules that are active is less than estimated. For example, if the fraction of AlPcS4 molecules that are active is 4 times less than estimated and the drug is homogenously distributed throughout the cell, then the diffusion coefficient must also be increased by 42/3 to generate the same curves shown in Fig. 6. In addition, the diffusion coefficient of oxygen close to the sensitizer molecules (if it is not homogenously distributed within the cell) may be different then the average value for the entire cell.Implications of 1O2 quencher depletion to PDT dosimetry
In general, most advanced PDT dosimetry techniques try to estimate the amount of 1O2 that is generated during treatment.6 The fraction of 1O2 that reacts with A is typically assumed to remain constant and close to unity. Given the changes in τΔ reported by Hackbarth et al. and the experimental results of this study, it appears that such an assumption is not valid for some photosensitizers. Explicit dosimetry techniques will overestimate the [1O2] that reacts during PDT if [A] is significantly depleted. Ideally, measurements of [PS], fluence, and [3O2] are made during explicit PDT dosimetry. Under well oxygenated conditions it is assumed that the product of [PS] and fluence will be indicative of the [1O2] that reacts within the cell. Using the Monte Carlo program with the parameters that best described the experimental data, the concentration of 1O2 molecules that react with A for a treatment in which 30 mM of 1O2 is generated was calculated for various [PS]. If the reaction constants were known and perfect explicit dosimetry was performed, the [1O2] expected to react would be 20 mM (if it was assumed that all generated 1O2 reacts then it would be 30 mM). In Table 4 the actual [1O2] that reacts with A is shown. Since explicit dosimetry does not take into account quencher depletion, at typical in vivo [PS] (<10 μM) the [1O2] that reacts with 1O2 quenchers would be at least 15% less than expected.| [PS] (μM) | Reacted [1O2] (μM) |
|---|---|
| 3333.3 | 19.1 |
| 26.7 | 17.8 |
| 9.7 | 16.6 |
| 2.5 | 13.4 |
| 0.5 | 8.6 |
As an alternative to explicit dosimetry, direct dosimetry measures the 1270 nm luminescence signal from 1O2. In principle the luminescence signal should be corrected for 1O2 lifetime.9 If the lifetime is measured and if the reaction constants are known then corrections for quencher depletion could be made. Due to the weak luminescence intensity, the technique is difficult to implement clinically42 and in instances where in vivo measurements have been made12,43,44 the 1O2 lifetime was not accounted for. If the luminescence signal is not corrected for τΔ then the errors associated with direct dosimetry would be greater than those associated with explicit dosimetry. This is because the increase in 1O2 lifetime would be interpreted as a greater generation of 1O2, when, in fact, it means that less 1O2 is reacting with 1O2 quenchers.
Conclusions
For AlPcS4-PDT of Mat LyLu cells in suspension, the PDT efficiency was dependent on the [AlPcS4]. This result is consistent with a model of PDT in which both the PS and A remain stationary during the treatment. Good fits to the experimental data were achieved using the stationary model when Dcell, τΔ(start), τΔ(end), and [A]0 were equal to 1.6 × 10−10 m2 s−1, 0.4 μs, 1.2 μs and 90 mM respectively. If the sensitizer is not uniformly distributed throughout the cell or if the fraction of AlPcS4 molecules that are active is less than estimated then the value of Dcell must be increased to describe the experimental results. The reduction in PDT efficiency observed during these experiments suggests that modern PDT dosimetry techniques will significantly underestimate the [1O2] that reacts during AlPcS4-PDT unless singlet oxygen quencher depletion is accounted for.Acknowledgements
This research was supported by the Canadian Cancer Society Research Institute.References
- C. Foote, Definition of type I and type II photosensitized oxidation, Photochem. Photobiol., 1991, 54, 659 CrossRef CAS.
- B. W. Henderson and T. J. Dougherty, How does photodynamic therapy work?, Photochem. Photobiol., 1992, 55, 145–157 CrossRef CAS.
- M. J. Niedre, A. J. Secord, M. S. Patterson and B. C. Wilson, In vitro tests of the validity of singlet oxygen luminescence measurements as a dose metric in photodynamic therapy, Cancer Res., 2003, 63, 7986–7994 CAS.
- K. R. Weishaupt, C. J. Gomer and T. J. Dougherty, Identification of singlet oxygen as the cytotoxic agent in photoinactivation of a murine tumor, Cancer Res., 1976, 36, 2326–2329 CAS.
- B. C. Wilson, M. S. Patterson and L. Lilge, Implicit and explicit dosimetry in photodynamic therapy: a new paradigm, Lasers Med. Sci., 1997, 12, 182–199 CrossRef CAS PubMed.
- B. C. Wilson and M. S. Pattersonm, The physics, biophysics and technology of photodynamic therapy, Phys. Med. Biol., 2008, 53, R61–R109 CrossRef CAS PubMed.
- M. S. Patterson, B. C. Wilson and R. Graff, In vivo tests of the concept of photodynamic threshold dose in normal rat liver photosensitized by aluminum chlorosulphonated phthalocyanine, Photochem. Photobiol., 1990, 51, 343–349 CrossRef CAS.
- J. S. Dysart, G. Singh and M. S. Patterson, Calculation of Singlet Oxygen Dose from Photosensitizer Fluorescence and Photobleaching During mTHPC Photodynamic Therapy of MLL Cells, Photochem. Photobiol., 2005, 81, 196–205 CrossRef CAS.
- M. Niedre, M. S. Patterson and B. C. Wilson, Direct near-infrared luminescence detection of singlet oxygen generated by photodynamic therapy in cells in vitro and tissues in vivo, Photochem. Photobiol., 2002, 75, 382–391 CrossRef CAS.
- J. S. Dysart and M. S. Patterson, Photobleaching kinetics, photoproduct formation, and dose estimation during ALA induced PpIX PDT of MLL cells under well oxygenated and hypoxic conditions, Photochem. Photobiol. Sci., 2006, 5, 73–81 CAS.
- M. T. Jarvi, M. S. Patterson and B. C. Wilson, Insights into photodynamic therapy dosimetry: simultaneous singlet oxygen luminescence and photosensitizer photobleaching measurements, Biophys. J., 2012, 102, 661–671 CrossRef CAS PubMed.
- M. J. Niedre, C. S. Yu, M. S. Patterson and B. C. Wilson, Singlet oxygen luminescence as an in vivo photodynamic therapy dose metric: validation in normal mouse skin with topical amino-levulinic acid, Br. J. Cancer, 2005, 92, 298–304 CAS.
- M. A. Weston and M. S. Patterson, Simple photodynamic therapy dose models fail to predict the survival of MLL cells after HPPH-PDT in vitro, Photochem. Photobiol., 2009, 85, 750–759 CrossRef CAS PubMed.
- T. C. Zhu, E. I. Parsai and C. G. Orton, Point/counterpoint. PDT is better than alternative therapies such as brachytherapy, electron beams, or low-energy X rays for the treatment of skin cancers, Med. Phys., 2011, 38, 1133–1135 CrossRef.
- A. Baker and J. R. Kanofsky, Quenching of singlet oxygen by biomolecules from L1210 leukemia cells, Photochem. Photobiol., 1992, 55, 523–528 CrossRef CAS.
- J. Moan and K. Berg, The photodegradation of porphyrins in cells can be used to estimate the lifetime of singlet oxygen, Photochem. Photobiol., 1991, 53, 549–553 CrossRef CAS.
- B. Liu, T. J. Farrell and M. S. Patterson, A dynamic model for ALA-PDT of skin: simulation of temporal and spatial distributions of ground-state oxygen, photosensitizer and singlet oxygen, Phys. Med. Biol., 2010, 55, 5913–5932 CrossRef PubMed.
- S. Mitra, Photodynamic Therapy: Biophysical Mechanisms and Molecular Responses, PhD thesis, University of Rochester, 2004 Search PubMed.
- M. A. Weston and M. S. Patterson, Calculation of singlet oxygen dose using explicit and implicit dose metrics during benzoporphyrin derivative monoacid ring A (BPD-MA)-PDT in vitro and correlation with MLL cell survival, Photochem. Photobiol., 2011, 87, 1129–1137 CrossRef CAS PubMed.
- S. Hackbarth, J. Schlothauer, A. Preuß and B. Röder, New insights to primary photodynamic effects–Singlet oxygen kinetics in living cells, J. Photochem. Photobiol., B, 2010, 98, 173–179 CrossRef CAS PubMed.
- S. Hackbarth, J. Schlothauer, A. Preuß, C. Ludwig and B. Röder, Time resolved sub-cellular singlet oxygen detection – ensemble measurements versus single cell experiments, Laser Phys. Lett., 2012, 9, 474–480 CrossRef CAS.
- D. Gryglik, M. Lach and J. S. Miller, The aqueous photosensitized degradation of butylparaben, Photochem. Photobiol. Sci., 2009, 8, 549–555 CAS.
- M. A. Idowu, Photophysical and Photochemical behaviour of metallophthalocyanines: Effect of nanoparticles and molecules of biological importance, PhD thesis, Rhodes University, 2009 Search PubMed.
- J. S. Dysart and M. S. Patterson, Characterization of Photofrin photobleaching for singlet oxygen dose estimation during photodynamic therapy of MLL cells in vitro, Phys. Med. Biol., 2005, 50, 2597–2616 CrossRef CAS PubMed.
- J. C. Finlay, S. Mitra, M. S. Patterson and T. H. Foster, Photobleaching kinetics of Photofrin in vivo and in multicell tumour spheroids indicate two simultaneous bleaching mechanisms, Phys. Med. Biol., 2004, 49, 4837–4860 CrossRef CAS.
- I. Georgakoudi, M. G. Nichols and T. H. Foster, The mechanism of Photofrin photobleaching and its consequences for photodynamic dosimetry, Photochem. Photobiol., 1997, 65, 135–144 CrossRef CAS.
- M. T. Jarvi, M. J. Niedre, M. S. Patterson and B. C. Wilson, The influence of oxygen depletion and photosensitizer triplet-state dynamics during photodynamic therapy on accurate singlet oxygen luminescence monitoring and analysis of treatment dose response, Photochem. Photobiol., 2011, 87, 223–234 CrossRef CAS PubMed.
- R. Edrei, V. Gottfried, J. E. V. Lier and S. Kimel, Sulfonated phthalocyanines: photophysical properties, in vitro cell uptake and structure-activity relationships, J. Porphyrins Phthalocyanines, 1998, 2, 191–199 CrossRef CAS.
- S. Dhami, A. J. D. Mello, G. Rumbles, S. M. Bishop, D. Phillips and A. Beeby, Phthalocyanine fluorescence at high concentration: Dimers or reabsorption effect?, Photochem. Photobiol., 1995, 61, 341–346 CrossRef CAS.
- T. Nyokong, Effects of substituents on the photochemical and photophysical properties of main group metal phthalocyanines, Coord. Chem. Rev., 2007, 251, 1707–1722 CrossRef CAS PubMed.
- J. Moan, V. Iani and L. W. Ma, In vivo fluorescence of phthalocyanines during light exposure, J. Photochem. Photobiol., B, 1998, 42, 100–103 CrossRef CAS.
- J. Moan, K. Berg, H. Anholt and K. Madslien, Sulfonated aluminium phthalocyanines as sensitizers for photochemotherapy. Effects of small light doses on localization, dye fluorescence and photosensitivity in V79 cells, Int. J. Cancer, 1994, 58, 865–870 CrossRef CAS.
- B. W. Pogue, J. A. O'Hara, E. Demidenko, C. M. Wilmot, I. A. Goodwin, B. Chen, H. M. Swartz and T. Hasan, Photodynamic therapy with verteporfin in the radiation-induced fibrosarcoma-1 tumor causes enhanced radiation sensitivity, Cancer Res., 2003, 63, 1025–1033 CAS.
- R. W. Boyle and D. Dolphin, Structure and biodistribution relationships of photodynamic sensitizers, Photochem. Photobiol., 1996, 64, 469–485 CrossRef CAS.
- N. L. Oleinick and H. H. Evans, The photobiology of photodynamic therapy: cellular targets and mechanisms, Radiat. Res., 1998, 150, S146–S156 CrossRef CAS.
- A. Michaeli and J. Feitelson, Reactivity of singlet oxygen toward amino acids and peptides, Photochem. Photobiol., 1994, 59, 284–289 CrossRef CAS.
- A. Michaeli and J. Feitelson, Reactivity of singlet oxygen toward large peptides, Photochem. Photobiol., 1995, 61, 255–260 CrossRef CAS.
- H. P. Kao, J. R. Abney and A. S. Verkman, Determinants of the translational mobility of a small solute in cell cytoplasm, J. Cell Biol., 1993, 120, 175–184 CrossRef CAS.
- M. A. O'Loughlin, D. W. Whillans and J. W. Hunt, A fluorescence approach to testing the diffusion of oxygen into mammalian cells, Radiat. Res., 1980, 84, 477–495 CrossRef CAS.
- S. Hatz, L. Poulsen and P. R. Ogilby, Time-resolved singlet oxygen phosphorescence measurements from photosensitized experiments in single cells: effects of oxygen diffusion and oxygen concentration, Photochem. Photobiol., 2008, 84, 1284–1290 CrossRef CAS PubMed.
- M. K. Kuimova, G. Yahioglu, J. A. Levitt and K. Suhling, Molecular rotor measures viscosity of live cells via fluorescence lifetime imaging, J. Am. Chem. Soc., 2008, 130, 6672–6673 CrossRef CAS PubMed.
- M. T. Jarvi, M. J. Niedre, M. S. Patterson and B. C. Wilson, Singlet oxygen luminescence dosimetry (SOLD) for photodynamic therapy: current status, challenges and future prospects, Photochem. Photobiol., 2006, 82, 1198–1210 CrossRef CAS PubMed.
- S. Lee, D. H. Vu, M. F. Hinds, S. J. Davis, A. Liang and T. Hasan, Pulsed diode laser-based singlet oxygen monitor for photodynamic therapy: in vivo studies of tumor-laden rats, J. Biomed. Opt., 2008, 13, 064035 CrossRef PubMed.
- H. J. Laubach, S. K. Chang, S. Lee, I. Rizvi, D. Zurakowski, S. J. Davis, C. R. Taylor and T. Hasan, In vivo singlet oxygen dosimetry of clinical 5-aminolevulinic acid photodynamic therapy, J. Biomed. Opt., 2008, 13, 050504 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry and Owner Societies 2014 |