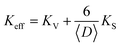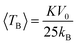Tuning the surface anisotropy in Fe-doped NiO nanoparticles

Abstract

Ni_1−xFe_xO nanoparticles have been obtained by the co-precipitation chemical route. X-ray diffraction analyses using Rietveld refinement have shown a slight decrease in the microstrain and mean particle size as a function of the Fe content. The zero-field-cooling (ZFC) and field-cooling (FC) magnetization curves show superparamagnetic behavior at high temperatures and a low temperature peak (at T = 11 K), which is enhanced with increasing Fe concentration. Unusual behavior of the coercive field in the low temperature region and an exchange bias behavior were also observed. A decrease in the Fe concentration induces an increase in the exchange bias field. We argue that these behaviors can be linked with the strengthening of surface anisotropy caused by the incorporation of Fe ions.

---

1. Introduction

In the last few decades, nanoscience has been an exciting area of research, as much from an application point of view as for the fundamental research. In this scenario, magnetic nanoparticles (NPs) have been extensively studied mainly owing to their unique physical properties compared with their bulk counterparts.^1–6 It is well known that below a critical size, magnetic NPs behave as a single-domain, in contrast with the multi-domain structure observed in their bulk form. In a rough approximation, the energy states of the magnetization vector of the particles can be modeled as a two-level system separated by barriers that depend on their size and magnetic effective anisotropy (E_b = k_effV).^2–4,7–11 It is worth noting that in most cases it is very difficult to separate the contributions of the different kind of anisotropies, e.g., magnetocrystalline, magnetoelastic, shape and surface anisotropies to k_eff. However, in the particular case of small-moment nickel oxide (NiO), the surface anisotropy appears to be dominant.^9,12 In some of these cases, the appearance of a peak at low temperature characterizes a system with a large surface effect, meaning the surface anisotropy is dominant compared with the other anisotropies. Some authors suggest that this effect is related to uncompensated surface moments due to the bond breaking of Ni ions on the surface.^3,9,12,13

In this work, we report structural and magnetic data that show a reinforcement of the surface anisotropy of NiO NPs doped with iron. We discuss this strengthening on the basis of the increase of surface anisotropy caused by the insertion of Fe ions into the NiO crystalline structure.

2. Experimental details

Ni_1−xFe_xO NPs (x = 0, 0.01, 0.05 and 0.10) were prepared by annealing a precursor powder obtained by the co-precipitation method following the steps of our previous work.¹⁴ The precursors were chemically obtained at room temperature by mixing an aqueous solution of nickel nitrate Ni(NO₃)₂·6H₂O (and iron nitrate Fe(NO₃)₂·3H₂O, in the case of the doped samples) and a 1 mol l⁻¹ solution of NaOH to maintain a pH value of 12. The resulting precipitate was washed several times in order to completely remove Na ions, centrifuged and dried in air at 80 °C. Finally, the precursors were synthesized at 350 °C for 3 hours.

The crystalline structures of the samples were investigated by X-ray diffraction (XRD) using a Rigaku powder diffractometer with Bragg–Brentano geometry mode θ − 2θ (with Cu Kα radiation operated at 40 kV and 40 mA). Rietveld refinement was carried out by DBWS software using a modified pseudo-Voigt function as the profile function. From these analyses, we have also extracted information on the full width at half maximum (FWHM) for {111}, {002} and {022} crystallographic families. These analyses allow us to estimate the crystallite size and lattice distortion (microstrain) through the Williamson–Hall equation,¹⁵

where β is the FWHM of the XRD peak, θ is the diffraction angle, k is a constant (close to 1 for cubic structure and spherical crystallites), λ is the incident X-ray wavelength, t is the crystallite size and ε is the microstrain. The particle shape and size were measured by means of transmission electron microscopy (HR-TEM JEOL 3010, LNNano/LNLS/CNPEM). X-ray Photon Spectroscopy (XPS) measurements were recorded with SPECSLAB II (Phoibos-Hs 3500150 analyzer, SPECS, 9 channels) using non-monochromatic Al Kα (hν = 1486.6 eV) radiation at the soft X-ray spectroscopy beamline at the LNLS/CNPEM (Brazilian Synchrotron Light Laboratory, Brazil). The samples were analyzed as a function of emission angle (15°, 45° and 75°) to investigate surface and internal regions of the particles. Magnetic measurements as a function of the field and temperature were carried out using a SQUID magnetometer (Quantum Design MPMS EverCool system).

3. Results and discussion

3.1 Structural properties

Fig. 1 presents the X-ray diffraction patterns of Ni_1−xFe_xO (x = 0, 0.01, 0.05 and 0.10) nanoparticles synthesized at 350 °C obtained via the co-precipitation method. We also show the difference between the experimental and calculated patterns which have been evaluated via the Rietveld method. Unlike the results reported by Mallick et al.,¹⁶ all XRD patterns shown in Fig. 1 indicate the same cubic structure of NiO without the presence of any spurious phases with Fe concentrations in the range from 0 to x = 0.10.

Fig. 1 X-ray diffraction and Rietveld refinement patterns for Ni_1−xFe_xO (x = 0, 0.01, 0.05 and 0.10) nanoparticles synthesized at 350 °C.

As one can see, there is a broadening in the FWHM of the Bragg peaks when increasing the doping concentration, which is associated with the growth process the particles. Part of this broadening is due to the slight decrease in the average crystallite sizes from pure to doped samples (see Table 1). However, we observed that the change in the FWHM broadening can also be associated with the crystallinity of the doped samples once we have used the same synthesis conditions. Indeed, we have observed an increase in the microstrain of the doped samples as a function of the iron substitution. In this scenario, we attributed the FWHM broadening to X-ray reflection occurring at plane families where likely there is a larger iron incorporation. Another important feature produced by iron incorporation is the disorder of the crystalline structure created by stacking faults in the crystal due the difference between Fe³⁺ (0.64 Å) and Ni²⁺ (0.69 Å) ionic radii. Finally, in agreement with our previous statements, our XRD data show a decrease in the lattice parameter as a function of iron doping (see Table 1).

Table 1 Lattice parameters, particle size and microstrain for Ni_1−xFe_xO (x = 0, 0.01, 0.05 and 0.10) nanoparticles synthesized at 350 °C

Sample	a (Å)	Size (nm)	Microstrain
Pure	4.1852(5)	13(2)	0.0073
1% Fe	4.1827(5)	10(1)	0.0073
5% Fe	4.1818(6)	10(1)	0.0080
10% Fe	4.1706(9)	8(1)	0.0095

---

Fig. 2 displays representative transmission electron microscopy images in high resolution mode of the Fe-doped NiO with 1% (Fig. 2a) and 10% (Fig. 2b) Fe content. The main planes of the NiO structure (111), (200) and (220) are readily seen in the images with lattice fringes shown in both samples. Although the sample doped with 1% Fe shows sphere-like particles (Fig. 2a), we have observed that some nanoparticles also possess a rod-like shape similar to that found in the doped sample with 10% Fe. These results show that the mean sizes of the rod-like particles are 17 × 6 nm for the sample with 1% Fe and 13 × 5 nm for the sample with 10% Fe. The histograms presented in Fig. 2 show that the mean particle sizes obtained indicate differences between the results estimated by the Williamson–Hall equation and the TEM analyses. These differences can be explained considering that the XRD analysis have taken into account a spherical morphology.

Fig. 2 HR-TEM images of samples of Fe-doped NiO nanoparticles, with (a) 1% Fe and (b) 10% Fe. Insets show lattice fringes corresponding to the crystalline planes of NiO and histograms of the particle size distribution calculated from TEM.

Fig. 3 displays the experimental and calculated XPS spectra for the 10% Fe-doped sample in the region corresponding to the binding energy range of 704–730 eV, which includes the Fe 2p_3/2 and Fe 2p_1/2 peaks recorded at 15°, 45° and 75°. The peaks shown, including the shake-up peaks, are a convolution of the peaks for Fe with different oxidation states (Fe²⁺ and Fe³⁺). The calculated areas after fitting for each peak are presented in Table 2. These analyses show an increase in the amount of Fe³⁺ with increasing emission angle, indicating that the surface of the particles contain more Fe³⁺ than Fe²⁺. Based on the magnetization results, the core particles present an antiferromagnetic-like spin configuration and the composition on the particle surface is close to a ferrimagnetic structure. This disordering of the surface spin can lead to a spin-glass-state in the low temperature region.

Fig. 3 Experimental and calculated Fe 2p XPS spectra for 10% Fe-doped NiO nanoparticles at different angles. The deconvolution of each spectrum is also included.

Table 2 The results of deconvolution of the Fe 2p_3/2 peak: area ratio of the oxidation state (A_Fe³⁺/A_Fe²⁺) as a function of emission angle for 10% Fe-doped sample

Emission angle	15°	45°	75°
A Fe ^+3/AFe^+2	1.8	2.1	2.3

---

3.2 Magnetic properties

Fig. 4 shows the ZFC–FC magnetization curves measured at H = 100 Oe for Ni_1−xFe_xO (x = 0, 0.01, 0.05 and 0.10) nanoparticles synthesized at 350 °C. It is evident that the ZFC–FC curves display typical superparamagnetic (SPM) behavior for all samples in the high temperature regime and a blocked state at temperatures lower than 160 K. It is known that the blocking temperature is associated with the mean particle size and anisotropy. But when a large surface effect appears, an effective uniaxial anisotropy must be considered¹⁷ as described by this phenomenological expression:
where 〈D〉 is the particle diameter and K_V and K_S are the core and surface uniaxial anisotropy, respectively. In this case, the constant K in the expression is used to calculate the average blocking temperature 〈T_B〉
where V₀ is the particle volume and k_B is the Boltzmann constant. Although our results show that all samples have an average blocking temperature near to 160 K, once the average particle for the pure sample is larger than for the Fe-doped samples, a decrease in anisotropy is observed. On the other hand, the broadening of the ZFC–FC curves is a consequence of the large distribution of energy barriers, which can be associated with the particle size distribution. In this sense, our results show that the irreversibility temperatures of the Fe-doped samples vary in the lower temperature regions with increasing dopant concentration, indicating a likely reduction in the particle size distribution.

Fig. 4 ZFC–FC magnetization curves at H = 100 Oe for Ni_1−xFe_xO (x = 0, 0.01, 0.05 and 0.10) nanoparticles synthesized at 350 °C. The insets show in detail the ZFC region for observation of T_B for the Fe-doped samples with 5 and 10% Fe.

Besides, the magnetization measurements show for all samples an unusual increase in magnetization (at T = 11 K), which is enhanced with increasing dopant concentration. This unusual behavior has been interpreted as an effect of the finite size of particles, that is, the breaking of a large number of exchange bonds on the surface of the particles, which drives the spins to a strongly frustrated state.^4,9,12,13 Although, the decrease in the particle size increases the surface to volume ratio, this decrease in the size is not sufficient to change significantly the magnetic properties, mainly the peak at low temperature. In this scenario, the origin of the blocking effects and the low temperature peak for the Ni_1−xFe_xO nanoparticles come from the core and surface of the particle, respectively. Our results show that most of the iron ions can be incorporated on the surface of the particle. One must note when analyzing Fig. 4 that while the maximum value of the ZFC curves are almost constant (M_max ∼ 0.010 emu g⁻¹), the intensity of the low temperature peak increases with the iron concentration.

The field dependence of the ZFC–FC curves for the Ni_0.9Fe_0.1O sample is displayed in Fig. 5. Our M vs. H loops measured at T = 5 K remain separated with a field of 50 kOe for the 10% Fe-doped sample as one can see in the inset of Fig. 5. This splitting means that magnetic moments can present a switching field of 50 kOe, which can be indicative of “high field irreversibility”,² in good accordance with the results shown in the inset (left) of Fig. 6c. This behavior has been associated with frozen magnetically ordered regions in the surface shell.^4,9 In this scenario, results shown in Fig. 4 provide strong evidence about the change in spin states on the particle surface as a function of iron doping. Unlike the results reported by Winkler et al.,⁹ for NiO nanoparticles, we have noted that at H = 50 kOe the curves for the Ni_0.9Fe_0.1O sample still remain split, indicating a strengthening of surface anisotropy with the Fe doping.

Fig. 5 ZFC–FC magnetization curves for the Ni_0.90Fe_0.10O sample taken at different applied fields. The inset shows the split between the ZFC–FC curves at low temperature.

Fig. 6 Hysteresis curves measured at (a) 300 K and (b) 5 K taken in the ZFC mode for Fe-doped NiO nanoparticles. The insets show (a) the original loop and (b) the doping dependence on the exchange bias field (H_EB). (c) Hysteresis loops taken in ZFC and FC modes at 5 K for the Ni_0.90Fe_0.10O sample and the inset shows the original loops in the low field region.

Fig. 6 shows M vs. H curves recorded at temperatures of 300 K (Fig. 6a) and 5 K (Fig. 6b) for all samples studied in this work. At T = 5 K, the M vs. H loops present hysteretic behavior for all samples, however the magnetization never reaches the saturation value. On the other hand, the high field behavior shows a linear contribution, which increases with the iron doping, suggesting an increase of the surface contribution to the magnetization. It is also evident that, in the 10% Fe-doped sample, the hysteresis curves measured at low temperature, the coercive field (H_C) is slowly narrowed. In fact, these results confirm the uncompensated spin systems either on the surface or in the core of the NiO nanoparticles. It is more evident in doped samples with a high concentration of doping (5% and 10%), when the surface effect is large. At room temperature, the M vs. H loops also display a hysteresis, which can be attributed to the contribution from larger particles. However, the coercive field and reversibility temperature decrease with the iron doping, indicating a change in the particle size distribution. Furthermore, we have observed in the M vs. H loops the exchange bias phenomenon for doped systems, which increases with a decrease in the amount of doping, as can be observed in the inset of Fig. 6b. To illustrate the shift of the coercive field, we show in Fig. 6cM vs. H loops measured in ZFC and FC (with an applied field of 50 kOe) mode taken at 5 K. Recent studies performed by Punnoose et al. have shown this phenomenon for CuO nanoparticles.¹⁸ They have suggested that uncompensated exchange couplings of the surface spins lead to a significant magnetic moment per particle, even though the spins in the core are antiferromagnetically ordered. Sharma et al. have reported exchange bias in Ni–NiO nanoparticles and they have associated the decrease in the exchange bias field (H_EB) with an increase in the ferromagnetic phase present on the particle surface.¹⁹ So our results suggest a similar magnetic behavior where the origin of the coupling between the ferromagnetic surface spins with antiferromagnetic (core particle) spins result in shifted hysteresis loops of the ferromagnetic surface spins.

These anomalous behaviors are further confirmed from the dependence of the coercive field (H_C) and remanent magnetization (M_R) as functions of temperature (see Fig. 7). First of all we can see that H_C does not decay with the square root of temperature following a Néel relaxation and the Bean–Livingston approaches.¹ Instead, the coercive field and remanent magnetization decrease in the temperature range where the surface effects are stronger, reaching a minimum at T = 10 K. After that, H_C reaches a maximum at T = 15 K and then decreases to zero to higher temperatures. The significant decrease in H_C observed close to T = 10 K can be related to a competition between the blocked and unblocked particles, which is very usual behavior in superparamagnetic systems. On the other hand, the increment in H_C in the temperature range of 15 < T < 25 K is a consequence of the competition between the magnetic interactions existing on the blocked particles. In fact, one can infer that the surface effects become dominant over those of the particle core and it is more difficult to align the uncompensated spins on the particle shell. Therefore, when decreasing the temperature, a strong contribution from the blocked particles increases the H_C values and consequently the M_R.⁵ Besides, it is not unreasonable to state that this increase in the total magnetization can be related to the formation of short-range spin clusters on the particle surface.^12,13,20

Fig. 7 Coercive field and remanent magnetization as a function of temperature for the Ni_0.90Fe_0.10O sample.

4. Conclusion

In conclusion, single phases of Ni_1−xFe_xO (x = 0, 0.01, 0.05 and 0.10) nanoparticles were synthesized via the co-precipitation method. XRD analysis indicates that there is a slight decrease in the average particle size and an increase in the particle microstrain with increasing iron concentration. The ZFC–FC measurements display two different magnetic behaviors: (i) a progressive blocking process of the core particle moments at around 160 K and then (ii) below 20 K, an anomalous magnetic behavior with an increase in the magnetic moment, which can be associated with spin clusters at the particle surface driving the system into a collective freezing of spins. This latter effect was enhanced with increasing iron concentration. Exchange bias effects were observed in the doped samples and the bias field increased with decreasing amount of Fe. These results are attributed to the interactions between ferromagnetic (particle surface) and antiferromagnetic (core) states. These facts, together with the structural results allow us to state that Fe ions are located on the particle surface once there is a strong change in the surface anisotropy as a function of iron doping. Finally, the anomalous behavior of M_R and H_C at low temperature can also be linked with the strengthening of the surface effects of Fe-doped NiO nanoparticles.

Acknowledgements

This research was supported by CNPq funding agency (Project 577512/2008-0, 477114/2008-3) and FAPITEC.

References

1. C. P. Bean and J. D. Livingston, The Anisotropy of Very Small Cobalt Particles, J. Phys. Radium, 1959, 30, S120.
2. R. H. Kodama, A. E. Berkowitz, E. J. McNiff Jr and S. Foner, Surface spin disorder in NiFe₂O₄ nanoparticles, Phys. Rev. Lett., 1996, 77, 394–397.
3. R. H. Kodama, S. A. Makhlouf and A. E. Berkowitz, Finite Size Effects in Antiferromagnetic NiO Nanoparticles, Phys. Rev. Lett., 1997, 79, 1393–1396.
4. E. De Biasi, C. A. Ramos, R. D. Zysler and H. Romero, Large Surface Magnetic Contribution in Amorphous Ferromagnetic Nanoparticles, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 144416.
5. W. C. Nunes, W. S. D. Folly, J. P. Sinnecker and M. Novak, Temperature Dependence of the Coercive Field in Single-Domain Particle Systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 014419.
6. P. Allia, M. Coisson, P. Tiberto, F. Vinai, M. Knobel, M. A. Novak and W. C. Nunes, Granular Cu-Co Alloys as Interacting Superparamagnets, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 144420.
7. J. L. Dormann, D. Fiorani and E. Tronc, On the Models for Interparticle Interactions in Nanoparticle Assemblies: Comparison with Experimental Results, J. Magn. Magn. Mater., 1999, 202, 251–267.
8. J. L. Dormann, D. Fiorani and E. Tronc, Magnetic Relaxation in Fine-Particle Systems, Adv. Chem. Phys., 1997, 98, 283–494.
9. E. Winkler, R. D. Zysler, M. V. Mansilla and D. Fiorani, Surface Anisotropy Effects in NiO Nanoparticles, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 132409.
10. E. De Biasi, C. A. Ramos and R. D. Zysler, Size and Anisotropy Determination By Ferromagnetic Resonance in Dispersed Magnetic Nanoparticle Systems, J. Magn. Magn. Mater., 2003, 262, 235–241.
11. E. Tronc, D. Fiorani, M. Nogues, A. M. Testa, F. Lucari, F. D'Orazio, J. M. Greneche, W. Wernsdorfer, N. Galvez, C. Chaneac, D. Mailly and J. P. Jolivet, Surface Effects in Noninteracting and Interacting Gamma-Fe(2)O(3) Nanoparticles, J. Magn. Magn. Mater., 2003, 262, 6–14.
12. C. T. Meneses, J. G. S. Duque, E. De Biasi, W. C. Nunes, S. K. Sharma and M. Knobel, Competing Interparticle Interactions and Surface Anisotropy in NiO Nanoparticles, J. Appl. Phys., 2010, 108, 013909.
13. W. Duan, S. H. Lu, Z. L. Wu and Y. S. Wang, Size Effects on Properties of NiO Nanoparticles Grown in Alkali salts, J. Phys. Chem. C, 2012, 116, 26043–26051.
14. C. T. Meneses, W. H. Flores, F. Garcia and J. M. Sasaki, A Simple Route to the Synthesis of High-Quality NiO Nanoparticles, J. Nanopart. Res., 2007, 9, 501–505.
15. G. Williamson and W. Hall, X-ray Line Broadening From Filed Aluminium and Wolfram, Acta Metall., 1953, 1, 22–31.
16. P. Mallick, C. Rath, R. Biswal and R. C. Mishra, Structural and Magnetic Properties of Fe-doped NiO, Indian J. Phys., 2009, 83, 517–523.
17. M. Knobel, W. C. Nunes, L. M. Socolovsky, E. De Biasis, J. M. Vargas and J. C. Denardin, J. Nanosci. Nanotechnol., 2008, 8, 1–20.
18. A. Punnoose, H. Magnone, M. S. Seehra and J. Bonevich, Bulk to Nanoscale Magnetism and Exchange Bias in CuO Nanoparticles, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 174420.
19. S. K. Sharma, J. M. Vargas, E. De Biasi, F. Beron, M. Knobel, K. R. Pirota, C. T. Meneses, S. Kumar, C. G. Lee, P. G. Pagliuso and C. Rettori, The nature and enhancement of magnetic surface contribution in model NiO nanoparticles, Nanotechnology, 2010, 21, 035602.
20. R. Berger, J. C. Bissey, J. Kliava, H. Daubric and C. Estournes, Temperature dependence of superparamagnetic resonance of iron oxide nanoparticles, J. Magn. Magn. Mater., 2001, 234, 535–544.

---