Resistive switching in iron-oxide-filled carbon nanotubes

Abstract

Iron-oxide-filled carbon nanotubes exhibit an intriguing charge bipolarization behavior which allows the material to be applied in resistive memory devices. Raman analysis conducted with an electric field applied in situ shows the Kohn anomalies and a strong modification of the electronic properties related to the applied voltage intensity. In addition, the I_D/I_G ratio indicated the reversibility of this process. The electrical characterization indicated an electronic transport governed by two main kinds of charge hopping, one between the filling and the nanotube and the other between the nanotube shells.

---

Introduction

Many studies have been conducted to develop electronic memories for new and enhanced technological applications, such as nonvolatile memories based on metal oxides.^1,2 These materials commonly exhibit a switching mechanism based on the migration of oxygen vacancies or a filamentary conducting path, both of which are motivated by high voltages applied to the material.^1,3 Regarding this fact, one possibility is the use of an oxide encapsulated by carbon nanotubes (CNTs), which can be used in electrical memory applications.⁴ The encapsulation of oxides by carbon walls preserves their pristine characteristics, and the extraordinary mechanical and manufacturing properties of carbon nanotubes (CNTs) are transferred to the new material.^5,6 These nanomaterials exhibit new electrical, optical, and mechanical properties due to the synergistic effect between the carbon nanotube (CNT) and its filling.^7–10

In this paper, we investigate and discuss the intriguing electrical behavior of iron-oxide-filled multiwalled carbon nanotubes (Fe-MWCNTs) and explain how the effects are advantageous for application in a resistive memory device. To identify the material electronic state over a range of several applied voltages, the Raman spectra were acquired during the device operation, and the main Raman active modes of the carbon nanotubes were studied. The applied voltage dependence on the G band indicated Kohn anomalies, which are strongly related to the material's electronic state. The ratio between the D band and G band intensities (I_D/I_G) also provided important information about the material electronic structure and the memory device operation. The electronic characterization indicates the existence of two main hopping charge transports, one between the carbon nanotube walls and another between the filling and the carbon nanotube. The combination of these processes with iron-oxide oxygen migration is specific to this type of carbon nanotube and allows the bipolar resistive switching between two different electronic states. The switching behavior exhibited by a carbon nanotube provides this material class with new features and opens up the possibility of its application in resistance random access memory (ReRAM).

Experimental

Fe-MWCNT production

The Fe-MWCNTs used in this work were produced from ferrocene pyrolysis under a controlled atmosphere based on a previous study by Schnitzler et al.¹¹ The images of the samples revealed that approximately 87% are composed of filled multiwalled carbon nanotubes, with an average diameter between 40 and 100 nm¹² and a length of 20 μm. Although the Fe-MWCNTs presented some imperfections, such as bucky-onions and carbon nanopolyhedra in small quantities, no purification method was applied to preserve the original characteristics of the sample. The diffractometry and the HRTEM analyses for this material indicated the presence of Fe₂O₃, Fe₃O₄, and metallic iron filling in the MWCNTs.¹¹ Some electrical and magnetic characterizations of these nanotubes are also presented in ref. 4 and 8.

Characterization

To study the material's electrical properties, a device with a planar geometry was designed (inset, Fig. 1a). The device was assembled onto a well cleaned glass substrate, where a titanium layer (10 nm thick) and a gold layer (100 nm thick) were thermally evaporated in a low-pressure chamber to produce the electrical contacts. These electrodes have a micrometric gap (7 μm) between them, where the Fe-MWCNTs are deposited. This micrometric separation was achieved by a carbon microfiber shadow mask with a 7–9 μm diameter placed on the substrate before the metal evaporation. The Fe-MWCNT dispersion used at the deposition was prepared from 0.3 mg of Fe-MWCNTs dispersed in chloroform (20 mL) using an ultrasonic bath (90 min). The nanotube dispersion was then deposited between the electrodes by casting at 70 °C until film formation was observed. A scanning electron microscopy (SEM) image from the device active region is shown in the inset of Fig. 1a. This image clearly shows the Fe-MWCNT net covering both electrodes, allowing electronic transport between them.

Fig. 1 (a) Characteristic current intensity versus voltage curve (I–V) for the Fe-MWCNT planar device; the inset presents curves for different initial applied voltages, 0 to 30 V and −30 to 30 V; a schematic representation of the measurement set-up, with the Raman laser incident; and a device SEM image. (b) Fe-MWCNT Raman spectra for an applied voltage range of −40 to 40 V in both directions (indicated by the arrows). The darker line indicates zero voltage applied.

The electrical current versus applied voltage (I–V) was obtained from an Agilent semiconductor parameter analyzer (4155C) with a limited compliance current of 100 μA to avoid damaging the sample. The I–V analyses, shown in Fig. 1a, exhibit the characteristic curve shape of a net of Fe-MWCNTs between two identical electrodes. This measurement analyzes the electrical current intensity from an external voltage applied from −30 to 30 V (forward direction, increasing) and from 30 to −30 V (backward direction, decreasing), indicated by arrows on the figure, at a voltage step of 0.05 V with a scan rate of 2 V s⁻¹. Two intense electric current peaks are identified in the I–V curve: one in the positive region for the forward applied voltage and the other in the negative region for the backward applied voltage. The highest positive electrical current peak, near 6 V, only occurs after the negative voltage has been applied; likewise, the negative electrical current peak near −6 V only occurs after the positive voltage has been applied. Thus, the application of the opposite voltage on the sample is necessary to yield a peak in the next voltage region. The inset in Fig. 1a demonstrates this feature; when the voltage is at 0 V, there is no electrical current peak. Therefore, if a new measurement is performed starting with a negative applied voltage, the peak appears in the same region as before. It is important to note that the I–V curve presents small perturbations after the peak, which is attributed to the different CNTs (sizes and diameters) present in this sample. For similar devices, this current peak is not detected when regular, unfilled MWCNTs are used, as tested by our group (ESI†) and shown in other studies.^13,14

Results and discussion

The I–V analyses revealed a bipolar behavior, which should correspond to modifications of the material electronic state. Therefore, we used Raman spectroscopy to identify modifications due to the electron–phonon interactions on the material surface. Raman spectroscopy has been extensively applied to characterize carbon materials, such as carbon nanotubes and graphene.^15,16

A schematic illustration of the set-up used simultaneously to apply an external voltage and acquire the Raman intensity is shown in Fig. 1a. The Raman spectra were acquired from a Renishaw spectrophotometer with an excitation line achieved from a 2.41 eV Ar⁺ laser focused by a 50× lens (Leica) with a spectral resolution of 1 cm⁻¹. Before the measurements, the laser beam was focused on the sample with the chosen power (1.40 mW) for 15 min to ensure that the equilibrium temperature is reached before the spectra are acquired. Care was taken to acquire all spectra from the same location on the sample. The spectra were acquired in one accumulation process with a hold time of 10 s. Before the start of each acquisition, a specific voltage was applied between the electrodes for 1 min. This process was repeated for several voltages ranging from −40 to 40 V (forward direction) and from 40 to −40 V (backward direction). The main result is shown in Fig. 1b. The Raman laser spot, with a diameter of approximately 1 μm, was focused exactly on the center of the gap to avoid any interference from the metal electrodes. The arrows in Fig. 1b indicate the applied voltage direction and reference values. All modes also exhibit a blue shift when the forward direction voltage is applied, regressing to the initial position as the voltage is applied backwards.

All the common intense active modes for MWCNTs are found between 1200 and 3000 cm⁻¹. For the Raman spectrum at zero applied voltage (V = 0), the Lorentzian line shape analyses revealed the G band, located at ∼1580 cm⁻¹, as well as the D band at ∼1354 cm⁻¹, the D′ band at ∼1618 cm⁻¹, and the G′ band at ∼2700 cm⁻¹; all of these wavenumbers are in agreement with previously published values.^17–21

The Lorentzian line shape analyses for the G band position as a function of applied field voltage are presented in Fig. 2a. All sp² carbon layer networks share a doubly degenerate phonon mode called the G band, corresponding to the E_2g symmetry about the Brillouin zone center.²¹Fig. 2a shows the dependence of the G band on the applied voltage, which clearly shows an almost linear phonon energy increase with the forward applied voltage and an abrupt change during the energy reduction for the backward applied voltage. A blue shift/red shift of ∼7 cm⁻¹ is observed when the voltage is applied in a forward/backward direction. Importantly, at zero applied voltage, the band positions have similar values in the forward and backward directions; however, in the region between 2 and 10 V (electrical current peak region), there is a difference of at least 3 cm⁻¹ between the forward direction and the backward direction at the same voltage. The same feature is observed for the negative applied voltage. The same analyses for the D (Fig. 2b) and the G′ band (Fig. 2c) revealed a shift of ∼7 cm⁻¹ for the backward direction and small values for the forward direction. This mode also presented a difference of ∼3 cm⁻¹ between the forward direction and the backward direction applied voltages. The relative intensity difference between the D band and the G band (I_D/I_G) analyses is presented in Fig. 2d. I_D/I_G increases, presenting an abrupt change from −10 V to 10 V, with a difference of ∼0.25 between the initial negative voltage applied and the final positive voltage applied. Despite the small differences between the forward and backward directions in the I_D/I_G analysis, the curve shapes are the same, which indicates the reversibility of the process, considering that the relative intensity is almost the same at the cycle's start and end. The case of the D′ band shift was similar, as shown in Fig. 1b, and it is possible to identify a blue shift (4 cm⁻¹) as the voltage increased to 40 V and the same red shift as the voltage decreased again.

Fig. 2 Raman mode energies as a function of the applied voltage in both directions. The solid square represents −40 to 40 V (forward), and the empty circle represents 40 to −40 V (backward). (a) The G band applied voltage dependence; (b) the D band applied voltage dependence; (c) the G′ band applied voltage dependence; and (d) the I_D/I_G relative intensity applied voltage dependence.

Fig. 2a shows the G band, which presents a non-linear shift related to the voltage applied to the Fe-MWCNTs. It is important to note that the curve shape for this Raman active mode differs depending on the direction of the applied voltage. The Raman measurements presented share some similarities with electron–phonon coupling in gate voltage dependence experiments,^22–24 relating the material's electronic doping, promoted by the applied field, with phonons from the optical measurements. However, most of the recent studies concerning this physical phenomenon are theoretical or experimental studies using very well purified monolayer or bilayer graphene,^22,25–27 single-walled carbon nanotubes,^23,28–30 graphite,³¹ or MWCNTs,³² all of which use a transistor device as a single element between the source and drain electrode. Here, we discuss the effect of the applied voltage under Fe-MWCNTs, which are comprised of a metal oxide filling covered by several graphene layers. Although we are testing a complex material, a comparison with these models would be valuable.

Analyzing the values presented with the forward voltage ramp between −40 and 40 V, the G band shifts are identified between 1576 and 1583 cm⁻¹, the first of which is typical for small CNT metallic tubes¹⁵ and the second of which is characteristic of graphite-like materials.²¹ When the opposite voltage ramp is applied (backward voltage), the materials still present graphite-like frequencies, with an abrupt change for lower frequencies down to −40 V. However, our samples have a large diameter (40 to 100 nm) and a diameter reduction motivated by an applied voltage that cannot be used in order to explain the energy phonon reduction.

To explain these results, it is important to remember that Fe-MWCNTs are a strongly electron-doped material due to the CNT filling and are composed of iron oxides, which are strongly correlated materials. Thus, the CNTs tested here present a different electron charge distribution than do regular MWCNTs, and a metallic behavior is expected due to the electrical characteristics of the MWCNTs and the additional charge from the filling.

In fact, the G band blue shift, presented by metallic CNTs under an external voltage applied, is an expected feature due to the large electric field applied, which induced changes in the charge density at the superficial carbon layer, resulting in a shifted phonon frequency.³³ This phonon blue shift, regarding an external voltage applied, is explained by the electron–phonon coupling renormalization which is related to the Kohn anomaly in the E_2g mode phonon dispersion.^24,34 From Fig. 2a it is possible to verify this phenomenon up to 40 V. This fact indicates a Fermi surface distortion above the K point, due to the high electron doping, which is responsible for the phonon blue shift.^30,33

The red shift for negative applied voltages is a unique result, as the previous results for monolayer graphene,³³ SWCNTs,²⁴ and MWCNTs³² only presented a blue shift, even for negative gate voltages. These results corroborate our control sample in which the non-filled MWCNTs were tested (see ESI†). The almost totally filled MWCNT characteristic should enhance the contribution of the innermost shells, further distorting the surface charge density. Thus, an increase of the contribution of the innermost carbon layers to the Raman spectra is expected. In fact, regarding the electron–phonon coupling and the Kohn anomaly, a phonon energy reduction should be motivated by a Fermi surface distortion below the Fermi surface at 0 V. Although this behavior is not yet fully explained for MWCNTs, some recent studies attributed the red shift to the intensification of new bands, promoting the interlayer interaction in graphene structures.^22,35 We are not able to prove or disprove this theory due to the number of carbon layers in our system. Moreover, some studies present this red shift as distortions of the occupied electronic levels,^24,30 which can complement and justify our results due to the large electronic doping in our system promoted by the carbon nanotube filling.

The D band originated from a double resonance intravalley highly dispersive process activated by the presence of defects.³⁶ This double resonance process, characteristic of this band, is strongly dependent on the material electronic configuration at the K and K′ regions.^29,37 Thus, this characteristic allows the D band to shift when an external agent promotes electronic distortions at the first Brillouin zone center. In our system, the applied voltage distorts the superficial electronic distribution, which can shift the D band, as observed in Fig. 2b. The D band is an expected feature, similar to the G band, as the charge density is also capable of modifying the double resonance phonon generation.³⁴

The D band overtone, G′, is very sensitive to the stacking order and is always present in graphite-like materials.^38,39 Some dispersive behavior is also expected for this mode, and its energy shift should present a similar shape to that of the D band.^18,34 This shift was also observed in Fig. 2c, in which the curve shape is similar to that of Fig. 2a.

The ratio between the D band and G band intensities (I_D/I_G) can provide some important information about the material structure.^16,21Fig. 2d presents the I_D/I_G ratio versus the applied voltage, which shows the same shape as the other curves, besides the small differences between the forward and backward directions. This feature testifies to the good reversibility of this process. Even if we consider that an increase in this ratio represents an increase in disorder, this disorder returns to the same beginning level. This good reversibility is a desired feature for memory devices, which must constantly switch between high- and low-conductivity states. Another observation from Fig. 2d is that the ratio saturates near ±15 V, which means that at this voltage, most of the material elements have reached maximum conductivity.

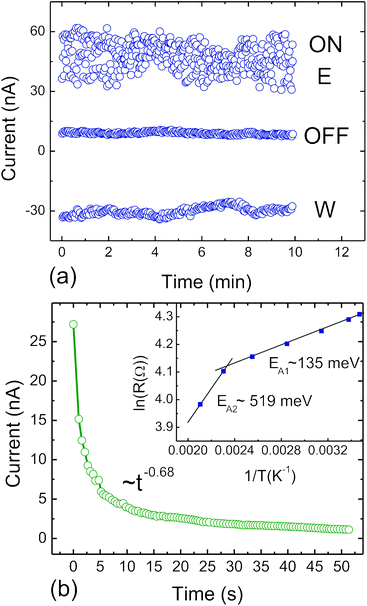
Based on these results, it is possible to conclude that there are two different electronic states promoting phonons with different energies for the same applied voltage (±6 V), which are related to the direction of the electric field. Here, we suggest that the shift difference occurs due to the reminiscent charge polarization. Once the voltage is applied in different directions, the device is still under the same electronic conditions until the space charge at the filling changes its polarization; for this sample, this phenomenon begins at ±10 V. This feature leads to the possibility of using this material as a resistive memory device capable of writing, reading, and erasing information many times.⁴Fig. 3a shows the same Fe-MWCNT device working as a resistive memory device for a duration of 10 min.

Fig. 3 (a) Fe-MWCNT resistive memory operating for 10 min with the voltage current dependence; the operation process is comprised of write (−10 V), read ON (+7 V), erase (+10 V), and read OFF (−7 V). (b) Current versus time (I–t) with 7 V applied after a pulse of −10 V; the inset is the resistance versus temperature curve (R–T) for Arrhenius analyses showing activation energies.

Here, it is possible to identify the processes of write (W), read (ON), erase (E), and read again (OFF). In this test, the information was written using an applied voltage of −10 V; the recorded information was read at 7 V, at which it is possible to identify the high-conductivity state (ON); the information was erased by applying 10 V; and the information was accessed again at 7 V, at which the low-conductivity state (OFF) can be verified. All of these processes (write, read, erase, and read again) were conducted within 28 ms with an ON/OFF difference of approximately 40 nA. This ON/OFF difference is related to the device construction parameters, and high values can be obtained by changing the device dimensions.

The Raman analyses revealed the strong modification of the material's electronic state due to the applied external field and its reversibility. These measurements corroborate the electrical behavior of the iron oxide filling the CNT, as reported here and in ref. 4. However, the mechanism of this behavior is still under discussion.

The electrical behavior exhibited by the Fe-MWCNTs (Fig. 1a) is similar to that of electrically polarized systems with some atom or oxygen ions/vacancies displacements,^40–42 or structure distortions⁴³ induced by an external electric field. To eliminate the atom displacement possibility, we performed a polarization versus voltage test using a Sawyer–Tower circuit (ESI†), which indicates the leakage current instead of the ferroelectric properties. Usually, the leakage current can be induced by an oxygen vacancy concentration, space charge trapping, dipole complexes, or electrical charge hopping.⁴⁴ The time-dependent current under a constant applied voltage (7 V) after one pulse of the opposite voltage (−10 V) is presented in Fig. 3b. This discharge curve can be described using the empirical Curie-von Schweidler equation,⁴⁵ simplified as I(t) ∼ t^−α, where it was found that α = 0.68 ± 0.01 at 300 K, which can be assigned to space-charge polarization and electron charge hopping.^46,47

The energy needed to activate the electronic transport in this material was determined by measuring the electrical resistance versus temperature. The inset of Fig. 3b shows the Arrhenius analysis, which confirms the thermal-activated transport with two different activation energies: E_A1, with a value of ∼135 meV, and E_A2, with a value of ∼519 meV. These results were obtained by monitoring the temperature as a function of the device electrical resistivity in an inert atmosphere (N₂), as shown in the equation below, where R_(T) is the temperature-dependent electrical resistance, R₀ is the intrinsic electrical resistance, and the k_BT is the Boltzmann constant multiplied by the temperature.

R_(T) = R₀ exp[−E_A/(k_BT)] (1)

Fe-MWCNTs are a complex material combining two different classes of materials. Thus, it is important to consider that any electronic transport should occur in at least two different regions. Analyzing the activation energies, we attribute E_A1 to the MWCNT inter-shell transport (inter-layer), which agrees with the hopping energy between the nanotube layers, as presented in ref. 13. E_A1 was ascribed to the filling-MWCNT transport (filling-tube). We found this E_A2 value to be in agreement with the hopping energy range (300 to 800 meV) for electronic hopping between a metal or metal oxide to a carbon layer.^48–50 Here, we consider the inter-tube electrical resistance to be a constant due to its linear contribution and non-thermal activation,⁵¹ which should not affect the main shape of the I–V characteristic curve. It is well-known that a pure MWCNT net presents an electronic conduction described by a Poole–Frenkel model with the inter-layer transport activated by cross-shell defects.¹³

Charge polarization is not often observed in CNTs; in fact, this feature is commonly found in metal oxide materials.^1,52 In a previous study,⁴ we demonstrated that α-Fe₂O₃ with similar characteristics also presents a non-linear I–V curve and the memory effect. Thus, it remains unclear as to how the filling contributes to the electronic transport on the carbon nanotube network. According to some recent studies regarding CNTs,^13,32,53 the applied electric field increase promotes charge injection from the outermost layer down to the innermost MWCNT layer and vice versa. For pure MWCNTs, this results in a nonlinear conductivity governed by at least two different regimes dependent on the electric field intensity.⁵⁴ In particular, the contributions of the innermost shells are more intense for filled MWCNTs, and the presence of a foreign material inside the nanomaterial can strongly modify its electronic transport. Likewise, the work presented by Chimowa et al. demonstrates that an increase in the metallic material filling content in the MWCNT results in a more weakly localized conductivity promoted by the participation of the filling in the electronic properties.⁵³

Considering these facts, it becomes evident that the filling strongly contributes to the electronic transport of the Fe-MWCNTs presented herein. However, our device's conductivity experiences an abrupt change in the region of ∼6 V, and our filled-MWCNT contains iron oxide species, which commonly present an intriguing electrical behavior. We propose that the electronic conductivity process is regulated by two hopping processes: one between the MWCNT layers (inter-layer hopping) and one between the filling and the tube (filling-tube hopping). This latter process is responsible for the current peak, which only occurs if the charges from the filling are polarized by a large, opposite voltage.⁵⁵ Therefore, when the voltage increases up to a certain region, in this case ∼6 V, to activate the filling-tube hopping, the MWCNT layers begin to receive a limited number of new charges from the filling, resulting in an increase in the electrical current. In this case, the limited number of charges turns out to be responsible for the apparent negative differential resistance shown at the I–V curve.⁵⁵

The bipolarization process, commonly induced by an opposite applied voltage, is necessary to polarize the space charges in the filling, which is typical for superficial oxygen ion migration on oxides.^3,41,56,57 In fact, in our theoretical study about hematite,⁵⁷ this material presents relevant modifications on its electronic structure due to the presence of oxygen vacancies.

The combination of these processes, in which the electrical current is tuned or not depending on the previous voltage applied, allowed the construction of a resistive memory device based on the Fe-MWCNT resistive switch. A schematic illustration of the Fe-MWCNT discharge is provided in Fig. 4.

Fig. 4 Sketch illustrating the charge transport at the discharge moment.

Here, we represent the charge hopping between the MWCNT layers (black circles). When the device achieves a specific voltage, the ionic charges in the filling (white circles), polarized by a previous opposite voltage, undergo a secondary hopping process, transferring new charges to the nanotube layers, which are responsible for the current peak at a specific voltage.

Conclusions

In conclusion, we have presented Raman analysis and electrical characterization of Fe-MWCNTs, which reveals a charge bipolarization on this material. The Raman studies with an electric field applied in situ demonstrate the presence of Kohn anomalies, and a strong modification of the electronic state was observed. The I_D/I_G analysis demonstrates that this process has good reversibility and indicated the maximum voltage needed for recording information. The electronic transport was shown to be governed by the hopping between the nanotube shells and the hopping between the filling and the nanotube. The combination of the iron-oxide electrical behavior and the MWCNT characteristics allows the application of this material in resistive memory devices.

Acknowledgements

The authors acknowledge financial support from the Brazilian agencies CAPES, CNPq, F. Araucária/CNPq, the National Institute of Science and Technology in Carbon Nanomaterials, and the National Network of Carbon Nanotubes Research. Cava C. E. thanks Rodrigo Salvatierra for fruitful discussions.

Notes and references

1. A. Sawa, Mater. Today, 2008, 11, 28–36.
2. J. Doo Seok, T. Reji, R. S. Katiyar, J. F. Scott, H. Kohlstedt, A. Petraru and H. Cheol Seong, Rep. Prog. Phys., 2012, 75, 076502.
3. M. J. Rozenberg, M. J. Sánchez, R. Weht, C. Acha, F. Gomez-Marlasca and P. Levy, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 115101.
4. C. E. Cava, R. Possagno, M. C. Schnitzler, P. C. Roman, M. M. Oliveira, C. M. Lepiensky, A. J. G. Zarbin and L. S. Roman, Chem. Phys. Lett., 2007, 444, 304–308.
5. F. Rossella, C. Soldano, V. Bellani and M. Tommasini, Adv. Mater., 2012, 24, 2453–2458.
6. G. Korneva, H. Ye, Y. Gogotsi, D. Halverson, G. Friedman, J.-C. Bradley and K. G. Kornev, Nano Lett., 2005, 5, 879–884.
7. E. Nossol and A. J. G. Zarbin, Adv. Funct. Mater., 2009, 19, 3980–3986.
8. A. E. P. de Araújo, J. G. S. Duque, M. Knobel, M. C. Schnitzler and A. J. G. Zarbin, J. Magn. Magn. Mater., 2007, 312, 32–34.
9. M. Koehler, C. D. Canestraro, M. C. Schnitzler, M. M. Oliveira, A. J. G. Zarbin, L. S. Roman and M. G. E. d. Luz, EPL, 2007, 79, 47011.
10. C. D. Canestraro, M. C. Schnitzler, A. J. G. Zarbin, M. G. E. da Luz and L. S. Roman, Appl. Surf. Sci., 2006, 252, 5575–5578.
11. M. C. Schnitzler, M. M. Oliveira, D. Ugarte and A. J. G. Zarbin, Chem. Phys. Lett., 2003, 381, 541–548.
12. R. V. Salvatierra, C. E. Cava, L. S. Roman and A. J. G. Zarbin, Adv. Funct. Mater., 2013, 23, 1490–1499.
13. S. Agrawal, M. S. Raghuveer, R. Ramprasad and G. Ramanath, IEEE Transactions on Nanotechnology, 2007, 6, 722–726.
14. S. Fan, M. G. Chapline, N. R. Franklin, T. W. Tombler, A. M. Cassell and H. Dai, Science, 1999, 283, 512–514.
15. A. Jorio, R. Saito, G. Dresselhaus and M. S. Dresselhaus, Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 2004, vol. 362, pp. 2311–2336.
16. L. G. Cançado, A. Jorio, E. H. M. Ferreira, F. Stavale, C. A. Achete, R. B. Capaz, M. V. O. Moutinho, A. Lombardo, T. S. Kulmala and A. C. Ferrari, Nano Lett., 2011, 11, 3190–3196.
17. P. Tan, S.-L. Zhang, K. T. Yue, F. Huang, Z. Shi, X. Zhou and Z. Gu, J. Raman Spectrosc., 1997, 28, 369–372.
18. A. Jorio, M. A. Pimenta, A. G. S. Filho, R. Saito, G. Dresselhaus and M. S. Dresselhaus, New J. Phys., 2003, 5, 139.
19. P. Tan, L. An, L. Liu, Z. Guo, R. Czerw, D. L. Carroll, P. M. Ajayan, N. Zhang and H. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 245410.
20. A. G. S. Filho, A. Jorio, G. S. Ge, G. Dresselhaus, R. Saito and M. S. Dresselhaus, Nanotechnology, 2003, 14, 1130.
21. M. A. Pimenta, G. Dresselhaus, M. S. Dresselhaus, L. G. Cancado, A. Jorio and R. Saito, Phys. Chem. Chem. Phys., 2007, 9, 1276–1290.
22. L. M. Malard, D. C. Elias, E. S. Alves and M. A. Pimenta, Phys. Rev. Lett., 2008, 101, 257401.
23. H. Farhat, K. Sasaki, M. Kalbac, M. Hofmann, R. Saito, M. S. Dresselhaus and J. Kong, Phys. Rev. Lett., 2009, 102, 126804.
24. J. C. Tsang, M. Freitag, V. Perebeinos, J. Liu and P. Avouris, Nat. Nanotechnol., 2007, 2, 725–730.
25. J. Yan, E. A. Henriksen, P. Kim and A. Pinczuk, Phys. Rev. Lett., 2008, 101, 136804.
26. T. Ando, J. Phys. Soc. Jpn., 2007, 76, 104711.
27. J. Yan, Y. Zhang, P. Kim and A. Pinczuk, Phys. Rev. Lett., 2007, 98, 166802.
28. K. T. Nguyen, A. Gaur and M. Shim, Phys. Rev. Lett., 2007, 98, 145504.
29. E. R. Margine, P. E. Lammert and V. H. Crespi, Phys. Rev. Lett., 2007, 99, 196803.
30. Y. Wu, J. Maultzsch, E. Knoesel, B. Chandra, M. Huang, M. Y. Sfeir, L. E. Brus, J. Hone and T. F. Heinz, Phys. Rev. Lett., 2007, 99, 027402.
31. C.-H. Park, F. Giustino, M. L. Cohen and S. G. Louie, Nano Lett., 2008, 8, 4229–4233.
32. S. Nanot, M. Millot, B. Raquet, J.-M. Broto, A. Magrez and J. Gonzalez, Phys. E, 2010, 42, 2466–2470.
33. S. Pisana, M. Lazzeri, C. Casiraghi, K. S. Novoselov, A. K. Geim, A. C. Ferrari and F. Mauri, Nat. Mater., 2007, 6, 198–201.
34. A. C. Ferrari, Solid State Commun., 2007, 143, 47–57.
35. M. Bruna and S. Borini, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125421.
36. F. Tuinstra, J. Chem. Phys., 1970, 53, 1126.
37. C. Thomsen and S. Reich, Phys. Rev. Lett., 2000, 85, 5214–5217.
38. H. Wilhelm, M. Lelaurain, E. McRae and B. Humbert, J. Appl. Phys., 1998, 84, 6552–6558.
39. A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov, S. Roth and A. K. Geim, Phys. Rev. Lett., 2006, 97, 187401.
40. H. W. Jang, A. Kumar, S. Denev, M. D. Biegalski, P. Maksymovych, C. W. Bark, C. T. Nelson, C. M. Folkman, S. H. Baek, N. Balke, C. M. Brooks, D. A. Tenne, D. G. Schlom, L. Q. Chen, X. Q. Pan, S. V. Kalinin, V. Gopalan and C. B. Eom, Phys. Rev. Lett., 2010, 104, 197601.
41. D. S. Jeong, H. Schroeder and R. Waser, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 195317.
42. K. Szot, W. Speier, G. Bihlmayer and R. Waser, Nat. Mater., 2006, 5, 312–320.
43. S. Lee, A. Pirogov, M. Kang, K.-H. Jang, M. Yonemura, T. Kamiyama, S. W. Cheong, F. Gozzo, N. Shin, H. Kimura, Y. Noda and J. G. Park, Nature, 2008, 451, 805–808.
44. I. Stolichnov and A. Tagantsev, J. Appl. Phys., 1998, 84, 3216–3225.
45. A. K. Jonscher, Dielectric relaxation in solids, Chelsea Dielectrics Press, 1983.
46. H. Kliem, IEEE Transactions on Dielectrics and Electrical Insulation, 2005, 12, 709–718.
47. X. G. Tang, J. Wang, Y. W. Zhang and H. L. W. Chan, J. Appl. Phys., 2003, 94, 5163–5166.
48. M. Bruzzi, P. Piseri, S. Miglio, G. Bongiorno, E. Barborini, C. Ducati, J. Robertson and P. Milani, Eur. Phys. J. B, 2003, 36, 3–13.
49. V. K. Singh, M. K. Patra, M. Manoth, G. S. Gowd, S. R. Vadera and N. Kumar, New Carbon Mater., 2009, 24, 147–152.
50. P. Li, D. E. Miser, S. Rabiei, R. T. Yadav and M. R. Hajaligol, Appl. Catal., B, 2003, 43, 151–162.
51. A. Allaoui, S. V. Hoa, P. Evesque and J. Bai, Scr. Mater., 2009, 61, 628–631.
52. S. Yu, Y. Wu and H. S. P. Wong, Appl. Phys. Lett., 2011, 98, 103514.
53. G. Chimowa, E. C. Linganiso, D. Churochkin, N. J. Coville and S. Bhattacharyya, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 205429.
54. S. Agrawal, M. S. Raghuveer, H. Li and G. Ramanath, Appl. Phys. Lett., 2007, 90, 193104.
55. D. B. Strukov, G. S. Snider, D. R. Stewart and R. S. Williams, Nature, 2008, 453, 80–83.
56. O. Warschkow, D. E. Ellis, J. Hwang, N. Mansourian-Hadavi and T. O. Mason, J. Am. Ceram. Soc., 2002, 85, 213–220.
57. C. E. Cava, L. S. Roman and C. Persson, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 045136.

---

Footnote

† Electronic supplementary information (ESI) available: See DOI: 10.1039/c3nr04320g

---