Interplay between microstructure and magnetism in NiO nanoparticles: breakdown of the antiferromagnetic order†
N.
Rinaldi-Montes
*a,
P.
Gorria
a,
D.
Martínez-Blanco
a,
A. B.
Fuertes
b,
L.
Fernández Barquín
c,
J.
Rodríguez Fernández
c,
I.
de Pedro
c,
M. L.
Fdez-Gubieda
d,
J.
Alonso
d,
L.
Olivi
e,
G.
Aquilanti
e and
J. A.
Blanco
a
aDepartamento de Física, Facultad de Ciencias, Universidad de Oviedo, Calvo Sotelo s/n, 33007, Oviedo, Spain. E-mail: nataliarin@gmail.com
bInstituto Nacional del Carbón (CSIC), Apartado 73, 33080, Oviedo, Spain
cCITIMAC, Facultad de Ciencias, Universidad de Cantabria, 39005, Santander, Spain
dUniv. Basque Country, EHU, Dept. Elect & Elect. and BCMaterials, E – 48080, Bilbao, Spain
eSincrotrone Trieste S.C.p.A., S.S. 14 Km 163.5, 34149 Basovizza, Trieste, Italy
First published on 9th October 2013
Abstract
The possibility of tuning the magnetic behaviour of nanostructured 3d transition metal oxides has opened up the path for extensive research activity in the nanoscale world. In this work we report on how the antiferromagnetism of a bulk material can be broken when reducing its size under a given threshold. We combined X-ray diffraction, high-resolution transmission electron microscopy, extended X-ray absorption fine structure and magnetic measurements in order to describe the influence of the microstructure and morphology on the magnetic behaviour of NiO nanoparticles (NPs) with sizes ranging from 2.5 to 9 nm. The present findings reveal that size effects induce surface spin frustration which competes with the expected antiferromagnetic (AFM) order, typical of bulk NiO, giving rise to a threshold size for the AFM phase to nucleate. Ni2+ magnetic moments in 2.5 nm NPs seem to be in a spin glass (SG) state, whereas larger NPs are formed by an uncompensated AFM core with a net magnetic moment surrounded by a SG shell. The coupling at the core–shell interface leads to an exchange bias effect manifested at low temperature as horizontal shifts of the hysteresis loop (∼1 kOe) and a coercivity enhancement (∼0.2 kOe).
Introduction
The steadily increasing interest in magnetic nanoparticles (NPs) over the past decade has been motivated by the unusual size-dependent magnetic behaviours and by their numerous applications in modern nano-electronics, magnetic separation or biomedical areas.1–7 The growing research activity in this field has been propelled by the development of new chemical routes that allowed the synthesis of NPs with tuneable size distributions and being embedded in different insulating matrices.8–16 It is worth noting that NPs of the same material and similar size but synthetized using different fabrication routes show a strong dependence of the magnetic properties on the morphology, microstructure or the nature of the matrix.1,8,10,13 Moreover, 3d metal oxide NPs with different core–shell morphologies are also good candidates for a number of applications due to the possibility of tuning the magnetic response and/or the coating with a functional layer.2,4,13–15 Therefore, a comprehensive study combining advanced structural characterization techniques and meticulous magnetic measurements is needed to elucidate the microstructure–magnetism interplay at the nanoscale.Nickel oxide (NiO) has been under extensive research for decades due to its importance in numerous technological applications (i.e., catalysis, batteries, ceramics, etc.). Nowadays, nanosized NiO particles have generated a renewed interest because the combination of their unique properties (i.e., high surface area, short diffusional paths, exceptional magnetic properties, etc.) opens an avenue for their use in fields as diverse as catalysis,17–19 anodic electrochromism,20 capacitors,21 smart windows,22 fuel and solar cells23,24 or biosensors.25 Specially intense research effort is being made to combine NiO with graphene in order to develop highly functional energy storage systems26,27 and electrochemical sensors.28
From a magnetic standpoint, bulk NiO is an antiferromagnetic (AFM) material with a Néel temperature (TN) of ∼523 K. An intriguing aspect is that when the size of magnetic materials is reduced down to the nanometric scale they start to exhibit a magnetic behaviour that may differ markedly from their massive counterparts.7,12,17,29 If the crystallite size is reduced, the ratio between surface and volume atoms increases and the surface coordination number is modified. Frequently, the presence of defects and broken bonds is detected not only for the atoms sitting at the surface but also in the first submerged layers. The magnetic structure of materials with a negative exchange coupling between magnetic sublattices (antiferromagnetic, AFM, and ferrimagnetic, FMI, in general) is particularly sensitive to this local periodicity-breaking.30–34 Low temperature high net magnetic moment and hysteresis,35–45 together with training and exchange bias (EB) effects46,47 have been reported as unusual features in NiO NPs. This anomalous magnetic scenario has been modelled in different ways. Kodama first proposed a theoretical multi-sublattice structure based on Monte Carlo calculations.39 Recently, several experimental works have considered that each NP would be formed by a spin–glass (SG) shell strongly coupled to the AFM core. The core–shell morphology is also consistent with the reported presence of two peaks in the zero-field-cooling magnetization curve.35–38,40–42,44
Unfortunately, previous works on NiO NPs were limited to focus either on the structure of the NPs48–50 or on their magnetic behaviour.35–47 Moreover, studies covering both aspects are scarce and mainly devoted to the defect structure at the surface of NPs of a given size.51–53 This neglects other structural possibilities to explain the general trend and, what is more, the use of a single sample refrains the establishment of NP size effects on the magnetism of the system, only possible through a systematic study of a series of samples with different size distributions. Consequently, our conviction is that microstructure and magnetic properties are so intimately linked at the nanoscale that only a joint analysis combining experimental techniques can provide a global approach. In order to achieve this purpose, we have prepared three samples with controlled sizes (2.5, 4 and 9 nm); characterized their crystal structure and microstructure by X-ray diffraction (XRD), high-resolution transmission electron microscopy (HRTEM) and X-ray absorption spectroscopy (XAS); and studied the magnetic properties through the temperature and magnetic field dependences of the magnetization.
Experimental
Preparation of the materials
A commercial activated carbon (AC) was used as a nano-template for the synthesis of NiO NPs. The AC material, supplied by Osaka Gas (Japan), has a large Brunauer–Emmett–Teller (BET) surface area of 2350 m2 g−1, a high pore volume of 1.47 cm3 g−1 and porosity made up of mesopores of up to 6–7 nm in diameter (∼2.5 nm in average). The synthetic method is based on a pyrolysis process that takes place within the restricted volume formed by the AC porosity. In a typical fabrication procedure, 1 g of AC was impregnated with a solution formed by 1 g nickel(II) nitrate hexahydrate in 4 mL of ethanol. The impregnated sample was vacuum dried at 323 K for several hours and subsequently heat-treated in N2 atmosphere or air up to the fixed temperature. In the case of the S1 sample, the heat treatment was carried out under N2 up to 573 K and kept at this temperature for 1 h. Under these conditions, Ni salt decomposed into NiO and the obtained sample consisted of very small NiO aggregates inserted into a carbon matrix, which constituted 80 wt%. If the temperature is increased, NiO will reduce by means of carbon and Ni NPs will be formed. Samples S2 and S3, were obtained by heat treatment in air at 573 K for 3 h and at 673 K for 1 h, respectively. By following this later path, NiO nucleates forming larger NPs as the heating temperature increases and, at the same time, the gasification of the carbon matrix occurs (C + O2 → CO2), which is promoted by the catalytic action of NiO NPs. In the case of the S3 sample, the carbon matrix was completely removed, while the S2 sample still contains around 25 wt% of carbon as deduced from thermo-gravimetric analysis.Characterization methods
The crystalline structure of the samples was investigated by means of room temperature X-ray powder diffraction (XRD). The patterns were collected on a Philips X'Pert PRO MPD diffractometer operating at 45 kV and 40 mA, equipped with a germanium Johansson monochromator that provides Cu Kα1 radiation (λ = 1.5406 Å), and a PIXcel solid angle detector.High-resolution TEM (HRTEM) images were recorded on a JEOL-JEM-2100F microscope (200 kV). The samples were prepared by sprinkling a small amount of powder over ethanol and then several drops of this solution were deposited onto carbon films, which were placed on copper grids. In order to determine the size distribution of each sample, around 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 NPs were counted, using the PSA macro for ImageJ,54 and modelled with a lognormal distribution fit.
000 NPs were counted, using the PSA macro for ImageJ,54 and modelled with a lognormal distribution fit.
X-Ray absorption fine structure (XAFS) spectroscopy technique probes the local environment surrounding the absorbing atom. XAFS experiment is both local, due to the short (∼10 Å) mean free path of the photoelectron, and essentially instantaneous, given that the lifetime of the hole in the atomic core is only on the order of 10−16 to 10−15 s. The room temperature Ni K-edge XANES (X-ray absorption near-edge structure) and EXAFS (extended X-ray absorption fine structure) spectra were obtained in transmission mode, at the XAS beamline at Elettra-Sincrotrone Trieste (Italy) using standard ionization chambers for the detection of intensities. Ni metal foil spectrum was also recorded simultaneously to calibrate the energy. In order to achieve the best signal-to-noise ratio, the powdered samples were deposited homogeneously onto a Kapton tape and layers were added until the desired transmission value was obtained. The absorption spectra were analysed according to standard procedures using IFFEFIT package.55 Data reduction, background removal and normalization were carried out using the Athena software and the spectra were modelled using Artemis, ATOMS and FEFF6 software.55
The M(T) and M(H) curves were measured using a Quantum Design PPMS-9T magnetometer. First, the sample was cooled in zero-field (ZFC) from 300 K down to 2 K. Then a magnetic field (Happl) was applied and kept constant, and afterward the MZFC(T) curve was measured by increasing the temperature from 2 K to 300 K. Finally, the MFC(T) curve was recorded while cooling the sample starting from 300 K down to 2 K. The magnetization vs. applied magnetic field cycles, M(H), was measured between −85 and 85 kOe at low (2 K) and room (300 K) temperatures. In order to study the EB effect, the sample under a constant applied magnetic field (Hcool) of 10 kOe was cooled down from 300 to 2 K. After that, a M(H) cycle was recorded between −85 and 85 kOe. The EB field (HEB) was defined as the horizontal shift of the central point of the loop measured at a given Hcool, relative to the Hcool = 0 loop, i.e., HEB = −(HC1 + HC2)/2, where HC1 and HC2 are the left and right coercive fields.
Results and discussion
Structural characterization
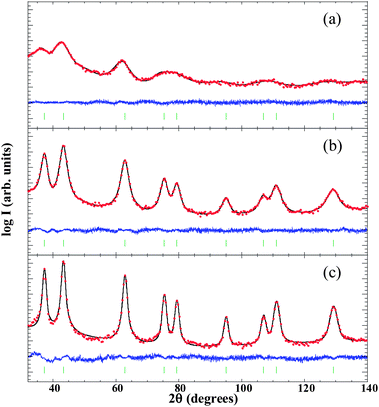
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m crystal structure because, even if NiO experiences rhombohedral distortion (∼0.1%) below the Néel temperature (TNiON ∼ 523 K), it is within the error of the present structural analysis.58 In samples S1 and S2 we have also used an amorphous contribution due to the scattering coming from the porous carbon matrix. The mean NP diameters estimated for S1, S2 and S3 were 2(1), 5(1) and 10(1) nm (the numbers in parentheses correspond to a measure of the degree of anisotropy, not to the estimated error), respectively. This finding is in good agreement with the broadening of diffraction peaks as the size of the NPs is reduced due to a lower number of diffracting crystalline planes. The value of the cell parameter obtained for both S2 and S3 was 4.18(1) Å, very close to the reported value for bulk NiO (abulkNiO = 4.178 Å).59 On the other hand, aXRD was found to be 4.22(1) Å in the smallest NPs (S1). The lattice expansion experienced by the NPs of 2.5 nm and its effect on the interatomic distances will be further explored by means of EXAFS measurements.
m crystal structure because, even if NiO experiences rhombohedral distortion (∼0.1%) below the Néel temperature (TNiON ∼ 523 K), it is within the error of the present structural analysis.58 In samples S1 and S2 we have also used an amorphous contribution due to the scattering coming from the porous carbon matrix. The mean NP diameters estimated for S1, S2 and S3 were 2(1), 5(1) and 10(1) nm (the numbers in parentheses correspond to a measure of the degree of anisotropy, not to the estimated error), respectively. This finding is in good agreement with the broadening of diffraction peaks as the size of the NPs is reduced due to a lower number of diffracting crystalline planes. The value of the cell parameter obtained for both S2 and S3 was 4.18(1) Å, very close to the reported value for bulk NiO (abulkNiO = 4.178 Å).59 On the other hand, aXRD was found to be 4.22(1) Å in the smallest NPs (S1). The lattice expansion experienced by the NPs of 2.5 nm and its effect on the interatomic distances will be further explored by means of EXAFS measurements.
| Sample code | Synthesis parameters | HRTEM | XRD | |||
|---|---|---|---|---|---|---|
| Atmosphere | Temperature (K) | Time (h) | NP size (nm) | NP size (nm) | Cell parameter (Å) | |
| S1 | N2 | 573 | 1 | 2.5(0.6) | 2(1) | 4.22(1) |
| S2 | Air | 573 | 3 | 4(1) | 5(1) | 4.18(1) |
| S3 | Air | 673 | 1 | 9(2) | 10(1) | 4.18(1) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m crystalline structure (see selected area electron diffraction [SAED] pattern in a 200 nm2 region in Fig. 2g and the crystalline planes in Fig. 2h–i). During the synthesis process the carbon matrix had been almost completely gasified so that the weight percentages of NiO were 75% and 100% in S2 and S3, respectively. In order to confirm the chemical composition of the samples energy-dispersive X-ray spectroscopy (EDX) measurements were performed, providing a Ni
m crystalline structure (see selected area electron diffraction [SAED] pattern in a 200 nm2 region in Fig. 2g and the crystalline planes in Fig. 2h–i). During the synthesis process the carbon matrix had been almost completely gasified so that the weight percentages of NiO were 75% and 100% in S2 and S3, respectively. In order to confirm the chemical composition of the samples energy-dispersive X-ray spectroscopy (EDX) measurements were performed, providing a Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O atomic ratio of 1
O atomic ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in all the investigated regions.
1 in all the investigated regions.
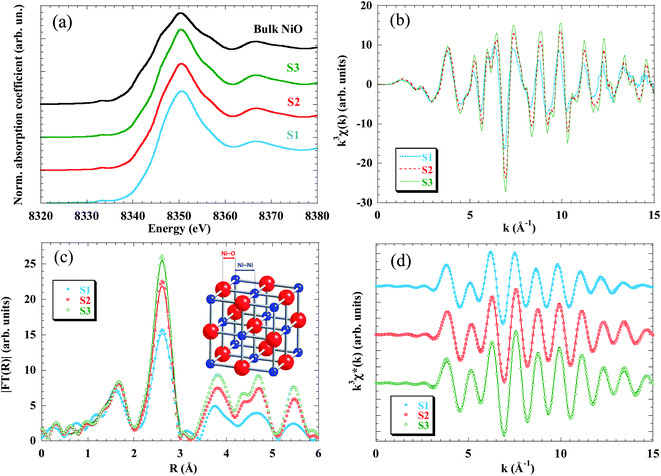
In order to get quantitative information about the local structure around the Ni atoms, the inverse Fourier transform of the two main peaks, 0.5 Å ≤ R ≤ 3 Å, (Fig. 3d) was fitted to the well-known EXAFS function:55
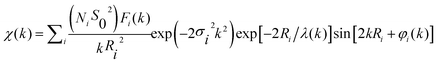 | (1) |
The quantitative results of the fits, performed in the k-range 3.5 ≤ k ≤ 15 Å−1, considering only Ni–O and Ni–Ni single-scattering events, are reported in Table 2. While the number of neighbours that constitute the first shell (NNi–O ∼ 6 in all samples) does not change as compared to the bulk NiO, the average coordination number of the second shell (that corresponds to the Ni–Ni pair) decreases from 11 to 9.6 as the particle size is reduced.
| Sample code | 1st shell (Ni–O) | 2nd shell (Ni–Ni) | ||||
|---|---|---|---|---|---|---|
| N | R (Å) | σ 2 (Å2) | N | R (Å) | σ 2 (Å2) | |
| S1 | 6.2(6) | 2.07(1) | 0.009(2) | 9.6(4) | 2.985(2) | 0.009(1) |
| S2 | 6.0(4) | 2.07(1) | 0.007(1) | 10.0(2) | 2.957(2) | 0.006(1) |
| S3 | 5.8(6) | 2.08(1) | 0.006(1) | 11.0(3) | 2.957(2) | 0.005(1) |
| Bulk NiO | 6.0(1) | 2.09(1) | 0.006(1) | 12.0(1) | 2.955(1) | 0.005(1) |
The evolution of the coordination number is in good agreement with the amplitude reduction observed in the second peak of the Fourier transform. The decrease of the average coordination number with particle size was already found in previous EXAFS studies in NPs48,49,62 and is due to the fact that surface Ni atoms are undercoordinated and that the recorded EXAFS signal is the average over all the Ni absorbing centres. In the present samples the ratio of surface to bulk atoms strongly increases when reducing the size from 9 nm (S3) to 2.5 nm (S1). Considering as “surface atoms” those located in a one-unit-cell-thick outer layer, they represent only ∼25% in S3 and ∼50% in S2, but the percentage increases up to ∼70% in S1. These results are in good agreement with the expected reduction of the coordination number due to the cluster size (see, for example, Calvin et al.63 and Fig. S3 in the ESI†).
Regarding the interatomic distance, we found that the Ni–O bond length remains constant in the three samples (RNi–O = 2.07 Å) and also coincides with the one obtained from the bulk sample. On the other hand, the Ni–Ni pair distance experiences a pronounced relaxation only in the S1 sample (RNi–Ni = 2.985 Å). This expansion leads to a cell parameter of 4.22 Å (a = √2RNi–Ni), which is in good agreement with the aforementioned results obtained from XRD analysis.
Finally, the Debye–Waller factor, σ2, is k-dependent and its damping effect is more noticeable in high-k oscillations. The σ2 can be understood as a superposition of dynamic (σd2) and static (σs2) terms. The σd2 factor is temperature-dependent and should not change appreciably between samples, since all the EXAFS spectra were recorded at 300 K. So the increase of σ2 with decreasing particle size is ascribed to the static term, which indicates a higher structural disorder in good agreement with the lack of coordination of the Ni atoms located at the surface.
Summarizing the results extracted from the XAS analysis, it has been proved that NPs are affected by surface effects as the particle size decreases, this feature being especially pronounced in smaller NPs (S1), whereas larger ones (S3) exhibit almost bulk-like behaviour. Surface effects consist of average undercoordination, bond relaxation and static disorder and should be understood as arising from the breaking of the periodicity that the lattice experiences at the boundary of the particle. No evidence of crystallinity loss can be deduced from EXAFS data.
Magnetic characterization
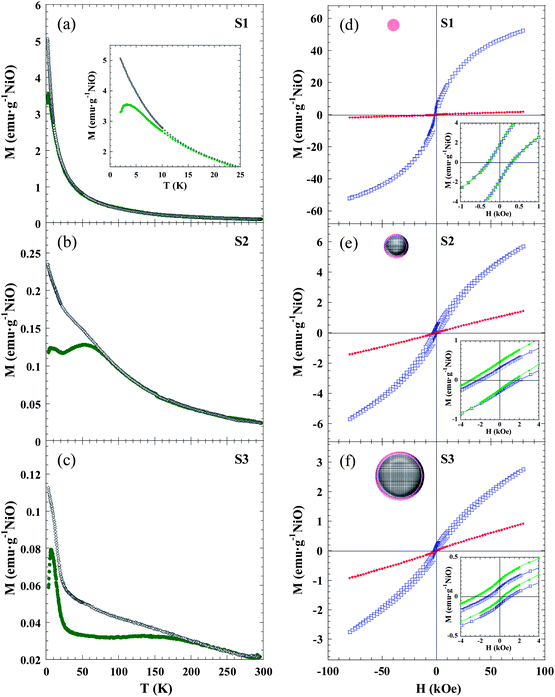
The temperature dependence of the magnetization was investigated in ZFC and FC regimes under an applied magnetic field of 1 kOe (Fig. 4a–c). The MZFC(T) curves of samples S2 and S3 reveal identical features, and three characteristic temperatures of the system, i.e. Tf, TB and Tirr, can be identified: (i) a low temperature sharp peak at TS2f ∼ 6.2 K and TS3f ∼ 6.7 K; (ii) a broad maximum centred at TS2B ∼ 53 K and TS3B ∼ 145 K; and (iii) a splitting temperature between MZFC(T) and MFC(T) curves at TS2irr ∼ 91 K and TS3irr ∼ 270 K. The same qualitative behaviour was observed in the curves measured at 0.1 kOe (Fig. S4 in the ESI†). This phenomenology in NiO NPs can be understood through a core–shell model.35 Then, each particle would be formed by: (i) an AFM ordered core with uncompensated magnetic sublattices (giving rise to a net magnetic moment) due to the reduction in the number of exchange coupled moments caused by finite size effects; and (ii) a magnetically disordered shell, which thermally fluctuates as a SG-like system.36–38,40–42,44 In this context, the magnetically ordered cores will exhibit SPM behaviour above a certain temperature. When the particle size is not monodispersed there is a distribution in the anisotropy energy barriers, and the NP magnetic moments become blocked progressively, each one at a blocking temperature Tb ∼ KV/25kB, as explained by the Néel–Brown model for uniaxial and non-interacting NPs. In our case, TB is usually associated with the mean value of Tb and Tirr is the irreversible temperature, which determines the highest value for the Tb in the system. The latter explains why in S2 and S3 both TB and Tirr increase as the particle size is raised. On the other hand, Tf would correspond to the temperature for the SG-like freezing of the surface spins due to a disordered magnetic moment arrangement. In order to support this assumption, low temperature (2–20 K) AC susceptibility measurements were carried out at five different frequencies (f) between 1 Hz and 1 kHz. The preliminary data analysis of the frequency shift of Tf give values between 0.03 and 0.06 for the Ω parameter [Ω = ΔTf/Tf Δ(log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f)], which are within the expected range for SG (0.004–0.06) rather than that for SPM (0.1–0.3) systems.64
f)], which are within the expected range for SG (0.004–0.06) rather than that for SPM (0.1–0.3) systems.64
The S1 sample exhibits markedly different behaviour with respect to S2 and S3 samples. Only TS1f ∼ 3 K and TS1irr ∼ 15 K can be identified in the ZFC and FC curves, whereas there is not any maximum that could be ascribed to a blocking temperature (TB). The latter seems to suggest that, while in S2 and S3 the disordered region is limited to the surface shell, in S1 the NPs are so small that all the spins in the particle are influenced by surface effects and a magnetically-ordered core is not formed (see NP schematic pictures in Fig. 4d–f). The fact that sample S1 is more affected by size effects than S2 and S3 is in good agreement with EXAFS results. In the case of S1, the non-coincidence of TS1f and TS1irr would arise from the fact that there is a distribution in the particle size.
Furthermore, the magnetic field dependence of magnetization can be understood on the basis of the previously stated microstructural picture that can be summarized as follows. S2 and S3 NPs consist of an ordered uncompensated AFM core with a net magnetic moment, and a surface disordered shell, both components having two different regimes: blocked/SPM, separated by TB for the core, and SG/paramagnetic separated by Tf for the shell. Fig. 4d–f shows the M(H) curves of S1, S2 and S3 measured under ZFC conditions at low (2 K) and room (300 K) temperatures. The most relevant magnetic magnitudes are presented in Table 3.
| Sample code | Temperature dependence, M(T) | Field dependence, M(H) | ||||||
|---|---|---|---|---|---|---|---|---|
| T f (K) | T B (K) | T irr (K) | M 2K–ZFC80kOe (emu g−1 NiO) | M 2K–ZFCr (emu g−1 NiO) | H 2K–ZFCC (kOe) | H 2K–FCC (kOe) | H 2K–FCEB (kOe) | |
| S1 | 3.0(1) | — | 15(1) | 52.4 | 1.80 | 0.27 | 0.27 | 0 |
| S2 | 6.2(1) | 53(5) | 91(3) | 5.7 | 0.30 | 2.04 | 2.18 | 0.86 |
| S3 | 6.7(1) | 145(15) | 270(10) | 2.8 | 0.12 | 1.13 | 1.41 | 1.14 |
The value of the magnetization measured at 80 kOe (M2K–ZFC80kOe) in S1 is more than one order of magnitude larger than the corresponding values of S2 and S3, due to the higher number of disordered magnetic moments present in the NPs of 2.5 nm compared to larger ones. At T = 2 K the three samples exhibit remanence (M2K–ZFCr) and coercivity (H2K–ZFCC), due to the blocked/frozen states of all the magnetic entities. The observed value of M2K–ZFCr is roughly one order of magnitude higher for the S1 sample respect to those for S2 and S3, and could be ascribed to the formation of Ni2+ clusters below Tf. The high H2K–ZFCC value in S2 and S3, compared to S1, is due to the interfacial anisotropy that the frozen surface SG exerts on the core magnetic moment of the NP. The importance of interfacial effects was further proved by the hysteresis loops measured at T = 2 K in FC conditions (Hcool = 10 kOe).
The S2 and S3 samples show characteristic features of the EB effect, namely a shift toward the negative field axis (H2K–FCEB) and coercivity enhancement (H2K–FCC). The EB is a phenomenon associated with the exchange anisotropy created at the interface between materials with different anisotropy energies, typically an AFM and a FM,65 but EB has also been studied in different combinations of magnetic components (FM, AFM, ferrimagnetic, SG).31,66
The EB in the studied samples is attributed to the magnetic coupling between the NP core net magnetic moment, which behaves as a SPM macrospin above TB, and the spins at the NP shell.67,68 When the NPs are cooled down from T > TB to Tf < T < TB under an external magnetic field, the core moment lines up along the field direction, while SG spins remain random. In this situation, the core blocked macrospin is able to follow the applied field when it reverses its direction. Further cooling down to T < Tf gives rise to the exchange coupling between the interfacial SG spins and the adjacent spins belonging to the core blocked macrospin. This magnetic interaction determines the direction along which the spins become oriented. Therefore, when the applied field is reversed (at T < Tf), a microscopic torque at the core–shell interface appears, tending to keep the core blocked macrospin in its original direction.
When comparing these results with previous studies on NiO NPs,47 we observed a similar trend of HEB growth with the particle diameter. On the other hand, we found higher values of H2KC in the 4 nm NPs (S2) than in the 9 nm ones (S3), both in ZFC and FC regimes. The research developed by Ali et al. on exchange-biased bilayered FM/SG systems revealed that HEB increased monotonically with the SG thickness until it is saturated at a certain value, while HC exhibits a maximum well below the saturation point of HEB.67 Therefore, in the case of FM/SG interfaces, the degree by which a region of the glass is bound to the FM depends on the characteristics of the spin configuration at the interface. The HEB is provided by the glassy regions that remain largely intact on reversal the FM, whereas those that change on reversal of the FM contribute to HC. Thus, we believe that the values of HEB and HC in NiO NPs depend not only on the particle size, but also strongly on the characteristics of the surface shell. The topological structure of the surface is associated with the degree of magnetic frustration, which determines the thickness of the SG shell and also the roughness and magnetic coupling at the core–shell interface.
In brief, the AF coupling in nanoscale NiO is found inside each NP core when the particle size is larger than 4 nm. On the other hand, surface disordered magnetic moments are at the origin of SG behaviour, which dominates the magnetic response of the shell and also that of the whole NP when the particle size is ∼2 to 3 nm.
Conclusions
The influence of the microstructure on the magnetic properties of three nanosized NiO samples with diameters of 2.5, 4 and 9 nm was studied. The EXAFS technique allowed proving that surface effects became more relevant as the particle size was reduced, even if crystallinity still remained. Magnetic measurements revealed that there was a competition between surface spin disorder and antiferromagnetism, leading to a different magnetic arrangement in smaller NPs as compared to larger ones. In the NiO NPs of 2.5 nm frustration prevailed and Ni2+ magnetic moments were found to be in a SG state; while as the particle size increased, the nucleation of an AFM core became favourable and only the shell exhibited a magnetically-disordered SG state (NPs of 4 and 9 nm). The existence of an uncompensated AFM core was indirectly detected through the presence of a net magnetic moment arising from the reduction in the number of exchange coupled moments caused by finite size effects, which behaved as a superparamagnet. Interestingly, only NPs with an AFM core exhibited an exchange bias effect, which was described by a SPM/SG model in which the NP core net magnetic moments were pinned by the frozen magnetic moments at the surface disordered shell. The dependence of HEB and HC on the particle size was strongly affected by the characteristics of the surface shell.The disappearance of the AFM core when NiO NPs are small enough and the variation of HEB and HC with the topological structure of the surface and the roughness at the core–shell interface confirm the deep interplay between the structure and the magnetism of materials at the nanoscale and suggest that it is possible to tune their magnetic properties by controlling the morphological aspects. The present findings could be of special interest in NPs made of materials that are AFM in their bulk form, but could present unique physical–chemical properties that may be valuable at the nanoscale in the production of small and smart materials.
Acknowledgements
N. Rinaldi-Montes is thankful to Ministerio de Educación, Cultura y Deporte (MECD) for doctoral grant FPU12/03381. This work was accomplished with financial support from project MAT2011-27573-C04. Thanks are due to Carlos Álvarez Villa and Zakariae Amghouz (SCT's Univ. Oviedo) for their help in obtaining TEM and HRTEM images, respectively; Beatriz Vallina (SCT's Univ. Oviedo) for providing assistance with XRD measurements and Elettra-Sincrotrone Trieste (Italy) for allocating beam time for EXAFS experiments.References
- D. L. Huber, Small, 2005, 1, 482 CrossRef CAS PubMed.
- Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, R167 CrossRef CAS.
- A. B. Fuertes and P. Tartaj, Chem. Mater., 2006, 18, 1675 CrossRef CAS.
- A. H. Haviv, J. M. Greneche and J.-P. Lellouche, J. Am. Chem. Soc., 2010, 132, 12519 CrossRef CAS PubMed.
- P. Gorria, M. Sevilla, J. A. Blanco and A. B. Fuertes, Carbon, 2006, 44, 1954 CrossRef CAS PubMed.
- C. T. Meneses, W. H. Flores and J. M. Sasaki, Chem. Mater., 2007, 19, 1024 CrossRef CAS.
- M. P. Fernandez-Garcia, P. Gorria, M. Sevilla, A. B. Fuertes, R. Boada, J. Chaboy, G. Aquilanti and J. A. Blanco, Phys. Chem. Chem. Phys., 2011, 13, 927 RSC.
- A. C. Johnston-Peck, J. Wang and J. B. Tracy, ACS Nano, 2009, 3, 1077 CrossRef CAS PubMed.
- P. Gorria, M. P. Fernandez-Garcia, M. Sevilla, J. A. Blanco and A. B. Fuertes, Phys. Status Solidi RRL, 2009, 3, 4 CrossRef CAS.
- G. Salazar-Alvarez, J. Qin, V. Sepelak, I. Bergmann, M. Vasilakaki, K. N. Trohidou, J. D. Ardisson, W. a. A. Macedo, M. Mikhaylova, M. Muhammed, M. D. Baro and J. Nogues, J. Am. Chem. Soc., 2008, 130, 13234 CrossRef CAS PubMed.
- Y. Mao, J. Parsons and J. S. McCloy, Nanoscale, 2013, 5, 4720 RSC.
- M. P. Fernandez-Garcia, P. Gorria, J. A. Blanco, A. B. Fuertes, M. Sevilla, R. Boada, J. Chaboy, D. Schmool and J. M. Greneche, Phys. Rev. B, 2010, 81, 094418 CrossRef.
- A. A. El-Gendy, E. M. M. Ibrahim, V. O. Khavrus, Y. Krupskaya, S. Hampel, A. Leonhardt, B. Buechner and R. Klingeler, Carbon, 2009, 47, 2821 CrossRef CAS PubMed.
- A. B. Davila-Ibanez, N. J. Buurma and V. Salgueirino, Nanoscale, 2013, 5, 4797 RSC.
- B. R. Knappett, P. Abdulkin, E. Ringe, D. A. Jefferson, S. Lozano-Perez, T. C. Rojas, A. Fernandez and A. E. H. Wheatley, Nanoscale, 2013, 5, 5765 RSC.
- M. P. Fernandez-Garcia, P. Gorria, M. Sevilla, M. P. Proenca, R. Boada, J. Chaboy, A. B. Fuertes and J. A. Blanco, J. Phys. Chem. C, 2011, 115, 5294 CAS.
- J. Park, E. Kang, S. U. Son, H. M. Park, M. K. Lee, J. Kim, K. W. Kim, H. J. Noh, J. H. Park, C. J. Bae, J. G. Park and T. Hyeon, Adv. Mater., 2005, 17, 429 CrossRef CAS.
- J. Xiao, B. Chen, X. Liang, R. Zhang and Y. Li, Catal. Sci. Technol., 2011, 1, 999 CAS.
- Y. H. Pai and S. Y. Fang, J. Power Sources, 2013, 230, 321 CrossRef CAS PubMed.
- H. Zeng, J. Li, J. P. Liu, Z. L. Wang and S. H. Sun, Nature, 2002, 420, 395 CrossRef CAS PubMed.
- X. Yan, X. Tong, J. Wang, C. Gong, M. Zhang and L. Liang, Mater. Lett., 2013, 95, 1 CrossRef CAS PubMed.
- J. M. Tarascon and M. Armand, Nature, 2001, 414, 359 CrossRef CAS PubMed.
- X. Wang, L. Li, Y. Zhang, S. Wang, Z. Zhang, L. Fei and Y. Qian, Cryst. Growth Des., 2006, 6, 2163 CAS.
- E. A. Gibson, M. Awais, D. Dini, D. P. Dowling, M. T. Pryce, J. G. Vos, G. Boschloo and A. Hagfeldt, Phys. Chem. Chem. Phys., 2013, 15, 2411 RSC.
- M. Tyagi, M. Tomar and V. Gupta, Biosens. Bioelectron., 2013, 41, 110 CrossRef CAS PubMed.
- Y. Jiang, D. Chen, J. Song, Z. Jiao, Q. Ma, H. Zhang, L. Cheng, B. Zhao and Y. Chu, Electrochim. Acta, 2013, 91, 173 CrossRef CAS PubMed.
- G. Zhou, D. W. Wang, L. C. Yin, N. Li, F. Li and H. M. Cheng, ACS Nano, 2012, 6, 3214 CrossRef CAS PubMed.
- X. Zhu, Q. Jiao, C. Zhang, X. Zuo, X. Xiao, Y. Liang and J. Nan, Microchim. Acta, 2013, 180, 477 CrossRef CAS.
- Magnetic Properties of Fine Particles, J. L. Dormann and D. Fiorani, North Holland, Amsterdam, 1992 Search PubMed.
- S. Morup, D. E. Madsen, C. Frandsen, C. R. H. Bahl and M. F. Hansen, J. Phys.: Condens. Matter, 2007, 19, 213202 CrossRef.
- J. Nogues, J. Sort, V. Langlais, V. Skumryev, S. Surinach, J. S. Munoz and M. D. Baro, Phys. Rep., 2005, 422, 65 CrossRef PubMed.
- V. Skumryev, S. Stoyanov, Y. Zhang, G. Hadjipanayis, D. Givord and J. Nogues, Nature, 2003, 423, 850 CrossRef CAS PubMed.
- O. Iglesias, A. Labarta and X. Batlle, J. Nanosci. Nanotechnol., 2008, 8, 2761 CAS.
- Q. Pankhurst, L. Fernández Barquín, J. S. Lord, A. Amato and U. Zimmermann, Phys. Rev. B, 2012, 85, 174437 CrossRef.
- E. Winkler, R. D. Zysler, M. V. Mansilla, D. Fiorani, D. Rinaldi, M. Vasilakaki and K. N. Trohidou, Nanotechnology, 2008, 19, 185702 CrossRef CAS PubMed.
- E. Winkler, R. D. Zysler, M. V. Mansilla and D. Fiorani, Phys. Rev. B, 2005, 72, 132409 CrossRef.
- M. P. Proenca, C. T. Sousa, A. M. Pereira, P. B. Tavares, J. Ventura, M. Vazquez and J. P. Araujo, Phys. Chem. Chem. Phys., 2011, 13, 9561 RSC.
- S. Thota and J. Kumar, J. Phys. Chem. Solids, 2007, 68, 1951 CrossRef CAS PubMed.
- R. H. Kodama, S. A. Makhlouf and A. E. Berkowitz, Phys. Rev. Lett., 1997, 79, 1393 CrossRef CAS.
- S. D. Tiwari and K. P. Rajeev, Phys. Rev. B, 2005, 72, 104433 CrossRef.
- M. Ghosh, K. Biswas, A. Sundaresan and C. N. R. Rao, J. Mater. Chem., 2006, 16, 106 RSC.
- C. T. Meneses, J. G. S. Duque, E. de Biasi, W. C. Nunes, S. K. Sharma and M. Knobel, J. Appl. Phys., 2010, 108, 013909 CrossRef.
- M. Tadic, M. Panjan, D. Markovic, I. Milosevic and V. Spasojevic, J. Alloys Compd., 2011, 509, 7134 CrossRef CAS PubMed.
- W. J. Duan, S. H. Lu, Z. L. Wu and Y. S. Wang, J. Phys. Chem. C, 2012, 116, 26043 CAS.
- Y. G. Morozov, D. Ortega, O. V. Belousova, I. P. Parkin and M. V. Kuznetsov, J. Alloys Compd., 2013, 572, 150 CrossRef CAS PubMed.
- S. Sabyasachi, S. Majumdar and S. Giri, Solid State Commun., 2011, 151, 1515 CrossRef CAS PubMed.
- S. A. Makhlouf, H. Al-Attar and R. H. Kodama, Solid State Commun., 2008, 145, 1 CrossRef CAS PubMed.
- M. A. Peck and M. A. Langell, Chem. Mater., 2012, 24, 4483 CrossRef CAS.
- A. Anspoks, A. Kuzmin, A. Kalinko and J. Timoshenko, Solid State Commun., 2010, 150, 2270 CrossRef CAS PubMed.
- F. Jiao, A. H. Hill, A. Harrison, A. Berko, A. V. Chadwick and P. G. Bruce, J. Am. Chem. Soc., 2008, 130, 5262 CrossRef CAS PubMed.
- S. Mandal, K. S. R. Menon, S. K. Mahatha and S. Banerjee, Appl. Phys. Lett., 2011, 99, 232507 CrossRef.
- S. Mandal, S. Banerjee and K. S. R. Menon, Phys. Rev. B, 2009, 80, 214420 CrossRef.
- A. Anspoks, A. Kalinko, R. Kalendarev and A. Kuzmin, Phys. Rev. B, 2012, 86, 174114 CrossRef.
- R. A. Sperling, P. Rivera Gil, F. Zhang, M. Zanella and W. J. Parak, Chem. Soc. Rev., 2008, 37, 1896 RSC.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537 CrossRef CAS PubMed.
- J. Rodriguez-Carvajal., Satellite Meeting on Powder Diffraction of the XV IUCr Congress, 1990, vol. 127 Search PubMed.
- H. Rietveld, J. Appl. Crystallogr., 1969, 2, 65 CrossRef CAS.
- M. Towler, N. Allan, N. Harrison, V. Saunders, W. Mackrodt and E. Apra, Phys. Rev. B, 1994, 50, 5041 CrossRef CAS.
- S. Sasaki, K. Fujino and Y. Takeuchi, Proc. Jpn. Acad., Ser. B, Phys. Biol. Sci., 1979, 55, 43 CrossRef CAS.
- J. I. Langford, D. Louer and P. Scardi, J. Appl. Crystallogr., 2000, 33, 964 CrossRef CAS.
- D. Martinez-Blanco, P. Gorria, J. A. Blanco, M. J. Perez and J. Campo, J. Phys.: Condens. Matter, 2008, 20, 335213 CrossRef.
- A. I. Frenkel, C. W. Hills and R. G. Nuzzo, J. Phys. Chem. B, 2001, 105, 12689 CrossRef CAS.
- S. Calvin, M. M. Miller, R. Goswami, S. F. Cheng, S. P. Mulvaney, L. J. Whitman and V. G. Harris, J. Appl. Phys., 2003, 94, 778 CrossRef CAS.
- J. A. Mydosh, Spin Glasses: An Experimental Introduction, Taylor & Francis, London, 1993 Search PubMed.
- J. Nogues and I. K. Schuller, J. Magn. Magn. Mater., 1999, 192, 203 CrossRef CAS.
- S. Giri, M. Patra and S. Majumdar, J. Phys.: Condens. Matter, 2011, 23, 073201 CrossRef CAS PubMed.
- M. Ali, P. Adie, C. H. Marrows, D. Greig, B. J. Hickey and R. L. Stamps, Nat. Mater., 2007, 6, 70 CrossRef CAS PubMed.
- F. T. Yuan, J. K. Lin, Y. D. Yao and S. F. Lee, Appl. Phys. Lett., 2010, 96, 162502 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: TEM size distributions, normalized XAS spectra, variation of the coordination number due to cluster size reduction and ZFC-FC curves at 0.1 kOe. See DOI: 10.1039/c3nr03961g |
| This journal is © The Royal Society of Chemistry 2014 |