Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Influence of nitrogen donor ligands on the coordination modes of copper(II) 2-nitrobenzoate complexes: structures, DFT calculations and magnetic properties†
Raj Pal
Sharma
*a,
Anju
Saini
a,
Divyakshi
Monga
a,
Paloth
Venugopalan
a,
Julia
Jezierska
b,
Andrew
Ozarowski
c and
Valeria
Ferretti
*d
aDepartment of Chemistry, Panjab University, Chandigarh-160014, India. E-mail: rpsharma@pu.ac.in
bFaculty of Chemistry, University of Wroclaw, 50-383 Wroclaw, 14 F. Joliot Curie Str., Poland
cNational High Magnetic Field Laboratory, Florida State University, Tallahassee, Florida 32310, USA
dCenter for Structural Diffractometry and Department of Chemical and Pharmaceutical Sciences, University of Ferrara, via, Fossato di Mortara 17-27, I-44121, Ferrara, Italy. E-mail: frt@unife.it
First published on 5th November 2013
Abstract
Three novel copper(II) 2-nitrobenzoate complexes, [Cu(γ-pic)2(2-nitrobenzoate)2] 1, [Cu(β-pic)2(2-nitrobenzoate)2(H2O)2] 2 and [Cu2(H2tea)2(2-nitrobenzoate)2]·2(H2O) 3 (where γ-pic = 4-methylpyridine, β-pic = 3-methylpyridine and H2tea = mono deprotonated triethanolamine), were isolated by addition of γ-pic, β-pic and H3tea to the hydrated copper(II) 2-nitrobenzoate, [Cu2(2-nitrobenzoate)4(H2O)2]·2H2O, suspended in a methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water (4
water (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) mixture. The newly synthesized complexes have been characterized by elemental analyses, thermogravimetric analysis (TGA), spectroscopic techniques (EPR, IR and UV/Visible), magnetic susceptibility measurements, single crystal X-ray structure determination and DFT study. All compounds crystallize in the monoclinic crystal system with the P21/c space group. X-ray structure determination revealed the presence of monomers in both 1 and 2 and dimer in 3 with the deprotonated oxygen atom of the H2tea ligand bridging two Cu(II) atoms. Two co-crystallized water molecules are also present in 3. The crystal lattice is stabilized by C–H⋯O hydrogen bonding interactions in 1 and O–H⋯O, C–H⋯O hydrogen bonding interactions in 2 and 3. The dimeric complex exhibits relatively strong ferromagnetic exchange with J = −100 cm−1 (corresponding to H = JS1S2). The zero-field splitting parameters (zfs) of the dimer triplet states D and E were derived from HF EPR spectra recorded at moderately low temperatures. The sign of D was determined from low-temperature HF EPR spectra.
1) mixture. The newly synthesized complexes have been characterized by elemental analyses, thermogravimetric analysis (TGA), spectroscopic techniques (EPR, IR and UV/Visible), magnetic susceptibility measurements, single crystal X-ray structure determination and DFT study. All compounds crystallize in the monoclinic crystal system with the P21/c space group. X-ray structure determination revealed the presence of monomers in both 1 and 2 and dimer in 3 with the deprotonated oxygen atom of the H2tea ligand bridging two Cu(II) atoms. Two co-crystallized water molecules are also present in 3. The crystal lattice is stabilized by C–H⋯O hydrogen bonding interactions in 1 and O–H⋯O, C–H⋯O hydrogen bonding interactions in 2 and 3. The dimeric complex exhibits relatively strong ferromagnetic exchange with J = −100 cm−1 (corresponding to H = JS1S2). The zero-field splitting parameters (zfs) of the dimer triplet states D and E were derived from HF EPR spectra recorded at moderately low temperatures. The sign of D was determined from low-temperature HF EPR spectra.
Introduction
In recent years, crystal engineering based on organic and/or inorganic molecular building blocks has been rapidly expanding owing to the novel and diverse topologies and potential applications in host–guest chemistry, catalysis, electrical conductivity and magnetism.1–6 One of the important strategies is to establish the likely connections between organic and/or inorganic molecular building blocks by exploiting non-covalent interactions.7,8 In the case of transition metal complexes, these interactions are established mainly among the ‘organic’ parts of the molecules, and can be modulated through a suitable choice of the ligands. Copper(II) complexes are among the most widely studied coordination compounds because of their wide range of applications,9–15 in particular when the ligands are alkyl/aryl carboxylate anions, which can exhibit a wide variety of coordination modes (monodentate, symmetric\asymmetric chelating, and bidentate\monodentate bridging). Moreover, properties of copper(II) carboxylates and the coordination abilities of carboxylate ions can be varied to a large extent using nitrogen donor ligands with appropriate functionalization.16–19 A combined stereo-electronic effect that emerges as a result of both the carboxylate anion and the ancillary N-donor ligand would dictate the final nature and structure of the complex formed. That is, in a nutshell, the chosen carboxylate ligand may show a propensity to exhibit different coordination modes depending upon the type of N-donor ligand chosen.In this direction, with the aim of comparing the structural and packing features of complexes in which different N-donor ligands participate, we have chosen two very similar nitrogen-donor ligands γ-pic (4-methyl pyridine) and β-pic (3-methyl pyridine) which are rigid in their molecular topology along with a third N-donor ligand triethanolamine (H3tea) which is highly flexible in terms of molecular conformation. This ligand after deprotonation (i.e. H2tea) will be endowed with two –OH groups which may take part either singly or in a combined way in the hydrogen bonding as effective proton donors. In addition, a theoretical approach that can model these structures and their bonding features would be rewarding. Thus, this paper reports the synthesis, characterization and DFT study of three novel copper(II) complexes with different nitrogen donor ligands, [Cu(γ-pic)2(2-nitrobenzoate)2] (1), [Cu(β-pic)2(2-nitrobenzoate)·2(H2O)2] (2) and [Cu2(H2tea)2(2-nitrobenzoate)2]·2(H2O) (3).
Particular attention has been devoted to complex 3 where the presence of the H2tea ligand favours the formation of a dinuclear molecule in which two Cu atoms are bridged by two oxygen atoms. In general, the magnetic behavior of transition metal complexes containing more than one metal atom with unpaired electrons is affected by the metal–metal interaction. The case discussed in this paper is that of weakly interacting metal ions (with the Cu…Cu distance in the range 3–5 Å), where the coupling between their electrons leads to low-lying excited states of different spin which can be thermally populated. The resulting magnetic behavior can be antiferromagnetic or ferromagnetic, and the ferromagnetic/antiferromagnetic coupling is strictly related to structural parameters such as the Cu–O–Cu angle and the Cu⋯Cu distance. Accordingly, the magnetic characterization of 3 has been performed both from a theoretical and experimental point of view.
Experimental
Three copper(II) carboxylate complexes were synthesized by reacting copper(II) 2-nitrobenzoate with an appropriate N-donor ligand in a methanol–water mixture and allowing the solution to evaporate at room temperature as shown in Scheme 1.All three complexes have been characterized and investigated by elemental analyses, TGA, spectroscopic (FT-IR, UV/Visible, EPR) and magnetic susceptibility studies, conductance measurements, as well as by single-crystal X-ray crystallography and DFT.
Syntheses
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol
1 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water mixture and γ-pic was added till a clear dark blue coloured solution was obtained. When the solution was allowed to evaporate at room temperature, blue coloured crystals appeared after 3 days. Complex 1 is soluble in methanol and insoluble in water and acetone. Complex 1 decomposed at 190 °C. Anal. calcd for C26H22CuN4O8 (%): C, 53.65; H, 3.78; N, 9.63; Cu, 10.92. Found: C, 52.45; H, 3.66; N, 9.52; Cu, 10.73. IR/cm−1 (KBr): 3565(m), 3317(m), 3128(b), 3208(m), 3085(w) 1607(s), 1564(ms), 1524(s), 1443(w), 1389(s), 1350(m), 1151(m), 1071(ms), 1034(ms), 977(w), 959(w), 862(m), 835(m), 805(m), 795(m), 785(m) 752(m), 700(m), 648(m), 589(w), 554(m), 493(ms), 459(m). UV/Visible (CH3OH) λmax = 732 nm (εmax = 94.07 mol−1 L cm−1).
water mixture and γ-pic was added till a clear dark blue coloured solution was obtained. When the solution was allowed to evaporate at room temperature, blue coloured crystals appeared after 3 days. Complex 1 is soluble in methanol and insoluble in water and acetone. Complex 1 decomposed at 190 °C. Anal. calcd for C26H22CuN4O8 (%): C, 53.65; H, 3.78; N, 9.63; Cu, 10.92. Found: C, 52.45; H, 3.66; N, 9.52; Cu, 10.73. IR/cm−1 (KBr): 3565(m), 3317(m), 3128(b), 3208(m), 3085(w) 1607(s), 1564(ms), 1524(s), 1443(w), 1389(s), 1350(m), 1151(m), 1071(ms), 1034(ms), 977(w), 959(w), 862(m), 835(m), 805(m), 795(m), 785(m) 752(m), 700(m), 648(m), 589(w), 554(m), 493(ms), 459(m). UV/Visible (CH3OH) λmax = 732 nm (εmax = 94.07 mol−1 L cm−1).
Details of the TGA and spectroscopic characterization of complexes 1–3 are available in the ESI.†
Materials and physical measurements
Analytical grade reagents were used without any further purification. Carbon, hydrogen and nitrogen were measured micro-analytically using an automatic Perkin Elmer 2400 CHN elemental analyzer and copper was determined gravimetrically.20FT-IR spectra were recorded as KBr pellets using a Perkin Elmer Spectrum RXFT-IR system. The electronic spectrum was recorded in H2O using a Hitachi 330 spectrophotometer. The thermogravimetric analysis (TGA) was conducted using an SDT Q600 instrument. The samples contained in the alumina pan were heated from 25 °C to 1000 °C at a constant rate of 10 °C min−1 in a nitrogen environment with a flux (flow rate) of 10 mL min−1. Conductance measurements were performed using a Pico Conductivity Meter (Model CNO4091201, Lab India) in aqueous medium at 25 °C by using double distilled water. Magnetic measurements for 1 and 2 at room temperature were carried out using the Gouy's method with following specifications: pole face diameter: 10.2 cm; pole gap: 4.0 cm; current: 7.0 & magnetic induction: 0.6 Tesla. Magnetic susceptibility measurements for 3 over the temperature range 1.8–300 K were performed at a magnetic field of 0.5 T using a Quantum Design SQUID MPMSXL-5 magnetometer. Correction for the sample holder as well as the diamagnetic correction χD which was estimated from the Pascal constants were applied.21
X-band EPR High-field and high-frequency EPR spectra at temperatures ranging from ca. 6 K to 290 K were recorded for 3 on a home-built spectrometer at the EMR facility of the NHMFL.22
The instrument is a transmission-type device in which microwaves are propagated in cylindrical lightpipes. The microwaves were generated by a phase-locked Virginia Diodes source generating a frequency of 13 ± 1 GHz and producing its harmonics of which the 2nd, 4th, 6th, 8th, 16th, 24th and 32nd were available. A superconducting magnet (Oxford Instruments) capable of reaching a field of 17 T was employed. The EPR spectra at X- and Q-bands were measured using a Bruker Elexsys E500 spectrometer equipped with a NMR teslameter and frequency counters. The simulations of the experimental spectra were performed using computer programs employing full diagonalization of the spin Hamiltonian matrix, written by one of us.
Crystallography
The crystallographic data for 1, 2, and 3 were collected using a Nonius Kappa CCD diffractometer at room temperature using graphite-monochromated MoKα radiation (λ = 0.71073 Å). Data sets were integrated using the Denzo-SMN package23 and corrected for Lorentz-polarization and absorption effects.24 The structures were solved by direct methods (SIR97)25 and refined by full-matrix least-squares methods with all non-hydrogen atoms being anisotropic. As for hydrogen atoms, those belonging to methyl groups in 1 and all the C–H in 2 and 3 were included on calculated positions, riding on their carrier atoms; the others were located in the difference-Fourier map and refined isotropically. All other calculations were performed using SHELXL-9726 implemented in the WINGX system of programs.27 The experimental details are reported in Table 1.| 1 | 2 | 3 | |
|---|---|---|---|
| Chemical formula | C26H22CuN4O8 | C26H26CuN4O10 | C26H36Cu2N4O14·2(H2O) |
| M r | 582.02 | 618.05 | 791.70 |
| Crystal system, space group | Monoclinic, P21/c | Monoclinic, P21/c | Monoclinic, P21/c |
| a, b, c (Å) | 7.8506 (1), 21.8740 (4), 8.1508 (2) | 8.0020 (2), 12.2397 (3), 14.5180 (3) | 7.6633 (2), 27.2585 (7), 8.5840 (2) |
| β (°) | 103.0120 (6) | 105.1790 (11) | 117.5840 (11) |
| Z | 2 | 2 | 2 |
| V (Å3) | 1363.75 (5) | 1372.32 (6) | 1589.29 (7) |
| μ (mm−1) | 0.86 | 0.86 | 1.42 |
| Crystal size (mm) | 0.52 × 0.47 × 0.17 | 0.26 × 0.20 × 0.18 | 0.55 × 0.26 × 0.12 |
| No. of measured, independent and observed [I > 2σ(I)] reflections | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 268, 3883, 3325 268, 3883, 3325 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455, 3294, 2519 455, 3294, 2519 |
6658, 3325, 2884 |
| R int | 0.034 | 0.039 | 0.056 |
| R[F2 > 2σ(F2)], wR(F2), S | 0.038, 0.115, 1.08 | 0.043, 0.136, 1.02 | 0.045, 0.142, 0.99 |
| No. of reflections | 3883 | 3294 | 3325 |
| No. of parameters | 211 | 196 | 249 |
| Δρmax, Δρmin (e Å−3) | 0.31, −0.44 | 0.32, −0.61 | 0.54, −1.03 |
Quantum mechanical calculations
The ‘in vacuum’ fully optimized geometries of [Cu(γ-pic)2(2-nitrobenzoate)2] (1) and [Cu(β-pic)2(2-nitrobenzoate)·2(H2O)2] (2) complexes have been obtained by density functional theory (DFT) calculations carried out at the B3LYP/6-31G(d,p) level of theory using the Firefly system of programs.28,29ORCA software30 was used to perform the “broken symmetry” DFT calculations of exchange parameters J for 3. All atoms were retained at the positions determined by the X-ray structures. The “broken symmetry” procedure applied to a dimeric copper(II) complex first performs a Self-Consistent Field (SCF) calculation for a high-spin molecule (HS) with the spin equal to 1. In the next stage, another SCF calculation is performed taking the spin on one Cu atom ‘up’ and ‘down’ on another, which is referred to as the broken symmetry state (BS). Finally, the magnitude of J (for the spin Hamiltonian 1) is evaluated as J = 2(EHS − EBS)/(〈S2〉HS − 〈S2〉BS), where E are the energies and 〈S〉2 are the expectation values of the spin-squared operator in the HS and BS states.
Ahlrichs-type basis set TZVPP31 for copper(II) and all coordinated atoms, and VDZ31a for other atoms were used, combined with the B3LYP32 functional. Ahlrichs polarisation functions from basis H–Kr R and auxiliary bases from the TurboMole library were also used.31b
Results and discussion
The composition of 1, 2 and 3 was established by elemental analysis. The mode of coordination of the carboxylate ligand in these complexes was indicated by IR spectral criterion Δv = vcarboxylato(asym) − vcarboxylato(sym) as reported in literature.33,34Molecular geometry and coordination
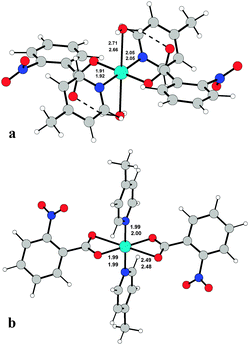
To determine the structures unambiguously and to analyse the packing modes, single X-ray crystal structure determination of complexes 1, 2 and 3 was undertaken. Fig. 1–3 report the ORTEPIII diagrams for 1–3, respectively.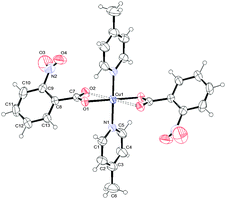 | ||
| Fig. 1 ORTEPIII view and the atom numbering scheme for 1. Thermal ellipsoids are drawn at the 50% probability level. Contact distances are shown as dashed lines. | ||
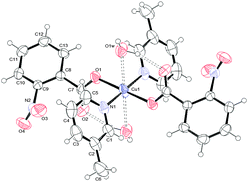 | ||
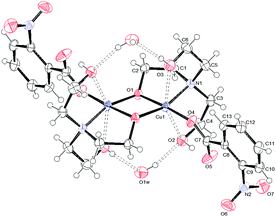
| Fig. 2 ORTEPIII view and the atom numbering scheme for 2. Thermal ellipsoids are drawn at the 40% probability level. Contact distances and hydrogen bonds are shown as dashed lines. | ||
 | ||
| Fig. 3 ORTEPIII view and the atom numbering scheme for 3. Thermal ellipsoids are drawn at the 40% probability level. Contact distances and hydrogen bonds are shown as dashed lines. | ||
Relevant geometrical parameters are reported in Table 2. In 1 and 2, the Cu atom lies on an inversion center, while in 3 a symmetry center is positioned just in the middle of the binuclear complex. In both 1 and 2 complexes, the Cu atom is linked to two picoline and two monodentate benzoate ligands, bonded via O1. In addition, it is involved in two further second-order interactions, giving a final (4 + 2) coordination: in 1 the carboxylic oxygens (O2) are at a Cu–O distance of 2.518(1) Å, while in 2 two centrosymmetrically related water molecules are at a distance of 2.739(2) Å (Table 2). The angles formed by the O2–Cu1 and O1w–Cu1 lines with the normal to mean basal planes measure 32.60(4) and 6.08(7)° in 1 and 2, respectively. Complex 3 is dimeric with the de-protonated oxygen atom of the H2tea ligand forming a bridge between two centrosymmetrically related Cu(II) atoms. The coordination geometry of 3 can be described, in analogy with those reported in the literature for analogous Cu(II) benzoate,35 3-chlorobenzoate36 and 4-methylbenzoate37 complexes, as distorted tetragonal bipyramidal (or highly distorted octahedral), with each H2tea molecule acting as a tetradentate ligand or as square-planar with two additional interactions like in 1 and 2.
| a Symmetry code: (1 − x,−y, −z). | |||
|---|---|---|---|
| 1 | |||
| Cu1–N1 | 2.005(1) | Cu1…O2 | 2.518(1) |
| Cu1–O1 | 1.987(1) | ||
| N1–Cu1–O1 | 89.24(5) | N1–Cu1–O2 | 88.19(5) |
| Cu⋯Cu contacts | |||
| Cu⋯Cu | 7.8506(1) | 8.1508(2) | |
| 2 | |||
| Cu1–N1 | 1.997(2) | Cu1⋯O1W | 2.739(2) |
| Cu1–O1 | 1.971(2) | ||
| N1–Cu1–O1 | 91.02(7) | N1–Cu1–O1w | 91.10(8) |
| O1–Cu1–O1w | 96.00(7) | ||
| Cu…Cu contacts | |||
| Cu…Cu | 8.0020(2) | 9.4945(1) | |
| 3 | |||
| Cu1–O1 | 1.946(2) | Cu1⋯O3 | 2.478(2) |
| Cu1–N1 | 2.042(2) | Cu1–O4 | 1.966(3) |
| Cu1⋯O2 | 2.576(2) | Cu⋯Cua | 2.9187(4) |
| Cu1–O1a | 1.934(2) | ||
| O1–Cu1–N1 | 85.00(9) | N1–Cu1–O3 | 76.3(1) |
| O1–Cu1–O2 | 90.59(9) | N1–Cu1–O4 | 98.70(9) |
| O1–Cu1–O3 | 97.2(1) | O2–Cu1–O4 | 88.83(9) |
| N1–Cu1–O2 | 78.40(9) | O3–Cu1–O4 | 85.0(1) |
| O1–Cu1–O1a | 82.46(9) | Cu1–O1–Cu1a | 97.5(1) |
Actually, the equatorial plane in 3 is defined by one carboxylate oxygen atom of 2-nitrobenzoate, two bridging alkoxo oxygen atoms and one nitrogen while O2 and O3 atoms of H2tea are located at much longer distances (Table 2); the Cu atom is displaced by 0.023 Å from the least-square plane passing through (O1, N1, O4) and the angles formed by Cu1–O2 and Cu1–O3 lines with the normal to this plane are 16.44(9) and 11.19(8)°, respectively. For each dimeric moiety, two water molecules of crystallization are present in the crystal.
The Cu–N distances are similar in all the three complexes and do not show any significant discrepancy from structural parameters of related Cu compounds. The Cu–O distances display a wide range of values, from 1.934(2) Å (oxo-bridge, complex 3) to 2.739(2) Å (water molecule, complex 2), that can be more appropriately considered as a contact distance. The histogram of the Cu–O(benzoate) distances, obtained from a search on the CSD database (278 hits) considering both the oxygens linked to the metal, is clearly bimodal showing two distinct bond length distributions around 2.0 and 2.6 Å, respectively, in perfect agreement with the structural data of 1 and 3. Moreover, Fig. 4, obtained by the same CSD search, suggests that these two distances are intercorrelated; if one increases, the other decreases. Geometrical data of complex 1 (red point) are perfectly in line with the others. The points enclosed in a circle, which do not follow the curve trend, refer to particular structures: of polymeric type, with huge ligands, or having Cl− anions as ligands.
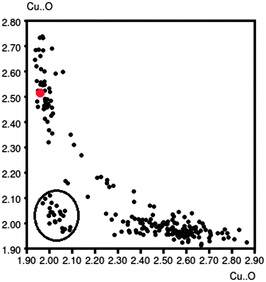 | ||
| Fig. 4 Intercorrelation between the Cu–O distances in Cu(II) benzoate complexes. Data for compound 1 are reported as red points. | ||
As far as the binuclear complex 3 is concerned, a comparison with the similar Cu–H2tea complexes above mentioned35–37 shows that the molecular arrangement around the Cu atoms and the geometrical parameters are strictly comparable in all of them; benzoates are acting as monodentate ligands, with the oxygen of anionic H2tea bridging two metals, and one OH group of the H2tea being involved in an intramolecular hydrogen bond with the free benzoate oxygen. Moreover, two cocrystallized water molecules for each binuclear complex are always present connecting different molecules in exactly the same way as in complex 3 (vide infra), suggesting that in these structures, the presence of water is essential for the robustness of the crystalline framework.
It is interesting to note that complexes 1 and 2 present a different Cu environment in spite of having almost identical ligands (p-methyl and o-methyl pyridine, respectively). In order to explore whether the choice of different picoline molecules can affect the possibility of water inclusion in the first or the second coordination sphere, the equilibrium geometry of both complexes has been obtained by DFT calculations starting from the same initial point, i.e. by adding two Cu-coordinated water molecules to the picoline/benzoate skeleton at a distance of 2.40 Å or using an initial geometry with no coordinated water molecules. The results are reported in Fig. 5. For the diaquo complexes, the Cu–O, Cu–N distances are strictly comparable and the energies of the calculated molecules are practically identical: the γ-picoline complex is more stable than the β-picoline one by 0.36 kcal mol−1. The same results have been obtained for complexes without water, but in this case the γ-picoline compound is more stable by 2.13 kcal mol−1; this extra-stability is however not sufficient to explain the different coordination of the two compounds, which probably depends mostly on the solvent used (or in general on the crystallization conditions).
As mentioned at the outset, one of our objectives was to delineate the variation/change in the conformation of the carboxylate ligand upon the addition of three different N-donor ligands, two rigid (picolines) and one flexible (H3tea). Indeed, as anticipated, the –NO2 moiety is out of plane from the aromatic ring in all three, but the extent of variation is quite large, ranging from 42.4(3), 53.9(3) and 81.6(4)° for 1, 2 and 3 respectively (note that this variation is highest with the most flexible N-donor ligand H3tea).
In an analogous manner, the –COO− moiety also gets rotated with respect to the aromatic plane, the highest rotation being observed in 1 and 2 (42.6(2) and 42.3(3)°) and almost in-plane of the aromatic ring in 3 (5.2(2)°). Here also that distinction prevails; the rigid N-donor ligands are similar in behavior and the flexible one shows considerable deviation. It is clear that each of these structures would try to maximize the resonance energy by keeping both –NO2 and –COO groups in plane with the aromatic ring, but the opposing steric repulsion needs to be compensated by allowing them to move away from the plane to the extent that the lattice energy is minimum (most stable arrangement). Thus, in the most flexible deprotonated ligand H2tea (3) –COO− is only few degrees away from the plane, but at the same time the –NO2 is almost orthogonal. In the rigid N-donors 1 and 2 the situation is in between, both the groups deviate to the extent of some 45°. These findings are supported by the survey of the conformation of the nitrobenzoate moiety in Cu complexes with N-donor ligands already present in literature. 21 structures of this type were found in the CSD; for each of them the NO2− and COO− out-of-plane was evaluated through the measure of the torsion angles O1–N–C1–C2 and O2–C3–C2–C1 (see Fig. 6). As shown in the plot, the two angles are strongly intercorrelated in the same way as found for the present complexes; the COO− group is rarely coplanar with the phenyl moiety, and this happens when both the oxygens are ‘busy’ in covalent or strong H-bonding interactions within a same molecular complex, in which the Cu atom is linked to small or highly conformationally adaptable N-donor ligands.
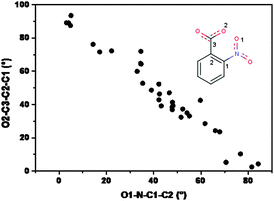 | ||
| Fig. 6 Scatter plot of the out of plane angles for NO2 and COO− groups in Cu(2-nitrobenzoate) complexes. | ||
This observation becomes interesting when we consider the mode of coordination in 1, 2 and 3. In 1, the carboxylate group is monodentate but the second oxygen is still interacting with the Cu atom, (Table 2) whereas in 2 one of the Cu–O distance becomes so large (3.185(2) Å) that the coordination is obviously monodentate and it is much higher yet in 3 (3.378(3) Å). That is, the nature of the N-donor ligand definitely exerts influence on the coordination mode and this in turn affects the structure and the packing architecture of the crystallized complex.
Packing
The hydrogen bonding structural parameters for the three complexes are reported in Table 3. In 1, the presence of a number of good hydrogen bonding acceptors but a lack of good hydrogen bonding donors allows only the formation of C–H⋯O bonds. The C–H⋯O1 contact on the two sides of the molecule generates ribbons linking the complexes along the c direction. These ribbons are in turn connected along the b direction through C–H⋯O2 interactions. Conversely, in 2 and 3 the presence of water molecules or hydroxyl groups leads to strong O–H⋯O interactions, both intermolecular and intramolecular. In 2, the coordinated water molecules, besides being involved in intramolecular interactions, act as H-bond donors towards the O2 atoms of an adjacent molecule, giving rise to the R22(12) ring as shown in Fig. 7.| D–H⋯A | D–H | D⋯A | H⋯A | Angle |
|---|---|---|---|---|
| a x − 1, y, z. b x, y, z + 1. c 1 − x, −y, −z. d x + 1, y, z. e x, 1/2 − y, z + 1/2. f 1 − x, y − 1/2, 1/2 − z. g x, 1/2 − y, z − 1/2. h −x, −y, −z. i 1 − x, −y, −z. j x + 1, y, z + 1. | ||||
| Complex 1 | ||||
| C2–H2⋯O2a | 0.95(2) | 3.268(2) | 2.36(3) | 160(2) |
| C4–H6⋯O1b | 0.90(3) | 3.451(2) | 2.56(3) | 168(2) |
| Complex 2 | ||||
| O1W–H2W⋯O2c | 0.93(4) | 2.728(3) | 1.83(4) | 163(4) |
| O1W–H1W⋯O2d | 0.89(4) | 2.892(3) | 2.06(4) | 154(4) |
| C3–H3⋯O1We | 0.93 | 3.426(4) | 2.53 | 161 |
| C6–H62⋯O3f | 0.96 | 3.440(5) | 2.56 | 151 |
| C12–H12⋯O2g | 0.93 | 3.397(3) | 2.49 | 163 |
| Complex 3 | ||||
| O2–H2⋯O5 | 0.85(5) | 2.631(4) | 1.80(5) | 165(4) |
| O1W–H2W⋯O2 | 0.84(5) | 2.870(4) | 2.05(6) | 164(5) |
| O1W–H1W⋯O1h | 0.82(7) | 2.997(4) | 2.28(7) | 146(6) |
| O3–H3⋯O1Wi | 0.71(6) | 2.711(4) | 2.01(6) | 171(6) |
| C1–H1B⋯O1Wj | 0.97 | 3.397(4) | 2.61 | 138 |
 | ||
| Fig. 7 O–H⋯O hydrogen bond arrangement in 2. Intermolecular and intramolecular hydrogen bonds are shown as dashed and dotted lines, respectively. | ||
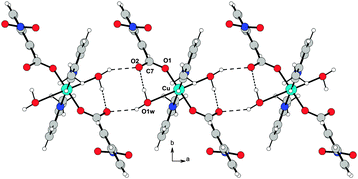
The resulting overall packing is made of parallel ribbons running along the a direction. In 3, the interaction network is somewhat similar but more complex than 2 due to the presence of a large number of hydrogen bond donor and acceptor groups. Water molecules of crystallization act as linkers by bridging the adjacent molecules; they behave as hydrogen bond donors towards O1 and O2 atoms and as acceptors to the O3 atom. This results in formation of molecular ribbons running along the a direction (Fig. 8). In both structures the crystal lattice is further stabilized by weak C–H⋯O interactions.
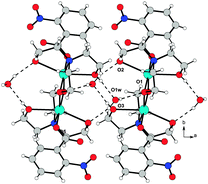 | ||
| Fig. 8 O–H⋯O hydrogen bond arrangement in 3. Intermolecular hydrogen bonds are shown as dashed lines. For the sake of clarity, intramolecular O–H⋯O interactions are not shown. | ||
Magnetic and EPR measurements
Magnetic moments higher than the spin-only value of 1.73 are observed in copper(II) complexes (3d9), due to spin–orbit coupling. Monomeric copper(II) complexes generally show magnetic moments in the range 1.75 to 2.2 μB at room temperature. The EPR spectra of the powdered complexes with gx = 2.056, gy = 2.066 and gz = 2.258 parameters for 1 (Fig. 9a) and gx = 2.057, gy = 2.057 and gz = 2.262 for 2 (Fig. 9b) are typical for axial symmetry of Cu(II) coordination polyhedron (with a very weak rhombic distortion) for 1 and axial symmetry for 2. The g parameter values for 1 and 2 correspond to the dx2−y2 orbital of the unpaired electron ground state and are characteristic of the N2O2 donor set provided by the ligands in the xy Cu(II) plane. The low field “parallel” part of the spectrum for 2 exhibits signals due to hyperfine interaction between unpaired electrons and copper nucleus (nuclear spin I = 3/2) with A∥ = 169 × 10−4 cm−1 (Fig. 9b). It is a rare case when the hyperfine splitting is resolved in a powder EPR spectrum of a Cu(II) complex suggesting a greater isolation of Cu(II) centers than in 1 due to water molecules at axial positions which are involved in hydrogen bonds with carboxyl groups. The Cu–Cu distances are in fact greater in 2 than in 1 (Table 2).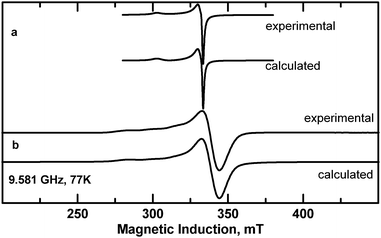 | ||
| Fig. 9 X-band EPR spectra of powdered complexes (a) 1 and (b) 2 at 77 K (experimental and calculated with the parameters given in the text). | ||
Magnetic susceptibility and EPR spectra of 3
The temperature dependence of the effective magnetic moment of 3 is shown in Fig. 10.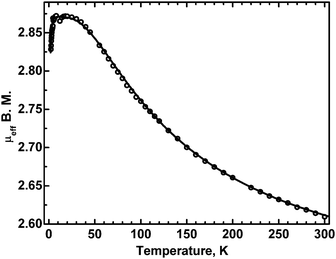 | ||
| Fig. 10 The effective magnetic moment of 3 as a function of temperature. Dots: experimental, solid line – calculated with J = −100 cm−1 (see the text). | ||
The moment is seen to increase with decreasing temperature, to reach a plateau between 25 and 4.5 K, followed by a decrease at the lowest temperatures. This is a characteristic pattern of a ferromagnetically coupled dimer. The exchange interactions, responsible for that behavior, can be described by the classical Heisenberg–Dirac–VanVleck Hamiltonian
| Ĥ = JŜ1Ŝ2 | (1) |
The magnetic susceptibility per mole of a dimeric copper(II) complex can be calculated from
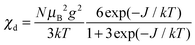 | (2) |
| Ĥ = JŜ1Ŝ2 + D12{Ŝz1Ŝz2 − Ŝ1·Ŝ2/3} + E12(Ŝx1Ŝx2 − Ŝy1Ŝy2) + μBB{g1}Ŝ1 + μBB{g2}Ŝ2 | (3) |
The spin Hamiltonian matrix was diagonalised to find the energy levels and the magnetic susceptibility per mole of the dimer was calculated from
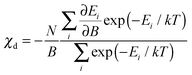 | (4) |
In order to estimate the magnitude of the isotropic exchange integral J in eqn (1)–(3), a DFT calculation has been performed using the procedure described in the previous section. Correct sign of J was found while its magnitude was overestimated (−176 cm−1).
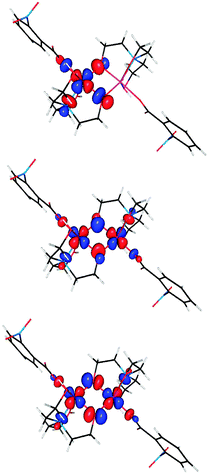
The interactions which contribute to ferromagnetism of dinuclear complexes involve pairs of overlapping ‘magnetic orbitals’ localized on each metal ion.40 Representative orbitals are plotted in Fig. 11.
As for EPR spectra, a spin-triplet (S = 1) spectrum was seen at all temperatures over the range 3–300 K. Spectra were of the best quality at moderately low temperatures of about 200 K. Because of the large energy difference between the triplet and singlet states, the spectra could be interpreted in terms of the coupled-spin Hamiltonian with S = 1 (instead of using eqn (3)):
| Ĥ = μBB{g}Ŝ + D{Ŝz2 − S(S + 1)/3} + E(Ŝx2 − Ŝy2) | (5) |
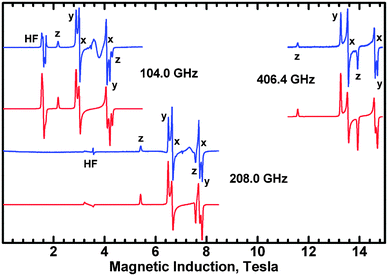
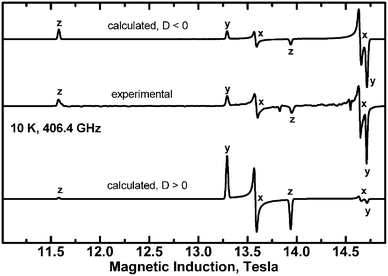
Interestingly, the zero-field splitting tensor and the g tensor were found to be non-coaxial. Spectra at all frequencies (Fig. 12) were successfully simulated assuming that the zfs tensor is rotated versus the g tensor by 11 degrees about the X axis. At 200 K, the following parameters were found: gx = 2.060, gy = 2.060, gz = 2.303, D = −1.135 cm−1, E = −0.0430 cm−1. The parameters derived from the X-band spectra (Fig. 13) at 77 K are very similar: gx = 2.06, gy = 2.06, gz = 2.30, |D| = 1.125 cm−1, |E| = 0.040 cm−1, with signals due to the monomeric impurities present at 300 mT. The spin Hamiltonian parameters are temperature-dependent and at 10 K (Fig. 14) they are gx = 2.056, gy = 2.045, gz = 2.320, D = −1.042 cm−1, E = −0.0075 cm−1, with the same angle of rotation of the zfs and g tensors as found at 200 K (11 deg). The reason for the deviation between the axes of the g and zfs tensors observed in the EPR spectra is the misalignment between the equatorial ligand plane and the Cu–Cu direction.
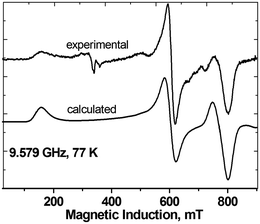 | ||
| Fig. 13 The X-band EPR spectra of powdered complex 3 at 77 K, experimental and calculated with the parameters given in the text. | ||
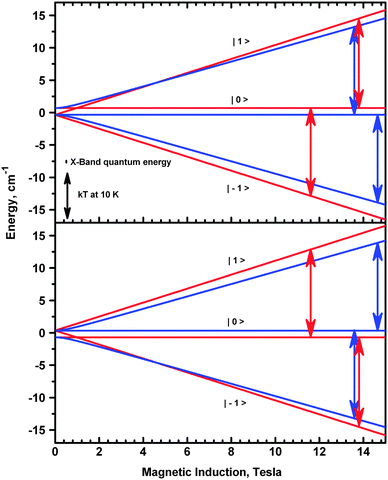
Since the complex is ferromagnetic, EPR spectra could be detected at very low temperatures allowing determination of the sign of D and E.41 This is possible thanks to the Zeeman splitting being comparable to the thermal energy, kT (Fig. 15).
In copper(II) dimers, there are two contributions to the zero-field splitting parameters D and E. One is the magnetic dipole–dipole interaction, while the other one is associated with the anisotropy of the exchange interactions. These contributions cannot be determined separately in an experiment. The dipolar part depends on the Cu–Cu separation. Its largest component is oriented along the Cu–Cu direction, while the largest component of the exchange-related zfs is expected to be parallel to the gz direction. The latter should be at least approximately perpendicular to the plane of the equatorial ligands. The angle between the Cu–Cu vector and the normal to the equatorial ligand plane is 86 deg. We assume for simplicity that this angle equals 90 deg and define a system of coordinates in which the axis X is along Cu–Cu, and the axis Z is perpendicular to Cu–Cu and is tilted 4 deg from the normal to the plane defined by the equatorial ligands. In these coordinates one can write formulae for the dipole–dipole related Ddip and Edip parameters using the point-dipole approximation:
| Ddip = (2gz2 + 2gx2 − gy2)μB2/4RCu–Cu3 |
| Edip = −(2gx2 + gy2)μB2/4RCu–Cu3 | (6) |
The experimentally determined D and E parameters are the sum of the dipole–dipole and exchange-related parts, therefore
| Dex = D − Ddip = −1.20 cm−1 |
| Eex = E − Edip = 0.007 cm−1 |
The exchange-related zero-field splitting thus appears to be remarkably axial (|E| ≪ |D|). Maurice et al. derived formulae for Dex and Eex for two coupled Cu2+ ions with the dx2−y2 ground state orbital.42
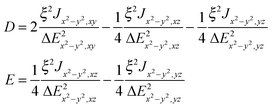 | (7) |
The quantities ξ/ΔEx2−y2,xyetc. in eqn (7) appear also in the theory of the g tensor in Cu(II). For example, Δgz = gz − 2.0023 = 8ξ/ΔEx2−y2,xy and it is possible to eliminate the unknown ΔE values from eqn (7):
| Dex = [Jx2−y2,xyΔgz2 − 2Jx2−y2,xzΔgy2 − 2Jx2−y2,yzΔgx2]/32 | (7a) |
Conclusions
Three novel complexes were isolated by addition of γ-picoline, β-picoline and triethanolamine to the hydrated copper(II) 2-nitrobenzoate, [Cu2(2-nitrobenzoate)4(H2O)2]·2H2O suspended in a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–water mixture. It has been found that the addition of different types of N-donor ligands (rigid and flexible) has a profound influence on the orientation of –NO2 and –COO− moieties in these complexes and, above all, on the coordination geometry around the Cu atom. Detailed structural analysis of 1, 2 and 3 confirms that the addition of different N-donor ligands to copper(II) carboxylates may affect their physico-chemical behaviour such as magnetism. The dimeric complex 3 exhibits relatively strong ferromagnetic exchange with J = −100 cm−1 (corresponding to H = JS1S2). The zero-field splitting parameters (zfs) of the dimer triplet state D = −1.135 cm−1, E = −0.043 cm−1 were derived from the HF EPR spectrum recorded at moderately low temperatures. The sign of D was determined from low-temperature HF EPR spectra.
1 methanol–water mixture. It has been found that the addition of different types of N-donor ligands (rigid and flexible) has a profound influence on the orientation of –NO2 and –COO− moieties in these complexes and, above all, on the coordination geometry around the Cu atom. Detailed structural analysis of 1, 2 and 3 confirms that the addition of different N-donor ligands to copper(II) carboxylates may affect their physico-chemical behaviour such as magnetism. The dimeric complex 3 exhibits relatively strong ferromagnetic exchange with J = −100 cm−1 (corresponding to H = JS1S2). The zero-field splitting parameters (zfs) of the dimer triplet state D = −1.135 cm−1, E = −0.043 cm−1 were derived from the HF EPR spectrum recorded at moderately low temperatures. The sign of D was determined from low-temperature HF EPR spectra.
Acknowledgements
The high-field EPR spectra were recorded at the NHMFL which is supported by the NSF through the cooperative agreement DMR-1157490, the State of Florida and the Department of Energy. One of us (RPS) thanks the U.G.C.(New Delhi), India, for financial assistance vide sanction letter F.No. 40-60/2011(SR). JJ is grateful to Ministry of Science and Higher Education of the Polish Republic for financial support in the purchase of the Bruker ELEXSYS E 500 EPR spectrometer.Notes and references
- (a) C. A. Schalley, Supramolecular Chemistry, Thematic Series, Beilstein J. Org. Chem., 2009, 5 Search PubMed; (b) C. A. Schalley, Supramolecular Chemistry II, Thematic Series, Beilstein J. Org. Chem, 2011, 7 Search PubMed; (c) H. Xu, X. Zhang, J. Sun and S. Cui, Supramolecular Chemistry: from molecular architecture to functional assemblies, Encyclopedia of Life Support System, 2010.
- (a) C. S. Liu, P. Q. Chen, E. C. Yang, J. L. Tian, X. H. Bu, Z. M. Li, H. W. Sun and Z. Y. Lin, Inorg. Chem., 2006, 45, 5812 CrossRef CAS PubMed; (b) J. W. Steed and P. A. Gale, Supramolecular Chemistry: From molecules to nanomaterials, Wiley, 2012, vol. 8 Search PubMed.
- (a) L. J. Zhou, Y. Y. Wang, C. H. Zhou, C. J. Wang, Q. Z. Shi and S. M. Peng, Cryst. Growth Des., 2007, 7, 300 CrossRef CAS; (b) P. Diaz, J. Benet-Buchholz, R. Vilar and A. J. P. White, Inorg. Chem., 2006, 45, 1617 CrossRef CAS PubMed.
- S. H. Rahaman, H. Chowdhury, D. Bose, G. Mostafa, H.-K. Fun and B. K. Ghosh, Inorg. Chem. Commun., 2005, 8, 1041 CrossRef CAS PubMed.
- M. M. Bishop, S. J. Coles, H. W. L. Andrew, L. F. Linndoy, A. Parkin, O. T. Thorn-Seshold and P. Turner, Supramol. Chem., 2005, 17, 567 CrossRef CAS.
- J. Lang, K. Vagnerova, J. Czernek and P. Lhotak, Supramol. Chem., 2006, 18, 371 CrossRef CAS.
- J. P. Zhang and S. Kitagawa, J. Am. Chem. Soc., 2008, 130, 907 CrossRef CAS PubMed.
- A. Westcott, J. Fisher, L. P. Harding, P. Rizkallah and M. J. Hardie, J. Am. Chem. Soc., 2008, 130, 2950 CrossRef CAS PubMed.
- M. M. O. Pena, J. Lee and D. J. Thiele, J. Nutr., 1999, 129, 1251 CAS.
- N. W. Solomons, J. Am. Coll. Nutr., 1985, 4, 83 CrossRef CAS.
- P. F. Larson, Angew. Chem., Int Ed., 2009, 48, 5091 Search PubMed.
- B. Wu, X.-J. Yang, C. Janiak and P. G. Lassahn, Chem. Commun., 2003, 902 RSC , and references cited therein.
- J. R. J. Sorenson, Chem. Br., 1989, 25, 169 CAS , and references cited therein.
- C. Marzano, M. Pellei, F. Tisato and C. Satini, Anticancer Agents Med. Chem., 2009, 9, 185 CrossRef CAS.
- I. Iakovidis, I. Delimaris and S. M. Piperakis, Mol. Biol. Int., 2011, 1 Search PubMed.
- Dublin Institute of Technology Intellectual Property Ltd, US Pat. EP2407164A1, 2012 Search PubMed.
- F. Q. Liu, Q. X. Wang, K. Jiao, F. F. Jian, G. Y. Liu and R. X. Li, Inorg. Chim. Acta, 2006, 359, 1524 CrossRef CAS PubMed.
- J. Moncol, M. Korabik, P. Segl'a, M. Koman, D. Mikloš, J. Jaškova, T. Glowiak, M. Melnìk, J. Mrozinski and M. R. Sundberg, Z. Anorg. Allg. Chem., 2007, 633, 298 CrossRef CAS.
- M. Barceló-Oliver, Á. García-Raso, Á. Terrón, E. Molins, M. J. Prieto, V. Moreno, J. Martínez, V. Lladó, I. López, A. Gutiérrez and P. V. Escribá, J. Inorg. Biochem., 2007, 101, 649 CrossRef PubMed.
- M. A. Malati, Experimental Inorganic Chemistry, Horwood Publishing, Chichester, 1st edn, 1999 Search PubMed.
- (a) C. J. O'Connor, Prog. Inorg. Chem., 1982, 29, 203 CrossRef CAS; (b) G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532 CrossRef CAS.
- A. K. Hassan, L. A. Pardi, J. Krzystek, A. Sienkiewicz, P. Goy, M. Rohrer and L.-C. Brunel, J. Magn. Reson., 2000, 142, 300 CrossRef CAS PubMed.
- Z. Otwinowski and Z. Minor, Processing of X-Ray Diffraction Data Collected in Oscillation Mode, in Methods in Enzymology, ed. C. W. Carter and R. M. Sweet, Macromolecular Crystallography, Part A, Academic Press, San Diego, 1997, 307 Search PubMed.
- R. H. Blessing, Acta Crystallogr., 1995, A51, 33 CrossRef CAS.
- A. Altomare, M. C. Burla, M. Camalli, G. Cascarano, C. Giacovazzo, A. Guagliardi, A. G. Moliterni, G. Polidori and R. Spagna, J. Appl. Crystallogr., 1999, 32, 115 CrossRef CAS.
- G. M. Sheldrick, SHELXL97, Program for Crystal Structure Refinement, University of Göttingen, Göttingen, Germany, 1997 Search PubMed.
- J. Farrugia, J. Appl. Crystallogr., 1999, 32, 837 CrossRef.
- A. A. Granovsky, Firefly (PC GAMESS) version 7.1.G, Copyright (c) 1994, 2009, Firefly Project, Moscow, Russia.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347 CrossRef CAS.
- F. Neese, ORCA – An ab initio, Density Functional and Semiempirical Program Package, Version 2.9.1, 2012, free download from http://www.cec.mpg.de/forum/downloads.php CrossRef; F. Neese, The ORCA program system WIREs, Comput. Mol. Sci., 2012, 2, 738 CrossRef.
- (a) H. Schaefer, R. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef; (b) R. Ahlrichs, unpublished. The Ahlrichs auxiliary basis sets were obtained from the TurboMole basis set library under ftp.chemie.uni-karlsruhe.de/pub/jbasen.
- (a) D. A. Becke, Phys. Rev. A, 1988, 38, 30980 CrossRef; (b) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef; (c) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7406 CrossRef; (d) R. A. Kendall and H. A. Früchtl, Theor. Chem. Acc., 1997, 97, 158 CrossRef CAS.
- K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, John Wiley & Sons, New York, 5th edn, 1997 Search PubMed.
- J. Bellamy, The Infrared Spectra of Complex Molecules, Chapman & Hall, London/New York, 1980 Search PubMed.
- (a) A. M. Kirillov, M. N. Kopylovich, M. V. Kirillova, M. Haukka, M. F. C. G. da Silva and A. J. L. Pombeiro, Angew. Chem., Int. Ed., 2005, 44, 4345 CrossRef CAS PubMed; (b) R. M. Escovar, J. H. Thurston, T. Ould-Ely, A. Kumar and K. H. Whitmire, Z. Anorg. Allg. Chem., 2005, 631, 2867 CrossRef CAS.
- A. M. Kirillov, M. N. Kopylovich, M. V. Kirillova, E. Yu. Karabach, M. Haukka, M. F. C. G. da Silva and A. J. L. Pombeiro, Adv. Synth. Catal., 2006, 348, 159 CrossRef CAS.
- A. M. Kirillov, M. Haukka, M. N. Kopylovich and A. J. L. Pombeiro, Acta Crystallogr., 2007, E63, m526 Search PubMed.
- V. H. Crawford, H. W. Richardson, J. R. Wasson, D. J. Hodgson and W. E. Hatfield, Inorg. Chem., 1976, 15, 2107 CrossRef CAS.
- (a) W. E. Hatfield, in Magneto-structural correlations in exchange coupled systems, ed. R. D. Willet, D. Gatteschi and O. Kahn, NATO ASI Series., Reidel, Dordrecht, 1985, p. 555 Search PubMed; (b) D. Venegas-Yazigi, D. Aravena, E. Spodine, E. Ruiz and S. Alvarez, Coord. Chem. Rev., 2010, 254, 2086 CrossRef CAS PubMed; (c) E. Ruiz, P. Alemany, S. Alvarez and J. Cano, J. Am. Chem. Soc., 1997, 119, 1297 CrossRef CAS.
- (a) O. Kahn and B. J. Briat, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 268 RSC; (b) A. Rodríguez-Diéguez, M. E. López-Viseras, J. E. Perea-Buceta, A. J. Mota and E. Colacio, Inorg. Chim. Acta, 2012, 385, 73 CrossRef PubMed; (c) N. Onofrio and J.-M. Mouesca, Inorg. Chem., 2011, 50, 5577 CrossRef CAS PubMed; (d) A. Rodríguez-Fortea, P. Alemany, S. Alvarez and E. Ruiz, Inorg. Chem., 2002, 41, 3769 CrossRef PubMed.
- (a) A. Ozarowski, Inorg. Chem., 2008, 47, 9760 CrossRef CAS PubMed; (b) A. Ozarowski, I. B. Szymanska, T. Muziol and J. Jezierska, J. Am. Chem. Soc., 2009, 131, 10279 CrossRef CAS PubMed.
- R. Maurice, K. Sivalingam, D. Ganyushin, N. Guihery, C. de Graaf and F. Neese, Inorg. Chem., 2011, 50, 6229 CrossRef CAS PubMed.
- (a) D. L. Reger, A. E. Pascui, M. D. Smith, J. Jezierska and A. Ozarowski, Inorg. Chem., 2012, 51, 7966 CrossRef CAS PubMed; (b) D. L. Reger, A. E. Pascui, M. D. Smith, J. Jezierska and A. Ozarowski, Inorg. Chem., 2012, 51, 11820 CrossRef CAS PubMed.
- A. Ozarowski and D. Reinen, Inorg. Chem., 1986, 25, 1704 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: TGA, IR and UV characterization details, and figures depicting TGA curves, IR spectra and crystal packing for the three complexes. CCDC 915710 (1), 915711 (2) and 915712 (3). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c3nj00736g |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2014 |