Influence of aromatic ligand on the redox activity of neutral binuclear tetranitrosyl iron complexes [Fe₂(μ-SR)₂(NO)₄]: experiments and quantum-chemical modeling

Abstract

Reduction of neutral binuclear nitrosyl iron complexes of “μ-S” structural type [Fe₂(SR)₂(NO)₄] with R = 3-nitro-phenol-2-yl, 4-nitro-phenol-2-yl, 5-nitropyridine-2-yl and pyridine-2-yl in aprotic solution has been studied by a cyclic voltammetry (CVA) method at a wide range of potential scan rates. A complex with R = 3-nitro-phenol-2-yl was synthesized for the first time; therefore it was studied by X-ray and Mössbauer spectroscopy. The parameters of the Mössbauer spectrum are: isomer shift δ_Fe = 0.115(1) mm s⁻¹, quadrupole splitting ΔE_Q = 1.171(1) mm s⁻¹, and line width = 0.241(1) mm s⁻¹ at 85 K. From the current–voltage curve, the transfer of the first electron was found to be reversible, and the redox-potentials of these reactions were determined. The further reduction of the complexes was determined to be irreversible because the product of the second electron addition is instable and decomposes partially during the potential scan. Calculations of geometric and electronic structures of monoanions and dianions of the complexes under study and their theoretical redox-potentials were performed by DFT methods. Introduction of the electron-acceptor NO₂ group into the phenyl and pyridine rings of sulfur-containing ligands of the nitrosyl iron complexes was found to affect the geometry of the anions and the distribution of the additional negative charge, as well as to increase the redox-potential and to facilitate reduction of these complexes.

---

1. Introduction

The interest in the redox-reactions of synthetic sulfur–nitrosyl iron complexes, which are biomimetics of nitrosyl ferredoxins, nitric monoxide (NO) natural reservoirs^1–4 providing NO transport in the cells of living organisms, is due to the importance of a wider basic problem, i.e., correlation between the structure of these highly-reactive nitrosyl complexes and the mechanisms of their biological activity in vivo.⁵ Studies of the redox-properties of “esters of Roussin red salt” [Fe₂(μ-SR)₂(NO)₄] (R = an alkyl group) were first reported in ref. 6 and 7. Complexes of this structural type with aromatic ligands are known to easily generate NO upon thermal and photo activation,⁸ as well as upon hydrolysis in 1% aqueous solutions of dimethylsulfoxide.⁹ As follows from our research, they can be used as effective and less toxic (compared to complexes with R = an alkyl group) NO donors in chemotherapy of tumors.^10–12 However, their insolubility in water and physiological solutions limits their clinical application. Therefore, new experimental approaches are necessary for the production of bio-available medicinal forms. One of these approaches is based on the complex investigation of redox-reactions of neutral sulfur–nitrosyl complexes [Fe₂(μ-SR)₂(NO)₄]^13,14 with R = an aryl group, including quantum-chemical calculation of the redox-potentials of these systems in solutions and experimental study of their redox-activity by the CVA method, with the aim to predict the possibility to transform neutral complexes into ionic forms.

The present work aims at the theoretical and experimental determination of the reduction potentials for neutral binuclear nitrosyl iron complexes of “μ-S” structural type [Fe₂(SR)₂(NO)₄] with aromatic ligands (analogs of DNA pyridine bases), namely, a complex with 3-nitro-phenyl (1) synthesized for the first time, and complexes with 4-nitro-phenyl (2),¹⁵ 5-nitropyridine-2-yl (3)¹⁶ and pyridine-2-yl (4)⁷ in comparison with isostructural complexes with phenyl (5),¹³ 4,6-dimethyl-2-pyrimidyl (6) and 6-methylpyridyl (7).¹⁴ In this work, X-ray study of single crystals of 1 has been performed, and the geometrical and electronic structures of mono- and dianions of complexes 1–4 have been calculated by DFT methods, and the influence of the aromatic ligand in the complex on its redox activity has been studied.

2. Experimental

2.1. Reagents and materials

All materials and solvents were purchased commercially and used as supplied, unless otherwise mentioned. Analytical grade solvents used for the studies were further purified before use.

2.2. Synthesis and characterization of complexes 1–4

Crystals of complexes 1–3 were synthesized according to the procedure described in ref. 16.

For the synthesis of complex 1, 0.8 g of Na₂[Fe₂(S₂O₃)₂(NO)₄]·4H₂O (1.4 mM) in 20 ml of distilled water (purged with argon for 0.5 hours) and 0.78 g (3.1 mM) of Na₂S₂O₃·5H₂O¹⁸ were placed in a three-necked flask also purged with argon, and 1 g (5.3 mM) of 3-nitrophenyl hydrazinium salt (obtained according to ref. 16) in 20 ml of water was added dropwise under intense mixing. The reaction mixture was kept in the closed flask for 3 hours, then was filtered through a porous filter, washed with ether, and dissolved in methylene chloride. A part of the methylene chloride was removed by evaporation, and the solution was kept in a freezer at −18 °C. The next day small crystals of the precipitate were filtered and dried in air. Yield 0.5 g (78%). Fe₂S₂C₁₂H₈N₆O₈: found, %: C – 26.85, H – 1.89, N – 15.53, S – 11.57, Fe – 20.9; calculated, %: C – 26.69, H – 1.49, N – 15.55, S – 11.87, Fe – 20.68.

The IR-spectrum (cm⁻¹) of 1 was recorded on a Perkin-Elmer Spectrum 100X at room temperature: 3094(w), 3064(w), 1821(m), 1778(s), 1761(s), 1523(s), 1461(w), 1417(w), 1349(s), 1296(w), 1271(w), 1167(w), 1121(w), 1069(w), 997(w), 926(w), 896(w), 874(w), 806(m), 743(s), 733(s).

Complexes 2–4 were synthesized according to the procedures described in ref. 15–17, respectively. Fe₂S₂C₁₂H₈N₆O₈: found, %: C – 26.58, H – 1.56, N – 15.19, O – 23.37, Fe – 20.2, S – 11.78; calculated, %: C – 26.69, H – 1.49, N – 15.55, O – 23.70, Fe – 20.8, S – 11.88. C₁₀H₆N₈O₈S₂Fe₂: found, %: C – 22.20; H – 1.28; N – 19.84; S – 12.17; Fe – 21.20; calculated, %: C – 22.14; H – 1.12; N – 20.67; S – 11.83; Fe – 20.61. Fe₂S₂C₁₀H₈N₆O₄: found, %: C – 26.58; H – 1.80; N – 18.60; S – 14.15; Fe – 24.80; calculated, %: C – 26.60; H – 1.77; N – 18.58; S – 14.16; Fe – 24.77.

Elemental analysis of crystals 1–4 was performed at the Analytical Center of IPCP RAS. The iron content was determined by the method of atomic absorption spectrometry on the atomic absorption spectrophotometer AAS-3 of Carl Ceiss Jena in the flame of acetylene–air using deuterium background corrector. A hollow cathode lamp was used. The determination of the iron content was performed on the resonance line 248.3 nm.

2.3. ⁵⁷Fe Mössbauer absorption spectra

The ⁵⁷Fe Mössbauer absorption spectra of 1 were recorded on a WissEl operating in constant acceleration mode. ⁵⁷Co in a Rh matrix was used as the source. The spectra at low temperatures were measured using a continuous flow helium cryostat CF-506 (Oxford Instruments) with controllable temperature. The Mössbauer spectra were processed by the least-squares method assuming the Lorentzian form of the individual spectral components.

2.4. X-ray diffraction analysis

X-ray diffraction analysis of 1 was carried out on a CCD diffractometer Agilent XCalibur with an EOS detector (Agilent Technologies UK Ltd, Yarnton, Oxfordshire, England). Data collection, determination and refinement of unit cell parameters were carried out using the CrysAlis PRO program suite [Agilent (2011). CrysAlis PRO version 171.35.19, Agilent Technologies UK Ltd, Yarnton, Oxfordshire, England]. X-ray diffraction data were collected at 200(2) K using MoKα (λ = 0.71073 Å) radiation. Coverage of unique data was 99.8% complete to 52.64° (2θ). The structure was solved by the direct methods. The positions and thermal parameters of non-hydrogen atoms were refined isotropically and then anisotropically by the full-matrix least-squares method. Selected crystallographic parameters and the data collection and refinement statistics are given in Table 1. The bond lengths and bond angles in structure 1 are listed in Table 2. All calculations were performed with the SHELXTL program package.¹⁹ CCDC 939149.

Table 1 Crystal data and structure refinement for 1

Parameter	Value
Empirical formula	C12H8Fe2N6O6S2
Formula weight	540.06
Temperature/K	200(2)
Crystal system, space group	Triclinic, P1̄
Unit cell dimensions
a/Å	6.6056(7)
b/Å	8.199(1)
c/Å	9.642(1)
α/deg.	75.65(1)
β/deg.	71.705(8)
γ/deg.	78.57(1)
Volume/Å^3	476.2(1)
Z	1
Density (calculated)/g cm^−3	1.883
Absorption coefficient/mm^−1	1.799
F(000)	270
Crystal size	0.25 × 0.3 × 0.35 mm^3
Theta range for data collection	3.08 to 26.32°
Index ranges	−8 ≤ h ≤ 8, −9 ≤ k ≤ 10, −12 ≤ l ≤ 12
Reflections collected	3291
Independent reflections [R(int)], parameters	1935 [0.0217]/136
Goodness-of-fit on F^2	0.900
Final R indices [I > 2σ(I)]	R 1 = 0.0344, wR2 = 0.0673
R indices (all data)	R 1 = 0.0485, wR2 = 0.0734
Largest diff. peak and hole	0.59 and −0.48 e Å^−3

---

Table 2 Selected bond lengths [Å] and angles [deg.] for 1

Bond	d/Å	Bond	d/Å
Fe(1)–N(1)	1.675(3)	Fe(1)–N(2)	1.658(3)
N(1)–O(1)	1.169(3)	N(2)–O(2)	1.169(4)
Fe(1)–S(1)	2.2698(9)	Fe(1)–S(1)^a	2.279(1)
S(1)–C(1)	1.793(3)	N(3)–C(3)	1.469(4)
O(3)–N(3)	1.240(4)	O(4)–N(3)	1.230(4)

---

Bond angle	ω/deg.	Bond angle	ω/deg.
a Symmetry transformations used to generate equivalent atoms: −x + 2, −y + 1, −z.
Fe(1)–N(1)–O(1)	168.7(3)	Fe(1)–N(2)–O(2)	169.2(3)
N(1)–Fe(1)–S(1)	111.86(9)	N(2)–Fe(1)–S(1)	106.2(1)
C(1)–S(1)–Fe(1)	111.2(1)	N(2)–Fe(1)–N(1)	116.3(1)
O(3)–N(3)–C(3)	117.8(3)	O(4)–N(3)–C(3)	118.9(3)
C(2)–C(3)–N(3)	117.9(3)	C(4)–C(3)–N(3)	119.3(3)
C(2)–C(1)–S(1)	118.6(2)	C(6)–C(1)–S(1)	121.0(3)
O(4)–N(3)–O(3)	123.3(3)

---

2.5. Quantum-chemical calculations

Quantum-chemical calculations were performed using Gaussian 03 version D.²⁰ DFT calculations were performed using local GGA BP86 (Burke exchange and Perdew 86 correlation) functionals in basis tzvp. From the calculations, there are no imaginary frequencies, thus suggesting that all optimized geometries are the minimums. The Gibbs free energy in dichloromethane solution was calculated in the frame of the polarized continuum model (PCM).

2.6. Voltamperic measurements

Voltamperic measurements were performed in a dry inert atmosphere (Ar) in CH₂Cl₂ + 0.25 M Bu₄NPF₆ using an Elins P-30I potentiostate in a range of potential scan rates from 10 to 200 mV s⁻¹. The solution was preliminarily deaerated with Ar, and during CVA measurements there was no gas bubbling through the solution. A glass-carbon disc of 3 mm diameter pressed into a Teflon cylinder and polished by abrasive was used as the main electrode, and platinum mesh was used as a counter electrode. Potentials (E) are shown with respect to an aqueous saturated calomel electrode (sat.c.e) (except otherwise marked). Correction for ohmic resistance of the solution was determined from CVA measurement in a 0.01 M solution of ferrocene + 0.25 M Bu₄NPF₆ in CH₂Cl₂ and was ∼0.5 kOhm. Values of the currents of the cathode and anode peaks were measured with respect to the extrapolation lines for the initial parts of the corresponding cathode and anode branches. The methods for purification of the solvent and the base electrolyte were similar to those in ref. 21. The values of the potentials of the oxidation–reduction peaks of the complexes presented in Table 3 have been corrected for the ohmic resistance of the solution.

Table 3 Values of the potentials for the oxidation–reduction peaks of complexes 1–4

Complex	Concentration	E C1, mV sat.c.e.	E A1, mV	E C2, mV	E A2, mV	E C3, mV	E A3, mV	E C4, mV	E A4, mV
1	12 mg in 5 ml	−510	−440	−1115	−1025	−1495	−1385	—	—
2	6 mg in 3 ml	−445	−385	−965	−890	−1630	−1510	—	—
3	9 mg in 5 ml	−440	−375	−850	−555	−1295	−1225	−1535	−1455
4	5 mg in 5 ml	−620	−530	−660	—	—	—	—	—

---

3. Results and discussion

Compound 1 has a centrosymmetric binuclear structure (Fig. 1), which is similar to the structure of earlier studied thiosulfate nitrosyl iron complexes^18,22 and neutral complexes [Fe₂(μ-SR)₂(NO)₄] (R = Me, Et, n-C₅H₁₁, CMe₃²³ or Py¹⁷).

Fig. 1 The molecular structure of complex 1. The additional “A” letters in the atom labels indicate that these atoms are at equivalent positions (2 − x, 1 − y, −z).

The interatomic distance Fe(1)–Fe(1A) is 2.731(1) Å. The length of the carbon–sulfur bond in the SR ligand is 1.793(3) Å, this being consistent with the analogous bonds in μ-S binuclear complexes,²⁴ and exceeding considerably the length of the S=C bond (1.684 Å).²⁵ This suggests that the thiol form of the ligand participates in the formation of the complex under study.

The nitrogroup deviates from the plane of the phenyl cycle by 12.3°.

Similar to ref. 22 and 23, in 1 there are only small differences in the structure of the NO groups, which are shown in the difference of the Fe–N and N–O bond lengths and valence angles Fe–N–O (Table 2).

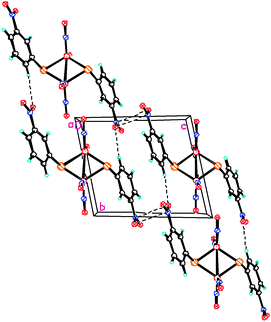
Fig. 2 shows the fragment of the projection of the crystalline structure on the crystallographic plane (YZ). The dotted lines show the shortened intermolecular contacts between the nitrogroups of molecule 1, O(3)⋯N(3){1 − x, 2 − y, 1 − z} 2.938(4) Å, and weak intermolecular hydrogen bonds, O(4)*⋯H(4)–C(4) and O(3)#⋯H(6)–C(6) with the following parameters: d(O4*⋯H4) = 2.54 Å, d(O4*⋯C4) = 3.409(5) Å, ∠(O4*⋯H4A–C4) = 155° [O4* is at (−x, 2 − y, 1 − z)], and d(O3#⋯H6) = 2.54 Å, d(O3#⋯C6) = 3.444(5) Å, ∠(O3#⋯H6–C6) = 166° [O3# is at (x, y − 1, z)], respectively.

Fig. 2 Fragment of the projection of the crystalline structure on the crystallographic plane (YZ).

The ⁵⁷Fe Mössbauer spectrum of polycrystals of 1 is a single doublet; its parameters (quadrupole splitting ΔE_Q = 1.171(1) mm s⁻¹, isomer shift δ_Fe = 0.115(1) mm s⁻¹ and width of absorption lines = 0.241(1) mm s⁻¹ at a temperature of 85 K) are similar to those for other complexes of the “μ-S” structural type.^2,15–17,23 This points to structural equivalence of the two iron atoms in 1 and is consistent with X-ray data.

The molecular structures of complexes 2–4 are presented in Fig. 3 (the X-ray data for the complexes are shown in the original papers^15–17).

Fig. 3 The molecular structures of complexes 2–4.^15–17

Fig. 4–7 present the I,E-dependences measured with different scan speeds (10–200 mV s⁻¹) in solutions of 1–4 in different potential ranges. For complexes 1 and 2 there are three cathode and three anode peaks. For complex 3 there are four cathode and three (four for the increased scan speed) anode peaks, and for 4 there are two cathode peaks and one anode peak. In Table 3 the potential values for these peaks are shown.

Fig. 4 I,E-curves measured with different scan speeds of the potential in a solution of complex 1 + 0.25 M Bu₄NPF₆ in CH₂Cl₂, mV s⁻¹: 1 – 10, 2 – 20, 3 – 50, 4 – 100, 5 – 200.

Fig. 5 I,E-curves measured with different scan speeds of the potential in a solution of complex 2 + 0.25 M Bu₄NPF₆ in CH₂Cl₂, mV s⁻¹: 1 – 10, 2 – 20, 3 – 50, 4 – 100, 5 – 200.

Fig. 6 I,E-curves measured with different scan speeds of the potential in a solution of complex 3 + 0.25 M Bu₄NPF₆ in CH₂Cl₂, mV s⁻¹: 1 – 10, 2 – 20, 3 – 50, 4 – 100, 5 – 200.

Fig. 7 I,E-curves measured with different scan speeds of the potential in a solution of complex 4 + 0.25 M Bu₄NPF₆ in CH₂Cl₂, mV s⁻¹: 1 – 10, 2 – 20, 3 – 50, 4 – 100, 5 – 200.

For all complexes (1–4) the addition of the first electron is electrochemically reversible, i.e., at the scan rate 10–20 mV s⁻¹ it is only controlled by the substance diffusion to the electrode surface. In general, a linear dependence of the currents of the anode and cathode peaks (I_a and I_k) on υ^0.5 is observed, with the curve almost passing the zero mark (Fig. 8). The difference of the potentials for the first anode and cathode peaks at low scan speeds is 60–70 mV, and the peaks themselves have a symmetric form, thus pointing to a reversible type of electron transfer. The value of the formal potential for this process E⁰ = (E_A + E_C)/2 is −0.475 V for 1, −0.415 V for 2, −0.410 V for 3 and −0.575 V for 4. The growth of the scan rate of the potential is accompanied by the increase of the potential difference of the cathode and anode peaks (ΔE_C1A1) (Fig. 9), i.e., the process becomes electrochemically irreversible. Almost equal values of currents I_a and I_k point to an inconsiderable contribution of irreversible chemical reactions in the total process. For complexes 1 and 2, ΔE_C1A1 reaches a thermodynamical value and does not depend on scan speed at υ ≤ 20 mV s⁻¹, so the value of the heterogeneous constant of the electron transfer can be determined (k₀ ∼ 0.02 cm s⁻¹). For complexes 3 and 4 the value of ΔE_C1A1 decreases monotonically with the decrease of υ, and does not reach a thermodynamical value even with the smallest scan speed. In this case, k₀ can be estimated assuming parallel dependencies of ΔE, lg υ for the studied complexes. Then, k₀ ∼ 0.01 cm s⁻¹ and ∼0.005 cm s⁻¹ for complexes 3 and 4, respectively.

Fig. 8 Dependencies of the cathode (1–4) and anode current (1′–4′) on the square root of the scan speed of the potential for the first electron transfer in solutions of complexes 1–4.

Fig. 9 Dependencies of the potential of the anode and cathode peaks for the first electron transfer on the scan speed of the potential in solutions of complexes 1–4.

The addition of the next electrons occurs irreversibly. This is confirmed both by the potential difference of the peaks (>75 mV) and their asymmetry. It should be noted that the addition of the second electron occurs electrochemically irreversibly for complexes 1 and 2. With the used potential scan speeds, the electrode reaction occurs in a kinetic mode so the potential difference of the cathode and anode peaks is above 75 mV, and the anode and cathode peaks are symmetrical (Fig. 4 and 5). For complexes 3 and 4 the transfer of the second electron is strictly irreversible, this being evidenced by the absence of the oxidation current for the product of the second electron addition to the complex intermediate in the anode part of the curve (Fig. 6 and 7). Consequently, this product is unstable and decomposes during measuring of the cyclic voltamperogram, with a characteristic time τ < 1 s. For complex 3, with the increase of scan speed, the anode peak appears on the CVA, which might correspond to the oxidation of particles forming upon decomposition of the product of the second electron addition to the complex.

For complexes 1 and 2 the addition of a third, and for complex 3 also of a fourth electron occurs. However, these results are difficult to analyze because the transfer of the next electrons might occur not on the complexes, but on the products of homogeneous transformations of the intermediates forming upon the addition of the second electron.

Thus, from the scope of the experimental data, the following scheme of electrochemical transformation for the studied complexes of “μ-S” type seems to be the most probable:

Calculations of the geometrical and electronic structures of the monoanions of complexes 1–4 have been performed by the DFT method using the local BP86 functional and the tzvp basis. For comparison with thiophenol [Fe₂(μ-PhS)₂(NO)₄]⁻ (5), their most important geometrical parameters are presented in Table 4. On the whole, they differ inconsiderably for all the complexes under consideration; however, there are some tendencies that cannot be due to errors of the DFT calculations. It should be noted that key distances in the optimized geometries of 4 and 5 are similar, i.e., there are no considerable changes upon replacement of the phenyl ring by the pyridine one. However, for the electron-acceptor substituent the situation is different. As we can see in the table, introduction of the NO₂ substituent in the ring leads to shortening of the N–O bond in the nitrosyl group. For complexes 1–3 this bond is shorter than in 4 and 5, and for the pyridine ring the effect is stronger than for the phenyl ring. The presence of the substituent in the ring does not influence considerably the length of the Fe–N bond. As for the Fe–S bond, it shortens a little upon the introduction of the NO₂ group in the ring in the case of the para-position in the phenyl ring (anion of complex 2) but rather essentially in the case of the pyridine ring (anion of complex 3). The length of the S–C bond was affected only by the introduction of the nitro-group in the para-position of the phenyl ring of the sulfur-containing ligand (anion of complex 2). Thus, the introduction of the electron-acceptor NO₂ group in the phenyl and pyridine ring of sulfur-containing ligands in nitrosyl iron complexes affects the distribution of the bond lengths in the anions, and for the pyridine ring this influence is more considerable than for the phenyl ring.

Table 4 Selected main geometric parameters (Å, degree) for the anions of complexes 1–4 and complex 5 (for comparison)

Bond	1	2	3	4	5
N1–O1	1.185	1.188	1.182	1.190	1.192
N2–O2	1.188	1.188	1.182	1.190	1.192
Fe1–N1	1.657	1.657	1.657	1.655	1.655
Fe1–N2	1.658	1.658	1.657	1.655	1.655
Fe1–S1	2.297	2.313	2.280	2.311	2.318
Fe2–S1	2.303	2.312	2.280	2.313	2.318
S1–C1	1.806	1.790	1.796	1.801	1.806
Fe1–N1–O1	169.5	170.0	168.9	168.2	169.6
Fe1–N2–O2	170.3	170.0	168.9	168.7	169.6
N1–Fe1–N2	117.5	117.5	116.5	115.9	117.1

---

For all the neutral complexes, as well as for their anions, the charges on the atoms were calculated based on approximation of natural bond orbitals (NBO) in the frame of the Gaussian 03 program²⁰ and according to Bader.²⁶ In Table 5 the charges on the key atoms of the complexes are shown. The values obtained from these two methods are somewhat different. Analysis according to Bader produces a charge close to 1 on the iron atom, this being consistent with a common electronic structure of iron–sulfur nitrosyl complexes.²⁷ For complexes 4 and 5, both methods suggest that upon transition from the neutral molecule to the monoanion the charge on the iron atom becomes more positive, while the NO group becomes more negative. Consequently, the Fe–N bond in the anion of these complexes is more polar than in the neutral molecule, and therefore the anion is expected to be a better NO donor than the neutral complex. This is true for complex 2, too, which has the NO₂ group in the para-position of the phenyl ring. In 1 (the NO₂ group is in the meta-position) and 3 (the NO₂ group is in the pyridine ring) the charge on the iron atom does not change when going to the monoanion. Considerable changes in the charge on the sulfur atom occur when the NO₂ group is in the pyridine ring (complexes 3 and 4).

Table 5 Charges on the atoms for complexes 1–5 and for their anions based on the approximation of the natural bond orbitals (NBO) and according to Bader

Complex	Q	Charge	Fe	NO	S
1	Q(NBO)	0	0.26	−0.08	0.04
		−1	0.34	−0.19	−0.07
	Q(Bader)	0	0.85	−0.31	−0.18
		−1	0.82	−0.40	−0.22
2	Q(NBO)	0	0.25	−0.07	0.05
		−1	0.34	−0.21	−0.11
	Q(Bader)	0	0.85	−0.31	−0.18
		−1	0.88	−0.45	−0.25
3	Q(NBO)	0	0.27	−0.08	0
		−1	0.29	−0.15	−0.06
	Q(Bader)	0	0.86	−0.31	−0.20
		−1	0.86	−0.39	−0.21
4	Q(NBO)	0	0.27	−0.08	−0.01
		−1	0.34	−0.21	−0.14
	Q(Bader)	0	0.86	−0.32	−0.21
		−1	0.88	−0.44	−0.27
5	Q(NBO)	0	0.26	−0.09	0.04
		−1	0.35	−0.25	−0.14
	Q(Bader)	0	0.86	−0.33	−0.19
		−1	0.89	−0.48	−0.29

---

We tried to calculate a relative (in %) re-distribution of the negative charge in the monoanion as compared to the neutral molecule. For this purpose, the difference of the charges in the neutral molecule and in the monoanion was determined for each atom. Then, assuming that the value of the charge should be −1, its distribution for each atom was determined (Fig. 10). Comparison of 4 and 5 shows that for the pyridine ring, the most part of the additional negative charge is on the ligand, this being due to the presence of the electron-acceptor atom in the ring. If there is a NO₂ group in the pyridine ring, the additional charge appears there as well, thus, the charge on the Fe(NO₂)-unit and the sulfur atom becomes much lower. When the NO₂ group is introduced in the para-position of the phenyl ring (complex 2), there is a smaller percentage of the additional negative charge on the Fe(NO)₂ units and the sulfur atom as compared to complex 5, and this trend increases for the NO₂ group in the meta-position (complex 1). Thus, the presence of the electron-acceptor NO₂ group in the aromatic ring of the sulfur-containing ligand of the nitrosyl iron complex affects the distribution of the additional negative charge, thus influencing the redox-behavior of these compounds.

Fig. 10 Relative distribution of the additional negative charge (%) on atoms and atomic groups (bold – from the NBO method, italic – according to Bader).

The redox-potentials of the complexes were calculated using the DFT method (BP86/tzvp), which had proved to be appropriate for these types of calculations^14,28 and is often used successfully for calculation of the structure and some other properties. It should be noted that the local functional BP86 yields the results for the structure, electronic structure and physical-chemical properties of the iron nitrosyl complexes of various types that are the closest to the experimental data.^13,29

The procedure for calculating the redox-potentials of the nitrosyl complexes in solution is based on the Born–Haber thermodynamic cycle, which relates the electron addition in the condensed phase with the corresponding process in the gaseous phase via free energies of solvation of reagents and products. Taking into account E⁰ = −ΔG⁰/nF, the values of the redox-potentials for the nitrosyl complexes under study with respect to a standard hydrogen electrode (SHE) can be calculated as:

where F is the Faraday constant, and G⁰ is the standard free energy of the complex [Fe₂(SR)₂(NO)₄]ⁿ, which consists of the sum of its total energy in the gaseous phase, a thermal correction to Gibbs free energy and the solvation free energies. 4.34 eV (ref. 30) is the free energy of the standard process of hydrogen formation from the protons on the standard hydrogen electrode (SHE): H⁺(aq) + e⁻(g) → 1/2H₂(g).

In Table 6, the results for the calculations of the first and the second redox-potentials of the reduction process in dichloromethane as compared to the experimental data are shown. The experimental data were calculated with respect to a SHE. The conversion constant between the SHE and a standard calomel electrode is 0.244 V.³¹ For comparison, the calculated and experimental data for the nitrosyl iron complex with the phenyl substituent are presented in Table 6. As can be seen, the calculated values of the first redox-potentials are close to the experimental ones. Besides, the theoretical values of the first redox-potentials for all the complexes with ligands containing NO₂ substituents are more positive than the redox-potentials for complexes 4 and 5. This confirms our assumption that the presence of the electron-acceptor NO₂ substituent in the aromatic ring affects the redox-processes in iron–sulfur nitrosyl clusters, i.e., increases the redox-potential and facilitates the reduction of these complexes.

Table 6 Calculated redox-potentials of the reduction process (V/SHE) for the complexes under study as compared to the experimental data

	Experimental		Calculated
	E ^0/−1	E ^−1/−2	E ^0/−1	E ^−1/−2
1	−261	−866	−339	−1055
2	−151	−571	−225	−920
3	−156	−676	−116	−1000
4	−376	—	−669	−1928
5	−360	−870	−536	−1693

---

As for the second calculated redox-potential, for these systems it also differs from the experimental data, as it is for the complex with the phenyl substituent [Fe₂(M-PhS)₂(NO)₄].¹³ We believe that this is due to the destruction of the forming dianion, namely, to the dissociation over the Fe–S bond,¹³ this being indirectly confirmed by the irreversibility of the second redox-potential for these complexes in the electrochemical experiment.

4. Conclusions

Using the CVA method, the values of the reduction potentials for neutral complexes [Fe₂(SR)₂(NO)₄] of “μ-S” structural type have been determined in an aprotic solvent, and the scheme for their reduction has been suggested. As it follows from the calculations with DFT, the introduction of the electron-acceptor NO₂ group in the phenyl and pyridine rings of sulfur-containing ligands affects the structure of their anions, and for the pyridine ring this influence is more considerable than for the phenyl one. In addition, the presence of the electron-acceptor NO₂ group in the aromatic ring of the sulfur-containing ligand of the nitrosyl iron complex affects the distribution of the additional negative charge, thus influencing the redox-behavior of these compounds. The calculated first redox-potentials of the reduction of the complexes are close to the experimental values. Generally, more positive redox-potentials for the reduction of neutral complexes, [Fe₂(μ-SR)₂(NO)₄] with R = 3-nitro-phenyl, 4-nitro-phenyl and 5-nitropyridine-2-yl, provides opportunities for production of stable anionic forms of nitrosyls with functional ligands containing acceptor substituents in the aromatic ring.

Acknowledgements

The work has been financially supported by RFBR N 11-03-01033.

Notes and references

1. R. Butler and I. L. Megson, Chem. Rev., 2002, 102, 1155.
2. K. Szacilowski, A. Chmura and Z. Stasicka, Coord. Chem. Rev., 2005, 249, 2408.
3. Z. J. Tonzetich, L. E. McQuade and S. J. Lippard, Inorg. Chem., 2010, 49, 6338.
4. H. Lewandowska, M. Kalinowska, K. Brzoska, K. Wojciuk, G. Wojciuk and M. Kruszewski, Dalton Trans., 2011, 40, 8273.
5. H. Kalyvas and D. Coucouvanis, Inorg. Chem., 2006, 45, 8462.
6. J. A. Crayston, C. Glidewell and R. J. Lambert, Polyhedron, 1990, 9, 1741.
7. C. Glidewell and R. J. Lambert, Polyhedron, 1992, 11, 2803.
8. J. L. Bourassa and P. C. Ford, Coord. Chem. Rev., 2000, 200–202, 887.
9. N. A. Sanina, L. A. Syrtsova, N. I. Shkondina, T. N. Rudneva, E. S. Malkova, T. A. Bazanov, A. I. Kotel'nikov and S. M. Aldoshin, Nitric Oxide: Biol. Chem., 2007, 16, 181.
10. N. A. Sanina, T. N. Roudneva, I. V. Sulimenkov, N. P. Konovalova, T. E. Sashenkova and S. M. Aldoshin, Russ. J. Gen. Chem., 2009, LIII, 164.
11. N. A. Sanina, O. S. Zhukova, S. M. Aldoshin, N. S. Emel'yanova and G. K. Gerasimova, RU pat., 2429242 C2, 2011, p. 13.
12. N. A. Sanina, K. A. Lysenko, O. S. Zhukova, T. N. Roudneva, N. S. Emel'yanova and S. M. Aldoshin, US pat., 8,067,628 B2, 2011, p. 21.
13. N. A. Sanina, A. G. Krivenko, R. A. Manzhos, N. S. Emel'yanova, K. V. Bozhenko and S. M. Aldoshin, Izv. Akad. Nauk, Ser. Khim., 2012, 10, 1844.
14. R. Wang, M. A. Camacho-Fernandez, W. Xu, J. Zhang and L. Li, Dalton Trans., 2009, 777.
15. S. M. Aldoshin, D. V. Korchagin, G. V. Shilov, N. A. Sanina, G. I. Kozub and T. A. Kondrat'eva, Eur. J. Inorg. Chem., 2014 , submitted, CCDC 957763.
16. G. I. Kozub, N. A. Sanina, T. A. Kondrat'eva, G. V. Shilov, D. V. Korchagin, N. S. Ovanesyan and S. M. Aldoshin, Russ. J. Coord. Chem., 2012, 38, 10–689.
17. O. A. Rakova, N. A. Sanina, G. V. Shilov, Y. M. Shul'ga, V. M. Martynenko, N. S. Ovanesyan and S. M. Aldoshin, Russ. J. Coord. Chem., 2002, 28(5), 341.
18. N. A. Sanina, S. M. Aldoshin, T. N. Rudneva, N. I. Golovina, G. V. Shilov, Yu. M. Shul'ga, V. M. Martynenko and N. S. Ovanesyan, Russ. J. Coord. Chem., 2005, 31(5), 323.
19. G. M. Sheldrick, SHELXTL v. 6.14, Structure Determination Software Suite, Bruker AXS, Madison, Wisconsin, USA, 2000.
20. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision D.01, Gaussian, Inc., Wallingford, CT, 2004.
21. O. A. Rakova, N. A. Sanina, G. V. Shilov, V. V. Strelets, I. B. Borzova, A. V. Kulikov and S. M. Aldoshin, Russ. J. Electrochem., 2001, 27, 1.
22. (a) N. A. Sanina, O. A. Rakova, S. M. Aldoshin, I. I. Chuev, E. G. Atovmyan and N. S. Ovanesyan, Russ. J. Coord. Chem., 2001, 27(3), 198; (b) C. Glidewell, R. J. Lambert, N. B. Hursthouse and M. Motevalli, J. Chem. Soc., Dalton Trans., 1989, 9, 2061.
23. (a) J. T. Thomas, J. H. Robertson and E. G. Cox, Acta Crystallogr., 1958, 11, 599; (b) C. Glidewell, M. E. Harman, M. B. Hursthouse, I. L. Johnson and M. Motevalli, J. Chem. Res., Synop., 1988, 212–213(M), 1676.
24. N. A. Sanina and S. M. Aldoshin, Russ. Chem. Bull., 2011, 60(12), 1223.
25. J. Jolley, W. I. Cross, R. G. Pritchard, C. A. McAuliffe and K. B. Nolan, Inorg. Chim. Acta, 2001, 315, 36.
26. R. F. W. Bader, Atoms in Molecules - A Quantum Theory, Oxford University Press, Oxford, 1990.
27. N. A. Sanina, N. S. Emel'yanova, A. N. Chechlov, A. F. Shestakov, I. V. Sulimenkov and S. M. Aldoshin, Russ. Chem. Bull., 2010, 59(12), 2215.
28. (a) P. Winget, C. J. Cramer and D. G. Truhlar, Theor. Chem. Acc., 2004, 112, 217; (b) L. E. Roy, E. Jakubikova, M. G. Guthrie and E. R. Batista, J. Phys. Chem. A, 2009, 113, 6745; (c) M. Namazian, H. R. Zare and M. L. Coote, Biophys. Chem., 2008, 132, 64; (d) C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2007, 111, 408; (e) Y. Song, J. F. Zhou, Y. Song, Y. Wei and H. Wang, Bioorg. Med. Chem. Lett., 2005, 15, 4971; (f) Y. Song, Spectrochim. Acta, Part A, 2007, 67, 611; (g) A. L. Speelman and J. G. Gillmore, J. Phys. Chem. A, 2008, 112, 5684; (h) S. N. Datta, J. Sudhamsu and A. Pandey, J. Phys. Chem. B, 2004, 108, 8007; (i) T. J. Tugsuz, J. Phys. Chem. B, 2010, 114, 17092; (j) P. J. Silva and M. J. Ramos, Comput. Theor. Chem., 2011, 966, 120; (k) Y. Shimodaira, T. Miura, A. Kudo and H. J. Kobayashi, J. Chem. Theory Comput., 2007, 3, 789; (l) M. H. Baik and R. A. Friesner, J. Phys. Chem. A, 2002, 106, 7407; (m) M. Uudsemaa and T. Tamm, J. Phys. Chem. A, 2003, 107, 9997.
29. (a) S. M. Brothers, M. Y. Darensbourg and M. B. Hall, Inorg. Chem., 2011, 50, 8532; (b) T. N. Roudneva, N. A. Sanina, K. A. Lyssenko, S. M. Aldoshin, M. Yu. Antipin and N. S. Ovanesyan, Mendeleev Commun., 2009, 19, 253; (c) N. S. Emel'yanova, A. F. Shestakov and N. A. Sanina, Int. J. Quantum Chem., 2013, 113, 740; (d) N. Emel'yanova, N. Sanina, A. Krivenko, R. Manzhos, K. Bozhenko and S. Aldoshin, Theor. Chem. Acc., 2013, 132, 1316.
30. A. Lewis, J. A. Bumpus, D. G. Truhlar and C. J. Cramer, J. Chem. Educ., 2007, 84, 934.
31. V. V. Pavlishchuk and A. W. Addison, Inorg. Chim. Acta, 2000, 298, 97.

---

Footnote

† CCDC 939149. For crystallographic data in CIF or other electronic format see DOI: 10.1039/c3nj00704a

---