Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optimal vacancy concentrations to maximize the N–V yield in nanodiamonds†
Amanda S.
Barnard
*
CSIRO Materials Science and Engineering, 343 Royal Parade, Parkville, Victoria 3052, Australia. E-mail: amanda.barnard@csiro.au
First published on 28th January 2014
Abstract
In recent years fluorescent diamond nanoparticles have begun to fill the need for optically bright and stable, non-toxic probes for a growing range of biomedical applications. Significant attention has been given to finding ways of obtaining small particles with a higher yield of the optically active N–V defects, on-demand, by processing mass produced samples post defacto. While it has been established that a combination of irradiation (to introduce an abundance of vacancies) and annealing (to increase vacancy mobility) can achieve these goals, it is desirable to know how many vacancies to introduce a priori. In this paper a numerical model is developed to predict and compare the yield of different nitrogen/vacancy complexes in nanodiamond, as a function of the individual nitrogen and vacancy concentrations, the particle size and annealing temperature. The results reveal that, irrespective of the temperature and nitrogen content, this processing strategy is unlikely to work for detonation nanodiamond, but tuning these concentrations can promote the formation of N–V or H3 defects over ∼20 nm.
For many years diamond nanoparticles were the proverbial ‘solution in search of a problem’. Although they presented a range of attractive properties,1 the degree of structural control required to facilitate some of the more traditional applications remained challenging, and hindered the development of nanodiamond-based applications and devices. The luminescence emanating from optically active defects within the particles, which are also known from bulk diamond (and often referred to as color centers) is however a property that appears to be robust against the persistent polydispersivity typical of nanodiamond samples. Bright, stable and spectroscopically distinct luminescence is easily obtained, provided that a sufficient concentration of defects can be created and maintained.
Defects in nanodiamond typically include intrinsic point defects, incidental impurities which result from the synthesis and/or purification processes, and defect complexes such as the range of optically active defects and color centers2–4 that may be incidental or deliberate. The most simple defect in diamond is a single neutral lattice vacancy, which is commonly referred to as a GR1 defect (where GR stands for general radiation). Vacancies are omnipresent in diamond, and so this defect has been extensively studied in various states.5
Since nitrogen is also widespread in diamond, numerous studies have also focussed on characterizing and understanding the properties of different types of N-related defects, including the single substitutional nitrogen impurity, known as the C-center. However, arguably the most widely studied defect in nanocrystalline diamond is the paramagnetic nitrogen–vacancy complex (N–V)6 which forms when a vacancy (GR1) migrates to bind with a C-center.7,8 The energy-level structure of the negatively charged N–V defect results in emissions characterized by a narrow zero-phonon line (ZPL) at 637 nm (the neutral N–V center has a zero-phonon line at 575 nm)9 accompanied by a wide structured side band of lower energy due to transition from the same excited state, but with formation of phonons localized on the defect. The optical emission from N–V centers in diamond nanocrystals has been shown to strongly depend on the crystal size8,10–13 and the charge state is related to the temperature.15
Defects such as GR1 centers and N–V centers are mobile within diamond, and may migrate if a driving force is sufficient to overcome the kinetic energy barriers associated with diffusion. The diffusion of an N–V center is vacancy-assisted, and the rate limiting step is the C–N exchange energy.14 During this migration, if an N–V center interacts with another single nitrogen atom (or a migrating vacancy interacts with a nitrogen dimer, known as an A-center) then a H3 center is formed. The H3 center consists of two N atoms surrounding a vacancy. It is one of the most studied in diamond,2,16 and may be formed abundantly by irradiation with 1 to 2 MeV electrons to doses of 1018 to 1020 electrons per cm2 and annealing at 1200 K for 20 hours in vacuum.17 If we continue this logical progression, then if a N–V center migrates to an A-center, or alternatively a H3 center migrates to a C-center (which is far less likely), then a N3 center may be formed. The N3 center consists of three nitrogen atoms surrounding a vacancy (whereas a vacancy completely surrounded by four N atoms is known as a B-center). Both the H3 and N3 provide photoluminescence and cathodoluminescence, are known to be thermally stable, and exhibit high quantum efficiency up to temperatures in excess of 500 K.18
A summary of the point group symmetry, zero phonon line (ZPL), central wavelength (λ0) and photoacoustic imaging quantum yield for the GR1, N–V−, H3 and N3 defects is provided in Table 1, where we can see that the quantum yield for each of these defects is quite different. The quantum yield is defined as the number of photons emitted via photoluminescence versus the number of photons absorbed during excitation.19 The N–V and H3 defects are the most efficient, which somewhat explains their popularity in the scientific community. In addition to the quantum yield, the wavelength itself is very important, as it determines the penetration depth of the radiation. The penetration depth for 532 nm light is 0.6 mm, for 670 nm is 2.4 mm, and for 750 nm is 2.6 mm. This is insufficient to penetrate human skin, irrespective of the quantum yield.
| Defect | Point group | ZPL (nm) | λ 0 (nm) | Q |
|---|---|---|---|---|
| GR1 | T d | 741 | 898 | 0.014 |
| N–V0 | C 1h | 575 | 600 | — |
| N–V− | C 3v | 638 | 685 | 0.99 |
| H3 | C 3v | 504 | 531 | 0.95 |
| N3 | C 2v | 415 | 445 | 0.29 |
Coupled with the lack of cytotoxicity and excellent biocompatibility,21 it is easy to see why nanodiamonds have now found applications in biomedicine; in drug delivery,8,22–26 diagnostic labeling,20,27–31 and most recently as a highly sensitive nanometer-scale thermal probe,32 and bimolecular detection.33–35 In the last two examples the functionality is due to the presence of N–V centers. An advantage of the characteristic spectrum of the N–V0 and N–V− defects is that they are well separated from the endogenous fluorescence region, as shown in the comparative results of ref. 27 for N–V fluorescence from 35 nm nanodiamonds and flavin.
However, as pointed out above, efficiency in each case is contingent on sufficient defects being present in each particle, and herein lies the problem. Although these optical defects do occur naturally, greater efficiency can be gained if their abundance can be controlled. Efficient applications require smaller particles with a higher yield of the N–V defects, on-demand, and so most studies treat their samples with a combinations of irradiation and annealing to increase the N–V yield (brightness, stability and longevity), post defacto.
The most widely used method for increasing the quantity of N–V centers is by thermal annealing (at temperatures above 800 °C in vacuum) of type Ib nanodiamond containing atomically dispersed nitrogen atoms that has been irradiated with 1–2 MeV electron beams.27 The increase in yield can be as high as eight times.36 It has also been demonstrated using integrated absorption intensity of the sharp zero-phonon line (637 nm) at liquid nitrogen temperature, that an N–V− density of 25 ± 6 ppm can be obtained with a substrate irradiated with a 3 MeV proton beam, at a dose of 1 × 1016 H+ per cm2.37 This type of treatment does not sufficiently damage the nanodiamond enough to prevent it's use in very sensitive applications.38 Alternatively, it has been shown that the implantation of carbon ions at an appropriate energy can introduce additional vacancies that, when combined with strategic implantation of nitrogen ions into an N-containing diamond lattice, can dramatically increase the N–V production yield by over 50%.39
Therefore, to provide some insights as to the consequences of the generous insertion of nitrogen and lattice vacancies, and to provide a tool that can be use guide future work, a simple model that draws on a limited set of input parameters would be very useful. In the following paragraphs we will see that the optimal concentration of vacancies that need to be generated during these processes, for a given nitrogen concentration, can be predicted by modifying existing probabilistic models12 to accommodate changes in the N and vacancy concentrations independently (as a function of the particle size and the annealing temperature). This new multivariate model is more flexible, more inclusive, and can be used in conjunction with any consistent set of input parameters to predict the optimal conditions for N–V generation, a priori.
Let us begin by assuming that the probability of observing a defect containing species i and j (Pobs(i, j), where i and j can represent substitutional atoms and lattice vacancies) is related to the probability of that defect being included (Pinc(i, j), either following implantation or a special process during synthesis) and the probability of the defect diffusing and annihilating with the free surfaces (or escaping, Pesc(i, j))
| Pobs(i, j) = Pinc(i, j) [1 − Pesc(i, j)]. | (1) |
From previous works it has been shown, in good agreement with experiment,12 that
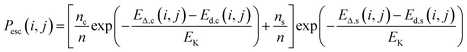 | (2) |
The probability of a defect being included, Pinc(i, j), will be a function of the individual probabilities of i and j being included (Pi and Pj, weighted by the number of components ni and nj in each nij defect, respectively), and the probability of i and j combining, such that
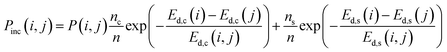 | (3) |
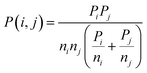 | (4) |
| Pi = Ci[1 − Pesc(i)], | (5) |
In the case of nanodiamond, many of the individual values for all Ed and EΔ have been published before. The values of the defect energies, defect energies and diffusion barriers can be generated using any simulation method, provided consistency is preserved by calculating each parameter with the same computational method and convergence criteria. During the implementation of the model herein, all numerical parameters were generated using the density functional tight-binding theory with self consistent charges, as described in ref. 4, 12, 40, 42 and 43. As described in the these references, >50 defect sites with in a nanodiamond have been sampled to obtain good statistics for each defect/particle combination and clearly define the separation between the core and the shell. For convenience, the different defect energies (Ed) and the barrier heights (EΔ, based on the energy of the configuration identified as the transition state), is provided in Table 2; and details of the computational method and raw data are provided in the ESI.†
| Configuration | GR1 | V–N–V | N–V | H3 | N3 | N |
|---|---|---|---|---|---|---|
| Bucky-diamond | ||||||
| E d,c | 6.74 | 2.15 | 6.87 | 7.25 | 7.25 | 1.86 |
| E d,s | 1.76 | −7.68 | 1.65 | 4.62 | 2.55 | 0.40 |
| E Δ,c | 1.80 | 8.61 | 6.68 | 4.51 | 9.95 | 667.8 |
| E Δ,s | −3.18 | −10.14 | 13.28 | 19.20 | 2.19 | 1327.9 |
| Passivated nanodiamond | ||||||
| E d,c | 6.62 | 6.76 | 6.77 | 6.75 | 7.18 | 4.26 |
| E d,s | 3.40 | 6.50 | 4.80 | 4.29 | 6.52 | 2.29 |
| E Δ,c | 1.80 | 8.61 | 6.68 | 4.51 | 9.95 | 667.8 |
| E Δ,s | −1.42 | 8.34 | 4.70 | 2.05 | 9.29 | 665.8 |
The final result will provide the total number of observed (stable) defects, as a function of the annealing temperature, the observation temperature, the concentration of nitrogen present in the particle and the concentration of vacancies that are introduced. The greatest advantage of this model is that it can be used on N–V, H3 and N3 simultaneously, under the same conditions, and include other possible defects such as the V–N–V complex that would form if an extra vacancy migrated to an existing N–V. Since the V–N–V is not optically active, this would quench the luminescence, and is therefore highly unfavorable.
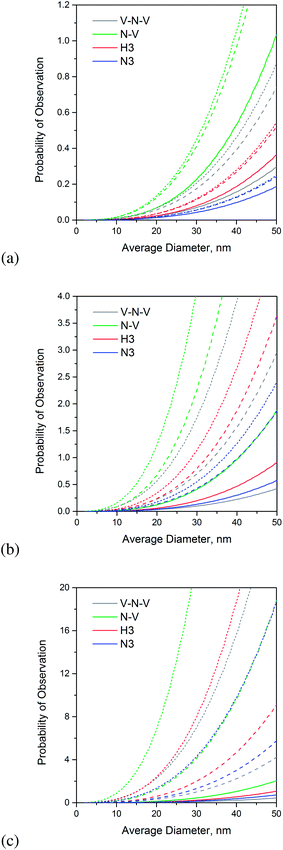
In Fig. 1 we find the predicted (maximum) probability of observation of these different defects formed from complexes of nitrogen and lattice vacancies (i and j), for hydrogen passivated nanodiamonds (all sp3-bonded). Fig. 1(a)–(c) provide results for nitrogen concentrations of 1 ppm, 10 ppm and 100 ppm, respectively. In each case the corresponding 1 ppm, 10 ppm, and 100 ppm vacancy content are represented by solid, dashed and dotted lines of the same color. Unsurprisingly the expected number of defects per particle (indicated by the final probability of observation) increases with increasing nitrogen concentration, though it is interesting to see the impact of the vacancy concentration. When the nitrogen concentration is small all the maximum defect concentration quickly saturates, and there is limited benefit to adding more vacancies. Most of the extra vacancies diffuse and escape, since there are insufficient nitrogen impurities for them to partner with. As the nitrogen concentration increases we can see a benefit to increasing the vacancy concentration, which can be used to tune the yield.
Irrespective of the vacancy and nitrogen concentration however, it is reassuring to see that the N–V defect has the highest probability of observation in passivated nanodiamonds. Saturation with a high concentration of vacancies does not give rise to a higher probability of the dark V–N–V defects (as many of these vacancies diffuse and escape instead), and a low supply of vacancies does not increase the probability of the H3 or N3 defects, since the N–V defect is still much more energetically favorable. This is not necessarily the case in clean, reconstructed bucky-diamonds.
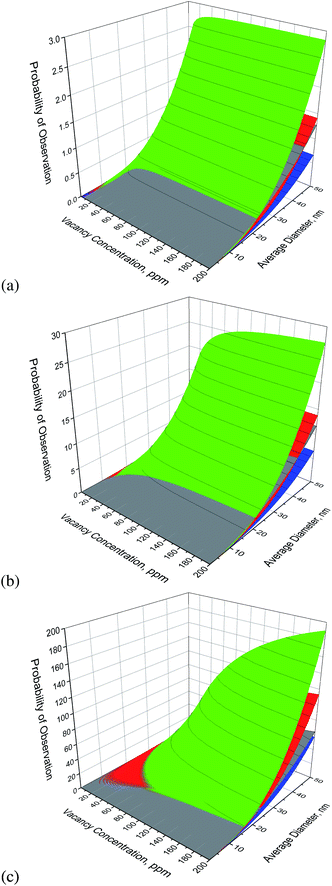
In Fig. 2(a)–(c) we find the results for bucky-diamonds with nitrogen concentrations of 1 ppm, 10 ppm and 100 ppm, respectively. In this case the predicted number of defect complexes is provided as a function of the vacancy concentration, as well as the average particle diameter. This is because, unlike the passivated nanodiamonds, the N–V is not always the most likely outcome. At small sizes the dark V–N–V defect is more likely than the N–V, over almost the entire range of vacancy and N concentrations. The size at which N–V becomes more probable decreases with the N/V ratio, and over-saturating with vacancies should only be considered for larger high-pressure high-temperature (HPHT) nanodiamonds. Keeping the concentration of vacancies low does not necessarily increase the probability of N–V, and actually means that the H3 defect becomes more likely than the N–V if the vacancy contraction is too small. This is because the energy barrier for the vacancy-assisted diffusion of the N–V defect is lower than the H3, and H3 defects are more unlikely to escape.
At this point is should be pointed out that this study has not included the possibility of vacancy clustering, and the formation of voids. This is because, at this stage, insufficient information is available on the structure of voids (either in the core, or in the shell), and in particular the structure of the inner (negative) surface of the void interior. When this information becomes available in the future the model can be extended, but will take a different form depending on whether the surfaces of the void are graphitized or not. It is also important to point out that this model makes no assertions about the doping states of any of these defects once produced. This model is entirely based on thermodynamics and statistical mechanics, and the electronic structure of the defect is assumed at the outset. The intention is to predict how to make more defects, not predict what states those defects are likely to be in. If one were particularly interesting in the latter, this information could be routinely obtained from the original simulations used to parameterise the model, provided they were undertaken at sufficiently high level of theory.
Using this model it is apparent that the ideal vacancy concentration for a given sample will depend on the type (size) of the nanodiamond, and the pre-existing (or intentionally added) nitrogen content at the time of implantation. For a 28 nm nanodiamond with 50 ppm nitrogen, a concentration of >7 ppm of vacancies is recommended to ensure that N–V formation is preferred over H3, and it is always preferred over V–N–V. That is a very convenient ratio, and provides plenty of scope for (more imprecisely) increasing the N and vacancy concentrations to manage the overall yield. With an equal concentration of N and vacancies (50 ppm) the N–V yield in bucky-diamond is predicted to be ∼12, and in a passivated nanodiamond it is predicted to be ∼9; which is in excellent agreement with the observations and measurements of Hui et al. of 8 ± 1.41 As other authors have demonstrated that the concentration of vacancies and nitrogen can be tuned simultaneously, by varying the implantation energy,27,36–39,44–48 it is suggested that similar experiments, combined with predictions obtained using this model, will provide further insights.
The temperature will also affect the yield, as it will encourage vacancy diffusion; but it also encourages vacancy ‘escape’, leaving fewer to join with N complexes to form functional defects. However, with the bucky-diamond shell to provide the high kinetic energy barrier varying the annealing temperature is unlikely to negatively impact the yield. This indicates that it is better to irradiate as-grown nanodiamond powders, and then functionalize the surfaces for specific applications later on.
Acknowledgements
Computational resources for this project were supplied by the National Computing Infrastructure (NCI) national facility under Partner Allocation Scheme, Grant q27.References
- V. N. Mochalin, O. Shenderova, D. Ho and Y. Gogotsi, Nat. Nanotechnol., 2012, 7, 11–23 CrossRef CAS PubMed.
- J. Walker, Rep. Prog. Phys., 1979, 42, 1605 CrossRef CAS.
- Y. D. Glinka, K.-W. Lin, H.-C. Chang and S. H. Lin, J. Phys. Chem. B, 1999, 103, 4251–4263 CrossRef CAS.
- A. S. Barnard, Analyst, 2009, 134, 1751–1764 RSC.
- F. Jelezko and J. Wrachtrup, Phys. Status Solidi A, 2006, 203, 3207–3225 CrossRef CAS.
- A. T. Collins, G. Davies, H. Kanda and G. S. Woods, J. Phys. C: Solid State Phys., 1988, 21, 1363–1376 CrossRef CAS.
- K. Iakoubovskii and G. J. Adriaenssens, J. Phys.: Condens. Matter, 2001, 13, 6015 CAS.
- Y.-R. Chang, H.-Y. Lee, K. Chen, C.-C. Chang, D.-S. Tsai, C.-C. Fu, T.-S. Lim, Y.-K. Tzeng, C.-Y. Fang, C.-C. Han, H.-C. Chang and W. Fann, Nat. Nanotechnol., 2008, 3, 284–288 CrossRef CAS PubMed.
- G. Davies, J. Phys. C: Solid State Phys., 1979, 12, 2551 CrossRef CAS.
- J. R. Rabeau, A. Stacey, A. Rabeau, S. Prawer, F. Jelezko, I. Mirza and J. Wrachtrup, Nano Lett., 2007, 7, 3433–3437 CrossRef CAS PubMed.
- B. R. Smith, D. Inglis, B. Sandnes, J. R. Rabeau, A. V. Zvyagin, D. Gruber, C. Noble, R. Vogel, E. Ōsawa and T. Plakhotnik, Small, 2009, 5, 1649–1653 CrossRef CAS PubMed.
- C. Bradac, T. Gaebel, N. Naidoo, J. R. Rabeau and A. S. Barnard, Nano Lett., 2009, 9, 3555–3564 CrossRef CAS PubMed.
- Y. Shen, T. M. Sweeney and H. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 033201 CrossRef.
- A. Mainwood, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 7934 CrossRef CAS.
- B. T. Webber, M. C. Per, D. W. Drumm, L. C. L. Hollenberg and S. P. Russo, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 014102 CrossRef.
- M. D. Crossfield, G. Davies, A. T. Collins and E. C. Lightowlers, J. Phys. C: Solid State Phys., 1974, 7, 1909 CrossRef CAS.
- The Properties of Diamond, ed. J. E. Field, Academic, New York, 1979, pp. 23–77 Search PubMed.
- S. C. Rand and L. G. DeShazer, Opt. Lett., 1985, 10, 481–483 CrossRef CAS.
- T. Plakhotnik and R. Chapman, New J. Phys., 2011, 13, 045001 CrossRef.
- H.-C. Chang, in Nanodiamonds, First Applications in Biology and Nanoscale Medicine, ed. D. Ho, Springer Science + Business Media, New York, 2009 Search PubMed.
- A. M. Schrand, S. A. C. Hens and O. A. Shenderova, Crit. Rev. Solid State Mater. Sci., 2009, 34, 18–74 CrossRef CAS.
- H. Huang, E. Pierstorff, E. Ōsawa and D. Ho, Nano Lett., 2007, 7, 3305–3314 CrossRef CAS PubMed.
- R. Lam, M. Chen, E. Pierstorff, H. Huang, E. Ōsawa and D. Ho, ACS Nano, 2008, 2, 2095–2102 CrossRef CAS PubMed.
- X.-Q. Zhang, M. Chen, R. Lam, X. Xu, E. Ōsawa and D. Ho, ACS Nano, 2009, 3, 2609–2616 CrossRef CAS PubMed.
- M. Chen, E. D. Pierstorff, R. Lam, S.-Y. Li, H. Huang, E. Ōsawa and D. Ho, ACS Nano, 2009, 3, 2016–2022 CrossRef CAS PubMed.
- E. K. Chow, X.-Q. Zhang, M. Chen, R. Lam, E. Robinson, H. Huang, D. Schaffer, E. Ōsawa, A. Goga and D. Ho, Sci. Transl. Med., 2011, 3, 73ra21 Search PubMed.
- C.-C. Fu, H.-Y. Lee, K. Chen, T.-S. Lim, H.-Y. Wu, P.-K. Lin, P.-K. Wei, P.-H. Tsao, H.-C. Chang and W. Fann, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 727–732 CrossRef CAS PubMed.
- C. Y. Cheng, E. Perevedentseva, J. S. Tu, P. H. Chung, C. L. Cheng, K. K. Liu, J. I. Chao, P. H. Chen and C. C. Chang, Appl. Phys. Lett., 2007, 90, 163903 CrossRef PubMed.
- J.-I. Chao, E. Perevedentseva, P.-H. Chung, K.-K. Liu, C.-Y. Cheng, C.-C. Chang and C.-L. Cheng, Biophys. J., 2007, 93, 2199–2208 CrossRef CAS PubMed.
- K.-K. Liu, W.-W. Zheng, C.-C. Wang, Y.-C. Chiu, C.-L. Cheng, Y.-S. Lo, C. Chen and J.-I. Chao, Nanotechnology, 2010, 21, 315106 CrossRef PubMed.
- Y.-K. Tzeng, O. Faklaris, B.-M. Chang, Y. Kuo, J.-H. Hsu and H.-C. Chang, Angew. Chem., Int. Ed., 2011, 50, 2262–2265 CrossRef CAS PubMed.
- G. Kucsko, P. C. Maurer, N. Y. Yao, M. Kubo, H. J. Noh, P. K. Lo, H. Park and M. D. Lukin, Nature, 2013, 500, 54–59 CrossRef CAS PubMed.
- Y. C. Lin, E. Perevedentseva, L. W. Tsai, K. T. Wu and C. L. Cheng, J. Biophotonics, 2012, 5, 838–847 CrossRef CAS PubMed.
- A. Ermakova, G. Pramanik, J.-M. Cai, G. Algara-Siller, U. Kaiser, T. Weil, Y.-K. Tzeng, H. C. Chang, L. P. McGuinness, M. B. Plenio, B. Naydenov and F. Jelezko, Nano Lett., 2013, 13, 3305–3309 CrossRef CAS PubMed.
- Y. Kuo, T. Y. Hsu, Y. C. Wu and H. C. Chang, Biomaterials, 2013, 34, 8352–8360 CrossRef CAS PubMed.
- X. Song, G. Wang, X. Liu, F. Feng, J. Wang, L. Lou and W. Zhu, Appl. Phys. Lett., 2013, 102, 133109 CrossRef PubMed.
- T.-L. Wee, Y.-K. Tzeng, C.-C. Han, H.-C. Chang, W. Fann, J.-H. Hsu, K.-M. Chen and Y.-C. Yu, J. Phys. Chem. A, 2007, 111, 9379–9386 CrossRef CAS PubMed.
- M. A. Zurbuchen, M. P. Lake, S. A. Kohan, B. Leung and L.-S. Bouchard, Sci. Rep., 2013, 3, 2668 Search PubMed.
- B. Naydenov, V. Richter, J. Beck, M. Steiner, P. Neumann, G. Balasubramanian, J. Achard, F. Jelezko, J. Wrachtrup and R. Kalish, Appl. Phys. Lett., 2010, 96, 163108 CrossRef PubMed.
- A. S. Barnard and M. Sternberg, J. Comput. Theor. Nanosci., 2008, 5, 2089–2095 CrossRef CAS PubMed.
- Y. Y. Hui, Y.-R. Chang, T.-S. Lim, H.-Y. Lee, W. Fann and H.-C. Chang, Appl. Phys. Lett., 2009, 94, 013104 CrossRef PubMed.
- A. S. Barnard and M. Sternberg, Nanotechnology, 2007, 18, 025702 CrossRef.
- A. S. Barnard, in Nanodiamond, ed. O. A. Williams, Royal Society of Chemistry, Cambridge, 2014 Search PubMed.
- J. R. Rabeau, P. Reichart, G. Tamanyan, D. N. Jamieson, S. Prawer, F. Jelezko, T. Gaebel, I. Popa, M. Domhan and J. Wrachtrup, Appl. Phys. Lett., 2006, 88, 23113 CrossRef PubMed.
- J. Meijer, B. Burchard, M. Domhan, C. Wittmann, T. Gaebel, I. Popa, F. Jelezko and J. Wrachtrup, Appl. Phys. Lett., 2005, 87, 261909 CrossRef PubMed.
- B. Naydenov, V. Richter, J. Beck, M. Steiner, P. Neumann, G. Balasubramanian, J. Achard, F. Jelezko, J. Wrachtrup and R. Kalish, Appl. Phys. Lett., 2010, 96, 163108 CrossRef PubMed.
- D. M. Toyli, C. D. Weis, G. D. Fuchs, T. Schenkel and D. D. Awschalom, Nano Lett., 2010, 10, 3168 CrossRef CAS PubMed.
- Z. Huang, W.-D. Li, C. Santori, V. M. Acosta, A. Faraon, T. Ishikawa, W. Wu, D. Winston, R. S. Williams and R. G. Beausoleil, Appl. Phys. Lett., 2013, 103, 081906 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of electronic structure simulations used to generate input parameter in this case. See DOI: 10.1039/c3mh00157a |
| This journal is © The Royal Society of Chemistry 2014 |