Systematic study of exciton diffusion length in organic semiconductors by six experimental methods†
Jason D. A.
Lin
a,
Oleksandr V.
Mikhnenko
ab,
Jingrun
Chen
c,
Zarifi
Masri
d,
Arvydas
Ruseckas
d,
Alexander
Mikhailovsky
a,
Reilly P.
Raab
a,
Jianhua
Liu
a,
Paul W. M.
Blom
e,
Maria Antonietta
Loi
b,
Carlos J.
García-Cervera
c,
Ifor D. W.
Samuel
d and
Thuc-Quyen
Nguyen
*a
aCenter for Polymers and Organic Solids, Department of Chemistry and Biochemistry, University of California, Santa Barbara, CA 93106, USA. E-mail: quyen@chem.ucsb.edu; Fax: +1 805 893 4120; Tel: +1 805 893 4851
bZernike Institute for Advanced Materials, University of Groningen, Nijenborgh 4, 9747 AG Groningen, The Netherlands. E-mail: m.a.loi@rug.nl; Tel: +31 50 363 4119
cDepartment of Mathematics, University of California at Santa Barbara, Santa Barbara, CA 93106, USA. E-mail: cgarcia@math.ucsb.edu; Fax: +1 805 893 2385; Tel: +1 805 893 3681
dOrganic Semiconductor Centre, SUPA, School of Physics and Astronomy, University of St. Andrews, St Andrews, KY169SS, UK. E-mail: idws@st-andrews.ac.uk; Tel: +44 (0) 1334 46 3114
eMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: blom@mpip-mainz.mpg.de; Tel: +49 6131 379-121
First published on 23rd January 2014
Abstract
Six experimental methods have been used to investigate the exciton diffusion length in materials with systematic chemical modifications. We find that exciton diffusion length correlates with molecular ordering. We discuss situations in which certain experimental techniques are more appropriate.
Exciton diffusion plays a vital role in the function of many organic semiconducting opto-electronic devices. Exciton diffusion length (LD) is the characteristic distance that excitons are able to diffuse during their lifetime in a given material. A short LD limits the dissociation of excitons into free charges in planar-heterojunction organic solar cells.1,2 Conversely, a long LD in organic light emitting diodes (OLEDs) can limit luminous efficiency if excitons diffuse to non-radiative quenching sites such as oxidation defects,3 electrodes,4 and polarons.5 Exciton diffusion has been studied in a number of small molecules1,2,6–17 and conjugated polymers.9,18–32 However, it remains challenging to understand the relationship between the chemical structure and the exciton diffusion length. There are only a few works which investigate exciton diffusion length as a function of chemical structure.1,11,13,21,27,33 In particular the effect of conjugation length on the exciton diffusion has not been addressed.
Several methods have been used to measure exciton diffusion length; however, it is unclear which methods are more reliable for a given situation. Reported techniques to measure exciton diffusion length include photoluminescence (PL) surface quenching,1,11,21,22,24–26,34–37 time-resolved PL bulk quenching modeled with a Monte Carlo simulation,16,27 exciton–exciton annihilation,15,23,26,29,38 modeling of solar cell photocurrent spectrum,6,9,10,18,35,39–45 time-resolved microwave conductance,17,46,47 spectrally resolved PL quenching,13,33,48,49 and Förster resonance energy transfer theory.13,33,50 Currently, there is little known on how the value of the measured exciton diffusion length of the same material can vary depending on the technique employed. Consequently, it is difficult to draw conclusions regarding the structure–property relationships across previous studies.
In this work, a thorough investigation has been performed to study the dependence of exciton diffusion length on chemical structure using six experimental techniques. We have utilized phenyl substituted diketopyrrolopyrrole (DPP) small molecules (Fig. 1) as our model system. The chemical structure has been systematically modified in regards to conjugation length and functional groups. We show that decreasing the conjugation length increases molecular ordering, which is correlated with an enhancement of exciton diffusion length.
In general, a diffusion length is defined as the root mean squared displacement of a particle from its initial position during time τ (ref. 51):
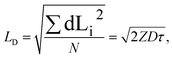 | (1) |
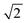 factor is often omitted in eqn (1) and the values of LD are often reported for the one-dimensional case:
factor is often omitted in eqn (1) and the values of LD are often reported for the one-dimensional case: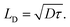 | (2) |
To be consistent with literature, we use eqn (2) in this work to define the exciton diffusion length.
Fig. 1 shows the chemical structures of the compounds that were used in this work. When going from compound A to B the conjugation length is increased by two thiophene units. Comparing B to C highlights the impact of the functional group by the replacement of the linear alkyl chains on the lactam nitrogen units with ethyl–hexyl groups. These variations in chemical structures have been shown to induce different molecular packing and film morphology,52 which may impact the exciton diffusion length.
To understand how the experimental technique influences the resulting value of the exciton diffusion length we have used six methods to independently measure the exciton diffusion length for compounds shown in Fig. 1. The exciton diffusion length was measured using steady-state PL surface quenching (SS-SQ), time-resolved PL surface quenching (TR-SQ), exciton–exciton annihilation (EEA), time-resolved PL bulk quenching modeled with a Monte Carlo simulation (BQ-MC), time-resolved PL bulk quenching fitted with the Stern–Volmer equation (BQ-SV), and estimated using Förster resonant energy transfer (FRET) theory.
In the surface quenching techniques – such as SS-SQ and TR-SQ – steady-state or time-resolved PL is measured to determine the exciton quenching efficiency in bilayer films as a function of organic semiconductor thicknesses with a thin quenching layer. The exciton diffusion length is correlated to the maximum thickness of the material at which the majority of generated excitons can reach the quenching interface. In the EEA technique, time-resolved PL is measured at variable excitation fluence to detect the decay of excitons due to the diffusion limited collision and annihilation. The exciton diffusion length is correlated to the exciton density at which the majority of generated excitons can be quenched via EEA. In the bulk (or volume) quenching techniques, organic semiconductor is mixed with exciton quenching molecules to form homogeneous blends. Exciton quenching efficiency in blend films is measured as a function of quencher concentration. The quenching can be analysed by a Monte Carlo simulation or the Stern–Volmer equation leading to exciton diffusion parameters. In the BQ-MC technique, the experimentally measured exciton lifetime in pristine material is inputted into the Monte Carlo simulation where the diffusion coefficient is fitted to match the experimentally measured quenching efficiency at a given PCBM concentration. In this technique, the exciton diffusion length is correlated to the distance an exciton is required to travel to reach a quencher molecule. The BQ-MC and BQ-SV are similar in regards to film fabrication and measurement. In contrast to BQ-MC, the BQ-SV method can be only applied to materials that show monoexponential PL decay dynamics. However, the analysis in the BQ-SV technique does not require the Monte Carlo simulation software. For the FRET theory method, the diffusion coefficient is estimated from the Förster radius and the distance between chromophores. Then the exciton diffusion length is calculated using formula (2). In the following, we will only briefly discuss the key differences between the techniques. Further details regarding the sample preparation, measurement, data analysis, and assumptions for each technique can be found in the ESI.†
In regards to sample preparation, surface quenching techniques are the most time consuming due to high demands for the sample quality. An efficient exciton quencher is required that can form a stable and sharp interface with the organic semiconductor, which is non-trivial as discussed in the ESI.† A relatively large number of samples is required (10–20) with variable thickness of organic semiconductor in the range of typically 5–50 nm. In addition a precise thickness measurement is necessary using atomic force microscopy and/or spectroscopic ellipsometry. Surface quenching techniques also assume consistent morphologies across thick and thin films. This is likely not the case for semi-crystalline materials. Samples for the bulk quenching techniques – such as BQ-MC and BQ-SV – are relatively simple to prepare since the aforementioned requirements for the film thickness, surface roughness, and interface effects do not apply. However, a good quenching agent must be available, which would homogeneously mix with the organic semiconductor. Fortunately, [6,6]-phenyl-C61-butyric acid methyl ester (PCBM) can be used as such an agent in most of the cases. The bulk quenching techniques require a smaller number of samples, typically only 8 spin-coated films. These methods account for clustering of the quenchers and cannot be used if the miscibility with the quenching agent is poor. And finally, the EEA and FRET theory techniques have the simplest fabrication procedures since all measurements are done on a pristine film.
When it comes to the experimental measurements, the steady-state techniques – such as SS-SQ – are the most challenging because they require careful estimation of the amount of light absorbed and emitted.24 Therefore, the time-resolved techniques – such as TR-SQ, BQ-MC, BQ-SV, and EEA – are preferred over the steady-state measurements. However, the time-resolved techniques usually require expensive equipment, such as ultra-fast pulsed lasers and sophisticated detectors. Thickness measurements with very high precision must be conducted for surface quenching methods that is time and resource consuming. The EEA technique requires high intensities of the pulsed lasers and good photostability of a material under study.
The data analysis procedures for the different techniques studied here range from advanced modeling and simulation to relatively simple fitting to an equation. The data modeling for the surface quenching techniques can be either simple or extensive, depending on the materials. The most complex situation occurs in the bi-layer method if the organic semiconductor and the exciton quencher have both significantly different refractive indexes and strong Förster coupling (Section 1 of ESI†). Otherwise, the exciton diffusion can be modeled with a simple analytical formula.22 The data of the EEA technique can be modeled using an analytical model; however, the annihilation radius has to be determined using additional experiments.26 Modeling for the bulk quenching techniques – such as BQ-MC – is not straightforward in general. However, a free software package is available for use [http://mikhnenko.com/eDiffusion]. If the bulk quenching data shows mono-exponential PL decay then analysis can be readily performed by fitting to the Stern–Volmer formula as in the BQ-SV method. Finally, FRET theory provides a relatively easy way to estimate the exciton diffusion coefficient since no fitting or modeling software is needed. However, this technique requires knowledge of a number of parameters which are often difficult to measure experimentally such as the average dipole orientation, intermolecular distance, and index of refraction (Section 5 of ESI†). In general, this is an indirect method and it must be used with caution.
Table 1 summarizes the sample preparation, measurement, and analysis in the techniques employed in this work. It shows that surface quenching techniques such as SS-SQ and TR-SQ require a large number of samples, measurements, and modeling in comparison to bulk quenching techniques such as EEA, BQ-MC, and BQ-SV.
| Technique | Abbrev. | Sample preparation | Measurement | Data analysis | Best for |
|---|---|---|---|---|---|
| Steady-state surface quenching | SS-SQ | • 10 Pristine films with varying organic semiconductor thickness | • Steady-state PL spectrum as a function of thickness | • Calculate quenching efficiency | •Amorphous smooth films. Good quenching interface is required |
| • 10 Bilayer films with a quenching layer and varying organic semiconductor thickness | • Thickness | • Model optical constants, electrical field, generation rate, and exciton density | |||
| • Optical constants | • Fit for exciton diffusion length | ||||
| Time-resolved surface quenching | TR-SQ | •Equivalent to SS-SQ | • Time-resolved PL decay as a function of thickness | •Equivalent to SS-SQ | •Equivalent to SS-SQ |
| • Thickness | |||||
| • Optical constants | |||||
| Exciton–exciton annihilation | EEA | •3–5 Pristine films | • Time-resolved PL at different excitation densities | • PL decay fitting with an analytical model | •Amorphous materials |
| • Film density | |||||
| • Thickness | |||||
| Bulk quenching with Monte Carlo modeling | BQ-MC | •8–10 Blend films with varying concentrations of quencher | • Time-resolved PL decay | • Calculate quenching efficiency | •Moderately crystalline or amorphous materials |
| • Film density | • Use Monte Carlo simulation to model PL | ||||
| Bulk quenching with Stern–Volmer modeling | BQ-SV | •Equivalent to BQ-MC | •Equivalent to BQ-MC | • Calculate quenching efficiency | •Equivalent to BQ-MC |
| • Use analytical model to fit the data | |||||
| FRET theory | •3–5 Pristine films | • Steady-state absorption and PL spectrum | • Estimate distance between molecules | •Materials with very small quantities available | |
| • PL quantum yield | • Calculate Förster radius and diffusion coefficient | ||||
| • Film density | |||||
| • Thickness | |||||
| • Index of refraction | |||||
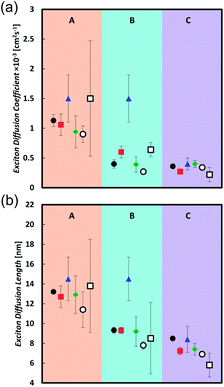
Table 2 and Fig. 2 summarize the measurements of the exciton diffusion coefficient and exciton diffusion length. Very good agreement between different techniques is obtained in the compound C, whereas in compounds A and B the technique based on exciton–exciton annihilation gives a higher exciton diffusion coefficient than the techniques based on the bulk quenching and surface quenching.
| Technique | Diffusion coefficient × 10−3 (cm2 s−1) | Exciton diffusion length (nm) | ||||
|---|---|---|---|---|---|---|
| A | B | C | A | B | C | |
| SS-SQ | 1.13 ± 0.1 | 0.4 ± 0.07 | 0.36 ± 0.04 | 13.2 ± 0.1 | 9.32 ± 0.3 | 8.49 ± 0.16 |
| TR-SQ | 1.06 ± 0.18 | 0.6 ± 0.1 | 0.27 ± 0.03 | 12.7 ± 1.1 | 9.3 ± 0.3 | 7.22 ± 0.36 |
| EEA | 1.5 ± 0.4 | 1.5 ± 0.4 | 0.4 ± 0.1 | 14.5 ± 2.2 | 14.5 ± 2.2 | 8.4 ± 1.3 |
| BQ-MC | 0.94 ± 0.27 | 0.39 ± 0.13 | 0.4 ± 0.06 | 12.9 ± 1.9 | 9.2 ± 1.5 | 7.4 ± 0.6 |
| BQ-SV | 0.9 ± 0.14 | 0.27 ± 0.02 | 0.34 ± 0.02 | 11.4 ± 1.8 | 7.79 ± 0.04 | 6.9 ± 0.3 |
| FRET theory | 1.53 ± 0.97 | 0.64 ± 0.45 | 0.22 ± 0.12 | 13.8 ± 4.7 | 8.5 ± 3.6 | 5.8 ± 1.2 |
In this series of compounds we find that the diffusion coefficient is significantly increased by decreasing the conjugation length and slightly enhanced by decreasing the molecular bulkiness of solubilizing groups. Compound A has the shortest conjugation length and shows the largest diffusion coefficient around 1 × 10−3 cm2 s−1 with exciton diffusion length of 13 nm. In comparison, compounds B and C yield similar diffusion coefficients around 0.4 × 10−3 cm2 s−1 and an exciton diffusion length of 9 and 8 nm, respectively. When comparing B and C within the same technique a general trend shows that the exciton diffusion coefficient and length for B is either equal to or slightly greater than that of C.
The variance in diffusion coefficients between compounds A, B, and C can be due to different degrees of molecular ordering in the thin films. Previous works have shown that a greater degree of molecular ordering can enhance the exciton diffusion coefficient.11,33,53,54
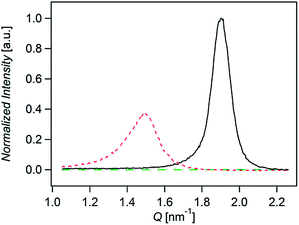
Fig. 3 shows the normalized X-rays scattering intensity versus scattering vector Q for thin films of compounds A, B, and C. The normalization accounts for film thickness, structure factor, multiplicity, unit cell volume, and the Lorenz-polarization factor (Section 6 in ESI†). We also took into account the orientation of the crystallites by measuring the angular distribution of the scattered (Fig. S12 ESI†). Integration of peaks areas in Fig. 3 shows that the relative crystallinity of A is roughly 1.6 times greater than B. Compound C does not show any scattering. Therefore the relative crystallinity follows A > B > C, which is similar to the trend we observe in the diffusion coefficients. In this way we find that the diffusion coefficient correlates with the relative crystallinity.
In regards to the measurement of exciton diffusion length it is important to consider the degree of anisotropy in films. For instance, anthracene single crystals show LD = 36, 60, and 100 nm in the c, a, and b crystalline directions respectively.55 In our analysis of the angular distribution of the scattered intensity (Fig. S10 ESI†) we found that crystallites in films of A and B are textured out of plane and therefore anisotropic. While our x-ray diffraction measurements confirm the presence of anisotropy, it does not quantify the degree of anisotropy since the volume fraction of amorphous and crystalline regions is not known.
To probe anisotropy in both crystalline and amorphous regions we utilized spectroscopic ellipsometry. Spectroscopic ellipsometry can be used to model the magnitude of absorption for in and out of plane directions which is correlated to the average dipole orientation of molecules in film. We find that there is no detectable anisotropy in films A, B, and C (Section 7 in ESI†). This result suggests that the volume fraction of crystallites in films of A and B is small relative to the volume fraction of the amorphous phase.
A predominantly isotropic medium in films of A, B, and C is further supported by the following observations. The exciton diffusion length in the direction out of plane is probed by the surface quenching techniques. We found that the obtained value is very similar to the exciton diffusion length probed in three dimensions using the bulk quenching techniques. Moreover, all three materials make homogeneous mixture with PCBM molecules for PCBM concentrations of 1017–1018 cm−3 (Fig. S7†). This concentration range corresponds to the average distance between PCBM molecules of 10–20 nm. Thus the crystallites (if present) must be smaller than this distance that corresponds to the length-scale of exciton diffusion. Therefore materials A, B, and C can be considered isotropic on the scale of exciton diffusion length.
The correlation between relative crystallinity of the films with exciton diffusion length can be rationalized using the consideration that the Förster energy transfer facilitates singlet exciton diffusion in organic semiconductors. The efficiency of the FRET is rapidly decreasing with the distance between the chromophores. Therefore materials with shorter intermolecular distances are expected to have higher exciton diffusion coefficient, for similar Förster radii. Although it is difficult to estimate the intermolecular distance in mostly amorphous materials, it is likely that materials with higher affinity to form crystallites pack more densely on average. Indeed, our champion material A exhibits the highest affinity to form crystallites resulting in the largest diffusion coefficient in the series. While materials B and C show weaker affinity to form crystallites and thus lower diffusion coefficient.
From a practical stance, it is useful to investigate how the measured exciton diffusion length of a single material varies depending on the measurement technique employed. Consistent result across different techniques is achieved in the amorphous material C. In contrast, the EEA technique gives greater diffusion coefficients for compounds A and B which is attributed to exciton migration to crystalline regions where exciton–exciton collision and annihilation is enhanced. This result shows that caution should be taken when comparing exciton diffusion lengths of semi-crystalline materials measured by different techniques.
In this work we have covered six techniques to measure the exciton diffusion length. We find that certain techniques are more appropriate given the material properties along with the instrumentation and analysis software available. We find the BQ-MC technique to be ideal for the measurement of exciton diffusion length for a broad range of materials due to its facile sample fabrication along with its minimal assumptions in modeling. However, BQ-MC does require an organic semiconductor which is miscible with PCBM, instrumentation for time-resolved spectroscopy, and simulation software. When the organic semiconductor exhibits mono-exponential decay the BQ-SV technique can be used which does not require simulation software. The EEA and FRET Theory techniques are better suited for organic semiconductors, which have poor miscibility with PCBM and are highly crystalline, since the measurements are performed on pristine films. The EEA technique is also advantageous in situations when an efficient quencher is not available. In general, surface quenching techniques such as SS-SQ and TR-SQ are the most demanding in regards to sample fabrication, measurement, and analysis. However, surface quenching techniques directly measure exciton diffusion length and can be accurately employed when the organic semiconductor and the exciton quencher are able to form a sharp and efficient quenching interface.
Conclusions
In summary, we have compared and contrasted six techniques to measure exciton diffusion length. Very good agreement between different techniques is obtained in amorphous films, whereas in semi-crystalline films the technique based on exciton–exciton annihilation gives a higher exciton diffusion coefficient and subsequently larger diffusion length than the techniques based exciton quenching. All the approaches are useful and the combined results give insight into structure–property relations for exciton diffusion. Different techniques have different advantages and disadvantages, and we discussed key differences in fabrication, measurement, and analysis. Consistent results are obtained with surface and with bulk quenching techniques, which indicates that diffusion in the direction perpendicular to the plane of the film and 3D diffusion in the bulk are not different, and hence isotropic. We find that bulk quenching techniques are convenient for systematic studies of exciton diffusion length since the sample preparation procedure is quite simple and fast and the analysis can be done using open source Monte-Carlo software or fitting to the Stern–Volmer equation. We investigated the dependence of exciton diffusion length on systematic chemical modifications. It is shown that decreasing the conjugation length of compound B to form compound A results in an enhancement in the exciton diffusion coefficient from 0.4 × 10−3 cm2 s−1 to 1 × 10−3 cm2 s−1 and exciton diffusion length from 9 nm to 13 nm. We attribute this to an increase in relative molecular ordering upon decreasing the conjugation length. It is also shown that decreasing the molecular bulkiness by replacement of the ethyl–hexyl groups by the linear alkyl chains has little effect on the resulting exciton diffusion parameters.Acknowledgements
The authors thank the National Science Foundation (NSF) Division of Materials Research, NSF-SOLAR for the financial support. TQN thanks the Camille Dreyfus Teacher Scholar Award and the Alfred Sloan Research Fellowship program. Z.M. is grateful to the Government of Brunei Darussalam for financial support. Work at St Andrews is supported by the Engineering and Physical Sciences Research Council of the UK and by the European Research Council of the European Union. We thank Alex Sharenko for useful discussion.Notes and references
- Y. Terao, H. Sasabe and C. Adachi, Appl. Phys. Lett., 2007, 90, 103515 CrossRef
.
- S. M. Menke, W. A. Luhman and R. J. Holmes, Nat. Mater., 2013, 12, 152–157 CrossRef CAS PubMed
.
- H. Antoniadis, L. J. Rothberg, F. Papadimitrakopoulos, M. Yan, M. E. Galvin and M. A. Abkowitz, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 14911–14915 CrossRef CAS
.
- A. L. Burin and M. A. Ratner, J. Phys. Chem. A, 2000, 104, 4704–4710 CrossRef CAS
.
- E. J. W. List, C. H. Kim, W. Graupner, G. Leising and J. Shinar, Mater. Sci. Eng., B, 2001, 85, 218–223 CrossRef
.
- D. Qin, P. Gu, R. S. Dhar, S. G. Razavipour and D. Ban, Phys. Status Solidi A, 2011, 208, 1967–1971 CrossRef CAS
.
- O. V. Mikhnenko, R. Ruiter, P. W. M. Blom and M. A. Loi, Phys. Rev. Lett., 2012, 108, 137401 CrossRef PubMed
.
- B. A. Gregg, J. Sprague and M. W. Peterson, J. Phys. Chem. B, 1997, 101, 5362–5369 CrossRef CAS
.
- T. Stübinger and W. Brütting, J. Appl. Phys., 2001, 90, 3632–3641 CrossRef
.
- C. L. Yang, Z. K. Tang, W. K. Ge, J. N. Wang, Z. L. Zhang and X. Y. Jian, Appl. Phys. Lett., 2003, 83, 1737–1739 CrossRef CAS
.
- S.-B. Rim, R. F. Fink, J. C. Schöneboom, P. Erk and P. Peumans, Appl. Phys. Lett., 2007, 91, 173504 CrossRef
.
- A. Holzhey, C. Uhrich, E. Brier, E. Reinhold, P. Bäuerle, K. Leo and M. Hoffmann, J. Appl. Phys., 2008, 104, 064510 CrossRef
.
- R. R. Lunt, N. C. Giebink, A. A. Belak, J. B. Benziger and S. R. Forrest, J. Appl. Phys., 2009, 105, 053711 CrossRef
.
- H. Gommans, S. Schols, A. Kadashchuk, P. Heremans and S. C. J. Meskers, J. Phys. Chem. C, 2009, 113, 2974–2979 CAS
.
- S. Cook, A. Furube, R. Katoh and L. Han, Chem. Phys. Lett., 2009, 478, 33–36 CrossRef CAS
.
- O. Mikhnenko, J. Lin, Y. Shu, J. E. Anthony, P. W. M. Blom, T.-Q. Nguyen and M. A. Loi, Phys. Chem. Chem. Phys., 2012, 14, 14196–14201 RSC
.
- M. C. Fravventura, J. Hwang, J. W. A. Suijkerbuijk, P. Erk, L. D. A. Siebbeles and T. J. Savenije, J. Phys. Chem. Lett., 2012, 3, 2367–2373 CrossRef CAS PubMed
.
- J. J. M. Halls, K. Pichler, R. H. Friend, S. C. Moratti and A. B. Holmes, Appl. Phys. Lett., 1996, 68, 3120–3122 CrossRef CAS
.
- A. Haugeneder, M. Neges, C. Kallinger, W. Spirkl, U. Lemmer, J. Feldmann, U. Scherf, E. Harth, A. Gügel and K. Müllen, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 15346–15351 CrossRef CAS
.
- D. E. Markov, J. C. Hummelen, P. W. M. Blom and A. B. Sieval, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 045216 CrossRef
.
- D. E. Markov, C. Tanase, P. W. M. Blom and J. Wildeman, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 045217 CrossRef
.
- D. E. Markov, E. Amsterdam, P. W. M. Blom, A. B. Sieval and J. C. Hummelen, J. Phys. Chem. A, 2005, 109, 5266–5274 CrossRef CAS PubMed
.
- A. J. Lewis, A. Ruseckas, O. P. M. Gaudin, G. R. Webster, P. L. Burn and I. D. W. Samuel, Org. Electron., 2006, 7, 452–456 CrossRef CAS
.
- S. R. Scully and M. D. McGehee, J. Appl. Phys., 2006, 100, 034907 CrossRef
.
- C. Goh, S. R. Scully and M. D. McGehee, J. Appl. Phys., 2007, 101, 114503 CrossRef
.
- P. E. Shaw, A. Ruseckas and I. D. W. Samuel, Adv. Mater., 2008, 20, 3516–3520 CrossRef CAS
.
- O. V. Mikhnenko, H. Azimi, M. Scharber, M. Morana, P. W. M. Blom and M. A. Loi, Energy Environ. Sci., 2012, 5, 6960–6965 CAS
.
- A. J. Ward, A. Ruseckas and I. D. W. Samuel, J. Phys. Chem. C, 2012, 116, 23931–23937 CAS
.
- Z. Masri, A. Ruseckas, E. V. Emelianova, L. Wang, A. K. Bansal, A. Matheson, H. T. Lemke, M. M. Nielsen, H. Nguyen, O. Coulembier, P. Dubois, D. Beljonne and I. D. W. Samuel, Adv. Energy Mater., 2013, 3, 1445–1453 CrossRef CAS
.
- E. Hennebicq, G. Pourtois, G. D. Scholes, L. M. Herz, D. M. Russell, C. Silva, S. Setayesh, A. C. Grimsdale, K. Müllen, J.-L. Brédas and D. Beljonne, J. Am. Chem. Soc., 2005, 127, 4744–4762 CrossRef CAS PubMed
.
- X. Zhang, Z. Li and G. Lu, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 235208 CrossRef
.
- S. Athanasopoulos, E. V. Emelianova, A. B. Walker and D. Beljonne, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 195209 CrossRef
.
- R. R. Lunt, J. B. Benziger and S. R. Forrest, Adv. Mater., 2010, 22, 1233–1236 CrossRef CAS PubMed
.
- Y. Wu, Y. C. Zhou, H. R. Wu, Y. Q. Zhan, J. Zhou, S. T. Zhang, J. M. Zhao, Z. J. Wang, X. M. Ding and X. Y. Hou, Appl. Phys. Lett., 2005, 87, 044104 CrossRef
.
- M. Theander, A. Yartsev, D. Zigmantas, V. Sundström, W. Mammo, M. R. Andersson and O. Inganäs, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 12957 CrossRef CAS
.
- Y. C. Zhou, Y. Wu, L. L. Ma, J. Zhou, X. M. Ding and X. Y. Hou, J. Appl. Phys., 2006, 100, 023712 CrossRef
.
- O. V. Mikhnenko, F. Cordella, A. B. Sieval, J. C. Hummelen, P. W. M. Blom and M. A. Loi, J. Phys. Chem. B, 2008, 112, 11601–11604 CrossRef CAS PubMed
.
- P. E. Shaw, A. Ruseckas, J. Peet, G. C. Bazan and I. D. W. Samuel, Adv. Funct. Mater., 2010, 20, 155–161 CrossRef CAS
.
- A. K. Ghosh and T. Feng, J. Appl. Phys., 1978, 49, 5982–5989 CrossRef CAS
.
- J. Wagner, T. Fritz and H. Böttcher, Phys. Status Solidi A, 1993, 136, 423–432 CrossRef CAS
.
- V. Bulović and S. R. Forrest, Chem. Phys. Lett., 1995, 238, 88–92 CrossRef
.
- L. A. A. Pettersson, L. S. Roman and O. Inganäs, J. Appl. Phys., 1999, 86, 487 CrossRef CAS
.
- P. Peumans, A. Yakimov and S. R. Forrest, J. Appl. Phys., 2003, 93, 3693 CrossRef CAS
.
- S.-B. Rim and P. Peumans, J. Appl. Phys., 2008, 103, 124515 CrossRef
.
- A. Huijser, T. J. Savenije, A. Shalav and L. D. A. Siebbeles, J. Appl. Phys., 2008, 104, 034505 CrossRef
.
-
T. J. Savenije and L. D. Siebbeles, in Laser Science, Optical Society of America, 2010, p. LWC5 Search PubMed
.
- J. E. Kroeze, T. J. Savenije, M. J. W. Vermeulen and J. M. Warman, J. Phys. Chem. B, 2003, 107, 7696–7705 CrossRef CAS
.
- K. J. Bergemann and S. R. Forrest, Appl. Phys. Lett., 2011, 99, 243303 CrossRef
.
- B. P. Rand, D. Cheyns, K. Vasseur, N. C. Giebink, S. Mothy, Y. Yi, V. Coropceanu, D. Beljonne, J. Cornil, J.-L. Brédas and J. Genoe, Adv. Funct. Mater., 2012, 22, 2987–2995 CrossRef CAS
.
- T. K. Mullenbach, K. A. McGarry, W. A. Luhman, C. J. Douglas and R. J. Holmes, Adv. Mater., 2013, 25, 3689–3693 CrossRef CAS PubMed
.
-
M. Pope and C. E. Swenberg, Electronic processes in organic crystals and polymers, Oxford University Press, 1999 Search PubMed
.
- C. Kim, J. Liu, J. Lin, A. B. Tamayo, B. Walker, G. Wu and T.-Q. Nguyen, Chem. Mater., 2012, 24, 1699–1709 CrossRef CAS
.
- L. D. A. Siebbeles, A. Huijser and T. J. Savenije, J. Mater. Chem., 2009, 19, 6067–6072 RSC
.
- G. Wei, R. R. Lunt, K. Sun, S. Wang, M. E. Thompson and S. R. Forrest, Nano Lett., 2010, 10, 3555–3559 CrossRef CAS PubMed
.
- R. C. Powell and Z. G. Soos, J. Lumin., 1975, 11, 1–45 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3mh00089c |
| This journal is © The Royal Society of Chemistry 2014 |