Paramecium swimming and ciliary beating patterns: a study on four RNA interference mutations

Abstract

Paramecium cells swim and feed by beating their thousands of cilia in coordinated patterns. The organization of these patterns and its relationship with cell motility has been the subject of a large body of work, particularly as a model for ciliary beating in human organs where similar organization is seen. However the rapid motion of the cells makes quantitative measurements very challenging. Here we provide detailed measurements of the swimming of Paramecium cells from high-speed video at high magnification, as they move in microfluidic channels. An image analysis protocol allows us to decouple the cell movement from the motion of the cilia, thus allowing us to measure the ciliary beat frequency (CBF) and the spatio-temporal organization into metachronal waves along the cell periphery. Two distinct values of the CBF appear at different regions of the cell: most of the cilia beat in the range of 15 to 45 Hz, while the cilia in the peristomal region beat at almost double the frequency. The body and peristomal CBF display a nearly linear relation with the swimming velocity. Moreover the measurements do not display a measurable correlation between the swimming velocity and the metachronal wave velocity on the cell periphery. These measurements are repeated for four RNAi silenced mutants, where proteins specific to the cilia or to their connection to the cell base are depleted. We find that the mutants whose ciliary structure is affected display similar swimming to the control cells albeit with a reduced efficiency, while the mutations that affect the cilia's anchoring to the cell lead to strongly reduced ability to swim. This reduction in motility can be related to a loss of coordination between the ciliary beating in different parts of the cell.

---

Insight, innovation, integration

Genetic disorders in the cilia or the basal body are known to cause several human diseases, although the contribution of the ciliary beating and metachronal waves to these diseases are often poorly understood. This motivated us to study ciliary beating on Paramecium cells as they swim freely within microfluidic channels, in order to elucidate the relationship that exists between the beating frequency, organization, and swimming efficiency. Advanced image analysis was used to provide quantitative measurements of the ciliary movement, which we related to the swimming of the cells. These measurements were repeated for different RNAi silenced genes associated with the ciliary structure or their anchoring to the cell surface, showing a strong effect of some genes on the swimming efficiency.

Introduction

A common strategy for swimming at cellular scale consists of oscillating a flagellum or the cilia covering the surface of the cell. However these oscillations can only lead to cell motility if the shape of the undulations is not time-reversible.¹ This is the case for instance for the waves propagating on the flagellum of the sperm cell or the corkscrew motion of the flagella of E. coli, which both display a clear directionality. In ciliates, where the cell is covered by a large number of cilia, the time reversal symmetry is broken on two scales: first on the scale of a single cilium, which typically performs first a power stroke that moves the cell forward, followed by a recovery stroke in which the cilium moves close to the cell body and therefore has a weaker effect on moving the cell backwards. Second, the beating of individual cilia is synchronized into waves, called the metachronal waves, that also travel along the cell body in a well defined direction.^2,3

The behavior that is described above, which has long been known for protozoa such as Paramecium, is also observed in a wide variety of other situations. Indeed, it also describes many physiological processes in humans, such as mucous clearance from airways, egg transport in fallopian tubes, or the motion of the spinal fluid in the nervous system.⁴ As a result, a malfunction in the beating patterns in these organs, whether genetic or acquired, can lead to different diseases (ciliopathies) that result from the accumulation of fluid (hydrocephaly),⁵ a confusion of the left-right asymmetry during development⁶ or the loss of mechanical role of the airway epithelium.⁷ Therefore, the study of cilia beating and coordination, as well as the signalization which conditions them is an essential step to understand how cilia movement is affected by some genetic dysfunction.

The fact that the ciliated cells in the human organs are anchored to a fixed solid boundary while the fluid is pushed by the beating motion simply corresponds to a change of reference frame, in comparison with micro-swimmers, and does not change the underlying mechanics. The strong similarity in behavior between ciliates and human organs, in addition to the conserved structure of cilia and the genes that affect them across species,⁸ have motivated the study of micro-swimmers as simple models for the observation of the fluid-solid coupling due to ciliary beating.

These issues have motivated a surge of interest in recent years in the study of ciliary motion and fluid flow. In particular, a large body of theoretical and numerical work has looked to identify the relation between the swimming velocity, the emergence and organization of the metachronal waves, and the motion of individual cilia.^9–11 Hydrodynamic interactions between individual cilia have also been studied in addition to the optimality of this organization in terms of energy use or feeding ability.^12,13 In addition, experimental work on ciliated eukaryotes has recently allowed the measurement of ciliary beating dynamics and subsequent flow fields.^14–17

They complete older works, such as those of Machemer;¹⁸ here they determined that Paramecium movement relies on the coordinated beating of some five thousand cilia covering the whole cell body, ensuring the cell to swim forward along a spiraling line under normal conditions. This movement may be converted to a backward swimming, due to cilia beating reversal, when the cell encounters an obstacle or changes direction.² The forward straight swimming is also affected by mechanical or chemical signals which can change the swimming mode by stimulating ciliary ion channels.¹⁹ In addition to these global descriptions of Paramecium, two sub-populations of beating cilia can be distinguished in terms of cell swimming: body (somatic) cilia and the cilia of the peristomal region, which both contribute to the cell's swimming, and cilia of the gullet which drive the feeding bacteria into the oral cavity and a group of cilia at the rear of the cell which do not beat and whose role is both cell orientation and sensing. Peristomal cilia, involved both in cell locomotion and feeding, beat stronger backward and in a better coordination than the somatic cilia.² However, the mechanism which allows neighboring cilia on the cell's surface to beat differently remains mysterious, as well as whether those two categories of cilia respond to the same stimuli.

A few recent experimental studies have nevertheless provided a new level of detail on the beating pattern and the swimming. Machemer²⁰ and Jung²¹ have measured the cilia beat frequency (CBF) on swimming cells and found that the value is homogeneous along the cell body. Jung et al. report that the different cilia have distinct behavior in response to an increase in viscosity of the surrounding fluid.²¹

Here we perform detailed quantitative measurements of the cell swimming and its relation with the ciliary beating on five populations of cells: one control strain and four RNAi silenced strains, where the silenced genes are associated with cilia functions or ciliopathies that occur in humans. Two of the silenced genes encode proteins that participate in the cilia structure itself, while the other two affect the anchoring of the cilia to the cell base. We use high-speed video recordings (2000 frames per second) of the cells as they swim in the semi-confined environment of a microfluidic channel which limits their movement to a two-dimensional plane. Image analysis is then used to obtain the cell velocity as well as the movement of the cilia, in the moving reference frame, along the edge of the cell. This then allows us to reconstruct graphically the metachronal waves and to obtain the CBF at every location of the cell and to explore their relation in the different cell populations. The introduced method could further be used for other species of microswimmers and provides an interesting approach to study ciliary beating anomalies in ciliopathies.

Material and method

Strains and culture conditions

Wild-type cells of stock d4-2 are a derivative of the wild-type stock 51 of Paramecium tetraurelia.²² Cells were grown at 27 °C in a buffered infusion of wheat grass powder BHB (l'Arbre de vie, Luçay le Male, France), supplemented with 0.4 μg mL⁻¹ β-sitosterol and inoculated with nonpathogenic Klebsiella pneumoniae. At least 1 hour before analysis the cells were concentrated and transferred to Dryl's solution (1 mM NaH₂PO₄, 1 mM Na₂HPO₄, 2 mM Na₃ citrate, 1.5 mM CaCl₂, pH 6.8).

Gene silencing in Paramecium tetraurelia

The genes to be silenced were individually cloned between two T7 promoters in the L4440 feeding vector modified with the Gateway® vector conversion system (Invitrogen, 11828-029). These constructs were used for transformation of a RNase III–deficient strain of Escherichia coli with an IPTG-inducible T7 polymerase, HT115 (DE3). RNAi was induced as previously described.²³ Briefly, paramecia were cultured in double-stranded RNA-expressing bacteria and sub-cloned daily whilst maintained at a cell density of 20 paramecia per ml. Phenotypes were screened every 24 h. Control cells were grown under the same conditions with HT115 bacteria carrying an empty plasmid. The efficiency of the RNAi was ascertained by phenotypic inference of more than 80%. Genes identification numbers in Paramecium are as follows: DPCD (GSPATT00031641001), MKS1 (GSPATT00011904001), Striatin 6 (St6) (GSPATT00036966001 and GSPATT00034214001), Tubuline new16 (T16) (GSPATT00024605001).

Microwell experiments

Cell tracking control experiments (Fig. 1) were realized with paramecia freely swimming in 0.2 ml in depression slides maintained at a temperature between 20 and 25 °C recorded with a DS-2MBW CCD camera (Nikon) and Nikon NIS-Elements V3 software mounted on a Eclipse Ti microscope (Nikon) equipped with a 2× objective, NA 0.06 WD 7.5 Plan UW and a 0.7× DXM auxiliary lens. Video sequences were processed at 2 frames per s with the freely available software ImageJ (W. Rasband, NIH, http://rsb.info.nih.gov/ij/) and the plugin Manual_Tracking (Fabrice.Cordelieres@curie.u-psud.fr). The graph shows swimming velocity as means ± SE of control (n = 20) and St6, MKS1, T16 and DPCD silenced cells (n = 20) (*P < 0.0001, unpaired Student's t-test). Swimming tracks (6–9 points/track) show the regular swimming pattern of control cells whereas silenced cells show slower and disorganized swimming paths. Scale bars: 0.5 mm.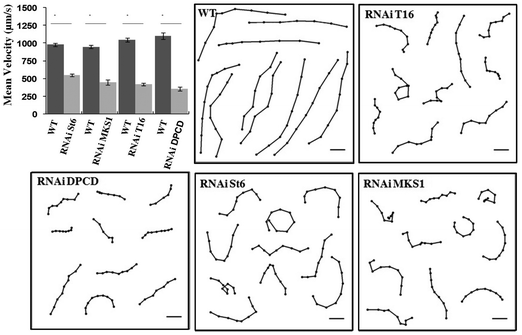

Fig. 1 Mean velocity plot (mean ± SE) and swimming tracks of control (WT) and RNAi silenced cells swimming freely in depression slides.

Microfluidic device fabrication

The swimming of Paramecium cells was observed in microfluidic channels which were fabricated using dry-film soft lithography techniques. First a photo-resist layer, of a thickness of 50 μm, was deposited on a glass slide using an office laminator (PEAK Photo laminator PS320) at a roller temperature of 100 °C. The microchannel shape was then produced by exposing the film to UV-light (Hamamatsu L9588) through a photomask. The channel structure was then developed by immersion in an aqueous bath of 1% potassium chloride by mass. Poly-dimethyl siloxane (PDMS) was then poured over the master and cured for 2 h at 70 °C. Afterwards, the PDMS-channels were cut out and bonded to a thin microscope cover slip (Menzel Glaeser, 24 × 50 mm) by exposing both surface to an oxygen plasma (Harrick Scientific) for 1 min.

Experimental set-up and method

The experimental set-up for observing the swimming of Paramecium in microchannels consisted of a controllable syringe pump (Cetoni neMESYS), an inverted microscope (Nikon TE200) and a high-speed camera (Photron 1024PCI). The suspension containing the cells was transferred into a glass syringe, after a centrifugation step to concentrate the cells, and subsequently injected inside the PDMS-channels in short bursts (flow rate 5 μL min⁻¹ during 30 to 60 s). The injected Paramecium cells were acclimated for 2–5 min before starting the imaging in the channel at 2000 frames per second (FPS) through a 60× (1.4 NA) objective. We recorded and analyzed forward swimming cells, exclusively. The image was focused at the periphery of the cell, near the center plane of the microchannel. The video sequences consisted of 200 to 400 images at 1024 × 512 pixel resolution. The resolution of the image was 3.6 pixels per micron.

Cell tracking protocol and image analysis inside a microchannel

A cell tracking code was developed in order to perform all of the image analysis in the reference frame of the swimming cell. The tracking tool, which uses the CR-toolbox for Matlab (http://https://sites.google.com/site/crtoolbox/), allows the region of the cilia to be isolated from the image for its subsequent analysis. The user manually identifies, on the first image of the sequence, the cell border and the area corresponding to the cilia video. This area is highlighted in green in Fig. 2A while the cell is highlighted in blue. The algorithm then tracks a set of features on the cell on successive images, thus yielding the center of mass and orientation of the cell as a function of time.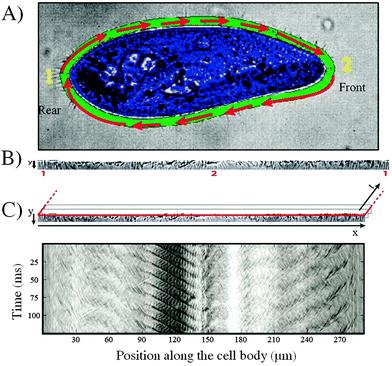

Fig. 2 Cell tracking and extraction of image sequences obtained from a Paramecium cell swimming in a microchannel. (A) Definition of the border (green) and cell area (blue) for the tracking of a swimming cell (1. indicates the rear of the cell; 2. indicates the front of the cell). (B) Extracted and unfolded image sequence of the ciliary motion (Movie S1 provided in ESI†). (C) Extraction of the space-time diagram, 1. Red line indicates the selected resliced plane for the image sequence. 2. Space-time diagram constructed for a resliced plane at position y = 0.

The region corresponding to the cilia on each image is then unfolded into a rectangle and a stack is made of the individual images, yielding a video of the ciliary beating in Cartesian coordinates, in the reference frame of the swimming cell (Fig. 2B). A sample movie of the cilia image sequence is provided with the ESI† (see Movie S1). Finally, a space-time diagram (chronograph) of the ciliary movement is produced by selecting a horizontal line on the cilia video and plotting the gray scale along this line as a function of time, as shown in Fig. 2C. In all of the chronographs, the left hand side corresponds to rear of the cell (region labeled 1 on Fig. 2A). Increasing x corresponds to going around the cell in a clockwise fashion, with the front of the cell (region labeled 2 on Fig. 2A) appearing near the middle of the plot. In this particular example, the front of the cell corresponds to a position x = 140 μm. Moving further in x then covers the bottom part of the cell, before closing the loop at the right hand side of the graph. For all of the data presented here, the space-time diagram is obtained one pixel away from the cell border. This ensures that the number of pixels is preserved between the original image and the rectangular mapping, while also increasing the signal to noise ratio.

The cell velocity was determined by numerically differentiating the coordinates obtained from the tracking tool. The typical size of the cell was taken as its perimeter, measured as the length of the spatial vector on the space-time diagram (Fig. 2C).

Ciliary beat frequency (CBF) and wave velocity

The space-time diagram was then used to obtain the ciliary beat frequency (CBF) and the direction and speed of the metachronal waves along the Paramecium. The CBF was calculated at each position along the cell's body by performing an auto-correlation of the gray values along a column of the chronograph. This method provided highly resolved measurements in space of the CBF along the cell. A quantitative measure of the metachronal wave speed proved to be more difficult. Due to their low speed, only a few waves (typically 3–10) were observed over the course of an experiment, which was insufficient to determine variations in wave speed between different cells. Therefore wave speeds were estimated by simply observing the local slope on the space-time diagram.

Statistics

For velocity data, means are expressed in standard error of the mean (mean ± SE). For CBF data, means are expressed in standard deviation of the mean (mean ± SD).

Results and discussion

Experimental observations: cell shape and velocity

The goal of our experiments is to compare the ciliary beating of steady-state swimming cells, either control paramecia or cilia-related mutants. Thus, the first part of our work is aimed at defining swimming patterns and cell morphology of control versus cilia-related knock-down cells in our micro-channels.

(a) Control strain. Fifty-six control cells were observed and their motion analyzed in our experiments. Control paramecia in the microchannels display a characteristic elongated oval shape, and a straight, fast swimming behavior without adherence to the channel walls (Fig. 3A, Movie S2, ESI†). Rotations around the major cell axis, commonly observed for Paramecium swimming in an unconstrained volume³ were inhibited by using channels of 50 μm depths. Nevertheless, the confinement did not seem to affect the swimming behavior and our values of the velocities are in good agreement with the literature: the mean cell velocity was 784 ± 31 μm s⁻¹ with a maximum velocity of 1376 μm s⁻¹.² Minimum velocities in the range of 50 to 100 μm s⁻¹ were associated with “young” cells, just issued from cell division, which have not reached their full body length or ciliature (see Movie S3, ESI†).

Fig. 3 Shape and swimming velocity of control and knock-down Paramecium cells in straight microchannels of 50 μm depth and 100 μm widths. Experimental observation of the shape for (A) control, (B) St6 RNAi, (C) T16 RNAi, (D) MKS1 RNAi and (E) DPCD RNAi cells. The red arrow is indicating the swimming direction in the channels. (F) Table of the respective cells dimensions as means ± SD. For the determination of the length and width, the Paramecium cell was modeled as an ellipse. (G) The bar plot shows the swimming velocity as means ± SE of control (n = 56), St6 (n = 18), MKS1 (n = 15), T16 (n = 20) and DPCD (n = 13) silenced cells.

(b) Mutants (gene silenced cells). Our method of ciliary beating analysis was then applied to various RNAi-induced knock down mutants of Paramecium impaired in cilia-related genes and whose swimming behavior was noticeably altered in cell tracking experiments in microwells (see Fig. 1).

Four genes have been selected of which two are involved in ciliopathies (DPCD and MKS1) and two (St6 and T16) are structural proteins associated with cilia or their anchoring structures, the basal bodies.

• DPCD (for “deleted in primary ciliary diskynesia”) deletion was shown to induce primary ciliary dyskinesia (PCD) in knockout mice, as a result of impaired organization of axonemal dyneins.^24,25 In Paramecium two homologous genes encode DPCD proteins which share 43% identity with their human counterpart.

• Mutations in MKS1 are causing Meckel Gruber syndrome, a severe ciliopathy which affects the development and homeostasis of several organs such as the central nervous system, kidneys, liver, or the skeleton. MKS1 has been shown to be associated with sensory signaling function of cilia and is essential for the cilium stability.²⁶

• St6 is one component of the striated rootlets which anchor the basal body to the intracellular side of the cortex and extend over the cell cortex along the basal body rows. A multigenic family encodes the several striated rootlet proteins that we have analyzed by mass spectrometry. We have ascertained by the synthesis of an antibody that St6 belongs to the striated rootlets and shown that St6 RNAi impairs their assembly.

• T16 is a non conventional Paramecium tubulin. Paramecium possesses a complex multigenic tubulin family with some highly divergent members which form a phyletic branch, distinct from the α, β, γ, δ and ε tubulins. Our analysis of the role of these tubulins has revealed a strong phenotypic effect on cell swimming whilst an anti-peptide antibody directed against the T16 protein labels the cilia tip, suggesting that this tubulin participates in the cilia microtubule shaft.

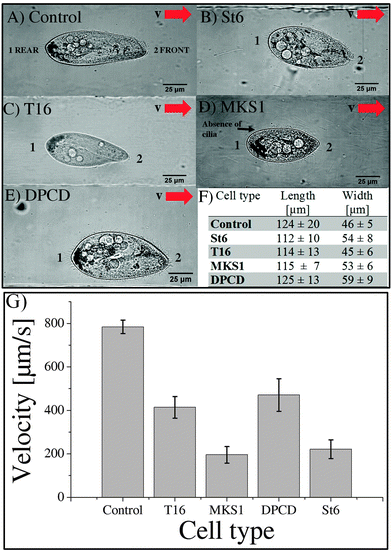
Eighteen St6, twenty T16, fifteen MKS1 and thirteen DPCD knock-down mutants were analyzed for their swimming behavior and ciliary beating in the microchannels. The phenotype of the control and all investigated mutants as well as the mean cell velocities are shown in Fig. 3.

The images in Fig. 3A–E are representatives of control and each knock-down cell type investigated during swimming in a microchannel. The mean swimming velocity for all cell types, extracted from cell tracking as described in materials and methods, are shown in Fig. 3G. The average length and width of the different cell types are listed in Fig. 3F. While the length of RNAi cells is comparable to control (less than 10% variation for St6, T16 and MKS1), their width displays larger variations, up to a 28% increase in the case of DPCD cells. However, these shape differences do not correlate with swimming velocities, as further highlighted by the examination of cell shape variation for each cell type (see S4 in ESI†).

The T16 phenotype which displays a similar shape as the control cell (Fig. 3A, C, F) has a swimming velocity reduced by 43% (see Movie S5, ESI†) with an average velocity of 413 ± 50 μm s⁻¹ and a maximum velocity of 789 μm s⁻¹.

The DPCD phenotype appeared to be much “fatter” compared to all other cell types (Fig. 3A, E, F). It showed no loss in cilia but a reduced swimming velocity of 471 ± 75 μm s⁻¹ with variability including some cells swimming at a maximum velocity of 1060 μm s⁻¹ (see Movie S6, ESI†). The most affected DPCD cells displayed impaired straight forward swimming patterns but conserved their avoiding reactions when meeting the channel wall.

The swimming velocity was most affected in the MKS1 and St6 knock-down cells with a decrease of more than 70% as compared to the average velocity of control cells. The phenotype of the St6 cells (Fig. 3B) led to a strong reduction of swimming velocity with an average value of 221 ± 43 μm s⁻¹ and a maximum velocity of 644 μm s⁻¹ (see Movie S7, ESI†). Some St6 mutants showed partly inactive cilia resulting in insufficient beating as well as an affinity to stick to the channel walls. This resulted in a staggered swimming behavior.

Similar to the St6, the MKS1 phenotype (Fig. 3D) resulted in abnormal ciliary beating patterns, with cilia being immotile or beating weakly. Furthermore, some MKS1 cells showed partial lack of cilia. This phenotype resulted in the loss of the straight forward swimming and an increased drifting of the cells (see Movie S8, ESI†). We determined a strongly reduced average swimming velocity of 196 ± 38 μm s⁻¹ with a maximum velocity of 410 μm s⁻¹. Interestingly, experiments realized in maze-like microchannels revealed that MKS1 cells have lost their mechano-sensation, evidenced by the inability of those cells to change direction when knocking into the channel walls (see Movies S9 MKS1 and S10 control in ESI†).

In conclusion, all the mutants examined display a significant reduction in swimming velocity which appears to be independent of their shape (see S11, ESI†). The most affected cells are St6 and MKS1 mutants.

CBF & metachronal wave propagation

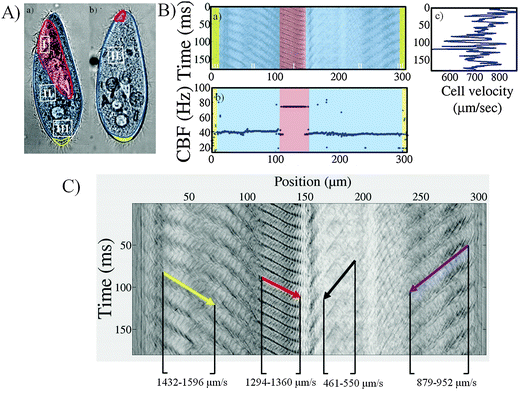
We now turn to the detailed analysis of the high-speed videos to visualize ciliary motion in space and time and extract the CBF and wave speed. We describe the results for the control strain before comparing this behavior with that of the mutant populations. Here, we measured two main ciliary beating frequencies; the body CBF which indicates the somatic cilia on the body surface and the mouth CBF which indicates the peristomal cilia. The cilia of the gullet are located inside the mouth and were not measured in our experiments.

(a) Control strain

Fig. 4 displays the three populations of cilia on a Paramecium control cell image (Fig. 4A). A typical space-time diagram and the corresponding CBF and velocity plot of a control cell are shown in Fig. 4B. The wave pattern and the slope, which corresponds to the wave velocity, are highlighted in Fig. 4C. The abscissa of the space-time diagram corresponds to the distance on the cell's periphery, starting at the middle of the cell's rear. The colored region on the space-time diagram (Fig. 4Ba) indicates the characteristic cilia organization on the Paramecium cortex, corresponding to the illustration on Fig. 4A.

Fig. 4 Extracted space-time diagram and CBF values from the cell body and mouth region (A) microscope images of a Paramecium cell in front (a) and back (b) view. The colors highlight the different cilia organization with the mouth/peristomal region (I) (in red) where cilia are paired, a mixed zone (in blue) of single and paired cilia on the body surface (II) and the cell's rear (in yellow) where cilia are single including a dozen of non-beating longer cilia (III). (B) Space-time diagram of a control cell where corresponding regions of the cell are in the same colors (a), CBF as a function of position along the cell perimeter (frequency plot) (b) and cell velocity as a function of time (c). (C) Space-time diagram where the direction of metachronal wave propagation has been indicated by arrows. The slopes, which correspond to the wave velocities, are displayed at selected regions.

The distribution of the CBF on this cell is plotted in Fig. 4Bb. Two frequencies can be distinguished on this cell: F₁ = 39 Hz, across large regions of the cell, and F₂ = 77 Hz corresponding to the mouth region, where the beating serves for cell feeding. We confirmed this in our experiments using tracer particles (1 μm polystyrene spheres) which regularly flow towards the oral groove (see movie S12, ESI†). This discrepancy in frequencies between the cell body and mouth region was observed for almost all control cells, yielding mean CBF values of 35 ± 4 Hz for the cell cortex and 66 ± 8 Hz for the mouth region. The minority of cells which escaped this rule were tracked while facing with their back to the video, thus masking the mouth waves and preventing the measurement of the mouth CBF.

The mouth CBF was generally observed to be nearly twice the cell body CBF. The fact that the frequency was not exactly twice however implies that it is not simply a harmonic of the CBF. Rather, it likely results from the specific organization of the peristomal cilia (see also ref. 27), which are paired in each cortical unit. In contrast with the mouth region where the CBF is very regular, the rear of the cell (x > 290 μm and x < 20 μm on Fig. 4Ba) is characterized by the presence of caudal cilia that are longer and that rotate without coordination. The CBF measurements in these areas appear as noise in the CBF plots.

The velocity trace of the cells was found to fluctuate even during a smooth swimming period, as shown in Fig. 4Bc where the instantaneous velocity of a control cell is plotted alongside the spatio-temporal diagram. We were not able to relate the velocity fluctuations to any variations in the ciliary activity. Instead, the typical time scale of the fluctuations, which can be estimated from Fig. 4Bc at around 10 ms, was consistent with the viscous diffusion time scale for Paramecium, as discussed by Hamel et al.²⁸

In Fig. 4C the wave's propagation has been indicated by arrows in the space-time diagram. The oblique patterns correspond to the waves that travel from the rear of the cell towards the front, i.e. from the edges of the graph towards the central region (at 150 μm in abscissa). This observation of antiplectic metachronal waves agrees with previous observations. The slope of the oblique lines corresponds to the wave speed, projected in the plane of observation. This value is not constant along the cell body. Instead we observe that the wave speed vary in the range of 1600 to 460 μm s⁻¹. In contrast, the peristomal wave displayed remarkable invariance, originating at the oral groove and travelling towards the tip of the cell, regardless of the cell's swimming direction or speed. The signature of this wave on the edge of the cell is observed in the range x = 100 to 140 μm on Fig. 4C. The features discussed here were observed on almost all control cells. However, although the wave velocities varied from cell to cell, it was not possible to find a correlation between the wave velocities and the cell swimming velocity.

(b) Mutants (gene silenced cells)

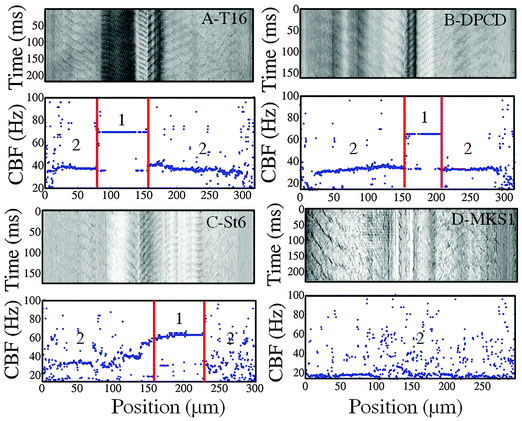
We turn now from the control to the knock-down cells which were analyzed in the same manner. The spatio-temporal measurements including the space-time diagrams and frequency plots were carried out for all cell types; a few representative examples are shown in Fig. 5.

Fig. 5 Space-time diagrams and corresponding ciliary beat frequency plots of T16 (A), DPCD (B), St6 (C) and MKS1 (D) knock-down cells. (1) CBF mouth location depends on the position of the mouth region during the CBF measurements. (2) CBF body location.

The space-time diagrams and frequency plots of T16 and DPCD knock-down cells (Fig. 5A and B) are similar to the ones obtained with control cells: they display distinctive CBF values for body and mouth regions with respective values either equivalent to the control cells for DPCD (34 ± 5 Hz; 66 ± 9 Hz) or slightly reduced for T16 (32 ± 6 Hz; 60 ± 8 Hz) silenced cells.

On the opposite, the space-time diagrams of most St6 and MKS1 cells are characterized by fuzzy CBF signals with strong fluctuation, restricted to the cell body region for St6 knock-down cells but affecting both body and mouth regions for MKS1 silenced cells (Fig. 5C and D). In contrast with the other cell types, the St6 silenced cells displayed some phenotypical variance that we interpreted as a variability of RNAi efficiency. Indeed, some cells retained two well defined frequencies over most of the cell body in addition to visible wave propagation while others displayed large regions with immotile cilia or cilia beating very slowly (see S13, ESI†). These regions of uncoordinated ciliary beating generated the noisy appearance of the space-time diagrams over the cell body region while the mouth region was not concerned by these uncoordinated beating patterns.

Moreover, the most affected St6 cells displayed a distorted morphology with the presence of a bulge near the mouth. This impaired the visualization of waves which appeared to travel transverse to the cell's major axis. As a result, the mouth waves appeared as standing waves on the space-time diagrams (see image S14, ESI†). However, although those distortions had a strong effect on the mouth wave propagation, they did not affect the CBF which displays a homogeneous reduction of 20% compared to the control cells, both for body and mouth regions (29 ± 5 Hz and 61 ± 7 Hz, respectively).

MKS1 silencing caused the strongest reduction in the CBF of the body region of approximately 30% with a mean value of 22 ± 6 Hz. A striking characteristic of those cells is the absence of ciliary motion and wave propagation in the mouth region although we did not note cilia loss in this region. However, like in St6 RNAi cells, the most affected MKS1 silenced cells displayed partial loss of cilia in the body region. Cells lacking too many cilia were excluded from the analysis, the corresponding diagrams being too noisy to extract a mean CBF value. Overall, MKS1 RNAi cells were characterized by a loss of synchrony of the ciliary beating illustrated by the absence of regular waves on the cell body and in even more remarkably in the peristomal region, as well as the very noisy space-time diagrams (demonstrated in the space-time diagram S15 in the ESI†).

Interestingly, although all the mutants are characterized by a low swimming velocity, their cilia beating dynamics is not affected in the same way. Surprisingly, knock-down of T16 and DPCD, which are core proteins of the axoneme and involved in structural stability does not significantly impact beating frequency. This has to be compared to another Paramecium mutant Bug 22²⁹ affected in cilia rigidity, shown to be strongly impacted in swimming velocity and cilia beating trajectory but beating frequency was not reduced. Thus, in these examples, it seems that beating frequency is more affected by mutations in proteins involved in cilia anchoring than in axonemal stability.

CBF vs. swimming velocity

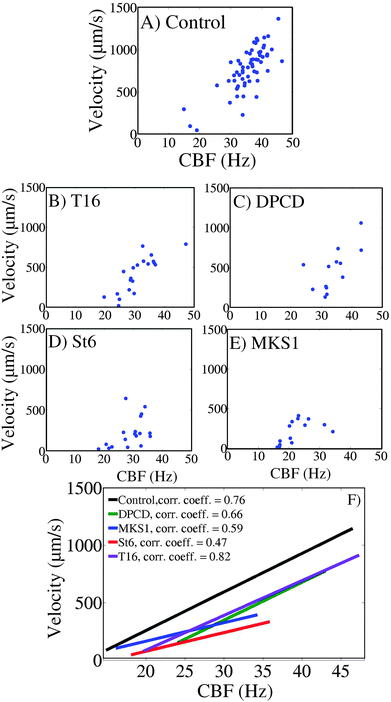
The relationships between CBF and swimming velocity were then explored as an appraisal of “ciliary beating efficiency”. In Fig. 6A–E for each cell type, the mean velocity of each individual cell has been plotted against the body CBF. The data reveal a good correlation between body CBF and cell velocity as confirmed by the linear regression illustrated in Fig. 6F. In the control cells, apart from a few cells which were almost immotile during the recording, swimming is characterized by values of CBF over 30 Hz (range between 15 and 47 Hz) and velocities between 500 and 1500 μm s⁻¹.

Fig. 6 Relation of swimming velocity and CBF. (A–E) Velocity-frequency plots for all investigated control, St6, DPCD, T16 and MKS1 RNAi cells. (F) Velocity versus CBF correlation plot for the body region. The plot represents the single fits for all the cell types. Black line: control cells. Green line: DPCD knock-down mutants. Blue line: MKS1 knock-down mutants. Red line: St6 knock-down mutants. Violet line: T16 knock-down mutants.

This also applies to the knock-down mutant DPCD where most cells swim with a CBF over 30 Hz (range of 22 to 42 Hz) with corresponding velocities between 500 and 1000 μm s⁻¹. T16 knock-down cells display a wider range of swimming patterns with half of the cells being slower (with a cell velocity below 500 μm s⁻¹) and corresponding CBF below 30 Hz. However, these two knock-down mutants display like the control cells a strong correlation between swimming velocity and body CBF, as attested by the curves in Fig. 6F. Accordingly, the curves for DPCD and T16 (Fig. 6F respectively violet and green lines), although shifted towards lower velocities, are almost parallel to the control cell's curve, showing that the same increase in CBF will produce the same progression in swimming velocity. This indicates a ciliary beating which is less efficient in terms of swimming in the DPCD and T16 than in control cells. However, the acceleration of the ciliary beating brings the same effect on swimming acceleration for the three cell types.

Contrasting with DPCD and T16, the MKS1 and St6 knock-down mutants are uniformly characterized by very low swimming velocities (below 500 μm s⁻¹). However, whereas MKS1 knock-down cells all display very low CBF values (below 30 Hz), St6 knock-down cells have a wider distribution of their CBF (values ranging mostly from 20 to 35 Hz), similar to the T16 RNAi mutant. The correlation coefficients calculated from the best linear regression curves obtained from these two strains (Fig. 6F respectively blue and red lines) have smaller values, indicating that the correlation between the cell velocity and CBF is not so strong. Furthermore, the change in the slope for these two RNAi mutants indicate that in addition to a bad cilia beating efficiency, their ability to accelerate in response to the increase of CBF is impaired. In the case of the St6 phenotype, an increase of CBF about 10 Hz resulted in a halved velocity change in comparison to the control (Fig. 6F St6 plot, 180 μm s⁻¹, and control plot, 360 μm s⁻¹). However, the correlation curve obtained for MKS1 knock-down cells must be treated with some caution since it is underlying a statistical uncertainty because of the partial deciliation induced by MKS1-RNAi. Thus, while most cells swim slowly due to slow CBF, the slow swimming velocity of the rare cells which have a CBF over 30 Hz could result from a lack of cilia rather than a low cilia beating efficiency. However, since it is not possible to evaluate the ciliary loss of each MKS1 RNAi cell, and that we know that ciliary instability is a characteristic of the MKS1 silencing, we decided to consider the whole MKS1 RNAi cell population and treat them all together.

Strikingly, the St6 knock-down cells are the ones which display the least efficient cilia beating among the five strains examined in this experiment, with a ratio of cell velocity against CBF which is the lowest over the whole CBF scale. In conclusion, the St6 knock-down mutant is characterized both by an inefficient ciliary beating and an inability to increase its speed concurrent with an increased beating frequency.

Note that the linear relationship between the swimming velocity and the CBF is an indication that the ciliary beating pattern is independent of the frequency for a given cell population. This is expected in the low Reynolds number regime, if the fluid-structure coupling with the cilia is weak. The slope of the velocity/CBF curves defines a length scale which is in the range of 10 to 35 μm, suggesting the presence of a characteristic length scale for each cell population. We verified this by measuring the spatial correlation coefficient C on each of the space-time diagrams (see e.g. plot S16, ESI†). These curves display a decrease to zero over a length scale comparable with the slope of the velocity/CBF curves. Indeed, a typical correlation length L_C is extracted from each measurement by looking for the distance at which C crosses the value of 0.1 (in order to reduce the sensitivity to the noise near C = 0). The values of L_C are plotted on Fig. 7, with respect to the corresponding slopes of the velocity/CBF curves (see Fig. 6F). They show a nearly linear relationship and confirm the presence of such a typical length within the spatial organization of the ciliary beating. While we expect that this length scale L_C is related to the observed wavelength of the metachronal waves, the current measurements do not allow us to clearly extract this information and more analysis is required to make a direct link between the lengths scales that interact.

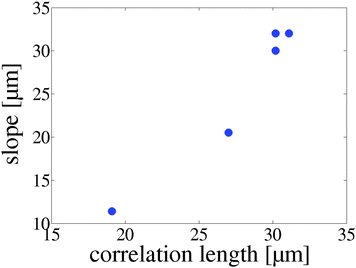Fig. 7 Slope–correlation length (L_C) plot where each dot represent a cell population. L_C was obtained using a spatial correlation function on each cell population (see plot S16, ESI†).

Finally, we emphasize that it is possible for Paramecium to beat its cilia at a finite frequency while remaining nearly stationary. This confirms visual observations that the different ciliary strokes are possible and that the cell can perform different ciliary movements than the standard power-stroke/recovery stroke. This implies in turn that the CBF, while strongly affecting the cell velocity, is not the only factor determining the swimming pattern and speed. As regards the mouth CBF, a similar plot displayed correlation with the swimming velocity except for St6 and MKS1, for which no correlation could be found (see plot S17, ESI†).

Summary and conclusion

We provide quantitative measurements of the ciliary beating of a freely swimming Paramecium. This is achieved by filming the cells at high-speed as they swim in a semi-confined microfluidic channel, which allows them to swim in a straight line without leaving the plane of focus of the microscope. By subtracting the measured cell velocity from the ciliary motion, we are able to obtain images that capture the beating in the moving reference frame. This provides us with a visualization of the metachronal waves along the cell body, which are indeed antiplectic. These waves however travel in and out of the plane of visualization, making it impossible to extract the real wave velocity; only its projection in the plane of observation is available. We were nevertheless not able to find any correlation between the wave velocity and the cell swimming velocity.

Conversely, precise measurements were possible for the ciliary beat frequency (CBF) at all locations on the cell periphery. The cells were found to display two distinct beat frequencies: one frequency along the cell body, showing a strong correlation with the swimming velocity, and another higher frequency emanating from the peristomal region which showed a correlation with the swimming velocity for certain cell types. Since this value is in conflict with previous measurements,²¹ we attempted to check if this higher frequency was an artifact, due to the doubling of the cilia in this region, but this does not appear to be the case from our videos. Instead, the effect may be attributed to the higher effort that is exerted by the doubled cilia which would then beat at a frequency nearly double the frequency elsewhere. This observation of a distinctive behavior of the peristomal cilia, intended to create a flux towards the gullet, supports the pioneering observations of Kuznicki et al.,³⁰ who noticed that those cilia beat independently of the other group of cilia and in a better coordination. This was recently confirmed by²¹ who demonstrated that the beating of those cilia, in contrast with the body cilia is insensitive to variations in viscosity, brushing up to date the questions of the control of the movement of neighboring groups of cilia in ciliated protozoa.³¹

Finally, the measurements were repeated on control cells and four different RNAi induced knock-down mutants. Those knock-down cells have been selected because their phenotype was characterized by a significant reduction in swimming velocity as revealed by cell tracking in microwells (Fig. 1). The reduced cell velocity was confirmed in the microfluidic channels for all knock down mutants although with distinctive characteristics. The mean velocity of control cells was lower in the channels (780 μm s⁻¹) than in the wells (1100 μm s⁻¹), suggesting that this could result from the confinement in the microchannels, as suggested by.³ However, although the slowdown in the microchannels of the St6 and MKS1 mutants, which are fatter than the control cells, agrees with this hypothesis, the increased velocity in microchannels of the DPCD mutant which has the largest width refutes it. We did not observe a clear correlation between the ratio cell width against channel diameter and cell velocity in our experiments. Nevertheless, it is likely that the spiraling parameter, which influences cell's velocity³ is affected differently in the various phenotypes, making it difficult to draw any conclusions about the drag effect of channel boundaries in our experiments. However, it highlights the advantages of microfluidic channels to compare mutants whose particular unconfined swimming behavior impedes precise comparative measurements of their swimming velocities.

This method also proved to be very valuable in the analysis of the impact of knock-down mutations on cilia beating and subsequent cell swimming behavior. Although all the knock-down mutants were characterized by a decreased cell velocity compared to control cells, two categories could be distinguished with T16 and DPCD cells in one part (with a reduction in mean velocity less than 50% compared to control cells), and St6 and MKS1 whose mean velocity is reduced by more than 70% compared to control cells. We also show that in our conditions, cell velocity variation is not attributable to differences in cell morphology.

Our analysis demonstrates that although the ciliary beating efficiency of all knock-down mutants is lower in terms of swimming velocity compared to control cells, as attested by the ratio cell velocity against CBF, their ability of increasing their swimming velocity according to the acceleration of ciliary beating is unchanged for DPCD and T16 cells and highly affected in MKS1 and furthermore for St6. This suggests that in addition of impairing individual cilia beating (such as beating shape, kinetics or strength), St6 and MKS1 knock-down affect the efficiency of collective cilia movement. This is further supported by our experiments which show distinctive space-time diagrams for the two knock-down mutants categories, from which consistent values of CBF were observed over the whole cell periphery in DPCD and T16 knock-down cells, whereas noisy graphs of MKS1 and St6 silenced cells attest of a lack of cilia beating coordination along the cell's surface. Interestingly, this analysis is pertinent when considering the nature of the knock-down mutants: DPCD and T16 are both structural proteins of the ciliary microtubule scaffold and therefore expected to influence a cilium's individual movement. On the other hand, MKS1 and St6 influence cilia anchoring on the cell surface: St6 being involved in kinetodesmal fibers which anchor the basal body in the Paramecium cortex, and MKS1, localized at the transition zone between basal body and cilium's core, is essential for cilium stability.³² Our work thus provides experimental evidence for the respective contribution of cilium structure and anchoring on cilia movement and synchronization, as previously analyzed in theoretical models.¹²

In conclusion, our results contribute to understanding the movements of micro-swimmers but can also contribute to the characterization of the defects involved in ciliary diseases, which are still often restricted to the characterization of the structural defects of cilia.³³ Our analysis suggests that the coordination of the ciliary beating should be considered as a major factor in the etiology of ciliary dyskynesia and highlights the benefit of the use of ciliated protozoa like Paramecium for which sophisticated genetic tools enables to phenocopy mutation involved in ciliary diseases.

Acknowledgements

The project was generously supported by the Pole de Recherche et Enseignement Supérieur PRES UniverSud as well as partially supported by the grant from Genopole: program ATIGE and from the ANR: project 06-PCVI-0029. The authors gratefully thank Chris Bertram, Fulvio Martinelli and Sebastien Michelin for helpful advice on the ciliary beating measurements and analysis.

References

1. E. Lauga and T. R. Powers, The hydrodynamics of swimming microorganisms, Rep. Prog. Phys., 2009, 72, 096601.
2. S. Dryl, Behavior and Motor response of Paramecium, in Paramecium, A current survey, ed. W. J. V. Wagtendonk, Elsevier, Amsterdam, London, New York, 1974.
3. S. Jana and S. Jung, Paramecium swimming in capillary tube, Phys. Fluids, 2012, 24, 041901.
4. W. Supatto and J. Vermot, From cilia hydrodynamics to zebrafish embryonic development, Curr. Top. Dev. Biol., 2011, 95, 33–66.
5. Z. Mirzadeh, et al., Cilia organize ependymal planar polarity, J. Neurosci., 2010, 30(7), 2600–2610.
6. D. Babu and S. Roy, Left-right asymmetry: cilia stir up new surprises in the node, Open Biol., 2013, 3(5), 130052.
7. M. W. Leigh, et al., Clinical and genetic aspects of primary ciliary dyskinesia/Kartagener syndrome, Genet. Med., 2009, 11(7), 473–487.
8. L. Vincensini, T. Blisnick and P. Bastin, 1001 model organisms to study cilia and flagella, Biol. Cell., 2011, 103(3), 109–130.
9. W. J. Yi, et al., Directional disorder of ciliary metachronal waves using two-dimensional correlation map, IEEE Trans. Biomed. Eng., 2002, 49(3), 269–273.
10. S. Gueron, et al., Cilia internal mechanism and metachronal coordination as the result of hydrodynamical coupling, Proc. Natl. Acad. Sci. U. S. A., 1997, 94(12), 6001–6006.
11. S. Michelin and E. Lauga, Phoretic self-propulsion at finite Péclet numbers, J. Fluid Mech., 2014, 747, 572–604.
12. J. Elgeti and G. Gompper, Emergence of metachronal waves in cilia arrays, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(12), 4470–4475.
13. N. Osterman and A. Vilfan, Finding the ciliary beating pattern with optimal efficiency, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(38), 15727–15732.
14. D. R. Brumley, et al., Hydrodynamic synchronization and metachronal waves on the surface of the colonial alga Volvox carteri, Phys. Rev. Lett., 2012, 109(26), 268102.
15. M. Polin, et al., Chlamydomonas swims with two “gears” in a eukaryotic version of run-and-tumble locomotion, Science, 2009, 325(5939), 487–490.
16. J. S. Guasto, K. A. Johnson and J. P. Gollub, Oscillatory flows induced by microorganisms swimming in two dimensions, Phys. Rev. Lett., 2010, 105(16), 168102.
17. K. Drescher, et al., Direct measurement of the flow field around swimming microorganisms, Phys. Rev. Lett., 2010, 105(16), 168101.
18. H. Machemer, Ciliary activity and metachronism in Protozoa, in Cilia and Flagella, ed. M. A. Sleigh, Academic Press, London, New York, 1974.
19. C. Kung, et al., In vivo Paramecium mutants show that calmodulin orchestrates membrane responses to stimuli, Cell Calcium, 1992, 13(6–7), 413–425.
20. H. Machemer, Ciliary activity and the origin of metachrony in Paramecium: effects of increased viscosity, J. Exp. Biol., 1972, 57(1), 239–259.
21. I. Jung, T. R. Powers and J. M. Valles, Jr., Evidence for two extremes of ciliary motor response in a single swimming microorganism, Biophys. J., 2014, 106(1), 106–113.
22. T. M. Sonneborn, Methods in Paramecium research, in Methods in Cell Physiology, ed. D. M. Prescott, Academic Press, New York, 1979, pp. 241–339.
23. P. Dupuis-Williams, et al., Functional role of epsilon-tubulin in the assembly of the centriolar microtubule scaffold, J. Cell Biol., 2002, 158(7), 1183–1193.
24. Y. Kobayashi, et al., Hydrocephalus, situs inversus, chronic sinusitis, and male infertility in DNA polymerase lambda-deficient mice: possible implication for the pathogenesis of immotile cilia syndrome, Mol. Cell. Biol., 2002, 22(8), 2769–2776.
25. M. Zariwala, et al., Investigation of the possible role of a novel gene, DPCD, in primary ciliary dyskinesia, Am. J. Respir. Cell Mol. Biol., 2004, 30(4), 428–434.
26. A. R. Barker, R. Thomas and H. R. Dawe, Meckel-Gruber syndrome and the role of primary cilia in kidney, skeleton, and central nervous system development, Organogenesis, 2014, 10(1), 96–107.
27. F. Iftode and A. Fleury-Aubusson, Structural inheritance in Paramecium: ultrastructural evidence for basal body and associated rootlets polarity transmission through binary fission, Biol. Cell., 2003, 95(1), 39–51.
28. A. Hamel, et al., Transitions between three swimming gaits in Paramecium escape, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(18), 7290–7295.
29. C. Laligne, et al., Bug22p, a conserved centrosomal/ciliary protein also present in higher plants, is required for an effective ciliary stroke in Paramecium, Eukaryotic Cell, 2010, 9(4), 645–655.
30. L. Kuznicki, T. L. Jahn and J. R. Fonseca, Ciliary activity of Paramecium micronucleatum. I. Evolution of techniques II. Body cilia III. Oral groove and cytopharynx IV. Metachrony, Proc. 3rd Int. Conf. Protozool., Progress in Protozoology, 1969.
31. B. Parducz, On the nature of metachronal ciliary control in Paramecium, J. Protozool., 1962, 9, 27.
32. F. R. Garcia-Gonzalo, et al., A transition zone complex regulates mammalian ciliogenesis and ciliary membrane composition, Nat. Genet., 2011, 43(8), 776–784.
33. W. A. Stannard, et al., Diagnostic Testing of Patients Suspected of Primary Ciliary Dyskinesia, Am. J. Respir. Crit. Care Med., 2010, 181(4), 307–314.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ib00181h

---