Epidermal homeostasis and radiation responses in a multiscale tissue modeling framework

Abstract

The surface of the skin is lined with several thin layers of epithelial cells that are maintained throughout a lifetime by a small population of stem cells. High dose radiation exposures could injure and deplete the underlying proliferative cells and induce cutaneous radiation syndrome. In this work we propose a multiscale computational model for skin epidermal dynamics that links phenomena occurring at the subcellular, cellular, and tissue levels of organization, to simulate the experimental data of the radiation response of swine epidermis, which is very similar to human epidermis. Incorporating experimentally measured histological and cell kinetic parameters, we obtain results of population kinetics and proliferation indices comparable to observations in unirradiated and acutely irradiated swine experiments. At the sub-cellular level, several recently published Wnt signaling controlled cell-cycle models are applied and the roles of key components and parameters are analyzed. This integrated model allows us to test the validity of several basic biological rules at the cellular level and sub-cellular mechanisms by qualitatively comparing simulation results with published research, and enhances our understanding of the pathophysiological effects of ionizing radiation on the skin.

---

Insight, innovation, integration

A cell-based, multiscale tissue model simulates the cellular dynamics of epidermal renewal, radiation injury and healing of skin tissue. This work highlights the importance of considering proliferation kinetics as well as the spatial organization of tissues when conducting in vivo investigations of radiation responses.

Introduction

The skin epidermis is the outermost surface of the body that functions as a barrier to protect animals from dehydration, mechanical stress, and infections. It undergoes a constant turnover through continuous self-renewal and differentiation of a small population of epidermal stem cells.¹ These underlying proliferative cells of the skin are sensitive to radiation and could be injured and even depleted by high dose exposures. Radiation damage to the skin includes erythema, pigmentation, dry and moist desquamation in the early phase (<4 weeks), and atrophy and fibrosis (or necrosis) in the later phase (>6 weeks).² The ED₁₀ (a dose in which 10% of a population receives the effect) has been estimated to be 4 Gy for erythema and 14 Gy for the more serious moist desquamation.^3,4 However, how these values vary with the dose-rate or possible dose fractionation scheme, and different qualities of radiation (protons, neutrons, and heavy ions) has not been studied extensively. Of interest are skin damage from new cancer therapy modalities including hyper-fractionation and Hadron therapy with protons and carbon beams, exposure to dirty-bombs or hot particles, and exposures to astronauts from solar particle events.

Most of our knowledge of the mechanisms responsible for the development of radiation-induced damage to the skin and underlining tissues are derived from extensive studies in animals spanning the past several decades. Of the available laboratory species, the swine is regarded as the best animal model as its skin bears many characteristics similar to human skin.⁵ For example, the dimensions of epidermis and dermis are approximately the same in the young swine and adult human;⁶ the swine skin and human skin have a similar histological appearance;^7,8 the structural organization of the epidermis in the young swine, at the microscopic level, is similar to that in adult humans.⁹ In addition, the population kinetics, the density of the basal cells, and cell-cycle parameters in swine epidermis are comparable to those in the human epidermis.^5,10 All these similarities between the two species comprise the impetus in biomedical research with particular attention to swine skin in radiobiological studies.^11–20

To be applicable for radiation protection in humans, the observations in animal studies have to be extrapolated to humans. Mathematical modeling is an essential step to bridge the gaps in the investigations of different species. In addition, bio-mathematical modeling provides a powerful tool to handle the complexities of biological systems governed by sophisticated regulatory processes. It allows connecting experimental results to fundamental biological principles and the opportunity to explore the roles of a single parameter in a complex biological system, which can lead to new and more informative experiments.²¹ This approach has become an increasingly large field of study in recent years. Bio-mathematical models range from simple ones in which cellular automata are coupled with reaction–diffusion equations for oxygen and glucose that act on a macroscale,^22,23 to more complex models that incorporate blood flow, vascular remodeling^24,25 and details of subcellular processes such as the cell cycle and protein expression.^26,27 The frameworks for running simulations of such models are large and complex. As a result, several collaborative software projects such as CompuCell3D²⁸ and Chaste (cancer, heart and soft-tissue environment)²⁹ have been developed to tackle such problems. In this paper, we describe a multiscale skin epidermis model based on Chaste,²⁹ and how we modified to simulate the skin epidermal homeostasis and various responses after acute radiation exposure previously investigated in swine experiments.

The remainder of this paper is organized as follows. In the next section, after a brief description of the characteristics of the structure of skin epidermal epithelium and the functions of the various types of cellular compositions for maintaining epidermal homeostasis, a multiscale tissue model for swine epidermis under normal conditions and after acute irradiation is introduced, with the rationale to determine the control parameters based on experimental studies. In this work we do not distinguish epidermal stem cells from transit amplifying cells in the proliferative layers of the epidermis. Such a distinction can be made in future work. In the Results section, the model is used to carry out simulations, by comparison with experimental data in previous swine skin studies under normal conditions and after acute exposure. The reproduction rates vs. mitotic index, and the cellular counts vs. the incidence of moist desquamation are also discussed. The advantages and limitations of our approach and the directions of future research are summarized in the final section.

Methods

Epidermis of the skin

The epidermis of the skin is separated from the underlying dermis by a basement membrane (BM) that is rich in extracellular matrix and tyrosine kinase growth factors, which provide stimuli to the innermost basal layer of the epidermis to proliferate and maintain the overall cellular population of the epidermis.³⁰ This is accomplished by a small amount of epidermal stem cells, which can both self-renew over lifelong periods, and differentiate progressively upward to generate multiple suprabasal layers. The first generation of daughter cells (transit amplifying cells) can divide several times, expanding either along the BM plane to occupy the basal layer, or upward to detach from the BM. The non-divisible cells (also called prickle cells) after this phase go to the spinous and granular layers, which remain transcriptionally active. Spinous cells synthesize an extensive network of keratin filaments interconnected to desmosomes to generate an integrated mechanical infrastructure in the differentiating layers, while granular cells produce lipid-rich lamellar granules. Granular cells also make lysine- and glutamine-rich proteins that become irreversibly cross-linked by transglutaminase to form the cornified envelope. As granular cells transit to the stratum corneum, all metabolic activity ceases, cytoplasmic organelles are lost, and the cornified envelope serves as a scaffold for lipid bilayers that are extruded to make the epidermal barrier at the skin surface.^31,32

Though the epidermis of all regions is formed with this type of stratified structure, its thickness varies considerably with body site. In addition, the basal layer of the human epidermis is not ideally flat but shows a varying degree of undulation—with ridges or pegs (rete pegs) extending into the dermis. Therefore the distribution of proliferating cells in different regions of the epidermis is not the same. In addition, it has been established that cell division in the human epidermis is not exclusively confined to the basal layer. A single pulse injection of [3H]thymidine into the human skin suggests that about 32% of labeled nuclei are in the suprabasal layers.³³ This feature significantly differs from species with thin epidermis such as that of the common laboratory rodents, in which no suprabasal cells have the capability of proliferation.³⁴ The pig and the primate, which have a thick epidermis, nevertheless show similar results to humans of a multilayer of proliferative cells in the epidermis.^7,35 That is one of the reasons that swine skin is regarded as the closest model for human skin, especially in the radiation response studies.^17–20,36

Multiscale tissue model

With the versatile tools of Chaste,²⁹ we modeled a patch of interfollicular epidermis as a two-dimensional rectangular surface with periodic boundary conditions on the left and right sides (for details see ref. 37). For all simulations, the initial height of the patch is set to 6 cell diameters, where we estimate that a cell diameter is approximately 8 μm.³⁸ The 6 layers represent one basal layer at the bottom, and five suprabasal layers of other viable cells of the epidermis. If a non-dividing cell stays in the population exceeding a pre-defined time (312 hours in our model), it is assumed to enter the stratum corneum, and is no longer monitored in the modeling system.

The key component of this multiscale epidermal model is a lattice-free, cell-centre model developed by Meineke et al.³⁹ and extended by van Leeuwen et al.³⁷ In this model each cell is represented by a discrete point and adjacent cell centers are connected by linear springs with defined mechanical properties. Neighboring cells are determined by a Delaunay triangulation to avoid extremely small angles that may form for a cell relative to two neighboring cells, in keeping with the physical tendency of cells to avoid compaction stresses otherwise encountered, while cell shapes are determined by an associated Voronoi tessellation, which is a means to define cell boundaries given the cell centers as just defined, by drawing the set of all line segments formed by the set of all points in the plane equidistant between the two nearest cell centers. This has the effect of making cell sizes more or less uniform and avoiding instant, far-reaching changes in cell arrangement when new cells insert within a filled lattice.³⁹

The equations of motion are developed by neglecting inertial effects and balancing the viscous drag on cell centers with cell–cell interaction forces associated with the compression and extension of the springs. The equations of motion are

where r_i is the position of cell centre i, n is the total number of cells, s_ij(t) and k_ij are the natural length and strength, respectively, of the spring connecting cell centers i and j, S_i is the set of cells that are adjacent to cell i, μ_i is the drag coefficient, which depends on cell i type, and t is the time. The drag term models cell-stroma adhesion.

When cell i divides, its daughter cell j is placed a distance 0.1 cell diameters from cell i, in a randomly chosen direction. To model cell growth during the M phase, the rest length of the spring connecting the parent and daughter cells, s_ij(t), increases from 0.1 to 1 during the last hour of the cell cycle; s_ij(t) = 1 for all other connections.

Wnt signaling cell-cycle models

Extensive experimental evidence demonstrates that Wnt signaling plays a central role in regulating the proliferation, differentiation and motility of skin cells during their morphogenesis.^1,40–42 In particular, it has been proposed that a spatial gradient of extracellular Wnt factors along the vertical axis determines position-dependent rates of cell proliferation, differentiation and death.⁴³ The Wnt signaling pathway involves a set of extracellular Wnt factors which can bind to specific receptors on the cell membrane. The binding triggers a cascade of intracellular reactions, leading eventually to the inhibition of a protein complex containing the APC tumor suppressor. As this destruction complex is responsible for maintaining a low level of β-catenin in cytoplasm, inactivation of the complex results in a high concentration of β-catenin, which then relocates into the nucleus, binds to a transcription factor of the TCF/LEF family, and induces transcription of Wnt targets. These include genes coding for proteins involved in cell cycle control, migration and apoptosis.⁴¹

Several Wnt signaling cell-cycle models have been applied in previous computational studies of intestinal tissue renewal.^37,44 We adopted two types of models in our epidermis modeling. In the simple Wnt cell cycle model (SWCC), the cell cycle of the proliferation cells is assumed to vary stochastically, with the duration of the G₁ phase being sampled from a normal distribution with mean 107 h and s.d. 11 h, while the durations of the S, G₂ and M phases are set to 9.5 h, 9.0 h, and 0.8 h, respectively. These values are adopted from the collected data of cell kinetic parameters for the basal layer in 4–7 month old Large White pigs.⁴⁵ When the total cell-cycle time elapses, a cell divides producing two daughter cells, both sensitive to their surroundings. If the extracellular Wnt level is favorable, the newborn cells are assigned new cell-cycle times. Under adverse conditions, cells leave the cell cycle and differentiate.³⁷

For the Wnt signaling pathway controlled cell cycle model (WCC), there are two different approaches previously applied to crypt dynamics.^37,44 In the model proposed by van Leeuwen et al., a system of nonlinear ordinary differentiation equations (ODEs) are used to predict the temporal changes in the concentrations of ten components of the Wnt pathway within a single cell, which include the dual roles of β-catenin in Wnt signal transduction and cell–cell adhesion.³⁷ Coupled with the cell-cycle model proposed by Swat et al.,⁴⁶ cells exposed to a strong Wnt signal can progress more quickly through the cell cycle than cells exposed to low Wnt concentrations. This produces position-dependent characteristics for cell proliferation and differentiation rates if a spatially varying Wnt signal is provided.³⁷ In addition, the cell-cycle model's inherent bistability property also affords a threshold Wnt level below which the G₁/S checkpoint can never be passed.⁴⁶ Therefore in some regions with unfavorable Wnt concentration, the cell growth is arrested (i.e., quiescent or terminal differentiated). In the modeling study of Mirams,⁴⁴ the cell-cycle model proposed by Swat et al. was also applied in the same way, but only one equation was used to predict the temporal changes in the concentrations of the key components of the Wnt pathway within a single cell.⁴⁴ This was achieved via a systematic asymptotic analysis, and the simplified Wnt model was demonstrated to retain the essential behavior of the full Wnt pathway.⁴⁴

As both models are coupled using the same cell-cycle model, they demonstrate a similar feature in Wnt-dependent cell cycle durations (Fig. 1). According to the analysis of the cell-cycle model,⁴⁶ the cell is deemed to enter the S phase only when the level of a key component, E2F1, crosses a threshold. The duration of the G₁ phase of a cell is thus determined by the course of the temporal evolution of E2F1, which is manifested by integration of the set of Wnt-dependent ODEs of the cell-cycle model over time. Fig. 1 shows that for both models there is a general trend for a shorter G₁ phase when the cell is exposed to a stronger Wnt stimulus, and a rapidly increasing G₁ duration when Wnt concentration reduces to a certain level (0.64 for the van Leeuwen model, and 0.47 for the Mirams model). Therefore cells proliferate quickly under a strong Wnt stimulus, proliferate less rapidly as the stimulus reduces and become quiescent at low Wnt stimuli. This feature could explain quite well the observed proliferation patterns in a healthy crypt, as the duration of the G₁ phase of stem cells in crypt is measured from typically around 6 hours to 25 hours.⁴⁴ However, for swine and human skins, the typical G₁ durations for proliferative cells are in the range of 100 to 160 hours.⁵ In order to use these published models without adjusting the model parameters in our multiscale epidermis model, we simply assigned the Wnt concentration of the basal layer to be in the narrow range so that the corresponding G₁ duration is around 100 hours.

Fig. 1 Variation of G₁ phase duration of two Wnt signaling cell cycle models with Wnt stimuli. Default parameter values in Chaste 3.0²⁹ are used.

As the two Wnt-dependent cell cycle models are indistinguishable in describing the proliferation pattern of the epidermis, we chose the simple one proposed by Mirams.⁴⁴ Following the previous studies of crypt dynamics,^37,44 we superimposed in the epidermal model a fixed spatial gradient in Wnt along the vertical direction, so that Wnt levels are highest (0.471) at the bottom and lowest (0.000) near the top, and each cell is promptly assigned a Wnt concentration [Wnt] depending on its vertical distance from the bottom (i.e., height):

where y_i is the height of the cell center, and y_top− y_bottom is the initial height of the virtual patch, which is kept fixed during simulation. We also set a threshold (0.350) for differentiated cells so that in the patch there are two layers of cells at the bottom that have the capability for proliferation. During simulations each cell is instantly assigned a G₁ time determined from the extra- and intra-cellular molecular interaction network, while the durations of G₂, M and S phases are assumed to be the same constants as in SWCC. The same Wnt profile is applied for SWCC simulations. In these simulations, however, the G₁ duration of proliferative cells in the virtual epidermis is not affected by Wnt concentrations but by the proliferation status and stochastic assignment.

Radiation induced cell killing and epidermal regeneration

Previous experimental studies on swine skin demonstrated a distinct strain difference in radiation responses.⁴⁷ In this study we exclusively employed the experimental data of the Yorkshire pig¹² to corroborate our multiscale epidermal model. For this strain of pig, ED₅₀ (a dose in which 50% of a population receives the effect) for moist desquamation is 2300 R (22.31 Gy).¹² Experiments established that acute exposures ranging from 16.49 Gy to 26.19 Gy induce epidermal erosion from 17 days post-irradiation, which reaches its maximum dimension between the 24th and 28th days, followed by healing either completely (<22.31 Gy) or maximally (> = 22.31 Gy) at about 36 days. For unhealed fields a second reaction of necrosis or ulceration develops between 36 and 70 days.¹²

Based on the experimental observations,^12,47 we assumed that the spinous and granular cells are radio-resistant, and the proliferative cells (located mainly in basal layer and first suprabasal layer) are sensitive with a D₀ of 7.76 Gy. Note this value is about two times that of the combined data for the dose response of small, large, and giant islands in the swine skin experiment,¹² as we supposed the islands could arise either from a single cell or from multiple congregated cells.

As the degenerative phase lasts for about 4 weeks after exposure, we implemented a delayed random cell killer to direct cellular depletion from the epidermal population, by assuming that the damaged cells start apoptosis at time points sampled from a normal distribution with a mean of 22 days and s.d. of 5 days. This followed from the observed normal distribution of degenerate cells in the basal and first suprabasal layers in another previously conducted swine experiment.⁴⁷

To simulate the regenerative phase, we simply assumed that the surviving proliferative cells change their proliferation rate between the 14th and 25th days after exposure. This is supported by the shortened cell turnover time observed in the proliferative layers in the swine skin experiment.⁴⁷ In SWCC simulations, an altered state with a shorter G₁ duration (28 hours) was assigned to all surviving proliferative cells after simulation time reached the 14th day while in WCC simulations, a higher Wnt concentration (0.475) was assigned to the bottom of the epidermal patch on the 14th day (the corresponding G₁ duration is about 27 hours (see Fig. 1)). This is supported by recent experimental observations of the Wnt signaling activation during the re-epithelialization phase of wound healing.⁴⁸ After 25 days of simulation, the proliferation rates of the cells were assumed to return to the normal state for both models.

It has been observed that if the skin dose is high enough, there is a second cell depletion period after the regenerative phase, which is related to the vascular damage and complete ulceration of the upper dermis.^5,12,14 The dose-dependent incidence identified for the Large White pigs indicates an ED₅₀ of 20.86 Gy,⁵ which can be modeled using an error function.⁴⁹ As the ED₅₀ value for Yorkshire pigs is 22.31 Gy, we made a simple shift of this function, i.e.,

where D is the skin dose in Gy, to denote the probability of losing the physiological support of the basement membrane in this strain of pigs (see also the ESI,† Fig. S1).

In our model simulations, immediately after the finish of the regenerative phase, a uniform random number between 0 and 1 was generated. If the random number was smaller than P, the boundary forces added to the basal layer cells (see below) were nullified, leading to the initiation of the second cell depletion process. All these efforts to model radiation induced cell killing and epidermal regeneration are summarized in the schematic diagram of Fig. 2.

Fig. 2 Schematic diagram of radiation response of epidermal proliferative cells. The portion of surviving cells are determined by D₀, which have accelerated proliferation rate from day 14 to day 25, and normal rate or decreasing count afterwards, depending on the possibility of dermal necrosis, while the damaged cells go through delayed degeneration with a normal distribution of time.

Additional model assumptions

The ability of epidermal domains to be maintained can be explained by one of two different mechanisms, which are not necessarily mutually exclusive. The delamination model assumes that the stem cell divides symmetrically along the BM plane, leading to one daughter cell with the highest proliferative capability and attachment potential to the BM, and another one which can be detached from BM and promoted into suprabasal layers. Another model assumes asymmetrical division of the stem cell relative to BM, leading to one proliferative basal daughter and one detached, suprabasal daughter.³¹ In this study we applied the delamination model, as we found the basal cells can be naturally promoted to the higher layers by the compulsive forces rendered by the dividing neighbors. This was implemented by directing the daughter cell to locate randomly either on the right or the left side of the stem cell. Following van Leeuwen et al.,³⁷ we did not pin stem cells at the base of the patch, but allowed them to move freely in response to local spring-mediated biomedical forces. Therefore the stem cells were not set to be immortal and not sharply distinguished from the less proliferative transit amplifying cells.

To balance the compulsive forces that prop up the basal cells, we found it necessary to add a boundary force for the basal layer. For cells below 0.48 (dimensionless height), a spring force with the same magnitude of equilibrium neighboring cells was added pointing down to the BM plane. Without this treatment we found that the basal cells are eventually lost from the system. This feature also helped us to simulate the second cell depletion phenomenon observed in experiments.

Results

Epidermal homeostasis

In a set of representative simulations of one epidermal proliferative unit (EPU),⁵⁰ an epidermal patch with 10 cells width was initially started at equilibrium, each pair of neighboring cells being separated by a natural distance (i.e., 1) so that they formed a regular, hexagonal lattice (Fig. 3(a)), while the ages of the cells were set randomly to avoid synchronization. For both cell cycle models (SWCC and WCC), the steady states were reached at around 600 hours, in which the cell production rate equals the cell removal rate (ESI,† Videos S1 and S2).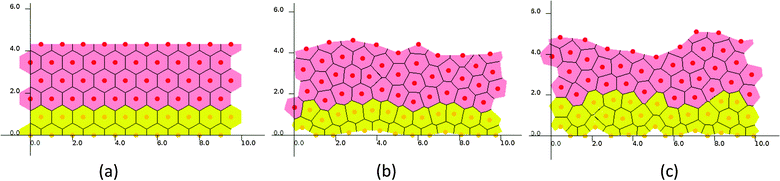

Fig. 3 Snapshots of one EPU simulations. (a) Initial state and steady states of (b) the SWCC model and (c) the WCC model.

Though the two simulations started from an identical initial state, and the same Wnt profile and threshold for terminal differentiation, some subtle differences in cellular proliferation pattern and histological parameters could be discerned (ESI,† Videos S1 and S2, and Fig. 3). For example, the proliferation cells in SWCC simulations are exclusively confined in the two layers attached to BM (Fig. 3(b)), but in the WCC steady state, some cells in the third layer are still proliferative (Fig. 3(c)). These cells already enter an unfavorable Wnt region; however, their proliferation state is determined by the concentrations of cell cycle components, which are correlated with the Wnt stimuli. This can be considered to be a multiscale effect which is induced by interactions across different time and space scales (extracellular Wnt factors, Wnt signaling, cell cycle control, proliferation and migration).³⁷

To quantify the proliferation and histology differences between these two cell cycle models in further detail, extensive simulations were conducted with 10 EPUs (100 cells of width) for 70 days from the steady states.

The virtual epidermal patches maintained by the two cell cycle models are morphologically indistinguishable during the lengthy simulations (Fig. 4). The heights and proliferation cell populations are the most used parameters to document morphological changes in radiobiological studies on skin.^12,47Fig. 3 shows that these parameters are nearly the same for the two patches sustained by different cell cycle models. Both models produce a higher cell density in the basal layer than in the first suprabasal layer (Fig. 4(b) and (c)). This feature is probably caused by the boundary forces added to associate cells with the BM plane, rather than the cell cycle models. As is described in the Methods section, for the SWCC model, the cells in these two layers have exactly the same cell cycle parameters. It should be noted that this feature is consistent with experimental observation. In Large White pigs, the cell density is around 140 cells per mm in the basal layer, and 75 cells per mm in the first suprabasal layer.⁴⁷

Fig. 4 Cellular dynamics of 70 day simulations of 10 EPUs. (a) Heights, (b) basal cell counts, and (c) cell counts of the first suprabasal layer.

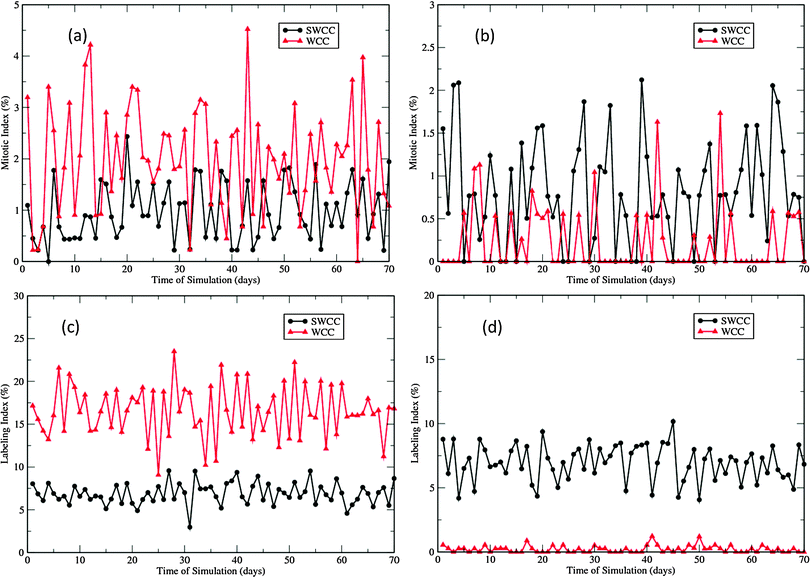
The differences in proliferation patterns generated by the two cell cycle models are characterized by the two proliferation indices presented in Fig. 5. The labeling index (LI) experiments involve injecting intradermally with a substance (3HTdR or BrdU) that is incorporated into cells during the S-phase of the cell cycle. When a labeled cell divides, it produces two labeled daughter cells. On the other hand, the mitotic index (MI) is measured by visually detecting the mitotic cells, though in some experiments some substance (e.g., vincristine) is administered to aid visualization.⁵¹ These two parameters are widely used in cell kinetics studies to generate information about the cytokinetic organization and dynamics. In our multiscale epidermal simulations, the cells in the S-phase were labeled at the 23rd hour of each day, and the labeled cells and mitotic cells were counted one hour later, followed by removal of the label tracer of the whole population. Fig. 5 shows the two indices of the basal and the first suprabasal layers in the 70 day simulations.

Fig. 5 Proliferation indices in the 70 day epidermal homeostasis simulations of 10 EPUs. (a) Mitotic indices of basal layer in two types of simulations (SWCC and WCC). (b) Mitotic indices of the first suprabasal layer in simulations. (c) Labeling indices of the basal layer in simulations. (d) Labeling indices of the first suprabasal layer in simulations.

In the SWCC driven simulations, the LIs of the basal layer and the first suprabasal layer are nearly the same (∼7.5%, see Fig. 5(c) and (d)). This is not unexpected as the gradient of the imposed Wnt profile does not affect the cell cycle parameters. However, there is a subtle difference in the MIs (Fig. 5(a) and (b)). The void MIs are more frequently measured in the first suprabasal layer than in the basal layer, though the average indices are almost the same (∼1%). This difference is probably due to the lower cell density in the first suprabasal layer and the small number of mitotic cells that are monitored. In contrast, such differences are quite distinctive in the WCC driven simulations. The proliferation indices in the basal layer are significantly higher than those in the first suprabasal layer (Fig. 5). It should be noted that neither of the models generate the correct proliferation pattern measured in experiments. In the cell kinetics studies of Large White pigs, the proliferation indices in these two layers demonstrate some differences, but the differences are not so drastically (8.1% vs. 4.1%, 0.3% vs. 0.2%, for LIs and MIs, respectively).⁵¹ In the Yorkshire pig experiments, the two layers were not treated separately, and the overall LI was reported to be 3.9%, and the measured MIs varied between 1.7 and 3.2%.⁸ Such discrepancy will be addressed in the following discussions.

Responses to acute irradiation

Three phases of histologic changes

Acute exposures of 16.49, 22.31, and 26.19 Gy were introduced in the 10 EPU patches after each patch had entered the steady state. These doses correspond to those applied to the skin of Yorkshire pigs in a previously conducted experiment.¹² For each level of exposure, four independent simulations were carried out, and morphological features, cell density, radiation damage, as well as proliferation indices were monitored for up to 70 days following exposure.

In all simulations the three experimentally observed phases of epidermal histologic changes, i.e., degenerative (cell loss) phase, regenerative (cell replacement) phase, and post-regenerative (hyperplasia followed by returning to the normal state or second cell loss) phase,¹² could be clearly discerned (ESI,† Videos S3 and S4). There are some differences in the timeline of these phases simulated by the two cell cycle models, but the overall sequence and duration are quite consistent with the experimental observations.¹²

The degenerative phase starts promptly after exposure, with prickle cells intact but a majority of transit amplifying cells marked for apoptosis. As D₀ for transit amplifying cells is set to 7.76 Gy, the numbers of surviving transit amplifying cells after the three levels of exposures are about 24, 11, and 7, respectively (since the radiation damage is introduced in a random manner, the number as well as the location of the surviving cells are assigned stochastically for different single simulations) (see Fig. 2). These few cells cannot provide enough supply to the prickle cell layers, as well as to the degenerating proliferative layers, leading to cell degeneration and loss dominated phase during the first 2 to 3 weeks following exposure. At the end of this period, the overall population reaches the nadir as the prickle cells are nearly depleted at all levels of exposure. Nevertheless, the pool of surviving proliferative cells is multiplied several fold at this point (ESI,† Videos S3 and S4).

Though we set the same period for regenerative phase in the models (from the 14th to the 25th day), the manifested cell replacement in simulations is dependent upon the underlying cell cycle models. With the same dose of exposure, the WCC driving simulations show some regeneration activities even before the Wnt level increases on the 14th day, much earlier than the SWCC driving simulations (ESI,† Videos S3 and S4, and Fig. 6). As a result, cell regeneration in WCC simulations is much more effective than in SWCC simulations during the first week of this period. After this, the SWCC simulations take a faster pace and produce “overshoots” at the end. This hyperplasia is not so noticeable in WCC simulations (ESI,† Videos S3 and S4, and Fig. 6). In both types of simulations, the regenerating islands¹² are formed with several cells in the beginning and expand and merge with each other during the rest time of this period. In some areas where the regenerating islands are too few or expand too slowly, the surface becomes denuded for a certain time (ESI,† Videos S3 and S4). These correspond to the areas of ulceration observed in experiments.¹²

Fig. 6 Height changes of the virtual epidermal patches after different levels of exposure. (a) SWCC simulations. (b) WCC simulations. The movie files for the 26.19 Gy simulations are provided as ESI,† Videos S3 and S4.

The simulated post-regeneration phase is characterized by hyperplasia of the regenerated epithelium immediately after the regeneration period and later a return to a control level of cellularity for all simulations of 16.49 Gy exposure, and second cell loss for 22.31 Gy and 26.19 Gy exposures (ESI,† Videos S3 and S4, and Fig. 6). As the dermal necrosis incidence function is set to ensure that the EP₅₀ is around 22.31 Gy (ESI,† Fig. S1), about half of the total number of simulations at this level of exposure could maintain the integrity of the BM plane as well as the whole epidermal structure. For exposures of 26.19 Gy, all simulations experienced full depletion of all cellular population, but with variant stopping times before they can fully proceed to 70 days following radiation (ESI,† Videos S3 and S4).

Morphological changes

Fig. 6 documents the changes of the height of simulated epidermal patches after the three levels of radiation. In simulations the height was actually used to monitor the position of the tip cell in the patch, therefore it is correlated with the thickness of the viable layers of the epidermis, as long as the whole epidermal structure is maintained. This applies to simulations up to 25 days after radiation, when the end of the regeneration phase is reached. The SWCC results are quite consistent with the observed dynamics of prickle-cell linear density for the three exposures in Yorkshire pigs.¹² Particularly, in experiments, the initial depletion rates are found to be independent of the radiation dose, but the severity of cell depletion and the rate of recovery are dose dependent.^12,45 While these features can be observed in both types of simulations (Fig. 6), the timelines of these changes simulated by the SWCC model are closer to experimental observations than by the WCC model.

The sudden increase of the heights after the regeneration phase in simulations of high exposures (22.31 Gy and 26.19 Gy) is caused by the abrupt release of the basal cells attached to the BM plane. As the dermal necrosis incidence function is applied at this point, after high exposures the BM plane is destroyed and the epidermal structure is totally ruined. Therefore the patch height after this point in high dose simulations is not related to the thickness of viable layers but the size of the remnant cellular congregation (ESI,† Videos S3 and S4). As attractive forces are applied to all cells in the models, the rapid expansion of the prickle cell pool eventually leads to a circular shape in 2D simulations. (The horizontal axis and vertical axis in the supplemental videos are not on the same scale, so the remnant pool at the end of simulation looks like an ellipse.) In a 3D real epidermis, the cells can move in all directions and will therefore occupy more horizontal space, which will give rise to sphere-like islands with much less heights. This is exactly the type of regenerative and unhealable islands observed in experiments.^12,45

With 26.19 Gy exposures, the whole patches are totally lost after around 50 days in WCC simulations, while the remnant islands still survive till the end of 70 days in SWCC simulations (ESI,† Videos S3 and S4, and Fig. 6). This is not unexpected, as in WCC simulations the maintenance of the epidermis is highly dependent on the basal layer (Fig. 4), while in SWCC simulations the less affected first suprabasal layer contributes almost equally as the basal layer to the maintenance (Fig. 5). In experiments there is some progression in healing in the late phase (after 56 days) that is involved in the remnant islands.¹² This might be related to the repairing of the underlying BM plane, or migration of cells from neighboring undamaged areas, which were not considered in this study.

The morphological changes can also be discerned from the recorded cellular counts of the proliferative layers in simulations (Fig. 7). These cell counts are in fact the cell line densities as the widths of the patches are kept fixed during simulations. Compared with experimental observations,^12,45 the degeneration rates of both layers are much slower and nadir densities at the end of degeneration phase are much higher in simulations (Fig. 7). This is due to the fact that, in simulations, all cells in the layers are counted, irrespective of whether they are marked for apoptosis or not. In experiments, most cells exhibiting pyknosis and shrinkage necrosis were excluded from analysis.^12,45 That is also the reason that the regeneration phase is not easily manifested in simulations, especially for the SWCC simulations (Fig. 7). At this time point the major component of these two layers are surviving and regenerated cells, which are closer to the population measured in experiments.^12,45

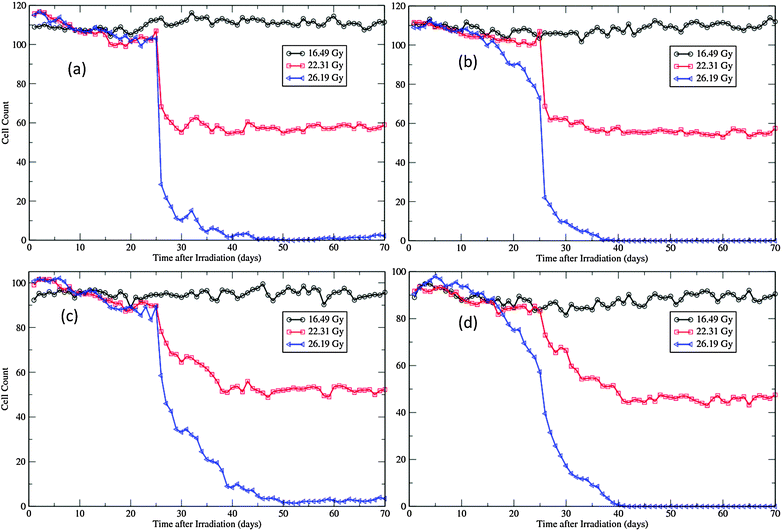Fig. 7 Cellular dynamics in the proliferative layers of the virtual epidermal patches after different levels of exposure. (a) Basal cell count in SWCC simulations. (b) Basal cell count in WCC simulations. (c) Cell count in the first suprabasal layer in SWCC simulations. (d) Cell count in the first suprabasal layer in WCC simulations. The movie files for the 26.19 Gy simulations are provided as ESI,† Videos S3 and S4.

Proliferation index changes

Fig. 8 and 9 describe the changes of proliferation indices of the virtual epidermis patches after exposure. It should be noted that all radiation induced apoptotic cells are excluded in the calculation of the two proliferation indices. In the swine experiment the indices were measured up to 40 days after exposure, due to the severe ulcerations induced by high dose exposures after this stage.¹² In simulations, as the dermal necrosis incidence function was introduced at 25 days after exposure, such ulcerations could be observed much earlier than in experiment (Fig. 7). Therefore the high MIs in Fig. 8 after the regeneration phase (>25 days) do not mean high proliferation rates at this stage; they are just the direct effect of fast reduction of the proliferative cellular population.

Fig. 8 Changes of MIs of the virtual epidermal patches after different levels of exposure. (a) MIs of basal layer in SWCC simulations. (b) MIs of basal layer in WCC simulations. (c) MIs of the first suprabasal layer in SWCC simulations. (d) MIs of the first suprabasal layer in WCC simulations.

Fig. 9 Changes of LIs of the virtual epidermal patches after different levels of exposure. (a) LIs of basal layer in SWCC simulations. (b) LIs of basal layer in WCC simulations. (c) LIs of the first suprabasal layer in SWCC simulations. (d) LIs of the first suprabasal layer in WCC simulations.

For both SWCC and WCC simulations, the MI changes during the degeneration and regeneration phases (<25 days) are quite consistent with the experimental observations.¹² The dose-dependent MI response can be clearly discerned from the data. For higher doses, the degree of initial depression of MIs is higher, and that of the following enhancement of MIs is also higher (Fig. 8). In experiment, the duration of depressed MIs for exposures of 22.31 Gy and 26.19 Gy were about 15 days, while for exposure of 16.49 Gy it was about 7 days.¹² The peak MIs for three levels of exposure were about 3.5%, 4.5%, and 6.5%, respectively.¹² It is interesting to note that all peaks of MIs measured in experiment were around 25 days after exposure.¹²

Depression of LI was observed in both layers during the degeneration phase for all simulations (Fig. 9, compared with Fig. 6(a) and (c)). For SWCC simulations, the responses of LI in two layers are nearly identical (Fig. 9(a) and (c)). For all levels of exposures, after a period of enhancement during the regeneration phase, the simulated LIs do not return to normal (see Fig. 5(a) and (c)), but oscillate with a period of about 6 days till the end of simulations. This kind of cell cycle synchronization is probably induced by the two times change of G₁ phase durations for the whole pool of proliferative cells at the same specific time points (the 14th day and 25th day, respectively, after radiation exposure), which is an oversimplified treatment to change the cellular state. In reality, such changes should occur gradually throughout a spread of time, as each cell has a unique microenvironment and proliferative capability in this scenario. The high LIs observed in post-regeneration phase in high exposure simulations are due to the fact that only very few proliferative cells are left in these layers at this stage (discussed above).

Interestingly, the artificial oscillation of LIs in SWCC simulations was not observed in WCC simulations (Fig. 9(b) and (d)), though the two times change of G₁ phase durations were applied in the WCC model at exactly the same time points as in the SWCC model (see the Methods section). This implicates that the cells equipped with the more sophisticated cell cycle model driven by Wnt signaling can generate results closer to reality than those with the simplified model, which is a well known fact about regulation of epidermal stem cells.³⁰

Discussion

Though there exists a rather simple stratified structure for interfollicular epidermis, the major part of the skin of all mammals, the regulations of its normal homeostasis and of wound repair are highly complex processes that involve many biological interactions not only within a particular time and length scale, but also across scales.³⁰ To construct a meaningful multiscale model that can generate comparable results with experimental observations while to keep it computationally tractable, it is essential to choose carefully as to which processes are modeled, and to simplify them as much as possible. In this paper, we present a model that describes epidermal renewal and radiation injury and re-epitheliation, which considers coupling of the following fundamental processes:

• Subcellular level: Wnt signalling, cell–cell adhesion and cell-cycle control;

• Cellular level: cell division, migration and differentiation;

• Macroscale level: extracellular Wnt profile, cell–cell adhesion, and basal cell-BM adhesion.

Following Meineke et al.³⁹ and van Leeuwen et al.,³⁷ we model the connections between cells as springs and use the Voronoi tessellation associated with the cell centers to determine size and shape of every cell in the aggregate. The cell-cycle progression, cell–cell adhesion and differentiation states are influenced by intra-, inter- and extracellular cues. Incorporating experimentally measured histological and cell kinetic parameters into this well-developed multiscale tissue framework, we obtain results of population kinetics and proliferation index comparable to observations in unirradiated and acutely irradiated swine experiments.

Among the new insights gained from our modeling simulations, we highlight the following. First, tissue organization and homeostasis can be attained by delicate balancing of cell proliferation, differentiation, and cell–cell interactions. In this study, it demonstrates that simple cell cycle models (i.e., SWCC and WCC) with specified phase durations of the cell cycle within the polygonal cell model equipped with spring-like cell–cell interactions are versatile enough to describe all essential features of swine skin homeostasis, such as constant thickness and cell density, periodic renewal, proliferative patterns, etc. Mechanisms for skin stratification have been proposed to be very complex, involving many intra-/inter-cellular signaling pathways and networks of structural proteins.⁵⁰ The modularized approach in this study provides a simple way of categorization to characterize these complex processes, and exhibits the potential of extending this framework to other tissues such as gastrointestinal tract, lung epithelium, etc.

Second, this study confirms that BM plays important roles in maintaining epidermal homeostasis, radiation induced moist desquamation, and the following wound healing. Earlier experiments have established that, after single acute exposures of 1700 to 2700 R, there is no consistent endothelial cell loss and dermal microvasculature damage during the first 4 weeks; but after that, abrupt dose-dependent changes underlying the BM plane are initiated and persist till the end of observation.¹⁴ This is exactly replicated by the dermal necrosis incidence function introduced on the 25th day of our simulations, which determines whether an exposed area will be healed or not, and is essential to generate results compatible to those observed in experiment.¹² A recent experiment found that, by grafting autologous adipose tissue-derived stroma cells in high dose exposed minipigs, the healing of skin wounds can be greatly accelerated.¹⁹ Though the focus of this study is the epidermal layers of the skin, it is a known fact that the normal functionality and structure of the epidermis is highly dependent upon the integration of the underlying tissue.³¹

Third, our study indicates that the drastic reduction of cell cycle time calculated in early studies of regenerating cells¹² may be overestimated by mistakenly taking into consideration the non-dividing cellular pool. Our simulations indicate that, during the 12 days regenerating phase, the prickle cells increase from nearly nothing to the control level and above, while the damaged proliferative layers are replaced gradually (ESI,† Videos S3 and S4). Therefore the ratio of basal cells and prickle cells is not constant but constantly changing. The calculation in ref. 12 assumed the ratio of prickle to basal cells to be the same as in the steady state (i.e., 3.5), leading to a very short cell cycle time (13.6 hours) for the regenerating basal cells, that is about 30-fold reduction from the basal cell doubling time in the intact population (about 10 to 16 days). In contrast, our simulations assumed a much moderate reduction (for SWCC, the G₁ duration decreases from 107 hours to 28 hours, while durations for S, G₂, and M are unchanged; for WCC, the reduction is similar). This radiation induced proliferation change is more compatible with that observed in another experiment using the Large White pigs (the cell colony cell cycle time is 16–22 hours in the basal layer, and 44–49 hours in the first suprabasal layer).

From this modeling study, we learned that the time course and degree of severity of various skin responses after radiation are highly dependent on the underlying model parameters of cell kinetics and cellular-tissue configurations. A major bottleneck to apply this mathematical modeling approach to solve biomedical problems is the limited availability of high-quality quantitative data. Due to this limitation, in this study, we had to use parameters from different sources and even from different strains. For example, the turnover time for swine epidermal basal cells was reported to range from 118 to 389 hours in different studies.⁵¹ The reason that we chose the narrow range (118–140 h) is that it generates results that are most compatible with the observations in radiation studies (such as in ref. 12 and 45). However, the steady states generated from this narrow range of cell cycle time have quite different proliferation patterns (MIs and LIs) from experiments. Another set of model parameters we cannot ascertain is that in the Wnt dependent cell cycle model, which has been used to describe the gut crypt dynamics.⁴⁴ The mechanisms for Wnt signaling in regulation of different tissues might be the same, but the detailed interactions among molecules are probably different as in different tissue microenvironments. Particularly, we chose the Wnt level at the bottom of virtual epidermal patch to be in the region that a subtle Wnt alteration can induce very rapid change in the cell cycle time (Fig. 1), in order to set the G₁ duration to be around 100 h. This makes a vast difference for proliferation in the basal and the first suprabasal layers (Fig. 4). Compared with the experimental proliferation indices, it seems that a better Wnt dependent cell cycle model for the epidermis can be achieved by adjusting parameters so that the G₁ duration is around 100 h while the Wnt level is close to the dimensionless maximum (i.e., 1). Further improvement in the model is necessary once more biological dynamics data are available.

We have considered Wnt dependent cell cycle models in this study; however other morphogens and growth factors should be considered in future work. In particular TGFβ plays an important role in cutaneous wound healing,⁵² and studies have revealed an interaction⁵³ between TGFβ and Wnt-β-catenin signaling.⁴⁸ Studies of these interactions could be considered in future work using the Chaste framework; however it will require a good degree of model development compared to the present work.

As the mammalian epidermis has a relatively simple structure, and is easy to access and to grow its cells in vitro, it is regarded as the most suitable target tissue for testing various cell regulation and cell manipulation theories.⁵⁴ With recent vigorous endeavors focused on this system, many basic mechanisms of epidermal homeostasis involving stem cells regulation have been unfolded.^1,55 The proposal of existence of epidermal stem cells 40 years ago is an important step in the studies of skin homeostasis and wound healing.⁵⁴ The concept that the renewing tissues of the body contain a small pool of self-maintaining stem cells, upon which the entire tissue is dependent, is also now accepted as applicable to all renewing tissues. However, a major obstacle in these areas has been a lack of molecular markers and of the precise in vivo localization of the putative stem cells. In this study we did not distinguish the epidermal stem cells and the transit amplifying cells in the proliferative layers of the epidermis. It has been reported that, during wound repair, epidermal transit amplifying cells can increase the number of rounds of DNA replication than they exhibit under normal conditions.⁵⁶ There is also evidence supporting the reversibility of epidermal stem cells and transit amplifying cell compartments, and the differentiation plasticity of epidermal transit amplifying cells.^57,58 These finding seems to propose the flexibility of epidermal stem cells, i.e., the stem cells pool is not confined to a certain cell population or localized in a defined microenvironment, but is dynamically stimulated/modified by surrounding cues. This is the setting we applied in our model. Alternatively, we can easily manipulate the stem cells in our model to locate at specified positions and to respond to stimuli differently from the transit amplifying cells. By collaborating with experimental groups, the present model of the epidermis may help to enhance our understanding on some unsolved properties of stem cells.

The modular tools of the mutiscale tissue framework Chaste allow experienced users to conduct many in silico experiments easily. In a follow up to this paper that focuses on the epidermal response of acute radiation, we will investigate the dose-rate and fractionation effects of radiation on the skin, as the current therapeutic practice routinely applies medium dose rate and fractionation of exposure onto targets to alleviate the detrimental effects of high dose acute irradiation. These are related to the cellular killing module and have been previously considered in hematopoietic modeling study in our group.⁵⁹ We will apply a similar scheme to the radiosensitive cells in the virtual epidermal patch and adjust the corresponding parameters so that the model predictions are consistent with experimental data previously observed in animal studies.⁶⁰ This approach will help to find the optimal therapeutic protocols that could minimize the detrimental effects to skin while maximizing the killing efficiency to the target cells. A second exciting line of research is to incorporate a radiation track structure and investigate the effects of high-energy protons, neutrons, and heavy ions on the skin. Basic radiobiological responses such as cell survival curves, mutation, chromosomal aberrations and representative mouse tumor induction curves from these sources can be achieved by computational tools developed in our groups such as GERMcode⁶¹ and RITRACK.⁶² We will develop interfaces to merge these well-established tools with Chaste and conduct in silico simulations to compare the skin responses of conventional photon techniques and new Hadron therapy with protons and carbon beams. This would also help us to understand the pathophysiolgical mechanism of skin damage due to exposure to radiation (ref. 63) and highly charged and energetic particles in space exploration.⁶⁴

Competing interests

The authors have declared that no competing interests exist.

Acknowledgements

This work was supported by NASA Space Radiation Risk Assessment project and the University of Nevada, Las Vegas. We are thankful for the discussion with Dr Olga Smirnova, and appreciate the hospitality of the Chaste team for the 2012 Chaste Cell-based Modelling Workshop.

References

1. C. Blanpain and E. Fuchs, Epidermal homeostasis: a balancing act of stem cells in the skin, Nat. Rev. Mol. Cell Biol., 2009, 10, 207–217.
2. NSCR, National Council on Radiation Protection and Measurements. Limit for exposure to “hot particles” on the skin, vol. 106, NCRPM, Bethesda, MD, 1989.
3. F. E. Haskin, F. T. Harper, L. H. Gooseens, B. C. P. Kraan, J. B. Grupa and J. Randall, Probabilistic accident consequence uncertainty analysis: early health effects uncertainty assessment. Main Report, US Nuclear Regulatory Commission, Washington, D.C., 1997.
4. D. J. Strom, Health impacts from acute radiation exposure, vol. PNNL-14424, Pacific Northwest National Laboratory Report Richland, Wash., 2003.
5. J. W. Hopewell, The skin: its structure and response to ionizing radiation, Int. J. Radiat. Biol., 1990, 57, 751–773.
6. G. M. Morris and J. W. Hopewell, Pig epidermis: a cell kinetic study, Cell Tissue Kinet., 1985, 18, 407–415.
7. W. Montagna and J. S. Yun, The Skin of the Domestic Pig, J. Invest. Dermatol., 1964, 42, 11–21.
8. J. O. Archambeau and G. W. Bennett, Quantification of morphologic, cytologic, and kinetic parameters of unirradiated swine skin: a histologic model, Radiat. Res., 1984, 98, 254–273.
9. G. M. Morris and J. W. Hopewell, Changes in the cell kinetics of pig epidermis after repeated daily doses of X rays, BJR Suppl., 1986, 19, 34–38.
10. J. W. Hopewell, Mechanisms of the action of radiation on skin and underlying tissues, BJR Suppl., 1986, 19, 39–47.
11. J. W. Hopewell and C. M. Young, Changes in the microcirculation of normal tissues after irradiation, Int. J. Radiat. Oncol., Biol., Phys., 1978, 4, 53–58.
12. J. O. Archambeau, G. W. Bennett, J. J. Abata and H. J. Brenneis, Response of swine skin to acute single exposures of X rays: quantification of the epidermal cell changes, Radiat. Res., 1979, 79, 298–337.
13. J. W. Hopewell and C. M. Young, The effect of field size on the reaction of pig skin to single doses of X rays, Br. J. Radiol., 1982, 55, 356–361.
14. J. O. Archambeau, A. Ines and L. F. Fajardo, Response of swine skin microvasculature to acute single exposures of X rays: quantification of endothelial changes, Radiat. Res., 1984, 98, 37–51.
15. J. O. Archambeau, A. Ines and L. F. Fajardo, Correlation of the dermal microvasculature morphology with the epidermal and the endothelial population changes produced by single X ray fractions of 1649, 2231 and 2619 rad in swine, Int. J. Radiat. Oncol., Biol., Phys., 1985, 11, 1639–1646.
16. J. L. Redpath, D. M. Peel, P. Dodd, R. H. Simmonds and J. W. Hopewell, Repopulation in irradiated pig skin: late versus early effects, Radiother. Oncol., 1985, 3, 173–176.
17. J. A. Mahl, B. E. Vogel, M. Court, M. Kolopp, D. Roman and V. Nogues, The minipig in dermatotoxicology: methods and challenges, Exp. Toxicol. Pathol., 2006, 57, 341–345.
18. D. Agay, H. Scherthan, F. Forcheron, N. Grenier, F. Herodin, V. Meineke and M. Drouet, Multipotent mesenchymal stem cell grafting to treat cutaneous radiation syndrome: development of a new minipig model, Exp. Hematol., 2010, 38, 945–956.
19. F. Forcheron, D. Agay, H. Scherthan, D. Riccobono, F. Herodin, V. Meineke and M. Drouet, Autologous adipocyte derived stem cells favour healing in a minipig model of cutaneous radiation syndrome, PLoS One, 2012, 7, e31694.
20. E. A. Ahmed, D. Agay, G. Schrock, M. Drouet, V. Meineke and H. Scherthan, Persistent DNA damage after high dose in vivo gamma exposure of minipig skin, PLoS One, 2012, 7, e39521.
21. S. Adra, T. Sun, S. MacNeil, M. Holcombe and R. Smallwood, Development of a three dimensional multiscale computational model of the human epidermis, PLoS One, 2010, 5, e8511.
22. A. A. Patel, E. T. Gawlinski, S. K. Lemieux and R. A. Gatenby, A cellular automaton model of early tumor growth and invasion, J. Theor. Biol., 2001, 213, 315–331.
23. K. Smallbone, R. A. Gatenby, R. J. Gillies, P. K. Maini and D. J. Gavaghan, Metabolic changes during carcinogenesis: potential impact on invasiveness, J. Theor. Biol., 2007, 244, 703–713.
24. S. R. McDougall, A. R. Anderson, M. A. Chaplain and J. A. Sherratt, Mathematical modelling of flow through vascular networks: implications for tumour-induced angiogenesis and chemotherapy strategies, Bull. Math. Biol., 2002, 64, 673–702.
25. M. R. Owen, T. Alarcon, P. K. Maini and H. M. Byrne, Angiogenesis and vascular remodelling in normal and cancerous tissues, J. Math. Biol., 2009, 58, 689–721.
26. T. Alarcon, H. M. Byrne and P. K. Maini, A cellular automaton model for tumour growth in inhomogeneous environment, J. Theor. Biol., 2003, 225, 257–274.
27. A. Shirinifard, J. S. Gens, B. L. Zaitlen, N. J. Poplawski, M. Swat and J. A. Glazier, 3D multi-cell simulation of tumor growth and angiogenesis, PLoS One, 2009, 4, e7190.
28. R. M. H. Merks and J. A. Glazier, A cell-centered approach to developmental biology, Physica A, 2005, 113–130.
29. J. Pitt-Francis, P. Pathmanathan, M. O. Bernabeu, R. Bordas and J. Cooper, etal., Chaste: a test-driven approach to software development for biological modelling, Comput. Phys. Commun., 2009, 2452–2471.
30. E. Fuchs and V. Horsley, More than one way to skin, Genes Dev., 2008, 22, 976–985.
31. E. Fuchs, Scratching the surface of skin development, Nature, 2007, 445, 834–842.
32. M. I. Koster and D. R. Roop, Mechanisms regulating epithelial stratification, Annu. Rev. Cell Dev. Biol., 2007, 23, 93–113.
33. N. S. Penneys, J. E. Fulton Jr., G. D. Weinstein and P. Frost, Location of proliferating cells in human epidermis, Arch. Dermatol., 1970, 101, 323–327.
34. W. J. Hume and C. S. Potten, Advances in epithelial kinetics—an oral view, J. Oral Pathol., 1979, 8, 3–22.
35. R. M. Lavker and T. T. Sun, Epidermal stem cells, J. Invest. Dermatol., 1983, 81, 121s–127s.
36. The Minipig in Biomedical Research, ed. P. A. McAnulty, A. D. Dayan, N.-C. Ganderup and K. L. Hastings, The Minipig in Biomedical Research, CRC Press, Boca Taton, FL, 2012.
37. I. M. van Leeuwen, G. R. Mirams, A. Walter, A. Fletcher, P. Murray, J. Osborne, S. Varma, S. J. Young, J. Cooper, B. Doyle, J. Pitt-Francis, L. Momtahan, P. Pathmanathan, J. P. Whiteley, S. J. Chapman, D. J. Gavaghan, O. E. Jensen, J. R. King, P. K. Maini, S. L. Waters and H. M. Byrne, An integrative computational model for intestinal tissue renewal, Cell Proliferation, 2009, 42, 617–636.
38. D. Drasdo and M. Loeffler, Individual-based models to growth and folding in one-layered tissues: Intestinal crypts and early development, Nonlinear Anal., 2001, 245–256.
39. F. A. Meineke, C. S. Potten and M. Loeffler, Cell migration and organization in the intestinal crypt using a lattice-free model, Cell Proliferation, 2001, 34, 253–266.
40. R. B. Widelitz, Wnt signaling in skin organogenesis, Organogenesis, 2008, 4, 123–133.
41. T. Reya and H. Clevers, Wnt signalling in stem cells and cancer, Nature, 2005, 434, 843–850.
42. C. Niemann and F. M. Watt, Designer skin: lineage commitment in postnatal epidermis, Trends Cell Biol., 2002, 12, 185–192.
43. C. Gaspar and R. Fodde, APC dosage effects in tumorigenesis and stem cell differentiation, Int. J. Dev. Biol., 2004, 48, 377–386.
44. G. R. Mirams, PhD thesis, The University of Nottingham, 2008.
45. G. M. Morris and J. W. Hopewell, Cell population kinetics in pig epidermis: further studies, Cell Tissue Kinet., 1987, 20, 161–169.
46. M. Swat, A. Kel and H. Herzel, Bifurcation analysis of the regulatory modules of the mammalian G1/S transition, Bioinformatics, 2004, 20, 1506–1511.
47. G. M. Morris and J. W. Hopewell, Changes in the cell kinetics of pig epidermis after single doses of X rays, Br. J. Radiol., 1988, 61, 205–211.
48. C. Fathke, L. Wilson, K. Shah, B. Kim, A. Hocking, R. Moon and F. Isik, Wnt signaling induces epithelial differentiation during cutaneous wound healing, BMC Cell Biol., 2006, 7, 4.
49. O. A. Smirnova, S. Hu and F. A. Cucinotta, Dynamics of acutely irradiated skin epidermal epithelium in swine: modeling studies, Health Phys., 2013 , in press.
50. C. Blanpain and E. Fuchs, Epidermal stem cells of the skin, Annu. Rev. Cell Dev. Biol., 2006, 22, 339–373.
51. G. M. Morris, M. Rezvani, J. W. Hopewell, H. Franke and M. Loeffler, Epidermal cell kinetics in pig skin, Epithelia, 1988, 1, 231–242.
52. C. Amendt, A. Mann, P. Schirmacker and M. Blessing, Resistance of keratinocytes to TGFβ-mediated growth restriction and apopotosis induction accelerated re-epithelialization in skin wounds, J. Cell Sci., 2002, 115, 2189–2198.
53. S. S. Cheon, Q. Wei, A. Gurung, A. Youn and T. Bright, et al., Beta-catenin regulated wound sizwe and mediates the effect of TGF-beta in cutaneous healing, FASEB J., 2006, 20, 692–701.
54. C. S. Potten and C. Booth, Keratinocyte stem cells: a commentary, J. Invest. Dermatol., 2002, 119, 888–899.
55. E. Fuchs and T. Chen, A matter of life and death: self-renewal in stem cells, EMBO Rep., 2013, 14, 39–48.
56. M. S. Lehrer, T. T. Sun and R. M. Lavker, Strategies of epithelial repair: modulation of stem cell and transit amplifying cell proliferation, J. Cell Sci., 1998, 111(Pt 19), 2867–2875.
57. R. M. Lavker and T. T. Sun, Epidermal stem cells: properties, markers, and location, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 13473–13475.
58. E. Clayton, D. P. Doupe, A. M. Klein, D. J. Winton, B. D. Simons and P. H. Jones, A single type of progenitor cell maintains normal epidermis, Nature, 2007, 446, 185–189.
59. S. Hu and F. A. Cucinotta, Characterization of the radiation-damaged precursor cells in bone marrow based on modeling of the peripheral blood granulocytes response, Health Phys., 2011, 101, 67–78.
60. G. J. van den Aardweg, J. W. Hopewell and R. Guttenberger, The kinetics of repair of sublethal radiation-induced damage in pig skin: studies with multiple interfraction intervals, Radiat. Res., 1996, 145, 586–594.
61. F. A. Cucinotta, I. Plante, A. L. Ponomarev and M. H. Kim, Nuclear interactions in heavy ion transport and event-based risk models, Radiat. Prot. Dosim., 2011, 143, 384–390.
62. I. Plante, A. Ponomarev and F. A. Cucinotta, 3D visualisation of the stochastic patterns of the radial dose in nano-volumes by a Monte Carlo simulation of HZE ion track structure, Radiat. Prot. Dosim., 2011, 143, 156–161.
63. J. Valentin, Protecting people against radiation exposure in the event of a radiological attack. A report of The International Commission on Radiological Protection, Ann. ICRP, 2005, 35, 1–110 , iii–iv.
64. G. Dietze, D. T. Bartlett, D. A. Cool, F. A. Cucinotta, X. Jia, I. R. McAulay, M. Pelliccioni, V. Petrov, G. Reitz and T. Sato, ICRP Publication 123: Assessment of Radiation Exposure of Astronauts in Space, Ann. ICRP, 2013, 42, 1–339.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3ib40141c

---