Chemometric modeling of organic contaminant sources in surface waters of a mediterranean river basin
Alejandro G.
García-Reiriz
*a,
Alejandro C.
Olivieri
a,
Elisabeth
Teixidó
b,
Antoni
Ginebreda
c and
Romà
Tauler
c
aDepartment of Analytical Chemistry, Faculty of Biochemistry and Pharmaceutical Sciences, National University of Rosario, Rosario Institute of Chemistry (IQUIR-CONICET), Suipacha 531, Rosario, S2002LRK, Argentina. E-mail: garciareiriz@iquir-conicet.gov.ar
bAgència Catalana de l'Aigua, Provença 204-208, 08036 Barcelona, Spain
cDepartment of Environmental Chemistry, IDAEA-CSIC, Jordi Girona 18-26, 08034 Barcelona, Catalonia, Spain
First published on 25th November 2013
Abstract
Chemometric methods are applied to the analysis and interpretation of large multivariate datasets obtained in environmental monitoring studies. Concentrations of multiple organic compounds were measured in river samples taken from several sampling sites, at various geographical locations, during a number of campaigns and/or sampling time periods. Samples were collected and analyzed as part of an extensive multi-annual monitoring program from a mediterranean river basin (in Catalonia, at the northeast of Spain) by the Water Quality Regional Agency. Due to the great amount of multivariate data stored in environmental databases and to their complexity, chemometric modeling methods such as Principal Component Analysis (PCA) and Multivariate Curve Resolution with Alternating Least-Squares (MCR-ALS) coupled with appropriate mapping representations are proposed for the evaluation of the environmental quality of the studied rivers. Results achieved in this study are intended to be a contribution to water quality assessment and evaluation of contamination of surface waters in river basins, and to support public policies of environmental control and management of the regions under study.
Environmental impactChemometric methods are applied to the analysis and interpretation of large multivariate datasets obtained in environmental monitoring studies. This work shows the application of chemometric methods to large datasets stored by official environmental agencies to give better data interpretation possibilities and summarizing for their improved quality management and interpretation. Environmental database was chemometric modeling with methods such as Principal Component Analysis (PCA) and Multivariate Curve Resolution with Alternating Least-Squares (MCR-ALS) coupled with appropriate mapping representations to evaluation of the environmental quality of the studied rivers. Results achieved in this study are intended to be a contribution to water quality assessment and evaluation of contamination of surface waters. |
1. Introduction
Environmental databases constitute a suitable option for monitoring and control of water systems. A potential disadvantage associated with large databases is the difficulty in their interpretation for decision making. A good alternative for analysis is to resort to multivariate methods. They extract information on the behaviour of the variables involved in the several different studied dimensions (e.g. time and space). When combined with geo-positioning tools, identification of the main sources of contamination is possible, whether they are point or diffuse, or of anthropologic or geologic origin.1In this work, a database from the Agencia Catalana de Agua (Catalonian Water Agency), containing information on a large number of potential contaminants, was studied using different chemometric techniques. Chemometrics provides powerful tools for the modeling and interpretation of large environmental multivariate datasets generated in environmental monitoring programs.2,3 The goal of these studies is the computation, screening and graphical display of patterns in large datasets, looking for possible contamination sources and their distribution. Principal Component Analysis (PCA) is one of these multivariate methods for data analysis, which is frequently used in environmental exploratory studies.4,5 PCA allows the transformation and visualization of complex datasets into a new and simpler perspective, in which the more relevant environmental information can be easily perceived. By using PCA, contamination patterns may be identified and their geographical and temporal distributions may be investigated. PCA has been applied in previous studies by several authors for various types of environmental datasets, such as those stemming from water, biota and sediments.6–10 Another method applied here is Multivariate Curve Resolution Alternating Least Squares (MCR-ALS), a powerful chemometric tool with an increasing application for the analysis of environmental monitoring datasets.11 It has been recently validated for the identification of environmental pollution patterns in surface water.12 This latter study was intended to model pollution in surface water of the Ebro River delta (a smaller area of around 300 km2), during the main growing-season of the rice crop. Other chemometric methods have also been applied to the investigation of environmental data, such as partial least-squares (PLS),8,9 parallel factor analysis (PARAFAC) and Tucker3 models.13 The use of multivariate factor analysis, such as those proposed in the present work, has also been discussed in several books.2,14 In the present work, the research is focused on a large environmental dataset, obtained during a study of natural surface waters from the rivers of Catalonia (northeast of the Iberian Peninsula), including the analysis of multiple organic contaminants. In the framework of this extensive multi-annual environmental monitoring program from the Water Catalan Agency, organic contaminant compounds in the entire geographical area of Catalonia were analyzed during the years 1997–2004. The occurrence of organic compounds in natural surface waters is attributed to the presence of several industrial, agricultural and urban wastewater points and diffuse contamination sources. The Catalonia geographical area is one of the most industrialized areas of Spain, and it is of interest to evaluate its environmental situation. Although this investigation provides results which could be considered only of concern for the particular area under study, the obtained results and conclusions are of general interest from an environmental point of view to other river basin areas, especially those which are close to the Mediterranean coasts, which have the same type of climate, hydrology, vegetation and human activities (industrial, agricultural, urbanization) operating over the river water systems. This work is also of interest from a chemometric point of view, specifically for the comparison of the results furnished by PCA and MCR-ALS, which are often used in environmental studies.2,15 Other recent publications are concerned about the presence of persistent organic compounds in Catalonia,16–19 which were also analyzed in several types of environmental compartments. Additionally, other recent examples exist proposing rather similar approaches for the resolution and interpretation of major contamination sources of surface waters operating in several river basins around the world.20 The two main objectives of this work are thus: (1) the investigation of the main long-term diffuse contamination sources of organic contaminants in the Catalonia river basin area, and (2) the estimation of their geographical distribution in order to contribute to the evaluation of the environmental health of the surface waters of the region under study. To achieve these two goals, multivariate data methods of analysis based on PCA and MCR-ALS are applied and compared.
Diffuse and point pollution in the Catalonia River basin area, arising from agriculture, industry and human sewage, is an issue of great concern, since changes in climatic conditions and land use practices have produced large scale adverse impacts on both the water quality and quantity. Through the environmental monitoring program performed at several sampling sites and environmental compartments of the network, a large amount of concentration values of chemicals spread into the Catalonia river basin were obtained. In order to derive useful environmental information from the data, the application of modern chemometric methods based on new multivariate factor analysis21 tools is proposed. The basic assumption of these methods when they are applied to environmental data tables is that each value of a measured variable in a particular sample is due to the sum of contributions from individual independent sources of different origin. Each one of these sources is characterized by a particular chemical composition profile and is distributed among samples in a different way. As a result of the application of chemometric methods, the main point and diffuse sources of contamination in the environment and their origin may be identified and their distribution profiles among samples (geographical, temporal, among environmental compartments) are characterized.
The distribution of contamination sources and their impact over the territory can be assessed by the use of geographical information systems,22,23 by means of cartographic techniques of symbols and pollution prediction maps. Geo-statistical methods24–26 based on mathematical and statistical functions are used, which allow the estimation of continuous surfaces using the measured variables to predict unknown values by interpolation and, at the same time, give an estimation of the errors associated with these predictions.
Finally, it is worth mentioning that the proposed techniques and tools can contribute to the management of the river basins under the application of the Water Framework Directive (2000/60/EC)
2. Experimental
Samples were not taken in a special monitoring design in the zone under study. Sampling was performed at locations previously decided by the Catalan Water Agency, and they were taken once per year, although not every site was studied every year. They were obtained over a period of eight years, from 1997 to 2004. The geographical area under study where these compounds were analyzed covered several small and medium sized rivers in the Catalonia region, such as (from North to South Catalonia coast) Muga, Fluvià, Ter, Daró, Riudaura, Tordera, Besòs, Llobregat, Foix, Gaià, Francolí, Riu de Canyes, Noguera Pallerasa, Noguera Ribagorçana, Segre, Ebre, and Garona rivers (see the location of these rivers in Fig. 1). With the exception of the last five rivers, the remaining ones are typical Mediterranean rivers, characterized by short length and small catchment areas, steep slopes and drastic flow variations during the dry summer season, and sudden flow increases after the fall and spring rains that often cause floods and damage.These datasets have been analyzed as they were provided by the Catalan Water Agency, and no attempt was made to have an optimal design of the best sampling sites for the purpose of environmental source identification. It should thus be noted that because of these sampling limitations, information about temporal evolution of the river contamination sources in Catalonia rivers could only be obtained in a limited way. These results should be confirmed with new data obtained using a better designed monitoring sampling plan, including the data obtained in more recent years. Some work is pursued at present in this direction.
Water samples were collected from the already numbered points of the quality network established by the Catalan Institution of water (‘Agencia Catalana de l'Aigua’), indicated in Fig. 1. Samples were kept in 1 liter glass bottles fitted with Teflon-lined caps, leaving no headspace. After sampling, they were preserved in the fridge (not exceeding 5 °C) until the moment of performing the analysis.27
The following volatile compounds were analyzed in the samples: ethylbenzene, m- and p-xylene, and toluene using headspace analysis with gas chromatography with a flame ionization detector (GC-FID).28,29 Headspace analysis was performed with a Varian Genesis headspace autosampler connected to a Varian Star 3600 gas chromatograph. Samples were equilibrated at 70 °C for 4 min, mixed at 80% of full power for 7 min, and after mixing, stabilized for 1 min. The sample loop volume was 1 mL, the line and valve were maintained at 150 °C and vials were pressurized at 7 psi. These conditions resulted in the highest sensitivity and reproducibility. Compounds were separated on a 75 m × 0.53 mm i.d. × 3 μm film DB-624 fused-silica column from J&W. The GC operating temperatures were: injector 160 °C, detector 300 °C, oven 40 °C (5 min) programmed at 5 °C min−1 to 250 °C. Helium at 9 psi was the carrier gas.
Other volatile compounds, 1,1,1-trichloroethane, 1,2-dichloropropane, 1,2,4-trichlorobenzene, 1,2-dichlorobenzene, bromodichloromethane, bromoform, chloroform, dibromochloromethane, tetrachloroethylene, carbon tetrachloride, and trichloroethylene, were analyzed by headspace analysis with gas chromatography with an electron capture detector (GC-ECD).28,29 Headspace analysis was performed with a Varian Genesis headspace autosampler connected to a Varian Star 3600 gas chromatograph. Samples were equilibrated at 70 °C for 4 min, mixed at 80% of full power for 7 min, and, after mixing, stabilized for 1 min. The sample loop volume was 1 mL, the line and valve were maintained at 150 °C and vials were pressurized at 7 psi. These conditions resulted in the highest sensitivity and reproducibility. Compounds were separated on a 30 m × 0.32 mm i.d. × 1.8 μm film DB-624 fused-silica column from J&W. The GC operating temperatures were: injector 160 °C, detector 300 °C, oven 40 °C (5 min) programmed at 6 °C min−1 to 140 °C (1 min) and at 15 °C min−1 to 220 °C (5 min), and helium was the carrier gas at 7 psi.
The following compounds, chlorpyrifos, diazinon, fenitrothion, malathion, acenaphthene, acenaphthylene, anthracene, phenanthrene, fluoranthene, fluorene, pyrene, 4,4′-dichlorodiphenyldichloroethane (DDD), 4,4′-dichlorodiphenyldichloroethylene (DDE), 4,4′-dichlorodiphenyltrichloroethane (DDT), α-, β-, δ- and γ-hexachlorocyclohexane, endosulfan I, endosulfan II, endosulfan sulfate, and hexachlorobenzene, were analyzed by liquid–liquid extraction according to the method 625 from the U.S. Environmental Protection Agency.30 One liter of sample was added with internal standards (anthracene-d10 and decachlorobiphenyl) and extracted twice with dichloromethane (150 mL and 100 mL) by stirring for 10 min. The organic extracts were combined and dried with anhydrous Na2SO4. Dichloromethane was removed under reduced pressure, first in a round bottom flask and further in a conic flask, until a volume of 0.5 mL. The concentrate was transferred to a 1 mL conical vial, the flask was washed with isooctane, and dried under N2 stream until a final volume of 100 μL for high-resolution gas chromatography with mass spectroscopy detection (HRGC/MS) and/or with electron capture detection (HRGC/ECD) analysis. A surrogate standard mixture (nitrobenzene-d5, 2-fluorobiphenyl and 4-terphenyl-d14) was added to the extract.
Final extracts were analyzed by HRGC. Organochlorine pesticides (4,4′-dichlorodiphenyl-dichloroethane (DDD), 4,4′-dichlorodiphenyldichloroethylene (DDE), 4,4′-dichlorodiphenyltrichloroethane (DDT), α-, β-, δ- and γ-hexachlorocyclohexane, endosulfan I, endosulfan II, endosulfan sulfate, and hexachlorobenzene) were quantified by HRGC/ECD and their structural identity was confirmed by HRGC/MS. The other pesticides and PAH (chlorpyrifos, diazinon, fenitrothion, malathion, acenaphthene, acenaphthylene, anthracene, phenanthrene, fluoranthene, fluorene, and pyrene) were identified and quantified by HRGC/MS.
HRGC/MS was performed on an integrated quadrupole GC/MS MD-800 from Fisons (Manchester, UK). Helium was used as a carrier gas (at a constant flow of 1.2 mL min−1) in a DB-5MS column (30 m × 0.25 mm i.d., 0.25 μm film thickness). The program was from 90 °C (held for 5 min) to 240 °C at 6 °C min−1 and to 310 °C (maintained for 10 min) at 10 °C min−1. The injector temperature was 280 °C, and the injection mode was splitless for 90 s. The scanning was in 40–500 m/z at 1 scan per second. MS spectra were compared with the NIST spectral library (62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 235 spectra) and with Wiley spectral library 5th edn (138
235 spectra) and with Wiley spectral library 5th edn (138![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111 spectra), and each compound was identified according to its best mass spectrum fitting. The HRGC/ECD analysis was performed on a Shimadzu GC-9A model gas chromatograph equipped with an ECD-9 model detector from the same firm. Helium was used as a carrier gas at a flow rate of 2.6 mL min−1 in a DB-5 column (30 m × 0.2 mm i.d., 0.25 μm film thickness). The program was from 130 °C (held for 1 min) to 140 °C (maintained for 1 min) at 12 °C min−1, and from 140 °C to 310 °C at 4 °C min−1; the final temperature was further held for 10 min. The injector and detector temperature was 290 °C and the injection mode was splitless for 1 min.
111 spectra), and each compound was identified according to its best mass spectrum fitting. The HRGC/ECD analysis was performed on a Shimadzu GC-9A model gas chromatograph equipped with an ECD-9 model detector from the same firm. Helium was used as a carrier gas at a flow rate of 2.6 mL min−1 in a DB-5 column (30 m × 0.2 mm i.d., 0.25 μm film thickness). The program was from 130 °C (held for 1 min) to 140 °C (maintained for 1 min) at 12 °C min−1, and from 140 °C to 310 °C at 4 °C min−1; the final temperature was further held for 10 min. The injector and detector temperature was 290 °C and the injection mode was splitless for 1 min.
Pentachlorophenol was derivatized to its acetyl pentachloro derivative by treatment with 0.7 mL of acetic anhydride. For the extraction, 1 mL of hexane was previously added to 100 mL of sample, and 0.7 g of NaHCO3 were added to the water sample as a buffer. The organic extract was transferred to a 1 mL vial for analysis by HRGC/MS. Final extracts were analyzed by HRGC/MS with an integrated quadrupole GC/MS MD-800 from Fisons (Manchester, U.K.). Helium was used as a carrier gas (at a constant flow of 1.2 mL min−1) in a DB-5MS column (30 m × 0.25 mm i.d., 0.25 μm film thickness). Chromatograms were recorded under time-scheduled selected ion monitoring (SIM) using acquisition windows from 5 to 28 min, and 266, 264, 268, 308 m/z values. The dwell time was set at 0.08 s. The program was from 90 °C (held for 2 min) to 130 °C (0 min) at 15 °C min−1, and from 130 °C to 310 °C at 10 °C min−1; the final temperature was further held for 5 min. The injector temperature was 280 °C, and the injection mode was splitless for 90 s.31,32
3. Chemometric methods
3.1. Data pre-treatment
Datasets were organized in one data table or data matrix. The rows of this data matrix identified samples from the various geographical sites and sampling dates, while columns (variables) represent the analyzed chemical compounds. Dimensions of the data matrix were 303 × 37, corresponding to 303 observations (sampling sites and times) and 37 analyzed compounds. Prior to the application of chemometric data processing, the different variables contained in the data matrix were evaluated. Variables the concentrations of which were only 5% over the limit of detection were removed, because they did not provide useful information. In other cases, for other variables having a significant amount of values above their detection limit, the remaining values below the limit of detection were replaced by half of this limit.20 The distribution of variables was studied, and values which were very far from the mean of the distribution were replaced by the maximum value of the specific variable in the same sample site when this value was excluded.Scaling the elemental values over the sample is generally recommended, because the different compound concentrations can have large variations among them. Normalizing the concentrations will provide more equal weight to chemical species with substantially different concentrations. However, it should be kept in mind that scaling will lose information on the relative size and relative errors associated with the various data variables.
In determining the best data pretreatment method, a compromise was sought to find the method which provided the easiest and more optimal interpretation of possible contamination sources. The following data pretreatment methods were investigated: (1) concentration values were log-transformed, i.e. the decimal logarithm of all data matrix values was calculated; this transformation of experimental data has been recommended for skewed datasets,33,34 such as those usually found in environmental studies, where a large amount of the values are low, with a minor global contribution of high values, (2) log concentration values of each compound in the several samples were mean centered, i.e. the mean of the log concentration values of the same compound in the several samples (the mean of each column variable of the data matrix) was subtracted from each log concentration value, (3) log concentration values of each compound in the several samples were scaled, i.e. each log concentration value was divided by the standard deviation of the log concentration values of the same compound in the several samples (standard deviation of each column variable of the data matrix), (4) log concentration values of each compound in the several samples were auto-scaled, i.e. previous mean centering and unit variance scaling pretreatment methods were combined, (5) data were scaled based on either the whole set of values or on a yearly basis, (6) MinMax transformation (also known as range-scaling or feature scaling), and (7) MinMax of log concentration values (the two last ones explained in more detail below).
Of all the data pre-processing methods mentioned above, the MinMax with logarithmical transformation was the most successful one, hence some additional details are provided below. The specific expression for the MinMax transformation is:
 | (1) |
3.2. PCA
PCA assumes a bilinear model to explain the observed data variance using a reduced number of components, which are orthogonal. For a detailed description of this well-known methodology in chemometrics and other multivariate statistical data analysis methods see ref. 4 and 5. The bilinear decomposition may be written by the element wise equation: | (2) |
| D = XYT + E | (3) |
3.3. MCR-ALS
MCR-ALS35,36 works with the data array arranged in a column-wise augmented data matrix Daug, as that for PCA (described in the previous section). The bilinear decomposition of the augmented matrix Daug is performed according to the same expression already given for PCA [i.e.eqn (3)]. Although only the recovered information in YT appears to be explicitly related to one of the three modes, the matrix X implicitly contains the information related to the matrices X and Z in the remaining two modes, and they can be recovered by appropriate refolding followed by singular value decomposition (SVD) analysis, as described before for PCA. In contrast to PCA, however, during the ALS optimization phase of MCR-ALS, the selected constraints were non-negativity for the profiles in both modes (for the augmented scores mode and for the loadings in the second mode), while the loadings in the second mode were normalized to equal length.3.4. MCR-ALS for trilinear models
Trilinear models can be implemented iteratively as a constraint during ALS optimization in the MCR-ALS method.37,38 The application of MCR-ALS using this constraint should not be considered to be equal to a standard bilinear decomposition of the augmented two-way data matrix Daug. During the ALS optimization, each individual profile of the augmented scores matrix X is constrained to fulfill the trilinearity condition independently and iteratively. The same procedure used previously for the recovery of the loadings in the three modes from the augmented scores matrix obtained by PCA or MCR-ALS is applied now inside/during the ALS optimization instead of at the end of the optimization as in PCA. Each column of the X matrix is appropriately folded at each ALS iteration step to give a matrix with the number of rows equal to the number of sampling sites and eight columns corresponding to each of the years (1997–2004). SVD of this folded scores matrix gives the loadings in the first and third modes for the considered component. These two loadings describe the common variation captured by ALS in the two modes (sampling sites and years) for that particular component. The Kronecker product39–41 of these two new loading vectors gives the new augmented scores vector which substitutes the corresponding column of the X scores matrix. When this constraint is inserted during each step of the ALS iterative optimization procedure, it forces the shape of the loadings vector in the first mode (describing the sampling site variation of the considered component) to be the same for the eight years. Moreover, it captures the intensity (scale) variation of this component in the loadings of the third mode, showing the scale differences of this component among the eight years. This is precisely what is implied by the trilinear PARAFAC42 model and, in practice, results obtained by MCR-ALS with the trilinearity constraint applied to all the components of the system should give practically the same results as the application of PARAFAC model based methods. However, the main advantage of the trilinearity constraint in MCR-ALS over the PARAFAC model based methods is that this procedure in MCR-ALS is applied independently for each component and that it is not compulsory to apply it for all the resolved profiles in X. Actually, several columns of the X matrix can be constrained in several manners during MCR-ALS. This makes a clear distinction with PARAFAC where all resolved components should fulfill the sought trilinear condition.4. Results and discussion
In Table 1, a summary of the descriptive statistics obtained in the analysis of the previously referred compound using the procedure described above is given. In this table, for every compound analyzed, the minimum (usually at the limit of detection), the maximum value, the mean, the median, the standard deviation and the % of values above the detection limit are given. This database contains 37 compounds measured in several sampling sites from Catalonia rivers between the years 1997 and 2008, during a total of 8 years. The sampling sites were 35 but samples were not taken from all sites in all campaigns. For this reason, the size of the matrix was 303 × 37, where the first mode includes all samples taken in different sites and times, and the second mode contains the measured chemical compounds. In this table, variables are given in their own different scales, which can be very different in some cases, the use of an appropriate scaling preprocessing method being necessary to give them a similar weight during their analysis. When minimum, maximum, average and median values are observed, it is easily concluded that data distribution is not following a normal distribution of values and that probably are better described by a log normal distribution of values. This indicates the possibility of using log transformation of data to better investigate the data variance and to decrease the weight of extreme variable values.| Min | Max | Mean | Median | Std. dev. | % data | |
|---|---|---|---|---|---|---|
| Ethylbenzene | 0.25 | 9.4 | 0.3 | 0.25 | 0.6 | 2.6 |
| m,p-Xylene | 0.25 | 33.2 | 0 | 0.25 | 2 | 5.3 |
| Toluene | 0.3 | 644 | 0 | 0.3 | 40 | 5.6 |
| Chlorpyrifos | 5 | 1452 | 10 | 5 | 90 | 13.5 |
| Diazinon | 5 | 3894 | 0 | 16 | 200 | 62.4 |
| Fenitrothion | 5 | 201 | 0 | 5 | 20 | 7.3 |
| Malathion | 5 | 338 | 0 | 5 | 30 | 2.0 |
| Acenaphthene | 2 | 919 | 0 | 2 | 50 | 17.2 |
| Acenaphthylene | 2 | 255 | 0 | 2 | 20 | 8.9 |
| Anthracene | 2 | 34 | 2 | 2 | 2 | 3.0 |
| Phenanthrene | 2 | 245 | 10 | 6 | 30 | 64.0 |
| Fluoranthene | 2 | 16 | 3 | 2 | 2 | 23.1 |
| Fluorene | 2 | 201 | 0 | 2 | 20 | 33.3 |
| Pyrene | 2 | 52 | 4 | 2 | 5 | 35.3 |
| PCL–phenol | 0.01 | 1.45 | 0.04 | 0.035 | 0.08 | 97.4 |
| 4,4′-DDD | 0.5 | 141 | 1 | 0.5 | 8 | 4.0 |
| 4,4′-DDE | 0.1 | 61.2 | 0 | 0.1 | 4 | 2.3 |
| 4,4′-DDT | 0.5 | 152 | 2 | 0.5 | 10 | 3.3 |
| α-Hexachlorocyclohexane | 0.1 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 675 675 |
0 | 0.1 | 1000 | 14.5 |
| β-Hexachlorocyclohexane | 0.5 | 2706 | 0 | 0.5 | 200 | 5.3 |
| δ-Hexachlorocyclohexane | 0.1 | 1679 | 0 | 0.1 | 100 | 3.0 |
| Endosulfan I | 0.1 | 544.7 | 0 | 0.1 | 30 | 12.5 |
| Endosulfan II | 0.5 | 273 | 0 | 0.5 | 20 | 9.2 |
| Endosulfan sulfate | 0.5 | 465 | 0 | 0.5 | 40 | 12.9 |
| Hexachlorobenzene | 0.1 | 74 | 1 | 0.1 | 6 | 8.3 |
| Lindane(γ-hexachlorocyclohexane) | 0.1 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 308 308 |
0 | 5.8 | 1000 | 90.1 |
| 1,1,1-Trichloroethane | 0.025 | 1.2 | 0 | 0.025 | 0.1 | 17.8 |
| 1,2-Dichloropropane | 3 | 93 | 4 | 3.5 | 8 | 99.7 |
| 1,2,4-Trichlorobenzene | 0.1 | 4.2 | 0.1 | 0.1 | 0.3 | 2.6 |
| 1,2-Dichlorobenzene | 0.25 | 12.3 | 0.3 | 0.25 | 0.7 | 1.3 |
| Bromodichloromethane | 0.025 | 3.12 | 0.1 | 0.025 | 0.2 | 34.3 |
| Bromoform | 0.05 | 6.71 | 0.1 | 0.05 | 0.4 | 21.8 |
| Chloroform | 0.025 | 8.6 | 0 | 0.025 | 1 | 41.6 |
| Dibromochloromethane | 0.025 | 6.39 | 0.1 | 0.025 | 0.4 | 34.3 |
| Tetrachloroethylene | 0.025 | 21.3 | 0 | 0.06 | 2 | 57.4 |
| Carbon tetrachloride | 0.025 | 0.94 | 0 | 0.025 | 0.1 | 19.1 |
| Trichloroethylene | 0.025 | 20 | 0 | 0.025 | 2 | 45.2 |
Since in this work source apportionment was intended, data were not initially mean centered. In multivariate curve resolution and source apportionment and receptor modeling studies, the main interest is in actual values and not in their deviations from the mean. MinMax was the finally preferred data pre-processing tool, because it minimized differences in variable scales, allowing the comparison of results without giving more weight or importance to a particular variable. MinMax was applied separately to samples of each campaign rather than jointly to the entire database, decreasing in this way the differences among the several campaigns and thus providing a better comparison of the variation of the compound concentrations within them. The first approximation to estimate the number of components was obtained by PCA, which indicates the number of possible major independent sources of pollution affecting the measured data. The number of components was estimated by examining the size of the changes in explained variance in PCA as a function of the number of principal components. Three components were proposed to model the MinMax pre-processed data matrix, which allowed us to explain 62.9% of the overall variance.
In Fig. 2, loadings obtained by PCA are shown. It can be observed that the first component (34.9% of the variance explained) describes the average contamination affecting the geographical region under study over the investigated years, and the other two are components describing the contrast with more specific contamination sources. The second component (15.5% of the variance explained) highlights the contamination coming from some pesticides such as hexachlorocyclohexane (alpha, beta and delta isomers, as well as the gamma isomer lindane), endosulfan (I, II and sulfate) and diazinon. Finally, the third component (12.9% of the variance explained) describes the different behavior of the halomethanes (bromodichloromethane, chloroform, dibromochloromethane), chlorinated ethenes (tetrachloroethylene, trichloroethylene), carbon tetrachloride, chlorobenzenes and halopropanes.
The corresponding PCA scores describe the geographical distribution of these contamination patterns, marking what sites were more highly contaminated on the average (PC1 scores) and what sites were more affected by more specific agricultural contamination sources (PC2 scores) and by more industrially related contamination sources (PC3 scores). Because PCA defines the same vector space as the one obtained by MCR-ALS decomposition using the same number of components (see below), PCA score plots have been omitted for brevity. An advantage of MCR-ALS over PCA is the possibility of applying natural constraints like non-negativity, making easier the physical interpretation of the results. For this reason, the discussion about the possible sources or patterns was mainly focused on MCR-ALS results.
4.1. MCR-ALS results of the complete dataset applying non-negativity constraints
MCR-ALS was first applied to the complete dataset (37 compounds in all sampling sites and in 8 years) with non-negativity constraints. The trilinearity constraint could not be applied in this case, since not all the sites were sampled in all the campaigns and therefore the dataset could not be arranged as a three-way data array. The explained variance was 61.1% for three components. These three components are interpreted in environmental terms as follows (see Fig. 3).The first component (Fig. 3 and 4) (33.8% of the total variance explained) is dominated by PAHs (polycyclic aromatic hydrocarbons, i.e. acenaphthene, phenanthrene, fluoranthene, fluorene, pyrene, etc.), THMs (trihalomethanes, chloroform, bromoform, bromodichloromethane) and minor contributions of other compounds such as chlorinated ethenes (tri and perchloroethylene). The former group of compounds reflects diffuse contamination related to combustion engines, characteristic of areas with heavy traffic and industry. The second group can be associated with disinfection by-products generated during the chlorination treatment of drinking water and returned to the environment through discharges from WWTP. As a whole, the contamination pattern described by this first component corresponds to areas with heavy industrial and urban pressure. It is mainly located in Barcelona and its surrounding metropolitan area.
The second component (Fig. 3 and 5) (14.8% of the total variance explained) is dominated by DDT related compounds (DDT and its metabolites DDD and DDE), hexachlorobenzene, halomethanes (bromodichloromethane, chloroform, dibromochloromethane), chlorinated ethenes (tetrachloroethylene, trichloroethylene), carbon tetrachloride, and minor contributions of chlorobenzenes and halopropanes. Such a profile is specifically related to the chloro-alkali industry located in the low Ebro (Flix), which at present manufactures these chlorinated solvents, but was also a major producer of DDT in the past. Even though the production of DDTs was discontinued after their banning in Europe, the reported presence of polluted sediments in the river still generates downstream Flix a background contamination of DDT (and mostly its metabolites DDE and DDD). Hexachlorobenzene is also generated in the same chloro-alkali chemical plant as a by-product during the electrolysis process.
 | ||
| Fig. 5 Same as Fig. 4, corresponding to the second MCR-ALS component. | ||
The third component (Fig. 3 and 6) (12.5% of the total variance explained) is dominated by pesticides such as diazinon, chlorpyrifos, fenitrothion, malathion, hexachlorocyclohexane (alpha, beta and delta isomers, as well as the gamma isomer lindane), endosulfan (I, II and sulfate), and other minor contributors such as pentachlorophenol and chlorinated solvents. The strong presence of these pesticides is consistent with its occurrence in agriculture dominated areas, such as Lleida or the rural areas in the neighborhood of the Barcelona metropolitan area (Maresme, Anoia etc.) or the floodplains and deltas of the main rivers, all of them characterized by intensive agriculture.
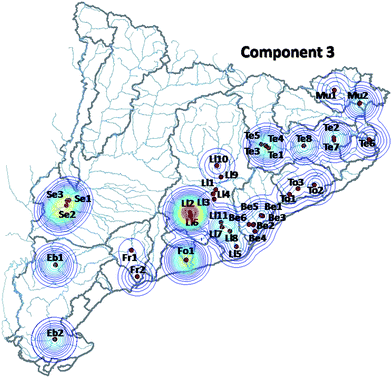 | ||
| Fig. 6 Same as Fig. 4, corresponding to the third MCR-ALS component. | ||
Fig. 4–6 summarize the geographical distribution of these three major contamination patterns previously described. These plots were obtained averaging the scores of all the campaigns in a single matrix to simplify their visualization.
4.2. MCR-ALS results of the reduced dataset by applying non-negativity and trilinearity constraints
From the 37 compounds included in the original database, 24 (see Table 1) were removed because the corresponding concentrations were not measured in all campaigns and all sites. The remaining 13 compounds were diazinon, phenanthrene, fluoranthene, fluorene, pyrene, pentachlorophenol, γ-hexachlorocyclohexane (lindane), 1,1,1-trichloroethane, bromodichloromethane, chloroform, dibromochloromethane, tetrachloroethylene and trichloroethylene. A new dataset was built with only these 13 compounds measured in 17 sampling sites at 8 campaigns. The whole dataset gave a data table or matrix of size 136 × 13, i.e. concentrations of the 13 compounds in the 136 different samples.MCR-ALS was then conducted in two manners: (1) by only applying the non-negativity constraint to loadings and scores, and (2) by applying non-negativity and also trilinearity constraints.37,38 This latter constraint is more restricted, leading to a decreased percentage of explained variance, but it has the advantage of separating the between year campaign patterns of the resolved components. It demands some data reorganization, in such a way that all campaigns display the same number of sampling sites, leaving only 17 studied locations. Results obtained by these two MCR-ALS analyses were rather similar, in terms of explained variances, 61.2% and 54.4% for the two approaches respectively, and also resulted rather similar in relation to the composition of the resolved components. This suggested that the data could be approximated by the trilinear model, giving more easily interpretable component profiles, especially in terms of the distribution and geographical representation (mapping) of the resolved components describing the different contamination patterns under study. For brevity only the results obtained using the trilinearity constraint are finally given in this discussion.
Fig. 7 shows the results corresponding to the non-negativity/trilinearity constrained MCR-ALS study. If the loading profiles corresponding to the different variables are compared, some patterns are observed always in the different components. Three different patterns grouping different compounds were identified (total explained variance of 54.4%): (1) the first component (30.1% of the total variance explained) is dominated by diazinon, phenanthrene, fluoranthene, fluorene, pyrene, lindane, tetrachloroethylene and trichloroethylene; (2) the second component (13.2% of the total variance explained) is dominated by phenanthrene, fluoranthene, fluorene, pyrene, bromodichloromethane, chloroform, and dibromochloromethane, and (3) the third component (11.1% of the total variance explained) is dominated by pentachlorophenol, 1,1,1-trichloroethane, tetrachloroethylene and trichloroethylene. Once identified the chemical composition of the main contamination patterns, the localization of these patterns and the corresponding possible sources are investigated.
The first MCR-ALS component or contamination pattern (30.1%) defined by the first group of compounds (see above) is mainly localized in the following sampling sites (see Fig. 7): (1) Anoia river, Vilanova del Camí, (2) Foix river, Castellet i la Gornal, and (3) Clamor de les Canals, Lleida. All these sampling points correspond to rural and middle sized villages and also according to the composition of this possible source identifies a general contamination source of mixed agricultural and population sources. Second (13.2%) and third (11.1%) components are focused on regions near Barcelona (Fig. 7) and give patterns corresponding to industrial and heavy population sources. Specifically, the second component corresponds to (1) Congost river, Montornès del Vallès, (2) Besòs river, Montcada i Reixac and Santa Coloma de Gramenet, Barcelonès, and (3) Riera de Rubí, Castellbisbal. Finally, the third component is localized in (1) Mogent river, Montornès Del Vallès, (2) Besòs river, Montcada i Reixac, (3) Besòs river, Santa Coloma de Gramenet, Barcelonès, and (4) Llobregat river, Abrera. As regarding the time evolution of these components, it can be concluded that both the first and third components have a growing trend over time, while the second one appears to be decreasing.
Results obtained with trilinearity and non-negativity constraints do agree with previous results obtained by modeling the whole dataset with MCR-ALS bilinear modeling. Again three MCR components were used to justify the observed data variance. Interpreting the composition and location of each component we can conclude that the first component can be associated with the presence of several pesticides related to agriculture activities, the second component can be associated with combustion engines characteristic of areas with heavy traffic and industry, and the third component profile can be specifically related to the chloro-alkali industry.
5. Conclusions
In this work, MCR-ALS is applied to investigate major contamination patterns affecting river basins of a particular geographical region over several years of monitoring and analysis. MCR-ALS with non-negativity and with or without trilinearity constraints resulted to be an efficient tool to resolve the major contamination patterns explaining the measured data variance. Three major contamination patterns were detected, which were respectively related to agriculture activities, industrial activities and the chlorination treatment of drinking water. Areas where these major contamination patterns were more relevant were then displayed using appropriate mapping tools.An additional conclusion of this work is the demonstration of data summarizing and interpretation possibilities obtained by the application of chemometric methods to large environmental datasets stored by official environmental agencies for their improved quality management and interpretation.
Acknowledgements
The authors acknowledge the following institutions for financial support: Agencia Española de Cooperación Internacional, Universidad Nacional de Rosario, CONICET (Consejo Nacional de Investigaciones Científicas y Técnicas), ANPCyT (Agencia Nacional de Promoción Científica y Tecnológica) and Catalan Water Agency (l'Agència Catalana de l'Aigua) for providing the data.References
- G. Hanrahan, in Environmental Chemometrics: Principles and Modern Applications (Analytical Chemistry), Taylor & Francis Group, Michigan, 2008 Search PubMed.
- D. L. Massart, in Handbook of chemometrics and qualimetrics, ed. B. G. M. Vandeginste, L. M. C. Buydens, S. de Jong, P. J. Lewi and J. Smeyers-Verbeke, Elsevier, Amsterdam, 1998 Search PubMed.
- J. W. Einax, in Chemometrics in environmental chemistry, ed. H. W. Zwanzinger and S. Geiss, VCH, Weinham, 1997 Search PubMed.
- I. T. Jolliffe, in Principal component analysis, Springer, New York, 2003 Search PubMed.
- S. Wold, K. Esbensen and P. Geladi, Principal component analysis, Chemom. Intell. Lab. Syst, 1987, 2, 37–52 CrossRef CAS.
- M. Manz, K. D. Wenzel, U. Dietze and G. Schüürmann, Persistent organic pollutants in agricultural soils of central Germany, Sci. Total Environ., 2001, 277, 187–198 CrossRef CAS PubMed.
- C. Backe, I. T. Cousins and P. Larsson, PCB in soils and estimated soil–air exchange fluxes of selected PCB congeners in the south of Sweden, Environ. Pollut., 2004, 128, 59–72 CrossRef CAS PubMed.
- S. P. Mujunen, P. Minkkinen, B. Holmbom and A. Oikari, PCA and PLS methods applied to ecotoxicological data: ecobalance project, J. Chemom., 1996, 10, 411–424 CrossRef CAS.
- U. Dietze, T. Braunbeck, W. Honnen, H. R. Köhler, J. Schwaiger and H. Segner, Chemometric discrimination between streams based on chemical, limnological and biological data taken from freshwater fishes and their interrelationships, J. Aquat. Ecosyst. Stress Recovery, 2001, 8, 319–336 CrossRef CAS.
- E. Peré-Trepat, M. Petrovic, D. Barceló and R. Tauler, Application of chemometric methods to the investigation of main microcontaminant sources of endocrine disruptors in coastal and harbour waters and sediments, Anal. Bioanal. Chem., 2004, 378, 642–654 CrossRef PubMed.
- R. Tauler, D. Barceló and E. M. Thurman, Multivariate correlation between concentrations of selected herbicides and derivatives in outflows from selected US midwestern reservoirs, Environ. Sci. Technol., 2000, 34, 3307–3314 CrossRef CAS.
- M. Terrado, D. Barceló and R. Tauler, Quality assessment of the multivariate curve resolution alternating least squares (MCR-ALS) method for the investigation of environmental pollution patterns, Environ. Sci. Technol., 2009, 43, 5321–5326 CrossRef CAS PubMed.
- R. Tauler, S. Lacorte, M. Guillamon, R. Cespedes, P. Viana and D. Barceló, Chemometric modeling of main contamination sources in surface waters of Portugal, Environ. Toxicol. Chem., 2004, 23, 565–575 CrossRef CAS PubMed.
- E. D. Malinowski, in Factor analysis in chemistry, John Wiley & Sons, New York, 3rd edn, 2002 Search PubMed.
- R. B. Cattell, in The scientific use of factor analysis in behavioral and life sciences, Plenum, New York, 1978 Search PubMed.
- E. Teixidó, L. Olivella, M. Figueras, A. Ginebreda and R. Tauler, Multivariate exploratory data analysis of the organic micropollutants found in the Llobregat River (Catalonia, Spain), Int. J. Environ. Anal. Chem., 2001, 81, 295–313 CrossRef.
- M. Terrado, D. Barceló and R. Tauler, Multivariate curve resolution of organic pollution patterns in the Ebro River surface water–groundwater–sediment–soil system, Anal. Chim. Acta, 2010, 657, 19–27 CrossRef CAS PubMed.
- J. Sánchez-Avila, J. Meyer and S. Lacorte, Spatial distribution and sources of perfluorochemicals in the NW Mediterranean coastal waters (Catalonia, Spain), Environ. Pollut., 2010, 158, 2833–2840 CrossRef PubMed.
- M. Petrovic, M. Farré, M. Lopez de Alda, S. Perez, C. Postigo, M. Köck, J. Radjenovic, M. Gros and D. Barcelo, Recent trends in the liquid chromatography-mass spectrometry analysis of organic contaminants in environmental samples, J. Chromatogr., A, 2010, 1217, 4004–4017 CrossRef CAS PubMed.
- I. M. Fharnham, A. K. Singh, K. J. Stetzenbach and K. H. Lohannesson, Treatment of nondetects in multivariate analysis of groundwater geochemistry data, Chemom. Intell. Lab. Syst., 2002, 60, 265–281 CrossRef.
- A. Smilde, in Multi-Way Analysis with Applications in the Chemical Sciences, ed. R. Bro and P. Geladi, John Wiley & Sons Ltd., New York, 2004 Search PubMed.
- D. Comas and E. Ruiz, in Fundamentos de los Sistemas de Información Geográfica, Arial Geografía, Barcelona, 1993 Search PubMed.
- J. Gutiérrez-Puebla and M. Gould, in Sistemas de Información Geográfica, Síntesis, Madrid, 1994 Search PubMed.
- F. Calvete and J. Carrera, in Geoestadística: Aplicaciones a la hidrología subterránea, Centro Internacional de Métodos Numéricos en Ingeniería, UPC, Barcelona, 1990 Search PubMed.
- N. Cressie, in Statistics for Spatial Data, JohnWiley & Sons Inc., New York, 1993 Search PubMed.
- P. Goovaerts, in Geostatistics for Natural Resources Evaluation, Oxford University Press, 1997 Search PubMed.
- E. Teixidó, L. Olivella, M. Figueras, A. Ginebreda and R. Tauler, Multivariate exploratory data analysis of the organic micropollutants found in the Llobregat River (Catalonia, Spain), Int. J. Environ. Anal. Chem., 2001, 81, 295–313 CrossRef.
- U.S. Environmental Protection Agency, Method 624 – Purgeables, 40 CFR Part 136, Federal Register 49, No. 209, 1984, p. 43373.
- T. A. Bellar, Method 503.1-Revision 2.0, Volatile aromatic and unsaturated organic compounds in water by purge and trap gas chromatography, U.S. Environmental Protection Agency, 1989 Search PubMed.
- U.S. Environmental Protection Agency, Method 625, Guidelines Establishing Test Procedures for the Analysis of Pollutants Under the Clean Water Act: Final Rule and Interim Final Rule and Proposed Rule, Federal Register, October 26, 1984, vol. 49(209), pp. 153–174.
- K. Abrahamsson and T. M. Xie, Direct determination of trace amounts of chlorophenols in fresh water, waste water and sea water, J. Chromatogr., 1983, 279, 199–208 CrossRef CAS PubMed.
- H. Lee, L. Weng and A. S. Chau, Chemical derivatization analysis of pesticides residues. VIII. Analysis of 15 chlorophenols in natural water by in situ acetylation, J.–Assoc. Off. Anal. Chem., 1984, 67(4), 789–794 CAS.
- J. Grimalt, L. Canton and J. Olive, Source input elucidation in polluted coastal systems by factor-analysis of sedimentary hydrocarbon data, Chemom. Intell. Lab. Syst., 1993, 18, 93–109 CrossRef CAS.
- V. Zitko, Principal component analysis in the evaluation of environmental data, Mar. Pollut. Bull., 1994, 28, 718–722 CrossRef CAS.
- R. Tauler, A. Smilde and B. Kowalski, Selectivity, local rank, 3-way data analysis and ambiguity in multivariate curve resolution, J. Chemom., 1995, 9, 31–58 CrossRef CAS.
- R. Tauler, Multivariate Curve Resolution Applied to Second Order Data, Chemom. Intell. Lab. Syst., 1995, 30, 133–146 CrossRef CAS.
- R. Tauler, I. Marques and E. Casassas, Multivariate curve resolution applied to three-way trilinear data: study of a spectrofluorimetric acid–base titration of salicylic acid at three excitation wavelengths, J. Chemom., 1998, 12, 55–75 CrossRef CAS.
- A. De Juan and R. Tauler, Comparison of three-way resolution methods for non-trilinear chemical data sets, J. Chemom., 2001, 15, 749–771 CrossRef CAS.
- A. Smilde, in Multi-Way Analysis, ed. R. Bro and P. Geladi, JohnWiley & Sons Ltd., Chichester, England, 2004 Search PubMed.
- D. S. Burdick, An introduction to tensor-products with applications to multiway data-analysis, Chemom. Intell. Lab. Syst., 1995, 28, 229–237 CrossRef CAS.
- H. A. L. Kiers, Towards a standardized notation and terminology in multiway analysis, J. Chemom., 2000, 14, 105–122 CrossRef CAS.
- R. Bro, PARAFAC. Tutorial and applications, Chemometrics Intell. Lab. Syst., 1997, 38, 149–171 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2014 |





