View PDF VersionPrevious ArticleNext Article

Open Access Article
This Open Access Article is licensed under a Creative Commons Attribution-Non Commercial 3.0 Unported Licence
DOI: 10.1039/C4CP01432D (Paper) Phys. Chem. Chem. Phys., 2014, 16, 17295-17304

Proton dynamics of two-dimensional oxalate-bridged coordination polymers

Satoshi Miyatsu a, Maiko Kofu a, Atsushi Nagoe ab, Takeshi Yamada ab, Masaaki Sadakiyo cd, Teppei Yamada c, Hiroshi Kitagawa bc, Madhusudan Tyagi e, Victoria García Sakai f and Osamu Yamamuro *ab
aInstitute for Solid State Physics, University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa, Chiba 277-8581, Japan. E-mail: yamamuro@issp.u-tokyo.ac.jp
bCore Research for Evolutional Science and Technology (CREST), Japan Science and Technology Agency (JST), 7 Gobancho, Chiyoda-ku, Tokyo 102-0076, Japan
cGraduate School of Science, Kyoto University, Kitashirakawa Oiwake-cho, Sakyo-ku, Kyoto 606-8502, Japan
dInternational Institute for Carbon-Neutral Energy Research (WPI-I2CNER), Kyushu University, 744 Moto-oka, Nishi-ku, Fukuoka 819-0395, Japan
eNIST Center for Neutron Research, National Institute of Standards and Technology, 100 Bureau Drive, Gaithersburg, Maryland 20899-6102, USA
fISIS Facility, Rutherford Appleton Laboratory, Harwell Science & Innovation Campus, Chilton, Didcot, OX11 0QX, UK

Received 2nd April 2014 , Accepted 1st July 2014

First published on 3rd July 2014

Abstract

A two-dimensional porous coordination polymer (NH4)2{HOOC(CH2)4COOH}[Zn2(C2O4)3] (abbreviated as (NH4)2(adp)[Zn2(ox)3] (adp = adipic acid, ox = oxalate)), which accommodates water molecules between the [Zn2(ox)3] layers, is highly remarked as a new type of crystalline proton conductor. In order to investigate its phase behavior and the proton conducting mechanism, we have performed adiabatic calorimetry, neutron diffraction, and quasi-elastic neutron scattering experiments on a fully hydrated sample (NH4)2(adp)[Zn2(ox)3]·3H2O with the highest proton conductivity (8 × 10−3 S cm−1, 25 °C, 98% RH). Its isostructural derivative K2(adp)[Zn2(ox)3]·3H2O was also measured to investigate the role of ammonium ions. (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O exhibit higher order transitions at 86 K and 138 K, respectively. From the magnitude of the transition entropy, the former is of an order–disorder type while the latter is of a displacive type. (NH4)2(adp)[Zn2(ox)3]·3H2O has four Debye-type relaxations and K2(adp)[Zn2(ox)3]·3H2O has two similar relaxations above each transition temperature. The two relaxations of (NH4)2(adp)[Zn2(ox)3]·3H2O with very small activation energies (ΔEa < 5 kJ mol−1) are due to the rotational motions of ammonium ions and play important roles in the proton conduction mechanism. It was also found that the protons in (NH4)2(adp)[Zn2(ox)3]·3H2O are carried through a Grotthuss mechanism. We present a discussion on the proton conducting mechanism based on the present structural and dynamical information.

1 Introduction

Metal–organic frameworks (MOFs), which are composed of metal ions and organic ligands, have attracted much attention in the last decade due to their applications in gas sorption,1–3 catalysis,4,5 and ionic conductivity.6–12 They are often called porous coordination polymers (PCPs) because they commonly possess a porous structure, a key characteristic of MOFs since the architecture (e.g., size, dimensionality) can be controlled by changing metal ions and ligands.13–15

We have focused on PCPs exhibiting proton conductivity. High-performance proton conductors have an important role in fuel cell applications.16–18 Protons are supplied by acidic groups such as –COOH and –OH (sometimes –NH2 group) on the pore wall and are carried by molecules (in most cases, water molecules) inside the pore.19–21,23,24 For example, in copper rubeanate (H2C2N2S2Cu; H2dtoaCu), the proton conductivity is mainly governed by the protons provided by the –NH2 group in the pore wall. H2dtoaCu adsorbs water in its pores to a maximum hydration of 3.7 molecules at a relative humidity (RH) of 100%. The conductivity at this concentration is 0.01 S cm−1, comparable to that of Nafion, currently the best commercial proton conductor. Our quasi-elastic neutron scattering (QENS) study has revealed that the water inside the pore behaves as bulk water (or free water) above the phase transition temperature, and is condensed on the pore surface below this temperature. This free water plays an important role as the proton carrier.25,26

(NH4)2(adp)[Zn2(ox)3] (adp = adipic acid, ox = oxalate) is one of the PCPs developed in recent years. It has been reported that (NH4)2(adp)[Zn2(ox)3] adsorbs as many water molecules as copper rubeanate and the proton conductivity of the trihydrate sample ((NH4)2(adp)[Zn2(ox)3]·3H2O) is also 0.01 S cm−1.22 Unlike copper rubeanate and Nafion which are amorphous solids, (NH4)2(adp)[Zn2(ox)3] can be synthesized as single crystals, leading to more homogeneous samples with high reproducibility, on which very precise structural work can be performed to investigate the mechanism of proton conduction.

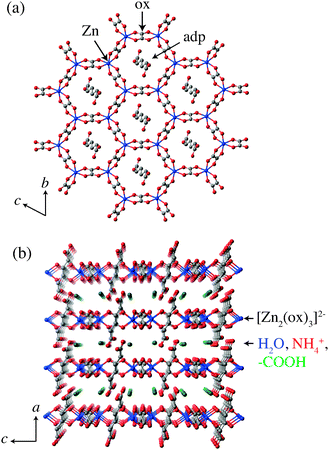
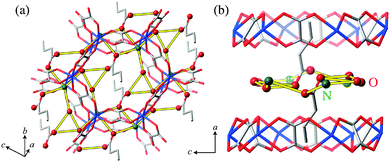
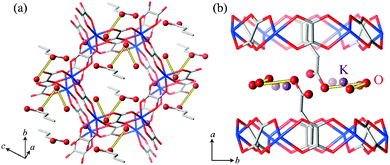
The crystal structure of (NH4)2(adp)[Zn2(ox)3], determined by single-crystal X-ray diffraction measurements,22 is shown in Fig. 1. Two-dimensional honeycomb sheets are formed by an oxalated-bridged framework [Zn2(ox)3]2− and adipic acids penetrate the sheets nearly vertically. There are carboxyl groups of adipic acids, ammonium ions and water molecules in the space between the zinc oxalate layers. We call this space “proton conducting layers”. It is presumed that protons are supplied by carboxyl groups and carried by water molecules and potentially by ammonium ions.


image file: c4cp01432d-f1.tif
Fig. 1 (a) Perspective view along the a-axis of (NH4)2(adp)[Zn2(ox)3]. A honeycomb layer structure is formed by [Zn2(ox)3]2− and adp. (b) Perspective view along the b-axis of (NH4)2(adp)[Zn2(ox)3]. H2O, NH4+, and –COOH groups are located between the layers. Red, green, gray, and blue colors correspond to oxygen, nitrogen, carbon, and zinc atoms, respectively. Water molecules are omitted.

The first purpose of this study is to investigate the phase behavior of (NH4)2(adp)[Zn2(ox)3]·3H2O and clarify the relation between the phase transition, which is associated with water molecules and/or ammonium ions, and the proton conductivity. For this purpose, we have performed adiabatic calorimetry and neutron powder diffraction measurements at temperatures between 5 and 300 K. Next, to reveal the proton-conducting mechanism, QENS measurements have been carried out in a time range between 0.1 ps and 10 ns. The incoherent neutron scattering cross-section of a hydrogen atom (σinc = 80 b, 1 b = 10−24 cm2) is much larger than the incoherent/coherent cross-sections of other atoms such as carbon (σinc = 0 b), nitrogen (σinc = 0.5 b), oxygen (σinc = 0 b), and deuterium (σinc = 2.1 b). Therefore, the self-motions of molecules/ions/functional groups with hydrogen atoms are preferentially detected through the incoherent scattering from hydrogen atoms. For all experiments, we have also investigated K2(adp)[Zn2(ox)3]·3H2O in which ammonium ions are substituted by potassium ions.27 Since K2(adp)[Zn2(ox)3]·3H2O is isostructural with (NH4)2(adp)[Zn2(ox)3]·3H2O, the comparison between the two samples is significant in revealing the function of ammonium ions. It should be pointed out that the proton conductivity of K2(adp)[Zn2(ox)3]·3H2O is 1.2 × 10−4 S cm−1 (25 °C, 98% RH), which is two orders of magnitude smaller than that of (NH4)2(adp)[Zn2(ox)3]·3H2O.27 In the last part of the paper, we discuss the mechanism of proton conductivity in (NH4)2(adp)[Zn2(ox)3]·3H2O on the basis of presently accessible structural and dynamical information.

2 Experimental

2.1 Samples

(NH4)2(adp)[Zn2(ox)3]·3H2O was prepared by a hydrothermal method with zinc oxide, adipamide, and H2(ox)·2H2O in water using an autoclave at 130 °C. In order to remove bulk water and ensure adsorption equilibrium, the sample was kept in a glove bag with relative humidity RH = 98% for a few hours. After this procedure, all sample handling was done in a glove bag at RH > 95%, to avoid transformation of the trihydrate into the dihydrate form below 85% RH.22 K2(adp)[Zn2(ox)3]·3H2O was synthesized from a mixture of zinc oxide, adipic acid, K2(ox)·H2O, and H2(ox)·2H2O in a water solvent using an autoclave at 130 °C.27 The sample was handled in the same manner.

In the neutron scattering experiments, the methylene chains of adipic acid were deuterated in both (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O, such that their contribution to the scattering signal is low, and the majority arises from the motions of the water, ammonium ions, and carboxyl groups.

2.2 Adiabatic calorimetry

The heat capacity measurements were performed using a custom-built adiabatic calorimeter.28 In adiabatic calorimetry, the heat exchange between the sample and the environment is virtually eliminated and the heat capacity is obtained from a simple relation C = ΔE/ΔT. The technique gives the most accurate absolute value of the heat capacity, with a precision and an accuracy of 0.05 and 0.1%, respectively.

(NH4)2(adp)[Zn2(ox)3]·3H2O (0.4153 g; 6.581 × 10−4 mol) was loaded into the sample cell with helium gas (0.1 MPa) for heat exchange, and the cell was sealed with an indium gasket. The temperature range for the heat capacity measurements was from 5 to 300 K. The temperature increment was 0.5 K at around 5 K, gradually increasing up to 2.5 K at around 300 K. The heat capacity of K2(adp)[Zn2(ox)3]·3H2O (1.001 g; 1.487 × 10−3 mol) was measured in the same way.

2.3 Neutron scattering

The dynamics of the molecules and ions in the proton-conducting layers of (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O were probed using three neutron spectrometers with different energy resolutions, to cover timescales between 0.1 ps and 10 ns (five orders of magnitude).
2.3.1 AGNES (direct geometry, time-of-flight type). We have performed elastic fixed-window scans and QENS measurements of (NH4)2(adp)[Zn2(ox)3]·3H2O on AGNES. AGNES is a time-of-flight chopper spectrometer which is owned by the Institute for Solid State Physics (ISSP), University of Tokyo. This instrument is installed on a cold neutron guide (C3-1) of JRR-3, Japan Atomic Energy Agency (JAEA).29,30 Neutrons with a wavelength of 4.22 Å (for the standard mode) or 5.50 Å (for the high resolution mode) are extracted with an array of five pyrolytic graphite (PG) (002) monochromators and pulsed using a double Fermi chopper. The pulsed neutrons are scattered by the sample and detected using 328 3He detector tubes arranged in a wide detector bank covering the scattering angles (2θ) between 10° and 130°. The energy resolutions (full-width at half maximum) and the energy windows are ΔEres = 120 μeV and −20 meV < ℏω < 3 meV in the standard mode and ΔEres = 49 μeV and −10 meV < ℏω < 1.5 meV in the high resolution mode. These settings correspond to time ranges between 0.1 and 50 ps and 1 and 100 ps, in the standard and high resolution modes, respectively.

In the fixed window scans at the standard mode, the intensity was recorded at 25 K, 50 K, 75 K, 100 K, 125 K, 150 K, 170 K, and every 10 K from 190 K to 300 K. Data were collected for 40 mins for each point. The QENS data were recorded in both modes at 10 K (for resolution), 100 K, 120 K, 150 K, 180 K, 210 K, 240 K, and 300 K with a counting time of 12 h.

2.3.2 IRIS (inverted geometry, time-of-flight type). We have performed the elastic fixed-window scans, QENS, and neutron powder diffraction measurements of (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O on IRIS. IRIS is a time-of-flight crystal analyzer spectrometer with diffraction capabilities located at the ISIS facility, Rutherford Appleton Laboratory (RAL), UK.31 In the QENS measurements, neutrons scattered from a sample are energy-analyzed by means of Bragg reflection from one of two large single crystal arrays (PG and muscovite mica) in close to backscattering geometry (2θB = 175° where θB is the Bragg angle of the analyzer crystal) and are counted in the detector array (27° < 2θ < 158°). The diffraction bank at 2θ = 170° enables us to measure the diffraction pattern simultaneously with QENS data in the range of the scattering vector, 1.6 Å−1 < Q < 2.1 Å−1. This bank is not for full structural analysis but for checking the structural change during the QENS measurement. In this study, IRIS was operated in the PG(002) configuration which provides an energy window of −0.5 meV < ℏω < 0.5 meV and an energy resolution ΔEres of 17.5 μeV, covering the relaxation time ranging from 10 ps to 150 ps.

In the fixed window scans, the intensity was recorded at 3.5 K and at every 10 K from 10 K to 300 K. The QENS data were collected at 5 K (for resolution), 100 K, 120 K, 150 K, 180 K, 210 K, 240 K, 270 K, and 300 K with a counting time of 4 h for (NH4)2(adp)[Zn2(ox)3]·3H2O and at 210 K, 240 K, 270 K, and 300 K with a counting time of 6 h for K2(adp)[Zn2(ox)3]·3H2O. The diffraction patterns were simultaneously recorded at every measurement temperature.

2.3.3 HFBS (inverted geometry, continuous type). We have measured (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O on HFBS. HFBS is a backscattering spectrometer installed on the NG2 guide at the NIST Center for Neutron Research in Gaithersburg, MD, USA.32 The HFBS instrument was operated in both the fixed window and dynamic window modes. In the dynamic window mode (QENS measurement conditions), the neutrons are Doppler shifted, providing a neutron wavelength band with its center at 6.27 Å. The neutrons scattered from the sample are energy-analyzed by means of Bragg reflection from Si(111) analyzers at 2.08 meV, and counted on 3He detector tubes. In this experiment, we used an energy window, −17 μeV < ℏω < 17 μeV, set by a Doppler frequency of 24 Hz. The energy resolution was 0.8 μeV, which can cover the range of relaxation time from 100 ps to 10 ns. In the fixed window mode, the Doppler drive was stopped and only elastic scattering was recorded.

The fixed window scan was performed from 4 K to 285 K continuously at a rate of 1 K min−1. The QENS data were recorded at 4 K (for resolution), 65 K, 70 K, 75 K, 80 K, 90 K, 100 K, 120 K, 150 K, 180 K, 200 K, 220 K, and 260 K for (NH4)2(adp)[Zn2(ox)3]·3H2O and at 100 K, 180 K, 200 K, 220 K, 240 K, 270 K, and 300 K for K2(adp)[Zn2(ox)3]·3H2O. The counting time was 10 h for each QENS measurement.

3 Results and discussion

3.1 Adiabatic calorimetry

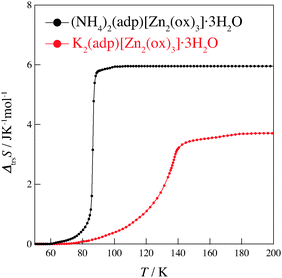
Fig. 2 and 3 show the heat capacities of (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O, respectively. Both (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O exhibited phase transitions at 86 K and 138 K, respectively. They both are higher order transitions without latent heat. This is confirmed by temperature drifts after heating; an endothermic drift is usually observed in first order transitions. The transition in (NH4)2(adp)[Zn2(ox)3]·3H2O is accompanied by a λ-type heat capacity anomaly. On the other hand, the heat capacity exhibits a step-like anomaly at the transition temperature in K2(adp)[Zn2(ox)3]·3H2O. To estimate the entropy change at the transitions, the baseline Cbase was estimated by fitting the heat capacities to a quartic function in the temperature range from 60 K to 80 K (below Ttrs) and from 90 K to 130 K (above Ttrs). For K2(adp)[Zn2(ox)3]·3H2O, the heat capacities were fitted by a cubic function in the temperature range from 70 K to 100 K and from 150 K to 200 K. The baselines are shown as the dashed lines in Fig. 2 and 3. The transition entropy ΔtrsS as a function of temperature is evaluated from the equation: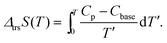
 
image file: c4cp01432d-t1.tif(1)
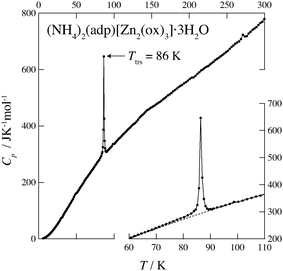image file: c4cp01432d-f2.tif
Fig. 2 Heat capacity of (NH4)2(adp)[Zn2(ox)3]·3H2O. The inset shows an enlarged plot around the phase transition. The dashed line represents the baseline for the transition. See text for the details.

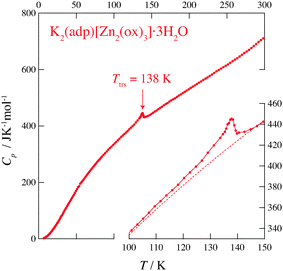image file: c4cp01432d-f3.tif
Fig. 3 Heat capacity of K2(adp)[Zn2(ox)3]·3H2O. The inset shows an enlarged plot around the phase transition. The dashed line represents the baseline for the transition. See text for the details.

Fig. 4 shows the transition entropies for (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O. The former drastically increases at T = 86 K while the latter gradually increases in a wide range of temperature. The total (integrated) transition entropies of (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O are estimated to be 5.95 ± 0.74 J K−1 mol−1 and 3.70 ± 1.56 J K−1 mol−1, respectively. The uncertainty of the transition entropy is due to the arbitrary properties of the baseline; various temperature regions and various orders of polynomial function for the fitting were tested to estimate the uncertainty of the baseline. The transition entropy of 5.95 J K−1 mol−1 is close to R[thin space (1/6-em)]ln[thin space (1/6-em)]2 (= 5.76 J K−1 mol−1), suggesting that the transition at 86 K is an order–disorder phase transition. This may be due to ammonium ions since no ordering transition is observed in K2(adp)[Zn2(ox)3]·3H2O and the transition associated with water molecules usually occurs at higher temperatures due to strong intermolecular hydrogen bonds. On the other hand, the transition entropy of K2(adp)[Zn2(ox)3]·3H2O (3.70 ± 1.56 J K−1 mol−1) is smaller than R[thin space (1/6-em)]ln2, so that we consider this transition is of a displacive type.


image file: c4cp01432d-f4.tif
Fig. 4 Transition entropies of (NH4)2(adp)[Zn2(ox)3]·3H2O (black) and K2(adp)[Zn2(ox)3]·3H2O (red).

3.2 Neutron powder diffraction

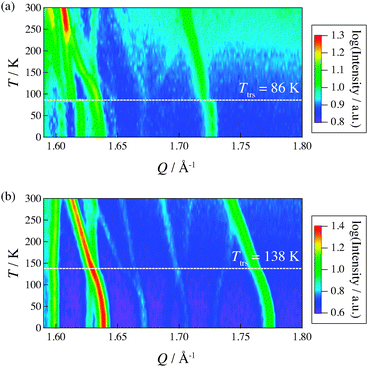
Fig. 5 shows two-dimensional contour intensity maps obtained from the neutron powder diffraction measurements on IRIS. The intensity is given on a logarithmic scale in order to make weak Bragg peaks as well as strong peaks visible.
image file: c4cp01432d-f5.tif
Fig. 5 Two-dimensional intensity maps obtained by neutron powder diffraction on IRIS for (a) (NH4)2(adp)[Zn2(ox)3]·3H2O and (b) K2(adp)[Zn2(ox)3]·3H2O. The intensity is given on a logarithmic scale. The white dashed line represents each transition temperature.

In (NH4)2(adp)[Zn2(ox)3]·3H2O, the Bragg peaks located at Q = 1.60–1.64 Å−1 drastically changed at the transition temperature 86 K. It should be noted that we could not recognize a significant structural change between 50 K and 100 K by single-crystal X-ray diffraction measurements. These results indicate that the phase transition is associated with hydrogen atoms; the hydrogen atoms are hardly detectable by X-rays. The present data also demonstrate that the deuteration of the methylene chain of adipic acid does not change the transition temperature much.

In K2(adp)[Zn2(ox)3]·3H2O, the weak peaks at 1.67 Å−1 and 1.70 Å−1 split above Ttrs = 138 K. Also, the position of Bragg peaks at 1.66 Å−1 and 1.74 Å−1 changed at the transition temperature. Unlike in the case of (NH4)2(adp)[Zn2(ox)3]·3H2O, the change in the diffraction pattern occurs gradually, which is consistent with the fact that the transition entropy gradually changes over a wide temperature range (see Section 3.1). To gain more insight into the arrangement of hydrogen atoms, further accurate neutron diffraction studies are required.

3.3 Mean square displacement

To investigate the temperature at which relaxation processes are activated within the time window of a given spectrometer, the mean square displacement, 〈u2〉, was obtained from an elastic fixed window scan. In the fixed window scan, we measure the elastic intensity I(Q,T) as a function of scattering vector Q and temperature T; the intensity is integrated around ℏω = 0 over a fixed energy region corresponding to the instrumental resolution. The mean square displacement, 〈u2〉, is evaluated from the equation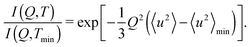
 
image file: c4cp01432d-t2.tif(2)
Here, the elastic intensity is normalized to the value at the minimum temperature Tmin; 〈u2〉min corresponds to the mean square displacement at T = Tmin. 〈u2〉 which varies linearly with respect to temperature for a harmonic oscillator and so the deviation from the straight line indicates the occurrence of anharmonic vibration and/or relaxation in the samples.

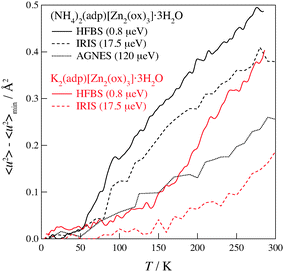
Fig. 6 shows the mean square displacements taken on the three neutron spectrometers with different energy resolutions. As for (NH4)2(adp)[Zn2(ox)3]·3H2O, 〈u2〉 drastically increases above a temperature between 50 and 100 K, indicating the onset of a relaxation. It is noteworthy that 〈u2〉 deviates from the linear relationship at 50 K in HFBS data, at 80 K in IRIS data, and at 100 K in AGNES data. It is reasonable that the HFBS data exhibit a lower onset temperature than the AGNES data, because a slower motion can be observed by an instrument with a higher energy resolution at a given temperature. The deviation also occurred at around 140 K in K2(adp)[Zn2(ox)3]·3H2O. One can naturally understand that the motions of hydrogen atoms get activated above the phase transition temperatures, since the high-temperature (disordered) phase usually has a loosely packed and/or weakly interacting structure. It is exceptional and interesting that the excess increase of 〈u2〉 appeared even below the transition temperature (86 K) in (NH4)2(adp)[Zn2(ox)3]·3H2O.


image file: c4cp01432d-f6.tif
Fig. 6 Mean square displacements of (NH4)2(adp)[Zn2(ox)3]·3H2O (black line) and K2(adp)[Zn2(ox)3]·3H2O (red line) as functions of temperature. The number in the parenthesis denotes the energy resolution of each instrument. The solid, dashed, and dotted lines correspond to the data taken on HFBS, IRIS, and AGNES, respectively.

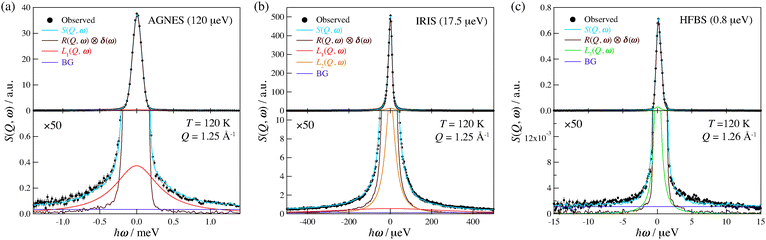
3.4 Quasi-elastic neutron scattering

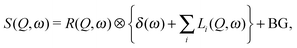3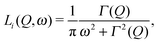.4.1 Analyses of QENS spectra. In order to examine the relaxational dynamics precisely, we have carried out QENS measurements of (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O using the three spectrometers having different energy resolutions. Fig. 7 shows, as an example, the dynamic structure factor, S(Q,ω), observed at Q ≃ 1.25 Å−1 and T = 120 K, taken on the three spectrometers. The data were fitted to the following equations:
 
image file: c4cp01432d-t3.tif(3)
 
image file: c4cp01432d-t4.tif(4)
where R(Q,ω) is the resolution function of each instrument. A delta function δ(ω) is attributed to the static component (or much slower motion than the instrumental resolution) mainly from hydrogen atoms and slightly from the coherent scattering contribution from other atoms, whereas Li(Q,ω) describes the relaxations of hydrogen atoms. In the case where the relaxation function is represented as a simple exponential decay (Debye relaxation), Li(Q,ω) is expressed by Lorentz functions as given in eqn (4). Γ(Q) is the half width at half maximum (HWHM) of the Lorentz function. The subscript of Li(Q,ω) implies that there exist multiple relaxation modes in the system. Since the number of observable relaxations depends on the energy resolution and window of the instrument, we accordingly change the number of Lorentz functions. BG is the constant background. The fitting procedures were carried out using the PAN program on the DAVE software.33 The fits converged well at all Qs and temperatures for all spectrometers. The results of the fits were satisfactory as shown in Fig. 7.
image file: c4cp01432d-f7.tif
Fig. 7 QENS profiles of (NH4)2(adp)[Zn2(ox)3]·3H2O obtained by (a) AGNES, (b) IRIS, and (c) HFBS spectrometers. All data are taken at Q ≃ 1.25 Å−1 and T = 120 K. The lower panels display the enlarged plot in the vertical axis. Error bars throughout the text represent one standard deviation. Solid curves represent the results of the fitting analyses. See text for the details.

To obtain the spatial information on the relaxations, we investigated the Q-dependence of the relaxations. The Q regions where strong diffraction peaks appear were omitted from the analysis. Fig. 8 displays Γ as a function of Q at 120, 180, and 240 K on AGNES and at 100 and 220 K on HFBS. No pronounced Q-dependence of Γ implies that these motions of hydrogen atoms are of a local origin. In the measurements on IRIS, similar behavior was observed. Hence, all of the hydrogen motions observed in (NH4)2(adp)[Zn2(ox)3]·3H2O are local relaxations.


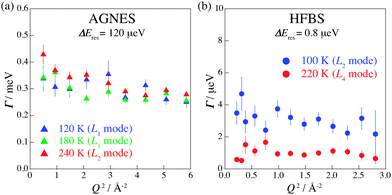image file: c4cp01432d-f8.tif
Fig. 8 Q-dependence of Γ estimated from the fitting for the data taken on (a) AGNES and (b) HFBS spectrometers.

The mechanisms of the proton diffusion assisted by water molecules are roughly divided into two: i.e., one is the Vehicle mechanism in which a water molecule having a proton, that is a hydronium ion (H3O+), carries a proton for a long distance34 and the other is the Grotthuss mechanism in which a hydronium ion reorients and passes a proton to a neighboring water molecules through a hydrogen bond.35,36 In (NH4)2(adp)[Zn2(ox)3]·3H2O, all of the motions related to hydrogen atoms are local relaxations as mentioned above. We thus conclude that the protons in (NH4)2(adp)[Zn2(ox)3]·3H2O are carried through the Grotthuss mechanism.

3.4.2 Arrhenius plot. Fig. 9 shows the Arrhenius plot of relaxation times for (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O. The relaxation times are evaluated from the relation, τ = 1/Γ, for the Lorentz functions. Here, the Γ data for all Q values are summed up because no Q dependence on Γ was observed as described before. The average Q value was 1.25 Å−1.
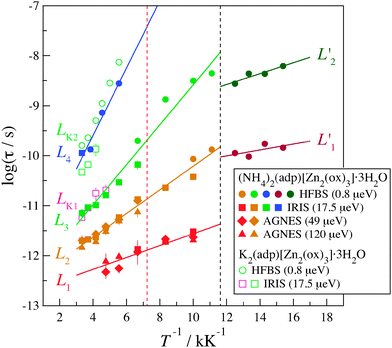
image file: c4cp01432d-f9.tif
Fig. 9 Arrhenius plot for the relaxation times of (NH4)2(adp)[Zn2(ox)3]·3H2O (filled symbols) and K2(adp)[Zn2(ox)3]·3H2O (open symbols) at Qav = 1.25 Å−1. The circle, square, diamond, and triangle symbols represent the data measured on HFBS (0.8 μeV), IRIS (17.5 μeV), AGNES (49 μeV), and AGNES (120 μeV), respectively; the number in the parenthesis denotes the energy resolution of each instrument. Each relaxation is labeled as Li (for (NH4)2(adp)[Zn2(ox)3]·3H2O) and LKi (for K2(adp)[Zn2(ox)3]·3H2O). The dashed black and red lines are the transition temperatures of (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O, respectively.

There exist four relaxation modes (L1, L2, L3, and L4) in (NH4)2(adp)[Zn2(ox)3]·3H2O. These relaxation modes were observed by two different instruments though their observation temperatures are sometimes different. This fact increases the reliability of the analysis and the related discussion. It is noteworthy that the data of each relaxation lie on each straight line, meaning that all relaxations follow the Arrhenius law in the whole temperature range. For each relaxation mode, the activation energy, ΔEa, of the relaxation is obtained from the slope of the plots assuming the Arrhenius equation

 
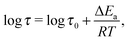image file: c4cp01432d-t5.tif(5)
where R (= 8.314 J K−1 mol−1) is the gas constant and τ0 is the relaxation time at infinite temperature. The activation energy for each relaxation is shown in Table 1. It is remarkable that the activation energies of L1 and L2 are very small compared with the rotational activation energies of H2O and NH4+ in condensed phases, e.g., 17 kJ mol−1 in bulk water and 20 kJ mol−1 in solid NH4Cl.

Table 1 Activation energy (ΔEa) for each mode in (NH4)2(adp)[Zn2(ox)3]·3H2O
Mode ΔEa (T > Ttrs) Mode ΔEa (T < Ttrs)
L 1 2.3 kJ mol−1 L 1′ 1.1 kJ mol−1
L 2 4.5 kJ mol−1 L 2′ 2.1 kJ mol−1
L 3 7.7 kJ mol−1
L 4 12.9 kJ mol−1

On the other hand, in K2(adp)[Zn2(ox)3]·3H2O, only two relaxations LK1 and LK2 were observed around the positions of L3 and L4 of (NH4)2(adp)[Zn2(ox)3]·3H2O, respectively. From the results mentioned above, it is reasonably concluded that L1 and L2 of (NH4)2(adp)[Zn2(ox)3]·3H2O are associated with the motions of NH4+ ions, while L3, L4, LK1, and LK2 are the motions of H2O molecules. The small activation energies of the L1 and L2 modes reflect the fact that the hydrogen bonds of ammonium ions are weaker than those of water molecules. We accept the possibility that the slowest mode (L4) is assigned to the relaxation of COOH groups of adipic acid.

Why do two different types of motions related to ammonium ions exist? From the structural data obtained by the single crystal X-ray diffraction,22 the two NH4+ ions are located at the crystallographically equivalent sites. On the other hand, there are two crystallographically distinct sites for the three H2O molecules; two H2O molecules are located in the two crystallographically equivalent sites, whereas the 3rd H2O molecule is positionally disordered between another two equivalent sites with an occupancy of 50%. The NH4+ ions may be affected by the presence or absence of adjacent water molecules, and may have different activation energies.

Next, we discuss the relation between the phase transitions and the relaxation motions. In (NH4)2(adp)[Zn2(ox)3]·3H2O, the relaxations obviously changed at the transition temperature as shown in Fig. 9. It was confirmed that there is no relaxation below the transition temperature in a shorter time region of L1′. This measurement was performed by DCS (NCNR, NIST, USA),37 a chopper spectrometer suitable for a time region between 10−10 s and 10−12 s. In general, molecular/ionic motions do not become faster below the transition temperature; therefore, it is speculated that the two relaxations observed below the transition temperature are the motions of ammonium ions. It is interesting to note that the activation energy below the transition temperature is lower than that above the temperature. It may suggest that the quantum tunneling plays a role in the relaxational process. Further studies are required to address this issue.

In K2(adp)[Zn2(ox)3]·3H2O, no relaxation was observed below the transition temperature. This suggests that the carboxyl groups and water molecules become frozen at the transition temperature, 138 K. Thus, the phase transition of (NH4)2(adp)[Zn2(ox)3]·3H2O at 86 K is entirely different from that of K2(adp)[Zn2(ox)3]·3H2O at 138 K.

3.4.3 Elastic incoherent structure factor. We have made further analysis on the two local relaxations of ammonium ions (L1 and L2). For the local motion, Γ(Q) does not give us any geometrical information, but the relative integrated intensities do via the elastic incoherent structure factor (EISF), A0(Q). This is defined as
 
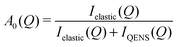image file: c4cp01432d-t6.tif(6)
where Ielastic and IQENS are the peak intensities of elastic and quasi-elastic scatterings, respectively. Fig. 10 shows the EISFs of the L1 and L2 relaxations measured at 120 K as a function of momentum transfer Q. For other relaxations, which were measured on HFBS, it was difficult to obtain analyzable A0(Q) probably because the detector efficiencies of HFBS were not corrected appropriately against Q in our experiment. It was also difficult to analyze the data at higher temperatures since two relaxations, e.g., L1 and L2, approach each other as shown in Fig. 9.
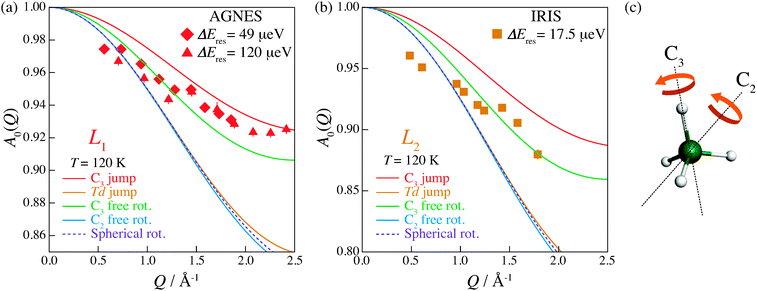
image file: c4cp01432d-f10.tif
Fig. 10 Elastic incoherent structure factor (EISF) of (NH4)2(adp)[Zn2(ox)3]·3H2O for (a) the L1 mode measured by AGNES and (b) the L2 mode measured by IRIS. Solid curves represent the calculated EISF based on several model functions. See text for the details. (c) Structure of ammonium ions composed of four hydrogen atoms (white) and a nitrogen atom (green). The twofold (C2) and threefold (C3) axes are exhibited.

The EISF varies as a function of Q, depending on the dynamical model.38,39 In an ammonium ion, four hydrogen atoms surround a central nitrogen atom with tetrahedral symmetry. The contribution from the incoherent scattering of nitrogen atoms can be neglected, so that the incoherent scattering reflects only the motion of the hydrogen atoms. We considered several dynamic models; a jump about a threefold axis (C3 jump), a jump among the apices of a tetrahedron (Td jump), a continuous rotation about a threefold axis (C3 free rot.), a continuous rotation about a twofold axis (C2 free rot.), and an isotropic rotation on the circumscribed sphere of the tetrahedron (Spherical rot.). Note that a jump about the C2 axis is indistinguishable from that about the C3 axis. The A0s for the reorientation of the ammonium ion are given by

 
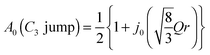image file: c4cp01432d-t7.tif(7)
 
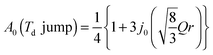image file: c4cp01432d-t8.tif(8)
 
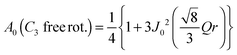image file: c4cp01432d-t9.tif(9)
 
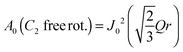image file: c4cp01432d-t10.tif(10)
 
A0 (Spherical rot.) = j02 (Qr),(11)
where r is the distance between the hydrogen and nitrogen atoms, and J0 and j0 are 0th order of the Bessel and spherical Bessel functions, respectively. In this calculation, r was fixed to be a literature value (1.0 Å). The calculated A0(Q)s are also plotted in Fig. 10. It can be concluded that the ammonium ions likely perform a continuous rotation around the C3 axis while jumping between two preferred orientations.

3.5 Proton conducting path

Finally, we discuss proton conducting pathways in (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O. As mentioned before, the protons are carried through the Grotthuss mechanism with H2O molecules, NH4+ ions (for (NH4)2(adp)[Zn2(ox)3]·3H2O), and –COOH groups of adipic acid located in the proton conducting layers. Since the positions of hydrogen atoms were not determined by the X-ray diffraction,22 we consider the oxygen and nitrogen atoms which can be associated with the hydrogen bonds. Table 2 lists the possible hydrogen bonds with bond lengths shorter than 3.1 Å that can be considered to be the largest limit for the hydrogen-bond formation. The number of hydrogen bonds in (NH4)2(adp)[Zn2(ox)3]·3H2O is three times larger than that in K2(adp)[Zn2(ox)3]·3H2O. These bonds are schematically shown in Fig. 11 and 12 for (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O, respectively. There exists an obvious hydrogen-bond network in the proton conducting layers of (NH4)2(adp)[Zn2(ox)3]·3H2O. On the other hand, hydrogen bonds neither form a network nor percolate over the proton conducting layer in K2(adp)[Zn2(ox)3]·3H2O. Evidently, the ammonium ions have a key role in forming the hydrogen-bond network; there are 3–4 hydrogen bonds between N(1) and O(n) (n = 8, 9, 10). We speculate that the high proton conductivity in (NH4)2(adp)[Zn2(ox)3]·3H2O is realized not only by many proton conducting paths but also by the high mobility of ammonium ions (rotation around the C3 axis with small activation energy). This would have to be confirmed through the determination of the exact positions of hydrogen atoms forming the hydrogen bonds.
Table 2 Possible hydrogen bonds in (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O. Only atoms associated with hydrogen bonds are considered; oxygen atoms of the carboxyl groups in adipic acids (O(7) and O(8)), oxygen atoms of water molecules (O(9) and O(10)), and nitrogen atoms of ammonium ions (N(1)). The sets with the bond length shorter than 3.1 Å are shown here
Sample Label From molecule/ion Label To molecule/ion Bond length d (Å)
(NH4)2(adp)[Zn2(ox)3]·3H2O O(9) H2O O(10) H2O 2.64(1)
N(1) NH4+ O(10) H2O 2.79(1)
N(1) NH4+ O(8) –COOH 2.84(2)
N(1) NH4+ O(9) H2O 2.85(1)
N(1) NH4+ O(8) –COOH 2.95(1)
O(7) –COOH O(10) H2O 2.99(1)
O(7) –COOH O(9) H2O 3.04(1)
K2(adp)[Zn2(ox)3]·3H2O O(9) H2O O(10) H2O 2.71(1)
O(8) –COOH O(10) H2O 3.04(1)


image file: c4cp01432d-f11.tif
Fig. 11 Possible hydrogen-bond arrangements in (NH4)2(adp)[Zn2(ox)3]·3H2O. Yellow thick lines represent hydrogen bonds whose length is shorter than 3.1 Å. (a) Perspective view along the a-axis. (b) Perspective view along the b-axis.

image file: c4cp01432d-f12.tif
Fig. 12 Possible hydrogen-bond arrangements in K2(adp)[Zn2(ox)3]·3H2O. Yellow thick lines represent hydrogen bonds whose length is shorter than 3.1 Å. (a) Perspective view along the a-axis. (b) Perspective view along the b-axis.

4 Conclusion

In this paper, in order to elucidate the relation between the proton conductivity and phase transitions, we have performed adiabatic calorimetry and neutron powder diffraction experiments for (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O, as well as QENS measurements to get insights into the mechanism for proton conduction. The adiabatic calorimetry revealed that (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O exhibit higher-order phase transitions at 86 K and 138 K, respectively. These transitions were also observed by the neutron powder diffraction measurement and the fixed window scan. In the QENS measurements, since Γ (HWHM of Lorentz function) is independent of Q, it is evident that the protons in (NH4)2(adp)[Zn2(ox)3]·3H2O are carried through the Grotthuss mechanism. By using the three spectrometers with different energy resolutions, we have succeeded to observe the overall feature of dynamics: there exist four and two relaxation motions in (NH4)2(adp)[Zn2(ox)3]·3H2O and K2(adp)[Zn2(ox)3]·3H2O, respectively. It is speculated that two fast rotational motions of ammonium ions having very small activation energy play a key role in the high proton conductivity in (NH4)2(adp)[Zn2(ox)3]·3H2O. We discuss the hydrogen-bond pathways in proton conducting layers using the previous structural data. We found that hydrogen-bond networks are well constructed by H2O and NH4+ in (NH4)2(adp)[Zn2(ox)3]·3H2O. This network can contribute to the Grotthuss mechanism of proton conduction. In order to further investigate the proton conducting mechanism, it is essential to determine the crystal structure and specifically the positions of the H atoms by means of a high resolution neutron diffractometer.

Disclaimer

The identification of commercial products does not imply endorsement by the National Institute of Standards and Technology nor does it imply that these are the best for the purpose.

Acknowledgements

The authors thank Dr John R. D. Copley (NCNR, NIST) for the DCS measurement, and Dr Kunihisa Sugimoto (SPring-8) and Dr Akihito Fujiwara (SPring-8) for the single-crystal X-ray diffraction measurement at low temperature. The HFBS experiment at NCNR was financially supported by Institute for Solid State Physics, the University of Tokyo, through the Travel Expense Support for the Overseas program. This work utilized facilities supported in part by the National Science Foundation under Agreement No. DMR-0944772.

References

  1. H. K. Chae, D. Y. Siberio-Perez, J. Kim, Y. Go, M. Eddaoudi, A. J. Matzger, M. O'Keeffe and O. M. Yaghi, Nature, 2004, 427, 523 CrossRef CAS PubMed.
  2. X. Zhao, B. Xiao, J. A. Fletcher, K. M. Thomas, D. Bradshaw and M. J. Rosseinsky, Science, 2004, 306, 1012 CrossRef CAS PubMed.
  3. R. Matsuda, R. Kitaura, S. Kitagawa, Y. Kubota, R. V. Beloslusov, T. C. Kobayashi, H. Sakamoto, T. Chiba, M. Tanaka, Y. Kawazoe and Y. Mita, Nature, 2005, 436, 238 CrossRef CAS PubMed.
  4. J. S. Seo, D. Whang, H. Lee, S. I. Jun, J. Oh, Y. J. Jeon and K. Kim, Nature, 2000, 404, 982 CrossRef CAS PubMed.
  5. C.-D. Wu, A. Hu, L. Zhang and W. Lin, J. Am. Chem. Soc., 2005, 127, 8940 CrossRef CAS PubMed.
  6. H. Kitagawa, Y. Nagao, M. Fujishima, R. Ikeda and S. Kanda, Inorg. Chem. Commun., 2003, 6, 346 CrossRef CAS.
  7. H. Ōkawa, M. Sadakiyo, T. Yamada, M. Maesato, M. Ohba and H. Kitagawa, J. Am. Chem. Soc., 2013, 135, 2256 CrossRef PubMed.
  8. M. Sadakiyo, H. Ōkawa, A. Shigematsu, M. Ohba, T. Yamada and H. Kitagawa, J. Am. Chem. Soc., 2012, 134, 5472 CrossRef CAS PubMed.
  9. G. Xu, K. Otsubo, T. Yamada, S. Sakaida and H. Kitagawa, J. Am. Chem. Soc., 2013, 135, 7438 CrossRef CAS PubMed.
  10. J. M. Taylor, R. K. Mah, I. L. Moudrakovski, C. I. Ratcliffe, R. Vaidhyanathan and G. K. H. Shimizu, J. Am. Chem. Soc., 2010, 132, 14055 CrossRef CAS PubMed.
  11. N. C. Jeong, B. Samanta, C. Y. Lee, O. K. Farha and J. T. Hupp, J. Am. Chem. Soc., 2012, 134, 51 CrossRef CAS PubMed.
  12. D. Umeyama, S. Horike, M. Inukai, Y. Hijikata and S. Kitagawa, Angew. Chem., Int. Ed., 2011, 50, 1 CrossRef.
  13. G. Ferey, C. Mellot-Draznieks, C. Serre and F. Millange, Acc. Chem. Res., 2005, 38, 217 CrossRef CAS PubMed.
  14. S. Kitagawa, R. Kitaura and S. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334 CrossRef CAS PubMed.
  15. O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705 CrossRef CAS PubMed.
  16. K. D. Kreuer, S. J. Paddison, E. Spohr and M. Schuster, Chem. Rev., 2004, 104, 4637 CrossRef CAS.
  17. K. D. Kreuer, Chem. Mater., 1996, 8, 610 CrossRef CAS.
  18. B. C. Steele and A. Heinzel, Nature, 2001, 414, 345 CrossRef CAS PubMed.
  19. Y. Nagao, R. Ikeda, S. Kanda, Y. Kubozono and H. Kitagawa, Mol. Cryst. Liq. Cryst., 2002, 379, 89 CrossRef CAS.
  20. Y. Nagao, M. Fujishima, S. Kanda, R. Ikeda and H. Kitagawa, Synth. Met., 2003, 133–134, 431 CrossRef CAS.
  21. T. Yamada, M. Sadakiyo and H. Kitagawa, J. Am. Chem. Soc., 2009, 131, 3144 CrossRef CAS PubMed.
  22. M. Sadakiyo, T. Yamada and H. Kitagawa, J. Am. Chem. Soc., 2009, 131, 9906 CrossRef CAS PubMed.
  23. S. Bureekaew, S. Horike, M. Higuchi, M. Mizuno, T. Kawamura, D. Tanaka, N. Yanai and S. Kitagawa, Nat. Mater., 2009, 8, 831 CrossRef CAS PubMed.
  24. A. Shigematsu, T. Yamada and H. Kitagawa, J. Am. Chem. Soc., 2011, 133, 2034 CrossRef CAS PubMed.
  25. T. Yamada, R. Yonamine, T. Yamada, H. Kitagawa and O. Yamamuro, J. Phys. Chem. B, 2010, 114, 8405 CrossRef CAS PubMed.
  26. T. Yamada, R. Yonamine, T. Yamada, H. Kitagawa, M. Tyagi, M. Nagao and O. Yamamuro, J. Phys. Chem. B, 2011, 115, 13563 CrossRef CAS PubMed.
  27. M. Sadakiyo, T. Yamada and H. Kitagawa, submitted.
  28. O. Yamamuro, M. Oguni, T. Matsuo and H. Suga, Bull. Chem. Soc. Jpn., 1987, 60, 1269 CrossRef CAS.
  29. T. Kajitani, K. Shibata, S. Ikeda, M. Kohgi, H. Yoshizawa, K. Nemoto and K. Suzuki, Physica B, 1995, 213–214, 872 CrossRef.
  30. O. Yamamuro, Y. Inamura, Y. Kawamura, S. Watanabe, T. Asami, H. Yoshizawa, Annual Report of Neutron Science Laboratory, Institute for Solid state Physics, University of Tokyo, 2005, 12, 12.
  31. C. J. Carlile and M. A. Adams, Physica B, 1992, 182, 431 CrossRef CAS.
  32. A. Meyer, R. M. Dimeo, P. M. Gehring and D. A. Neumann, Rev. Sci. Instrum., 2003, 74, 2759 CrossRef CAS PubMed.
  33. R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. W. Tregenna-Piggott, C. M. Brown, J. R. D. Copley and R. M. Dimeo, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341 CrossRef CAS.
  34. K. D. Kreuer, A. Rabenau and W. Weppner, Angew. Chem., Int. Ed. Engl., 1982, 21, 208 CrossRef.
  35. N. Agmon, Chem. Phys. Lett., 1995, 244, 456 CrossRef CAS.
  36. X. Ke and I. Tanaka, Solid State Ionics, 2004, 172, 145 CrossRef CAS PubMed.
  37. J. R. D. Copley and J. C. Cook, Chem. Phys., 2003, 292, 477 CrossRef CAS.
  38. M. Bée, Physica B, 1992, 182, 323 CrossRef.
  39. T. Yildirim, P. M. Gehring, D. A. Neumann, P. E. Eaton and T. Emrick, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 314 CrossRef CAS.
This journal is © the Owner Societies 2014