Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probing the type of anomalous diffusion with single-particle tracking
Dominique
Ernst
a,
Jürgen
Köhler
*a and
Matthias
Weiss
*b
aExperimental Physics IV, University of Bayreuth, 95440 Bayreuth, Germany. E-mail: juergen.koehler@uni-bayreuth.de
bExperimental Physics I, University of Bayreuth, 95440 Bayreuth, Germany. E-mail: matthias.weiss@uni-bayreuth.de
First published on 5th March 2014
Abstract
Many reactions in complex fluids, e.g. signaling cascades in the cytoplasm of living cells, are governed by a diffusion-driven encounter of reactants. Yet, diffusion in complex fluids often exhibits an anomalous characteristic (‘subdiffusion’). Since different types of subdiffusion have distinct effects on timing and equilibria of chemical reactions, a thorough determination of the reactants' type of random walk is key to a quantitative understanding of reactions in complex fluids. Here we introduce a straightforward and simple approach for determining the type of subdiffusion from single-particle tracking data. Unlike previous approaches, our method also is sensitive to transient subdiffusion phenomena, e.g. obstructed diffusion below the percolation threshold. We validate our strategy with data from experiment and simulation.
Introduction
A wide class of reactions in complex fluids, e.g. signaling cascades and protein complex formation in the cytoplasm of living cells, are governed by a diffusion-mediated encounter. For diffusion-limited reactions in three dimensions, a constant reaction rate k ∼ Dr in terms of the reactants' relative diffusion constant Dr was derived by Smoluchowski as early as 1916.1 Yet, this famous result becomes invalid if fluids have viscoelastic characteristics or if the accessible space in the fluid has a fractal dimension: under these circumstances the reactants' random walk becomes compact, and a proper reaction constant cannot be defined any more.2 Indeed, Smoluchowski's construction crucially relies on the fact that normal diffusion (Brownian motion) features a two-dimensional random walk so that motion in three-dimensional bulk fluids is non-compact. However, diffusion in viscoelastic fluids or in porous media may be governed by compact random walks and, as a consequence, the reaction coefficient k may become time-dependent.3,4Random walks are commonly evaluated by inspecting the mean square displacement (MSD) of molecules. For normal Brownian diffusion MSD ∼ Dt, whereas diffusion in viscoelastic media or in fractal geometries (e.g. percolation clusters) typically shows a sublinear scaling, MSD ∼ Γtα (α < 1, ‘subdiffusion’) with a generalized diffusion coefficient Γ. Diffusion anomalies have been observed in many complex fluids with a high concentration of macromolecules (‘crowders’), e.g. in living cells5–12 or in artificial fluids.13–17 Defining subdiffusion via the MSD's scaling, however, does not reveal the molecules' type of random walk that may feature distinct consequences on chemical reactions.
As of yet, three general types of subdiffusive random walks have been invoked to explain experimental observations of subdiffusion in complex/crowded fluids. Despite a common sublinear scaling of the MSD, they describe very different physical scenarios with quite different effects on chemical reactions. Here, we only give a brief overview and refer the reader for details to a very recent and extensive review by Höfling and Franosch.18
The first model relies on hindering free diffusion by randomly placing immobile obstacles in space (obstructed diffusion, OD). If the density of obstacles approaches the percolation threshold, tracer particles are forced to move in a fractal subspace which is reflected in a transient subdiffusion over several orders of magnitude in time.19 At the percolation threshold, a single scale-free cluster of obstacles emerges, and subdiffusion is seen on all time-scales.19 In two dimensions, the anomaly is then α ≈ 0.69, and fractal reaction kinetics are required to adequately describe chemical reactions.3,20
The second model violates the Markovian property of normal Brownian motion in that successive steps are anti-correlated. This so-called fractional Brownian motion (FBM) models a particle's motion in viscoelastic fluids,18 and reactions may show significant changes due to an enhanced rebinding of reactants.4,21 Please note that FBM in general also allows for correlated steps that lead to superdiffusion (not considered here).
The third model is based on assigning power-law distributed waiting times to a particle between periods of free Brownian motion (continuous time random walk, CTRW).22 If the normalizable distribution of waiting times has a divergent mean and divergent higher moments, subdiffusion can be observed over extended time scales. The more time has elapsed since starting an ensemble of tracers, the more particles have been assigned extraordinary long waiting times, and as a consequence more and more particles become immobilized. This aging effect, i.e. an increasing amount of ‘frozen’ particles, and the associated subdiffusive spreading is a property of the ensemble. In contrast, the time-averaged MSD of a single tracer particle shows no signs of anomalous diffusion.23,24 This discrepancy between single particles and an ensemble has been named weak ergodicity breaking and distinct effects on reactions are to be expected here (see, e.g., ref. 18 and 25 for an introduction).
Given these different types of subdiffusion and their distinct impact on chemical reactions, it is clear that elucidating the type of random walk of nanometer-sized objects is key for a quantitative understanding of reactions in crowded/complex fluids. Several reports have touched on this issue before by exploiting statistical features of the recorded random walk beyond the scaling of the MSD.17,26–32 Yet, a conclusive test that can be applied quickly to individual experimental trajectories while being capable of reporting also on the nature of transient subdiffusion phenomena has been lacking so far. In fact, most tests even have been limited to separating CTRW-like random walks from stochastic processes with a stationary distribution of increments like OD or FBM.
Here, we introduce a straightforward yet decisive test for the type of subdiffusive random walk in complex fluids from single-particle trajectories. Validating our approach with experimental trajectories obtained for nanobeads diffusing in complex fluids and simulations on transient subdiffusion of the OD type, we find that our approach is particularly more sensitive in reporting on transient subdiffusion phenomena than previously considered methods.
Materials and methods
Single particle tracking of fluorescent beads in sucrose and dextran solutions was done as described earlier.33,34 In brief, a cycling-orbit strategy35 was used to follow the center of mass of fluorescent nanobeads (diameter 20 nm), i.e. the diffusive motion of the bead was detected by changes in the fluorescence amplitude and phase. The diffusive motion was compensated by a piezo element. This setup allowed for a spatiotemporal resolution of trajectories in the 4 ms/10 nm range and trajectories of >105 positions could be recorded. We would like to note that the bead is only twofold larger than apoferritin, a cellular protein complex that has been studied in crowded media before.15 Moreover, a cycling-orbit tracking strategy can, in principle, also be applied to smaller beads. A too rapid diffusion and bleaching, however, may limit the number of recorded photons per time, hence increasing the positional uncertainty.Simulations of obstructed diffusion were performed on a two-dimensional square lattice (2000 × 2000 sites, periodic boundaries) using the blind ant algorithm: at each step, the particle blindly attempts to move to one of the four next-neighbor sites, and the move is accepted unless the site is blocked by an obstacle. A fraction 0 ≤ ϕ ≤ 0.35 of randomly chosen lattice sites was made inaccessible for random walkers, hence leading to transient subdiffusion. To meet the scales of the experiment, the lattice constant was chosen as Δx = 10 nm and the free diffusion constant was set to D0 = 1 μm2 s−1. Particle positions were recorded every 4 ms, and trajectories of 105 positions were acquired for each particle. For each value of ϕ = 0, 0.2, 0.35, 20 random obstacle configurations with a single diffusing particle were chosen to obtain 20 trajectories for each condition. Simulations therefore had comparable length and time scales and similar statistics as our experimental data. While increasing the number of trajectories certainly will enhance the statistics, we have refrained from doing so to have the same statistical fluctuations as seen in the experimental data.
Results
In order to highlight its applied nature, we outline our test for the type of subdiffusion by directly applying it to experimental single-particle tracking data recorded in sucrose and dextran solutions. We have shown previously that these data are governed by normal and fractional Brownian motion, respectively.17,36In order to determine the type of subdiffusive random walk, one first needs to separate diffusion processes with stationary distributions of increments (e.g. OD and FBM) vs. those with nonstationary distributions (e.g. CTRW). Given that a CTRW-type of motion is related to an ageing process, one may employ the recently reported emergence of a weak ergodicity breaking23,24 for this: for CTRW-like random walks, the ensemble-averaged MSD shows a diffusion anomaly α < 1 whereas the time-averaged MSD of single trajectories follows the scaling of a normal Brownian motion (α = 1). The ensemble-averaged MSD of j = 1,…,M trajectories is defined as
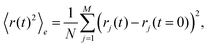 | (1) |
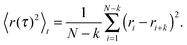 | (2) |
When evaluating the time-averaged MSD, one needs to infer the degree of anomaly on the time scales of interest. A straightforward approach to reveal the local diffusion anomaly value is given by the MSD's logarithmic derivative:
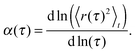 | (3) |
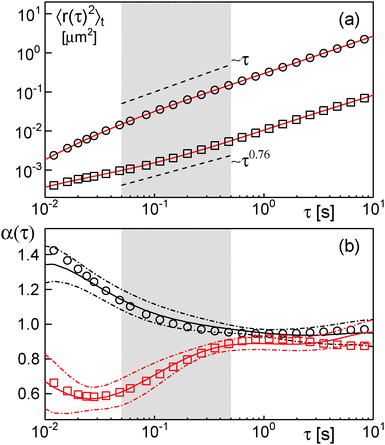 | ||
| Fig. 1 (a) Representative time-averaged MSD curves [eqn (2)] of single trajectories of nanobeads diffusing in solutions containing 60% sucrose (circles) or 30% dextran (squares). Full red lines are best fits of an 8th order polynomial. Fitting the MSD in the grey-shaded region (50–500 ms in accordance with our previous evaluation17) revealed an anomalous diffusion for dextran (α ≈ 0.76) but not for sucrose solutions (α ≈ 1). Dashed lines indicate the respective scaling. (b) Local diffusion anomaly [eqn (3)] for the same curves as determined via the polynomial fit (symbols as before). Full lines represent the mean anomaly (averaged over 21 trajectories) for sucrose (black) and dextran (red) solutions. Dash-dotted lines indicate the corresponding standard deviation of the mean. After an apparent superdiffusion due to inertial and statistical effects (cf. main text), α ≈ 1 for sucrose solutions. For dextran solutions, however, a clear subdiffusive regime is visible (α ≈ 0.8, grey shaded region) that converges asymptotically towards normal diffusion. | ||
In agreement with our previous results on the same trajectories,17,36α(τ) reported a vanishing diffusion anomaly, i.e. α ≈ 1, for large time scales for the motion of nanobeads in sucrose solutions (Fig. 1b). A slight superdiffusive signature for small times is due to inertial and statistical effects: Compensating for the particle's motion by moving the piezo element required a relaxation to the resting state. This contributed a non-diffusive signal to the MSD on the scale of few milliseconds.17 In addition, the unavoidable motion of particles during photon acquisition, i.e. position determination, adds a negative constant to the MSD that imitates a super-diffusive motion on short time scales (see ref. 39 for details).
In contrast, diffusion in dextran solutions was clearly subdiffusive for small times as judged on the basis of α(τ) (Fig. 1b). For about one order of magnitude, the anomaly value was significantly lower than unity, while α(τ) converged towards unity for large time scales. This result is in favorable agreement with earlier observations on subdiffusion of nano-particles in dextran solutions.6,14,15 Given that α(τ) reports a subdiffusive characteristic in the time-averaged MSD, trajectories taken in crowded dextran fluids cannot be a consequence of a CTRW-like random walk. In fact, we have shown earlier that the very same trajectories have all the features of FBM.36 Thus, inspecting the time-averaged MSD indeed yields a first test of whether random walk models with stationary or non-stationary increment distributions are to be considered.
To probe which random walk model with a stationary increment distribution might underlie single-particle tracking data, we quantify the trajectory's Gaussianity via
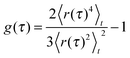 | (4) |
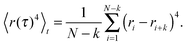 | (5) |
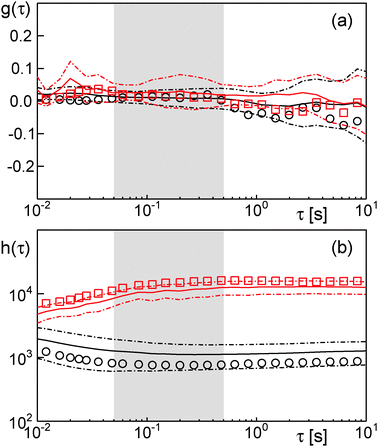 | ||
| Fig. 2 (a) The Gaussianty g(τ) [eqn (4)] fluctuates around zero for trajectories measured in sucrose (black) and dextran fluids (red). Hence, both data sets are due to Gaussian random walks. Symbols refer to the representative trajectories shown in Fig. 1 a, full lines are the mean of 21 trajectories, and dash-dotted lines indicate the corresponding standard deviation of the mean. (b) As expected from the Gaussianity, h(τ) [eqn (6)] is essentially constant in time (δ = 0) for trajectories in sucrose (black) and dextran fluids (red). Symbols and lines as before. | ||
To crosscheck the information on the type of random walk delivered by the Gaussianity, we inspected the scaling of a recently introduced quantity:31
| h(τ) = s(τ)/〈r(τ)2〉t ∼ τδ. | (6) |
Here, s(τ) is the number of distinct sites visited within a period τ, while the denominator is simply the time-averaged MSD. Due to different scaling laws of s(τ) for different types of random walks, δ = 0 was predicted for FBM, whereas δ < 0 for OD. Indeed, our experimental data are consistent with a scaling exponent δ = 0 (Fig. 2b), hence confirming the conclusions drawn from the Gaussianity.
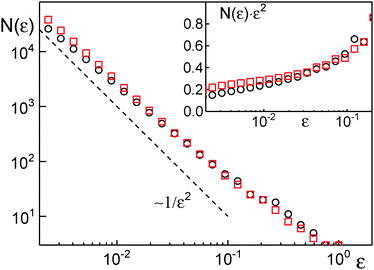
Despite the favorable agreement between both approaches, we would like to highlight the advantages of an analysis in terms of the Gaussianity over the scaling approach [eqn (6)]. First of all, our approach does not require to specify and to vary a box size for coarse graining. Briefly, for the scaling approach coarse graining is needed for defining the number of distinct vistited sites, s(τ), of a trajectory segment of (temporal) length τ. The most straightforward approach is to superimpose the trajectory with square boxes of edge length ε, and to count the number of non-empty boxes (= distinct visited sites), N(ε). If ε is too small, then each position of the trajectory will have its ‘own’ site, whereas a too large ε masks local features of the random walk. Both extremes are unfavorable for s(τ). As a matter of fact, the quantity N(ε) is the central quantity of a box-counting algorithm with which one can estimate the fractal dimension df of an object via the scaling N(ε) ∼ 1/εdf. Yet, N(ε) does not show a unique scaling for typical experimental trajectories (Fig. 3), i.e. the value of df depends on the choice of the box size ε. As the scaling exponent δ in eqn (6) depends crucially on df,31 the choice of ε is crucial for a proper analysis. Being aware of this, the authors of ref. 31 therefore proposed to vary the trajectory's coarse graining via ε to reveal the smallest δ possible for the trajectory, which, however, makes the analysis of experimental data considerably more laborious.
A second and more severe problem of the scaling approach is its intrinsic insensitivity to transient subdiffusion phenomena. Given that a proper determination of δ requires determination of the scaling of h(τ), δ-values are only meaningful when being extracted/averaged over at least one order of magnitude in time. Thus, transient and incomplete subdiffusion phenomena may be missed. To highlight this sensitive point, we have performed simulations of obstructed diffusion with ϕ = 0, 0.2, 0.35. While ϕ = 0 represents free diffusion, ϕ = 0.2 and ϕ = 0.35 represent an OD scenario that is well below the percolation threshold, i.e. only a weak and transient subdiffusion can emerge.19
As expected, evaluation of the temporal anomaly α(τ) [eqn (3)] revealed no significant subdiffusion for ϕ = 0. Also for ϕ = 0.2 no significant subdiffusion was visible, whereas a considerable transient anomaly is seen for ϕ = 0.35 (Fig. 4a). Evaluation of g(τ) clearly marked the free Brownian motion at ϕ = 0 as a Gaussian process whereas ϕ = 0.35 is clearly detected as a non-Gaussian process on short time scales (Fig. 4b). Even the random walk at ϕ = 0.2, albeit not showing a significant subdiffusion, is highlighted as a transient non-Gaussian process. This result clearly demonstrates the sensitivity of g(τ) for transient and even incomplete subdiffusion processes. In contrast, the scaling of h(τ) did not show major changes when inreasing the obstacle fraction from ϕ = 0 to ϕ = 0.2 or ϕ = 0.35 (Fig. 4c). This result underlines that the scaling of h(τ) may be a good measure for asymptotic subdiffusion processes whereas transient subdiffusion, maybe even combined with experimental noise, may not be detected. The Gaussianity, however, is a straightforward and sensitive quantity that can report on transient anomalous diffusion.
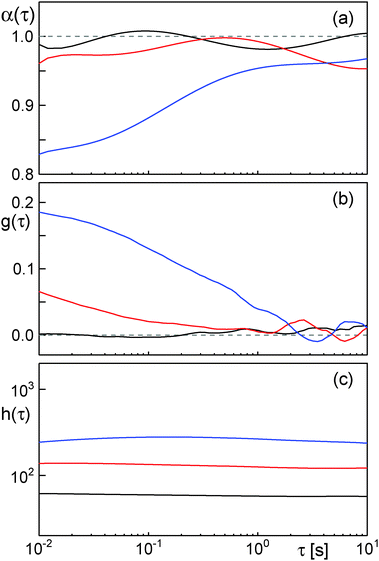 | ||
| Fig. 4 (a) Anomaly α(τ) [eqn (3)] (averaged over 20 trajectories) for obstructed diffusion with different volume fractions of obstacles. While for ϕ = 0 (black) and ϕ = 0.2 (red) no significant anomaly is observed, a significant transient subdiffusion is seen for ϕ = 0.35 (blue). (b) The averaged Gaussianity g(τ) clearly depicts the transient non-Gaussian nature of the random walk at ϕ = 0.35 (blue) for short time scales, whereas free diffusion at ϕ = 0 (black) is reported to be a Gaussian process. Interestingly, the Gaussianity already reports significant deviations from a normal Brownian walk at ϕ = 0.2 (red) while no significant subdiffusion has been detected via α(τ). (c) Albeit the simulated OD scenarios for ϕ = 0.2 (red) and ϕ = 0.35 (blue) have been clearly marked by the Gaussianity as non-Gaussian (sub)diffusion processes, the scaling of h(τ) does not significantly differ from that of normal Brownian motion at ϕ = 0 (black). Please note the same time axis for all plots. | ||
As a result of the above, we propose the following three-step protocol to uncover the anomalous random walk model from single-particle tracking data:
1. Check if the ensemble-averaged MSD [eqn (1)] deviates significantly from normal diffusion. If a subdiffusive characteristics, i.e. α < 1, is seen you can proceed with the next step.
2. Check if α(τ) [eqn (3)] of the time-averaged MSD [eqn (2)] shows subdiffusion. If a significant anomaly is visible then particles most likely do not undergo a CTRW and you can proceed with the next step. If α(τ) ≈ 1, a CTRW may be the most meaningful model for the particles' random walk.
3. Calculate the trajectory's Gaussianity [eqn (4)]. If g(τ) ≈ 0 then FBM is the most reasonable model, whereas positive values are a signature for obstructed diffusion.
Notably, for the case of mixed processes, e.g. CTRW in combination with OD40 or with FBM,12 a non-zero value of the Gaussianity due to the CTRW contribution is anticipated at least asympotically.18 The contribution of OD will then be superimposed on smaller time scales. However, a CTRW contribution will already be highlighted during the second point in the above to-do list. Given that diffusion processes with spatially smoothly varying diffusion constants41 or spatio-temporally changing temperature fields42 are in part reminiscent of a CTRW process,41 it is likely that only small modifications will be needed in the above approach to also clearly report on such processes.
In summary, we have proposed and conducted here a quick and versatile test for the type of subdiffusion that does not involve complex data handling. As seen above, our approach can even reveal transient and incomplete types of subdiffusive random walks within a few, easy steps. We therefore suggest this test as a helpful toolbox especially for evaluating experimental single-particle tracking data.
Acknowledgements
DE and JK gratefully acknowledge financial support from the Research Unit FOR608. MW is financially supported by the Human Frontier Research Program. We thank Daniel Zalami for his assistance with the data acquisition.References
- M. V. Smoluchowski, Phys. Z., 1916, 17, 557–571 Search PubMed.
- O. Benichou, C. Chevalier, J. Klafter, B. Meyer and R. Voituriez, Nat. Chem., 2010, 2, 472–477 CrossRef CAS PubMed.
- R. Kopelman, Science, 1988, 241, 1620–1626 CAS.
- M. Hellmann, D. Heermann and M. Weiss, EPL, 2011, 94, 18002 CrossRef.
- I. Tolic-Norrelykke, E. Munteanu, G. Thon, L. Oddershede and K. Berg-Sorensen, Phys. Rev. Lett., 2004, 93, 078102 CrossRef PubMed.
- M. Weiss, M. Elsner, F. Kartberg and T. Nilsson, Biophys. J., 2004, 87, 3518–3524 CrossRef CAS PubMed.
- G. Guigas, C. Kalla and M. Weiss, Biophys. J., 2007, 93, 316–323 CrossRef CAS PubMed.
- I. Golding and E. Cox, Phys. Rev. Lett., 2006, 96, 098102 CrossRef PubMed.
- S. Weber, A. Spakowitz and J. Theriot, Phys. Rev. Lett., 2010, 104, 238102 CrossRef PubMed.
- J. H. Jeon, V. Tejedor, S. Burov, E. Barkai, C. Selhuber-Unkel, K. Berg-Sorensen, L. Oddershede and R. Metzler, Phys. Rev. Lett., 2011, 106, 048103 CrossRef PubMed.
- K. Burnecki, E. Kepten, J. Janczura, I. Bronshtein, Y. Garini and A. Weron, Biophys. J., 2012, 103, 1839–1847 CrossRef CAS PubMed.
- S. M. Tabei, S. Burov, H. Y. Kim, A. Kuznetsov, T. Huynh, J. Jureller, L. H. Philipson, A. R. Dinner and N. F. Scherer, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4911–4916 CrossRef PubMed.
- I. Wong, M. Gardel, D. Reichman, E. Weeks, M. Valentine, A. Bausch and D. Weitz, Phys. Rev. Lett., 2004, 92, 178101 CrossRef CAS PubMed.
- D. Banks and C. Fradin, Biophys. J., 2005, 89, 2960–2971 CrossRef CAS PubMed.
- J. Szymanski and M. Weiss, Phys. Rev. Lett., 2009, 103, 038102 CrossRef PubMed.
- W. Pan, L. Filobelo, N. Pham, O. Galkin, V. Uzunova and P. Vekilov, Phys. Rev. Lett., 2009, 102, 058101 CrossRef PubMed.
- D. Ernst, M. Hellmann, J. Köhler and M. Weiss, Soft Matter, 2012, 8, 4886–4889 RSC.
- F. Höfling and T. Franosch, Rep. Prog. Phys., 2013, 76, 046602 CrossRef PubMed.
- F. Hofling, T. Franosch and E. Frey, Phys. Rev. Lett., 2006, 96, 165901 CrossRef PubMed.
- H. Berry, Biophys. J., 2002, 83, 1891–1901 CrossRef CAS PubMed.
- M. Hellmann, D. Heermann and M. Weiss, EPL, 2012, 97, 58004 CrossRef.
- R. Metzler and J. Klafter, Phys. Rep., 2000, 339, 1–77 CrossRef CAS.
- Y. He, S. Burov, R. Metzler and E. Barkai, Phys. Rev. Lett., 2008, 101, 058101 CrossRef CAS PubMed.
- A. Lubelski, I. Sokolov and J. Klafter, Phys. Rev. Lett., 2008, 100, 250602 CrossRef PubMed.
- E. Barkai, Y. Garini and R. Metzler, Phys. Today, 2012, 65, 29–35 CrossRef CAS.
- M. Magdziarz, A. Weron, K. Burnecki and J. Klafter, Phys. Rev. Lett., 2009, 103, 180602 CrossRef PubMed.
- S. Burov, R. Metzler and E. Barkai, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13228–13233 CrossRef CAS PubMed.
- V. Tejedor, O. Bénichou, R. Voituriez, R. Jungmann, F. Simmel, C. Selhuber-Unkel, L. Oddershede and R. Metzler, Biophys. J., 2010, 98, 1364–1372 CrossRef CAS PubMed.
- S. Burov, J. H. Jeon, R. Metzler and E. Barkai, Phys. Chem. Chem. Phys., 2011, 13, 1800–1812 RSC.
- F. Thiel, F. Flegel and I. M. Sokolov, Phys. Rev. Lett., 2013, 111, 010601 CrossRef PubMed.
- Y. Meroz, I. Sokolov and J. Klafter, Phys. Rev. Lett., 2013, 110, 090601 CrossRef PubMed.
- A. Berezhkovskii, L. Dagdug and S. Bezrukov, Biophys. J., 2014, 106, L09–L11 CrossRef CAS PubMed.
- D. Ernst, S. Hain and J. Köhler, J. Opt. Soc. Am. A, 2012, 29, 1277–1287 CrossRef PubMed.
- D. Ernst and J. Köhler, Phys. Chem. Chem. Phys., 2013, 15, 845–849 RSC.
- J. Enderlein, Single Mol., 2000, 1, 225–230 CrossRef CAS.
- M. Weiss, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 010101(R) CrossRef.
- M. Hellmann, J. Klafter, D. W. Heermann and M. Weiss, J. Phys.: Condens. Matter, 2011, 23, 234113 CrossRef PubMed.
- J. H. Jeon, E. Barkai and R. Metzler, J. Chem. Phys., 2013, 139, 121916 CrossRef PubMed.
- M. Goulian and S. M. Simon, Biophys. J., 2000, 79, 2188–2198 CrossRef CAS PubMed.
- A. V. Weigel, B. Simon, M. M. Tamkun and D. Krapf, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6438–6443 CrossRef CAS PubMed.
- A. G. Cherstvy and R. Metzler, Phys. Chem. Chem. Phys., 2013, 15, 20220–20235 RSC.
- A. Fulinski, J. Chem. Phys., 2013, 138, 021101 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2014 |