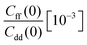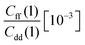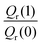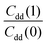Kinetic isotope effect in malonaldehyde determined from path integral Monte Carlo simulations
Jing
Huang
ab,
Marcin
Buchowiecki
cd,
Tibor
Nagy
a,
Jiří
Vaníček
*c and
Markus
Meuwly
*ae
aDepartment of Chemistry, University of Basel, Klingelbergstrasse 80, Basel, Switzerland. E-mail: m.meuwly@unibas.ch
bDepartment of Pharmaceutical Sciences, School of Pharmacy, University of Maryland, Baltimore, Maryland, USA
cInstitute of Chemical Sciences and Engineering, Ecole Polytechnique Fédérale de Lausanne, Lausanne, Switzerland. E-mail: jiri.vanicek@epfl.ch
dInstitute of Physics, University of Szczecin, Wielkopolska 15, 70-451 Szczecin, Poland
eChemistry Department, Brown University, Providence, Rhode Island, USA
First published on 29th October 2013
Abstract
The primary H/D kinetic isotope effect on the intramolecular proton transfer in malonaldehyde is determined from quantum instanton path integral Monte Carlo simulations on a fully dimensional and validated potential energy surface for temperatures between 250 and 1500 K. Our calculations, based on thermodynamic integration with respect to the mass of the transferring particle, are significantly accelerated by the direct evaluation of the kinetic isotope effect instead of computing it as a ratio of two rate constants. At room temperature, the KIE from the present simulations is 5.2 ± 0.4. The KIE is found to vary considerably as a function of temperature and the low-T behaviour is dominated by the fact that the free energy derivative in the reactant state increases more rapidly than in the transition state. Detailed analysis of the various contributions to the quantum rate constant together with estimates for rates from conventional transition state theory and from periodic orbit theory suggest that the KIE in malonaldehyde is dominated by zero point energy effects and that tunneling plays a minor role at room temperature.
1 Introduction
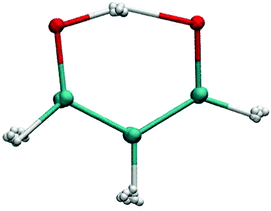
Determining the rate at which a chemical reaction proceeds remains a challenging computational problem, in particular for high-dimensional systems. Stated in the most general way, two ingredients are required: a suitable multidimensional potential energy surface (PES) which describes how the interaction energy changes as a function of the coordinates and a method to solve the quantum dynamical problem. For three- and four-atom systems, considerable progress has been made for both issues mentioned above. Nowadays, fully dimensional PESs can be computed and fitted to high-level ab initio calculations for systems containing 10 atoms or more.1–3 Despite their undisputed utility and the level of detail they provide, their routine use is, however, limited in various ways. First, from a practical perspective the analytical representation is highly non-trivial. This can be avoided by using ab initio molecular dynamics techniques, which, however, at a sufficiently high level of theory [MP2 or CCSD(T)] is extremely costly and usually not employed, except for the smallest systems.4 Second, due to the extensive parameterization (1633 parameters for typical PESs such as that for malonaldehyde2) the analytical PESs can be quite tedious in force evaluations which are needed in every scheme that computes rates from dynamics. Third, extending the validity of a fully dimensional PES from one compound to a chemically similar one is in general not possible. In other words, for every system, a new PES needs to be computed and fitted.Malonaldehyde (MA, see Fig. 1) has long served as a typical hydrogen transfer system to test and validate various computational approaches. Experimentally, the ground state tunneling splitting was determined to be 21.58314 cm−1 by different experiments with very high accuracy.5,6 Infrared spectra of MA have also been recorded at high resolution.7–10 Limbach et al. have studied the proton transfer rate in its di-imine derivative with nuclear magnetic resonance (NMR) spectroscopy.11 Using ab initio path integral Monte Carlo simulations, Tuckerman and Marx have demonstrated the importance of quantizing even the heavy-atom skeleton.4 One of the relevant quantities requiring a quantum mechanical treatment is the kinetic isotope effect (KIE). It relates the rate constants for hydrogen and deuterium transfer via KIE = kH/kD and can be determined in different ways.12,13 So far, the KIE for the intramolecular hydrogen transfer in MA has not been determined experimentally and computed estimates for the KIE at 300 K range from 1.54 to 5.1012 and from 6.49 to 11.41.13 Typical KIEs for organic reactions at 300 K are between 1 and 8, where the precise value depends strongly on the temperature and on the shape and height of the activation barrier.14,15 Significantly larger KIEs have been observed recently for enzymatic reactions at physiological temperature,16,17 which has spurred suggestions that quantum effects may be relevant even in biological systems. Whether enzyme active sites can increase their catalytic activity by enhancing these quantum mechanical effects such as zero point energy or tunneling is, however, still controversial.18–20
In the present work we combine a fully dimensional and validated (with respect to vibrations and tunneling splittings) PES21 based on molecular mechanics with proton transfer (MMPT)22 with the path integral Monte Carlo (PIMC) methodology in order to determine the primary H/D KIE on the intramolecular proton transfer in MA at various temperatures. Calculations of the KIE are based on the quantum instanton approximation for the rate constant23 and on thermodynamic integration with respect to the mass of the transferring particle.24,25
2 Methods
2.1 Quantum instanton approximation for kinetic isotope effects
The quantum-mechanical thermal rate constant is defined as the thermal average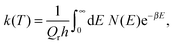 | (1) |
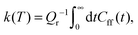 | (2) |
The quantum instanton (QI) method approximates the thermal rate constant as:23
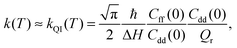 | (3) |
Within the QI approximation the KIE, defined here as the ratio of the hydrogen and deuterium transfer rate constants, can be computed as:24
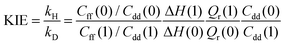 | (4) |
| m(λ) = mH(1 − λ) + mDλ. | (5) |
The intermediate values of λ facilitate calculation of the ratios Qr(1)/Qr(0) and Cdd(1)/Cdd(0) by thermodynamic integration (TI) with respect to mass,24
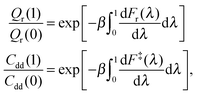 | (6) |
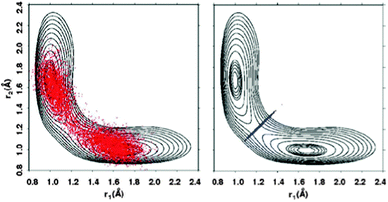
Finally, transition-state related quantities Cff(λ)/Cdd(λ) and ΔH(λ) required for eqn (4) are computed by constrained PIMC simulations with λ = 0 and 1.32–34 For the constrained simulations, a harmonic constraint ½k(rO1H − rO2H)2 with k = 20 a.u. is used to keep two path integral beads close to the dividing surface passing through the transition state. The effect of this constraint is illustrated in Fig. 2, where the two O–H distances r1 and r2 during PIMC simulations at 375 K with and without the constraint are projected onto a reduced two-dimensional (2D) PES for the proton transfer reaction. At low temperature – for hydrogen transfer below about 250 K – the optimal dividing surface bifurcates, and the two beads should be constrained separately to these two dividing surfaces.23,27 For simplicity, we neglect this effect.
2.2 Conventional transition state theory approximation for the kinetic isotope effect
Conventional Transition State Theory35 (CTST) within the rigid-rotor harmonic oscillator (RRHO) approximation without tunneling, overbarrier reflection and corner-cutting corrections was used to estimate the KIE in order to assess the importance of quantum effects in the investigated temperature range. According to CTST the rate coefficient is proportional to the ratio of the full translational–rovibronic partition functions in the transition state (Q‡) and in the reactant (Qr) calculated from the same reference energy level: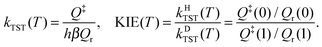 | (7) |
As above, values λ = 0 and 1 in the argument correspond to the H- and D-variants of MA, respectively. The ratio of transition state (Q‡) and reactant (Qr) partition functions was estimated considering only the lowest lying electronic states (E0) without rovibronic coupling. Note that the translational partition functions per unit volume (Qtrans) can be factored out exactly; moreover, since they are the same for the reactant and transition states, they cancel. The rovibrational partition (Qrovib) function was approximated with the product of rigid-rotor (Qrot,RR) and harmonic oscillator (Qvib,HO) partition functions.
Using elementary statistical mechanics, the final explicit expression for the KIE is
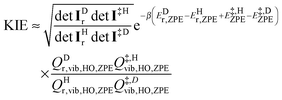 | (8) |
Beside CTST, the magnitude of tunneling rates was estimated from the experimentally determined tunneling splittings6,36 (21.6 cm−1 for H and 2.9 cm−1 for D). Accurate theoretical estimates (21.2 cm−1 for H and 3.0 cm−1 for D) for the tunneling splittings were obtained from the instanton theory by Mil'nikov et al.,37 who found the instanton path between the two minima at the CCSD(T)/(aug)-cc-pVDZ level using the method in ref. 38. The excellent agreement of these results with experiments supports the validity of calculations at the CCSD(T) level (e.g. MMPT surface) for quantitative investigations of MA and justifies the consistency of experimental results in combination with numerical results obtained directly from the MMPT surface.
Miller39 derived expressions that relate tunneling energy splittings (ΔE) to tunneling probabilities (Ptun) for a 1D symmetric double well potential based on periodic orbit theory,
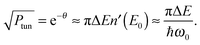 | (9) |
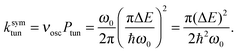 | (10) |
2.3 MMPT force field
The MMPT Force Field is used to compute the potential energies for MA during the PIMC simulations. A detailed account of the force field has been given in ref. 21 and 22. Briefly, MMPT uses parameterized three-dimensional potential energy surfaces fitted to MP2/6-311++G(d,p) ab initio calculations to describe the interactions within a general DH–A motif where D is the donor, H is the hydrogen, and A is the acceptor atom. Together with a standard force field—here CHARMM40 is used—the bonded interactions on the donor and acceptor side are smoothly switched on and off depending on the position of the transferring H-atom (DH–A or D–HA). Recent work shows that the parameterized MMPT force field for MA leads to equilibrium structures, infrared spectra, tunneling splittings, and proton transfer rates that compare favorably with experimental and previous computational work.21Fig. 2 shows the two-dimensional projection of the PES for the proton transfer in MA, and the corresponding proton transfer barrier height is 4.34 kcal mol−1, which is close to the ab initio value of 4.1 kcal mol−1 at the CCSD(T) level.23 Results and discussion
3.1 Simulation details
The PIMC simulations employed a combination of single-slice, multi-slice, and whole chain moves.41 The statistical errors of all the quantities were calculated by block averaging, which estimates statistical errors by removing inherent correlation in the Monte Carlo data.42 Test simulations were carried out to determine the required number P of imaginary time slices to converge the calculations. Fig. 3 shows the dependence of Cff/Cdd, ΔH, and dF‡(λ)/dλ on P for T = 375 K. In general P = 64 is sufficient for converging these quantities. The figure compares the thermodynamic estimator (TE)24 and centroid virial estimator (CVE)25 for the free-energy derivative dF‡(λ)/dλ. While the two estimators yield similar average results, the statistical root mean square error (RMSE) of dF‡(λ)/dλ computed with TE grows with P, whereas the RMSE of the CVE remains approximately constant up to P = 256. The RMSEs of Cff/Cdd and ΔH also increase significantly with P, as shown in Fig. 3. In particular, ΔH(0) and ΔH(1) have the largest statistical errors (see Table 1), and much longer simulations are required to evaluate them, especially at lower temperatures where larger P values are needed. This could be remedied by using more efficient estimators for ΔH and Cff/Cdd.34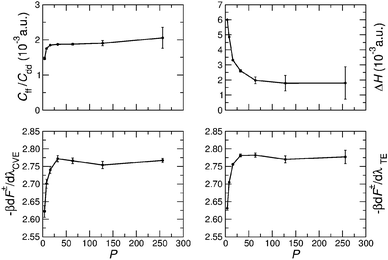 | ||
| Fig. 3 The dependence of Cff/Cdd, ΔH, (dF‡/dλ)CVE and (dF‡/dλ)TE on the number P of imaginary time slices for T = 375 K and λ = 0. | ||
| T (K) | ΔH(0) [10−3] | ΔH(1) [10−3] | KIE | ||||
|---|---|---|---|---|---|---|---|
| 1500 | 5.004 ± 0.039 | 4.769 ± 0.052 | 7.469 ± 0.242 | 8.776 ± 0.579 | 3.503 ± 0.001 | 4.054 ± 0.012 | 1.07 ± 0.08 |
| 750 | 2.988 ± 0.023 | 2.753 ± 0.024 | 4.061 ± 0.130 | 4.146 ± 0.131 | 5.332 ± 0.002 | 4.174 ± 0.003 | 1.42 ± 0.07 |
| 500 | 2.273 ± 0.018 | 2.118 ± 0.018 | 2.833 ± 0.099 | 3.090 ± 0.092 | 8.893 ± 0.005 | 4.609 ± 0.006 | 2.3 ± 0.1 |
| 375 | 1.890 ± 0.017 | 1.872 ± 0.018 | 1.959 ± 0.093 | 2.429 ± 0.083 | 15.421 ± 0.011 | 5.374 ± 0.010 | 3.6 ± 0.2 |
| 300 | 1.610 ± 0.019 | 1.694 ± 0.018 | 1.752 ± 0.102 | 2.345 ± 0.074 | 27.221 ± 0.027 | 6.647 ± 0.019 | 5.2 ± 0.4 |
| 250 | 1.426 ± 0.026 | 1.626 ± 0.023 | 1.686 ± 0.109 | 1.891 ± 0.092 | 48.578 ± 0.067 | 8.610 ± 0.035 | 5.5 ± 0.5 |
The free energy derivatives required for TI are evaluated for seven λ values (see below) with both unconstrained and constrained simulations. Unconstrained simulations include 2 × 108 steps, while constrained simulations are run for 4 × 108 steps each except those for λ = 0 and 1 where 8 × 108 steps are used to reduce the RMSE of ΔH. This results in 14 independent PIMC simulations and in a total number of 5 × 109 Monte Carlo moves from which the KIE was estimated at each temperature.
The ratios of the partition functions and of the delta–delta correlation functions are computed by TI for λ = j/6 with j = 0, 1,…, 6. The free energy derivatives needed as an input for TI at different temperatures are shown in Fig. 4. With decreasing temperature, dFr(λ)/dλ increases more rapidly than dF‡(λ)/dλ, and this is the major cause for the temperature variation of the KIE in MA (see Table 1).
 | ||
| Fig. 4 Free energy derivatives for the reactant (left) and transition states (right) with respect to the mass parameter λ used for thermodynamic integration. | ||
3.2 Kinetic isotope effect
Table 1 shows the computed KIE values from PIMC simulations on the MMPT PES together with intermediate variables required for eqn (4). The statistical errors are also listed, and the KIEs are determined to be within 10% uncertainty. At very high temperature (∼1500 K) the KIE is only slightly larger than 1, while at 300 K a KIE of 5.2 ± 0.4 is found.The temperature dependence of the KIE can be characterized in more detail by decomposing it into two factors, namely 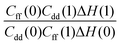 and
and 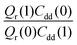 . As illustrated in Fig. 5, the ratio
. As illustrated in Fig. 5, the ratio 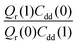 grows exponentially with the inverse temperature. An exponential fit based on the six temperatures considered in the present work leads to
grows exponentially with the inverse temperature. An exponential fit based on the six temperatures considered in the present work leads to 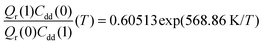 with a correlation coefficient of 0.999. This implies that
with a correlation coefficient of 0.999. This implies that 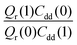 is an Arrhenius component and the tedious TI calculations can be reasonably replaced by the fitted formula. As for the pre-factor
is an Arrhenius component and the tedious TI calculations can be reasonably replaced by the fitted formula. As for the pre-factor 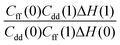 , its temperature dependence is more involved, partially because of the large uncertainties in ΔH(1) and ΔH(0). However, this factor is relatively temperature-insensitive and close to 1.17 over a large temperature range. With these observations an empirical formula of KIE = 0.708
, its temperature dependence is more involved, partially because of the large uncertainties in ΔH(1) and ΔH(0). However, this factor is relatively temperature-insensitive and close to 1.17 over a large temperature range. With these observations an empirical formula of KIE = 0.708![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(568.86 K/T) is expected to provide an estimate of the KIE for the proton transfer in MA above 300 K, which may be relevant for forthcoming experimental studies. A likely reason for this relatively simple exponential behavior is the small barrier height which implies that the main quantum-mechanical contribution to the KIE is due to zero-point energy in the investigated temperature range, as will be further discussed below.
exp(568.86 K/T) is expected to provide an estimate of the KIE for the proton transfer in MA above 300 K, which may be relevant for forthcoming experimental studies. A likely reason for this relatively simple exponential behavior is the small barrier height which implies that the main quantum-mechanical contribution to the KIE is due to zero-point energy in the investigated temperature range, as will be further discussed below.
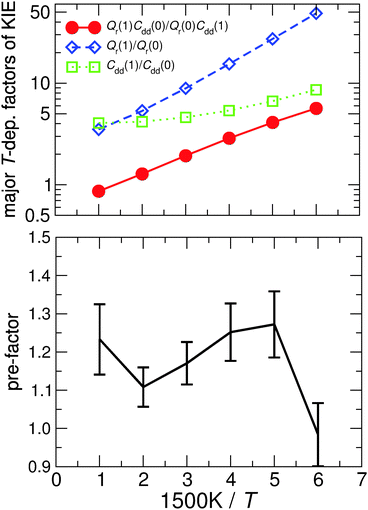 | ||
Fig. 5 The temperature dependence of different components of the KIE: the exponentially-dependent factor 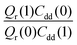 (top) and the pre-factor (top) and the pre-factor 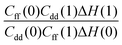 (bottom) are reported. See the text for details. (bottom) are reported. See the text for details. | ||
Our results demonstrate that meaningful and converged rates for proton transfer in relatively large systems can be obtained from extensive quantum simulations based on a validated fully-dimensional reactive MMPT-potential energy surface. Recently, the KIE at 300 K was computed from a distributed Gaussian EVB potential energy surface with different quantum methods.12 With this PES, the KIE computed as the ratio of the two rate constants ranges from 2.41 ± 0.86 to 4.05 ± 0.27 using quantum instanton and path integral-quantum transition state theory. Employing thermodynamic integration similar to that presented here, Wong et al.12 obtained a KIE of 4.27 ± 0.01 and 5.10 ± 1.81 with the two methods. Despite the fairly large differences among their four results, the last one agrees (within the statistical error) with our QI value of 5.2 ± 0.4.
Results for absolute rates and KIEs from CTST calculations are reported in Table 2 and compared with those from QI/MMPT. Calculations at the MP2/6-311++G(d,p) level of theory level were carried out with Gaussian09.43 For validation, the CTST results are compared with absolute rates determined previously at 300 K. The classical, “over-the-barrier” hopping rate for H-transfer from MD simulations on the MMPT surface is 2.4 ns−1.21 The factor of 540/2.4 = 225 difference between CTST and MD-based H-hopping rates on the MMPT surface is due to ZPE effects, for which classical MD does not account. Within the HO approximation, the ZPE difference between the reactant and the TS reduces the barrier height by 3.7 kcal mol−1, and thereby contributes to a Boltzmann factor of 470 at 300 K, explaining the factor of ≈102 difference. Independent classical MD calculations along the lines of previous work21 were carried out for estimating the “over-the-barrier” hopping rate in H and D isotopologues on the MMPT surface. This yields 5.3 ns−1 and 0.42 ns−1 at 300 K for H- and D-hopping, suggesting a KIE of ≈13, which is about twice as large as 6.9, the value obtained from CTST calculations on the MMPT surface.
| T (K) | CTST/MP2 | CTST/MMPT | QI/MMPT | MMPT | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k H | k D | KIE-ZPE | KIE-VIB | KIE | k H | k D | KIE-ZPE | KIE-VIB | KIE | KIE | δ KIE (%) | |
| 1500 | 22 | 15 | 1.31 | 1.15 | 1.5 | 35 | 21 | 1.46 | 1.11 | 1.6 | 1.1 | +48 |
| 750 | 13 | 6.7 | 1.71 | 1.12 | 1.9 | 18 | 7.9 | 2.13 | 1.05 | 2.2 | 1.4 | +61 |
| 500 | 8.4 | 3.4 | 2.24 | 1.10 | 2.5 | 11 | 3.4 | 3.10 | 1.04 | 3.2 | 2.3 | +41 |
| 375 | 5.7 | 1.8 | 2.93 | 1.08 | 3.2 | 7.6 | 1.6 | 4.52 | 1.04 | 4.7 | 3.6 | +31 |
| 300 | 3.8 | 0.90 | 3.84 | 1.06 | 4.1 | 5.4 | 0.80 | 6.60 | 1.04 | 6.9 | 5.2 | +32 |
| 250 | 2.6 | 0.50 | 5.02 | 1.04 | 5.2 | 4.0 | 0.40 | 9.62 | 1.03 | 10 | 5.5 | +82 |
Ground-state tunneling rates were calculated based on periodic orbit theory39 using the experimental ground-state splittings (21.6 cm−1 and 2.9 cm−1) and harmonic frequencies of the normal modes corresponding to O–H/D stretching (as upper estimates) obtained from the MMPT force field (2310 cm−1 and 3149 cm−1). Periodic orbit theory suggests ground-state tunneling rates of 44 ns−1 and 1.1 ns−1 for H and D isotopes, respectively, which are significantly slower (10% for H and 1–2% for D) than the CTST estimates for the over-the-barrier rates (540 ns−1 and 80 ns−1 at 300 K). Despite the fact the MMPT force field has a 1 kcal mol−1 higher barrier, CTST with electronic structure calculations at the MP2/6-311++G(d,p) level gives comparable rates of 380 ns−1 and 90 ns−1. This is due to differences in zero point energies between the MMPT and MP2 PESs. Our CTST results are comparable to hopping rates of 656 ns−1, 162 ns−1, and 222 ns−1, 92 ns−1 obtained by Wong et al.12 on their DG-EVB surface using PI-QTST and QI for H and D isotopologues, respectively.
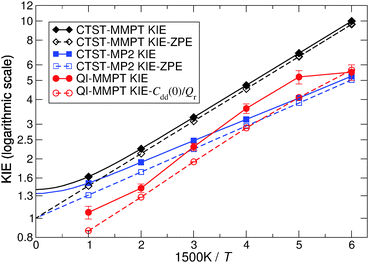
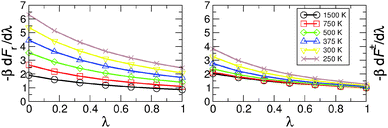
Kinetic isotope effects from QI and CTST calculations are compared in Fig. 6. The PIMC/QI KIE shows Arrhenius type (linear) behavior in the temperature range of 300 to 750 K, whereas deviations from it can be observed both at lower and higher temperatures. The curvature appearing at low temperature is due to tunneling, whereas at high temperature it is mainly due to convergence to the classical limit and probably also due to neglecting recrossing effects, which are higher for H than for D. Deviation from the Arrhenius-type behaviour due to tunneling was observed, e.g., already in early experiments on CO rebinding in myoglobin.44 The classical high-temperature limit from CTST – given by the ratio of harmonic imaginary frequencies in the transition state for the two isotopes24 – converges to a constant value of 1.398 at temperatures above 750 K, while its ZPE contribution (KIE-ZPE) tends to 1. On the other hand, classical MD simulations between 500 K and 2000 K also show that the rate for H- and D-transfers becomes T-independent above 1250 K. Such simulations include recrossing, which is neglected in CTST and QI, but classical MD on the PES neglects ZPE effects. The fact that at higher temperature the crossing rate from MD becomes constant was also observed in earlier simulations on H-transfer in a protonated ammonia dimer where it was also found that the maximum rate of transfer is slaved to the donor–acceptor vibrational frequency.22,45 Detailed investigations of such effects are, however, outside the scope of the present work.
The difference between QI and CTST at high and intermediate temperatures is mainly due to anharmonicity which is included in the QI but neglected in the CTST. However, it should be pointed out that high-temperature results of both QI and CTST for MA are somewhat academic since, at high temperature, the barrier is easily crossed and assumptions of classical or quantum transition state theories break down. Below 750 K, CTST estimates for the KIE are dominated by ZPE effects and vibrational excitation has little influence. CTST gives significantly different results for MMPT and MP2 at low temperature. This is probably related to the different harmonic frequencies in the MMPT and MP2 treatments. Another factor may be that during H-transfer the π-electron system of MA is rearranged and tautomerisation takes place. Such effects are included in MP2 calculations but are difficult to capture in a force field.
To explore the differences between QI theory and CTST and highlight the advantages of QI in the case of MA, the ZPE effects from QI calculations were estimated for both the reactant and transition states. According to Table 1, the two main factors contributing to the KIE when treated with the QI method are the ratios of Qr and Cdd, which are the Boltzmann factors of free energies of the isotopologues (see eqn (6)) for the reactant and the transition state, respectively. The asymptotic behaviour of the ratio of partition functions at low temperature is dominated by the Boltzmann factor of the ZPE differences, assuming a linear, Arrhenius-type behaviour (log vs. 1/T). An Arrhenius plot of these quantities (see Fig. 5) suggests a near-linear behaviour at low temperature. At 250 K Qr(1)/Qr(0) = 48.578 ± 0.067 and Cdd(1)/Cdd(0) = 8.610 ± 0.035 at the MMPT-QI level. This yields ZPE differences of ΔHDZPEr = 1.93 kcal mol−1 and ΔHDZPE‡ = 1.07 kcal mol−1 with a corresponding difference in ZPE-differences of Δ = 0.86 kcal mol−1 (Δ := ΔHDZPEr − ΔHDZPE‡) which is the quantity that appears in the exponent of the KIE calculated with CTST in eqn (8). For an improved estimate as T → 0 a general hyperbolic form of 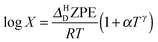 was fitted to the data at 500 K, 375 K, 300 K and 250 K, where X denotes the ratios Qr(1)/Qr(0) or Cdd(1)/Cdd(0), and α and γ are fitting parameters. This yields ΔHDZPEr = (1.805 ± 0.002) kcal mol−1 and ΔHDZPE‡ = (0.929 ± 0.016) kcal mol−1 and Δ = 0.87 kcal mol−1 for T → 0.
was fitted to the data at 500 K, 375 K, 300 K and 250 K, where X denotes the ratios Qr(1)/Qr(0) or Cdd(1)/Cdd(0), and α and γ are fitting parameters. This yields ΔHDZPEr = (1.805 ± 0.002) kcal mol−1 and ΔHDZPE‡ = (0.929 ± 0.016) kcal mol−1 and Δ = 0.87 kcal mol−1 for T → 0.
For low temperatures (T < 300 K) the CTST and QI kinetic isotope effects do not agree particularly well. The HO approximation on the MMPT surface yields ΔHDZPEr = 2.04 kcal mol−1 and ΔHDZPE‡ = 0.92 kcal mol−1 with a corresponding Δ = 1.12 kcal mol−1. Hence, for the TS excellent agreement is found between QI/PIMC-MMPT (0.92 kcal mol−1) and CTST/HO-MMPT (0.93 kcal mol−1), whereas for the reactant state the HO approximation is inadequate due to the large anharmonicity in the O–H stretching vibration. We conclude that the major contribution to the deviation between KIEs calculated by TST and QI at low temperature (see Table 2) is from ZPE differences in the reactant state (ΔHDZPEr), giving rise to a factor of 1.65 at 250 K. Another contribution to this difference may follow from the fact—mentioned in subsection 2.1—that at low temperature the optimal QI dividing surface bifurcates into two dividing surfaces.23,27 Our use of a single dividing surface determined by symmetry lowers the rate constant for hydrogen at and below about 250 K.23,27 Since the bifurcation occurs at even lower temperature for deuterium, the approximate QI rate probably slightly underestimates the KIE at 250 K. Nevertheless, our analysis above has shown that for significant vibrational anharmonicity (e.g. in the reactant state) due to the presence of low-lying barriers and of a neighboring well, the use of QI/PIMC becomes crucial, as it can capture these effects by exploring all relevant regions of the phase-space in contrast to the CTST/HO approximation, which uses only local information.
It is also possible to rationalize why, below 500 K, CTST-MP2 gives KIEs that are closer to the QI-MMPT values than the KIEs obtained with CTST-MMPT. The HO approximation on the MP2 surface gives ΔHDZPEr = 2.17 kcal mol−1 and ΔHDZPE‡ = 1.36 kcal mol−1 and a difference Δ = 0.81 kcal mol−1, which explains that the “better agreement” of CTST-MP2 with QI-MMPT at low temperature is simply due to an accidental cancellation of errors.
While CTST theory within the RRHO approximation can only be considered to be qualitative, it appears to correctly capture the magnitude of the KIE for this rigid molecule at the investigated, near-room and higher temperatures. It suggests that ZPE differences play the dominant role in the magnitude of the KIE, which is consistent with the small curvature of the Arrhenius plot of the KIE obtained from the QI-PIMC simulations.
4 Discussion and conclusions
Based on rigorous quantum simulations utilizing a validated PES for H-transfer in MA, the KIE was found to be 5.2 ± 0.4 at room temperature. As required, the KIE tends to 1 for higher temperatures and a strong temperature dependence for low temperatures is found. The latter can be primarily linked to the variation of the free energy as a function of the progression coordinate λ at the reactant and transition state, respectively. The working expression for the KIE (eqn (4)) allows the quantity of interest to be decomposed into a largely T-independent prefactor and a part which follows an Arrhenius behaviour. Such an empirical relationship can be valuable for experimental studies. Periodic orbit theory based tunneling rate estimates and detailed comparisons with CTST at various levels suggest that the KIE in MA is largely determined by zero-point energy effects and that tunneling plays a minor role.Our results suggest several ways to accelerate the PIMC calculations in future applications: the pre-factor in the KIE (consisting of Cff/Cdd and ΔH) is determined from simulations for H- and D-transfer (λ = 0,1), while the computation of the free energy part [Qr(1)/Qr(0) and Cdd(1)/Cdd(0)] involves TI at a series of intermediate λ values. As shown in Table 1, the relative error of Qr(1)/Qr(0) and Cdd(1)/Cdd(0) are orders of magnitude smaller than those of ΔH(0) and ΔH(1), implying that much shorter PIMC simulations would be sufficient for TI in calculating the KIE. Fig. 3 also shows that in free energy calculations a smaller number of imaginary time slices such as P = 32 could be used to further speed up the simulation. Another acceleration would result from using different numbers of beads for different parts of the system.46 For example, P = 64 can be used for atoms that are directly related to hydrogen transfer, while a much smaller number of beads, such as P = 4, is possibly sufficient for the remaining particles in the system. In the future we will explore the possibilities of lowering the P-values by using higher order factorization of the path integral and of lowering the statistical errors of Cff/Cdd and ΔH by implementing the CVE for these quantities.
In summary, a combination of an experimentally validated and efficient force field with rigorous and numerically robust means to compute quantum correlation functions yields KIEs in MA with statistical errors below 10% even at the lowest studied temperature of 250 K. The favorable scaling of the force field evaluation with the number of atoms and the possibility to reduce the number of beads required to describe atoms far from the proton transfer motif suggests the possibility of applying the present approach to the calculation of KIEs even in larger, biologically relevant systems.
Acknowledgements
This work was supported by the Swiss National Science Foundation through grants 200021-117810 (to MM), 200021_124936 (to JV), and the NCCR MUST (to JV and MM) and the authors thank Zhenhao Xu for exploratory MD simulations.References
- S. Huang, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2005, 122, 044308 CrossRef PubMed.
- Y. Wang, B. J. Braams, J. M. Bowman, S. Carter and D. P. Tew, J. Chem. Phys., 2008, 128, 224314 CrossRef PubMed.
- J. M. Bowman, B. J. Braams, S. Carter, C. Chen, G. Czako, B. Fu, X. Huang, E. Kamarchik, A. R. Sharma, B. C. Shepler, Y. Wang and Z. Xie, J. Phys. Chem. Lett., 2010, 1, 1866–1874 CrossRef CAS.
- M. E. Tuckerman and D. Marx, Phys. Rev. Lett., 2001, 86, 4946 CrossRef CAS.
- S. L. Baughcum, R. W. Duerst, W. F. Rowe, Z. Smith and E. B. Wilson, J. Am. Chem. Soc., 1981, 103, 6296–6303 CrossRef CAS.
- D. W. Firth, K. Beyer, M. A. Dvorak, S. W. Reeve, A. Grushow and K. R. Leopold, J. Chem. Phys., 1991, 94, 1812–1819 CrossRef CAS.
- Z. Smith and E. B. Wilson, Spectrochim. Acta, Part A, 1983, 39, 1117–1129 CrossRef.
- D. W. Firth, P. F. Barbara and H. P. Trommsdorf, Chem. Phys., 1989, 136, 349–360 CrossRef CAS.
- T. Chiavassa, R. Roubin, L. Piazzala, P. Verlaque, A. Allouche and F. Marinelli, J. Phys. Chem., 1992, 96, 10659–10665 CrossRef CAS.
- C. Duan and D. Luckhaus, Chem. Phys. Lett., 2004, 391, 129–133 CrossRef CAS PubMed.
- H. H. Limbach, B. Wehrle, H. Zimmermann, R. D. Kendrick and C. S. Yannoni, Angew. Chem., Int. Ed., 1987, 26, 247–248 CrossRef.
- K. F. Wong, J. L. Sonnenberg, F. Paesani, T. Yamamoto, J. Vanicek, W. Zhang, H. B. Schlegel, D. A. Case, T. E. Cheatham, W. H. Miller and G. A. Voth, J. Chem. Theor. Comput., 2010, 6, 2566–2580 CrossRef CAS PubMed.
- R. Iftimie and J. Schofield, J. Chem. Phys., 2001, 115, 5891–5902 CrossRef CAS.
- C. J. Collins and E. N. S. Bowman, Isotope effects in chemical reactions, Van Nostrand Reinhold, New York, 1971 Search PubMed.
- E. J. A. Kaye, Isotope effects in gas-phase chemistry, American Chemical Society, Washington, DC, 1992 Search PubMed.
- A. Kohen, R. Cannio, S. Bartolucci and J. P. Klinman, Nature, 1999, 399, 496–499 CrossRef CAS PubMed.
- Z. D. Nagel and J. P. Klinman, Chem. Rev., 2006, 106, 3095–3118 CrossRef CAS PubMed.
- P. Ball, Nature, 2004, 431, 396–397 CrossRef CAS PubMed.
- J.-K. Hwang and A. Warshel, J. Am. Chem. Soc., 1996, 118, 11745–11751 CrossRef CAS.
- S. C. L. Kamerlin and A. Warshel, Proteins, 2010, 78, 1339–1375 CAS.
- Y. Yang and M. Meuwly, J. Chem. Phys., 2010, 133, 064503 CrossRef PubMed.
- S. Lammers, S. Lutz and M. Meuwly, J. Comput. Chem., 2008, 29, 1048–1063 CrossRef CAS PubMed.
- W. H. Miller, Y. Zhao, M. Ceotto and S. Yang, J. Chem. Phys., 2003, 119, 1329–1342 CrossRef CAS.
- J. Vaníček, W. H. Miller, J. F. Castillo and F. J. Aoiz, J. Chem. Phys., 2005, 123, 054108 CrossRef PubMed.
- J. Vaníček and W. H. Miller, J. Chem. Phys., 2007, 127, 114309 CrossRef PubMed.
- W. H. Miller, S. D. Schwartz and J. W. Tromp, J. Chem. Phys., 1983, 79, 4889–4898 CrossRef CAS.
- T. Yamamoto and W. H. Miller, J. Chem. Phys., 2004, 120, 3086–3099 CrossRef CAS PubMed.
- M. Ceotto, S. Yang and W. H. Miller, J. Chem. Phys., 2005, 122, 044109 CrossRef PubMed.
- D. T. Major and J. Gao, J. Chem. Theor. Comput., 2007, 3, 949 CrossRef CAS.
- W. Wang and Y. Zhao, Phys. Chem. Chem. Phys., 2011, 13, 19362–19370 RSC.
- W. Wang and Y. Zhao, J. Chem. Phys., 2012, 137, 214306 CrossRef PubMed.
- Y. Zhao, T. Yamamoto and W. H. Miller, J. Chem. Phys., 2004, 120, 3100–3107 CrossRef CAS PubMed.
- T. Yamamoto and W. H. Miller, J. Chem. Phys., 2005, 122, 044106 CrossRef PubMed.
- S. Yang, T. Yamamoto and W. H. Miller, J. Chem. Phys., 2006, 124, 084102 CrossRef PubMed.
- M. J. Pilling and P. W. Seakins, Reaction Kinetics, Oxford University Press, 1995 Search PubMed.
- S. L. Baughcum, Z. Smith, E. B. Wilson and R. W. Duerst, J. Am. Chem. Soc., 1984, 106, 2260–2265 CrossRef CAS.
- G. Mil'nikov, K. Yagi, T. Taketsugu, H. Nakamura and K. Hirao, J. Chem. Phys., 2003, 119, 10–13 CrossRef CAS.
- G. Mil'nikov and H. Nakamura, J. Chem. Phys., 2001, 115, 6881–6897 CrossRef CAS.
- W. H. Miller, J. Phys. Chem., 1979, 83, 960–963 CrossRef CAS.
- A. D. MacKerell Jr., D. Bashford, M. Bellott, J. R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, I. W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef.
- M. Buchowiecki and J. Vaníček, J. Chem. Phys., 2010, 132, 194106 CrossRef PubMed.
- H. Flyvbjerg and H. G. Petersen, J. Chem. Phys., 1989, 91, 461–466 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, (Revision A.02), Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- J. Alben, D. Beece, S. Bowne, L. Eisenstein, H. Frauenfelder, D. Good, M. Marden, P. Moh, L. Reinisch, A. Reynolds and K. Yue, Phys. Rev. Lett., 1980, 44, 1157–1160 CrossRef CAS.
- M. Meuwly and M. Karplus, J. Chem. Phys., 2002, 116, 2572–2585 CrossRef CAS.
- Y. Li and W. H. Miller, Mol. Phys., 2005, 103, 203–208 CrossRef CAS.
| This journal is © the Owner Societies 2014 |