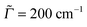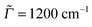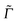Vibrationally resolved absorption, emission and resonance Raman spectra of diamondoids: a study based on time-dependent correlation functions
Shiladitya
Banerjee
and
Peter
Saalfrank
*
Universität Potsdam, Institut für Chemie, Karl-Liebknecht-Straße 24-25, D-14476 Potsdam-Golm, Germany. E-mail: peter.saalfrank@uni-potsdam.de
First published on 29th October 2013
Abstract
The time-dependent approach to electronic spectroscopy, as popularized by Heller and coworkers in the 1980's, is applied here in conjunction with linear-response, time-dependent density functional theory to study vibronic absorption, emission and resonance Raman spectra of several diamondoids. Two-state models, the harmonic and the Condon approximations, are used for the calculations, making them easily applicable to larger molecules. The method is applied to nine pristine lower and higher diamondoids: adamantane, diamantane, triamantane, and three isomers each of tetramantane and pentamantane. We also consider a hybrid species “Dia = Dia” – a shorthand notation for a recently synthesized molecule comprising two diamantane units connected by a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond. We resolve and interpret trends in optical and vibrational properties of these molecules as a function of their size, shape, and symmetry, as well as effects of “blending” with sp2-hybridized C-atoms. Time-dependent correlation functions facilitate the computations and shed light on the vibrational dynamics following electronic transitions.
C double bond. We resolve and interpret trends in optical and vibrational properties of these molecules as a function of their size, shape, and symmetry, as well as effects of “blending” with sp2-hybridized C-atoms. Time-dependent correlation functions facilitate the computations and shed light on the vibrational dynamics following electronic transitions.
1 Introduction
Diamondoids are a class of saturated hydrocarbons, made of repeated units of interconnected cyclohexane rings.1–3 They can be derived from the parent material diamond, by cutting out of the crystal small subunits and saturating the cutting positions with hydrogen. The simplest diamondoid is adamantane, C10H16, with its cage comprising sp3-hybridized C atoms. The next homologues are diamantane with two adamantane units, C14H20, triamantane C18H24, tetramantane C22H28, pentamantane, hexamantane and so forth.Starting with tetramantane, one speaks of higher diamondoids, in contrast to the lower diamondoids ada-, dia-, and triamantane. The higher diamondoids have been known for years1 and have always more than one structural isomer. For example, for tetramantane there exist four different isomers, called [1(2)3], [121] and two forms of [123] according to the so-called Balaban–Schleyer notation.1 For diamondoids higher than tetramantane, representatives belonging to the same family may have even distinct atomic compositions, and thus molecular weights.3 Even if the sum formula is the same, different isomers exhibit different shapes, and typically also different properties. For example, the two tetramantanes [123] mentioned above are enantiomers, i.e., molecules with different chirality.4
In general, diamondoids are chemically quite inert, hard compounds, with high thermal conductivity.5 Further, they are good (monochromatic) electron emitters with negative electron affinity,6 wide-gap semiconductors, transparent, absorbing light significantly around and above about 6 eV,7,8i.e., in the UV region. The diamondoids are excellent fluorescing materials, known to fluoresce both in the solid state and in gas-phase. Due to their flexible shape and composition and due to their ability to be functionalized (see below), one hopes that these molecules have tunable optical and electronic properties for possible applications. A prerequisite for their rational design, however, is the understanding of the optical properties of these materials, based on optical spectroscopy and/or theory.
In this context, the optical gaps and optical absorption of nine different, well-defined diamondoids (ada-, dia-, triamantane, the three tetramantanes ([1(2)3], [121], [123]), two (of ten) penta- and one hexamantane) have recently been measured in ref. 7. The different species can be characterized not only according to their size, but also their symmetry and shape: they form 1D, 2D, and 3D geometric families. Characteristic differences in absorption spectra were found depending on the geometric family, with the 3D structures exhibiting similar optical properties to the parent compound, diamond. Some but not all, absorption spectra showed sharp peaks, assigned to Rydberg states,7 and/or also a vibronic fine-structure was found for several species. While the observations could partially be assigned to structural features, symmetry and composition, a profound understanding of the optical spectra of diamondoids is still lacking.
Pristine diamondoids have also been studied with respect to their photoluminescence, i.e., fluorescence properties. For instance, intrinsic, broad-band photoluminescence of adamantane in the UV spectral region could be observed.9 A fine-structure in the fluorescence spectrum at an excitation energy of Eex = 6.6 eV vanishes at higher excitation energies.10 Also, the fluorescence of a series of (eight) diamondoids up to pentamantane has meanwhile been measured.10 For these compounds, the fluorescence maxima depend on size and shape of the diamondoid in question, ranging from 6.1 eV for adamantane to about 5.5 eV for [123]tetramantane. Some of the emission spectra show vibrational progressions, others are structureless. Again, the precise origin of these features is essentially unknown and requires further attention.
Diamondoids were also characterized by other spectroscopic methods. Schreiner et al. measured both optical and vibrational circular dichroism to distinguish the two enantiomeric forms of [123]tetramantane.4 Further, besides Raman spectra quite recently also resonance Raman (rR) spectra of diamondoids have been determined.11 Resonance Raman spectra give, unlike pure vibrational or electronic spectroscopy, simultaneous information on both, vibrational and electronic excitation in molecular systems.
To the best of our knowledge, no calculation of rR spectra of diamondoids has been presented so far. In fact, apart from the work cited above, almost all quantum chemical calculations up to now refer to molecules in their electronic ground states.12 If excited states were considered, e.g., for absorption spectra, this was usually done to arrive at vertical excitation energies only, without any vibrational fine-structure or inter-state couplings included.13 Also, HOMO–LUMO gaps (or fundamental gaps in the case of solid-state calculations) are often used as simplified measures for optical properties.14 While vibronics were hardly ever considered, Stokes shifts, on the other hand, i.e., the energy difference between vertical excitation and de-excitation energies due to different ground and excited state geometries, have been computed for selected pristine diamondoids.13
In order to systematically tune properties and arrive at functional nano-devices, pristine diamondoids are not the first choice: their properties depend on size and shape, but sometimes in an unforeseen way and to an extent which may be insufficient. Different strategies were suggested to chemically modify diamondoids resulting in hopefully specific functionality. Among these strategies are the following:
(i) “Doping”, e.g., replacing CH2 groups by isoelectronic O, or CH groups by isoelectronic N atoms. For example, replacing all four CH units in adamantane by N gives urotropine C6N4H12, whose absorption is altered and fluorescence is quenched in comparison to adamantane.9,15
(ii) “Electronic blending”, e.g., combining/connecting diamondoid subunits with unsaturated hydrocarbons containing sp2-hybridized C atoms. An example is a molecule which we call Dia = Dia below, in which two diamantanes are connected by a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C unit. More complicated species containing unsaturated subunits have been synthesized.16 Due to the enormous richness of synthetic possibilities and the fact that saturated subunits have entirely different electronic and optical properties than those with de-localized π-electrons, a great variety of properties can be expected for “electronically blended” hybrids – presently largely unexplored.
C unit. More complicated species containing unsaturated subunits have been synthesized.16 Due to the enormous richness of synthetic possibilities and the fact that saturated subunits have entirely different electronic and optical properties than those with de-localized π-electrons, a great variety of properties can be expected for “electronically blended” hybrids – presently largely unexplored.
(iii) “Functionalizing”, i.e., attaching functional groups such as alcohol, thiol,17,18 ester, cyano, amine, carboxyl, or introducing C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S units19 to/instead of one or several of the CH or CH2 units of the diamondoid. It is the hope to tune properties by using either electron donors or acceptors. For example, a theoretical prediction states that by introducing surface C
S units19 to/instead of one or several of the CH or CH2 units of the diamondoid. It is the hope to tune properties by using either electron donors or acceptors. For example, a theoretical prediction states that by introducing surface C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S units into diamondoids, their absorption onset can be shifted from the UV to the IR region.19
S units into diamondoids, their absorption onset can be shifted from the UV to the IR region.19
It is the purpose of the present paper to shed light on optical properties and excited states of several pristine diamondoids of increasing size, trying to explore and explain trends. This will be done for the lowest five diamondoids up to pentamantane, with formula C26H32. For diamondoids with isomers, we consider different isomeric forms. In general, we are interested in effects of size, shape, and symmetry of the diamondoids on their optical and vibronic properties. For this purpose, vertical and vibronically resolved spectra (for the lowest accessible excited states) will be considered to understand the vibrational fine-structure in absorption and emission spectra. Differences in HOMO–LUMO gaps, vertical excitation/de-excitation energies and non-vertical absorption/emission spectra, i.e., different measures for “optical gaps”, can be analyzed in this way. Further, we also study resonance Raman spectra of selected diamondoids, which provide further insight into electronic/vibrational excitations. As an example for a sp2/sp3 hybrid diamondoid, we investigate the Dia = Dia dimer. Here, a clear resonance is observed for the REP (Raman Excitation Profile) of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C vibration. As mentioned, vibronically resolved emission/absorption spectra as well as rR spectra of certain diamondoids are available and will be/are being prepared for publication.10,11 While not the main focus of our work, a comparison of the basic features of these spectra to ours will occassionally be given in the text below.
C vibration. As mentioned, vibronically resolved emission/absorption spectra as well as rR spectra of certain diamondoids are available and will be/are being prepared for publication.10,11 While not the main focus of our work, a comparison of the basic features of these spectra to ours will occassionally be given in the text below.
The paper is organized as follows. In Section 2, methods used in this work to compute vibrationally resolved absorption and emission spectra, as well as resonance Raman spectra, are described. All of these methods are based on time-dependent density functional theory in the linear-response regime, and on time-dependent correlation functions to efficiently compute spectra. The harmonic approximation is used for ground and excited states. In Section 3, results are presented and discussed. A final Section 4 concludes and summarizes this work.
2 Methods
The calculations of vibronic absorption, emission and resonance Raman (rR) spectra have been done based on time-dependent correlation function methods as popularized by Heller in the 1980s.20,21 Since then, the method has found wide applications in spectroscopy22–24 as an alternative to the time-independent, Franck–Condon approach.25 Also non-radiative transitions were treated using correlation function approaches.26,27 In many examples so far, and also here, the harmonic approximation was made for ground and excited states. In the excited states, geometry displacements, frequency alterations, and Duschinsky rotation were accounted for in this work, i.e., the IMDHOFAD model (Independent Mode Displaced Harmonic Oscillator with Frequency Alteration and Duschinsky rotation) was used in all what follows.28Ground and excited state geometry optimizations and normal mode analyses were performed with the help of hybrid density functional theory (DFT) and linear-response time-dependent DFT (TD-DFT). Unless otherwise stated, we have used the B3LYP functional29 and a TZVP (Triple Zeta Valence Polarised) basis set30 for our calculations. Most calculations were done with the GAUSSIAN09 program package.31 The normal modes and the vibrational frequencies were used to calculate the dimensionless origin shifts (between the ground state and excited state potential energy surfaces), the Duschinsky matrix and subsequently the spectra, using a FORTRAN code developed earlier.28 Vibronic analysis was also done for lowest (optically bright) excited singlet states. For higher-excited states, only vertical excitation energies were computed using TD-DFT.
In this work, we use the time-dependent correlation function approach for vibronic absorption, emission (fluorescence) as well as rR spectra involving two shifted harmonic singlet potential energy surfaces g and e. In all cases, the Condon approximation is made, i.e., the transition-dipole moment which depends on all nuclear degrees of freedom, ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) , is approximated as
, is approximated as
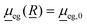 | (1) |
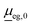 is the transition dipole at a reference geometry. The latter is chosen as the equilibrium geometries of the ground state g in the case of absorption and rR spectra, and of the excited state e in the case of emission, respectively.
is the transition dipole at a reference geometry. The latter is chosen as the equilibrium geometries of the ground state g in the case of absorption and rR spectra, and of the excited state e in the case of emission, respectively.
For the vibronic absorption spectrum, we calculate a cross section for excitation from the initial vibrational state |ϕgi(0)〉 in the ground electronic state, g, by (we use atomic units with ℏ = 1 throughout)20,22
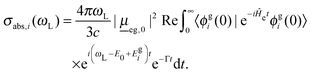 | (2) |
Here, ωL is the incident light frequency, c the velocity of light in a vacuum, E0 the adiabatic minima separation energy between the ground and excited states, and Egi is the vibrational energy of initial state |ϕgi(0)〉. Note that in the multi-atom case, |ϕgi(0)〉 is a product wave-function comprising 3N − 6 harmonic oscillator functions for each individual normal mode, where N is the number of atoms. At T = 0 K, only the vibrational ground state i = 0 (more precisely: i1 = i2 =⋯= iF = 0) contributes to the total spectrum. Further, e−iĤetϕgi(0) is a time-dependent wave-packet obtained by propagating the initial state under the influence of the field-free, excited state nuclear Hamiltonian Ĥe. Also, Re denotes the real part and Γ is a damping (lifetime, broadening) factor for the excited state. Similarly, the fluorescence emission cross section is given by
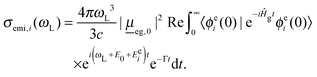 | (3) |
Here, |ϕei(0)〉 is now the product of 3N − 6 excited-state normal modes, which are propagated under the influence of the field-free ground state Hamiltonian, Ĥg.
Finally, the resonance Raman cross section is calculated as20,21
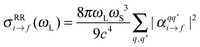 | (4) |
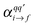 are the components of the Raman polarizability tensor (q,q′ = x, y, z). In the time-dependent formalism, the latter is given as
are the components of the Raman polarizability tensor (q,q′ = x, y, z). In the time-dependent formalism, the latter is given as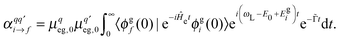 | (5) |
Here, |ϕgf(0)〉 is the stationary final vibrational wave-function and the other quantities are as mentioned previously (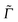 is a special broadening factor used for rR spectra, see below). In practice, we are interested in i = 0 → f = 1 scattering within a given mode. In selected cases, we have also tested overtone excitations, however, this has only a minor impact in most regions of the rR spectra, so these calculations are not further mentioned here.
is a special broadening factor used for rR spectra, see below). In practice, we are interested in i = 0 → f = 1 scattering within a given mode. In selected cases, we have also tested overtone excitations, however, this has only a minor impact in most regions of the rR spectra, so these calculations are not further mentioned here.
To calculate the vibronic absorption and emission cross sections, we need autocorrelation functions, e.g., for absorption at T = 0 K,
| I0(t) = 〈ϕg0(0)|e−iĤetϕg0(0)〉 | (6) |
| I10(t) = 〈ϕg1(0)|e−iĤetϕg0(t)〉. | (7) |
In the harmonic approximation, quasi-analytic expressions are available for these quantities (see, e.g., ref. 28 and references therein). These expressions exist for IMDHO (Independent Mode Displaced Harmonic Oscillator), IMDHOFA (IMDHO with Frequency Alteration), and IMDHOFAD (IMDHOFA with Duschinsky rotation) models, the latter of which is used here throughout. (The other, less complete models have been tested as well. They can be useful in cases where a full IMDHOFAD calculation cannot be done, and are not further mentioned here.) To evaluate the required (cross) correlation functions, the following ingredients are needed: the equilibrium geometries of ground and excited states ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) g0 and
g0 and ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) e0, the vibrational frequencies ωg1,…,ωg3N−6 and ωe1,…,ωe3N−6 of normal vibrations of g and e, and finally also the corresponding normal modes. Further details are summarized in Appendix A.
e0, the vibrational frequencies ωg1,…,ωg3N−6 and ωe1,…,ωe3N−6 of normal vibrations of g and e, and finally also the corresponding normal modes. Further details are summarized in Appendix A.
The cross-correlation function I10 for Raman amplitudes, for example, can also be written as a (3N − 6)-dimensional vector with components for each of the normal modes of the molecule. By Fourier transforming each component n of ![[I with combining low line]](https://www.rsc.org/images/entities/i_char_0049_0332.gif) 10, we get the Raman Excitation Profile (REP) along this particular mode n as a function of the excitation frequency ωL, i.e., a signal
10, we get the Raman Excitation Profile (REP) along this particular mode n as a function of the excitation frequency ωL, i.e., a signal 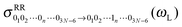 . We can also compute the Raman spectrum, i.e., including each mode, at a fixed excitation frequency, as a function of the Raman shift (i.e., the vibrational frequency).
. We can also compute the Raman spectrum, i.e., including each mode, at a fixed excitation frequency, as a function of the Raman shift (i.e., the vibrational frequency).
Autocorrelation and cross-correlation functions are computed on time grids with Δt = 0.3 fs and up to 131![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 072 points (giving a total propagation time of about 39 ps). The damping factors Γ correspond to Lorentzian line broadenings. They were chosen as Γ = 200 cm−1 for the vibronic absorption/emission spectrum in most cases and
072 points (giving a total propagation time of about 39 ps). The damping factors Γ correspond to Lorentzian line broadenings. They were chosen as Γ = 200 cm−1 for the vibronic absorption/emission spectrum in most cases and 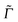 = variable for rR spectra. In the latter case, they account for broadening of the spectrum as a function of ωL. When calculating rR spectra as a function of vibrational frequencies instead, at a fixed ωL, a stick spectrum is obtained for which another (Lorentzian) broadening
= variable for rR spectra. In the latter case, they account for broadening of the spectrum as a function of ωL. When calculating rR spectra as a function of vibrational frequencies instead, at a fixed ωL, a stick spectrum is obtained for which another (Lorentzian) broadening ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) has to be used. Below we will mostly choose
has to be used. Below we will mostly choose ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) = 10 cm−1.
= 10 cm−1.
3 Results
3.1 Lower diamondoids: adamantane, diamantane, and triamantane
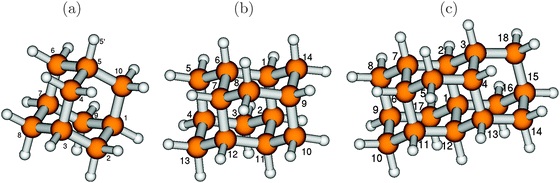
We begin by studying the effect of system size of diamondoids on absorption and emission spectra, by considering the lower-diamond series adamantane (C10H16, henceforth also abbreviated as “Ada”), diamantane (C14H20, “Dia”) and triamantane (C18H24, “Tria”). Optimized (B3LYP/TZVP) ground electronic state geometries, along with selected atom numbering, are shown in Fig. 1.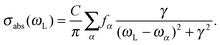 | (8) |
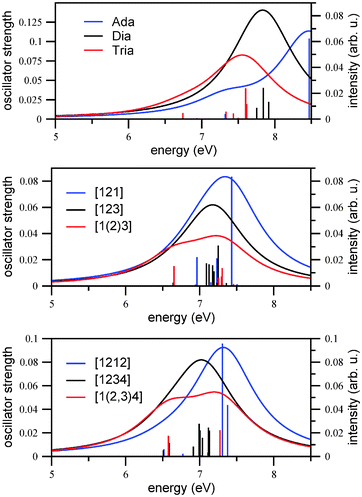
Here, fα is the oscillator strength for the transition from the ground state to excited state α, ωα is the corresponding transition energy, γ the Lorentzian width (different from those chosen for vibronically resolved spectra), and C is a constant. We chose C = 1 arbitrarily and γ = 0.5 eV (4033 cm−1). In practice, the first ten excited singlet states of each molecule were calculated using TD-B3LYP/TZVP. The result for Ada, Dia, Tria is shown in Fig. 2, upper panel.
From there, we first of all note that appreciable absorption sets in at energies of around 7 eV. The overall trend is such that the regions where absorption is maximal shift continuously to the red when going from adamantane to diamantane and then triamantane, suggesting the order Ada > Dia > Tria. In the case of adamantane, there is a shoulder at lower energies (slightly above 7 eV). While these observations are in qualitative agreement with previous measurements,7,32 the optical gaps determined there are lower than anticipated from Fig. 2, upper panel, namely 6.49 eV (adamantane), 6.40 eV (diamantane), and 6.06 eV (triamantane), respectively. In that reference, the optical gap was determined from the integrated oscillator strength, introducing a threshold of 5 × 10−4. Also, the fine-structure found in ref. 7 and 32 is not reproduced in our simple picture. In this context, we would like to mention that the use of the Minnesota functionals33 with greater Hartree–Fock exchange, like the M06-2X functional and the same basis set (TZVP), shifts the calculated values by about 0.7 eV further to the blue.
To gain more detailed insight, in Table 1 we show the vertical excitation energies and computed oscillator strengths for the three compounds, determined by TD-B3LYP/TZVP. We note that in none of the examples non-vanishing oscillator strengths are found below 6.74 eV, at least if broadening effects are neglected. For adamantane, the onset is at 7.32 eV, for diamantane it is at 7.61 eV, and 6.74 eV for triamantane (shown in bold in the table). From this criterion alone, one would expect the (wrong) order Dia > Ada > Tria. The reason why diamantane has a larger gap than expected, at least for un-broadened, vertical spectra, is that its lowest three excited states S1 to S3 are optically dark by symmetry, in contrast to the corresponding transitions in adamantane and triamantane. From Table 1 we recognize the well-known feature that in the highly symmetric molecules (Ada, point group Td, and Dia, D3d), due to the presence of degenerate irreducible representations also degenerate excited states arise. For instance, the HOMO of adamantane (B3LYP/TZVP, Kohn–Sham orbital) is threefold degenerate (T2 symmetry), and the HOMO − 1 of diamantane is twofold degenerate (Eg symmetry). This is in contrast to triamantane, which has only C2v symmetry and no degenerate irreducible representations. (Note that in the practical calculations without symmetry restrictions, as here, slight deviations from perfect degeneracies occur.)
| Ada (Td) | Dia (D3d) | Tria (C2v) | ||||
|---|---|---|---|---|---|---|
| State α | ω α (eV) | f α | ω α (eV) | f α | ω α (eV) | f α |
| 1 | 7.3223 | 0.0064 | 6.9696 | 0.0000 | 6.7430 | 0.0078 |
| 2 | 7.3227 | 0.0063 | 7.1297 | 0.0000 | 6.9349 | 0.0011 |
| 3 | 7.3232 | 0.0064 | 7.1300 | 0.0000 | 7.0544 | 0.0002 |
| 4 | 8.3673 | 0.0000 | 7.6115 | 0.0021 | 7.3320 | 0.0097 |
| 5 | 8.3675 | 0.0000 | 7.7516 | 0.0146 | 7.4281 | 0.0000 |
| 6 | 8.3677 | 0.0000 | 7.7520 | 0.0146 | 7.4339 | 0.0075 |
| 7 | 8.4070 | 0.0000 | 7.8437 | 0.0403 | 7.4929 | 0.0000 |
| 8 | 8.4073 | 0.0000 | 7.8438 | 0.0404 | 7.5005 | 0.0016 |
| 9 | 8.4546 | 0.0000 | 7.8660 | 0.0000 | 7.6019 | 0.0397 |
| 10 | 8.4703 | 0.1040 | 7.9168 | 0.0222 | 7.6162 | 0.0194 |
| l.a.t. | H (T2) → L (A1) | H (A1g) → L + 1 (A2u) | H (T2) → L (A1) | |||
For adamantane, the lowest three (almost) degenerate excited states at around 7.32 eV account for the lowest-energy absorptions, but a more intense contribution comes from a triply degenerate excited state at 8.47 eV. These can be compared to the experimental spectrum, where peaks are observed between (7–8) eV and about 8.5 eV, though these peaks exhibit many sharp features arising from Rydberg states,7,34 which TD-B3LYP does not calculate properly. For diamantane, the HOMO (A1g) → LUMO (A1g) is symmetry-forbidden, in agreement with findings from ref. 7, because in D3d, the dipole operator transforms as (Eu,A2u). Also the HOMO − 1 (Eg) → LUMO (A1g) transition is forbidden. As a consequence, the first available excited state involves a weak HOMO (A1g) → LUMO + 1 (A2u) transition at around 7.6 eV (see Table 1, last line). The strongest contributions to the vertical excitation spectrum come from two degenerate excited states at 7.84 eV. For triamantane, again, the HOMO → LUMO transition results in the first available excited state at 6.74 eV. The vertical spectrum shows peaks between 6.7–7.6 eV. The most intense transition corresponds to S9 at 7.60 eV. Comparison of the vertical spectra of the three molecules shows the common trend of a weak allowed transition at lower excitation energy, and an intense transition at relatively higher energy.
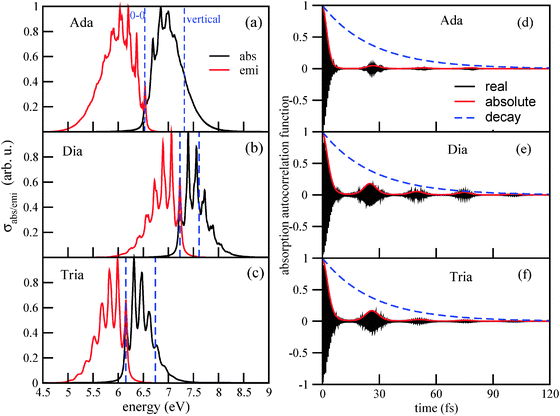
1. The main maxima of the vibronically resolved absorption spectra (ΔEvibro) are shifted with respect to the vertical transition energies ΔEvert, by several tenths of an eV to the red. For adamantane, the maximum is at 6.84 eV, and the vertical transition energy is at 7.32 eV. It should be said, though, that the maxima of vibronic spectra depend on the chosen broadening factors (see also Appendix B). For diamantane and triamantane, similar red-shifts are observed. The vertical transition energies, maxima of absorption signals, and HOMO–LUMO gaps (HOMO–LUMO + 1 in the case of diamantane), ΔEHL, are tabulated in Table 2.
| Molecule | ΔEHL | ΔE0–0 | ΔEvert | ΔEvibro | τ (abs) (fs) | ω (abs) (cm−1) | τ (emi) (fs) | ω (emi) (cm−1) |
|---|---|---|---|---|---|---|---|---|
| Ada | 8.15 | 6.54 | 7.32 | 6.84 | 26.5 | 1260 | 24.6 | 1360 |
| Dia | 8.37 | 7.23 | 7.61 | 7.39 | 24.6 | 1360 | 24.0 | 1390 |
| Tria | 7.49 | 6.16 | 6.74 | 6.31 | 25.0 | 1330 | 24.3 | 1370 |
From the table we note that vertical transition energies and HOMO–LUMO gaps (or orbital energy differences for lowest “allowed” transitions) are no good measures for the optical gap. The latter are by about 0.3–0.5 eV too large compared to maxima of absorption signals, the former by 1.0–1.3 eV. The adiabatic 0–0 transition energies ΔE0–0 agree better with ΔEvibro, being about 0.3 eV too low.
2. The absorption spectra are considerably broadened due to vibronic effects, with a band for the g → e transition spreading now over about 1 eV or more. The 0–0 transition is, of course, the lowest-energy excitation, amounting to 6.54 eV for Ada. The computed classical, adiabatic minima separation between S0 and S1 of adamantane is 6.88 eV, i.e., zero-point energy corrections are significant.
3. The absorption bands are characterized by a rich vibronic fine-structure. For adamantane, the first three peaks are at 6.54 eV (0–0), 6.69 eV, 6.84 eV and 6.95 eV. The vibrational progression corresponds to an energy spacing of about 0.15–0.16 eV. This suggests a frequency ω of about 1200–1300 cm−1. A corresponding vibrational period τ = 2π/ω is between 27.5 and 25.8 fs. For diamantane and triamantane, the absorption spectra show a more pronounced vibrational fine-structure than adamantane, but otherwise similar spacings and vibrational periods: for Tria, they are roughly the same as for Ada, while for Dia, the spacings are between 0.16 and 0.17 eV (1300–1370 cm−1), respectively.
4. Similar behavior is observed for the emission spectra. They are broadened, shifted (now to the blue relative to vertical transitions from e to g), and show rich vibronic fine-structure. The main maxima of emission spectra are shifted with respect to the absorption maxima, by up to about 1 eV.
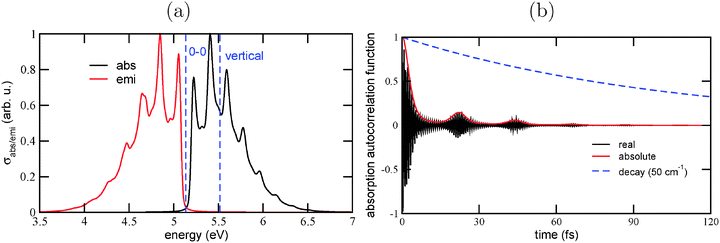
The reason for this behavior can be understood from the autocorrelation functions. The autocorrelation functions for absorption, 〈ϕg0|e−iĤet|ϕg0〉, are shown in Fig. 2(d)–(f). One observes a fast initial decay on a timescale τ0: the absolute value of the correlation function reaches 1/2 for the first time after 2.6 fs (Ada), 3.4 fs (Dia), and 3.2 fs (Tria). This determines the width of the envelope function of the absorption spectrum, up to pre-factors according to ΔE ∼ 1/τ0, and explains why the spectrum of Ada is broader than those of Dia and Tria: obviously, the excited wave-packet moves faster away from the Franck–Condon region in Ada than in Dia and Tria. The main position of the absorption signal is determined, of course, by the energy difference between ground and excited states, which shows up as fast oscillations (in the real and imaginary parts) of the correlation function. For Ada, these fast oscillations have a period of 0.61 fs, corresponding to an energy of 6.8 eV. For Dia and Tria, the fast periods are about 0.55 fs and 0.66 fs, corresponding to about 7.5 and 6.3 eV, respectively.
Secondly, one finds recurrences on a timescale τ = 25 – 26.5 fs depending on species, as reported as “τ(abs)” values in Table 2. A corresponding “effective vibrational frequency” ω(abs) = 2π/τ(abs) is also given in the table. It nicely reflects the energy spacings in the vibronically resolved absorption spectra, ranging from 1260 cm−1 (0.156 eV, for Ada) to 1360 cm−1 (0.169 eV, for Dia). The recurrences vanish more rapidly for adamantane than for diamantane and triamantane, leading to less pronounced vibronic fine-structure in its Fourier transform. Note that the decay of the recurrences is a system-specific, dynamical effect, since the same broadening Γ has been used for all species.
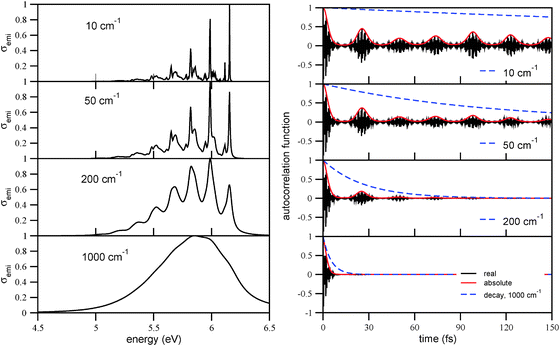
Analogous observations are made for emission spectra, and their correlation functions 〈ϕe0|e−iĤgt|ϕe0〉. Also for them, characteristic recurrence times τ are observed, which are in the range τ(emi) = 24.0–24.6 fs (see Table 2). The corresponding characteristic energies ω(emi) are in a range between 1360–1390 cm−1, or about 0.17 eV. In Appendix B, we analyze in detail the emission spectrum and the correlation function for triamantane. There, different broadening factors Γ will also be considered. A conclusion is that a particularly good agreement with experimental luminescence spectra32 is obtained for Γ ∼ 50–200 cm−1, which is why we chose Γ in this range. In Appendix B it is also shown that for too small broadening factors Γ, new vibrational fine-structures come up, which are not clearly resolved in experiment. These correspond to longer “beating times” τ2, τ3,…, leading to lower-frequency modes with characteristic energy spacings ΔE2, ΔE3…. The associated wavenumbers are in the order of a few hundred wavenumbers, and not further analyzed here.
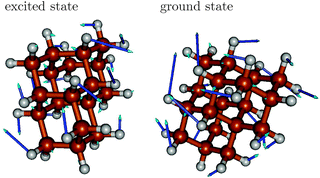
The vibrational progression in emission is dominated by ground state vibrations, while the fine-structure of absorption spectra is determined by excited state vibrations. In the excited state, the relevant vibrations are slightly “softer”, making vibrational periods longer. Analyzing the vibrational frequencies in ground and excited states, respectively, we find that typically several of them are in the appropriate range spanned by the respective ω values, however, always with similar character. As an example we show in Fig. 4 mode 76 of the excited state S1 of triamantane, with a frequency of 1320 cm−1. This is close to the ω value of 1330 cm−1 in Table 2. The mode strongly contributes to the vibronic fine-structure of the absorption spectrum of triamantane in Fig. 3(c). This interpretation will also be supported by analyzing rR spectra, vide infra. The mode describes a complicated combination of H–C–H (methylene) bending, C–H wagging and C–C stretching motions of triamantane, which are enforced upon electronic excitation of the molecule. A similar ground state mode (also mode 76, ω = 1355 cm−1) can be found (Fig. 4, right), close to ω(emi) of Table 2, which dominates the fine-structure of the emission spectrum of Tria.
The excited modes are related to geometric distortions upon electronic transitions. Upon electronic excitation, changes are moderate for several geometric parameters, but not for all. This leads to the observed differences between vertical and non-vertical excitation energies in Table 2. Selected bond lengths are reported in Table 3. The dihedral angles, though not mentioned here, do not show any appreciable change in moving from the ground state to the excited state. The C–C bond lengths for the diamondoids in the optimized ground states lie in the range of 1.53–1.54 Å, in the same range as in diamond, also consistent with previous findings.7 The C–H bond lengths lie in the range of 1.096 to 1.100 Å for all molecules. In the excited states, some of the C–C bonds are elongated, others contracted, mostly by small amounts. A clear exception is the C4–C5 bond of adamantane (atom numbering according to Fig. 1), which increases to 1.66 Å, i.e., by 0.12 Å. Also, the C2–C1 (and C8–C7) bonds stretch a bit, to 1.569 Å. In the excited state, the symmetry of adamantane is reduced from Td to Cs. Note that C–C elongation in the order of 0.1 Å for some bonds was found for adamantane upon ionization.35 In the Ada cation, however, all three C–C bonds parallel to one of the C–H bonds (i.e., bonds C4–C5, C2–C1, C8–C7 in Fig. 1(a)) were elongated by the same amount, leading to C3v symmetry.
| Molecule | Bond | Value (g) | Value (e) |
|---|---|---|---|
| Ada | C3–C4 | 1.540 | 1.515 |
| C4–C5 | 1.540 | 1.663 | |
| C2–C1 (C8–C7) | 1.540 | 1.569 | |
| C5–H5′ | 1.094 | 1.108 | |
| Dia | C3–C2 | 1.536 | 1.519 |
| C2–C1 | 1.547 | 1.521 | |
| Tria | C14–C15 | 1.537 | 1.520 |
| C15–C18 | 1.537 | 1.520 |
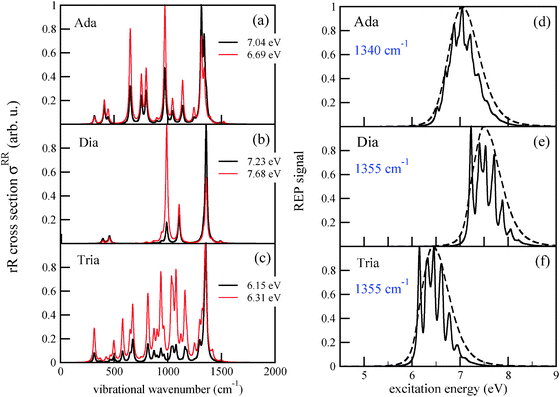
The spectrum of adamantane (Fig. 5(a)) shows many peaks, the most prominent ones being at around 1340 cm−1 and 970 cm−1, in particular the former with strong contributions from bending motions of different methylene groups and 650 cm−1, corresponding to twisting motions of the cyclohexane rings. The mode at 1340 cm−1 is (ground state) mode number 42. Its frequency is close to the frequency ω = 1360 cm−1 obtained from the characteristic recurrence time τ(emi) in the emission spectrum of adamantane, cf.Table 2. Hence, there is a tight connection between the intensity of the rR signal for the mode which is probed, and the mode(s) which is (are) excited during photoluminescence. The same effect is seen in the rR spectra of diamantane and triamantane, respectively. For the latter, the most intense peak is the one corresponding to ground state mode 76, with a frequency of 1355 cm−1 – the mode of Fig. 4 (right) of above.
In Fig. 5(a)–(c), the most intense peaks corresponding to every excitation frequency ωL were normalized to 1 in order to visualize the rR spectra for several excitation wavelengths in a single graph. In reality the peak intensities are strong functions of ωL, reflecting the resonant nature of the process. In Fig. 5(d)–(f) we show the Raman excitation profile (REP) for the mode(s) at 1340 cm−1 (for Ada), 1355 cm−1 (for Dia), and 1355 cm−1 (for Tria), which dominate the rR spectra in most cases, as a function of ωL. As expected, the profiles show maximal signals around the electronic excitation energies of the molecules, cf.Table 2. When adopting the same broadening as for absorption spectra (![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) = Γ = 200 cm−1), the REP spectra of the selected modes are strikingly similar to the vibronic absorption spectra of Fig. 3. Thus, the absorption process seems to be a decisive determinant for the Raman signal of the selected modes at around 1300 cm−1. Conversely, these modes (or their counterparts in the excited state) determine the vibrational fine-structure of absorption and emission spectra, at least under the chosen spectral resolution. The peaks in the REP spectra correspond to cases when the selected vibration is much intensified relative to other vibrations in the rR spectrum. Away from these peaks, the intensities of other peaks gain importance. For instance, in the rR spectrum of triamantane (Fig. 4(c)) several peaks are of similar intensity at ωL = 6.31 eV. In actual experiments, the fine-structure seen in the theoretical REP spectra may not be well resolved. In Fig. 4(d)–(f), we also show the REP spectra for the most intense Raman modes, when a broadening factor
= Γ = 200 cm−1), the REP spectra of the selected modes are strikingly similar to the vibronic absorption spectra of Fig. 3. Thus, the absorption process seems to be a decisive determinant for the Raman signal of the selected modes at around 1300 cm−1. Conversely, these modes (or their counterparts in the excited state) determine the vibrational fine-structure of absorption and emission spectra, at least under the chosen spectral resolution. The peaks in the REP spectra correspond to cases when the selected vibration is much intensified relative to other vibrations in the rR spectrum. Away from these peaks, the intensities of other peaks gain importance. For instance, in the rR spectrum of triamantane (Fig. 4(c)) several peaks are of similar intensity at ωL = 6.31 eV. In actual experiments, the fine-structure seen in the theoretical REP spectra may not be well resolved. In Fig. 4(d)–(f), we also show the REP spectra for the most intense Raman modes, when a broadening factor 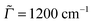 was used. Then, the REP spectra are structureless, but they still indicate a clear resonant behavior.
was used. Then, the REP spectra are structureless, but they still indicate a clear resonant behavior.
In passing we note that the Duschinsky rotation affects the relative intensities of some of the peaks, and should therefore be taken into account. For example, for Ada at an excitation energy of 6.69 eV, modes corresponding to the stretching vibration of different sets of C–H bonds (beyond 3000 cm−1, not shown here) show considerably high intensity with Duschinsky rotation, but not without.
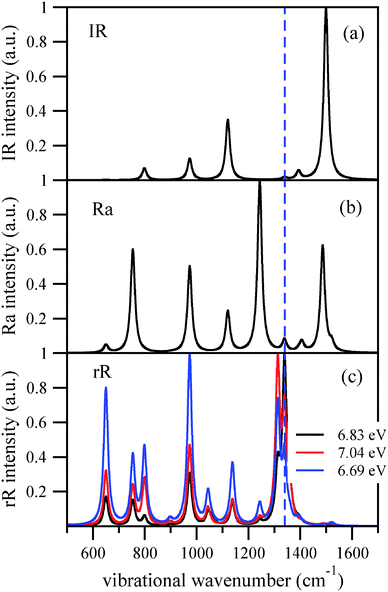
Finally we stress the well-known fact that IR, ordinary (non-resonant) Raman and resonant Raman spectra can be quite different. This is demonstrated in Fig. 6, for adamantane. The upper curve shows the IR spectrum, the middle panel the ordinary Raman spectrum (calculated from static polarizabilities), and the last panel the rR spectra for various excitation wavelengths again, calculated within the IMDHOFAD model. In this example, mode 42 at 1340 cm−1 which dominates the rR spectrum in most cases is practically dark in the IR spectrum and also weak in the ordinary Raman spectrum. The resonant enhancement of certain peaks makes rR spectroscopy a sensitive tool to study diamondoids.
3.2 Higher diamondoids: isomers of tetramantane and pentamantane
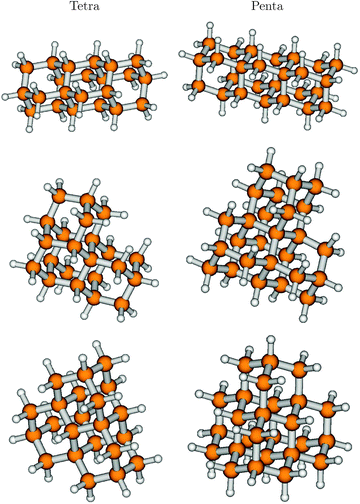
In ref. 7, also the effects of symmetry and shape of higher diamondoids, which come in different isomeric forms, were investigated. For instance, out of the four possible isomers (see above) of tetramantane (Tetra), C22H28, three structural isomers [121], [123], and [1(2)3] (one isomer) were studied. These are, in this order, precursors for one dimensional (1D), two-dimensional (2D) and three-dimensional (3D) higher homologues. We will therefore denote these species also as Tetra-1D, Tetra-2D, and Tetra-3D, respectively. The ground electronic states of all three molecules were optimized using B3LYP/TZVP, with geometries shown in Fig. 7, left column. The respective point groups are C2h, C2, and C3v.Further, we also considered three isomers of pentamantane of composition C26H32, which also form precursors to 1D, 2D, and 3D structures. These are [1212] (also “Penta-1D”, C2v), [1234] (“Penta-2D”, C2), [1(2,3)4] (“Penta-3D”, Td). The ground electronic states of all three molecules were also optimized using B3LYP/TZVP, with geometries shown in Fig. 7, right column.
In the middle and lower panels of Fig. 2, the vertical excitation spectra (stick spectra and broadened spectra) are shown for the Tetra and Penta isomers under investigation. For Tetra-1D the HOMO → LUMO, (HOMO − 1) → LUMO and (HOMO − 2) → LUMO transitions are all dipole-forbidden due to symmetry reasons and the first bright excited state is S3, which is a HOMO → (LUMO + 1) transition, at an excitation energy of 6.96 eV. For the two other isomers of tetramantane, the first excited state is bright, which is a HOMO → LUMO transition, at around 6.65 eV for both isomers. There are more degeneracies in the electronic states for the 3D isomer as compared to 1D and 2D isomers. Other than that, the three spectra of the tetramantanes are not dramatically different from each other, and also not from Ada, Dia, Tria as shown above. A main trend is that the absorption spectra of the tetramantanes are shifted slightly to the red relative to the lower diamondoids, as expected. This is in agreement with ref. 7, where optical gaps for the tetramantanes ranging from 5.94 to 6.10 eV were reported, and 6.06 to 6.49 eV for the lower diamondoids.
This trend further continues, to a smaller additional extent, for the pentamantanes. For all the isomers the first excited state is the bright one, dominated by a HOMO → LUMO transition. The transition is centered at 6.52 eV for the 1D isomer and 6.51 eV for the 2D isomer, whereas it is a little higher at 6.58 eV for the 3D isomer. Experimental optical gaps are also in a narrow range, between 5.8 and 5.9 eV. Like the isomers of tetramantane, there are more intense allowed transitions at higher energies. Also, the 3D isomer shows more electronic degeneracies than the other two isomers.
Vibronically resolved absorption and emission spectra of Tetra and Penta isomers, as shown in Fig. 8, are also not dramatically different from each other, and from those found for the lower diamondoids. The vibronic absorption and emission spectra of Tetra-1D, for example, in Fig. 8(a), show three peaks and two shoulders in the higher energy region. The first peak is located at the 0–0 transition energy, at 6.39 eV. The central peak, located at about 6.55 eV, is the most intense peak. The emission spectrum is practically a mirror image of the absorption spectrum. The vibronic absorption spectra of the other two isomers of tetramantane, Tetra-2D and Tetra-3D, retain the basic three peak nature, although the peak positions are down-shifted by about 0.3 eV.
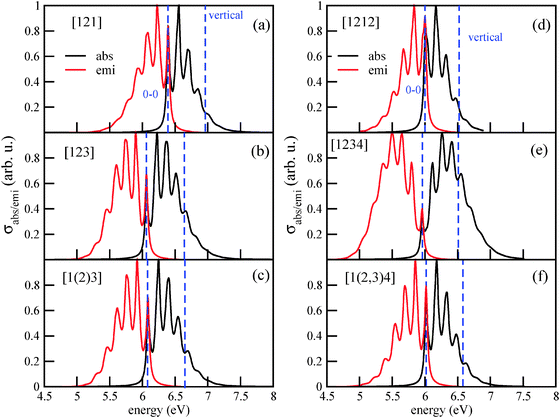 | ||
| Fig. 8 The vibronic absorption and emission spectra of three isomers of tetramantane (a)–(c) and pentamantane (d)–(f). | ||
The vibronic absorption and emission spectra of Penta-1D, Penta-2D and Penta-3D are shown in Fig. 8(d)–(f). Penta-1D and Penta-3D isomers have similar spectra, with the 0–0 transition centered at around 6 eV and the vertical transition at about 6.5 eV. Both absorption and emission spectra are highly fine-structured. In Table 4, first six rows, we list different measures for the excitation energies of the six higher diamondoids studied in this work.
| Molecule | ΔEHL | ΔE0–0 | ΔEvert | ΔEvibro |
|---|---|---|---|---|
| Tetra-1D [121] | 7.64 | 6.39 | 6.96 | 6.55 |
| Tetra-2D [123] | 7.35 | 6.06 | 6.64 | 6.22 |
| Tetra-3D [1(2)3] | 7.36 | 6.08 | 6.65 | 6.25 |
| Penta-1D [1212] | 7.21 | 6.00 | 6.52 | 6.17 |
| Penta-2D [1234] | 7.19 | 5.96 | 6.51 | 6.26 |
| Penta-3D [1(2,3)4] | 7.25 | 6.02 | 6.58 | 6.17 |
| Dia = Dia (E) | 6.23 | 5.14 | 5.52 | 5.41 |
| Dia = Dia (Z) | 6.22 | 5.11 | 5.50 | 5.38 |
For the absorption spectrum of [1(2,3)4] (Penta-3D), a direct comparison between theory and experiment7 is possible. The experimental absorption spectrum shows (apart from pre-edge spectral features and contributions due to higher excited electronic states) for the lowest absorption band a similar vibronic fine-structure as the one in Fig. 8(f). Both in theory and in experiment a vibrational level spacing of 0.155 eV is found. Also for emission spectra (of triamantane, cf. Appendix B), a similar good agreement is found. According to Fig. 8(f) and Table 4, the computed main maximum of the absorption spectrum is at 6.17 eV. In experiment, the main maximum is at about 6.6 eV. For the emission spectrum of triamantane, the experimental maximum is at 5.9 eV,10 and the theoretical one at around 6.0 eV (Fig. 3(c)). The maxima of the absorption and fluorescence bands show therefore an error of a few tenths of an eV in theory, while the vibronic spacings are very accurate. In stating this it should also be noted that the intensity of the individual vibronic peaks depends sensitively on broadening (see Appendix B). Hence the precise determination of main maxima both in theory and experiment is somewhat uncertain.
The vibrational fine-structure in absorption and emission spectra of higher diamondoids is characterized by similar peak spacings to that for the lower diamondoids (typically around 0.15–0.17 eV), and has similar origins: upon excitations and de-excitation, respectively, several modes are excited but a dominant contribution comes from vibrations of methylene groups between 1300 and 1400 cm−1 as before.
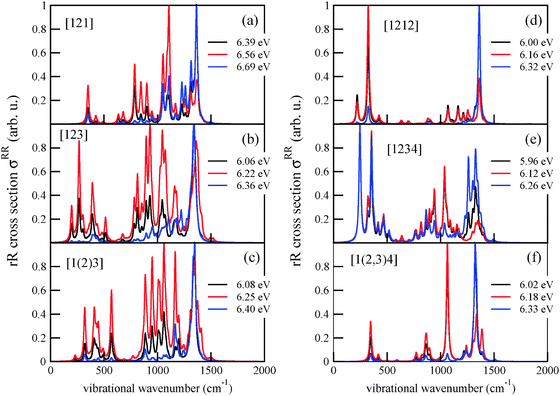
Not surprisingly, also the rR spectra (which are shown in Fig. 13, Appendix C) are often dominated by peaks around these wavenumbers, when excitation wavelengths close to the absorption maxima are used. For example, the rR spectra of Tetra-1D are dominated at an excitation energy of 6.39 eV, by mode 96 with a vibrational wavenumber of 1365 cm−1, corresponding to different bending motions of various methylene groups. At different excitation energies, other modes can become dominant in the rR spectrum. The rR spectra of Tetra-2D and Tetra-3D show their highest peak at around 1340 cm−1. For Penta-1D, the most intense scatterers are two modes corresponding to different methylene bending motions. At lower excitation energy, both modes are about equally intense while at higher energies (6.32 eV), one mode, with a frequency of about 1360 cm−1 dominates. The rR spectra of Penta-2D and Penta-3D show an analogous behavior: modes involving CH2 bending vibrations at around 1330 cm−1 (Penta-2D) and 1320 cm−1 (Penta-3D) dominate the spectrum at excitation wavelengths around the absorption peaks.
In summary the higher diamondoids studied here share many similarities with the lower diamondoids. The main effect is a moderate shift of excitation and fluorescence spectra to lower energies.
3.3 An artificial diamondoid: Dia = Dia
One way to perturb the electronic structure of diamondoids strongly is to introduce unsaturated C-atoms. Recently, Schreiner and coworkers synthesized, among other similar compounds, a molecule consisting of two diamantane units, connected by a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond.36 The compound comes in two stable forms, cis (Z) and trans (E), whose structures are shown in Fig. 9. The striking feature of this compound is the central C
C double bond.36 The compound comes in two stable forms, cis (Z) and trans (E), whose structures are shown in Fig. 9. The striking feature of this compound is the central C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, with an optimized bond-length of 1.345 Å for both isomers. The energies of both isomers are very similar, with the Z isomer being more stable by only 0.0017 eV (0.2 kJ mol−1) than the E isomer. Also, most optical and spectroscopical properties are quite similar, therefore we refer in what follows to the E-isomer only.
C bond, with an optimized bond-length of 1.345 Å for both isomers. The energies of both isomers are very similar, with the Z isomer being more stable by only 0.0017 eV (0.2 kJ mol−1) than the E isomer. Also, most optical and spectroscopical properties are quite similar, therefore we refer in what follows to the E-isomer only.
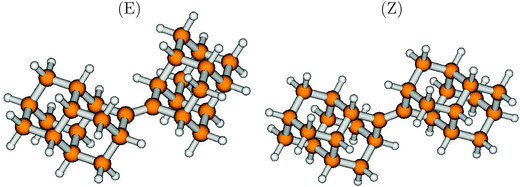 | ||
| Fig. 9 The ground electronic state geometries of Dia = Dia (E) and Dia = Dia (Z), optimized at the B3LYP/TZVP level of theory. | ||
The lowest allowed transition in Dia = Dia (E), S1, is 5.50 eV above the ground state according to Table 4. This is by more than 1 eV lower than all ΔEvert values found so far, cf.Tables 2 and 3. The transition is of the HOMO → LUMO type. The HOMO is a π-orbital localized at the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, while the LUMO is more de-localized towards the outer periphery and especially the C–H bonds of the molecule. The oscillator strength is 0.0039, i.e., relatively low. In fact, the vertical, broadened absorption spectrum of Dia = Dia (E) (not shown) is dominated by another state, S4, at an energy ΔEvert of 6.34 eV, with an oscillator strength of 0.83. This transition is dominated, for the E-isomer, by a HOMO → LUMO + 2 transition, where LUMO + 2 is the π*-orbital of the C
C bond, while the LUMO is more de-localized towards the outer periphery and especially the C–H bonds of the molecule. The oscillator strength is 0.0039, i.e., relatively low. In fact, the vertical, broadened absorption spectrum of Dia = Dia (E) (not shown) is dominated by another state, S4, at an energy ΔEvert of 6.34 eV, with an oscillator strength of 0.83. This transition is dominated, for the E-isomer, by a HOMO → LUMO + 2 transition, where LUMO + 2 is the π*-orbital of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. (In the case of the Z-isomer, the π*-orbital is LUMO + 1, and the brightest state is S5.)
C bond. (In the case of the Z-isomer, the π*-orbital is LUMO + 1, and the brightest state is S5.)
In Fig. 10, we show the vibronically resolved absorption and emission spectra for the lowest allowed transitions in Dia = Dia (E) in panel (a), and the corresponding correlation function for absorption in panel (b). Unlike in previous sections, in this case Γ = 50 cm−1 was chosen.
Also this figure demonstrates the clear red-shift of spectra in comparison to purely sp3-containing diamondoids. The maximum of the absorption spectrum is at about 5.4 eV (cf.Table 4), and the maximum of the emission spectrum is at around 4.7 eV. The tail of the emission spectrum reaches regions below 4 eV.
The luminescence and absorption spectra show once more a clear vibrational fine-structure. In the absorption spectrum, the main vibrational progression is characterized by a vibrational energy spacing of about 0.19 eV, or ω ∼ 1500 cm−1. The correlation function of absorption shows a main recurrence time τ of 22 fs, which fits nicely to the expected value τ = 2π/ω, which is also 22 fs. In the emission spectrum, we find a main progression with a spacing slightly above 0.20 eV, or about 1600 cm−1. As earlier, we interpret the higher frequency as being due to a dominating ground state vibration, and the lower frequency as being due to the corresponding softened vibration in the excited state. In fact, in the excited state the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond loses considerably its double-bond character, and the bond length increases to 1.409 Å. (In the E isomer, the bond is elongated to 1.412 Å.) Note that the geometry change in the central portion of the molecule is therefore substantial (photoelectron spectroscopic measurements on diamondoid molecules connected by the C
C bond loses considerably its double-bond character, and the bond length increases to 1.409 Å. (In the E isomer, the bond is elongated to 1.412 Å.) Note that the geometry change in the central portion of the molecule is therefore substantial (photoelectron spectroscopic measurements on diamondoid molecules connected by the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond indicate that the vibronic progression can be ascribed to the C
C bond indicate that the vibronic progression can be ascribed to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching mode36). As a consequence, the 0–0 transition is not seen in the absorption or the emission spectrum for the lowest bright state of Dia = Dia. This is different from what was found for pristine diamondoids, and a clear prediction from theory.
C stretching mode36). As a consequence, the 0–0 transition is not seen in the absorption or the emission spectrum for the lowest bright state of Dia = Dia. This is different from what was found for pristine diamondoids, and a clear prediction from theory.
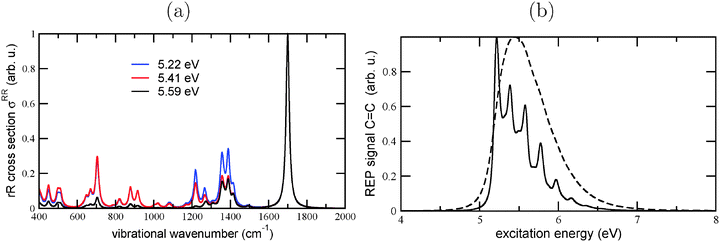
In carrying the analysis further, we also calculated the rR spectrum of Dia = Dia (E), for different excitation wavelengths, cf.Fig. 11(a). From there it can be seen that the clearly dominating mode, at an excitation energy of 5.59 eV, is the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C vibration at 1700 cm−1. (In the excited state, this vibration is softened to 1530 cm−1). Also at the other excitation energies (5.22 and 5.41 eV), the C
C vibration at 1700 cm−1. (In the excited state, this vibration is softened to 1530 cm−1). Also at the other excitation energies (5.22 and 5.41 eV), the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C vibration remains dominant, but lower-frequency modes gain some importance as well. In Fig. 11(b), we show the REP spectrum for this mode, for two different broadenings. Again, the overall shape of the REP spectrum is similar to the broadened absorption spectrum, emphasizing the importance of the C
C vibration remains dominant, but lower-frequency modes gain some importance as well. In Fig. 11(b), we show the REP spectrum for this mode, for two different broadenings. Again, the overall shape of the REP spectrum is similar to the broadened absorption spectrum, emphasizing the importance of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C vibrations for both absorption and resonantly enhanced Raman spectra.
C vibrations for both absorption and resonantly enhanced Raman spectra.
Experimentally, rR spectra of Dia = Dia in the gas phase and in the solid have recently been determined.11 A strong signal was found for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C vibration, also at around 1710 cm−1, similar to our findings. The experimental REP spectrum of the C
C vibration, also at around 1710 cm−1, similar to our findings. The experimental REP spectrum of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C vibration shows a resonance slightly above 5 eV (for the crystalline phase), and somewhat higher for the gas phase molecule. Our calculations support these observations, giving a clear microscopic interpretation of its origins in addition.
C vibration shows a resonance slightly above 5 eV (for the crystalline phase), and somewhat higher for the gas phase molecule. Our calculations support these observations, giving a clear microscopic interpretation of its origins in addition.
In passing we note that we also studied other hybrids of diamondoids with sp2-hybridized subunits, such as Ada = Ada and Ada = Dia. These have similar properties to those of Dia = Dia, and are therefore not further discussed here.
4 Summary and outlook
We studied vibrationally resolved absorption and emission spectra of nine selected pristine diamondoids, and an sp2/sp3 hybrid, Dia = Dia. Also, resonance Raman spectra were computed. For the vibronic spectra, two-state models comprising the ground and the first optically bright states were chosen, both calculated with (TD-)B3LYP/TZVP, and the IMDHOFAD model was adopted to account for vibrations. Time-dependent autocorrelation and cross-correlation functions were used for absorption/emission and rR spectra, respectively. These have two major advantages over time-independent methods: (i) they avoid the explicit, costly computation of Franck–Condon factors which makes them easily applicable to medium-sized molecules; (ii) they allow for a clear, instructive connection between stationary spectra by wave-packet dynamics.Considering the pristine diamondoids, effects of size, symmetry, and shape on optical properties were studied. For example, high symmetry leads to forbidden transitions. By increasing the size of the molecules, a general red-shift in absorption and emission occurs, an effect which rapidly saturates with increasing size, however. Simple measures such as the HOMO–LUMO gap were found to be no reliable indicators for the optical gaps of these materials. Also, vertical excitation (and de-excitation) energies are inaccurate. In fact, absorption and emission spectra of pristine diamondoids are highly structured vibronically, leading to a broadening and shift of optical bands. The vibronic fine-structure seen in experiment is mostly due to the excitation of combined C–C stretching and CH2 bending modes, at around 1350 cm−1. Upon electronic excitation/de-excitation, geometric changes occur which enforce these vibrations.
Resonance Raman spectroscopy is a powerful tool to unravel details of vibrations, complementary to IR, and much more sensitive than non-resonance Raman. In particular, the modes which determine the vibrational fine-structure in absorption are resonantly enhanced when the energy of the exciting photon matches the electronic excitation energy.
We also studied in some detail the sp2/sp3 hybrid, Dia = Dia. A striking feature is a strong red-shift of lowest absorption and emission bands. The vibrational fine-structure in absorption and emission is now dominated by the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C mode, which is weakened upon electronic excitation. This mode, occurring at around 1700 cm−1 in the ground state, is greatly enhanced in the resonance Raman spectrum, in striking agreement with experimental findings.
C mode, which is weakened upon electronic excitation. This mode, occurring at around 1700 cm−1 in the ground state, is greatly enhanced in the resonance Raman spectrum, in striking agreement with experimental findings.
In summary, for the diamondoids studied here, the time-dependent approach to vibronically resolved electronic spectroscopy allowed us to gain detailed insight into molecular motions induced by electronic transitions, and into optical properties in general. For several properties in addition to the benefit of interpretative power, theory also gives good quantitative agreement with experimental facts. Nevertheless, several tasks remain for the future: higher-energy transitions need to be studied, non-radiative couplings to other states should be considered, and the validity of underlying approximations (e.g., harmonic and Condon approximations) should be carefully evaluated. We are confident that the research line as advocated here, however, will eventually allow us to tackle the most important task: a systematic screening of diamondoids, including large and complex hybrid structures, with respect to their optical and electronic properties and their spectroscopic features.
Appendix A: expressions for (cross) correlation functions
In the IMDHOFAD model, the correlation function for absorption is given by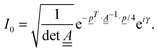 | (9) |
The cross-correlation function I10 for Raman amplitudes can be written as a (3N − 6)-dimensional vector with components for each of the normal modes of the molecule. This vector has the form
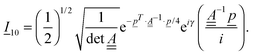 | (10) |
In the equations above 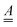 is a matrix of size (3N − 6) × (3N − 6),
is a matrix of size (3N − 6) × (3N − 6), ![[p with combining low line]](https://www.rsc.org/images/entities/i_char_0070_0332.gif) is a column vector of length (3N − 6) and γ a phase. The recipes for calculating these quantities are given in ref. 28. What are needed are the equilibrium geometries of ground and excited states
is a column vector of length (3N − 6) and γ a phase. The recipes for calculating these quantities are given in ref. 28. What are needed are the equilibrium geometries of ground and excited states ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) g0 and
g0 and ![[R with combining low line]](https://www.rsc.org/images/entities/i_char_0052_0332.gif) e0, the vibrational frequencies ωg1,…,ωg3N−6 and ωe1,…,ωe3N−6 of vibrations of g and e, and finally also the corresponding normal modes. From the normal modes one obtains the Duschinsky matrix
e0, the vibrational frequencies ωg1,…,ωg3N−6 and ωe1,…,ωe3N−6 of vibrations of g and e, and finally also the corresponding normal modes. From the normal modes one obtains the Duschinsky matrix 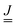 of size (3N − 6) × (3N − 6), and from frequencies, normal modes and geometries the dimensionless origin shifts
of size (3N − 6) × (3N − 6), and from frequencies, normal modes and geometries the dimensionless origin shifts 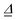 [a vector of length (3N − 6)] which are needed to evaluate
[a vector of length (3N − 6)] which are needed to evaluate 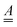 ,
, ![[p with combining low line]](https://www.rsc.org/images/entities/i_char_0070_0332.gif) , and γ.28
, and γ.28
Appendix B: emission spectrum of Tria and correlation function analysis
In order to analyze the correlation function approach and the choice of the broadening factor Γ in more detail, we show in Fig. 12, left panel, the luminescence spectrum of triamantane for broadening factors of Γ = 1000 cm−1, 200 cm−1, 50 cm−1, and 10 cm−1, respectively. With Γ = 1000 cm−1, the emission spectrum is broad and structureless, with the maximum at around 5.65 eV (lowest panel). This is not consistent with experiment,32 according to which the spectrum has a main maximum at around 6.0 eV, and a clear vibrational progression with a spacing of about 0.17 eV. The experimental spectrum is well compatible, however, with the choice Γ = 200 or Γ = 50 cm−1 in the figure. If, on the other hand, Γ is chosen very small (Γ = 10 cm−1), “too much” vibrational fine-structure appears compared to experiment. In passing we note that spectra similar to those corresponding to Γ = 200 or Γ = 50 cm−1 had already been obtained previously by a time-independent method.37Again, the structure of the emission spectra can nicely be correlated with the time-evolution of correlation functions, which are shown on the right panel of Fig. 12. The overall width of the band is determined by the initial decay of the correlation function on a timescale τ0 of a few fs. A second characteristic timescale τ is set by the recurrences of the correlation function, as above for absorption. The recurrence times τ for the emission spectra are 24.6 fs, 24.0 fs, and 24.3 fs for Ada, Dia, and Tria, respectively, hence slightly shorter than those for absorption according to Table 2. As a consequence, the characteristic frequencies ω = 2π/τ, which determine the vibronic progression of the emission spectra, are slightly larger than for absorption, namely 1360 cm−1 for Ada, 1390 cm−1 for Dia, and 1370 cm−1 for Tria, respectively.
Appendix C: rR spectra of higher diamondoids
Resonance Raman spectra were determined for all higher diamondoids, studied in this work. They are shown in Fig. 13 below, and partially discussed in the main text.Acknowledgements
We sincerely thank Dr Dominik Kröner (Potsdam), Thomas Möller (Berlin) and Janina Maultzsch (Berlin) for fruitful discussions, and for making experimental results available prior to publication. Financial support by the ‘Leibniz Graduate-School, Dynamics in New Light’, and by the “DFG-Forschergruppe 1282” (project Sa 547/11-1) is gratefully acknowledged.References
- J. E. Dahl, S. G. Liu and R. M. K. Carlson, Science, 2003, 299, 96 CrossRef CAS PubMed.
- P. R. Schreiner, et al. , Nature, 2011, 477, 308 CrossRef CAS PubMed.
- H. Schwertfeger and P. R. Schreiner, Chem. Unserer Zeit, 2010, 44, 248 CrossRef CAS.
- P. R. Schreiner, A. A. Fokin, H. P. Reisenauer, B. A. Tkachenko, E. Vass, M. M. Olmstead, D. Bläser, R. Boese, J. E. P. Dahl and R. M. K. Carlson, J. Am. Chem. Soc., 2009, 131, 11292 CrossRef CAS PubMed.
- H. Schwertfeger, A. A. Fokin and P. R. Schreiner, Angew. Chem., Int. Ed., 2008, 47, 1022 CrossRef CAS PubMed.
- W. L. Yang, et al. , Science, 2007, 316, 1460 CrossRef CAS PubMed.
- L. Landt, K. Klünder, J. E. Dahl, R. M. K. Carlson, T. Möller and C. Bostedt, Phys. Rev. Lett., 2009, 103, 047402 CrossRef.
- M. Steglich, F. Husiken, J. E. Dahl, R. M. K. Carlson and T. Henning, Astrophys. J., 2011, 729, 1 CrossRef.
- L. Landt, W. Kieleich, D. Wolter, M. Staiger, A. Ehresmann, T. Möller and C. Bostedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205323 CrossRef.
- T. Möller, private communication.
- R. Meinke, R. Richter, A. Merli, A. A. Fokin, T. V. Koso, V. N. Rodionov, P. R. Schreiner, C. Thomsen and J. Maultzsch, J. Chem. Phys. Search PubMed , (submitted).
- For example: G. Rasul, G. A. Olah and G. K. Suurya Prakasch, Proc. Natl. Acad. Sci. U.S.A., 2004, 101, 10868 CrossRef CAS PubMed; S. L. Richardson, et al. , Diamond Relat. Mater., 2006, 15, 707 CrossRef PubMed.
- E.g., F. Marsusi, J. Sabbaghzadeh and N. D. Drummond, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 245315 CrossRef.
- T. Sasagawa and Z. Shen, J. Appl. Phys., 2008, 104, 073704 CrossRef.
- A. A. Fokin, T. S. Zhuk, A. E. Pashenko, P. O. Dral, P. A. Gunchenko, J. E. P. Dahl, R. M. K. Carlson, T. V. Koso, M. Serafin and P. R. Schreiner, Org. Lett., 2009, 11, 3068 CrossRef CAS PubMed.
- A. A. Fokin, E. D. Butova, L. V. Chernish, N. A. Fokina, J. E. P. Dahl, R. M. K. Carlson and P. R. Schreiner, Org. Lett., 2007, 9, 2541 CrossRef CAS PubMed.
- L. Landt, M. Staiger, D. Wolter, K. Klünder, P. Zimmermann, T. M. Willey, T. van Bluren, D. Brehmer, P. R. Schreiner, B. A. Tkachenko, A. A. Fokin, T. Möller and C. Bostedt, J. Chem. Phys., 2010, 132, 024710 CrossRef PubMed.
- L. Landt, C. Bostedt, D. Wolter, T. Möller, J. E. P. Dahl, R. M. K. Carlson, B. A. Tkachenko, A. A. Fokin, P. R. Schreiner, A. Kulesza, R. Mitrić and V. Bonačić-Koutecký, J. Chem. Phys., 2010, 132, 144305 CrossRef PubMed.
- M. Vörös, T. Demjeén, T. Szilvási and A. Gali, Phys. Rev. Lett., 2012, 108, 267401 CrossRef.
- E. J. Heller, J. Chem. Phys., 1978, 68, 2066 CrossRef CAS.
- D. J. Tannor and E. J. Heller, J. Chem. Phys., 1982, 77, 202 CrossRef CAS.
- T. Petrenko and F. Neese, J. Chem. Phys., 2007, 127, 164319 CrossRef PubMed.
- J. Tatchen and E. Pollak, J. Chem. Phys., 2008, 128, 164303 CrossRef PubMed.
- C. Herrmann, J. Neugebauer, M. Presselt, U. Uhlemann, M. Schmitt, S. Rau, J. Popp and M. Reiher, J. Phys. Chem., 2007, 111, 6078 CAS.
- See, for example, M. Diercksen and S. Grimme, J. Chem. Phys., 2006, 122, 244101 CrossRef CAS PubMed; H. C. Jankowiak, J. L. Stuber and R. Berger, J. Chem. Phys., 2007, 127, 234101 CrossRef PubMed; J. Tatchen, N. Gilka and C. M. Marian, Phys. Chem. Chem. Phys., 2007, 9, 5209 RSC.
- M. Etinski, J. Tatchen and C. M. Marian, J. Chem. Phys., 2011, 134, 154105 CrossRef PubMed.
- Y. Niu, Q. Peng, C. Deng, X. Gao and Z. Shuai, J. Phys. Chem. A, 2010, 114, 7817 CrossRef CAS PubMed.
- S. Banerjee, D. Kröner and P. Saalfrank, J. Chem. Phys., 2012, 137, 22A534 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef.
- M. J. Frisch, et al., Gaussian 09 Revision A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- L. Landt, Electronic structure and optical properties of pristine and modified diamondoids, PhD thesis, Technical University Berlin, 2010 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2006, 120, 215 CrossRef.
- J. W. Raymonda, J. Chem. Phys., 1972, 56, 3912 CrossRef CAS.
- A. Patzer, M. Schütz, T. Möller and O. Dopfer, Angew. Chem., Int. Ed., 2012, 51, 4925 CrossRef CAS PubMed.
- T. Zimmermann, R. Richter, A. Knecht, A. A. Fokin, T. V. Koso, L. V. Chernish, P. A. Gunchenko, P. R. Schreiner, T. Möller and T. Rander, J. Chem. Phys., 2013, 139, 084310 CrossRef PubMed.
- R. Mitrić, V. Bonačić-Koutecký, private communication.
| This journal is © the Owner Societies 2014 |